Phase-contrast Micro-computed Tomography Measurements of the Intraocular Pressure-induced Deformation of the Porcine Lamina Cribrosa

Abstract

The lamina cribrosa is a complex mesh-like tissue in the posterior eye. Its biomechanical environment is thought to play a major role in glaucoma, the second most common cause of blindness. Due to its small size and relative inaccessibility, high-resolution measurements of LC deformation, important in characterizing LC biomechanics, are challenging. Here we present a novel noninvasive imaging method, which enables measurement of the three-dimensional deformation of the LC caused by acute elevation of intraocular pressure. Posterior segments of porcine eyes were imaged using synchrotron radiation phase contrast micro-computed tomography (PC μCT) at IOPs between 6 and 37 mmHg. The complex trabecular architecture of the LC was reconstructed with an isotropic spatial resolution of 3.2 μm. Scans acquired at different IOPs were analyzed with digital volume correlation (DVC) to compute full-field deformation within the LC. IOP elevation caused substantial tensile, shearing and compressive deformation within the LC, with maximum tensile strains at 30 mmHg averaging 5.5%, and compressive strains reaching 20%. We conclude that PC μCT provides a robust method for imaging the LC, and when combined with DVC, allows for full-field 3D measurement of ex vivo LC biomechanics at high spatial resolution.

I. Introduction

THE posterior segment of the eye is an anatomically complex region, composed primarily of neural tissues to detect light and transmit visual information, vasculature, and connective tissues. The eye maintains an intraocular pressure (IOP) as a result of a balance between fluid production and drainage. This IOP serves, in part, to prevent the eye from collapsing under external forces. The connective tissues provide mechanical strength to bear the IOP-induced loads. In the posterior eye, these tissues include the sclera (the white outer shell of the eye) and the lamina cribrosa (LC), a porous collagenous structure somewhat similar in appearance to trabecular bone and which spans the opening in the sclera where the optic nerve exits the eye. The pores of the LC serve as channels through which approximately 1.5 million retinal ganglion cell (RGC) axons traverse as they exit the eye in humans. The connective and neural tissues at the intersection of the optic nerve, the retina, and the sclera are collectively referred to as the optic nerve head (ONH).

The biomechanics of the ONH is of critical importance in glaucoma, the second leading cause of blindness worldwide [1]. Elevated IOP is the main risk factor for developing glaucoma [2], [3], and all current clinical treatments attempt to reduce IOP [2]. The loss of vision in glaucoma is caused by the progressive dysfunction and death of RGC axons, which is believed to begin within the pores of the LC [4]. One research hypothesis is that IOP-induced deformation of the LC precipitates axonal death [5], [6]. However, the mechanism by which this process occurs is poorly understood; therefore understanding LC biomechanics is a topic of substantial clinical and research interest. Unfortunately, the anatomical complexity, small size, and relative inaccessibility have made direct measurements of LC biomechanics challenging.

A number of groups have attempted to measure LC deformation in response to elevation of IOP, but to date all studies have been limited by the inability to image the complete LC. Initial studies, since the 1980s, measured the structural compliance of the anterior surface of the LC [7], [8] but could not access the deeper structures of the LC. Histologic approaches were later applied to eyes fixed at different IOPs to obtain snapshots of the deformed LC morphology [9], [10]. However, specimen preparation for histology can cause significant tissue distortion. Recent progress in second harmonic-generation (SHG) nonlinear microscopy has made it possible to measure IOP-induced LC displacements [11] and changes in the anterior LC structure [12] at high resolution in unfixed cadaveric eyes. However, light cannot penetrate deeply into the LC, a major limitation of using SHG nonlinear microscopy imaging to visualize the full LC. In vivo imaging techniques such as optical coherence tomography (OCT) are now emerging as a tool to perform LC biomechanics measurements in the clinic [13], [14], but even the most advanced OCT systems do not offer the resolution and depth penetration to resolve the beams of the LC through its full thickness [15].

Compared with light-based imaging methods, X-ray-based methods such as micro-computed tomography (μCT) offer superior tissue penetration and spatial resolution. Contrast in conventional X-ray imaging depends on the differential X-ray attenuation properties and thickness of anatomic structures. X-ray attenuation coefficients are proportional to tissue density or mineral content. This imaging technique provides excellent contrast in cancellous bone, where the calcified bone differs greatly in density from marrow and other structures. Unfortunately, in the LC, collagenous beams and neural tissue have relatively similar X-ray attenuation properties, which makes the tissue essentially undifferentiable using conventional X-ray μCT. We recently investigated a contrast-enhancing staining technique to obtain high-resolution scans of the LC with conventional μCT [16]. Specifically, collagen beams were stained with phosphotungstic acid (PTA), a chemical with much higher X-ray attenuation than collagen alone, allowing differentiation of the LC beams from neural tissue. However, PTA application markedly increased the stiffness of both the collagenous sclera and LC, preventing this method from being used for physiologically relevant imaging-based measurements of LC deformation in response to altered IOP.

Phase-contrast X-ray imaging overcomes this limitation, by taking advantage of differences in refractive indices between adjacent structures within a sample to derive image contrast. For soft tissues of comparable density, the X-ray phase shift is about three orders of magnitude larger than the X-ray absorption differential [17], [18]. Further, because phase-contrast imaging is more sensitive to the structures of interest in the LC, lower X-ray doses can be used, which represents a considerable advantage for possible future clinical applications.

Phase-contrast micro-computed tomorgraphy (PC μCT) can be carried out using fresh tissue. Therefore, we hypothesized that we could acquire scans of the LC at different IOP levels and use an image feature tracking algorithm such as digital volume correlation (DVC) to compute IOP-induced deformation of the LC. DVC was first applied to quantify strains in trabecular bone subjected to uniaxial strain by Bay et al. [19]. This technique is now commonly used to measure strain fields and load-induced micro-damage in hard material including bones [20], [21], [22], [23], but we are aware of only one instance in which it has been applied to compute strains in soft collagen-rich tissues [24].

In this study, we investigated the combined use of an inflation test and synchrotron radiation PC μCT imaging to measure the IOP-induced deformation of several LCs. Threedimensional scans of the entire ONH region were acquired at various IOP levels at an isotropic spatial resolution of 3.2 μm and processed to visualize how the fine structures of the LC deform under increasing pressure. Full-field deformation of the LC was calculated using digital volume correlation (DVC).

II. Methods

A. Inflation testing

Three porcine eyes were freshly harvested from animals approximately 9 months old (W.T. Maddock, Wales, UK). To ensure that we had enough specimens available during our window of time allocated at the synchrotron, we collected the eyes in advance and stored them at −4° C until the time of experiments. We confirmed that, on average, freezing did not significantly affect the mechanical properties of the sclera (Supplemental Material, Sec II). Before testing, the eyes were thawed at room temperature, cleaned of extra-orbital fat and muscle, hemisected, and glued at the corneal limbus to a 3D-printed UV curable resin holder, ensuring that the optic nerve was centered (Fig. 1A). The retina, choroid, and vitreous humor were gently excised. The mounted specimen was then placed inside a custom-made acrylic pressure chamber filled with phosphate buffered saline (PBS) (Fig. 1B). Pressure was hydrostatically adjusted between 6mmHg (baseline; at lower pressures the empty eye shell buckled under its own weight) and 37mmHg by manipulating the vertical position of a PBS reservoir connected to the base of the chamber. The pressure loading regimen covered the range of physiological pressures in normal (P = 12 – 22 mmHg) and hypertensive (P ≥ 22 mmHg) eyes [25]. We and others [26] reported minimal preconditioning effects for inflation testing of the sclera (Supplemental Material, Sec II). Therefore the specimens were not preconditioned before testing. However, they were inflated to 15 mmHg for 20 min to ensure the absence of leaks before scanning. The pressure chamber was immersed in a PBS bath to maintain constant hydration at room temperature during testing (Fig. 1C). A temperature probe recorded the PBS bath temperature and showed no temperature elevation after exposure to X-rays for 1 hour. The entire inflation apparatus was placed on a high-precision rotating stage with its rotation axis (aligned using a red laser) coincident with the optic nerve of the specimen (Fig. 1C).

Fig. 1. Inflation test used for PC μCT imaging.

A) Porcine specimen glued to the 3D-printed holder at the limbus, with the optic nerve centered. B) Specimen and holder from panel A mounted on the inflation chamber. The chamber was filled with PBS injected from the tubing connection at right and cleared of all air bubbles. C) The inflation chamber was then immersed in a PBS bath and connected to a PBS-filled reservoir, whose height could be manually adjusted to control pressure in the inflation chamber, i.e. the simulated IOP. The inflation apparatus was placed on a rotating stage that had translational degrees of freedom to ensure alignment between the rotation axis and the optic nerve axis.

B. Phase-contrast X-ray micro-computed tomography imaging

Experiments were performed on beamline I12, Joint Engineering, Environmental, and Processing at Diamond Light Source, the United Kingdom’s national synchrotron. The electron energy was 53keV. Bright spatially and chromatically coherent synchrotron X-rays were directed across the LC within the mounted eye (Fig. 1C). The X-ray phase shift was transformed by Fresnel diffraction into intensity variations, which were recorded using a 2D CCD X-ray detector with an effective pixel size of 3.2 μm (2560×2160 pixels) placed one meter behind the specimen. Since previous scanning electron microscopy studies measured an average pore diameter of 43μm in the porcine LC [27], the spatial resolution of our experimental system was sufficient to detect porcine LC microstructure. The field of view of the X-ray camera was 8.19mm x 6.91mm, allowing a region extending from 2mm anterior to the LC to 2 mm posterior to the LC to be scanned. Test scans showed that 1200 projections with an exposure time of 1.2 s per projection represented the best compromise between scan duration, image resolution, and contrast (total scan time: 40 min/pressure). PC μCT scans of porcine ONHs were repeated at different pressures between 6 and 37 mmHg (Table I). The specimens were equilibrated at each incremental pressure step for 15 minutes before initiating each scan to reduce the effects of creep that may occur during the scan [28], as tissue deformation during the scan would result in an imaging artifact. The phase retrieval method was based on a free propagation technique and implemented using the algorithm of Paganin et al. [29], and a Fourier-based technique was used to suppress ring artifacts [30] arising from defective pixels in the scintillator. To reduce the file size of the image volumes used for image processing, they were down-sampled by a factor of two (Matlab command imresize) and converted from 16-bit to 8-bit integer. The effective voxel size of the down-sampled image volume was 6.4 μm.

TABLE I.

Pressure levels at which PC μCT scans were acquired for the 3 specimens included in this study.

	6 mmHg (8 cm PBS)	15 mmHg (20 cm PBS)	22 mmHg (30 cm PBS)	30 mmHg (40 cm PBS)	37 mmHg (50 cm PBS)
Pig A	X			X
Pig B	X	X	X	X
Pig C	X	X	X	X	X

C. LC delineation and neural tissue volume fraction

Every 10^th sagittal slice of the reconstructed PC μCT scans was manually segmented with Matlab to define the bounding contours of the LC. These contours were parameterized using 49 elliptic Fourier harmonics and were linearly interpolated between adjacent segmented slices. The anterior surface of the LC and the insertion zone of the LC into the sclera could be easily detected thanks to sharp contrast differences in the phase-contrast scans. The posterior boundary was identified by a change in connective tissue density (brighter signal in the LC than in the septal architecture of the optic nerve). The test-retest reproducibility of this procedure is described below.

Delineations of the LC in sagittal slices were used to create a 3D mask encompassing the entire LC region in the image volume, which allowed further image processing of just the LC, excluding surrounding tissue. The porcine ONH contains a characteristic connective tissue structure near the posterior edge of the LC called the ventral groove, which was excluded from the masked LC region. The porcine LC is primarily composed of plate-like collagen-containing structures, forming honeycomb-like conduits around axons that are aligned with the optic nerve axis [16], [27]. We used Frangi’s vesselness filter, as described in Campbell et al. [16], to segment the LC in three dimensions from our PC μCT image volume. The quality of the segmentation was controlled by filter constants that were manually adjusted. To segment the 8-bit LC image volume in 3D, settings were α = 0.05, β = 1, scale range = 0.1 : 0.5 : 5 voxels, and γ = 250 The same set of parameters was used for the entire image volume and for each specimen. Each voxel’s grayscale value in the image processed with Frangi’s filter represents the probability that the voxel is a member of a beam. Three-dimensional renderings of the LC were generated by binarizing the output of the Frangi’s filter. A gray value threshold, different for each specimen but identical between the different scans of a specimen, that best reproduced the structure seen in the PC μCT images was empirically determined as judged by one author familiar with LC structure and anatomy (BC). After binarization, the local neural tissue volume fraction was calculated as the ratio of the number of negative voxels (identifying pores) to the total number of voxels within a summation kernel of 20×20×20 voxels convolved across the entire image volume.

D. IOP-induced deformation of the ONH

Determination of 3D deformation from image volumes is a non-trivial problem, and is strongly dependent on image quality. Unfortunately, for anatomically complex tissues such as the LC that undergo 3D deformations, there is no way to obtain gold standard measures of deformation. we therefore chose to quantify LC deformation using three different approaches, and to then compare the results. Reasonable agreement between the three sets of results would maximize our confidence in the accuracy of these approaches. A related matter concerns the mathematical description of the deformation of an object: this is typically done via the deformation gradient from which one can derive the Green Lagrange strain tensor. In 3D, the strain tensor has six independent components [31]. The three approaches we describe below (denoted as Approaches 1, 2, and 3) allow estimation of different numbers of components of the strain tensor. we present these approaches in increasing order of sophistication, each estimating an increasing number of strain components.

1). Approach 1: Average deformation of the LC and sclera

we here measured overall tissue dimensions to estimate region-averaged normal strains, assuming uniform deformation within the LC and the sclera. Sagittal slices oriented in the inferior-superior plane and representing nearly identical regions of tissue close to the center of the LC were selected from the reconstructed scans acquired at different IOPs (Fig. 2A). Truly identical slices could not be selected due to nonuniform displacement of tissue through the imaging plane. Binary masks of the scleral and LC cross-sections were manually created from hand-drawn contours (Fig. 2A–B). Image centerlines of the binary masks were obtained with the Matlab function bwmorph (Fig. 2B), which identifies the locations of points that are equidistant from region contours. The local inplane thicknesses of LC and sclera were computed as twice the Euclidian distance of the centerline to the nearest edges of the tissue using the function bwdist. Region-averaged peripapillary scleral and LC cross-sectional anterior-posterior thicknesses were calculated at each pressure to estimate IOP-induced compressive strains in those tissues. Specifically, anteriorposterior strains E_ap were calculated as:

$$E_{ap}=\frac{1}{2}[{(\frac{t_p}{t_b})}^2-1],$$ (1)

where t_p and t_b are the LC thicknesses at pressure p and baseline b = 6 mmHg, respectively. Using the same sagittal slice, transverse strain in the anterior LC, E_t, was defined from the change of contour length of the anterior LC boundary:

$$E_t=\frac{1}{2}[{(\frac{l_p}{l_b})}^2-1],$$ (2)

where l_p and l_b are the total contour lengths of the anterior LC from the superior to the inferior insertion of the LC into the sclera calculated at pressure p and at baseline, respectively. E_ap and E_t are approximations to two normal components of the strain tensor. We estimated the uncertainty in measurements of the thickness t, and the length l, by using a test-retest approach. Specifically, we calculated the standard deviation in the average values of those quantities obtained in five independent measurements from the scan at the baseline pressure of Pig B.

Fig. 2. Tissue thickness calculation from sagittal slices.

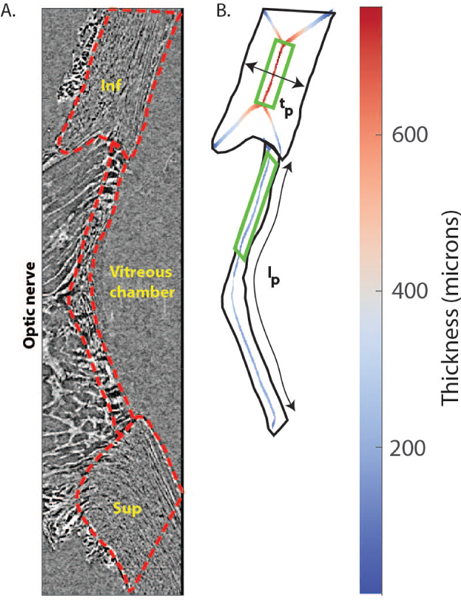
A) Sagittal slice passing through the center of the LC and oriented in the superior/inferior direction from the 6 mmHg scan of Pig B. The LC and scleral regions were manually delineated (red lines). B) Binary mask of the inferior sclera and LC. Pixels equidistant to the mask boundary (skeleton) are shown in the inferior sclera and LC, where color represents twice the distance between the centerline and the closest mask edge, i.e. the local thickness. Close to the corners of the sclera and LC, the skeletons have an “X” shape, where the mask boundaries in the anterior-posterior direction disrupt the centerline algorithm. Those regions were not included in the thickness calculation. Scleral and LC thickness were averaged in the indicated green rectangles (the entire scleral region comprised between the X-shaped lines, and the inferior half of the LC). The average thickness was used to compute compressive strain (Eq. 1). The anterior LC length l_p was used to compute transverse strain in Eq. 2. Legend: Sup = superior; Inf = inferior.

2). Approach 2: 2D strain mapping of maximum intensity projection images

The second approach utilized 2D digital image correlation (DIC) to quantify full-field strain measurements within different cross-sectional planes of the LC. Unlike Approach 1, we did not assume uniform deformation in Approach 2; i.e., the strain tensor was allowed to vary spatially across planar slices of the LC. We adopted this 2D approach because we expected that, as IOP was changed, the main mode of deformation in transverse planes (Fig. 3A) would be in-plane tensile deformation, while the main deformation mode in sagittal planes (Fig. 3B) would be compression. Thus, we expected that Approach 2 would provide a rapid and efficient way to characterize deformation patterns. This approach estimates 3 out of 6 components of the strain tensor for each analysis plane. DIC is an image analysis technique that tracks the displacements of non-uniform image features between baseline (P = 6 mmHg) and pressurized (P ≥6 mmHg) configurations [32]. The natural anatomic features of the LC provided excellent contrast and enough stochasticity for the DIC algorithm to spatially resolve local displacement. However, DIC could not be successfully performed on individual transverse slices because out-of-plane distortions prevented feature tracking as the eye deformed, i.e. the IOP-induced posterior bowing of the LC resulted in some features moving in opposite directions through the image plane; in combination with our very high spatial resolution in the through-plane direction, image features were thus lost from a single transverse slice as inflation pressure changed. Therefore, we instead created maximum intensity projections (MIPs) from 10 consecutive transverse slices to reduce the number of features that moved outside the region of interest due to through-plane deformation. Four such MIPs were generated from transverse slices located in the posterior, mid-posterior, mid-anterior, and anterior LC based on manual selection of the centermost slice of each MIP at each inflation pressure. Two additional MIPs were generated from 10 adjacent sagittal slices close to the center of the LC, oriented in the superior/inferior and nasal/temporal directions. The MIPs were imported into 2D DIC software (Istra 4D 4.4.1, Dantec Dynamics, Holtsville, NY) to compute planar displacements and strains at each inflation pressure increment. We used a DIC facet size of 41 × 41 pixels, with a 66% overlap (Supplemental Material, Sec. IV).

Fig. 3. Reconstructed PC μCT scan of the porcine ONH of Pig B.

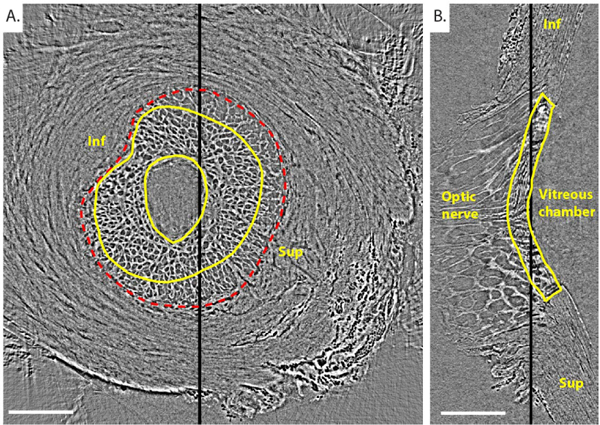
Transverse (A) and central sagittal (B) slices from a PC μCT scan of Pig B’s ONH imaged at 6mmHg IOP. The position of the transverse slice along the optic nerve axis is indicated with a thick black line on the sagittal slice. similarly, the position of the sagittal slice is indicated with a thick black line on the transverse slice. The edges of the LC are delineated in yellow in both views. The scleral canal is delineated in a red dashed line. The transverse slice contains prelamina tissue (inside central yellow contour), LC (between the 2 yellow solid contours), and postlaminar pial septae (inside the red scleral canal border but outside the outer yellow line). Inf and Sup indicate inferior (Ventral) and superior (Dorsal) orientations, respectively. we did not know whether the eyes were right or left, and thus the nasal and temporal orientations are not known. Scale bar = 1.25 mm.

3). Approach 3: 3D strain mapping of the full LC image volume

We carried out full 3D tracking of image features within the LC as the most sophisticated (but also most complex) approach to determine deformations and strains. Complete image volumes acquired at different inflation pressures were loaded into the 3D DVC correlation software DaVis 8.1.3 (LaVision, GmbH, Goettingen, Germary) to calculate 3D displacement and strain fields. DVC is a feature-tracking technique similar to DIC, except that DVC operates on full 3D image volumes rather than on just surfaces. Rigid body displacements were manually eliminated by spatially registering the scans before computing displacements. Specifically, three different, easily-identifiable LC features were manually tracked across the different scans, and the average translation vector was calculated and applied to every voxel of the undeformed image volume [33]. Strain values were independent of the choice of features used for registration. The Rigid body rotation was assumed to be negligible, following visual inspection of the scans. A multi-pass approach was adopted to maximize correlation, in which displacement gradients calculated in pass i were used to generate a new reference configuration in pass i +1 (Table II). The sub-volume size was progressively decreased to increase spatial accuracy. The final sub-volume size was 20×20×20 voxels with a 75% overlap, for which the strain resolution was estimated to be 20 microstrain (Supplemental Material, Sec. IV). Approach 3 calculates all 6 components of the strain tensor at each sub-volume, i.e. the entire spatially varying strain tensor.

TABLE II.

Parameters of multi-pass approach used in digital volume correlation to maximize correlation.

Step	Sub-volume size (voxels)	Number of passes	% overlap
1	128×128×128	2	50
2	96×96×96	3	50
3	40×40×40	3	50
4	20×20×20	3	75

It is standard practice to smooth the displacements to improve accuracy of strain estimation in optical methods for displacement calculation, since strain is extremely sensitive to noise in the displacement field [28], [34] (Supplemental Material, Sec. IV). Thus, for both DIC and DVC analyses, the components of the displacement vector were imported into Matlab and smoothed using cubic splines (csaps function, smoothing parameter 0.9999 for all displacement components). The smoothing parameter was chosen to reduce the local noise without affecting the physiological regional variations in displacement. It was manually iterated to improve the signal/noise ratio (as judged visually by one author (BC)), and the same parameter was used for the three specimens. The Matlab gradient function was applied to compute the derivatives of the displacements in the Green-Lagrange strain formulation. Volumetric strains were computed as the Jacobian (determinant) of the deformation tensor. For both DIC and DVC, deformation was analyzed only at voxels where the software returned high correlation values¹. Those corresponded to the trabecular regions, i.e. the entire LC and the post-laminar optic nerve where natural image features are abundant.

III. Results

A. Phase-contrast X-ray micro-computed tomography imaging

PC μCT imaging clearly resolved the connective tissue beam architecture of the LC (Fig. 3A, Supplemental Material, Sec. III)), with the entire LC and peripapillary sclera and parts of the optic nerve being visible (Fig. 3B). The LCs had an arc like shape in the central sagittal sections even at the baseline pressure of 6mmHg (Fig. 3B), and therefore, all transverse slices contained LC, pial septae (connective tissue with beam like structure posterior to the LC), scleral, and/or prelaminar tissues. In general, the postlaminar pial septae had a lower density of connective tissue compared to the LC. However, it was not possible to use such differences to delineate the LC/pial septae boundary in transverse views, as differences were subtle. Instead, a 3D mask created from the delineation of the LC in sagittal views, where density differences were more easily resolved, was used to delineate the LC from the pial septae in transverse slices. Videos of slice series in transverse and sagittal orientations are provided in the electronic supplementary material. PC μCT also successful imaged the inflated ONH. An animation of the deformation of the ONH caused by IOP elevation is shown in the electronic Supplementary Material.

B. Neural tissue volume fraction

Frangi’s vesselness filter successfully identified the location and orientation of connective tissue elements within the LC (Fig. 4 and electronic Supplementary Material). The parameters of Frangi’s filter were optimized to enhance the cribriform structure of the LC, but were not expected to segment the non-trabecular structure of the sclera. The probability map output by Frangi’s filter was binarized to segment the LC beams and then create a 3D rendering of the entire segmented LC (Fig. 5A and electronic Supplementary Material). We then used the binarized LC volumes to calculate neural tissue volume fractions. For example, in the transverse slice shown in Fig. 4A, neural tissue volume fraction was 0.40 ± 0.03 in the LC and 0.50± 0.04 in the pial septae (p = 0.001 using a Student’s t-test for the comparison of average porosity between the LC and the pial septa in 5 different transverse slices), quantifying the qualitative observation that the LC had a denser connective tissue structure than the pial septae (Fig. 5B).

Fig. 4. Frangi’s vesselness filter for connective tissue detection applied to the PC μCT scan of Pig B at 6mmHg.

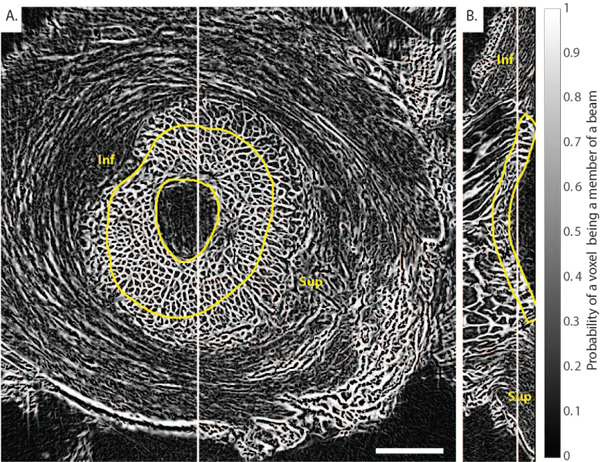
A) Transverse slice and B) sagittal slice. A modified version of Frangi’s vesselness filter was applied to enhance plate-like objects in the 3D image volume shown in Fig. 3. The image is a probability map that each voxel is a member of a beam. The method clearly identified the beam-like connective tissue constituents of the LC but did not evenly segment the non-trabecular structure of the sclera, as expected. Inf and Sup indicate inferior (Ventral) and superior (Dorsal) orientations, respectively. Scale bar = 1.25 mm.

Fig. 5. 3D rendering and neural tissue volume fraction of the LC of Pig B at 6 mmHg IOP.

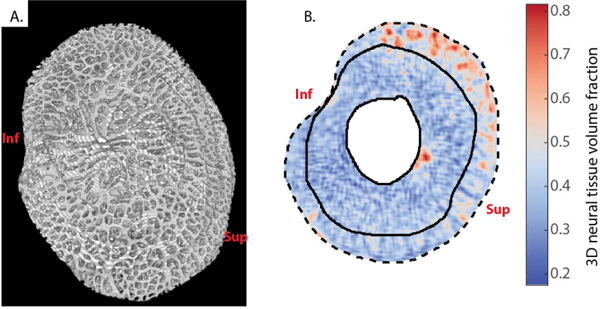
A) View from the posterior surface of the LC. The pores of the LC are clearly visible, and continuous conduits can be tracked from the anterior face to the posterior face of the LC, confirming the honeycomb-like structure of the porcine LC, although due to the tortuosity of these channels and their variable orientations, they are difficult to completely visualize in this static view. For a rotation of this 3D rendering, see supplementary video. The sclera, postlaminar pial septae of the optic nerve, and prelamina have been excluded from this reconstruction. B) 3D neural tissue volume fraction of the transverse slice shown in Figs. 3A and 4A. The sclera and the central prelaminar tissues are masked. The neural tissue volume fraction was smaller in the LC (delineated with solid lines) than in the pial septae (between the outside solid line and the dashed line, the latter delimiting the margin of the scleral canal). Inf and Sup indicate inferior (Ventral) and superior (Dorsal) orientations, respectively.

C. IOP-induced deformation of the ONH

1). Approach 1: Average LC and scleral deformation

Elevated IOP caused a posterior displacement of the sclera and LC (Fig. 6A), compressive deformation through the thickness of both the LC (Fig. 6B) and the sclera (Fig. 6C), and tensile deformation along the transverse direction in the anterior LC (Fig. 6D). Based on the test-retest results, the relative uncertainties in anterior-posterior strains in the sclera and LC were estimated to be 1.8% and 5.5%, respectively, while the relative uncertainty in the transverse LC strain was estimated to be 1.1% (Table III). Anterior-posterior strains in the LC at 30mmHg (relative to the baseline condition at 6mmHg) were 23.0%, 23.5% and 19.8% for Pigs A, B, and C respectively. The corresponding anterior-posterior strains in the sclera at 30 mmHg were 8.7%, 15.0% and 12.3%. The transverse strains of the anterior LC were smaller than the compressive strains, with values of 7.4%, 5.4%, and 6.8% at 30 mmHg for Pigs A, B, and C respectively, again referenced to baseline conditions at 6 mmHg of IOP. The comparison of LC deformations computed by Approach 1 (Average LC deformation) and Approach 2 (DIC) is presented in the electronic Supplemental Material. Overall, both approaches yielded similar estimates of the tensile deformation in the anterior LC. However, compressive strains in the LC computed with DIC were 40% lower than those computed with Approach 1, likely due to uncertainties associated with delineating the posterior LC in Approach 1.

Fig. 6. Approach 1 to estimate LC and scleral deformations and strains.

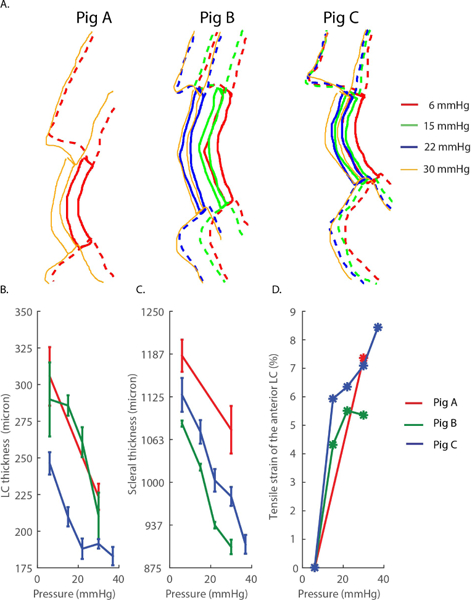
A) Manual delineation of the LC and scleral regions at inflation pressures between 6 and 30 mmHg for Pigs A, B, and C. B) Anterior-posterior thickness of LC as a function of the inflation pressure. C) Anterior-posterior thickness of the sclera as a function of the inflation pressure. In panels B and C, the error bars represent the standard deviation of the thickness over the region of interest described in Fig. 2 calculated from 3 repeated delineations. D) Tensile strain of the anterior LC as a function of the applied pressure. Tensile strains were estimated using Eq. 2.

TABLE III. Test-retest reproducibility of the manual delineation of the LC and sclera.

“Measurements” shows the mean ± standard deviation (SD) of measured scleral thickness, LC thickness, and anterior LC contour length obtained from 5 independent measurements using the scans of Pig B’s ONH at 6mmHg. The uncertainty arising from contour delineations translated into a relative uncertainty in strain estimation, here estimated by the ratio SD÷mean.

	Scleral thickness	LC thickness	Anterior LC arc length
Measurements	1063 ± 20 μm	293 ± 16.3 μm	3880 ± 41 μm
lower bound of the relative uncertainty in strain*	1.8%	5.5%	1.1%

^*Additional potential imaging-related uncertainties are not included in this estimate. Delineations were always performed by the same author (BC).

2). Comparison of strains computed by DIC (Approach 2) and DVC (Approach 3)

To evaluate whether 2D deformations computed by DIC were a good predictor of the full 3D deformations computed by DVC, the strain maps obtained by both methods were compared. We did not carry out statistical comparison between strains computed with DIC and DVC because we did not expect them to be exactly identical. Instead, a semi-quantitative comparison is presented in Fig. 7 and 8. Specifically, we compared the strain tensor components computed by DIC from a transverse MIP image to the corresponding in-plane components (E_xx, E_yy, E_xy) of the strain tensor computed by DVC in the middle of the image volume used to generate the MIP. Spatial distributions of strain at 30 mmHg were consistent between the two methods by visual inspection (Fig. 7C–D) and when quantified (Fig. 7B). Specifically, although the strain components E_yy and E_xx as computed by DVC were slightly larger than the corresponding components as computed by DIC, the difference was modest when spatially averaged over a region of interest, with a relative difference ≤ 25% at all pressures (Fig. 7B). We repeated the comparison between DIC and DVC strain calculation using a sagittal MIP image (Fig. 8). Again, the in-plane strain components computed by DIC and DVC showed similar spatial distributions (Fig. 8 C–D), and differences between strains computed by DIC and DVC and averaged over the region of interest shown in Fig. 8A did not exceed 15% at any pressure step (Fig. 8B). The reasonable agreement between the normal and shear deformation measurements obtained with DIC and DVC enhances confidence in the ability of DVC to measure LC biomechanics from these PC ĈT image volumes.

Fig. 7. Comparison of strains computed by DIC and DVC at 15 mmHg in a transverse MIP image of the LC of Pig B.

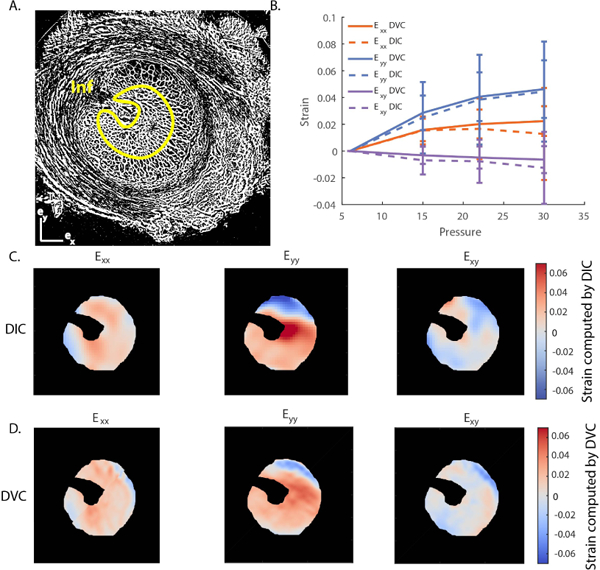
A) Binarized μCT slice corresponding to the central slice of a MIP located in the center of the LC used in the DIC calculation. B) Comparison of in-plane strain components (E_xx ,E_yy, E_xy ) computed by DIC and DVC, averaged over the region outlined in yellow in panel A, which corresponds to the LC tissue region. The error bars represent the standard deviation of the strain component over the region of interest. C) Contours of the in-plane strain components calculated by DIC. D) Contours of the in-plane strain components calculated by DVC corresponding to the location of the central slice of the MIP used for DIC analysis in panel C. Although strains were not identical on a voxel-by-voxel basis, there was good spatial agreement between regions of high and low strain computed by DIC and DVC. The ventral groove, the pial septa, and the sclera were masked in C and D. The position of the ventral groove (Inferior pole) is shown in A.

Fig. 8. Comparison of the strains computed by DIC and DVC at 15 mmHg in a sagittal MIP image of the LC of Pig B.

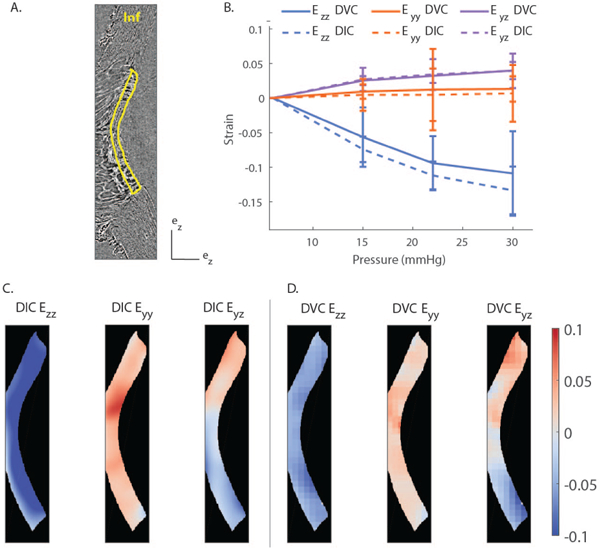
A) PC μCT slice corresponding to the center of the evaluated region. This MIP was close to the center of the LC and oriented in the superior/inferior direction. B) Quantitative comparison of in-plane strain components between DIC and DVC. The strains were averaged over the entire LC, delineated in yellow in panel A, and plotted as a function of the applied pressure. The error bar represent the standard deviation of the strain component over the region of interest. C) Contours of the in-plane strain components calculated by DIC. D) Contours of the in-plane strain components calculated by DVC corresponding to the location of the central slice of the MIP used for DIC analysis in panel C. There was good agreement between the regional variations and averaged values of the strains computed by DIC and DVC. The position of the Inferior pole is shown in panel A.

3). Full-field three-dimensional strains in the LC (Approach 3)

Approach 2 may be used to estimate the 3 out of the 6 strain components in the LC. Here we show that we can use DVC (Approach 3) to provide a full 3D description of the deformation, i.e. calculate all components of the strain tensor in the LC. In 3D, there are 3 orthogonal directions along which the LC undergoes pure stretch. In this coordinate system, the strain tensor is diagonal and the diagonal strain components are called the principal strains. The first principal strain, denoted as E₁, is a measure of the maximum tensile deformation and varied between 5.9% and 8.8% (Fig. 9B–C). More specifically in the anterior LC at 30 mmHg, E₁ = 8.8 ± 5.4% for Pig A, E₁ = 5.9 ± 2.1% for Pig B, and E₁ = 7.7 ± 4.4% for Pig C (mean ± standard deviation over the anterior region relative to baseline at 6 mmHg). The third principal strain, E₃, describes the maximum compression of the tissue. In the anterior slice of the LC at 30 mmHg, E₃ = –16.2 ± 6.9% for Pig A, E₃ = –15.3 ± 3.3% for Pig B, and E₃ = –7.8 ± 5.6% for Pig C (average ± standard deviation over the anterior region relative to baseline at 6 mmHg). In the entire LC, the first and second principal strains were tightly distributed around the mean (Fig. 10). In contrast, the compressive strains were more uniformly distributed between −30% and 0%, indicating that some regions of the LC are subjected to considerably more compressive strain than others.This was also evident in the maps of the principal strains (Supplemental Material, Sec. VI). Compressive strains were largest in the anterior central LC, and lowest in the posterior LC. Second principal strains were in general largest in the anterior LC regions and lowest in the posterior LC regions. The directions of first and second principal strains mostly lay in transverse planes, and therefore the directions of third principal strains were closely aligned with the ONH axis (Supplemental Material, movie 7).

Fig. 9. Principal strains computed by DVC for the three specimens.

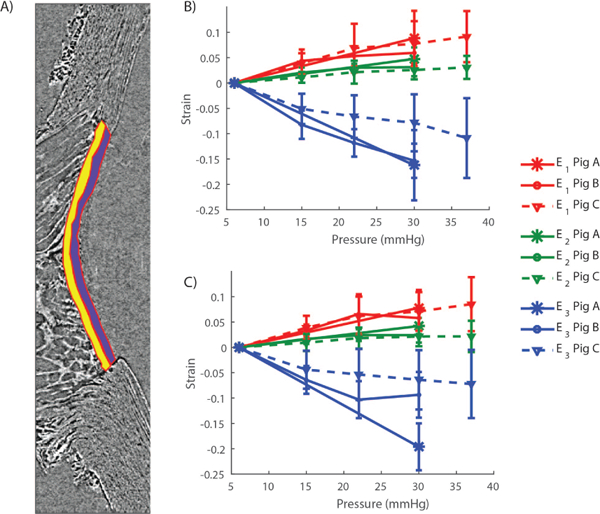
A) Principal strains were averaged over the anterior (purple) and posterior (yellow) LC. Both regions were manually delineated from the sagittal slice passing through the center of the LC. B) Principal strain/pressure curves in the posterior LC. C) Principal strain/pressure curves in the anterior LC. In panels B and C, the error bars represent the standard deviation of the strains over the regions shown in panel A.

Fig. 10. Histograms of the three LC principal strains computed with DVC at 30mmHg.

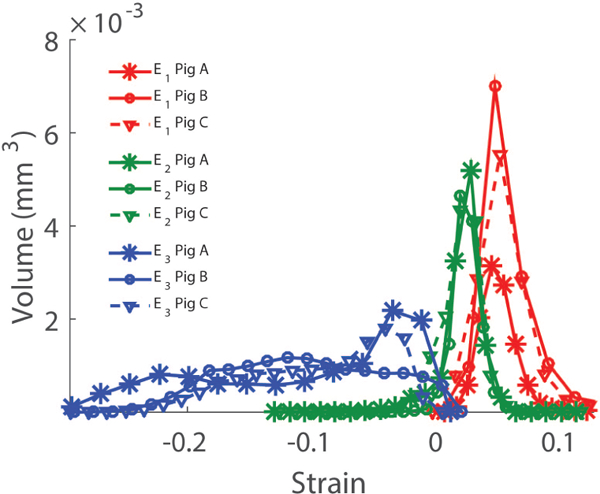
The histograms represent the total volume of LC tissue subjected to a given strain level.

The LC was not locally incompressible (Supplemental Material, Sec. VI). The volumetric strain contours closely matched the contours of the third principal strains. The anterior LC experienced large volumetric contraction up to 30%, while the posterior LC experienced almost equally large volumetric dilation. The average Jacobian over the entire LC was not equal to 1, indicating that the LCs as a whole were also not incompressible (J = 0.94 ± 0.11 for Pig A, J = 0.97 ± 0.08 for Pig B, and J = 0.97 ± 0.06 for Pig C, mean ± standard deviation over the entire LC).

IV. Discussion

We present a method based on phase-contrast micro-computed tomography to visualize connective tissue structures within the lamina cribrosa and to thus determine the full-field deformation of the LC in response to elevation of IOP using either DIC or DVC. The main findings of this study are:

• PC μCT provides a robust method for imaging the fine architecture of the LC at high spatial resolution under different loading conditions, without the use of exogenous contrast agents.

• DVC can be successfully applied to image volumes acquired at different IOPs to study LC biomechanics. Mechanical strains computed by using DIC on a combination of transverse and sagittal maximum intensity projection images were generally consistent with those computed with DVC, enhancing confidence in DVC as a robust method for strain measurements in the LC.

• The deformation field of the LC is complex. Large strain gradients were observed in both the transverse and sagittal planes. Compressive strains showed the largest spatial heterogeneity.

PC μCT using synchrotron radiation is becoming an increasingly popular method to image soft tissues without the need of a contrast agent, being successfully used to image the esophagus [35], kidney [36], and liver [17]. Here we show for the first time that it can also be employed to image the microstructure of the LC at high resolution, important for the study of ocular biomechanics, particularly for glaucoma. PC μCT overcomes many limitations of imaging techniques previously applied to the LC. First, as opposed to serial histology, which requires extensive tissue processing and alters tissue structure [9], [37], PC μCT is performed on intact tissue. Second, the entire ONH can be imaged with PC μCT. In contrast, large regions of the in vivo ONH cannot be resolved using OCT because of shadowing artifacts from blood vessels [38], [39], [40] and light penetration limitations. Similarly, multiphoton microscopy can penetrate at best about 600 into the LC [11], [12]. Finally, PC μCT does not require the application of contrast-enhancing agents necessary for conventional μCT that relies on X-ray absorption; such agents have been associated with significant changes in mechanical properties of the sclera and LC [16]. Therefore, PC μCT offers a unique and powerful tool to study ONH biomechanics.

We demonstrated that we could use registered PC μCT datasets of individual porcine eyes inflated to various IOPs to compute LC deformation. We first presented a first-order method (Approach 1) to compute average tensile and compressive strains in the LC. This method predicted average tensile strains in the LC of 5.4–8.7% and average compressive strains of 20–23% (at 30 mmHg relative to the baseline case of 6 mmHg). Although the tensile strains predicted with Approach 1 were close to those computed by DIC and DVC, Approach 1 overestimated the compressive deformation of the LC. To address the limitations of Approach 1, we went on to use more sophisticated 2D and 3D image correlation techniques to compute full-field deformation of LC tissue.

Strain profiles computed by DIC and DVC were compared in transverse and sagittal slices and showed generally good agreement for most strain components. We did not expect the strain profiles computed by DIC and DVC to be identical because 2D DIC cannot account for through-plane deformation. Since the LC is in a state of full 3D deformation, 2D strains computed by DIC should only be an approximation of the full 3D LC strains. However, the fact that tensile strains computed by DIC and DVC were consistent both in spatial distribution and relative magnitude in both sagittal and transverse MIP images gives us confidence that image correlation techniques are robust methods to determine deformation of the LC. Both DIC and DVC showed large spatial variations in the strain profiles within the LC, indicating that mechanosensitive tissues in the ONH may not be subjected to uniform strain conditions, consistent with previous observations by Sigal and coworkers [11]. Furthermore, our full 3D DVC LC strain calculation allowed us to study spatial variations of compressive strains, which was not possible in previous studies employing 2D image analysis techniques. Compressive strains varied from −30% to 0% depending on the position in the LC, with the anterior central LC subjected to the largest compressive strains. The direction of compressive strains was in general aligned with the ONH axis. The magnitudes of mechanical strains are known to cause phenotypic changes to astrocytes and other cells contained in the LC as shown by in vitro studies of cell monolayers cultured on flexible membranes and subjected to cyclic biaxial [41] and uniaxial stretch [42], [43].

The findings of this study demonstrate that the LC is not incompressible. The Jacobian or determinant of the deformation gradient measures the local volumetric deformation. For an isochoric deformation, J is uniformly equal to 1, J ≥ 1 indicates local dilation, and J ≤ 1 indicates local contraction. Local volume changes could be as high as 30%. One possible explanation for the observed volume change is that the LC is poroelastic and saturated fluid flows out of the pores of the LC during pressure elevation. The maps of the Jacobian suggest that fluid flows from the anterior LC (J ≤ 1 ) to the posterior LC (J ≥ 1), which is consistent with fluid being pushed out of the LC due to pressure acting on the anterior LC. There are anatomical features that would facilitate this motion of fluid. For instance, fluid may follow the anterior/posterior direction of axons, but is constrained to move posteriorly with the applied pressure. If fluid flow occurred during scanning, we would have observed motion in the reconstructed scans, which we did not. This suggests that the time scale for fluid diffusion must be shorter than 15min, the equilibration time used in this study. Most computational models of the LC assumed incompressibility. Our study suggests that this may not be the most accurate representation of the mechanical behavior of the LC.

This study represents the first full 3D experimental characterization of LC biomechanics, which has not previously been possible using other in situ imaging techniques. Because of the complexity of experimentally accessing the LC, much of the current state of the field in ONH biomechanics is based upon finite element modeling (FEM) to numerically estimate stresses and strains in the LC and ONH [44], [45], [46], [16]. In most finite element models to date, the LC is treated as a homogeneous structure and mechanical behavior of the LC is idealized, and therefore LC deformation predicted by FEM may not fully recapitulate the complex physiological deformation patterns of the LC. PC μCT combined with DVC provides both the reference geometry at high spatial resolution and the mechanical behavior of the ONH to calibrate material models of the ONH tissues (most of which are currently speculative) and should greatly improve the predictive capabilities of future computational models.

Several limitations should be considered when interpreting the results of this study. First, our PC μCT method relies on access to a synchrotron light source, which is necessarily limited by high facility cost and demand. There are multiple advantages of using synchrotron radiation for phase-contrast imaging: the partial coherence of the synchrotron-generated X-ray beam allows us the use of propagation methods to measure phase-shift, which does not require sophisticated detection equipment. Further, the signal-to-noise ratio is high even at low exposure time thanks to the high flux of the X-ray beam. Although conventional laboratory sources do not have these advantages at the moment, commercial PC μCT machines are being developed and should facilitate these experiments in future [47]. To ensure that we had specimens ready to test during our allocated window of time at the synchrotron, we collected the eyes in advance and maintained them frozen until the time of experimentation. Although we confirmed that freezing did not greatly affect the mechanical behavior of the sclera, it was not possible to directly measure the effects of freezing on the mechanical behavior of the LC. Previous studies reported that mechanical properties of other collagen-rich connective tissues (skin) were minimally affected if the tissue was frozen quickly after procurement [48]. Therefore, we expect the effects of freezing on LC mechanical behavior to be small, but this assumption should be tested. This study was conducted on cadaveric tissues. Postmortem swelling of the axon bundles may have occurred before testing [49], causing a volumetric strain in the baseline configuration that may not represent physiological conditions. However, we expect this effect to be uniform and small compared with the strains caused by elevation of IOP.

The specimens were not preconditioned before scanning. The effects of preconditioning on LC mechanics are not known. There is indirect evidence that suggests that the large volumetric strains we observed may not be caused by the absence of preconditioning. First, high compressive strains were also observed in the sclera, whose mechanical behavior is known to be minimally affected by preconditioning in inflation testing [26]. Second, the specimens were pressurized to 15 mmHg for 10 min before placing them on the stage to ensure that no leaks were present. Although this does not constitute a traditional preconditioning loading regimen, this pressure-hold protocol would have likely removed any excess unbound fluid in the pores of the LC as effectively as a commonly applied preconditioning protocol consisting of a series of pressure load-unload cycles to 15mmHg with no relaxation time between cycles [50]. Third, because we had to image a fully equilibrated specimen to prevent motion during scanning, we let the eye equilibrate at the baseline pressure for 15 min before scanning. We believe that the hydration of the LC would have reversed back to its pre-preconditioning state during that time, erasing all effects that preconditioning may have had. Lastly, we expect preconditioning to have a minimal effects on the mechanical behavior of ocular tissues subjected to inflation testing. Preconditioning is required in tensile and biaxial strip tests because sample preparation (dissection from surrounding tissue) disrupts the native collagen structure and because the applied loads are typically very different from those experienced in vivo. Inflation testing is different in that the specimen is subjected to physiological loading conditions and the structure of the specimen is kept intact [26], [28].

The displacements and strains computed with DVC are subject to uncertainty. We estimated strain resolution using synthetic image deformation applied to a test LC image set. We showed that, for our image sets, such uncertainties were at least an order of magnitude smaller than typical values for the three principal strains at 15mmHg, and therefore we are confident that our results are not substantially affected by strain resolution in our imaging method. Smoothing the displacements with cubic splines prevented excessively noisy strain contours but may have removed physiological high local strains. For instance, we did not detect any regions of very high strain (~50% strain) that were reported in a few eyes by Sigal et al. [11]. This may be due to anatomical differences between the human and porcine LC. Specifically, as opposed to the human LC, which contains primarily beam-like connective tissue, the porcine LC is composed of plate-like structures, which form long conduits for the axons. This may provide mechanical resistance against bending and kinking that does not exist in the human LC. Future work will examine and analyze connective tissue within PC μCT scans of human LCs.

In conclusion, we successfully used synchrotron radiation PC μCT to image the intact porcine LC without need for contrast agents. DVC and other image analysis techniques applied to scans of eyes inflated to increasing pressures allowed us to consistently characterize the strain environment within the entire LC. This work will drive future in vitro studies on the effects of mechanical stimuli on ONH astrocytes and will help further our understanding of biomechanical factors at play in glaucoma.