The structural, DC resistivity and magnetic properties of Zr and Co co-substituted Ni_0.5Zn_0.5Fe₂O₄

Abstract

The Zr and Co co-substituted Ni_0.5Zn_0.5Fe₂O₄ have been synthesized by sol-gel auto combustion method. The XRD patterns provide single phase cubic spinel with ($Fd\overline{3}m$($O_h^7$)) space group and extra peaks found in XRD patterns from x = 0.24 to x = 0.4. The experimental lattice parameter is increased from 8.3995Å to 8.4129 Å and the theoretical lattice parameter is increased from 8.3948Å to 8.4130Å with increasing dopant concentration. The substitute ions in place of ferric ions cause the significant changes in all structural parameters. The D.C resistivity is increased from 126597 Ω-cm to 684229 Ω-cm and the drift mobility is decreased from 4.9×10⁻³⁶ cm²/V-s to 1.88× 10⁻³⁶cm²/V-s with increasing dopant concentration. The activation energy is decreased from 0.2108 eV to 0.0905 eV with increasing doping concentration. The saturation magnetization is decreased from 71.1559 emu/gm to 28.2405 emu/gm and the net magnetic moment is decreased from 6.3556 Bhor magnetons to 2.5523 Bhor magnetons with increasing dopant concentration. The Y-K angles are increased from 20.0723̊ to 59.4274̊ with increasing dopant concentration. The anisotropy constant has increased from 100 to 351 with increasing dopant concentration. The permeability is decreased from 117 to 19.4524 with increasing dopant concentration.

1. Introduction

The iron based magnetic materials and metallic alloys are useless at higher frequency application due to their low resistivity for examples inductor cores in T.V circuits. The low resistivity of iron based magnetic and metallic materials allow the flow of electrons (electric current) through them, which produces the heat, hence these materials become inefficient due to waste of energy and this wastage energy is increased at high frequency [1, 2, 3]. However the ferrites are better performers at high frequency application than iron based magnetic and metallic alloys because of their high electrical resistivity and high temperature stability. These factors increase the usage of ferrites of high frequency application. The ferrites are choice for best core materials for frequency from 10 kHz to few MHz [4]. The important factors of ferrites are lower cost, higher temperature stability and high quality. The porosity is insignificant in metals, but its considerable important in ferrite such consideration helps us, why the ferrites have been used and studied for several years [5]. The ferrite properties are being improved on increasing trends in ferrite technology. The ferrites are categorized into soft and hard, the most common soft ferrites are Ni-Zn and Mn-Zn. The Mn-Zn ferrites have high permeability and low resistivity. Ni-Zn ferrites exhibit the high resistivity lower permeability. For high resistivity application Ni-Zn ferrites are suitable above 5 MHz frequency. The electrical conductivity in Ni-Zn ferrite is due to the presence of (Fe³⁺/Fe²⁺) in both A and B-sites [6]. The low permeability is assigned in Ni-Zn ferrites because of low saturation magnetization and net magnetic moment. In case of Mn-Zn ferrites high saturation magnetization and net magnetic moments are possible, hence Mn-Zn ferrites are used in beyond the1 MHz frequency applications [7]. By making the suitable modification with substitute ions the resistivity of ferrites is increase or decrease. The higher magnetic materials give the M-H loop with large area by means of great loss of energy. If the loop area is large the loss of energy is more and area of loops is less the loss if energy is less i.e. high magnetic materials induce the great loss of energy by means of eddy currents [8]. This will minimize by reduction the magnetization in material and increase the resistivity of ferrites. For present study the Ni_0.5Zn_0.5Fe₂O₄ is modified with Zr and Co ions to increase the resistivity of ferrites by decreasing magnetic ions (Fe³⁺). Since the ferrites possessed high resistivity by formation of Fe²⁺ions. But formation of Fe³⁺ions (Fe²⁺→Fe³⁺) will increase the electric conduction and also magnetization (If Fe³⁺ions present in material the magnetic properties are increase because one Fe³⁺ ion posses 5μB) [9]. For this present study our aim is increase the resistivity of Ni_0.5Zn_0.5Fe₂O₄ ferrites by substitution of Zr and Co ions. The present study deals the structural, DC resistivity and magnetic properties of Zr and Co co-substitute Ni_0.5Zn_0.5Fe₂O₄ at room temperature.

2. Experimental

The Conventional ceramic technique usually common technique to prepare the Ni-Zn ferrites but resultant product is not stoichiometric and homogeneous because the reactants are react at high temperature [10]. As a result the unwanted grain growth betides in processing of material. To lower processing material defects researchers developed alternative wet chemical method known as sol-gel auto combustion method. The sol-gel auto combustion method for tailoring the precursor materials was adopted in this investigation. For the present study Ni_0.5Zn_0.5Zr_xCo_xFe_2-2xO₄ have been prepared by sol-gel auto combustion method. All reagents Ni(NO₃)₂.6H₂O(Hi meadia 99.9% purity), Zn(NO₃)₂.6H₂O (Hi meadia 99.9% purity), Co(NO₃)₂.6H₂O(Hi meadia 99.9% purity), ZrO(NO₃).xH₂O (Hi meadia 99%), citric acid (C₆H₈O₇) (Hi meadia 99.9% purity) and ethelyglycol were used to tailoring of the material. Previous studies conducted by [11, 12] have been reported the making process of Ni_0.5Zn_0.5Zr_xCo_xFe_2-2xO₄. The precursor ferrite powder, ground fine and calcined at 800 °C for 3hrs. Later, 5% PVA added to calcined powders and ground for another 30–45 minutes then powders were sintered at 1200̊ C for 2hrs. The sinter powders were characterized using different methods. The reactions products were characterized by X-ray diffraction (XRD) at room temperature. Powders acquired from combustion and sintering were tested by x-ray powder diffraction (XRD) recorded at 2θ from 10° to 60° at a scanning rate of 1^◦ min⁻¹ using a Bruker D₈ with GADDS Co-Kα radiation (λ = 1.7895Å) and cryostream 700 recorded at 2θ from 10^° to 70̊ at a scanning rate of 2̊ min⁻¹. The surface structure examined by JEOL JSM-6610L model. The average grain size was measured by using the image-j software. TEM was carried out on the powders to confirm the particle size. The combustion powders are compressed by applying 5 tons pressure in 5 minutes to make the pellets and then the pellets sintered at 1200 °C for 2hrs. The sintered pellet surface layers carefully polished later washed in acetone. After that the pellet surfaces are coated with silver paste on the opposite faces to provide the electrodes. The Wayne-Kerr high frequency LCR meter Model 65120 used to carry out the inductance measurements in the frequency range 20Hz to 8 MHz at room temperature. Lake Shore 7410 VSM system used to characterize the DC magnetic properties of materials as a function of magnetic field at room temperature.

3. Results and discussion

The Zr and Co co-substituted Ni_0.5Zn_0.5Zr_xCo_xFe_2-2xO₄ (x = 0. 08, 0.16, 0.24, 0.32 and 0.4) ferrites have been prepared by sol-gel auto combustion method. In Fig. 1, the X-ray diffraction curves of the samples Ni_0.5Zn_0.5Zr_xCo_xFe_2-2xO₄ (x = 0. 08, 0.16, 0.24, 0.32 and 0.4) are illustred. For the dopant concentration x = 0.24 to x = 0.4, the extra peaks were observed using XRD. The extra peaks arose by decreasing intensities of (422) (511) (440) lattice planes. The lattice planes (220) and (422) are more sensitive for cations on tetrahedral site. The (222) lattice planes are sensitive for cations on octahedral site and the (511) planes are sensitive to oxygen ions parameter respectively. In cubic spinel structure (220) and (400) planes are sensitive to cation distribution on tetrahedral and octahedral sites, respectively. The magnetic moment of the ferrite determine by cations distributed among tetrahedral and octahedral sites. The substitution of Zr and Co ions in place of Fe³⁺ions creates the distortion in the unit cell due to large ionic radius of Zr and Co. This distortion may dominated by pure cubic structure upto x = 0.16, there after small intensity peaks developed around the (3 1 1) peak. The developed peaks around (3 1 1) may be due to the shifting of (3 1 1) peak to higher angles. The arised peaks around the may not disturb the pure cubic spinel phase and no character was changed by these peaks. The average position peak shifted by the angle of 1.31̊ supports the formation of Ni_0.5Zn_0.5Fe₂O₄ in different stoichiometry as a function of the Zr and Co substitution [13]. The lattice constant was calculated using the following formula reported by [14].

$$a=d\sqrt{h^2+k^2+l^2}$$ (1)

where is “a” lattice constant d is the space between the planes and h, k, l, are the Miller indices. The previous reported lattice constant value for Ni_0.5Zn_0.5Fe₂O₄ ferrite is 8.39 Å [15]. The lattice constant in this present study was found as 8.3995 Å. This is good in agreement with the earlier reported value. Theoretical and experimental lattice parameters are shown in Fig. 2 with increasing dopant concentration variation. From Fig. 2 it is found that the lattice constant decreased from the 8.3995 Å to 8.3611 Å for substitution x = 0.0 to 0.08 later increased to 8.4125Å for x = 0.4 with the addition of Zr and Co ions. The error bars mentioned in lattice parameter, the average error occurred in the lattice parameter as 0.0007Å and it is shown in Fig. 2 (a). The initial decrease in the lattice constant the substitute ions enters into specific lattice sites. Later, increase in the lattice parameter is missing match between the ionic radius of substitute ions and host site radius. By increasing the dopant concentration the substitute ions occupy a large amount of empty place, hence the lattice constant increased with increasing doping concentration [16]. The other structural parameters like to hope length L_A and L_B, bond length of tetrahedral and octahedral d_AL and d_BL, shared and unshared edges of tetrahedral and octahedral (d_AE,d_BEand d_BEU) increased with increasing dopant concentration because of the increase in the lattice constant [17, 18]. Calculated values listed in Table 2 and Table 3. The strain constant, averaged-space and theoretical lattice parameter increase with increasing dopant concentration as a result of large ionic radius ions substitute in place of Ferric ions Fe³⁺ (0.67Å) (Zr and Co have ionic radius 0.80Å and 0.79 Å the respectively). The substitution of large ionic radius ions in place of ferric ions expand the spinel lattice promptly. The equation used to determine the crystalline size is represented by Eq. (2).

$$D=\frac{0.94\ast \lambda }{\beta \cos \theta }$$ (2)

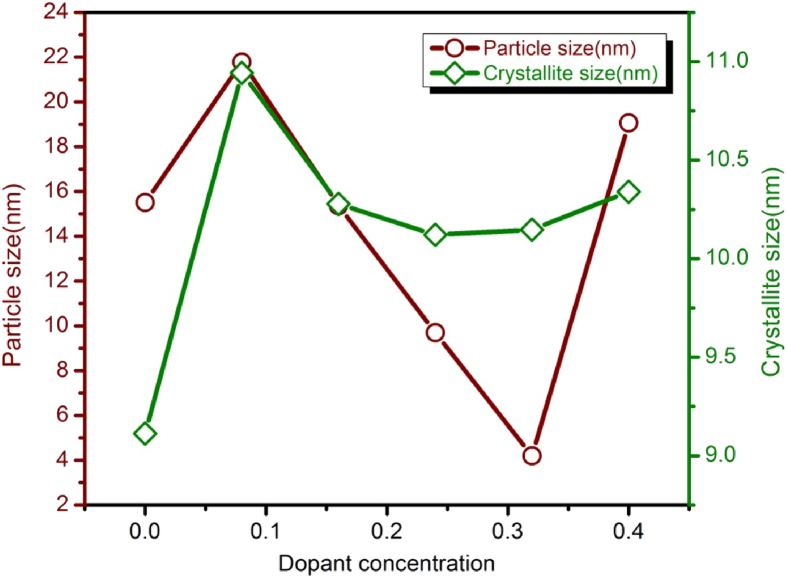
where λ is the wavelength and the β is the full width at half maximum of (311) peak. The crystallite size inversely depends on the FWHM in Eq. (2). The increase in the FWHM decreases the crystallite size and vice versa. The ratio of sintered density and X-ray density gives the porosity of samples. The porosity increased with increasing dopant concentration because of formation of Fe²⁺ions during the sintering [19]. The formation of Fe²⁺ions in the sintering of material lags the sintering rate of the samples so that the grains are not grown monotonically as result pores developed in the samples. The variation of particle size and crystallite size with dopant concentration is shown in Fig. 3.

Fig. 1.

X-ray diffraction patterns of Ni_0.5 Zn_0.5Zr_xCo_xFe_2-2xO₄ samples with x = 0.0, 0.08, 0.16, 0.24, 0.32, and 0.4.

Fig. 2.

Variation of experimental and theoretical lattice parameter with dopant concentration and Fig. 2(a) error bars of lattice parameter variation with dopant concentration.

Table 2.

The structural data of Zr and Co substituted Ni_0.5Zn_0.5Zr_xCo_xFe_2-2xO₄.

Dopant concentration	rA(Å)	rB(Å)	μ	d-space (average)	ε (strain)×10−3	I(220)/I(222)	I(220)/I(400)	I(422)/I(400)
0.0	0.4984	1.8298	0.4638	2.3632	7.4336	8.6936	2.2573	1.055
0.08	0.4973	1.8277	0.4633	2.2817	6.9218	2.6238	0.7545	0.2075
0.16	0.4993	1.8313	0.4641	2.4565	7.5134	8.1149	1.9547	0.6645
0.24	0.5004	1.8332	0.4646	2.4657	7.5060	2.2857	1.0408	0.4593
0.32	0.5011	1.8345	0.4649	2.4622	7.9988	3.6201	1.1418	0.6390
0.4	0.5013	1.8348	0.4650	2.6073	8.2814	1.6576	1.2943	0.5119

Table 3.

The structural data of Zr and Co substituted Ni_0.5Zn_0.5Zr_xCo_xFe_2-2xO₄.

Dopant concentration	F(θ)	LA(Å)	LB(Å)	dAL	dBL	dAE	dBE	dBEU
0.0	1.2601	3.6369	2.9696	1.7748	2.1233	2.8984	3.0409	3.5773
0.08	1.2601	3.6346	2.9677	1.7737	2.1220	2.8965	3.0389	3.5750
0.16	1.2563	3.6387	2.9710	1.7756	2.1244	2.8997	3.0423	3.5790
0.24	1.2622	3.6409	2.9728	1.7767	2.1256	2.9015	3.0442	3.5812
0.32	1.2609	3.6423	2.9740	1.7774	2.1265	2.9027	3.0454	3.5826
0.4	1.2601	3.6427	2.9744	1.7776	2.1267	2.9030	3.0457	3.5830

Fig. 3.

Variation of particle size and Crystallite size with dopant concentration.

3.1. Morphology study

3.1.1. SEM morphology

The SEM micrographs are shown in Fig. 4 the grain size measured by using image-j software. Fig. 5 shows the variations of sintered density, porosity and grain size with dopant concentration. From Fig. 5 the grain size and sinter density varies oppositly with porosity on increasing dopant concemtration. The porosity of sample decreases the grain size it is obviously shown in SEM micrographs. Density is important factor for micro-structural aspects and depending on material processing. In material processing primary particles are rearranged through the diffusion of grain boundaries. The grain growth rate improves due to necking process of primary particles through formation of liquid phase. During sintering of materials porosity arise due to occurrence of oxygen vacancy at higher temperature. The occurred porosity is increases with increasing sintering temperatures. In Ni-Zn ferrites Zinc evaporate at higher temperature. The volatize Zinc ions usually promote the formation of Fe²⁺. The loss of zinc resulted in unsaturated oxygen ions. Then the excess electrons on oxygen encourage neighboring Fe³⁺ ions form of Fe²⁺ions the due to the electrostatic interaction bond broken. This process develops the pore in the spinel lattice. To minimize this porosity the excess of ferric oxide partially dissolve into spinel lattice as γ-Fe₂O₃ in cation vacancies and partly as Fe₃O₄ with formation Fe²⁺ ions. This formation makes cation vacancies and oxygen vacancies concentration low as consequence the sintering rate becomes slow this may understand by using following Eq. (3).

6Fe₂O₃→4Fe₃O₄ + O₂ (3)

Fig. 4.

(a)–(f). SEM photo graphs of Zr and Co substituted Ni_0.5Zn_0.5Zr_xCo_xFe_2-2xO₄ (x = 0.00, 0.08, 0.16, 0.24, 0.32 and 0.4).

Fig. 5.

Variation of sintered density, porosity and grain size with dopant concentration.

Hence formation of Fe²⁺ions decreases the sintering rate as result the sinter density is decrease. The decrease sintering density consequence the grain size reduces.

3.1.2. TEM morphology

Fig. 6 shows TEM picture, the particle size estimated from TEM pictures by using the image-j software. The estimated particle size values are smaller compared to the data obtained from XRD measurements since particles show the agglomeration nature due to the particles reducing their dimensions into nano region. The All the structural variables are listed in Table 1, Table 2 and Table 3.

Fig. 6.

(a)–(f). Transmission electron micrographs of Ni_0.5Zn_0.5Zr_xCo_xFe_2-2xO₄ along with selected area Electron diffraction patterned of the samples (x = 0.00, 0.08, 0.16, 0.24, 0.32 and 0.4).

Table 1.

The structural data of Zr and Co substituted Ni_0.5Zn_0.5Zr_xCo_xFe_2-2xO₄.

Dopant concentration	Lattice parameter (aexp)Å	Lattice parameter (ath)Å	Crystallite size D (nm)	Sintered density (d)g/cm3	X-ray density dx g/cm3	Particle size (nm)	Grain size μm	Porosity%
0.0	8.3995	8.3948	9.1121	4.7657	5.3292	15.5051	2.3137	10.57
0.08	8.3941	8.3876	10.9423	5.0146	5.4084	21.7809	3.043	9.73
0.16	8.4035	8.4004	10.2774	4.9698	5.4640	15.364	2.7436	10.86
0.24	8.4086	8.4072	10.1211	4.9288	5.5108	9.6893	2.6048	13.63
0.32	8.412	8.4118	10.1474	4.8653	5.5806	4.1924	2.4618	15.85
0.4	8.4129	8.4130	10.3397	4.7936	5.6471	19.0597	2.2952	18.1

3.2. DC resistivity study

According to band theory of solids the oxides of transition metal should be semi metallic conductors than that of insulators or ordinary semiconductors, because the 3D bands in transition metal oxides occupied by electrons partly in all cases. Slater explained this phenomenon by semiconducting nature based on the super exchange coupling. The super exchange coupling provides the evidence for the semiconducting nature in ferrets. According to super exchange coupling the 3D bands of metallic oxides split with intervening gap. The lower band completely filled with electron and an upper band completely empty. For example, in Fe₃O₄ the Fe²⁺ions and Fe³⁺ions present in neighboring B-sites. The electronic exchange occurred between Fe³⁺ and Fe²⁺ ions only by a small energy barrier this leads high electronic conductivity as usual semiconductor mechanism. The semiconductor conductivity was described by the following Eq. (4).

$$\sigma ={\sigma }_o\exp \left(\frac{\Delta E}{{\kappa }_{B}T}\right)$$ (4)

where σ_o is the constant, ΔE is the activation energy, K_B is the bolts man constant, T is the absolute Temperature (K). The less or more curved lines obtained while a graph is drawn between the σ and 1/T. ΔE equals to 0.1eV for stoichiometries composition and ΔE reaches 0.5eV for low conductivity ferrites. The Arrhenius plot drawn between the inverse temperature and resistivity in the temperature range of 300 K–620 K is shown in Fig. 7 shows the semiconductor nature [20, 21]. The results revealed that an increase in inverse temperature decreases the DC resistivity exponentially. The electrical conductivity occurred from paramagnetic Fe²⁺ region to ferromagnetic Fe³⁺ region with increasing inverse temperature as a result the resistivity of ferrite samples decrease. The activation was energy calculated from the slopes of Arrhenius plots. Fig. 8 shows the activation energy with a variation of dopant concentration. The activation energy, decreased from the 0.2108 eV–0.0905 eV, with increasing doping concentration attributed to the increase of porosity of prepared samples. That is jumping frequency of electrons from the ferrous region (Fe²⁺) to the ferric region (Fe³⁺) decrease it may justify by the increase in resistivity because the activation energy behaves as DC electrical resistivity [22, 23]. The compositional dependence DC resistivity of ferrites increase from 1.2×10⁶ Ω-cm to 8.03×106 Ω-cm, for x = 0.08 to x = 0.24 later slightly decreased to 6.8×106 Ω-cm for x = 0. 4. The increase in DC resistivity as a result of formation of Fe²⁺ions in sintering process. The drift mobility of samples was detrmained from the following Eq. (5).

$${\mu }_d=\frac{1}{\eta e\rho }$$ (5)

where η = N_ad_sP_fe/M, “e” is charge of the electron, “ρ” is the resistivity of the sample. The drift mobility, increased from 4.9×10⁻³⁶ cm²/V-s to 6.14×10⁻³⁶ cm²/V-s for x = 0.0 to x = 0.08. Later it decreased to 1.88×10⁻³⁶ cm²/V-s for x = 0. 4. The drift mobility and DC resistivity variations are shown in Fig. 9. The high resistivity samples has low mobility and vice versa it is concluded by Fig. 9 [24]. The measured DC resistivity, activation energy and drift mobility values are listed in Table 4.

Fig. 7.

Variation of log ρ with inverse temperature.

Fig. 8.

Variation of activation energy with dopant concentration.

Fig. 9.

Compositional variation of D.C resistivity and Drift mobility.

Table 4.

The DC resistivity properties of Zr and Co substituted Ni_0.5Zn_0.5Zr_xCo_xFe_2-2xO₄.

Dopant concentration	DC resistivity Ω-cm	Drift mobility μd2×10−36 Cm2/V-s	Activation energy (ΔE)eV
0.00	126597	4.90	0.2108
0.08	327540	6.14	0.1857
0.16	604121	5.52	0.1669
0.24	803084	2.09	0.1455
0.32	784661	1.87	0.1267
0.4	684229	1.88	0.0905

3.3. Magnetic properties

The M-H loops for samples Ni_0.5Zn_0.5Zr_xCo_xFe_2-2xO₄ (x = 0.0, 0.08, 0.16, 0.24, 0.32, 0.4) was recorded on the room temperature using vibrating sample magnetometer (VSM). The shape and the width of the hysteresis loop depend on chemical composition, porosity, grain size. The area of M-H loops flourishing with increasing dopant concentration shown in Fig. 10. The ferromagnetic ion ordering by application of external magnetic field depicts the saturation magnetization. In ferrites the ferromagnetic order disturbs by the substitutes elements, hence the saturation magnetization is decreased. The magnetization of samples was estimated using the following Eq. (6).

$$M=M_B-M_A$$ (6)

Fig. 10.

(a)–(f). Hysteresis curves of M-H Zr and Co substituted Ni_0.5Zn_0.5Zr_xCo_xFe_2-2xO₄ (x = 0.00, 0.08, 0.16, 0.24, 0.32 and 0.4).

where M_A and M_B are the net magnetic moment of A and B-sites respectively. From Eq. (6) obviously resultant magnetization of the material is depending on the A-site magnetic moment. The Ni-Zn ferrite is the mixed ferrite in which ferric ions (Fe³⁺) are distributed among both A and B sites [25]. The substitution of Zr and Co in spinel lattice in place of ferric ions the net magnetic moment of resultant samples decreased gradually. Since the Zr and Co are exhibiting the non-magnetic and ferromagnetic ordering respectively. Despite Co shows the ferromagnetic ordering the net magnetic moment of B-site decreased as a result of the decrease of ferric (Fe³⁺) ions in B-site. The Zr⁴⁺ ions prefer to occupy the tetrahedral sites because of the tetrahedral site environment and replace the Fe³⁺ ions A-site to B-site. The A-site Fe³⁺ions spin moment always opposite to B-site Fe³⁺ ions spin moment as result saturation magnetization is decreased [26]. The net magnetic moment of prepared samples was reckoned using the following Eq. (7).

$${\eta }_B=\frac{molecularweight\times m_S}{5585\times d_S}$$ (7)

where m_s and d_s are the saturation magnetization and sintered density. The saturation magnetization and net magnetic moment with dopant concentration is shown in Fig. 11. The both parameters are decreased with increasing dopant concentration since they are directly related according to Eq. (7). The coercive field is the field where magnetization becomes zero in reverse direction in magnetization process. The coercive field for present samples increased from 48.6911 to 310.5979 for x = 0.00 to x = 0. 4. The decrease in porosity decreases coercivity and vice versa [27]. The coercive field and porosity varied in similar trend with increasing dopant concentration and is shown in Fig. 12. The Y-K angles was computed from the following Eq. (8).

$$n_B=\left(6+x\right)\cos {\alpha }_{Y-K}-5\left(1-x\right)$$ (8)

where x represents the substituting element concentration, the Y-K angles are gradually increase with increasing dopant concentration from 20.0723° to 59.4274. The increase in Y-K angles is indicated for A-site spin moments arranged for B-site spin moments with some angle. That is the spin of A-sub lattice arranged in B-sub lattice ferromagnetic ordering to antiferromagnetic ordering. A three lattice model by suggesting Yafett-Kittel, according to three lattice model the ferrites has A-lattice and B-lattice, but B lattice divided into two sub lattices of B1 and B2 [28] both are remain parallel. The A-site ions spin moments always opposite to B-site spins moments. The substitution of Zr ions replaces the Fe³⁺ions from A-site to B-site. The A-site Fe³⁺ions spin moments always opposite to B-site Fe³⁺ ions spins moments. Up to certain dopant concentration Fe³⁺ ions will arrange opposite later arranged in canting position. This canting position exhibits triangular spins arrangement in B lattices. This triangular arrangement increases with increase of substitution of impurities in ferrite lattice. Hence the ferromagnetic order changed as the anti ferromagnetic order in ferrite lattice. The decreasing trend shows the zero Y-K angles attributed decreasing A-B interaction suggested by the Neel's two lattice sub model favours the ferromagnetism with parallel spin arrangement in B lattice [29]. The composition variation of Y-K angles shown is in Fig. 13.

Fig. 11.

Variation of Net magnetic moment and saturation magnetization with dopant concentration.

Fig. 12.

Variation of Coercive field and porosity with dopant concentration.

Fig. 13.

Variation of Y-K angles with dopant concentration.

3.4. Permeability

The permeability is defined as in electromagnetism permeability is the measure of the ability of a material to support the formation of a magnetic field within itself. Hence the material obtains a degree of magnetization in response to the applied magnetic field. Eq. (9) is used to determain the extend magnetization of a material in response to an applied magnetic field.

$$\mu =\frac{L}{L_0}$$ (9)

where L is the inductance and L_o of torroids Figured as follows.

$$L_{o}4.606N^{2}Log\left(OD\right)t10$$ (10)

The compositional dependence of permeability with grain size is shown in Fig. 14. The permeability decreased from the 117.1649 to 19.4524 with increasing dopant concentration. The permeability directly proportional to saturation magnetization in case of contribution of electronic spin rotation and proportional to square of M_s in case of contributing the domain walls motion [30]. The Co ions are known to exhibit large anisotropic constant and magnetostriction both are inversely related to permeability hence decrease in permeability attributed to large anisotropy constant caused by the material. The variation of anisotropy constant understood using the single ion model. According to this model in Ni-Zn ferrite Fe³⁺ ions presented over A- and B-sites. For smaller doping concentration Ni²⁺ ions contribution is discarded in Ni-Zn ferrite. The A-site anisotropy is positive the B-site Fe³⁺ ion anisotropy is negative but larger. The increase in magneto crystalline anisotropy attributes the increase of dopant concentration of Zr and Co and also formation of Fe²⁺ and Co³⁺ ions. Therefore a decrease in permeability highly governed by Co ions anisotropy only [31]. The anisotropy constant and initial permeability with dopant concentration is shown in Fig. 14 (a). The frequency variation of initial permeability shown is in Fig. 15. It is known that the low-frequency dispersion associated with domain wall bowing and wall displacement. The application of field bows the pinned walls, the domain wall displacement is not triggered by any field [32]. The domain walls are not displaced up to certain frequency later the domain walls are displacing called critical field. The decrease in frequency dispersion indicates that the critical field increases due to incorporation of Co and Zr in general formula of ferrites [33] as result low initial permeability attains. The Q-factor determines the efficiency of the system with the applied field, it may neither electrical nor mechanical system. The wide frequency band is ascribed by a lower Q-factor of system and the narrow frequency band is caused by a high Q - factor of the system [34]. The frequency variation Q-factor shown is in Fig. 16. From Fig. 16 the Q-factor decreases with increasing dopant concentration due to increasing electrical resistivity. It is known that the main loss mechanism in Ni-Zn ferrite at high frequency is eddy current loss. The eddy current loss is expressed as follows in Eq. (11).

$$p_e=\frac{K{B}^2{f}^2{d}^2}{\rho }$$ (11)

where ‘P_e’ is the energy loss per unit volume, K is a geometric constant, B is the maximum induction, f is the frequency and‘d’ is the thickness of narrowest dimension perpendicular to the magnetic flux. From Eq. (11) the eddy current loss is inversely proportional to the resistivity of the samples [35, 36]. Fig. 16 shows the quality factor decreases with increasing Zr and Co concentration. The decrease in the Q-factor due to the increasing electrical resistivity of ferrite with applied field. This scenario is clearly shown by M-H loops with great losses of magnetic energy as a result the quality factor is decreased with increasing of resistivity of ferrites. All the measured magnetic properties are listed in Table 5.

Fig. 14.

Variation of permeability and grain size with dopant concentration and Fig. 14(a). Variation of permeability and anisotropy constant with dopant concentration.

Fig. 15.

Variation of permeability with frequency.

Fig. 16.

Variation of Q-factor with frequency.

Table 5.

The magnetic properties of Zr and Co substituted Ni_0.5Zn_0.5Zr_xCo_xFe_2-2xO₄.

Dopant concentration	Magnetic moment (ηB) Bohr magneton	Saturation magnetization (Ms) emu/gm	Permeability (μ)	Coercive field (Hc) Oe	Y-K angles(o)	Anisotropy constant(K) erg/cm3
0.00	6.3556	71.1569	117.1649	48.6911	20.0723	100.20
0.08	5.3574	58.8108	35.8440	42.395	34.4331	133.89
0.16	4.1472	47.1815	28.3499	54.9998	39.7553	177.41
0.24	2.9478	33.1309	27.6339	159.9546	48.9891	251.43
0.32	2.8595	31.7365	22.0879	214.8523	54.3232	337.34
0.4	2.5523	28.2405	19.4524	310.5976	59.4274	351.76

4. Conclusions

The Zr and Co co-substitute Ni_0.5Zn_0.5Fe₂O₄ have been prepared by sol-gel auto combustion method. The XRD patterns provide the single phase cubic spinel with ($Fd\overline{3}m$($O_h^7$)) space group. The extra peaks arise from dopant concentration of 0.24–0.4. This is indication for specific lattice sites preferred by substituting ions with decrease intensities of (422) (511) (440) planes. The particle agglomeration nature observed from TEM pictures due to the particles are reducue their dimension into nano range. The clear porosity observed in SEM micrographs due to the lagging of the sintering rate of material as result of formation of Fe²⁺ions. The DC resistivity and drift mobility vary in opposite directions with increasing dopant concentration because of the electrical conduction occurred from paramagnetic region to ferromagnetic region. The decrease in activation energy justified by the increase in porosity of samples since the creation of small vacancies in the sample will interrupt the electrical conduction. The increase in the area of M-H loops revels the loss of energy is high in materials by application of magnetic field justified by the Q factor of samples with a wide frequency band. The coercive field is increased as a result of increase in porosity. The non-collinear arrangement of Fe³⁺ions in B-site increases the Y-K angles because of increasing A-B interactions. The formation of Co³⁺ ions will induce the large anisotropy constant in prepared samples, hence increase in the anisotropy constant results in increasing dopant concentration.

Declarations

Author contribution statement

K. Jalaiah: Performed the experiments; Analyzed and interpreted the data; Wrote the paper.

K. Chandra Mouli, P.S.V. Subba Rao: Analyzed and interpreted the data.

R.V. Krishnaiah:Contributed reagents, materials, analysis tools or data.

K. Vijaya Babu: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.