Abstract
Objective
To examine the bidirectional effects of objectively measured nighttime sleep and sedentary activity among toddlers.
Method
Actical accelerometer data were analyzed for 195 toddlers participating in an obesity prevention trial (mean age = 27 months). Toddlers wore the accelerometers for up to 7 consecutive days. Nighttime sleep was defined as the number of minutes asleep between the hours of 8 pm and 8 am the following morning. Sedentary behavior (in minutes) was defined using previously established Actical cut points for toddlers. Variables were lagged and parsed into latent within- and between-person components, using dynamic structural equation modeling (DSEM).
Results
Toddlers spent an average of 172 min (∼3 hr) in sedentary activity and slept an average of 460 min (∼8 hr) per night. An autoregressive cross-lagged multilevel model revealed significant autoregression for both sleep and sedentary activity. Cross-lagged values revealed that decreased sleep predicted increased next-day sedentary activity, and sedentary activity predicted that night’s sleep. For 89% of the sample, the within-person standardized cross-lagged effects of sleep on sedentary were larger than the cross-lagged effects of sedentary on sleep.
Conclusions
Results suggest that, on average, nighttime sleep is a stronger predictor of subsequent sedentary behavior (compared with the reverse), and this is the case for the majority of toddlers. Findings highlight the importance of interindividual associations between sleep and sedentary activity. The present study is an example of how DSEM methods can be used to ask questions about Granger-causal cross-lagged relations between variables, both within and between individuals.
Keywords: research design and methods, statistical applications, sleep
Sleep and physical activity exist on a continuum of movement; both have been independently associated with children’s health (Chaput et al., 2017; Downing, Hnatiuk, & Hesketh, 2015; Tremblay et al., 2011). On average, shorter (vs. longer) sleep duration has been associated with higher adiposity, poorer emotional regulation, impaired growth, and higher risk of injuries in toddlers (Chaput et al., 2017). On average, more (vs. less) sedentary behavior has been linked to higher weight status, worse fitness, lower self-esteem and prosocial behavior, and lower academic achievement (Kuzik & Carson, 2016; Kuzik et al., 2017; Tremblay et al., 2011).
Limited research has assessed relations between sleep and sedentary behavior, particularly among young children (Kuzik et al., 2017). Short nighttime sleep duration has been associated with more sedentary behavior in cross-sectional studies (Busto-Zapico, Amigo-Vázquez, Peña-Suárez, & Fernández-Rodríguez, 2014). Sleepiness may decrease motivation to engage in active play and physical activity and increase the likelihood of sedentary behaviors, such as screen time (Magee, Caputi, & Iverson, 2014). Alternatively, sedentary behavior (including screen time) may lead to poor nighttime sleep quality and short sleep duration (Chaput et al., 2017; Taveras, Rifas-Shiman, Oken, Gunderson, & Gillman, 2008). Many studies that have examined sleep and sedentary behavior have been cross-sectional, preventing examination of directionality and relative strength of the relationship between them (Chaput et al., 2017). Longitudinal designs would enable us to examine the bidirectionality of this relationship and answer the questions: Does previous night’s sleep predict next-day sedentary behavior and/or does daytime sedentary behavior predict that night’s sleep? As well as address questions about relative strength of these relationships: Is sleep a stronger predictor of sedentary behavior or is sedentary behavior a stronger predictor of sleep?
Sedentary habits (including screen time) have been shown to persist during early childhood (0–5 years) and from early childhood to middle childhood (6–12 years) (Jones, Hinkley, Okely, & Salmon, 2013), suggesting that establishing healthy sedentary behaviors early in life may protect against both proximal and future negative health behaviors.
Nighttime sleep, specifically, has been linked to better emotional regulation and increased physical activity among young children (Chaput et al., 2017). Previous research has typically focused on sleep over a 24-hr period (Hirshkowitz et al., 2015), which may neglect the specific importance of nighttime sleep consolidation, as toddlers begin to sleep through the night and gradually spend less time asleep overall. This decline is especially marked during the second year of life, as children develop circadian rhythm patterns (Acebo et al., 2005; Bernier, Bélanger, Bordeleau, & Carrier, 2013; Mindell, Meltzer, Carskadon, & Chervin, 2009). Nighttime sleep specifically has been associated with sedentary behavior in infants (Vijakkhana, Wilaisakditipakorn, Ruedeekhajorn, Pruksananonda, & Chonchaiya, 2015) and physical activity among toddlers (Hager, Calamaro, et al., 2016), with no studies examining them both along a continuum of movement. Therefore, it is important to specifically examine nighttime sleep, given the emerging development of sleep consolidation in toddlerhood.
Much of the literature concerning sleep and physical activity has used subjective methods to examine differences between children (Downing et al., 2015). In a recent systematic review of sedentary behavior in children under 4 years, all studies (n = 24) used parent-reported screen time as a proxy for sedentary behavior, with the majority reporting only television time (rather than other electronic devices), and no studies used objective measures of sedentary behavior (Downing et al., 2015). Only recently have studies begun to use accelerometry to objectively examine sedentary behavior among toddlers (Gubbels, Van Kann, Cardon, & Kremers, 2018; Lee et al., 2017; Santos et al., 2017). Similarly, a recent systematic review of sleep in children under 4 found that 70% of studies used parental report to assess sleep duration (Chaput et al., 2017), despite well-documented evidence that parent report overestimates sleep duration, compared with objective measures (Girschik, Fritschi, Heyworth, & Waters, 2012). Research on both sleep and sedentary behavior has generally focused on identifying person-level characteristics (i.e., age, gender, socioeconomic status, and physical environment) that are related to activity on a typical day, with little attention to individual activity on a specific day (Cushing et al., 2017). Identifying individual-level fluctuating predictors of activity from day to day may be particularly relevant among children with alterations to their typical behavior (Cushing et al., 2017), such as experiencing or recovering from an illness.
Accelerometry is the most common method for objectively assessing physical activity and sedentary behavior and is increasingly used for sleep assessment (Quante et al., 2015). Although many modern accelerometers collect information relating to activity over time, data are often collapsed and temporal processes and dynamics are neglected (Hamaker & Wichers, 2017). If temporal information is examined, interesting and important questions can be asked about within-person contingencies regarding sleep and movement. Examples within pediatric psychology literature include research examining the effects of sleep on next-day moderate-to-vigorous physical activity (MVPA) among overweight youth (Krietsch, Armstrong, McCrae, & Janicke, 2016). Examining the unidirectional effects of sleep on movement, but not the bidirectional effects of movement on sleep, this study found that less sleep predicted increased MVPA the following day.
Cushing et al. (2017) aimed to study the bidirectional effects of individual fluctuations in affect and activity. Using separate multilevel analyses, they found bidirectional relations between individual-level fluctuations in affect and sedentary behavior (Cushing et al., 2017). This approach examined both average effects (e.g., “What is the relation between affect and activity on average?”) and random variability (e.g., “How consistent is this effect across people?”). This multilevel approach provided initial evidence that affect and movement are bidirectionally related within individuals but could not determine the relative magnitude of effects (e.g., “Does affect predict activity more than activity predicts affect?”).
To answer this question, many psychological researchers turn to cross-lagged models. In this approach, two or more variables are measured at two or more occasions and the cross-lagged associations are compared (controlling for effects the variables at previous time points have on themselves) (Schuurman, Ferrer, de Boer-Sonnenschein, & Hamaker, 2016). By taking multiple repeated measures and fitting them to a cross-lagged model, we can examine the association between variables while taking into account the time ordering of the process (Schuurman et al., 2016). Accelerometry data can be analyzed as longitudinal data if the time patterns are kept intact (i.e., by not collapsing data over time to obtain a single estimate of activity for an individual). This process enables analyses to address the bidirectional nature of activity (e.g. “Does sleep predict sedentary behavior more than sedentary behavior predicts sleep?”). Systems where variable “x” predicts future variables of “y” are referred to as “Granger Causality” (Granger, 1969) and have been widely applied in economics literature but only sparsely used in psychological research (Hamaker & Wichers, 2017). Though not true causality, comparing the relative strength of the cross-lagged associations can provide direction for future study and add clarity to theory (Schuurman et al., 2016).
We can also ask questions about the tendency of a variable to remain in a particular state. This stability, or “inertia”, can be thought of as the “carryover” of a variable, defined as the autoregression of that variable (one occasion predicting the subsequent occasion) (Hamaker & Wichers, 2017). For example, “Does last night’s sleep predict tonight’s sleep?” When data are collected multiple times from the same person, it is necessary to account for this carryover or stability (through modeling autoregression) before considering bidirectional effects or external predictors (Hamaker & Wichers, 2017). Thus, it is necessary to ask “Does today’s activity predict tonight’s sleep above and beyond last night’s sleep?”
Although cross-lagged models have been used to study such effects, these models estimate the average effect between people. Although alternatives have been proposed to separate out within- and between-person differences (Berry & Willoughby, 2017; Hamaker, Kuiper, & Grasman, 2015), such models do not generalize to any specific individual (i.e., they only estimate fixed slopes; the average across people). Multilevel models (as used in Cushing et al., 2017; Krietsch et al., 2016) allow for the separation of within-person dynamics and between-person differences (i.e., random slopes) (Schuurman et al., 2016), but often require a single outcome measure, and thus are unable to compare bidirectional effects. Dynamic structural equation modeling (DSEM) combines multilevel analyses while allowing for examination of paths typical of crossed-lagged autoregressive models. DSEM is a framework that combines multilevel modeling, structural equation modeling, time-series modeling, and time-varying effects modeling (Asparouhov, Hamaker, & Muthén, 2018). Structural equation models can handle multiple dependent variables and, thus, are suited for examining cross-lagged models and bidirectional effects.
The current study used the DSEM framework to create a multilevel bivariate autoregressive cross-lagged model to examine sleep and sedentary behavior among toddlers. The model comprises a time-series model at Level 1 that describes the within-person processes and at Level 2 that describes the between-person differences (Hamaker & Wichers, 2017). The aim of the current study was to examine and compare the bidirectional relations between nighttime sleep and next-day sedentary behavior among toddlers. We hypothesized that, on average, decreases in previous night sleep would predict increases in sedentary behavior the following day and that sedentary behavior would likewise predict the following night’s sleep. We further hypothesized that sleep would be a stronger predictor of sedentary behavior than the reverse. Finally, we hypothesized that there would be significant between-person variability around the autoregressive effects for sedentary behavior and nighttime sleep.
Method
Sample
The current study used baseline data from a larger randomized controlled trial aimed at obesity prevention. Biological mothers of ambulatory toddlers (age 12–32 months) were recruited from two clinical sites: suburban Special Supplemental Nutrition Program for Women, Infants, and Children (WIC) and urban Pediatric Ambulatory Center. Both sites served low-income, WIC-eligible (income <185% of poverty) families living in the surrounding communities. The suburban site was selected based on the racially diverse population it served, and the pediatric clinic was selected to sample low-income urban communities. Recruitment sites differed in location (suburban vs. urban) and the Pediatric Ambulatory Center served a greater proportion of African American families. Toddler eligibility criteria included at term birth with birth weight ≥2,500 g and no known congenital problems or disabilities. There were no weight inclusion criteria for toddlers or mothers. Eligible children were recruited while participating in routine well-child visits. The study was approved by university and state institutional review boards. All mothers provided written informed consent. Baseline assessments were conducted over two visits (1 week apart) by trained evaluators. At the first visit, mothers completed self-administered, computer-based questionnaires using voice-generating software and accelerometers were placed on the toddlers. During the second visit, accelerometers were removed. A total of 509 families were approached to participate—27 families actively refused, 174 passively refused, 4 were ineligible, and 27 were not randomized to the study. A total of 277 eligible mother–toddler dyads were recruited and completed the measurements. Self-reported income was used to calculate a poverty ratio based on 2009 thresholds determined by the US Census Bureau (2009). Based on income and family size, families were classified as either being above or below the poverty threshold as defined by the 2009 US Census Bureau.
Accelerometry
The Actical accelerometer (Philips Respironics) is a device with an omnidirectional sensor that can measure movement in one plane and can detect movements in the 0.5- to 3-Hz range. Voltage generated by the sensor is amplified and filtered via analog circuitry. The amplified and filtered voltage is passed into an analog to a digital converter, and the process is repeated 32 times per second (32 Hz). The resulting 1-s value is divided by four, then added to an accumulated activity value (activity counts) for the 1-min epoch (Pfeiffer, Mciver, Dowda, Almeida, & Pate, 2006). Acticals were placed on the child’s nondominant ankle, superior to the lateral malleolus, with a nonremovable, reinforced hospital band. Similar device placement has been used to detect sleep and physical activity among young children and shown to be significantly correlated with the gold standard of sleep measured by polysomnography (Galland, Kennedy, Mitchell, & Taylor, 2012; Sadeh, Acebo, Seifer, Aytur, & Carskadon, 1995) and direct observation of activity (Hager, Gormley, et al., 2016), respectively. The Actical is small, lightweight, and waterproof. It is worn during bathing, sleep, and play without interference. Toddlers wore the accelerometer next to the skin under socks for 7 consecutive days. Activity counts were collected in 1-min intervals (called “epochs”). During the second visit, the band was removed. Actical software (version 2.12) was used for data reduction. Only complete days (i.e., full 24-hr periods) with a daily average of 80 counts per minute were included in the analysis. For toddlers with more than 7 days of data, data were truncated after 7 days. Sleep was parsed from activity using the Sadeh algorithm (Sadeh et al., 1995). The Sadeh algorithm classifies each epoch as asleep or awake. The formula for the Sadeh algorithm is:
where PS is the probability of sleep; MW5 is the average number of activity counts during the scored epoch and a window of five epochs preceding and following the scored epoch; NAT is the number of epochs with an activity level of >50 but <100 activity counts in an 11-min window, including the scored epoch and the five epochs preceding and following the scored epoch; SD6 is the standard deviation of the activity counts during the scored epoch and the five preceding epochs; and ln(ACT) is the natural logarithm of the number of activity counts during the scored epoch + 1. If PS is >0, the epoch is scored as asleep; otherwise, it is scored as awake. Nighttime sleep was defined as the sum of 1-min sleep epochs occurring between the hours of 8 pm and 8 am the following morning. This definition of nighttime sleep was based on methods used in previous research on nighttime sleep among young children (Ma et al., 1993; Rigda, McMillen, & Buckley, 2000; So, Michael Adamson, & Horne, 2007) and recent survey research indicating that the average toddler bedtime is between 8 pm and 9 pm and awake time is between 6:30 am and 8 am (Mindell et al., 2016). The upper limits of those windows were selected to maximize the potential sleep that could reasonably be considered “nighttime.” Sedentary behavior (in minutes) was defined using previously established Actical cut points for toddlers (Hager, Gormley, et al., 2016). Cut points for counts per minute were 0–40 (sedentary), 41–2,200 (light), and ≥2,201 (MVPA). Activity cut points were only applied to epochs scored as “awake” per the Sadeh algorithm; thus, minutes of sedentary activity are separate from any daytime napping.
Data Analysis
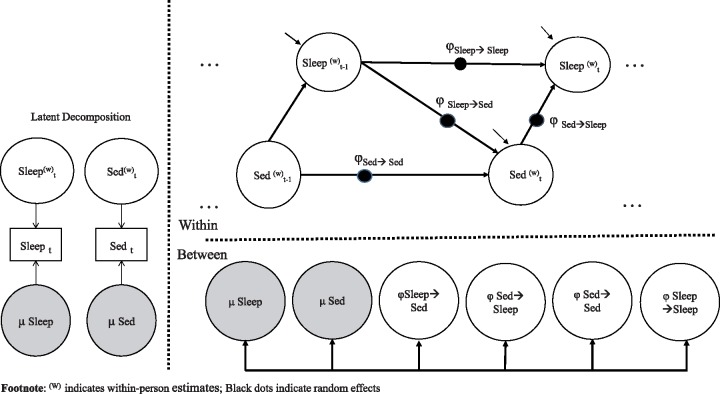
Descriptive statistics were conducted using IBM SPSS (Version 25). DSEM was conducted in Mplus Version 8.1 (Muthén & Muthén, 2015). The model was run using a Bayes full-information estimator with noninformative priors and no auxiliary variables. This approach produces results similar to full information maximum likelihood. We used 50,000 computed Markov chain Monte Carlo iterations, of which every 10th was recorded for estimation purposes. Data were assumed to be missing at random. Evidence for this assumption were based on t-tests of demographic factors associated with missingness and Little’s missing completely at random (MCAR) test. A Bayesian approach was used because it is flexible with regard to model specification and allows the bivariate model to be run simultaneously (Schuurman et al., 2016). In addition, Bayesian modeling allows for calculation of standardized regression coefficients that account for uncertainty about the new quantities, (Schuurman et al., 2016) and treats missing data as additional unknown quantities for which a posterior distribution can be estimated. Variables were parsed into latent within- and between-person components and lagged to control and estimate the impact of previous observations on subsequent outcomes (Hamaker & Wichers, 2017). An autoregressive lag-1 (AR-1) multilevel model was conducted predicting the outcomes of toddler sedentary behavior and nighttime sleep. A visual representation of the model is presented in Figure 1. It is worth clarifying the meaning of previous and current occasion, given the inherent lagged relations between nighttime sleep and next-day sedentary behavior. As an example, if the current nighttime sleep on Sunday (time “t”) is defined as sleep starting on 8 pm Sunday night to 8 am Monday morning, previous night sleep would be the previous sleep window from 8 pm Saturday night to 8 am Sunday morning (t-1; lag 1). In this example, current day at time “t” would refer to sedentary behavior on Sunday. Thus, to estimate the effects of sedentary behavior on subsequent nighttime sleep, current sleep at time “t” (on Sunday night) is regressed upon what appears to be current-day sedentary behavior at time “t” (on Sunday; lag 0), but which actually precedes sleep on Sunday night in time. To estimate cross-lagged effects of nighttime sleep on sedentary behavior, current sedentary behavior (time “t”) is regressed on nighttime sleep at the previous occasion (t-1; lag 1). The corresponding Mplus code is included in the supplementary materials (Supplementary 1).
Figure 1.
Multilevel cross-lagged autoregressive model for sedentary behavior and nighttime sleep.
Results
Data were processed from 195 Acticals. Missing Actical data (n = 82) were primarily owing to participant refusal to wear the Actical (n = 31/82, 37.8%) or having too few days to process (i.e., less than 2 full days, thus no data on nighttime sleep) (n = 38/82, 46.3.4%). The remaining missingness was owing to unexplained experimenter error (5/82, 6.1%), participants losing the Actical (3/82, 3.7%), device malfunction (3/82, 3.7%), or not having an available Actical at the time of data collection (2/82, 2.4%). T-tests revealed that demographic factors (including toddler gender, age, body mass index [BMI] z-score, maternal age, or poverty) were not associated with Actical refusal or missing Actical data (p > .05). In addition, Little’s MCAR test was nonsignificant χ2(38) = 46.795, p =.16. Toddlers in the final sample wore the Actical for an average of 5.36 days (SD = 1.76). The majority of the sample was African American (71.7%) and male (55.5%) (Table I). Seventy-eight percent of the sample reported an annual income below $30,000. Families recruited from the urban site were more likely to be African American, χ2(3) = 129.13, p < .001, and younger and report lower income (p>.05) compared with the suburban site. There were no significant recruitment site differences in toddler nighttime sleep, sedentary behavior, toddler BMI z-score, or missing data (p > .05). Baseline demographic variables are presented in Table I.
Table I.
Sample Demographics, n = 195
| Mean/% | SD | |
|---|---|---|
| Toddler age (months) | 20.3 | 5.6 |
| Toddler gender (male) | 55.4% | |
| Living at or below poverty line | 70.2% | |
| Toddler BMI z-score | 0.50 | 1.1 |
| Race/Ethnicity | ||
| African American | 71.7% | |
| Caucasian | 26.2% | |
| Other | 2.1% | |
| Days of Actical data | 5.36 | 1.72 |
| Average sedentary behavior (min) | 171.67 | 39.6 |
| Average nighttime sleep (min) | 460.23 | 85.86 |
The multilevel model unstandardized effects and variances are presented in Table II and their paths (corresponding to the associated symbols) are represented in Figure 1. The current model explained 28.7% of the within-person variability in nighttime sleep and 34.7% of the within-person variance in sedentary behavior.
Table II.
Unstandardized Effects
| B | Posterior SD | 95% CI LL | 95% CI UL | ||
|---|---|---|---|---|---|
| Means | |||||
| Sleep | μ Sleep | 468.04* | 7.31 | 453.72 | 482.45 |
| Sedentary | μ Sed | 170.81* | 3.51 | 163.95 | 177.67 |
| Slopes | |||||
| Sedentary→Sleep | ϕSed→Sleep | −0.30* | 0.11 | −0.51 | −0.09 |
| Sleep→ Sedentary | ϕSleep→Sed | −0.18* | 0.03 | −0.23 | −0.13 |
| Autoregression | |||||
| Sedentary | ϕSed→Sed | 0.17* | 0.05 | 0.07 | 0.28 |
| Sleep | ϕSleep→Sleep | 0.19* | 0.07 | 0.06 | 0.33 |
| Variances | |||||
| Sleep | Ψ μ Sleep | 2889.43* | 738.20 | 1655.89 | 4555.18 |
| Sedentary | Ψ μ Sed | 858.25* | 190.12 | 533.95 | 1284.63 |
| Sedentary→Sleep | Ψ ϕ Sed→Sleep | 0.30* | 0.12 | 0.12 | 0.58 |
| Sleep→ Sedentary | Ψ ϕ Sleep→Sed | 0.04* | 0.01 | 0.02 | 0.07 |
| Autocorrelation sleep | Ψ ϕ Sleep → Sleep | 0.20* | 0.05 | 0.12 | 0.31 |
| Autocorrelation sedentary | Ψ ϕ Sed→ Sed | 0.10* | 0.03 | 0.05 | 0.17 |
significance is based on the Credible Interval (CI) not containing zero
Attractor/Inertia Effects (Autoregression)
The multilevel AR-1 model allows researchers to estimate the average “inertia” of a variable (effect of a variable on itself from the preceding observation, lag 1) in the population, as well as for individuals in the sample. An autoregressive value close to 0 implies a strong attraction dynamic; meaning, after a high or low score, the individual will quickly recover to their equilibrium or “set point” (i.e., typical level of sleep or sedentary behavior). In contrast, an autoregressive value closer to 1 implies more carryover from one moment to the next, reflecting regulatory weakness. A child with a high sedentary autoregressive value would be likely to have several consecutive days in a row with high or low sedentary behavior above or below their set-point/equilibrium. Negative values of the autoregressive term have a different interpretation, because they imply reflexive back-and-forth shifting between scores above and below the equilibrium (called antipersistance) (De Haan-Rietdijk, Gottman, Bergeman, & Hamaker, 2016). Antipersistance might manifest as a sawtooth pattern where a night of short sleep is followed by a night of excessive sleep greater than that toddler’s typical nighttime sleep.
In the current study, the autoregressive value for sedentary behavior was both positive and significantly different from 0 (B = 0.174, 95% confidence interval [CI] .070 to 0.277) (see ϕSed→ Sed, Figure 1, Table II), indicating low carryover and no antipersistance. More specifically, sedentary behavior appears to have properties of an attractor dynamic, meaning that after a day of high or low sedentary activity, a child is likely to quickly return to his/her set point or equilibrium of typical sedentary activity the following day. This can present confusion when using standardized hypothesis testing, where regression coefficients are compared with a null value of 0. In an autoregressive model, 0 represents attraction to the set point, and no inertia. Zero is the strongest attraction an autoregressive dynamic can have. Readers are referred to Butner (2017) for a more in-depth explanation of attractors in autoregressive dynamic models.
The autoregressive value for sleep was positive and significantly different from 0 (B = 0.193, 95% CI 0.057 to 0.329) (see ϕSleep→ Sleep, Figure 1 and Table II), indicating previous night sleep predicts subsequent night sleep. Because the value is relatively close to 0, this indicates that after a night of more or less sleep than typical (i.e., a perturbation to the system), a child will return relatively quickly to their baseline “set point” on the following night.
Cross-Lagged Effects
Cross-lagged unstandardized values revealed that, on average, when comparing across individuals, toddlers with less than average nighttime sleep engaged in more sedentary behavior the following day (B = −0.178, 95% CI −0.231, −0.126) (see ϕSleep→ Sed, Figure 1 and Table II). Furthermore, sedentary behavior predicted sleep that night (B = −0.301, 95% CI −0.510 to −0.329) (see ϕSed→ Sleep, Figure 1 and Table II). Thus, overall, there was a pattern of less night sleep being followed by increased sedentary behavior the following day, in addition to increased sedentary behavior predicting decreased sleep at the next occasion.
Standardized Estimates
To compare the relative strength of cross-lagged effects and answer the question “does sleep predict next-day activity more than the reverse”, we examined the within-person standardized cross-lagged coefficient (averaged over cluster) (Schuurman et al., 2016). In the current study, the standardized effect of sedentary behavior on nighttime sleep was b = −.185 (95% CI −.278 to −.094), whereas the standardized effect of nighttime sleep on sedentary behavior was b = −.322 (95% CI −.403 to −.236). These values are standardized and averaged over cluster, indicating that in the current sample, the average within-person effect of sleep on sedentary behavior was stronger than the effect of sedentary behavior on sleep.
However, there was individual-level variation in the strength of the relationship between nighttime sleep and sedentary behavior across individuals. The standardized cross-lagged effect of nighttime sleep on sedentary was such that 95% of the Bayesian posterior draws for the average within-person effect were between −.403 and −.236, and 97% of the toddlers had a negative coefficient. The within-person standardized effect of sedentary behavior on sleep was such that 95% of the sample was expected to have a within-person effect between −.278 and −.094, and 92% of the toddlers had a negative average coefficient of sedentary behavior predicting nighttime sleep. This implies that for most toddlers in the sample, increased sedentary behavior predicts less sleep that night (and less sleep predicts more next-day sedentary behavior). However, there was significant variability around these effects. Therefore, examining the fixed effects only may be misleading. Indeed, a common criticism of single-level cross-panel designs is that they evaluate the average effects across individuals and ignore potential meaningful individual differences (Schuurman et al., 2016).
Therefore, to further investigate if nighttime sleep predicted more variability in sedentary behavior compared with the inverse (sedentary on sleep) within an individual, we examined the average cross-lagged coefficients for each individual in the sample. We calculated the proportion of the sample for whom the individual-level coefficients of nighttime sleep on sedentary were larger than the coefficients of sedentary on sleep. To compare the magnitude (separate from direction) of the relations, absolute values of the cross-lagged estimates were used to avoid negative/positive loadings potentially canceling each other out (Schuurman et al., 2016). For 89% of the current sample, the within-person standardized cross-lagged effects of nighttime sleep on sedentary behavior were larger than the cross-lagged effects of sedentary behavior on nighttime sleep. This indicates that not only is the average cross-lagged effect of nighttime sleep on sedentary behavior stronger than the cross-lagged effect of sedentary on sleep, but that this is the case for the majority of children in the sample.
Similarly, we examined the within-person standardized autoregressive coefficient (again, averaged over cluster) to compare the relative strength of the autoregressive effects and answer the question “Does sedentary behavior have more carryover compared with nighttime sleep?” Standardized within-person level autoregression estimates were .177 (95% CI .068 to .291) for sleep and .170 (95% CI .073 to .265) for sedentary behavior. To further explore the relative magnitude of the attractor/inertia dynamics, standardized autoregressive values were examined for each participant. Nighttime sleep values ranged from −.601 to .953. Absolute values in this case represent the strength of the attraction (with values closer to 0 being stronger attractors). The absolute value of autoregressive terms ranged from <.001 (very strong attractor) to .953 (weak attractor). Again, the autoregressive term being close to 1 indicates the strength of the attraction or repulsion, and the negative sign isolates if the pattern overshoots the set point in a sawtooth pattern (antipersistance) (Butner, 2017). For sleep, 14% of the sample had an autoregressive value below 0, indicating some level of antipersistance. A negative value implies that there is a set point for average nighttime sleep, but the children vacillate around their set point. Following a perturbation of sleep on a given night, sleep the following night overshoots the set point. Tangibly, this would be a night of short sleep followed by a night of relatively long sleep, but an eventual return to average baseline sleep.
For sedentary behavior, 10% of the toddlers in the sample had a negative autoregression value, indicating antipersistance. Absolute values for autoregressive estimates ranged from .002 to .546. When comparing the relative strength of the autoregressive terms, 53% of toddlers in the sample had an autoregressive value closer to 0 for nighttime sleep compared with sedentary behavior, indicating a quicker return to baseline levels following a perturbation.
Discussion
The aim of the current study was to examine and compare the strength of the bidirectional relations between nighttime sleep and sedentary behavior among toddlers. In doing this, we aimed to demonstrate the value of using a multilevel model to study Granger-causal cross-lagged relations between outcomes.
Consistent with previous literature, results indicated a bidirectional relation between nighttime sleep and sedentary activity (Chaput et al., 2017). Previous studies linking sedentary behavior to sleep have often relied on parent- or self-reported screen time as a proxy for sedentary behavior (Downing et al., 2015), and the current study builds on these results by using objective measures of sleep and sedentary behavior.
Results indicate that when toddlers have a day of high sedentary behavior, they are more likely to experience decreased nighttime sleep that night. In addition, if a toddler has less nighttime sleep, they will be more sedentary the following day. The average relation between nighttime sleep and next-day sedentary behavior was stronger than the reverse, and this was the case for the majority (89%) of toddlers in the sample. However, the strength of the relation between sleep and sedentary behavior varied across individuals.
With regard to carryover effects (i.e., inertia), both sleep and sedentary behavior showed relatively low inertia or carryover on average. However, nighttime sleep had slightly more carryover from one day to the next compared with sedentary behavior, and this was the case for the majority (53%) of toddlers in the sample. This means that if toddlers experience decreased sleep on one night, they are likely to experience some carryover the following night, but quickly return to their baseline level of sleep. Sedentary behavior had similar attractor dynamics (i.e. low inertia or carryover), meaning a deviation from typical sedentary behavior is followed by a relatively quick return to typical sedentary behavior the following day. However, significant between-person random variability around the strength of the carryover/inertia effects indicates that not all toddlers in the sample returned to their typical level of sleep or sedentary activity quickly or at the same rate. Some toddlers had relatively strong carryover from one day to the next. For toddlers with high carryover, a night of disrupted sleep is followed by continued nights of disrupted sleep before eventually returning to baseline. Furthermore, for 47% of the toddlers in the sample, sedentary behavior was actually more stable and had less carryover than sleep. The ability to capture these interindividual differences in a within-person process is an advantage of the multilevel analysis, which allows for each individual to have their own estimate of autoregression/carryover. If we were to only examine the average fixed effects of carryover (as in a cross-lagged panel model), we might erroneously conclude that sleep and sedentary behavior are relatively stable; however, this would only be true for a subset of the sample. A next step in this research could be to explain and predict these between-person differences in carryover (e.g. Why are some toddlers likely to have multiple nights of disrupted sleep while others return quickly to their baseline after disrupted sleep? And are toddlers with higher carryover (i.e., regulatory weakness) more likely to become overweight?).
The current article builds on intensive longitudinal models published in the Journal of Pediatric Psychology by Cushing et al. (Cushing, Brannon, Suorsa, & Wilson, 2014; Cushing et al., 2017). Like Cushing et al. (2017), the current study examined sedentary behavior (which is often understudied) and modeled within- and between-person variability. The current study extends these findings by examining multiple outcomes in a unified model that accounts for autoregression. Therefore, the cross-lagged effects in the current study can be interpreted as the effect of nighttime sleep on sedentary behavior (or vice versa) accounting for the previous occasions.
In addition, the current study demonstrates a method by which to compare the relative strength of both cross-lagged and autoregressive paths. In substantive terms, we were able to detect that, averaged across individuals, nighttime sleep had slightly more carryover or inertia from one day to the next compared with sedentary behavior. We can interpret this inertia term as a dynamic trend such that when nighttime sleep is perturbed from a toddler’s set point, poor sleep will carry over into following nights before eventually returning to equilibrium. Future research can use the DSEM technique to model this inertia to ask questions about the length or magnitude of these hypothetical cycles (i.e., how long do bouts of disrupted sleep typically last) as well as questions about individual differences that predict inertia (i.e., What characteristics are associated with a child who has more difficulty recovering from a night of decreased sleep?).
The current study is novel in several ways. A strength of the current study is the objective (accelerometer) methods to measure sleep and sedentary behavior, a method that is underutilized in pediatric psychology literature (Cushing et al., 2014). Furthermore, sleep and sedentary behavior in toddlers are often understudied topics (Downing et al., 2015). The study is further unique in that it treats accelerometer data as intensive longitudinal data, and directly compares the bidirectional cross-lagged effects between the multiple outcomes of sleep and sedentary behavior simultaneously in a unified autoregressive model.
The current study suggests that sleep and sedentary behavior are dynamically linked. If results are replicated, it suggests that interventions to address nighttime sleep may be influential for reduction of sedentary behavior and vice versa. Providers should be aware of this potential relationship especially in the context of assessing sleep. In addition to asking parents during toddler checkups about toddler sleep quality and duration, amount of sedentary behavior, such as screen time, may be important to assess as well. More specifically, if toddlers are having sleep problems, it may help to assess screen time and other sedentary behaviors. Many healthy sleep practices can help to achieve age-appropriate amounts of sleep, including having a consistent bedtime routine and removing screens from children’s bedrooms (Mindell, Li, Sadeh, Kwon, & Goh, 2015). Incorporating such strategies to target sleep may prove beneficial in the context of obesity interventions to reduce sedentary behavior. Ensuring that toddlers get adequate nighttime sleep may reduce sedentary behavior and help maintain a healthy weight. Similarly, if toddlers are partaking in less sedentary behavior and screen time, they may obtain adequate nighttime sleep duration (Ikeda, Kaneita, Kondo, Itani, & Ohida, 2012; Magee et al., 2014). Ultimately, the link between nighttime sleep and sedentary behavior may help explain findings linking sleep and obesity in young children (Busto-Zapico et al., 2014; Magee et al., 2014; Taveras et al., 2008).
Conclusions from the current study should be interpreted in the context of several limitations. Standardized comparison of cross-lagged effects shows that a parameter is statistically stronger, but not more important. Therefore, it is not clear from such a model that manipulation of nighttime sleep would necessarily lead to change in sedentary behavior. In addition, the current study used only up to 7 days of data. More time points are needed to directly examine trends or cycles in future studies (Schultzberg & Muthén, 2017). The current study had data loss as a result of participant refusal to wear the Actical. Although we used novel strategies to minimize data loss (i.e., using nonremovable bands and waterproof accelerometers), there may be additional strategies (i.e., incentives based on Actical days of wear) to maximize data retention in community samples. Although no demographic variables were related to participant refusal to wear the Actical, future research should strive to maintain greater data retention. Alternative multiple imputation strategies and auxiliary variable approaches may also be helpful (Enders, 2017; Graham, 2003) in light of emerging literature regarding multiple imputation in multilevel models with random slopes. In addition, the current study did not directly examine the impact of daytime napping. Although estimations of sedentary activity were separate from daytime sleep, daytime naps represent a portion of the movement continuum. Future studies can use the DSEM model to examine the dynamics of toddler napping behaviors as they relate to physical activity and nighttime sleep.
Given the novelty of the DSEM models used in the current study, several unresolved issues warrant consideration. An initial consideration is that the strength of lagged relationships depends on the interval between observations (Gollob & Reichardt, 1987), meaning that future studies may reach different conclusions about the reciprocal nature and the “causal dominance” of nighttime sleep and sedentary behavior, depending on the interval of time selected. This phenomenon (known as the “lag problem”) implies that simply because we modeled sedentary behavior and nighttime sleep at the level of a single day, it does not mean that the variables necessarily exert an influence on each other only at this interval (Hamaker, Asparouhov, Brose, Schmiedek, & Muthén, 2018). Different conclusions might be reached if researchers examine the dynamics between activity and sleep within a single day (i.e., does morning nap influence sedentary activity that afternoon).
Another way in which estimating dynamic relations can be complicated is through the presence of cycles (Liu & West, 2016). There may be monthly, weekly, and daily movements up and down in nighttime sleep and sedentary behavior, which could have led to spurious lagged relationships between variables. The VAR(1) model used in the current study assumes stationarity, that the dynamics between variables remain stable (Bringmann, Ferrer, Hamaker, Borsboom, & Tuerlinckx, 2018). However, this may not necessarily be the case when cycles exist. This might be particularly relevant for nighttime sleep and activity, given the potential effects of weekend/weekday cycles, seasonality, and developmental changes. Indeed, the current study did not examine cycles or trends (owing to limited sample size), which may have impacted results. More advanced time-varying-vector-autoregressive models (Bringmann et al., 2018) could be used to explore such potential trends and cycles in future studies. Ultimately, additional developments in the emergent area of dynamic systems modeling could impact current interpretation of study results in the future.
Passive sensors such as accelerometers can provide objective data with limited participant burden. Because passive sensors allow multiple points of data for a given individual, they can be treated as intensive longitudinal data (rather than collapsed to a single point across time). Although the current study only examined nighttime sleep, accelerometry can be used to measure additional aspects of sleep (i.e. sleep efficiency and sleep latency) that may be related to activity. The use of DSEM in pediatric research for intensive longitudinal data allows us to answer questions about the relative strength of bidirectional relations such as those between nighttime sleep and sedentary behavior. Future studies can use DSEM methods to predict autoregression (inertia) or model it as an independent variable (i.e., does high carryover for nighttime sleep predict weight gain). The present study is an example of how DSEM methods can be used to ask questions about Granger-causal cross-lagged relations between variables, both within and between individuals. Such methods can ideally inform personalized interventions in the future.
Funding
This work was supported by National Heart, Lung, and Blood Institute (F32-HL138963), the U.S. Department of Agriculture (grant no. CREES 2005-4808), and the Eunice Kennedy Shriver National Institute of Child Health and Human Development (R01-HD056099).
Supplementary Data
Supplementary data can be found at: https://academic.oup.com/jpepsy.
Conflicts of interest: None declared.
Supplementary Material
References
- Acebo C., Sadeh A., Seifer R., Tzischinsky O., Hafer A., Carskadon M. A. (2005). Sleep/wake patterns derived from activity monitoring and maternal report for healthy 1-to 5-year-old children. Sleep, 28, 1568–1577. [DOI] [PubMed] [Google Scholar]
- Asparouhov T., Hamaker E. L., Muthén B. (2018). Dynamic structural equation models. Structural Equation Modeling: A Multidisciplinary Journal, 25, 359–388. [Google Scholar]
- Bernier A., Bélanger M.-È., Bordeleau S., Carrier J. (2013). Mothers, fathers, and toddlers: Parental psychosocial functioning as a context for young children’s sleep. Developmental Psychology, 49, 1375.. [DOI] [PubMed] [Google Scholar]
- Berry D., Willoughby M. T. (2017). On the practical interpretability of cross‐lagged panel models: Rethinking a developmental workhorse. Child Development, 88, 1186–1206. [DOI] [PubMed] [Google Scholar]
- Bringmann L. F., Ferrer E., Hamaker E. L., Borsboom D., Tuerlinckx F. (2018). Modeling nonstationary emotion dynamics in dyads using a time-varying vector-autoregressive model. Multivariate Behavioral Research, 53, 293–314. [DOI] [PubMed] [Google Scholar]
- Busto-Zapico R., Amigo-Vázquez I., Peña-Suárez E., Fernández-Rodríguez C. (2014). Relationships between sleeping habits, sedentary leisure activities and childhood overweight and obesity. Psychology, Health and Medicine, 19, 667–672. [DOI] [PubMed] [Google Scholar]
- Butner J. (2017). Quantitative reasoning under a dynamical social science: Licensed under creative commons. Retrieved from http://systems.psych.utah.edu/quantitative-butner.html.
- Chaput J.-P., Gray C. E., Poitras V. J., Carson V., Gruber R., Birken C. S., MacLean J. E., Aubert S., Sampson M., Tremblay M. S. (2017). Systematic review of the relationships between sleep duration and health indicators in the early years (0–4 years). BMC Public Health, 17, 855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cushing C. C., Brannon E. E., Suorsa K. I., Wilson D. K. (2014). Systematic review and meta-analysis of health promotion interventions for children and adolescents using an ecological framework. Journal of Pediatric Psychology, 39, 949–962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cushing C. C., Mitchell T. B., Bejarano C. M., Walters R. W., Crick C. J., Noser A. E. (2017). Bidirectional associations between psychological states and physical activity in adolescents: A mHealth pilot study. Journal of Pediatric Psychology, 42, 559–568. [DOI] [PubMed] [Google Scholar]
- De Haan-Rietdijk S., Gottman J. M., Bergeman C. S., Hamaker E. L. (2016). Get over it! A multilevel threshold autoregressive model for state-dependent affect regulation. Psychometrika, 81, 217–241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Downing K. L., Hnatiuk J., Hesketh K. D. (2015). Prevalence of sedentary behavior in children under 2 years: A systematic review. Preventive Medicine, 78, 105–114. [DOI] [PubMed] [Google Scholar]
- Enders C. K. (2017). Multiple imputation as a flexible tool for missing data handling in clinical research. Behaviour Research and Therapy, 98, 4–18. [DOI] [PubMed] [Google Scholar]
- Galland B. C., Kennedy G. J., Mitchell E. A., Taylor B. J. (2012). Algorithms for using an activity-based accelerometer for identification of infant sleep–wake states during nap studies. Sleep Medicine, 13, 743–751. [DOI] [PubMed] [Google Scholar]
- Girschik J., Fritschi L., Heyworth J., Waters F. (2012). Validation of self-reported sleep against actigraphy. Journal of Epidemiology, 22, 462–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gollob H. F., Reichardt C. S. (1987). Taking account of time lags in causal models. Child Development, 58, 80–92. [PubMed] [Google Scholar]
- Graham J. W. (2003). Adding missing-data-relevant variables to FIML-based structural equation models. Structural Equation Modeling, 10, 80–100. [Google Scholar]
- Granger C. W. (1969). Investigating causal relations by econometric models and cross-spectral methods. Econometrica: Journal of the Econometric Society, 37, 424–438. [Google Scholar]
- Gubbels J., Van Kann D., Cardon G., Kremers S. (2018). Activating childcare environments for all children: The importance of children’s individual needs. International Journal of Environmental Research and Public Health, 15, 1400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hager E. R., Calamaro C. J., Bentley L. M., Hurley K. M., Wang Y., Black M. M. (2016). Nighttime sleep duration and sleep behaviors among toddlers from low-income families: Associations with obesogenic behaviors and obesity and the role of parenting. Childhood Obesity, 12, 392–400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hager E. R., Gormley C. E., Latta L. W., Treuth M. S., Caulfield L. E., Black M. M. (2016). Toddler physical activity study: Laboratory and community studies to evaluate accelerometer validity and correlates. BMC Public Health, 16, 936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamaker E., Asparouhov T., Brose A., Schmiedek F., Muthén B. (2018). At the frontiers of modeling intensive longitudinal data: Dynamic structural equation models for the affective measurements from the COGITO study. Multivariate Behavioral Research, 1–22. 10.1080/00273171.2018.1446819. [DOI] [PubMed] [Google Scholar]
- Hamaker E., Kuiper R. M., Grasman R. P. (2015). A critique of the cross-lagged panel model. Psychological Methods, 20, 102–16. [DOI] [PubMed] [Google Scholar]
- Hamaker E., Wichers M. (2017). No time like the present: Discovering the hidden dynamics in intensive longitudinal data. Current Directions in Psychological Science, 26, 10–15. [Google Scholar]
- Hirshkowitz M., Whiton K., Albert S. M., Alessi C., Bruni O., DonCarlos L., Hazen N., Herman J., Katz E. S., Kheirandish-Gozal L., Neubauer D. N., O'Donnell A. E., Ohayon M., Peever J., Rawding R., Sachdeva R. C., Setters B., Vitiello M. V., Ware J. C., Adams Hillard P. J. (2015). National Sleep Foundation’s sleep time duration recommendations: methodology and results summary. Sleep Health, 1, 40–43. [DOI] [PubMed] [Google Scholar]
- Ikeda M., Kaneita Y., Kondo S., Itani O., Ohida T. (2012). Epidemiological study of sleep habits among four-and-a-half-year-old children in Japan. Sleep Medicine, 13, 787–794. [DOI] [PubMed] [Google Scholar]
- Jones R. A., Hinkley T., Okely A. D., Salmon J. (2013). Tracking physical activity and sedentary behavior in childhood: A systematic review. American Journal of Preventive Medicine, 44, 651–658. [DOI] [PubMed] [Google Scholar]
- Krietsch K. N., Armstrong B., McCrae C. S., Janicke D. M. (2016). Temporal associations between sleep and physical activity among overweight/obese youth. Journal of Pediatric Psychology, 41, 680–691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuzik N., Carson V. (2016). The association between physical activity, sedentary behavior, sleep, and body mass index z-scores in different settings among toddlers and preschoolers. BMC Pediatrics, 16, 100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuzik N., Poitras V. J., Tremblay M. S., Lee E.-Y., Hunter S., Carson V. (2017). Systematic review of the relationships between combinations of movement behaviours and health indicators in the early years (0-4 years). BMC Public Health, 17, 849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee E.-Y., Hesketh K. D., Hunter S., Kuzik N., Rhodes R. E., Rinaldi C. M., Spence J. C., Carson V. (2017). Meeting new Canadian 24-hour movement guidelines for the early years and associations with adiposity among toddlers living in Edmonton, Canada. BMC Public Health, 17, 840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y., West S. G. (2016). Weekly cycles in daily report data: an overlooked issue. Journal of Personality, 84, 560–579. [DOI] [PubMed] [Google Scholar]
- Ma G., Segawa M., Nomura Y., Kondo Y., Yanagitani M., Higurashi M. (1993). The development of sleep-wakefulness rhythm in normal infants and young children. The Tohoku Journal of Experimental Medicine, 171, 29.. [DOI] [PubMed] [Google Scholar]
- Magee C., Caputi P., Iverson D. (2014). Lack of sleep could increase obesity in children and too much television could be partly to blame. Acta Paediatrica, 103, e27–31. [DOI] [PubMed] [Google Scholar]
- Mindell J. A., Leichman E. S., Composto J., Lee C., Bhullar B., Walters R. M. (2016). Development of infant and toddler sleep patterns: Real‐world data from a mobile application. Journal of Sleep Research, 25, 508–516. [DOI] [PubMed] [Google Scholar]
- Mindell J. A., Li A. M., Sadeh A., Kwon R., Goh D. Y. (2015). Bedtime routines for young children: A dose-dependent association with sleep outcomes. Sleep, 38, 717–722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mindell J. A., Meltzer L. J., Carskadon M. A., Chervin R. D. (2009). Developmental aspects of sleep hygiene: Findings from the 2004 National Sleep Foundation Sleep in America Poll. Sleep Medicine, 10, 771–779. [DOI] [PubMed] [Google Scholar]
- Muthén L., Muthén B. (Eds.), (2015). Mplus. (Vol. 5). Los Angeles, CA: Muthén & Muthén. [Google Scholar]
- Pfeiffer K. A., Mciver K. L., Dowda M., Almeida M. J., Pate R. R. (2006). Validation and calibration of the Actical accelerometer in preschool children. Medicine and Science in Sports and Exercise, 38, 152–157. [DOI] [PubMed] [Google Scholar]
- Quante M., Kaplan E. R., Rueschman M., Cailler M., Buxton O. M., Redline S. (2015). Practical considerations in using accelerometers to assess physical activity, sedentary behavior, and sleep. Sleep Health: Journal of the National Sleep Foundation, 1, 275–284. [DOI] [PubMed] [Google Scholar]
- Rigda R., McMillen I., Buckley P. (2000). Bed sharing patterns in a cohort of Australian infants during the first six months after birth. Journal of Paediatrics and Child Health, 36, 117–121. [DOI] [PubMed] [Google Scholar]
- Sadeh A., Acebo C., Seifer R., Aytur S., Carskadon M. A. (1995). Activity-based assessment of sleep-wake patterns during the 1st year of life. Infant Behavior and Development, 18, 329–337. [Google Scholar]
- Santos R., Zhang Z., Pereira J. R., Sousa-Sá E., Cliff D. P., Okely A. D. (2017). Compliance with the Australian 24-hour movement guidelines for the early years: Associations with weight status. BMC Public Health, 17, 867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schultzberg M., Muthén B. (2017). Number of subjects and time points needed for multilevel time-series analysis: A simulation study of dynamic structural equation modeling. Structural Equation Modeling: A Multidisciplinary Journal, 25, 1–21. [Google Scholar]
- Schuurman N. K., Ferrer E., de Boer-Sonnenschein M., Hamaker E. L. (2016). How to compare cross-lagged associations in a multilevel autoregressive model. Psychological Methods, 21, 206–21. [DOI] [PubMed] [Google Scholar]
- So K., Michael Adamson T., Horne R. S. (2007). The use of actigraphy for assessment of the development of sleep/wake patterns in infants during the first 12 months of life. Journal of Sleep Research, 16, 181–187. [DOI] [PubMed] [Google Scholar]
- Taveras E. M., Rifas-Shiman S. L., Oken E., Gunderson E. P., Gillman M. W. (2008). Short sleep duration in infancy and risk of childhood overweight. Archives of Pediatrics and Adolescent Medicine, 162, 305–311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tremblay M. S., LeBlanc A. G., Kho M. E., Saunders T. J., Larouche R., Colley R. C., Goldfield G., Gorber S. (2011). Systematic review of sedentary behaviour and health indicators in school-aged children and youth. International Journal of Behavioral Nutrition and Physical Activity, 8, 98.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- US Census Bureau. (2009). Poverty thresholds. Retrieved from https://www.census.gov/data/tables/time-series/demo/income-poverty/historical-poverty-thresholds.html
- Vijakkhana N., Wilaisakditipakorn T., Ruedeekhajorn K., Pruksananonda C., Chonchaiya W. (2015). Evening media exposure reduces night‐time sleep. Acta Paediatrica, 104, 306–312. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.