A simple empirical algorithm for optimising depletion power and resolution for dye and system specific STED imaging

Summary

Here we show an easy method for determining an effective dye saturation factor (‘P_STED’) for STED (Stimulated Emission Depletion) microscopy. We define P_STED to be a combined microscope system plus dye factor (analogous to the traditional ground truth I_s measurement, which is microscope independent) that is functionally defined as the power in the depletion beam that provides a resolution enhancement of 41% compared to confocal, according to the modified Abbe’s formula for STED resolution enhancement. We show that the determination of P_STED provides insight not only into the suitability of a particular dye and the best imaging parameters to be used for an experiment, but also sets the critical value for correctly determining the point spread function (PSF) used in deconvolution of STED images. P_STED can be a function of many experimental variables, both microscope and sample related. Here we show the utility of doing P_STED determinations by (1) exploiting the simple relationship between width and a threshold-defined area provided by a Gaussian PSF, for either linear or spherical objects and (2) linearising the normally inverse hyperbolic function of resolution versus power that can determine P_STED. We show that this rearrangement allows us to determine P_STED using only a few measurements: either at a few relatively low depletion powers, on traditional bead size measurements or by finding the total area of a naturally occurring sub-limit sized biological feature (in this case, microtubules). We show the derivation of these equations and methods and the utility of its use by characterising several dyes and a local imaging parameter relevant to STED microscopy. This information is used to predict the enhancement of resolution of the point spread function necessary for post-processing deconvolution.

Introduction

STED microscopy is a powerful super-resolution imaging technique for cellular biology. Resolution improvements of 8- to 10-fold over conventional imaging methods are now routinely realised, and the commercialisation of STED microscopes has put the technique in the hands of more and more biologists (for recent reviews see (Bianchini et al., 2015; Revelo & Rizzoli, 2015; Blom & Widengren, 2017; Roobala et al., 2018; Vicidomini et al., 2018). Even with these very ‘user accessible nanoscopes’, it is important to optimise many parameters to achieve the best results (Leutenegger et al., 2010; Galiani et al., 2012; Hebisch et al., 2017; Merino et al., 2017). These include choice of proper fluorophore and the selection of optimal STED laser and detection parameters. One must also adjust depletion powers for the desired resolution, while simultaneously preserving signal to noise ratio and avoiding excessive photo-bleaching, particularly for live cell imaging. Many microscopes also allow for emission time-gating; this requires one to choose the optimal window to collect the emission signal after excitation (gating is primarily influential when using continuous wave lasers for depletion) (Moffitt et al., 2011; Vicidomini et al., 2013; Vicidomini et al., 2014).

Optimisation of many of these parameters will often depend on sample properties and the dye in situ environmental conditions that are unchangeable or can only be adjusted in a non-precise manner. Post-processing through deconvolution of STED images can improve signal to noise and achievable resolution (Donnert et al., 2007; Zanella et al., 2013). Proper deconvolution requires a precise understanding of the point- spread-function found at a given depletion power and system settings - a shape which is often poorly extrapolated from idealised conditions. As pointed out by Barentine et al. (2018), the characteristics of sub-resolution beads make them ‘a poor proxy for the true resolution achieved when imaging cellular samples’ (Barentine et al., 2018). They took many cross section profiles of microtubules and developed a sophisticated algorithm for thereby determining the ultimate resolution limits. Instead, we suggest a simple algorithm - one that relies on taking just a few measurements - that enables quantification of the saturation factor in a STED experiment for two purposes: (1) giving feedback to the operator who is optimising imaging parameters and (2) providing the proper empirical parameter for optimal midrange (to the size of the calibration standard used) deconvolution of STED images.

To understand the proposed algorithm, it is necessary to define the STED saturation factor and the way STED depletion power determines resolution. The parameter I_s was first defined as the Stimulated Emission Depletion beam laser power required to deplete emission to a level of 50% (Harke et al., 2008). A combination of that purely photophysical parameter with specifics of the ‘donut’ beam architecture leads to the following super-resolution Eq. (1):

$$d=\mathbf{lambda}/\left(\mathbf{2}\mathbf{NA}\surd (\mathbf{1}+{\mathbf{STED}}_{\mathbf{sat}})\right),$$ (1)

where d is the idealised optical resolution, lambda is the observed wavelength, NA is the numerical aperture of the objective and STED_sat is the saturation factor. This differs from the classic Abbe’s formula only via nonzero STED_sat. The saturation factor is defined as:

$${\mathbf{STED}}_{\mathbf{sat}}=I/I_S.$$ (2)

Thus, d = d(confocal)/1.41 when I_STED = I_s (where I_STED is the power of the depletion beam). In this sense I_s is a ‘ground truth’ value for a dye under idealised conditions. In this work we define the term P_STED to be a practical or apparent Is that is dependent on microscope performance, user defined settings, and local sample conditions:

$${\mathbf{STED}}_{\mathbf{sat}}=P/P_{\mathbf{STED}}.$$ (3)

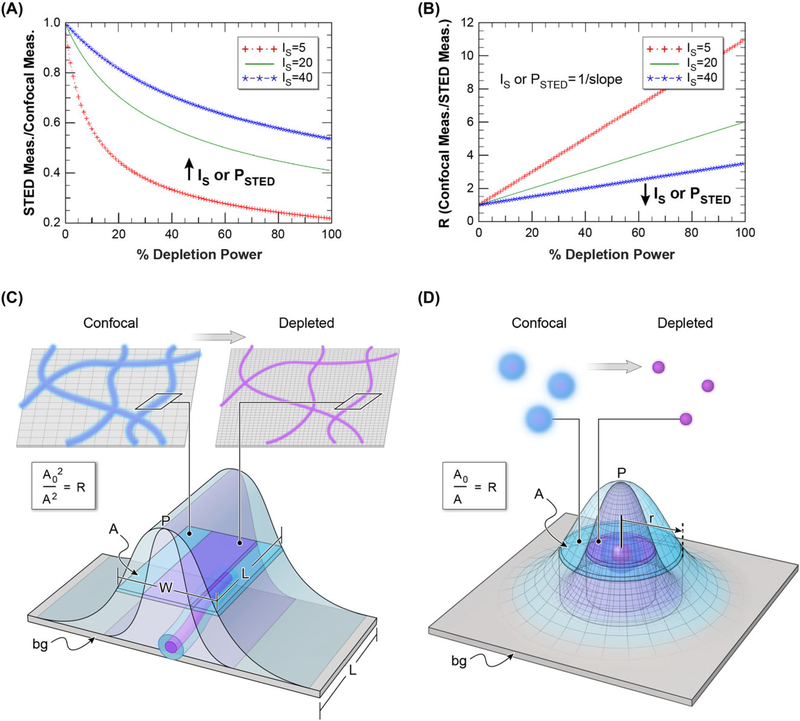
The proportional relationship of photophysical I_s (determined by stimulated emission cross section) to the apparent I_s (P_STED) depends largely on the particular electric field configuration of the donut near focus; their mutual constants for an ideal quadratic intensity donut are defined in Harke et al. (2008). The relationship between depletion power and resolution is also shown in Figure 1(A). Rearranging this PSF reduction formula, we can determine P_STED simply by rearranging the relationship of STED resolution (as a function of total depletion power) to diffraction limited confocal resolution (d_con>) in Eq. (1):

$$\begin{gathered} d/d_{\text{con}}=1/\surd (1+P/P_{\text{STED}})=> \\ R={\left(d_{\mathbf{con}}/d\right)}^{\wedge }2=1+P/P_{\mathbf{STED}}, \end{gathered}$$ (4)

where we define R as the STED ‘linearised ratio’. This relationship of R to STED depletion power is shown in Figure 1(B) where 1/slope = P_STED. Note we use P_STED, the effective I_s, based on in situ conditions for the sample, system settings (like emission time-gating) and optical nanoscope performance. This rearrangement of the fundamental STED equation shown in Eq. (4) simplifies the measurement of P_STED and related parameter STED_sat.

Fig. 1.

Graphical representation of the linearisation of the STED power versus resolution relationship. (A) STED depletion power versus resolution according to Eq. (1). Resolution here is defined as the apparent decrease in the size of a sub-diffraction sized object compared to a confocal image. P_STED is defined as the system specific STED saturation factor and varies as a function of dye or fluorescent protein and other imaging parameters such as depletion laser wavelength and emission time gating (shown in Figure 5). Lower values of P_STED indicate less STED laser depletion power is necessary to produce super-resolution images. (B) The linearisation of the power versus resolution shown in (A)where R is defined according to Eq. (4). This simple linearisation method allows for the easy determination of P_STED (the slope of the relationship between R and depletion power) with just a few measurements at low depletion powers (A). (C) Figure showing the relationship between area measurements of a line (such as microtubules) and the calculation of R as a function of increasing resolution with STED depletion. For lines the increasing resolution will result in decreased width whereas length is unchanged. Thus, R is not proportional to width × length but is instead proportional to total areâ2 (confocal areâ2/STED areâ2, or Bo/B). (D) Figure showing the relationship between area of a circular object (such as a bead) and the calculation of R. For punctate circular objects area is directly proportional to dimension squared; therefore, R is simply the ratio of areas (confocal area/STED area).

Traditionally, the measurement of STED_sat has been done by either exposing uncomplexed probes in solution to carefully matched coaxial Gaussian depletion beams or by directly examining the (Eq. (1) based) curve of STED depletion power to the apparent size of individual, fluorescently labelled subresolution beads. Although direct fitting to PSF data often preserves simple numerical weighting, the latter method is not always practical, due to the competing needs for high signal to noise images of the beads - for maintaining precise ‘size’ fitting - and concomitant fragility of the beads at high laser powers (both excitation and depletion). Further, one often cannot tell if the puncta being observed are made of single objects (vs. groups of two or more) until large powers are used. As shown in Figure 1, both puncta (beads) and sub resolution fibrous structures (like microtubules) can be used in the rearranged (linearised) method, when the threshold-defined area is employed. For subresolution fibrous targets, the ‘squeezable’ dimension D is obtained by using area to determine the average width of the ‘line’, since that width profile arises from the same approximate Gaussian one would obtain from a point object. Traditionally, FWHM (fraction = 0.5) is used to describe resolution. Once thresholded pixels are ‘tagged’, the Area Occupied A by the tagged (e.g., within FWHM) pixels can be used to obtain D values for the linear plot (see Fig. 1 for graphic representation of this process). In the case of uniformly well labelled, mostly linear, fibrous targets that are thin compared to confocal resolution Dc, the Area value is the product of D and the total length of the fibre in view, L. L is, of course, an un-known, but importantly, does not change with illumination. With area A = L × D, the needed (Dc/D)² value for the desired Eq. (4) plot is just the linearised ratio R = (Ac/A)². In a fashion, we are carrying out a wide line-profile averaging across the tubule as suggested in Barentine et al. (2018), except we are doing it by area rather than by doing many local fits. In contrast, punctate object area already contains the square of the squeezable dimension D; $A=\mathrm{\Sigma }{\text{pi}}^{*}{(D/2)}^2$ in that case (summed over all puncta). Hence the relationship for the linearised ratio parameter R is (Ac/A)² for fibre and is just (Ac/A) for punctate objects. Thus, plots of either type of area-derived R term above versus applied depletion power will yield lines whose intercepts are 1 and the slope is equal to 1/P_STED.

To test this relationship and simple algorithm, we measured P_STED for several dyes and different imaging conditions using the apparent reduction in signal area of fluorescently labelled subresolution beads and a natural structure (microtubules labelled by immunofluorescence in fixed DAOY cells) caused by a range of STED depletion powers, when compared to confocal imaging of the same field of view. We show that simple fitting of the subsequent curves following this linearisation method allows for a rapid, practical determination of P_STED, and subsequently STED_sat, for different fluorophores under different imaging conditions. We also show the utility of this measurement for correct deconvolution of STED images.

Methods

Sample preparation

Microtubules (MT) were visualised by immunofluorescence on fixed cells cultured on cover glass. DAOY human medulloblastoma cells were obtained from ATCC (Manassas, VA, USA), and cultured in DMEM media supplemented with 10% foetal bovine serum and penicillin/streptomycin, and grown at 3 7°C, in water saturated 5% CO₂. Cells were plated on #1.5 cover glass and allowed to attach and spread. When desired, the media was removed, cells washed with PBS, and fixed with −20°C methanol for 5 minutes. Methanol was removed and cells rehydrated with PBS for 5 minutes at room temperature. Fixed cells were blocked with 2 g L⁻¹ BSA in TBS and exposed to antialpha tubulin antibody (DM1A, Sigma Chemical Co, St Louis, MO, USA), diluted 1–1000 in BSA/TBS overnight at 4°C with rocking. Cells were washed 3 × 5’ with TBS, and exposed to antimouse secondary antibody labelled with various fluorophores (Life Technologies/ThermoFisher, Carlsbad, CA, USA) diluted 1–1000 in BSA/TBS for 1 hr with rocking. Cover glasses were drained, and mounted with ProLong Diamond (Invitrogen/Molecular Probes, Eugene, OR, USA).

Image acquisition and analysis

All images were acquired using a Leica SP8 3× STED microscope, a white-light laser for fluorescence excitation (470–670 nm), time-gated hybrid-PMTs, and a Leica 100 × (1.4 N.A.) STED White objective (Leica Microsystems, Inc., Wetzlar, Germany). ATTO 594 labelled beads and Alexa 594 labelled DAOY cells (microtubules) were imaged with 594 nm excitation, a 600–760 nm emission bandpass and 775 nm depletion from a pulsed laser (80 mHz). Beads labelled with Alexa 488 were imaged with 488 excitation, a 500–580 nm emission bandpass, and 592 nm (continuous wave) depletion. All beads used in this work were purchased from Gattaquant GMBH (Hiltpoltstein, Germany). Time-gating of the emission signal from the PMT was set to a range of 0.7–6.5 ns for experiments involving the 775 nm depletion laser, and to 1.0 or 1.5–6.5 ns for the 592 nm depletion laser.

Image processing was performed using the software program Metamorph (Molecular Devices, San Jose, CA, USA), or using custom-written programs in the IDL software language. Bead size measurements were performed using in-house programs written in the IDL software language (Harris Geospatial Solutions, Reston, VA, USA) by generating a maximum image projection from a stack z-stack through the beads (interslice distance set to 0.1 μm) and fitting each bead measured by a 2D Gauss function in IDL after thresholding to a value of the average of a background ROI plus 3× its standard deviation. For area measurements of beads, the threshold was set to 40% of the maximum of the signal. This was done to reduce the chance of including noise into the measurement and our simulations (not shown, but available upon request) demonstrated that thresholds lying between 20% and 80% do not significantly degrade the accuracy of the measurement. Nevertheless, we suggest the range 40–60% leads to the best accuracy. Bead size measurements after deconvolution (Hyugens, Scientific Volume Imaging B.V., the Netherlands) assuming an ‘idealised STED point spread function’, where noise was much reduced, were performed on many beads simultaneously using the stand-alone program PSFj (Knop Lab, http://www.knoplab.de/psfj/). MT area measurements were made using the software program Metamorph (Molecular Devices, San Jose, CA, USA) where the threshold was typically set to a value between the average of a background ROI plus 3× its standard deviation and a maximal value that did not provide loss of true MT fluorescence signal.

Results

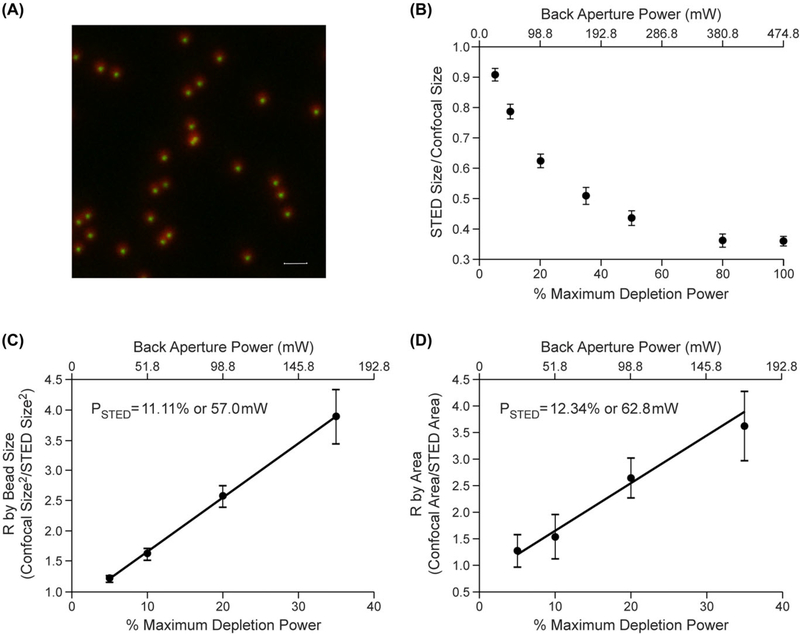
Figure 2 shows an image highlighting the decrease in apparent bead size with and without STED depletion for 20 nm sized beads labelled with the fluorescent dye ATTO 594. The measured size difference (expressed as a ratio with confocal) is graphically shown in 2B over a range of depletion power levels. This empirical relationship closely matches the function predicted by Eq. (1) that is simulated in Figure 1(A). For the same objects, Figures 2(C) and 2(D) display the linearisation method outlined in Eq. (4) and graphically shown in Figure 1(B) of R versus depletion power as measured from bead size (FWHM) and bead Area respectively. The slopes (and calculated P_STED) closely match, confirming that both linear measurements squared and the direct area measurements are valid ways of measuring P_STED (outlined in Eq. (4)). In both cases, the slopes remained highly linear over the range measured.

Fig. 2.

Example of measurement of P_STED using apparent size or total area measurement of a sub-resolution bead using the linearisation method. (A) Overlay image of the maximum image projection (MIP) from image stacks of 20 nm beads labelled with ATTO594 with 0% and 80% STED depletion power (775 nm pulsed laser). The scale bar represents 1 μm. (B) Ratio of STED depleted to confocal measured bead sizes as a function of depletion power (n = 10 to 14 individual bead measurements at each power) empirically showing the relationship outlined in Eq. (1). (C) P_STED measured from the reciprocal of the slope of the relationship of R versus depletion power as measured by bead size (FWHM). (D) The data from Figure 2 (C) linearised according to Eq. (3). P_STED was calculated from the reciprocal of the slope of the fitted line (R² > 0.99) in Figure 3(C). All error bars represent 1 standard deviation.

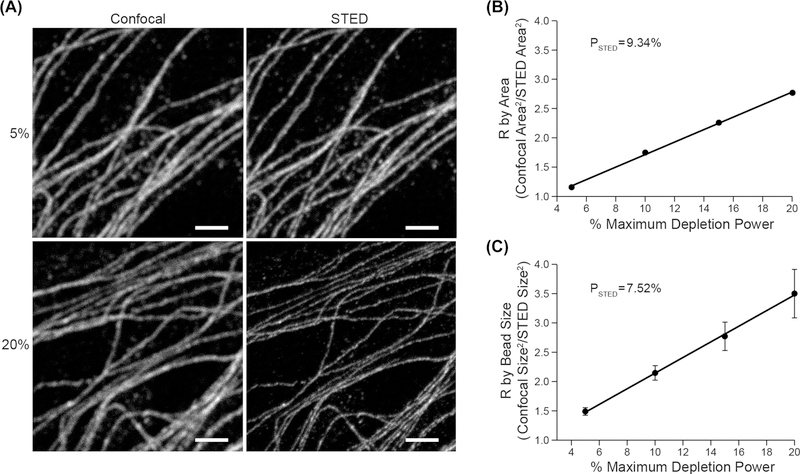
Figure 3(A) shows confocal and STED images of tubulin labelled with ALEXA 594 in DAOY cells over a range of depletion power levels. Figure 3(B) shows the linearisation method of determining P_STED by plotting R (as calculated for fibrous samples outlined above, i.e. area squared ratio) versus depletion power level. Figure 3(C) shows this same relationship as measured on Alexa 594 labelled sub-resolution beads. Note that the two calculated P_STED values as measured for the MT’s and the beads are again closely matched.

Fig. 3.

Example of measurement of P_STED using the apparent total area measurement of a subresolution naturally occurring cellular structure and the linearisation method. (A) Paired confocal and STED images of microtubules in DAOY cells labelled with Alexa 594 at two STED depletion powers (775 nm pulsed laser). Note the apparent size and area decrease as a function of depletion power. Scale bar represents 2 μm. (B) R as a function of STED depletion power (from Eq. (3)) as measured by total microtubule area for DAOY cells labelled with Alexa 594. (C). R as a function of STED depletion power and bead size (FWHM) for subresolution (approx. 20 nm) size Alexa 594 labelled beads. P_STED was calculated from the reciprocal of the slope of the fitted line (R² = 0.99) in B and C. Error bars in C represent 1 standard deviation.

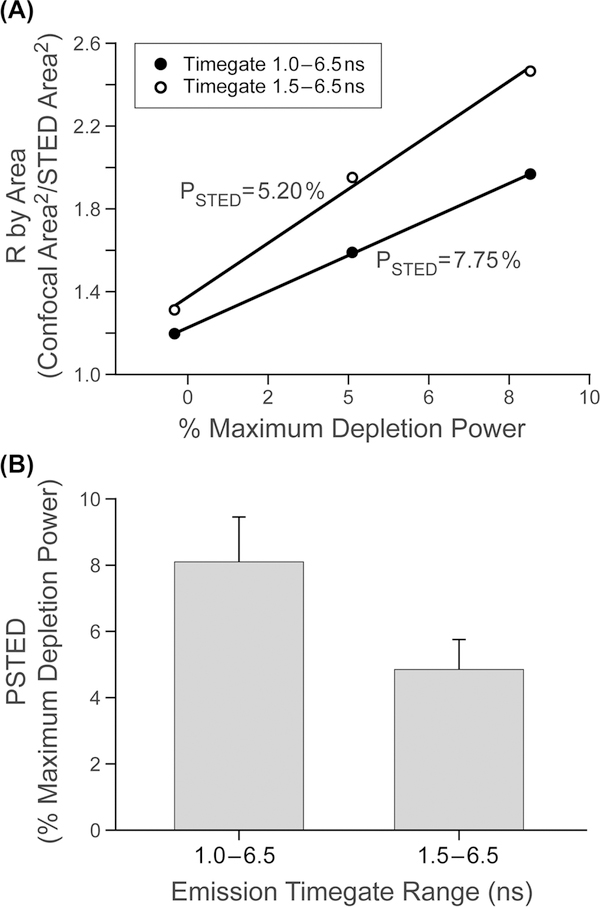
Figure 4 shows how a user specific variable (emission time-gating) can affect P_STED (for depletion with a continuous wave laser). Figure 4(A) shows an example single data set of R versus depletion power for two time-gate settings. Figure 4(B) shows the average P_STED values for replicate measurements (N = 8) of the same relationship shown in Figure 4(A) and shows the variability in making this measurement over a two day window and on separate samples. These figures show that when using that CW laser (592 nm), the longer time-gate (1.5–6.5 ns) was more efficient (lower P_STED value) at improving resolution than for the shorter time gate (1.0–6.5 ns) for the dye Alexa 488. The ability of an experimenter to rapidly make this measurement - and graphically observe the result - facilitates optimising the STED parameter of a system variable (in this case time gating) to produce the best resolution at the lowest depletion power.

Fig. 4.

Example of the use of the linearisation method to show the utility of P_STED measurement using two different emission time gates on the same dye. (A) Example plots of R as a function of STED depletion power for two different emission time gating windows (and 592 nm STED depletion) for the dye Alexa 488. P_STED was calculated from the reciprocal of the slope of the fitted lines (R² ≥ 0.99) in A. (B) Mean and standard deviation of P_STED as a function of time-gate window (n = 8).

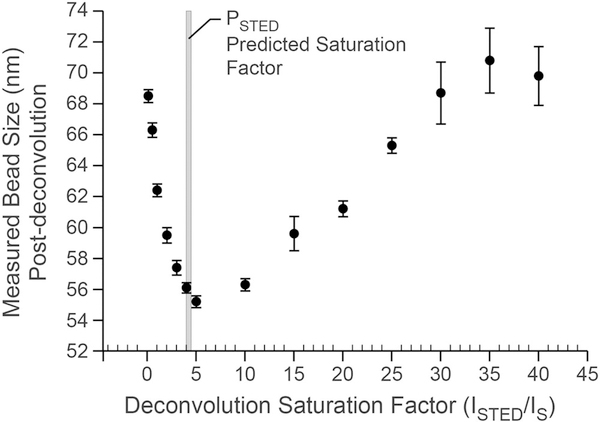
Figure 5 shows recovered bead sizes following deconvolution with varying saturation factors for ATTO 594 labelled beads from Figure 2(A) at a depletion power of 50%. The saturation factor predicts the point spread function of the microscope according to the STED depletion power versus resolution relationship outlined in Figure 1(A). Knowing this factor is critical to correctly deconvolving the data to give the best final resolution and contrast. The best resolution was found to be with a saturation factor of 5. This value is very close to the values predicted from the P_STED measurements shown in Figures 2(C) and (D) as shown in the drop-down line.

Fig. 5.

The P_STED measurement accurately predicts the optimal saturation factor for optimising resolution through deconvolution. Z-stack image data from the beads shown in Figure 2 at a depletion power of 50% were deconvolved assuming varying saturation factors and subsequently measured for size. Proper deconvolution assumes that the point-spread-function can be best approximated for optimal resolution. The relationship of size versus saturation factor shows a minimum size (best resolution) between saturation values of4–6. Saturation factors calculated from Figures 2(B) and 2(C) (50/11.1 = 4.5 from the bead size measurements and 12.34/50 = 4.1 from the bead area measurements) as shown in the drop-down line accurately predict the optimal saturation factor for deconvolution. Bead sizes were measured from n > 40 beads from one z-stack of a field of ATTO 594 labelled beads.

Discussion

In this work, we show that the apparent saturation factor for STED microscopy can be determined for a fluorophore by measuring either the average apparent size or, more easily, area of a subdiffractive object (in this case beads or microtubules) at a few relatively low STED depletion powers. Ideally this measurement would be made from sub-resolution bead sizes over the full range of depletion powers to populate a curve as shown in Figure 1(A). In most cases this is impractical due to many factors, including the fragility of sub-resolution beads at high depletion powers, the difficulty of quantification of bead sizes at low SNR due to loss of signal at high depletion powers, and the amount of time one must invest in measuring the entire curve on a day-to-day basis. The algorithm presented here simplifies the measurement of the saturation factor and allows for quickly optimising various components of a STED experiment, including choosing the appropriate depletion power, optimal user setting (for parameters like emission time-gating), and choosing the best dye, while seeking the least amount of STED induced bleaching. It also permits one to achieve optimal ‘final’ resolution by setting the correct deconvolution parameters to be used in postprocessing. This real-time knowledge can be used to avoid two main STED failure modes: excess photobleaching/photodamage and the generation of artefacts during deconvolution arising from incomplete knowledge of the point spread function.

It is important to note that the practical saturation factor for a fluorescent probe cannot always be inferred from a pure photophysical table of I_s values from published literature. The saturation factor gleaned from depletion power/ P_STED as measured by this algorithm is based on local parameters. Anything that affects the depletion power versus resolution relationship can affect the Is versus P_STED relationship in a particular microscope with a given sample. As discussed below, factors including the calibration of the microscope, the efficiency of the STED depletion beam, and the local characteristics of the fluorescent marker in the sample can all affect this relationship.

One of the prime factors that can affect P_STED is the spatial quality and timing of the STED depletion beam - which will be dependent on the nanoscope being used and the sample itself. For example, the absence of a completely dark centre for the depleting beam can act to reduce signal/noise ratio, and if this were due to a superposed constant power depletion spot with the same width as Dc, the linearity of the plot would be undisturbed to first order (simulation not shown). The slope, however, will reduce, making P_STED larger than in an ideal depletion beam. On the other hand, a constant non-dark fraction of I_STED found at the donut hole centre has been simulated by (Neupane et al., 2013). They find that even with only 10% brightness there, significant loss in theoretical resolving power occurs, with curves that resemble those shown below for other purposes (in Fig. 6) for target sizes of 80 nm+. A non-dark centre to the depletion beam can be due to multiple hardware considerations, such as mis-alignment or vibration or the quality of the optics involved. Distortion due to the sample inhomogeneities with index mismatch or simple spherical aberration effects that vary with depth into the sample also come into play (Gould et al., 2012). Worse, many of the important parameters (like donut beam electric field shaped are difficult to routinely calibrate in the working biological laboratory. The need for proper overfilling of the back aperture of the objective, which may differ between objectives but is generally fixed in the microscope body, makes it likely that changing objectives will change P_STED as well. Additionally both time-gating on the emission side (as shown in Figure 4B and the temporal structure of the depletion pulse can affeci P_STED. For instance, the arrival time of the depletion pulse for pulsed STED (after excitation) must be precise to avoid spontaneous emission before the depletion. Even the width of a STEE pulse is relevant; if too short (few picoseconds), ground state bottlenecks occur, raising P_STED. If too long, CW-like competition between spontaneous and stimulated emission could also increase Is (Harke et al., 2008).

Fig. 6.

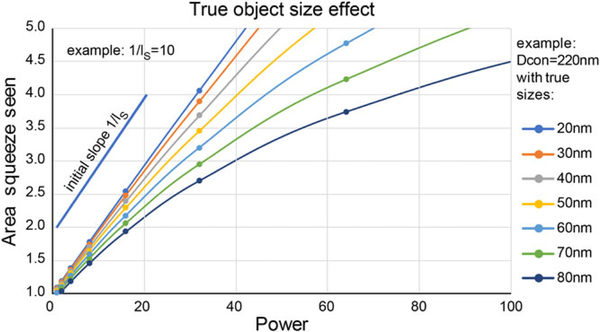
Simulation of the true object size effect on the linearised plot measurement of P_STED. As the true size of the object increases when compared to the confocal diffraction limited size, the initial linear region where the P_STED measurement can be made from the slope of R versus depletion power shrinks. For objects with a true size of 50 nm or less the apparent ratio remains linear to approximately 3× decrease in size compared to confocal.

Another factor affecting P_STED is the local chemical environment of the probe. In particular, P_STED is directly proportional to both the light absorption cross section and the lifetime of the probe in the emissive ‘on state’ (Harke et al., 2008; Blom & Widengren, 2017). For example, even if emission spectral shifts between ‘calibrating’ probes attached to, for example, latex beads versus probes actually on a protein seem subtle near the maximum, the weak tail of emission that is the feature struck by the STED beam may change cross section much more strongly. In general, anything that alters absorption or scattering in the sample (or, like bead index, changes the lifetime of the probe) may affect P_STED. Although there are many sites which give helpful information about the ‘best’ STED fluorophores (https://nanobiophotonics.mpibpc.mpg.de/dyes/, https://www.leica-microsystems.com/science-lab/quick-guide-to-sted-sample-preparation/, https://www.abberior-instruments.com/site/assets/files/2190/recommended_fluorescent_markers_for_sted_by_abberior_instruments-1.pdf) and new STED probes are being developed (Hense et al., 2015; Maksim et al., 2015; Rosales et al., 2015; Butkevich et al., 2016; Byrne et al., 2016; Laporte & Psaltis, 2016; Butkevich et al., 2017; Erdmann et al., 2017; Tavernaro et al., 2017), it is important to know how the dye is working locally on a given nanoscope.

In this work we have expressed the P_STED value as both the back aperture power of the depletion beam (Figure 2) and as a percent of the maximal depletion power (Figures 2–4). Accurate measurement of the back aperture power of the STED depletion beam can be difficult on some microscopes (due to beam blanking) and beyond the general capabilities of many labs. A more general parameter that can be put into practical day to day use is the ‘% maximal power of the depletion laser’ which on most microscopes is a software slider controlling the depletion power. Of course, if a pure reliable power measurement is available at the back aperture of the microscope this value would also be useful or could be used in conjunction with the software slider controlling the depletion power to predict the saturation factor.

Although this algorithm for measuring P_STED using a linearised plot is relatively straightforward, it is important to state the limits of its correct interpretation and implementation. One main factor is the true size of the sub-diffractive object used to make these measurements. Figure 6 shows a simulation of the relationship between the linearised ratio R of measured size of an object when imaged by confocal versus STED over a range of depletion powers. As the true object size increases, the range where the R versus power plot stays linear decreases. It is, therefore, important to restrict the depletion power range for accurate determination of the saturation factor. This is due to the fact that as measured D values approach ~ 3 times the actual object dimension Dobject, the observed Gaussian width D will more clearly be a convolution of the optical Gaussian with the object source function (spatial density of emitters). If one (customarily) treats the object itself as an approximate Gaussian distribution of emission in space, the net width observed will be D = sqr(Doptical² + Dobject²) > Doptical, and (Dc/D)² plots will fall below the line established by Doptical at lower applied STED depletion power, I. Thus, the line curves downward at larger intensities. As Figure 6 shows, for an idealised microscope with 220 nm confocal resolution, this breakpoint (for objects up to 50 nm in size) is approximately a factor of 2.5 reduction in size with STED depletion. If one decides on using even larger calibrating objects, it will be important to empirically determine the curvature for a given set of experimental parameters. This could lead to the need for a nonlinear fitting of the data, which although potentially valid, would require more information to extract the P_STED value.

To accurately determine P_STED it is also important to have a clean sample that fits the criteria listed in Figure 1 (either subresolution puncta like beads or a long thin subresolution fibrous sample like microtubules). Area measurements on fibrous samples like microtubules require measuring area in fields of view that have minimal background and ‘tangling’. Overlapped regions of microtubules will have larger areas and will not respond to depletion as well as areas with well separated microtubules. Simulations of this effect show that overlapped (e.g. ‘matted’) areas of >5% would skew the measured P_STED slope downward (larger perceived P_STED value) by >10%. Also, any background fluorescence from precipitated dye or other features that are not subresolution or are not filamentous will similarly affect the P_STED measurement. If the same region is used for multiple measurements and compared to confocal, then photobleaching must also be minimised to avoid decreasing the SNR to values that do not allow for accurate quantification of the true area of the labelled fluorescence signal. Photobleaching, if severe, could also alter the apparent threshold level, which should ideally be kept at a constant fraction of the actual PSF centre value. These factors could lead to a to a Y intercept that was significantly different than 1 and would require a re-evaluation of the microscope system or the sample.

Optimal use of this algorithm in more complex biological samples (those whose environment cannot be fully replicated by the DAOY or similar cells) may require supplemental use of, for example, exogenous fluorescent beads (or other fluorescent guide-stars such as nanodiamonds or quantum dots) to the sample. Alternately, the use of fluorescently labelled subdiffractive-sized features (actin, nuclear pore complexes, tubulin/microtubule associated protein etc.) in the complex sample can serve as a marker for determining the local saturation factor. In this manner, factors such as optical aberration with depth or sample type may be corrected - or at least accounted for - when planning an experiment or when postprocessing through deconvolution. Another example of this type of strategy is preparing the best depletion powers to match resolution in multicolour experiments. This sort of matching is helpful for quantifying nano-colocalisation.

In summary, from these considerations it is clear that system specific I_s (which we define as P_STED) remains a local parameter dependent on several instrument and probe characteristics. The procedure we describe above is useful in providing P_STED for the purpose of accurate knowledge of the 2D PSF for deconvolution, predicting resolution with depletion power, and for providing diagnostic information about nonideal conditions, through changes in either slope or curvature of the plots. Extending this algorithm to include a 3D PSF characterisation for microscopes that have XY and Z depletion beams is a next step for this tool development process.