The computational stance in biology

Abstract

The goal of this article is to call attention to, and to express caution about, the extensive use of computation as an explanatory concept in contemporary biology. Inspired by Dennett's ‘intentional stance’ in the philosophy of mind, I suggest that a ‘computational stance’ can be a productive approach to evaluating the value of computational concepts in biology. Such an approach allows the value of computational ideas to be assessed without being diverted by arguments about whether a particular biological system is ‘actually computing’ or not. Because there is sufficient difference of agreement among computer scientists about the essential elements that constitute computation, any doctrinaire position about the application of computational ideas seems misguided. Closely related to the concept of computation is the concept of information processing. Indeed, some influential computer scientists contend that there is no fundamental difference between the two concepts. I will argue that despite the lack of widely accepted, general definitions of information processing and computation: (1) information processing and computation are not fully equivalent and there is value in maintaining a distinction between them and (2) that such value is particularly evident in applications of information processing and computation to biology.

This article is part of the theme issue ‘Liquid brains, solid brains: How distributed cognitive architectures process information’.

1. Introduction: computational biology and biological computation

In 1960, the physicist Eugene Wigner published the now-classic ‘The Unreasonable Effectiveness of Mathematics in the Natural Sciences' in which he explored the reasons for the seemingly ubiquitous value of mathematics in the physical sciences [1]. Anyone familiar with the current biological literature might well expect to find an analogous paper entitled ‘The Unreasonable Effectiveness of Computation in the Biological Sciences’. As evidenced by many of the articles in this issue and others throughout the biological literature, the ideas of computation and computing are becoming increasingly pervasive in describing and explaining biological phenomena.

Computers and computation have been fellow travellers with biology since modern computers were invented in the past century. As in physics and most other sciences, computers quickly became essential tools for experimental control and data acquisition, for data analysis, for modelling and theory development, and for communication and publishing (e.g. [2,3]). Depending on which of ‘computation’ and ‘biology’ is noun and which is adjective, two broad scientific sub-disciplines have developed. While they are different enough to be distinguished, the boundaries are fuzzy and do not encourage any attempt at rigid distinction.

Computational biology (including bioinformatics) generally refers to the use of computational techniques in service of various branches of biological science, to ‘the understanding and modeling of the structures and processes of life’ (https://www.britannica.com/science/computational-biology) and to the ‘develop[ment of] algorithms or models to understand biological systems and relationships (https://en.wikipedia.org/wiki/Computational_biology). Bioinformatics focuses on the development and application of large-scale databases of biological information, in particular databases in molecular biology where the approach developed with protein and genetic data [4].

Biological computation, in contrast, focuses on the use of ideas from computation as theoretical and explanatory concepts in biology. In what is perhaps the clearest articulation of this perspective, Melanie Mitchell states:

the term biological computation refers to the proposal that living organisms themselves perform computations, and, more specifically, that the abstract ideas of information and computation may be key to understanding biology in a more unified manner… [I]t is only the study of biological computation that asks, specifically, if, how, and why living systems can be viewed as fundamentally computational in nature [5, p. 2].

It is this role of computation in biology that has seen such ubiquitous application in recent years and that will be the focus of this paper.

Both computation and information processing are abstract ideas that were originally developed in non-biological domains, for purposes other than a better understanding of biological phenomena. The fact that both sets of ideas have found valuable applications in biology speaks to their inherent generality. However, a fundamental issue is whether they are *too general*. That is, if every biological phenomenon is computational (or, similarly, if every biological phenomenon is information processing), then there seems to be little gained by the application of those concepts. I distinguish between information processing and computation in biological systems because I believe there are cases in which we are tempted to attribute computation to a biological phenomenon, when a lesser attribution of information processing (without computation) would be just as effective.

2. Alternative definitions of computation

In order to address the questions of ‘if, how, and why biological systems can be viewed as fundamentally computational in nature’, one needs a reasonably clear and generally accepted definition of ‘computation’, and how that concept is similar to and different from the related ideas of information and information processing.¹ Perhaps not surprisingly, there remain significant differences among computer science experts about those definitions. An excellent discussion of various alternatives is the symposium ‘What is computation?’ sponsored and published by the leading computer science and engineering organization, the Association for Computing Machinery (ACM) [12].

Contributors to the ACM symposium, all experts in computer science, offered a number of different definitions of computation, not mutually exclusive but offering different focus and emphasis.

(a). Formal definitions of computation

The mid-1930s was an extraordinary time in the history of computers and computer science. In just a few years Gödel, Church and Turing each made what would become key contributions to formal definitions of computing that were subsequently shown to be equivalent: recursive functions (Gödel), lamda expressions (Church) and most famously, the state sequence of an abstract machine with tape and control unit (Turing's ‘Universal Machine’) [13–15]. This work provides important background for early textbook definitions of computing:

The standard formal definition of computation, repeated in all the major textbooks, derives from these early ideas. Computation is defined as the execution sequences of halting Turing machines (or their equivalents). An execution sequence is the sequence of total configurations of the machine, including states of memory and control unit. The restriction to halting machines is there because algorithms were intended to implement functions: a nonterminating execution sequence would correspond to an algorithm trying to compute an undefined value. [12]

(b). Computation as algorithm

An algorithm is a step-by-step procedure for accomplishing a specified goal. Today the term is mostly commonly encountered in the computing context, but its more general definition applies widely in other contexts. A recipe is an algorithm, for example. Defining computation in terms of algorithms is closely related to the formal definitions just discussed, with particular emphasis on algorithms as sequences of steps needed to solve a specified mathematical problem or accomplish a given task [12].

(c). Computation as symbol manipulation

This perspective emphasizes that both the problem and its solution must be encoded in the form of symbols, that each step (state transition) in the computation is a manipulation of symbols that transforms one set of symbols (the problem set) into another (the solution set), and that many intervening symbol transformations may be needed for intermediate steps [16].

(d). Computation as process

As noted in the quotation from Denning above, the issues of whether a particular machine halts and whether it is possible in advance to determine whether a particular machine will or will not halt (the ‘halting problem’) were important considerations in Turing's original formulations [15]. Subsequently, a number of computer scientists have argued that computations that halt are a too-limited perspective and that many computations, such as operating systems, for example, are specifically designed NOT to halt but to run continuously. Indeed, for such systems halting is anathema, not the sign of a properly completed computation! This perspective has led to proposals that computation be viewed as process:

…the program is a description of the process, the computer is the enactor of the process, and the process is what happens when the computer (or, more correctly, the processor—since a computer may have multiple processors) carries out the program [17].

This view naturally incorporates both non-terminating and non-deterministic computations, which are significant advantages in the view of many.

(e). Digital versus analogue computation

In the variety of definitions considered thus far, computation has been mostly (and often implicitly) considered to be a discrete or digital (usually binary) process. The discrete states of a Turing machine are a clear example. But well before Gödel, Turing and Church [13–15], numerous applications of analogue computing, that is computing based on continuous processes, were used to solve important engineering problems. Lord Kelvin's tidal analyzer [18] and Vannevar Bush's differential analyzer [19] are early examples, and subsequent developments in electrical engineering resulted in a number of differential equation solvers. Should these important examples of problem-solving by machine be included in a formal definition of computing? As Denning asks: ‘Why is solving a differential equation on a supercomputer a computation but solving the same equation with an electrical network is not?’ [12, p. 6]. And as we will see below, analogue computing will become an important element in considering the application of computational concepts to biology.

(f). Computation as representations and transformations thereof

This perspective, offered by Denning [12] as an inclusive summary of many aspects of the preceding definitions, emphasizes the importance of the representational role of symbols and of the processing or transformational role of the operations on symbols in symbol manipulation.

(g). Computation as information processing

Continuing the effort to broaden definitions of computation, Rosenbloom [20] contends that computation should be defined very generally as information and transformations of information as opposed to other definitions that emphasize process, algorithm and representation. This close relationship between the concepts of information processing and computation is also evident in Mitchell's definition of biological computation above, in which a statement that ‘biological computation refers to the proposal that living organisms themselves perform computations' is followed immediately in the same sentence by ‘…more specifically, that the abstract ideas of information and computation may be key to understanding biology in a more unified manner’ [5, p. 2]. So are computation and information processing just different terms for the same underlying concepts? Or do they differ in identifiable and substantive ways?

3. Information processing and computation

Perhaps it should come as no surprise that the concepts of information and information processing, despite their ubiquitous use in contemporary science, engineering, commerce and public discourse, are also characterized by the lack of clear, generally agreed upon definitions (Rocchi [21] assembled over 25 definitions from the literature, and that was in 2010!).

Claude Shannon, in his landmark 1948 paper, ‘A Mathematical Theory of Communication’, is generally credited as the father of information theory (cf. [22,23]). But that paper, and the essence of Shannon's contribution [21], were as much about a theory of communication as a theory of information per se [24]. Shannon emphasized that his definition in terms of the signal actually transmitted relative to the ensemble of signals that could have been transmitted, was only one of many possible useful definitions:

The word ‘information’ has been given different meanings by various writers in the general field of information theory. […] It is hardly to be expected that a single concept of information would satisfactorily account for the numerous possible applications of this general field ([25], p. 180).

Focused primarily on the engineering problem of designing effective communication devices, Shannon took the radical step of defining information in a manner that completely eliminated meaning from the definition. ‘Shannon information’ was defined without regard to the content or meaning of the signal or its alternatives. This separation of information from meaning, of signals from semantics, has allowed ‘Shannon Information’ to become the dominant mathematical and scientific characterization of information, extensively applied not only to engineering problems, but to a wide variety of phenomena in the physical, biological and social sciences.

Should we allow the similarities and sometimes overlapping usages of information processing and computation to drive us to treat them synonymously? Despite Rosenbloom's [20] suggestion that we define computation as information processing, I contend that the two concepts are not identical and that there is real value in attempting to distinguish between them, despite their close relationships.

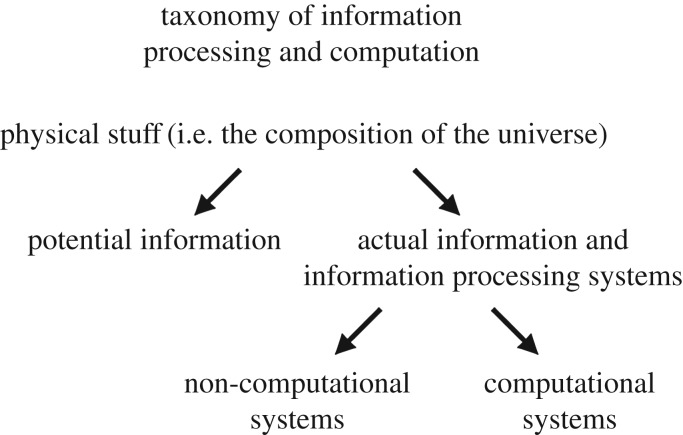
The sub-set/super-set relationship that I believe best characterizes the relationship between information processing and computation is illustrated in figure 1.

Figure 1.

Proposed taxonomy of information processing and computation.

Starting with the ‘physical stuff’ that constitutes the universe as a whole, each lower level in the diagram divides the preceding level into two distinct parts that completely characterize the preceding higher level.

The entire universe is divided into physical stuff that is Potential Information and Actual Information (and systems that process it). Potential information is just variance or entropy: variability in some properties of a set of objects. As Shannon showed, such variance across a set of physical objects or signals is essential for them to be used to transmit information. Actual information requires, in addition to the necessary variance among objects or signals, the demonstration that some system or other actually uses that variance to transmit information; that is, to reduce uncertainty about the problem under consideration.

To take what is perhaps a trivial example, the pattern of stones on the hillside outside my office may or may not be information in the Shannon sense. In my terminology, they clearly are potential information (as are the atoms and molecules that constitute the stones, as well as the location and height of the hills on which the stones rest). But whether or not they are actual information depends upon determining that some system or other is using those stones to convey information in the Shannon sense.

At the next level down, that sub-set of the universe that is Actual Information and Information Processing Systems is in turn divided into two exhaustive components: non-computational systems and computational systems. This division expresses the key idea that while all computational systems are information processing systems, not all information processing systems are computational.

How do we distinguish between information processing systems that are and are not computational? By applying the criteria offered in the definitions of computational systems above:

• Formal definitions: Are there aspects of the system that meet the formal definitions of computing?

• Algorithms: Are there elements or properties of the system that can be characterized as algorithmic?

• Symbol manipulation: Is there evidence in the system and its operation for symbol manipulation?

• Processes: Are there identifiable processes or subprocesses that are continuous rather than terminating (halting)?

• Representations and transformations: Do internal aspects of the system represent aspects outside the system itself and do aspects of the operation of the system constitute transformations of those representations?

To take obvious examples at each end of the continuum from computational to non-computational:

• 1.Most would be unwilling to attribute computation to planetary mechanics (e.g. ‘the earth computes its orbit’) even though it is perfectly possible to use computational techniques to model and predict planetary orbits with great precision.
• 2.Most would be willing to attribute computational capabilities to the laptop on which this manuscript is being written, because of our understanding that both the hardware that constitutes the system and the software used to provide instructions to the hardware meet many of the criteria listed above.

4. The computational stance in biology

But what about more interesting intermediate cases?

Does the human brain compute? If so, what and how?

Does an ant hill compute? What are the symbols? What is being represented?

Does a flock of birds compute? If so, what are the algorithms and processes?

It should come as no surprise that these intermediate cases all come from biology. All are cases in which one or more researchers has attributed computational properties to the systems in question, with varying degrees of explicitness in consideration of whether and to what degree computational properties apply. While I believe that arguments about whether a given biological system ‘actually computes’ can be counterproductive, I also believe that attributing such properties to a biological system simply because it is biological is unwarranted and unproductive.

Inspired by Dennett's analysis of physical, design and intentional ‘stances’ in the philosophy of mind [26,27] (see also [28,29]), I suggest that a ‘computational stance’ can be a productive approach to the application of computational ideas in biology.

My appropriation of the ‘stance stance’ is rather different in its particulars from the intentional stance in philosophy of mind. In particular, it does not raise the issues of realism that Dennett's critics are quick to offer (e.g. [28,30]). Nevertheless, by foregoing any deep arguments about ‘computational realism’ (i.e. that a biological system ‘really computes’), I am aware than some may consider the proposal to be so weak and timid as not to be worth their effort.

5. A real biological example

In order to illustrate the value of attempting to distinguish between a biological phenomenon that reflects computation versus another that reflects information processing but not computation, consider the famous ‘waggle dance’ of the honeybee [31].

von Frisch showed that honeybees communicate to their hive mates the location and distance of attractive food sources by means of a figure-eight-like dance with alternating left and right loops [31]. At the end of each loop, the honeybee ‘waggles’ its body in such a manner that the angle of the waggle represents the angle between the sun and the direction to the food source, and the duration of the waggle represents distance to the food source.

Many would consider the acquisition and storage of information about food sources, and communication of that information by foraging honeybees, a quintessential example of biological computation. In terms of the criteria for computation identified above, the dance behaviour can be effectively described as algorithmic: there is clear evidence of symbolic representation (direction and distance from the hive) and there are identifiable processes associated with different components of the dance. Taken together, Denning's ‘representations and transformations of those representations' are an effective characterization of the waggle dance phenomenon.

Now consider a related phenomenon exhibited by the same honeybees. More recent studies [32] have demonstrated that other honeybees in the hive can intervene to stop the waggle dance if they have had negative experiences (predators, for example) at the food source for which the waggle dance is being performed. This information is communicated by a head-butt against the dancer, which stops the dance and the recruitment of other observers to the food source.

By contrast with the waggle dance, this ‘danger’ or ‘stop’ signal communication is much simpler. At the level of the individual honeybee issuing the ‘stop’ signal, there is no complex symbolic representation of direction or distance, no elaborate sequence of behaviours, just the head-butt signal conveying information about a potential food site. Even though one could certainly describe the ‘stop’ signal phenomenon in computational terms, it is adequately explained at the level of the individual honeybee within the framework of information and communication in the Shannon, and Shannon and Weaver senses. At the level of the entire hive, however, Seeley et al. [33] have convincingly argued for a computational account.

6. Conclusion

Given the focus of this Special Issue, I have tried unsuccessfully to identify ways in which the criteria for computation can contribute to the discussion of the similarities and differences between ‘solid’ and ‘liquid’ brains. I conclude that the distinction between ‘solid’ and ‘liquid’ reflects structural and architectural differences—different physical implementations [34]—more than it reflects any systematic association with computation versus information processing.

My goal has not been to reach a principled determination about whether a particular biological system computes or not, because I do not believe such a principled determination is achievable (hence my emphasis on ‘the computational stance’). Rather, it is the process of examining whether and to what extent the biological system in question exhibits each of the criteria for computation that I believe will be helpful to understanding and explaining that system's operation. Ultimately, it is that criterion of utility for the explanatory goals that I believe to be more important than seeking a ‘does it compute or not?’ determination.

It is possible we may often find ourselves in the position identified by Frailey [17]:

Perhaps biological systems carry out processes that do not quite fit our notions of algorithmic, but they exhibit properties that are more readily understood because of what we know about computation.

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests.

Funding

We received no external funding for this article.