A brief history of liquid computers

Abstract

A substrate does not have to be solid to compute. It is possible to make a computer purely from a liquid. I demonstrate this using a variety of experimental prototypes where a liquid carries signals, actuates mechanical computing devices and hosts chemical reactions. We show hydraulic mathematical machines that compute functions based on mass transfer analogies. I discuss several prototypes of computing devices that employ fluid flows and jets. They are fluid mappers, where the fluid flow explores a geometrically constrained space to find an optimal way around, e.g. the shortest path in a maze, and fluid logic devices where fluid jet streams interact at the junctions of inlets and results of the computation are represented by fluid jets at selected outlets. Fluid mappers and fluidic logic devices compute continuously valued functions albeit discretized. There is also an opportunity to do discrete operation directly by representing information by droplets and liquid marbles (droplets coated by hydrophobic powder). There, computation is implemented at the sites, in time and space, where droplets collide one with another. The liquid computers mentioned above use liquid as signal carrier or actuator: the exact nature of the liquid is not that important. What is inside the liquid becomes crucial when reaction–diffusion liquid-phase computing devices come into play: there, the liquid hosts families of chemical species that interact with each other in a massive-parallel fashion. I shall illustrate a range of computational tasks, including computational geometry, implementable by excitation wave fronts in nonlinear active chemical medium. The overview will enable scientists and engineers to understand how vast is the variety of liquid computers and will inspire them to design their own experimental laboratory prototypes.

This article is part of the theme issue ‘Liquid brains, solid brains: How distributed cognitive architectures process information’.

1. Introduction

A substance offering no resistance to shear deformation is a fluid. A liquid is an incompressible fluid. Following the overall theme of this special issue ‘Liquid brains, solid brains’, co-edited by Ricard Solé, Melanie Moses and Stephanie Forrest, I focus on computing devices where a liquid plays a key role, either as a material substance for signal representation and transmission or as a substrate where computation takes place. A liquid plays a key role in the functioning and behaviour of several creatures, discussed in this special issue. Thus, for example, slime mould Physarum polycephalum is well known for coordinated channelling of fluid through its networks of protoplasmic tubes [1–4]. There is evidence of signal propagation with cytoplasmic flow [5], including morphological changes triggered by the cytoplasmic flow [6]. The networks of biochemical oscillators governing the shuffling of cytoplasm in the slime mould could be also responsible for the slime mould’s adaptive behaviour and learning [7–10]. At the level of social insect behaviour, fire ants exhibit fluid-like behaviour in their outbound traffic [11,12], and interactions between neighbouring ants in moving traffic could be seen as analogous to interaction between molecules in a fluid substrate [13].¹ My personal interest in liquid-based computers started in the early 1990s when I proposed a paradigm and experimental laboratory implementations of reaction–diffusion chemical computers [17,18], affective liquids [19] and liquid brains for robots [20,21]. In reaction–diffusion computers, information is processed via interaction of phase or diffusion wave fronts. Affective liquids are mixtures of chemical species representing emotional states [19], and stirred or thin-layer mixtures of doxastic and affective chemical-like species [22]. Liquid brains for robots are onboard controllers for robot navigation that employ a thin-layer excitable chemical reaction [23].

Echoing one of the threads of this special issue—‘a creature does not have to have a nervous system to cognize’—I demonstrate that a substrate does not have to be solid to compute. Liquid-based computing devices overlap with old schools analogue computation, as it was in the 1950s–1960s, and unconventional computation, as it fully flourishes in the 2000s. The field of analogue computation has been mainly populated by engineers and therefore most achievements have been highly practical. Unconventional computing, till recently, has been in the domain of computer science and therefore is full of theoretical papers. I estimate that for every thousand theoretical papers there is just one experimental laboratory paper. This is why an experimental laboratory prototype of an unconventional computing device is of utmost importance. Therefore in this paper I focus not on why a liquid can compute but on what practical computing devices can be made from liquid-phase substrates. I overview a variety of liquid computers, from hydraulic algebraic machines invented in the late 1890s to liquid marble logic designed just recently. The chronological order of selected liquid-based computing devices is shown in table 1. All the prototypes have only one thing in common: they use liquid to encode and process information. The exact implementations of the computing devices are very different one from another. Hydraulic mathematical machines employ mass transfer analogies; a fluid in such machines is mostly stationary except when bodies are immersed. Streams and jets of a fluid are employed in fluid mappers to explore geometrically constrained spaces and in fluid logic devices to realize logic gates via interaction of fluid jets. The streams are continuous. The liquid can also be ‘discretized’ in droplets and liquid marbles, and computation is implemented via liquid marbles colliding with each other or actuating mechanical devices. In hydraulic algebraic machines, integrators and droplet-based computers, the nature of the liquid is not critical because the liquid is used as an actuator or carrier of signals. What is inside the liquid becomes important when reaction–diffusion liquid-phase computing devices come into play: there, the liquid hosts families of chemical species that interact with each other in a massive-parallel fashion. Here I shall illustrate a range of computational tasks, including a computational geometry, implementable by oxidation wave fronts in nonlinear active chemical medium.

Table 1.

A brief history of liquid computers.

year	device	publications
1900	hydraulic algebraic machines	[24–26]
1936	hydraulic integrators	[27,28]
1949	Monetary National Income Analogue Computer	[29]
1949	fluid mappers	[30]
19602	fluidic logic	[32–36]
1985	Belousov–Zhabotinsky computers	[18,37–40]
1996	reaction–diffusion computers	[41–44]
2003	liquid brain for robots	[20,45]
2003	fluid maze solver	[46]
2007	droplet logic (pressure/flow-driven)	[47–50]
2010	chemotactic droplets solving mazes	[51,52]
2012	droplet logic	[53]
2017	liquid marbles logic	[54]

The examples discussed demonstrate the versatility of the liquid as a computing substrate. I believe the overview will encourage researchers and engineers to be more proactive in employing the liquid phase in their unconventional computing devices.

2. Hydraulic algebraic machines

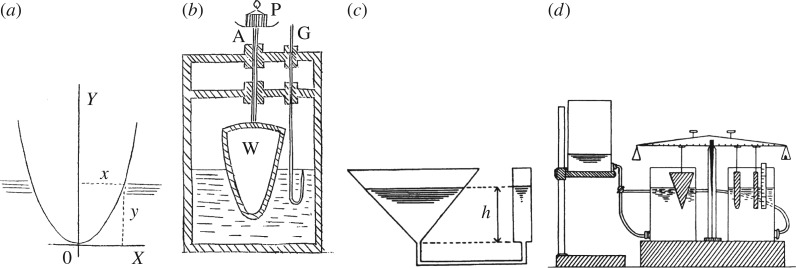
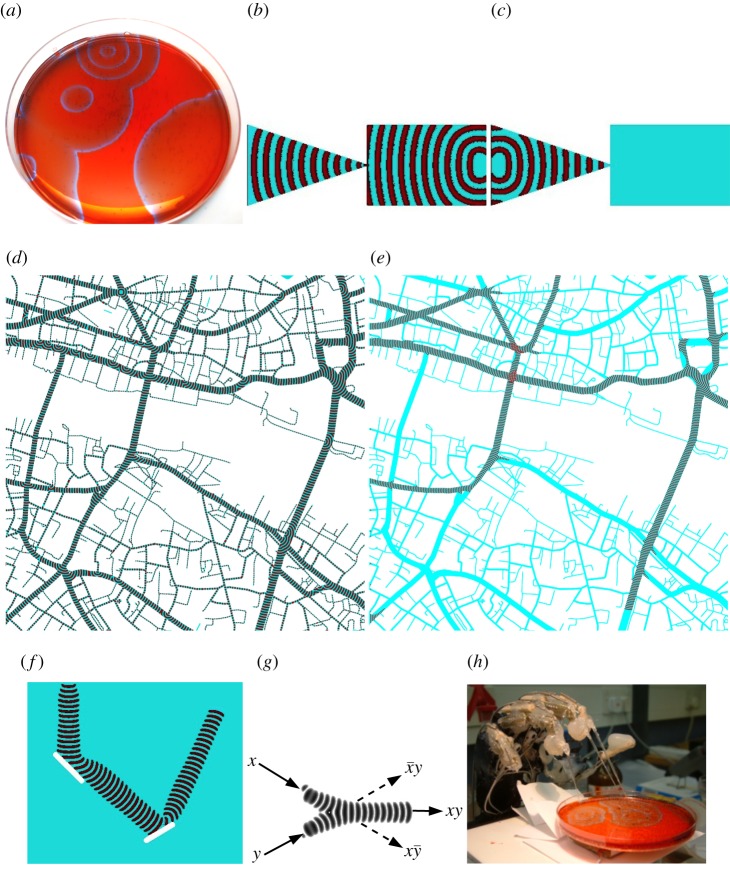
The first recorded liquid computers worked on the displacement of water in response to immersion of a body in a container. In 1901, Arnold Emch published a paper in The American Mathematical Monthly where he proposed to calculate the nth root of any number by immersing solid bodies in a liquid [24]. He assumed a paraboloid-shaped body is immersed in liquid as shown in figure 1a. When this body is immersed, the weight of the displaced water will be $W=\pi \cdot w\cdot {\int }_0^y{x}^2\hspace{0.17em}\text{d}y=\pi \cdot w\cdot {\int }_0^y{x}^2\hspace{0.17em}\text{d}y$, where w is the weight of one cubic foot of water. The function f(x) is selected such that the weight W of the displaced water equals the nth power of a given number $y:\hspace{0.17em}\pi \cdot w\cdot {\int }_0^y{x}^2\hspace{0.17em}\text{d}y=y^n$.

Figure 1.

(a,b) Illustration of the hydraulic method for extracting the nth root of any number proposed by Arnold Emch in 1901. Adapted from [24]. (c,d) Pictures from [26].

A device for the extraction of a square root of a given number N is shown in figure 1b. G is a hook-gauge showing the water level. The shape of the parabolic body immersed is defined by the equation $y=x^2\cdot \sqrt{(\pi w)/2}$. Let W be the weight of the water displaced, Q be the weight of the vessel, and P be an added weight to make $Q\cdot P=N=y^2$. Thus, $y=\sqrt{N}$. The value y is measured by gauge G as the difference of the water levels before and after the immersion.

A method of solving trinomial equation x³ + x = c, where c is a constant, was proposed by Demanet, cited by Gibb [26]. The device shown in figure 1c is an inverted cone joined to a cylinder, base 1 cm², with a tube. The height of the cone H and the cone’s radius R are selected so that $R/H=\sqrt{3}/\sqrt{\pi }$. A volume c cm² of water poured into the device will stay at the height h in both vessels. The volume of the water in the cylinder will be V = h³ (because $R=h\cdot (\sqrt{3}/\sqrt{\pi })$). The volume of the water in the cylinder used in the device is $1\cdot h$. Thus, we have h³ + h = c. The height h of the water is the solution of the equation.

A hydrostatic balance, inspired by Emch [24], was proposed by Meslin, cited in Gibb [26] to solve the equation $p\cdot x^m+q\cdot x^n+\dots =A$ (figure 1d [26]). Solid bodies are immersed in a liquid. Parameters of the bodies are selected so that when x units of length are immersed in the liquid the volumes are proportional to x^m, xⁿ, …. Coefficients p, q, etc., are represented by distances of the bodies’ hanging points relative to the axis of rotation of the beam (left means negative and right positive). After the bodies are immersed a weight |A| is suspended at a unit distance from the axis of rotation. The system becomes temporarily disturbed but the equilibrium is restored by the water redistributing between the vessels. After that the moments of the bodies relative to the axis of rotation of the beam will be $p\cdot h^m+q\cdot h^n+\dots$, and therefore h is the solution found.³

3. Hydraulic integrators

Flows of a liquid through a network of pipes with different diameters can analogously imitate thermal diffusion in geometrical constraint spaces, electrical conductivity and money flow in a country’s economy. In the early 1930s, two hydraulic computing devices were invented simultaneously in the USSR by Luk’yanov [27] and in the USA by Moore [28]. Both were designed to imitate heat transfer not by solving differential equations by hand or using existing calculators but by analogue modelling of the heat propagation with water (figure 2a). The devices relied on the following analogies between the liquid and the thermal characteristics of thermo-conductive building materials [27,28,55]. Levels of water in vessels represent difference of temperatures between the building materials and the air. The cut area of the vessels represents the thermal capacity of layers. Hydraulic resistance of the tubes connecting the vessels is analogous to the thermal resistance of the simulated material layers.

Figure 2.

Hydraulic equation solvers. (a) Luk'yanov’s hydraulic integrator (1936). This is a photo of Model no. 3 hydraulic integrator donated by the Ryazan Factory of Analog Computers to the Moscow Polytechnic Institute in 1956. Photo copyright © 2005–2018 Polytechnic Museum (Moscow, Russia). (b) Phillips Hydraulic Computer (1949). Science Museum Group Collection. Copyright © The Board of Trustees of the Science Museum. (Online version in colour.)

As stated by the Polytechnic Museum (Moscow, Russia) [56], there were around 150 hydraulic integrators produced in the USSR, some exported to Poland, the Czech Republic and China. A portable version of the Luk'yanov integrator was manufactured for schools.

Over a decade after the invention and relatively wide usage of the hydraulic integrators, in the late 1940s, William Phillips designed and prototyped his Monetary National Income Analogue Computer (MONIAC), also known as the Phillips Hydraulic Computer (figure 2b). There, a flow of money was imitated by a redistribution of water between the containers [29].

4. Fluid mappers and maze solvers

A current in a liquid is strongest along the shortest path (or paths) from a source to a sink (or sinks). Fluid mappers visualize the current streams, thus extracting shortest paths from the liquid computers. In 1900, Hele-Shaw & Hay proposed an analogy between stream lines of a fluid flow in a thin layer and the lines of magnetic induction in a uniform magnetic field [57]. They applied their ideas to solve a ‘problem of the magnetic flux distortion brought about by armature teeth’ [58]. In the 1940s Hele-Shaw and Hay analogies were advanced by Arthur Dearth Moore, who developed fluid flow mapping devices [30].

The Moore’s fluid mappers were made of a cast slab, covered by a glass plate, with input (source) and output (sink) ports. Crystals of potassium permanganate or methylene blue were evenly distributed at the bottom of the slab. Fluid flow lines were visualized by traces from the dissolving crystals. Moore shown that the fluid mappers can simulate electrostatic and magnetic fields, electric current, heat transfer and chemical diffusion [30]. The fluid mappers became popular, for a decade, and have been used to solve engineering problems of underground gas recovery and canal seepage [58,59], current flow modelling in the human body [60] (figure 3b) and design of fume exhaust hoods [61] (figure 3a).

Figure 3.

Fluid mappers and solvers. (a) A fluid mapper used in optimization of a canopy exhaust hood in 1954 [61]. (b) An imitation of the current flow in the human body by a thin-layer fluid flow, with domains of low permeability corresponding to the lungs and liver; the fluid enters the model from the left leg and leaves the model through the arms. The experiments were conducted in 1952. From [60]. (c) The fluid flow through a maze. The entrance is on the left; the exit is on the right. The flow simulation is done in Flow Illustrator http://www.flowillustrator.com/ for visual flow control dt = 0.01 and Reynolds number 500. The maze is black, red coloured areas are parts of the fluid making clockwise rotation and green coloured areas—counter-clockwise. (d) Maze solving with milk and water; snapshots from the video of experiments by Masakazu Matsumoto (https://youtu.be/nDyGEq_ugGo) with kind permission from Masakazu Matsumoto. (e) Labyrinth solving with coffee and milk: the path is traced by the coffee [62]. (Online version in colour.)

The Moore’s fluid mappers could solve mazes; however, Moore never reported this. The first published evidence of an experimental laboratory fluid maze solver dates back to 2003. In the fluidic maze solver developed in [46], the maze is a network of micro-channels. The network is sealed. Only the source site (inlet) and the destination site (outlet) are open. The maze is filled with a high-viscosity fluid. A low-viscosity coloured fluid is pumped under pressure into the maze, via the inlet. Owing to a pressure drop between the inlet and the outlet, liquids start leaving the maze via the outlet. The velocity of the fluid in a channel is inversely proportional to the length of the channel. High-viscosity fluid in the channels leading to dead ends prevents the coloured low-viscosity fluid from entering the channels. The shortest path—least hydrodynamic resistance path—from the inlet to the outlet is represented by the channels filled with coloured fluid (figure 3c). A similar approach could be used to solve a maze at a macro scale, e.g. with milk and water (figure 3d) or milk and coffee (figure 3e).

5. Droplet-tracing fluid mappers

Current and chemical gradients in liquid computers can be traced with droplets of another liquid. We can think of this as one liquid computer implementing a computation (developing current flow and/or chemical gradient) while another liquid computer (a droplet) extracts the results of the computation. The motion of droplets of one liquid in another liquid is determined by thermal and chemical gradients, and directed by flows outside and inside the droplet [63–68]. If the gradients represent the solution of a computational problem then droplets travelling along the gradients might be seen as solving the problem. Such an experimental prototype of a droplet traversing a pH gradient is presented in [52]. There, a polydimethylsiloxane maze is filled with a solution of potassium hydroxide. An agarose block soaked in hydrochloric acid is placed at the destination site. A pH gradient establishes in the maze. Then a droplet of a mixture of mineral oil or dichloromethane with 2-hexyldecanoic acid is placed at the start site. The droplet travels along the steepest gradient of the potassium hydroxide. The steepest gradient is along the shortest path. Therefore, the droplet travels from its start site to the destination site along the shortest path [52].

The exact mechanics of the droplet motion are explained in [52] as follows. Potassium hydroxide, which fills the maze, is a deprotonating agent. The gradient of the protonated acid determines a gradient of the surface tension. The surface tension decreases towards the destination site. A flow of liquid—the Marangoni flow—is established from the site of the low surface tension to the site of the high surface tension. The droplet is moved by the flow [52].

Another prototype chemotactic droplet maze solver was demonstrated in [51]. The maze is filled with a solution of sodium decanoate in water. The sodium chloride diffuses from its host nitrobenzene droplet at the destination site. A gradient of the saline concentration is established. The gradient is steepest along the shortest path leading from any site in the maze to the destination. A decanol droplet moves along the steepest gradient till it reaches the droplet at the destination site (figure 4).

Figure 4.

A decanol droplet (containing Oil Red O for colour) solves a maze. Adapted from [51] with kind permission of Jitka Čejková. (a) 0 s, (b) 20 s, (c) 60 s, (d) 140 s, (e) 180 s and (f) 200 s. (Online version in colour.)

The experimental prototypes of travelling droplets laid the foundation of an emergent field of liquid robots [69,70]. There, droplets are studied as adaptive actuating and/or propulsive devices capable of navigation in dynamically changing environments.

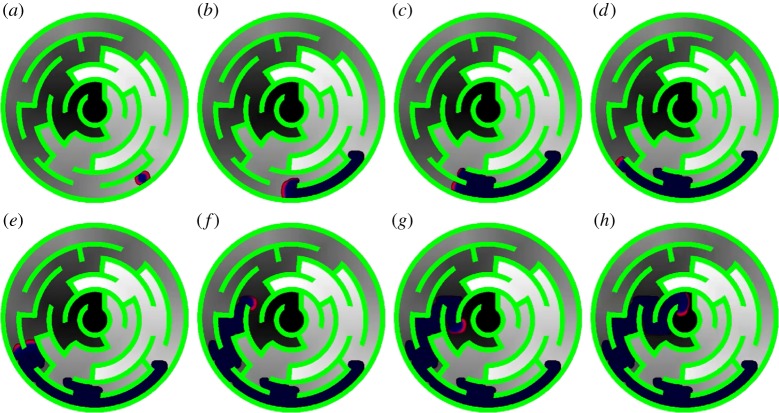
The droplets tracing gradients behave in a manner similar to the slime mould Physarum polycephalum, though without permanent marking of the path selected. A Physarum maze solver, proposed in [71], is based on attraction of the slime mould to volatiles emitted by bacteria colonizing a virgin oat flake. Thus, to solve a maze, we place an oat flake in the maze’s central chamber, and inoculate the slime mould into a peripheral channel. Chemoattractants from the oat flake diffuse along the maze’s channels (figure 5a). The Physarum explores its vicinity by branching out protoplasmic tubes into openings of nearby channels (figure 5b–e). When a wavefront of diffusing attractants reaches the Physarum, the Physarum halts lateral exploration and develops an active growing zone propagating along the gradient of the attractants’ diffusion (figure 5f–h). The thickest tube represents the shortest path between the sources of nutrients. Not only sources of nutrients can be placed at the destination site but also non-nutritional yet aromatic substances, e.g. roots of the medicinal plant Valeriana officinalis [72].

Figure 5.

(a–h) Simulation of maze solving by slime mould using diffusion equations for attractants and Oregonator wave propagation for the slime mould. Concentration of diffusing attractants is shown by levels of grey. Active zone of slime mould is shown by red. (Online version in colour.)

6. Fluidic logic

The first work on using fluids to implement logic gates can be traced back to the late 1950s/early 1960s [73–75]. The truth value of a variable was represented by high and low pressure in inlets and outlets and a computation was realized via interaction of fluid jet streams at junctions of the inlets. The basic principles of the fluidic devices are the laminar flow of a fluid, a jet interaction, a wall attachment and a vortex effect. The jet interaction is the phenomenon that occurs when fluid flows are arranged so that small opposing jets experience changes of direction which can be used as output signals. The wall attachment phenomenon is that the fluid attaches to a surface within a device and continues to flow over the surface until disturbed. The first devices, designed and fabricated in the 1960s, included beam deflection, turbulence, vortex and wall attachment amplifiers, AND, NOT, OR and XOR logic elements, counters and shift registers. The fluidic devices have been used in jet sensing, programmable sequence control, flameproof equipment, machine tool control, systems operating nuclear reactor coolant, servo-control in marine applications, missile and aircraft control, artificial heart-pumps, and lung ventilators [73–75].

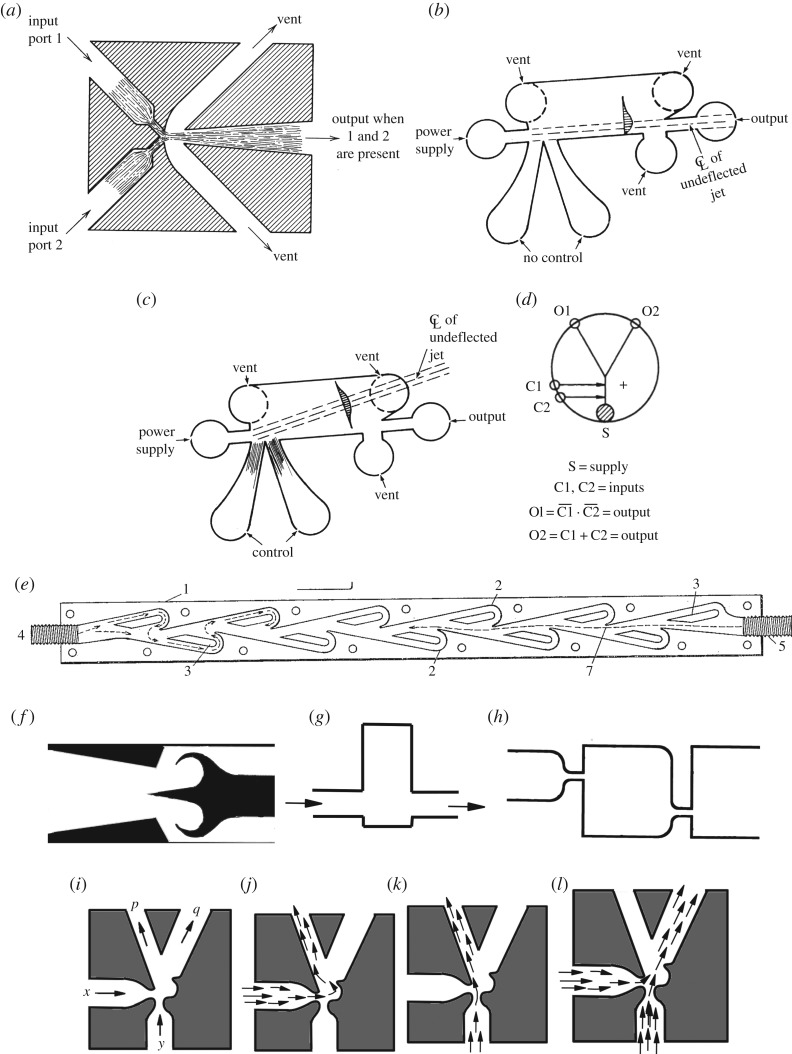
The AND–NOT gate (figure 6a) is the most well-known device in fluidics, on, a par with the bistable amplifier. Two nozzles are placed at right angles to each other. When there are jet flows in both nozzles they collide and merge into a single jet entering the central outlet. If the jet flow is present only in one of the input nozzles it goes into the vent opposite. The horizontal output channel implements x AND y and later channels x AND NOT y and NOT x AND y.

Figure 6.

(a) Fluidic AND–NOT gate [36,76]. (b,c) Fluidic deflection type NOR element. From [74]: (b) undeflected jet, (c) jet deflected by control stream; 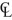, contour line. (d) A diagram of the monostable fluid NOR–OR amplifier [77]. (e) Tesla diode [31]. (f) Scroll diode [35,74]. (g) Basic delay. Adapted from [33]. (h) Delay and diode. Adapted from [32]. (i–l) Hobbs gate: a hook-type fluidic half-adder. (i) Structure of the gate. (j,k,l) Dynamics of the fluid streams for inputs (j) x = 1 and y = 0, (k) x = 0 and y = 1, (l) x = 1 and y = 1. Modified from [34].

A monostable beam deflection device comprises a power supply, controls/inputs and vents (figure 6b,c). When no inputs are present the fluid jet from the power source exits through the output (figure 6b). When one or both input jets are present, the jet from the power source is deflected into the vent and discharged (figure 6c) [74]. The fluid jet exits the output only if no input jet is present. This defines a NOR operation.

The monostable beam deflection device (figure 6b,c) can be transformed into a NOR–OR gate (figure 6d) by adding an output outlet instead of the vent [77]. When no control jets are present the jet from the power source exits via the outlet O1. If one or both signal jets are present, the jet from the power source is deflected into the outlet O2.

A fluidic diode is a two-terminal device that restricts, or even cancels, flow in one direction (backward direction). The Tesla diode [31] (figure 6e) and scroll diode [35,74] (figure 6f) are the most-known fluidic diodes (as well as the vortex diode, which is not discussed here).

The Tesla diode (figure 6e), called the ‘valvular conduit’ by its inventor [31], is composed of buckets and partitions arranged in such a manner that the forward flow propagates mainly along the axis (4–5 in figure 6e). In the backward direction (5–4 in figure 6e), fluid enters the branches and loops around to oppose the main flow.

In the fluidic scroll diode (figure 6f), the channel, or nozzle, converges in the backward direction and enters an annular cap. In the forward direction, the fluid flows through the throat and into a diffuser section. In the backward direction, the fluid enters the cap and is directed back towards an incoming flow, causing turbulence. A delay in the fluidic systems is implemented as a volumetric tank (figure 6g) with input and output pipes [33]. A step change in the input pressure appears as a similar change in the output pressure after a delay. The delay is caused by the turbulence. The amount of the delay is determined by the volume of the tank [33]. Another version of a delay element (figure 6h) combines orifices and volumes to have a low impedance in one direction of the flow.

A fluidic one-bit half-adder can be implemented on the basis of the gate proposed by Hobbs in 1963 [34] (figure 6i). Logical values are encoded into the presence of streams in the specified channels. When only input is True, x = 1, a power jet stream enters the gate via channel x. The stream is turned by the hook and follows the channel p (figure 6j). When only input y = 1 the power jet stream entering the gate via channel y locks on (gets attached to) the left boundary wall of its channel, and propagates along the channel p (figure 6k). If both inputs are True, streams entering x and y merge and follow the channel q (figure 6l). Thus, the stream exiting the channel p represents $p=x\oplus y$ and the stream exiting the channel q represents q = xy. The fluidic AND–NOT gate [36,76] had an unexpected ‘reincarnation’ in the logic gates implemented with swarms of soldier crabs [78–80] and plant roots [81,82]. In the crab gate, Boolean values True and False are encoded into the presence and absence of a swarm of soldier crabs in input or output channels (figure 7a). If a swarm is installed only in one of the input channels, it propagates along its original trajectory into the corresponding output channel, with minor dissipation of crabs into other channels. When both input channels have swarms of crabs, the crabs from different swarms collide at the junction. They change their velocity such that over 70–80% of crabs enter the central output channel (figure 7c). Thus, statistically, the central output channel represents function xy and lateral channels functions $\overline{x}y$ and $x\overline{y}$. The plant roots gate (figure 7b) proposed in [82] was an attempt to employ swarming behaviour of plant roots [84] in the implementation of logical functions. That is, roots propagating in the channels follow their original trajectories unless they encounter roots propagating in the other direction. When two swarms of propagating roots ‘collide’ their velocity changes towards a vector averaged over all swarm elements. Thus, if plant roots are present in both input channels they propagate into a central output channel xy.

Figure 7.

(a) A snapshot of the experimental set-up of AND–NOT gate implemented with soldier crabs. From [83] with kind permission of Yuta Nishiyama and Yukio Gunji. The crabs are placed in one or two input channels, shown at the bottom of the photos, and persuaded to move towards three output channels, shown at the top of the photos. (b) Experimental set-up of plant root gate. (c) Snapshots of operating crab gate for inputs 11: both input channels have swarms of crabs. See video at https://vimeo.com/242345427. (Online version in colour.)

7. Digital microfluidic logic

In fluidic logic devices, fluid jets are programmed by the geometry of channels and perform computation by interacting with each other. Boolean values are represented by pressure of the jets in the output channel. In digital microfluidics, signals are represented by droplets or bubbles travelling in the channel [47,48,50,53]. The droplets/bubbles also control pressure in the channels, thus affecting trajectories of other droplets/bubbles. An example of a fluidic gate, designed in [47], with two inputs x and y and two outputs is shown in figure 8a–d. An oil droplet is introduced into an aqueous phase. When the droplet enters the channel with the larger flow rate, the pressure drop increases across the channel containing two-phase emulsions, particularly at a low capillary number.

Figure 8.

(a–d) Microfluidic gate OR–AND, redrawn from [47]; oil droplets are coloured red and green for distinction only. Vertical channels are inputs, horizontal channels are outputs. (e–h) Snapshots of experimental implementation of microfluidic half-adder by Morgan et al. [85]: (e) x = 1, y = 0, (f) x = 0, y = 1, (g) x = 1, y = 1, (h) oil entering channel x is coloured to demonstrate a deflection of flow. Adapted from [85]. (Online version in colour.)

Cheow et al. [47] designed a ratio of tubes and flows (figure 8a) such that the following phenomena take place. If the flow through A to C exceeds the flow through A; the regime is laminar; therefore all flow from x goes via AC. An oil droplet entering A travels into C (figure 8b). The flow through the bridge between A and B exceeds half of the flow through B. Thus, an oil droplet entering B also travels into C (figure 8c). When a droplet from A enters channel C the hydrodynamic resistance of A increases. The flow via the bridge connecting A and B becomes less than half of the flow through B. The droplet entering B travels into channel D (figure 8d).

Using similar principles, Morgan et al. [85] implemented a one-bit half-adder. When only one of the input channels represents ‘1’ the droplets from this channel go into channel S (figure 8e,f). When both inputs are ‘1’ the droplets travel into lateral channels (figure 8g).

Other variants of fluidic gates are realized in [50] using surface tension-based passive pumping and fluidic resistance, and in [49].

8. Billiard-ball computing with droplets and marbles

In billiard-ball computing with droplets, the presence/absence of a droplet in a given time or space symbolizes True/False. The droplets compute when they collide with each other and change their velocity vectors as a result of the collision.

Most logic gates implemented in fluidic devices (§6) use the phenomenon of merging colliding jet streams (figure 6a) and excitation wave-fragments (figure 11g). Thus, input jet streams or wave-fragments x and y propagating, beyond the collision site, along their original trajectories represent functions $x\overline{y}$ and $\overline{x}y$. A stream or a wave-fragment propagating along a new trajectory represents the function xy. Discrete soft and liquid bodies do not always merge when they collide but often are reflected. Thus, they can implement collision-based gates.

Figure 11.

(a) A thin-layer BZ reaction; travelling oxidation wavefronts are blue. (b,c) Computer model of Agladze diode. (b) Forward propagation. Excitation wavefront propagates from the right to the left. (c) Backward propagation. Excitation wavefront propagates from the left to the right. (d,e) Exploration of London street networks with fully excitable (d) and sub-excitable (e) media. Time lapse snapshots two-variable Oregonator model. (f) Routing of a wave-fragment in a sub-excitable medium. The medium is sub-excitable but two rectangular shapes (white rectangles) are not excitable. Grid size is 500×500 nodes. The pictures are not snapshots of many wave fronts generated at the initial stimulation point, but time lapsed snapshots of a single wave-fragment recorded every 150th step of numerical integration. (g) Collision-based gate. Case shown when both inputs have value True; thus two wave-fragments collide. Time lapse overlays. One fragment is travelling from north-west to south-east, another fragment from south-west to north-east. The wave-fragments collide and fuse into a new localized excitation travelling east. (h) Robotic hand interacts with Belousov–Zhabotinsky medium. When the bending fingers touch the chemical medium, glass ‘nails’ fitted with capillary tubes release small quantities of colloidal silver into the solution and this triggers additional circular waves. Adapted from [131]. (Online version in colour.)

Collision-based computation, emerging from Fredkin–Toffoli conservative logic [86], employs mobile compact finite patterns, which implement computation while interacting with each other [87]. Information values (e.g. truth values of logic variables) are given either by the absence or the presence of the localizations or by other parameters of the localizations. These localizations travel in space and perform computation when they collide with each other. Thus, the localizations undergo transformations: they change velocities, form bound states and annihilate or fuse when they interact with other localizations. Information values of localizations are transformed as a result of collision and thus a computation is implemented.

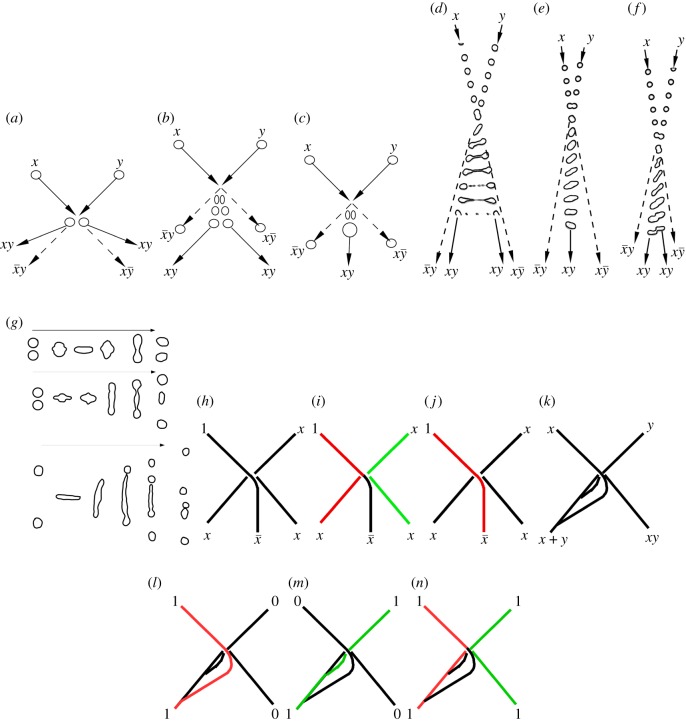
When two hard balls collide they are reflected in such a manner that the trajectory of a reflected ball is at an angle of less than 180° to the trajectory of the same ball not involved in the collision (figure 9a). If the presence of balls represents True values of Boolean variables x and y, then the trajectories of the reflected balls represent $\overline{x}y$ and $x\overline{y}$. This was the inspiration for the Fredkin gate [86]. When balls are soft they are compressed on impact and propagate for some period of time as conjunct bodies. Then their shapes are restored and they bounce back; thus their output trajectories are shifted in time–space (figure 9b). When soft bodies impact each other under particular regimes they might merge into a single ball and lose their momentum (figure 9c); in this case, we have only three output trajectories instead of four. The gate shown in figure 9c is a fusion gate analogous to figure 6a.

Figure 9.

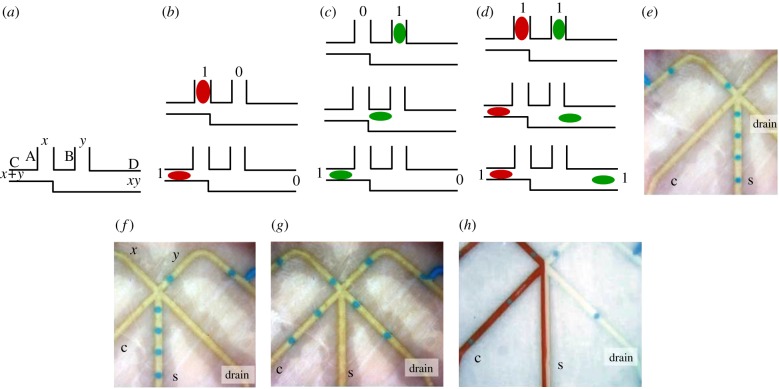
Collision-based computing with droplets and liquid marbles. (a) Hard balls gate, Fredkin gate. (b) Soft balls gate, Margolus gate. (c) Fusion/coalescence gate. (d–f) Gates derived from laboratory experiments [88] with droplets colliding with various offsets: (d) stretching separation, (e) coalescence and (f) reflexive separation. Illustrations of colliding droplets are redrawn from fig. 4 of [88]. (g) Outcome of binary droplet collision experimentally found by Ashgriz & Poo [89]; Weber numbers, from top to bottom are We = 23, We = 40 and We = 96. Collisions are redrawn from [89]. (h–n) Schemes of gates implemented with droplets on a hydrophobic surface in [53]. (h–j) NOT gate, scheme (h), x = 1 (i), x = 0 (j). (k–n) OR–AND gate, scheme (k), x = 1, y = 0 (l), x = 0, y = 1 (m), x = 1, y = 1 (n). In (h–n), the pathway of a droplet originated in channel x is coloured red, and in channel y green. (Online version in colour.)

Outcomes of the collisions between liquid droplets depend on the relationship between fluid inertia and tension (Weber number) of the colliding droplets and their offset. Binary collisions between droplets have been analysed exhaustively by Ashgriz & Poo in 1990 [89] and 20 years later by Rabe et al. [88]. Based on their results, we can derive the following experimental droplet gates: stretching separation (figure 9d) and reflexive separation (figure 9f) of colliding droplets represent a soft balls gate; coalescence of droplets (figure 9e) represents a fusion gate (figures 9c and 6a). For certain parameters of the droplet collisions, one or more stationary droplets are formed [89] (figure 9g); they could represent results of the AND gate and even be used as elementary memory units (the presence of a stationary droplet is ‘1’ and the absence is ‘0’).

Mertaniemi et al. [53] explicitly interpreted collisions between droplets on a hydrophobic surface in terms of Boolean logic gates. They programmed trajectories of droplets, and thus architectures of the logic gates, by the geometry of grooves, on the hydrophobic surface, along which the droplets travel. Examples of two gates are the NOT gate (figure 9h–j) and the OR–AND gate (figure 9k–n). In the NOT gate (figure 9h), there is a droplet travelling along the channel labelled ‘1’. When this droplet ‘1’ collides with the droplet travelling along the channel x, the droplet ‘1’ is reflected into the south-west channel x (figure 9i). When input x is False and only the droplet in channel ‘1’ is present, the droplet ‘1’ travels into the channel $\overline{x}$. The OR–AND gate (figure 9k) shows several channels leaving the collision site, and thus that the droplets x or y are always routed to the channel x + y when each of the droplets enters the gate alone (figure 9l,m). When both droplets enter the gate, they collide. Then one droplet enters the channel xy while the other droplet still travels to the channel x + y (figure 9n).

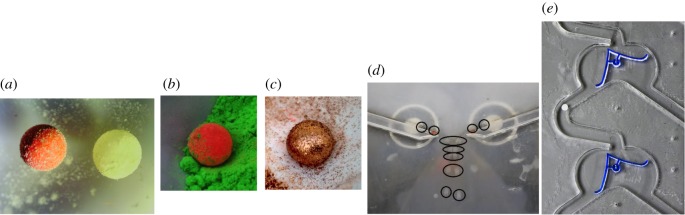
Instead of running droplets on a hydrophobic surface, we can coat the droplets with a hydrophobic power. The droplets then become liquid marbles. The liquid marbles, proposed by Aussillous & Quéré in 2001 [90], are liquid droplets coated by hydrophobic particles at the liquid/air interface (figure 10a–c). In 2016, I proposed to make experimental laboratory prototypes of computing devices allowing the liquid marbles to explore additional degrees of freedom to travel in different directions [92]. The first collision-based logic gate with liquid marbles was prototyped by Draper et al. [54]. An example of the liquid marble gate in action is shown in figure 10d.

Figure 10.

(a) Liquid marbles with Lycopodium coating and water cargo on the right and a mix of red Indian ink and water on the left; marbles are around 5 μl in volume. (b) Fifty microlitre water marble coated by red fluorescent fingerprint powder. (c) Fifty microlitre water marble coated by copper particles. (c) Soft balls gate, figure 9b, implemented with liquid marbles, filmed by a high-speed camera; the gate was prototyped by Draper et al. [54]. Adapted from [54]. (d) A fragment of the liquid marble binary counter presented in [91]. (Online version in colour.)

Computing schemes involving ‘proper’ collision-based gates require a synchronization of signals. Such synchronization is indeed achievable but places an additional burden on preparation of data for computation; thus, simultaneously with developments of synchronous circuits I considered producing experimental prototypes of asynchronous devices based on cantilever moving parts, actuated by liquid marbles [92].

In 1965, J. T. Godfrey [93] proposed a mechanical binary digital computer: the configuration of flip-flops arranged on an inclined surface and operated by metal balls rolling down the surface. The design inspired my group to prototype an asynchronous binary counter actuated by liquid marbles [90] (figure 10e). Droplet and liquid marble devices use the force of gravity to operate. This can be avoided by using self-propulsive liquid marbles, e.g. aqueous ethanol marbles on a water surface [94,95] or polypyrrole and carbon black marbles driven by light [96].

9. Reaction–diffusion computers

All living systems, from cells to brain cortex, display excitable dynamics as part of their dynamical patterns [97–99]. Creatures without a nervous system, e.g. plants [100–108], slime moulds [109–115] and fungi [116,117], employ excitation dynamics, manifested in calcium waves and action-potential-like spikes, in their decision-making processes. The electrical activity in plants, slime mould and fungi might be associated with calcium waves [111,118–125]. Decision-making with calcium waves propagating in living substrates strongly relates to the theory and practice of reaction–diffusion computing.

A reaction–diffusion computer [18,126,127] is a spatially extended chemical system that processes information by transforming an input concentration profile to an output concentration profile in a deterministic and controlled manner. In reaction–diffusion computers, the data are represented by concentration profiles of reagents, information is transferred by propagating diffusive and phase waves, computation is implemented via the interaction of these travelling patterns (diffusive and excitation waves), and results of the computation are recorded as a final concentration profile. Chemical reaction–diffusion computing is among the leaders in providing experimental prototypes in the fields of unconventional and nature-inspired computing.

The Belousov–Zhabotinsky (BZ) reaction—periodic oxidation of malonic acid in solution [128–130], has been a key substrate for implementing reaction–diffusion computers for nearly the last 40 years. In these computing devices, information is represented by travelling oxidation wave fronts (figure 11a) and the computation is programmed by geometrical constraining of the medium or configurations of the excitation initiation sites.

Research on BZ-based information processing started in the mid-1980s when Kuhnert, Agladze & Krinsky demonstrated that a thin layer of light-sensitive BZ reaction can implement contrast modification, detection of a contour and smoothing of the half-tone images projected onto the medium [39,132]. These results ignited an almost 40 year epoch of information processing with BZ medium. Work on image processing with BZ continued till the early 2000s [133–137].

In the mid-1990s, the Showalter laboratory produced a series of experimental prototypes of logic gates implemented via interaction of oxidation wavefronts in geometrically constrained BZ medium [40]. Following this, numerous devices were modelled and/or implemented in the experimental laboratory, including signal switches [138], counters [38], a one-bit adder [139], a many-bit binary adder [140] and decoder [141], three-valued logic gates [142] and a device for square root approximation [143].

Design of potential computing circuits was facilitated by the discovery of a chemical diode [37]. The diode is made of two plates covered with excitable solution. The corner of one plate is close to the plane side of the other plate. An excitation wavefront travelling in the forward direction reaches the contact site between the plates as a planar wave, it propagates through the contact site and then continues expanding in the triangular part of the device (figure 11b). The wave-fragment travelling in the backward direction slows down while propagating towards the corner of the triangular plate (figure 11c). At the contact point, the size of the wave-fragment becomes so small, for the level of the medium’s excitability, that it is annihilated without crossing the contact site between the plates.

The above prototypes constrained BZ medium in templates, that is, BZ computers were programmed by architecture. There is another option to realize logic gates using BZ. This is a collision-based, or dynamical, computation [86,87]; see §8. In 2001, Sendiña-Nadal et al. [144] experimentally demonstrated the existence of localized excitations—travelling wave-fragments that behave like quasi-particles in the photosensitive sub-excitable BZ medium. In the early 2000s, I proposed that the compact wave-fragments can represent Boolean values and execute logic gates by colliding with each other [145]. The wave-fragments can be routed in the medium by using non-excitable domains as reflectors (figure 11f). I employed the localizations to construct several logic gates and circuits [145–149].

BZ medium is also used for optimization tasks, e.g. to assist in maze solving [150–152] and to calculate the shortest collision-free path [87]. Recently, my group found that by tuning the excitability of the medium we can select the critical features of street networks [153,154]. In excitable BZ, oxidation wavefronts traverse all streets of the network (figure 11d). A pruning strategy is adopted by the medium with decreasing excitability when wider and ballistically appropriate streets are selected (figure 11e).

In the early 2000s, the first-ever excitable chemical controller mounted on-board a wheeled robot was constructed and tested under experimental laboratory conditions [20,45,87], and also a robotic hand was interfaced and controlled using BZ medium [128] (figure 11h). Litschel et al. [155] showed that by linking micro-reactors with BZ and establishing excitation and inhibitory connections between the neighbouring reactors, it is possible to generate travelling patterns of oscillatory activity resembling the neural locomotive patterns.

Control of a robot with oxidation wavefronts can be embedded directly in the actuating materials. This can be done by impregnating a pH-sensitive gel with a catalyst and immersing it in the catalyst-free BZ solution: a peristaltic motion will be observed [156]. Such an approach can be advanced to other types of smart materials and soft robots [157,158].

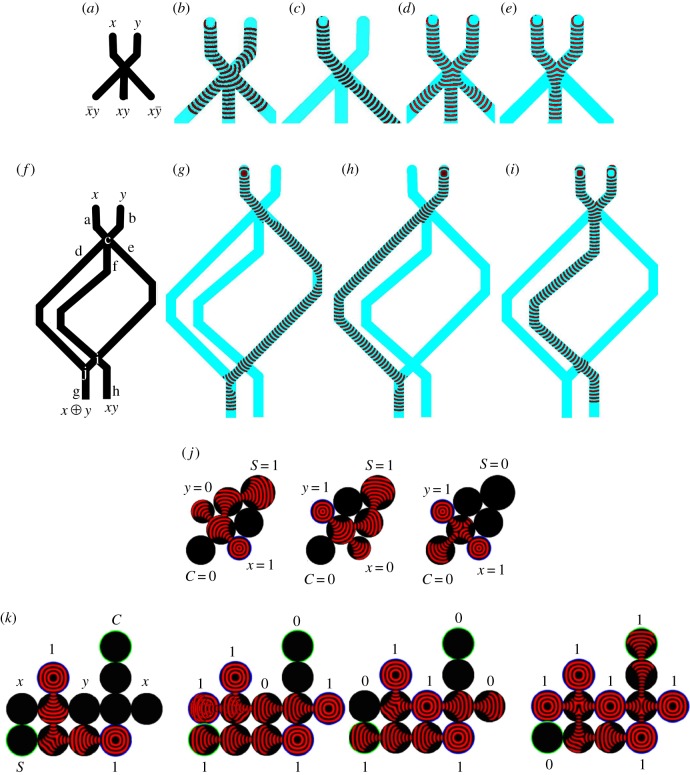
The collision-based gate shown in figure 11g can be also implemented in a geometrically constrained medium, where wave-fragments interact at the junctions of the excitable channels (figure 12) [159]. In excitable mode, stimulation of a single (figure 12b, input x) input leads to wavefronts propagating to all channels. In sub-excitable mode, a wave-fragment from the input channel propagates ballistically to an output channel (figure 12c), but when both input channels are excited the wave-fragments fuse and propagate into the central vertical channel (figure 12e). The fusion gates can be cascaded into a one-bit half-adder (figure 12f–i), and further to a many-bit full adder [159] and Fredkin and Toffoli logically reversible gates [161].

Figure 12.

(a–e) Fusion gate. (a) Scheme: inputs are x and y, outputs are xy, $\overline{x}y$, $x\overline{y}$. (b–e) Time lapse overlays of excitation waves. (b) Excitable mode, x = 1, y = 0. (c) Sub-excitable mode, x = 1, y = 0. (d) Excitable mode, x = 1, y = 1. (e) Sub-excitable mode, x = 1, y = 1. (f) A scheme of a one-bit half-adder: input channels are a and b, output channels are g and h, internal channels are d, e, f, and junctions are c, i and j. Input variables x and y are fed into channels a and b, results $x\oplus y$ and xy are read from channels g and h. (g–i) Time lapse overlays of excitation waves propagating in the one-bit half-adder for inputs (g) x = 1, y = 0, (h) x = 1, y = 0, (i) x = 1, y = 1. Sites of initial segment-wise perturbation are visible as discs. Grid size is 500×790 nodes. See details in [159]. (j) Composite half-adder implemented in two-dimensional BZ vesicles: $S=x\oplus y$, $C=x\cdot y$, where inputs and outputs are all connected to a central reactor disc which can achieve both the AND and XOR functions. Adapted from [160]. (k) Half-adder made from uniform BZ vesicles. Adapted from [160]. (Online version in colour.)

Fine-grained compartmentalization of BZ solutions can be achieved by preparing emulsions or liquid droplets of BZ solution in an oil and liposomes [162–168]. Then each of the droplets can be seen as a computing element interacting with its neighbours via reagents diffusing in oil. Information transmission, as presented by excitation wave fronts, between BZ droplets [164,165,169] has been demonstrated in laboratory experiments. Experimental laboratory computing devices made from arrays of BZ droplets or vesicles are the memory devices made from BZ–oil emulsion [170] and the NOR gate made from BZ droplets with inhibitory coupling [171]. Recently, my group demonstrated prototypes of BZ liquid marbles, BZ solution coated with a hydrophobic powder [172]. There is evidence of oxidation wavefront transmission between BZ liquid marbles, possibly via the gaseous phase; however, more experimental evidence is required to establish the design of potential computing architectures.

As demonstrated in computer experiments, by arranging a configuration of BZ droplets and by tuning sizes of pores between BZ vesicles, it is possible to implement Boolean gates, including collision-based polymorphic gates [173] and binary arithmetic circuits [160,174–176]. In the example shown in figure 12j, a one-bit half-adder is implemented in a simulated ensemble of two-dimensional BZ vesicles. The outputs from the XOR operation are recombined with an OR operation with additional discs in the top right. The circuit employs three methods of signal modulation: connection angle, disc size and aperture efficiency. Vesicles sizes and diameters of pores between vesicles are selected intentionally to perform the desired operations. The half-adder implemented in uniformly sized vesicles having the same diameters of pores is shown in figure 12k.

Recently, Gorecki et al. [177] demonstrated how to make a frequency of oscillation-based OR gate and one-bit memory in an array of coupled oscillatory BZ droplets and to evolve a classifier of BZ droplets [178].

BZ reaction is not the only chemical medium for unconventional computing. In the mid-1990s, Tolmachiov & Adamatzky developed prototypes of reaction–diffusion computing devices capable of approximation of the Voronoi diagram of a planar point set [44] and calculation of a skeleton of a planar shape [43]. Several experimental laboratory prototypes of precipitating processors have been built for implementation of an XOR gate [179], and computation of a skeleton of a planar shape [179] and Voronoi diagrams [180].

10. Discussion

Several contributions to this special issue have demonstrate that a creature does not need a nervous system, in its classical sense, to fuse sensorial inputs, process information and make a decision. The most exciting examples include learning by the slime mould, morphogenetic positional computing, distributed information processing in plant organs, and neuronal-like activity of bacterial biofilms. In the present paper, I show that a substrate does not need to be alive or posses any particular electrical or biochemical properties to compute: even a liquid, which you would be unable to keep in your hands, can perform sophisticated computing circuits.

Back in 2007, while at the ‘Unconventional Computation: Quo Vadis?’ conference in Santa Fe I met Norman Margolus (famous for his block cellular automata model of billiard-ball computers, co-design of the Cellular Automata Machine, and Margolus–Levitin theorem [181]). During our discussion about the nature of computation, Norman stated that ‘any object/substrate either does not compute or is a universal computer’. Fully agreeing with this statement, I would like to highlight that the time for theorizing that ‘natural systems’ compute is over. It is time to produce working laboratory prototypes of actual computing devices based on unconventional computing substrates. This is why in this paper I have exhibited a kaleidoscope of the working prototypes of liquid-based computing devices. I have shown that one can implement logic gates using interacting stream jets, colliding liquid droplets and marbles, and excitation wavefronts in nonlinear chemical medium. Most of the prototypes demonstrated are not liquid-specific. For example, gradient tracing by liquid droplets can be imitated by slime mould growing along a gradient of chemoattractants, and logic gates implemented by jet streams can be equally realized via collision between swarms of soldier crabs or growing plant roots.

The future potential of liquid-based computing is enormous. By selecting an appropriate cargo in liquid marbles, we can implement chemical reactions with two marbles. Thus information values carried by the marbles will not be just the binary physical presence of a marble at a given time in a given space but also concentrations of chemical species inside input and output marbles. A droplet or a marble filled with Belousov–Zhabotinsky (BZ) reaction medium can perform massive-parallel computation by itself because there are thousands of chemical micro-reactors that may act as elementary processors. At the same time, several BZ marbles can implement billiard-ball computing when rolling under gravity in a geometrically constrained space.

In this brief review, I have touched on all principal developments in liquid computing but liquid electronics. The breadth and depth of the liquid electronics ‘eco-system’ would require a separate review paper. Example ‘species’ of liquid electronics devices are liquid–solid phase reversible change of conductivity controlled by temperature [182], field-controlled electrical switch [183], liquid field effect transistor [184] and optical liquid droplet switch [185]. There is a also a huge, and largely unexplored, potential in combining mechanical properties of the liquid jets, droplets and marbles with electrical and optical properties of their solvents and solutes. All these provide scope for future studies.

The primary disadvantages of fluidic computers are now, as they were in the 1960s, lower operating speed (unless air jets are employed), higher power loss and entrapped air [186]. These problems become less important when considered in the context of reconfigurable bioinspired robots or control systems where speed is not critical.

What are the advantages of liquid computers? They do not need an electricity or any other artificial power source and can work just under gravity. This makes liquid computers invincible to electro-magnetic fields and fault tolerant (this is why some components from fluidic logic devices from the 1960s are still used in nuclear reactor control systems [187–189] and fighter jets [190–192]). In many prototypes of fluid computers, there are no moving parts (apart from fluid); therefore the devices have a lifetime substantially longer than mechanical or electrical computers. Fluidic devices can be integrated with and embedded in sensing and actuating materials; therefore they are impeccable controllers for soft-bodied robots [193]. The advantage of liquid droplets and marbles is the ease of their generation and manipulation; this is already well demonstrated by digital microfluidics applications [194–196].

Competing interests

The author declares that he has no competing interests.

Funding

No funding has been received for this article.