The Cognitive Lens: a primer on conceptual tools for analysing information processing in developmental and regenerative morphogenesis

Abstract

Brains exhibit plasticity, multi-scale integration of information, computation and memory, having evolved by specialization of non-neural cells that already possessed many of the same molecular components and functions. The emerging field of basal cognition provides many examples of decision-making throughout a wide range of non-neural systems. How can biological information processing across scales of size and complexity be quantitatively characterized and exploited in biomedical settings? We use pattern regulation as a context in which to introduce the Cognitive Lens—a strategy using well-established concepts from cognitive and computer science to complement mechanistic investigation in biology. To facilitate the assimilation and application of these approaches across biology, we review tools from various quantitative disciplines, including dynamical systems, information theory and least-action principles. We propose that these tools can be extended beyond neural settings to predict and control systems-level outcomes, and to understand biological patterning as a form of primitive cognition. We hypothesize that a cognitive-level information-processing view of the functions of living systems can complement reductive perspectives, improving efficient top-down control of organism-level outcomes. Exploration of the deep parallels across diverse quantitative paradigms will drive integrative advances in evolutionary biology, regenerative medicine, synthetic bioengineering, cognitive neuroscience and artificial intelligence.

This article is part of the theme issue ‘Liquid brains, solid brains: How distributed cognitive architectures process information’.

1. Introduction

Anatomical pattern control is one of the most remarkable processes in biology. Large-scale spatial order, involving numerous tissues and organs in exquisitely complex yet invariant topological relationships, must be established by embryogenesis—a process in which genetic clones of a single gamete cooperate to construct a functional body (figure 1a). This is often modelled as a feed-forward process with complex anatomy as an emergent result (figure 1b). However, a key part of robustness across many levels of organization is the remarkable plasticity revealed by regulative development and regeneration which can achieve a specific patterning outcome despite a diverse range of starting configurations and perturbations. For example, mammalian embryos can be split in half or fused, resulting in normal animals (figure 1c,d). Salamanders can regenerate perfect copies of amputated legs, eyes, jaws, spinal cords and ovaries. Remarkably, scrambled organs move to correct positions to implement normal craniofacial pattern despite radically displaced configurations at early developmental stages (reviewed in [1]).

Figure 1.

Illustrations of cognitive processes in embryogenesis and regeneration. Figure modified with permission after [1]. (a) An egg will reliably give rise to a species-specific anatomical outcome. (b) This process is usually described as a feed-forward system where the activity of gene-regulatory networks (GRNs) within cells result in the expression of effector proteins that, via structural properties of proteins and physical forces, will result in the emergence of complex shape. This class of models (bottom-up process driven by self-organization and parallel activity of large numbers of local agents) is difficult to apply to several biological phenomena. Regulative development can alter subsequent steps to reach the correct anatomical goal state despite drastic deviations of the starting state. (c) For example, mammalian embryos can be divided in half, giving rise to perfectly normal monozygotic twins each of which has regenerated the missing cell mass. (d) Mammalian embryos can also be combined, giving rise to a normal embryo in which no parts are duplicated. (e) Such capabilities suggest that pattern control is fundamentally a homeostatic process—a closed-loop system using feedback to minimize the error (distance) between a current shape and a target morphology. Although these kinds of decision-making models are commonplace in engineering, they are only recently beginning to be employed in biology [2,3]. This kind of pattern-homeostatic process must store a setpoint that serves as a stop condition; however, as with most types of memory, it can be specifically modified by experience. In the phenomenon of trophic memory (f), damage created at a specific point on the branched structure of deer antlers is recalled as ectopic branch points in subsequent years' antler regeneration. This reveals the ability of cells at the scalp to remember the spatial location of specific damage events and alter cell behaviour to adjust the resulting pattern appropriately—a pattern memory that stretches across months of time and considerable spatial distance and is able to modify low-level (cellular) growth rules to construct a pre-determined stored pattern that differs from the genome-default for this species. (g) A similar capability was recently shown in a molecularly tractable model system [4,5], in which genetically normal planarian flatworms were bioelectrically reprogrammed to regenerate two-headed animals when cut in subsequent rounds of asexual reproduction in plain water. (h) The decision-making revealed by the cells, tissues and organs in these examples of dynamic remodelling toward specific target states could be implemented by cybernetic processes at various positions along a scale of proto-cognitive complexity [6]. Panels (a,c,d) were created by Jeremy Guay of Peregrine Creative. Panel (c) contains a photo by Oudeschool via Wikimedia Commons. Panels (f) and (g) are reprinted with permission from [7] and [8] respectively. Panel (h) is modified after [6]. (Online version in colour.)

Cells can work together to maintain a body plan over decades, but occasional defections in this process result in a return to unicellular behaviours such as cancer. Yet, this process is not necessarily unidirectional, as normalization (tumour reprogramming) allows cells to functionally rejoin a metazoan collective [9]. Such dynamic plasticity and anatomical homeostasis (figure 1e) represent clear examples of pattern memory and flexible decision-making by cells, tissues and organs: systems-level functions such as recognizing damage, building exactly what is needed in the right location, and ceasing activity when the correct target morphology is achieved [2]. One of the key aspects of a homeostatic process is a stored setpoint, to which the system regulates. Classic data in deer antler regeneration (figure 1f) and recent work showing permanent reprogramming of planarian target morphology without genomic editing (figure 1g) reveal the ability to alter the anatomical setpoint in vivo. It is crucial to understand how living systems encode and regulate toward specific patterning outcomes, and where on Wiener's cognitive scale (figure 1h) the decision-making processes of patterning systems lie [6,10].

While significant progress has been made with respect to molecular pathways required for pattern control (e.g. [11]), the focus to date has been largely on understanding and manipulating the cellular hardware. The algorithms and ‘software’ that enable cells and molecular networks to make real-time decisions with respect to much larger systems-level properties (size of tail, position of eyes, etc.), and to adjust when the starting state or the setpoint is altered in real time, are still poorly understood. Likewise, a significant gulf exists between mechanistic models of gene-regulatory networks (GRNs) and attempts to understand the functional goal-directedness of large-scale patterning plasticity from a control theory or cybernetic perspective [12]. This knowledge gap is the main barrier to the highly anticipated revolution in regenerative medicine, which seeks to implement in biomedical settings the kind of top-down modular control observed throughout the tree of life. Triggering the repair of damaged complex organs, and building novel, functional constructs (living machines or ‘bio-bots’ [13]) in synthetic bioengineering applications, will require new approaches to complement molecular biology. Knowing which low-level rules to change, in order to obtain desired systems-level outcomes (e.g. adjusting cellular pathways to grow a limb of a different shape), is a well-known ‘inverse problem’ [14] that holds back advances in the many areas of biology and medicine that depend on rational control of anatomical structure. Thus, is it crucial to learn to intervene at the high-level decision-making modules of complex biological systems instead of only trying to micromanage the ‘machine code’ of molecular networks directly [15–18].

The field of neuroscience shows a path forward: not only does it include advances made at multiple levels of description (from synaptic molecules to representation of visual field contents in neural networks to high-order reasoning in primate societies), but it readily incorporates deep ideas from other fields such as dynamical systems theory (DST), thermodynamics and computer science [19–21]. How can the rest of biology benefit from a similar approach, in which multiple levels of analysis and intervention coexist, and in which a focus on computation and information merges with studies of molecular mechanism? Here, we attempt to sketch a roadmap toward filling in the missing pieces for the next generation of developmental and regenerative patterning: lowering the barrier for researchers in pattern regulation to begin to exploit powerful conceptual tools that will complement molecular genetics with the crucial computational, cognitive perspective.

Brains and neurons evolved from far more primitive cell types that were performing similar functions in the service of body patterning and physiology. We and others in the field of basal cognition have argued that, while nervous systems optimized the speed and efficiency of information processing for control of motile behaviour [22], many of the cognitive tricks of brains are reflections of much more ancient processes that performed information processing and decision-making with respect to body structure and function. Many systems, including bacterial films, slime moulds, plant roots and ant colonies, have been shown to exhibit brain-like behaviour [10,23,24]; indeed, the same molecular hardware underlying higher cognition (ion channels, neurotransmitters and synaptic machinery) was already present in our unicellular ancestor. While this is not yet a mainstream perspective, evolutionary contiguity and recent genomic analyses are consistent with the long-known fact that brains and aneural systems share not only molecular components but also computational functions, allowing many aneural and pre-neural systems to implement learning and adaptive behaviour. Despite the unquestioned suitability of hierarchical neural architectures for advanced types of representation, the physiological, behavioural and metabolic robustness of single cells reflects computational needs that are different in degree, not kind, from the obvious cognitive capacities of brains. In metazoans, the somatic and central nervous system computational systems interact, as brains provide instructive cues for organ patterning from the earliest stages of development [25] as well as signals needed for cancer suppression [26], while conversely, brains are able to adjust their cognitive programmes to function well in radically altered body architectures, such as effective vision via eyes made to develop on the backs of animals [27].

The basal cognition field, and the open puzzles of dynamic pattern regulation, challenge us to develop a broader understanding of what kind of physical systems can underlie cognitive processes. When does it make sense to analyse a system as a cognitive system as opposed to an exclusively biochemical perspective? What tools are available for unifying mechanistic or dynamical systems perspectives with information or computation-based ones? Here, we introduce the strategy of the Cognitive Lens—a view of biological systems from a fundamentally cybernetic perspective, asking what measurements, actions, representations, goal states, memories and decisions are being undertaken at the various levels of organization. This view seeks to complement (not replace) molecular descriptions of biological systems; moreover, we do not claim that any one perspective is uniquely correct [16]; next-generation biology requires a versatile toolkit with a variety of Lenses, any of which can be useful to different degrees in specific cases.

We have two main aims in introducing the Cognitive Lens, which is not yet often used outside of behavioural studies and neural systems. First, to briefly overview the idea (fully developed elsewhere, [28–30]) that a mechanism-based (bottom-up) perspective can be complemented with a cybernetic, top-down one for more efficient control of large-scale pattern in regenerative medicine and synthetic morphology settings. Second, to introduce biologists to deep concepts from other fields and illustrate their inter-relationships, in order to lower the barrier for the application of new kinds of models to patterning contexts (figure 2). We first review several key principles of cognition, computation and cybernetics. We then outline methods for quantitative analysis using various well-established mathematical tools and illustrate examples of systems analysed simultaneously by both DST and cognitive science. Regenerative biology serves as an ideal context in which cognitive explanations can facilitate better prediction and control of complex systems. Advances in taming the mechanism–cognition duality will be highly impactful for regenerative medicine, evolutionary biology, cognitive science and artificial intelligence.

Figure 2.

Mapping between various tools and the most related cognitive concepts. A taxonomy mind-map of tools to analyse cognitive phenomena, broadly decomposed into deterministic and statistical. The deterministic toolset further consists of dynamical and algorithmic sub-categories, while the statistical set consists of the information-theoretic and least-action principles sub-categories (see §3a–e for detailed explanation). The mapping between the tools and the cognitive phenomena is not necessarily one-to-one. For example, the dynamical concept of ‘attractor’ can be used to study both the cognitive concepts of ‘decision-making’ and ‘memory’. We explain some of the cognitive phenomena and the tools mentioned here in §§2 and 3; for definitions of those not described in those sections we refer the reader to the Glossary (box 1). Moreover, the list of tools and phenomena shown here is not exhaustive. For example, the well-known ‘Hamilton's principle’ (Glossary) is a type of least-action principle that belongs to the dynamical systems toolset (not shown here). Finally, the mappings between the tools and the phenomena that could be studied with them are proposals, some of which are described in §3. (Online version in colour.)

2. A cognitive perspective of biological patterning

(a). Overview

Metazoan embryogenesis reliably builds an exquisitely complex body plan, which (in many taxa) is actively defended from injury, ageing and cancer by a variety of processes that orchestrate individual cell behaviour towards a specific target morphology. The ability to reach a defined systems-level outcome from diverse starting states is homologous to familiar cognitive processes such as memory and goal-seeking behaviour. While complex outcomes certainly can emerge from iteration of low-level rules with no encoded goal state [30–32], data from regenerating planaria, deer antlers, crab claws and salamander limbs, reveal that target morphology can be re-written (reviewed in [1,14]). Bioelectric circuits in planarian flatworms can be transiently shifted to a state that induces a double-headed worm to form upon future rounds of amputation, while trophic memory in deer produces ectopic tines at locations of prior years' damage in the new antler rack. All of these examples are induced by physiological or mechanical stimuli (experience), not genomic editing, underscoring the parallels with memory: somatic tissues, like brains, can store different information to guide future behaviour (memory) in the substrate specified by the same genome. In other words, the pattern to which regenerative processes build can be permanently re-specified by altering biophysical properties that encode large-scale endpoints [2,8,33]. Thus, evolution makes use of beneficial features of both the emergent complexity (for filling in local details) and homeostatic feedback loops that store anatomical set-points (large-scale goal states). Control circuits that establish and maintain specific system-level patterning states further forge a conceptual link between developmental mechanisms and the cybernetic processes that occupy the transitional domain along the continuum ranging from purely physical events to information-processing computations.

We have elsewhere detailed the many parallels between patterning processes and cognitive ones [33], as well as highlighted the many known roles of neurotransmitters, bioelectric circuits, electrical synapse-mediated tissue networks, etc., in mediating decision-making among non-neural cells during morphogenesis [12]. Whereas brains process information to move the body through three-dimensional space, non-neural bioelectric networks control cell behaviour to move the body configuration through anatomical morphospace. The processes that guide behaviour and cognition are thus parallel to those that guide adaptive pattern remodelling, in both their functional properties and their molecular mechanisms. Likewise, the persistence of functional memories during the dynamic remodelling and even replacement of brain structures [34,35] is revealing the tight integration of cognitive content and body structure control. This suggests that techniques used to probe cognitive mechanisms could profitably be applied to understand the dynamics of pattern regulation. While this approach has driven advances and new capabilities in appendage regeneration [36], control of organ specification in embryogenesis [37] and cancer normalization [38], it is often resisted because of its teleological aspects: a focus on pattern homeostasis and the ability of cells to work towards implementing pre-specified (but re-writable) anatomical outcomes. Fortunately, cybernetics, control theory and other areas of engineering have long provided rigorous formalisms within which to understand goal-seeking devices and processes [39]. Thus, there is significant need and opportunity for new, quantitative theory to smoothly integrate data and models made at the level of molecular mechanisms with those formulated to understand decision-making in morphogenetic contexts from a cognitive perspective.

(b). Defining ‘cognition’

Disparate views exist on what precisely is meant by cognition, which we broadly classify into the following categories: informational, dynamical, statistical and learning. From an informational viewpoint, Neisser defines ‘cognition’ as any process where sensory information is transformed, reduced, elaborated, stored, recovered and used [40,41]. Lyon defines cognition as any set of information-processing mechanisms that enables an organism to sense and value its environment geared towards vital functions such as survival [42]. From a dynamical viewpoint, Maturana & Varela [43] define cognition essentially as life itself, in that they both require sensorimotor coupling or perception–action (a specific type of information-processing mechanism) routed via the environment. From a statistical point of view, cognition may be defined as a process that resists the dispersive tendencies imparted by the second law of thermodynamics by a system containing a boundary that separates it from the environment. Specifically, it imposes a lower bound on the dispersion of the sensory states, by selectively sampling them and using those states to actively infer their causes [44]. A more nuanced take argues that cognition can exist in a system only when a hierarchically separate self-organizing dynamic subsystem (e.g. nervous system or something analogous) within the more basal self-maintaining metabolic system appears, and the two interact to serve the organism's survival [41,45]. The perspective of learning is the simplest of all, where it is purported that any system capable of learning (with respect to intentions) and goal-seeking (to satisfy intention by implementing learned strategies) is a cognitive system [41,46,47]. Goodwin argues that a system that can learn and transmit higher-level ‘laws’ (e.g. those coded in the genome or in the brain that generates language) compared with the lower levels of physics and chemistry are cognitive systems, since these laws constitute the ‘knowledge’ contained by the system of its own behaviour in the context of some environment (e.g. morphogenesis) [47].

A spectrum of definitions of cognition is available in this emerging, interdisciplinary field (see [41] for more). It is well known that defining cognition is a difficult task and that there is no real consensus yet [41]. For this reason, we do not adopt any one definition, but rather focus on tools that can in principle help characterize any of the various forms of cognition. For illustration, in §3e we demonstrate how some of these tools can be applied to characterize one of the most well-known forms of cognition, namely learning. Moreover, our goal in this paper is not to definitively resolve an uncontroversial definition of cognition, but to present tools that can help with research. We believe that progress in experiment and analysis will result in refining an accepted definition, and that it would be premature to establish it at this time. A key aspect of our perspective is that the right question is not whether a given system is cognitive or not, but, eschewing an artificial binary classification, the degree to which a given system might be cognitive. We ask what kinds of information-processing models might provide the most efficient prediction and control of the information-processing drivers of the system behaviour, and where on the Wiener scale (figure 1h) it might lie. This view suggests the applicability of a wide range of conceptual tools (figure 2) to problems outside of neuroscience to which they are traditionally applied.

Cognition is thus a general phenomenon that is substrate-independent, and by implication a higher-level phenomenon, in the sense that diverse cell- and molecular-level mechanisms are dynamically harnessed toward system-level outcomes [2]. For this reason, we suggest that taking a cognitive view of biological processes will aid top-down control. As a further consequence of its higher-level form, cognition does not require a special organ like the brain (we illustrate this important point in §3f with the help of a learning-based example). Even single cells in a multi-cellular organism [46] or single-celled organisms like bacteria possess basal cognitive capacities [2,9], and interestingly use brain-like bioelectric dynamics [48]. Escherichia coli, for example, has pathways for perception and for adaptation, which enables it to efficiently perform chemotaxis, tolerating a broad range of environmental uncertainty by implementing a memory-based mechanism [9]. While some authors believe that life is fundamentally cognitive (requiring information processing at the genetic, physiological and behavioural levels to stay alive in a hostile environment), this is not necessarily the case. While today's living organisms, which have passed a very stringent selection filter, are no doubt significantly cognitive, it is possible that artificial constructs can (and soon will) be created by synthetic biologists which are alive but not cognitive, and thus would not be ecologically competitive outside the laboratory.

The various forms of cognition like those described above can be characterized using tools like those described herein. For example, the sulfur regulome of Pseudomonas can be viewed, through the lens of information theory (§3b), as an ‘information channel’ where information about the environmental features is received in an encoded form and transmitted in a decoded form [49]. Thus, an important aspect of the Cognitive Lens is that it can be applied to a wide class of systems, from evolved natural organisms, to synthetic bioengineered ‘biobots’, to artificially intelligent systems.

(c). Specific patterning mechanisms as a form of cognition

Cell signalling can be viewed as a type of dynamical cognition, since the outcome depends on history of the states (e.g. protein concentrations) and the recursive interactions that determine how the states unfold [50]. For example, the phenomenon of how various cell types emerge from a single type (the germ cell) can be described by a process of symmetry breaking caused by a small change in the interaction between genes (specifically known as ‘bifurcation’; see Glossary, box 1), where molecules in slightly different states suddenly polarize into extremal states (cell types) [50]. This context-dependency lies at the core of cognitive information processing.

Box 1. Ontology glossary (see also [39,51]).

• Active inference: A mechanism by which biological systems employ the ‘free energy principle’, where they minimize free energy either by updating the internal prediction model (beliefs) or by acting to fulfil the prediction.

• Adaptation: A set of actions taken by a system to adjust to the environment. It typically involves tuning of the parameters (e.g. via backpropagation) or the states of a system.

• Algorithmic information dynamics: An approach to characterize causation in dynamical systems that involves constructing algorithmic generative models that reproduce empirical data. It is purported to be a robust alternative to information theory, as it picks up subtle patterns in cases where the latter, which depends on aggregate properties, may not.

• Allostasis: A set of actions taken by a system to establish homeostasis possibly far in the future by anticipating threatening conditions.

• Attractor: A type of limit set to which trajectories converge over time.

• Backpropagation: A technique used to tune the parameters of an artificial neural network (ANN) such that it accomplishes a given task. It involves calculating the derivative of the output error with respect to the parameters, and then making small changes to the parameters in the direction in which the error decreases.

• Basin of attraction: The set of all trajectories that converge to an attractor.

• Bayesian inference: A statistical procedure for updating the likelihood of a hypothesis based on new evidence. The crux of the method relies on a simple law of probability known as Bayes’ rule.

• Bifurcation: A description of how the limit sets change as a function of the parameters of the system. Period-doubling bifurcation is a well-known case in chaotic dynamical systems where the number of attractors keeps doubling as the parameter value increases.

• Cellular automaton: A type of discrete dynamical system (DS) consisting of a set of cells embedded in a lattice, where each cell can be in one of two states, ON or OFF, and all cells have the same transition function.

• Dynamical system: A set of variables and parameters, and a set of equations describing how they relate with each other and how the states evolve over time.

• Free energy principle: A conceptual framework that describes how biological systems might maintain order. According to this principle, biological systems strive to minimize the difference between the observed and predicted (encoded as ‘beliefs’) sensory inputs—the ‘free energy’—thereby limiting sensory surprise.

• Flow: The set of all possible trajectories of a DS.

• Hamilton's principle: A formulation of the principle of stationary action which states that the path taken by a physical system is the one that requires the least total amount of action (e.g. energy).

• Homeostasis: A condition of a system where all variables, or a set of essential variables, maintain their states within viable conditions (e.g. body temperature, blood pressure, etc.)

• Inverse problem: In some complex systems, many agents follow local rules, resulting in a complex emergent outcome (e.g. anthills and intelligent ant colony behaviour emerging from simple rules executed in parallel by millions of ants, or body cells whose activity gives rise to a complex body). The inverse problem is the difficult task of knowing how to change rules at the small scale to result in a desired change in the large-scale (systems-level) outcome.

• Kolmogorov complexity: The length of the shortest algorithm that produces the observed empirical data.

• Learning: A set of actions taken by a system to accommodate mapping of new environmental stimuli to the system's own behaviour, typically in such a way as to enhance survival.

• Limit set: A small subset of the state space that trajectories never leave. A limit set can be a single point or a cycle of points in the state space.

• Memory: A state of a DS, in terms of the variable or parameter states, that represents some past event or environmental stimuli.

• Multistability: The property of a DS referring to its characteristic of containing multiple attractors.

• McCullogh–Pitts neuron: A highly simplified model of a neuron whose activity is ‘all or none’ [52]. The neuron fires if and only if the weighted sum of the activities of its input neurons crosses a certain threshold.

• Parameter: A component of a DS whose value remains fixed.

• Phase portrait: A pictorial representation of the limit sets of the system. It is useful in understanding the long-term behaviour of the system without worrying about the detailed structure of the trajectories.

• Saddle point: An equilibrium point in the state space that has some directions that are attractive and some that are repulsive.

• Stable equilibrium point: A fixed point in the state space where trajectories converge over time.

• State: The ordered set of values of the variables of a DS.

• State space: The set of all possible states of a DS.

• Statistical complexity: A set of statistical measures used to quantify the degree of deviation from randomness in a system.

• Trajectory: A geometric description of a solution of the system obtained by starting at some point in the vector space and following the vectors.

• Transition function: A rule or a mathematical function that dictates the dynamic behaviour of a single node (variable) in a DS.

• Ultrastability: The ability of a DS to change its parameters in response to environmental stimuli that threaten to disturb its homeostasis.

• Variable: A component of a DS whose value changes with time.

• Vector space: A geometric description of the system where every point in the state space is assigned a vector that describes how the states change (direction and magnitude).

Alan Turing proposed a mechanism underlying the emergence of heterogeneity in patterns, which can be classified as a type of informational cognition. He designed a reaction–diffusion system (molecules can both react, altering their concentrations, and diffuse) that generates patterns like stripes, spirals and spots that are strikingly realistic. Turing proposed that such a mechanism underlies the phenomenon of identical cells differentiating and creating patterns by reorganizing themselves [53]. Turing patterns are traditionally compared with biological patterns that are not based on neurons (e.g. shells). However, neural underpinnings of Turing patterns have also been investigated, thus demonstrating that Turing patterns can, in principle, show cognitive properties [54,55]. In a similar vein, associative memory has been shown to be possible in reaction–diffusion systems that are not neural in nature [56], and chemistry-based systems that do not explicitly model neurons have been shown to demonstrate neural-like behaviour [57,58]. Thus, non-neural systems can display cognitive properties as well. In summary, natural links exist between mechanisms of symmetry breaking and emergent spatial patterning and the mechanisms by which past events influence subsequent behaviour (contextual decision-making).

There are numerous examples of neural systems displaying learning-based cognition, but non-neural systems with similar capabilities have begun to surface as well. For example, GRNs have been shown to develop ‘associative memory’ [59–61]—a concept traditionally associated with neural networks, e.g. Hopfield networks [59,60,62]. Interestingly, similar phenomena have been described over a much longer timescale, where population dynamics during evolution can be described by not only gene frequencies but also a kind of associative memory paradigm [60,63–66], where ‘gene networks evolve like neural networks learn’ [60, p. 5]. The central idea of evolutionary associative memory is that phenotypes that are more often visited tend to become more robust owing to stronger evolved associations between the co-occurring genes underlying that phenotype [60]. An analogous ‘selectionist’ principle at play over developmental timescales was proposed by Edelman as a possible mechanism behind brain development and cognition [67]. Decision-making and memory have also been attributed to non-neural bioelectric networks that regulate embryogenesis and regeneration [1,68,69], and cytoskeletal structures inside single cells [70,71].

3. A cognitive toolkit to analyse biological patterning

David Marr proposed to analyse any cognitive system at three different levels (top to bottom): computational (what is the system trying to solve), algorithmic (how it solves the problem) and implementational (what mechanisms does it use to solve the problem) [72]. This strategy for biology is compatible with recent work on expanding explanatory paradigms beyond the molecular focus [16]. Below, we present a cognitive toolkit—a suite of well-established analytical methods that can be applied to understand and control complex biological outcomes. Importantly, these methods are agnostic, hence orthogonal, to the levels of analysis (figure 3). For example, the set of variables used in the dynamical systems analysis could refer to the spiking activity of neurons, cell types or behavioural performance of entire organisms (e.g. maze studies; also, figure 3 legend describes a more detailed example based on learning). Furthermore, we emphasize that the tools in this suite offer a view through which to analyse cognition in all of its manifestations, while being agnostic to its various substrates (whether living or non-living); we illustrate this in §3f with respect to a specific cognitive phenomenon, namely, learning.

Figure 3.

Cognitive systems. A schematic of an analysis approach for cognitive systems: what to analyse (Marr's three levels of analysis) and how to analyse (proposed tools of analysis spanning across the levels). Any tool can in principle be used to study any level (figure 2). Here is an example of how to relate dynamical systems tools with the three levels, in the context of the problem of associative learning (§3f). At the computational level, the associative learning problem may be specified as ‘associate two stimuli, natural and neutral, of which the natural stimulus evokes a response while the neutral one does not. In dynamical systems (DS) language, this may be translated as ‘a system with two attractors, each associated with a stimulus, corresponding to low-response and high-response’ (please see figure 6 for details). At the algorithmic level of analysis, the problem may be solved as ‘every time both stimuli are supplied, let the ability of the natural stimulus to evoke a response also strengthen the ability of the neutral stimulus to evoke the response such that over time the two stimuli become equivalent’. In DS terms, this may be translated as ‘let the internal state associated with the natural stimulus steer that associated with the neutral stimulus to the high-response attractor’. Finally, at the implementation level, the problem becomes ‘design a network with three nodes consisting of two stimuli and one response, where there is a connection between each stimulus and the response, such that the strength of the connection between the neutral stimulus and the response increases over time with the joint application of the two stimuli’. In DS terms, this is equivalent to ‘design a 3-variable (two weights and one response) coupled DS with a positive feedback loop such that the weight-state of the natural stimulus steers the weight-state of the neutral stimulus from the low-response basin of attraction through the basin-boundary to the high-response basin of attraction’. (Online version in colour.)

We broadly classify the tools to characterize cognitive phenomena into four categories (figure 3): dynamical systems, information-theoretic, least-action principles and algorithmic approaches. The same tool can be used to study different phenomena, and the same phenomenon can be studied using different tools (figure 3). For example, both the dynamical tool of attractors and the information-theoretic tool of mutual information can be used to characterize learning from complementary perspectives (described in more detail in §3f). Likewise, the statistical tool of Bayesian inference can be used to study both decision-making and memory (see, for example, [73,74]). Thus, a given cognitive phenomenon has various aspects (dynamical, statistical, etc., as described in §2b) that can be simultaneously studied using the toolkit. In the following, we describe each of the four types of tools in detail along with examples.

(a). Dynamical systems-based approaches

DST constitutes a set of analytical methods that help understand how processes, including cognitive ones, unfold over time, and how they are individually and collectively influenced by endogenous and exogenous entities [75–77]. It is specifically aimed at characterizing the overall behaviour of a complex dynamical system (DS) which is mathematically defined as a set of coupled differential or difference equations. These techniques depict the attractor states, the number and types of attractors, the basins of attraction associated with each attractor, the way these properties change as the parameters of the system are varied, etc. (see Glossary for definitions of the terms). DST methods have been extensively applied to study biological systems. For example, a technique known as ‘bifurcation analysis' (see Glossary) helps explain why a network of interconnected cells and signalling pathways can lead to cells assuming different identities (cell types) despite initial homogeneity [50]. Likewise, the ‘parameter’ of a DS (e.g. coupling strength among cells) can impart it with a potential to exhibit multiple stable states that may for instance correspond to multiple cell types. For example, dynamical systems approaches offer possible explanations for how a cancerous state might originate and stabilize over time [50,78]. Similarly, stochastic outcomes of planarian regeneration experiments [4,79] reveal the need to understand the circumstances that dictate stability of specific outcomes and the stimuli that might shift a system among the different stable anatomies.

A central insight of DS-based modelling is that a DS capable of some cognitive task, e.g. object discrimination, does not necessarily know how to solve the task via formal representation; problem-solving can emerge through a dynamic interaction between the DS and the environment [75]. One of the simplest applications of DST concepts is the view of cell type as an attractor state in the state space of gene expression [80,81]. Importantly, it is the same GRN that is instantiated in every normal cell, and yet the expression profile of one cell may differ from others. In other words, the fate of the cell type depends on the basin of attraction the cell finds itself in, which may be determined by contextual inputs [78]. One possible mechanism by which progenitor cells differentiate into specific types is by destabilizing the attractive state of the former, a process known as critical transition [82].

DS modelling has helped illuminate the control aspects of several patterning systems. For example, an analysis of a dynamical network model of Drosophila disc segmentation has shown that it is sufficient to control a small set of genes to guarantee specific segmentation patterning outcomes [83]. Likewise, an analysis of a dynamical network model of the leukaemia signalling network has revealed how to systematically steer the state of the system into a cancerous state or apoptotic state, also involving the control of small subsets of genes [84].

What kinds of dynamical systems are cognitive? Various views have been offered on this deep philosophical question [45], which can be broadly categorized as behaviour-based and organization-based. The former characterizes cognition as a specific form of behaviour (e.g. a closed-loop brain–body–environment interaction [75]), whereas the latter [45] posits a form of behaviour that is also weakly and bidirectionally coupled with the metabolic processes that scaffold the behavioural system itself (e.g. homeostasis is an integral part of cognition [85]). In this paper, we have stepped aside of this important issue, and rather focused on using dynamical systems as a tool to characterize cognition.

(i). Artificial neural networks

Artificial neural networks (ANNs) constitute a class of biologically inspired dynamical systems that are often used to make classifications (e.g. distinguish among images of dog breeds) and predictions (e.g. forecast stock prices). Conceptually, connectionist ideas at the dawn of the ANN field were important because they forged a rigorous link between simple physical signalling systems and logic operations and memory, which are the primitives of cognition [52,86–89]. This is because, for every set of logical propositions there is a McCulloch–Pitts neural network (see Glossary) that implements it, and vice versa [52]. More generally, for any DS (not just neural networks), there exists an ‘interpretation’ function that maps logical propositions to the regions of its state space [90]. The central idea that connects neural processing and patterning is succinctly laid out by Grossberg [21]: it is the same principle at play in the brain, where neurons sense information, communicate it among themselves and construct neural patterns, that must underlie patterning in systems outside of the brain as well. Accordingly, ANNs constitute an important class of models in various domains of developmental biology: Planarian morphogenesis [91], Drosophila embryogenesis [92] and many more [93]. In all these models, ANNs either learn or control the corresponding developmental process.

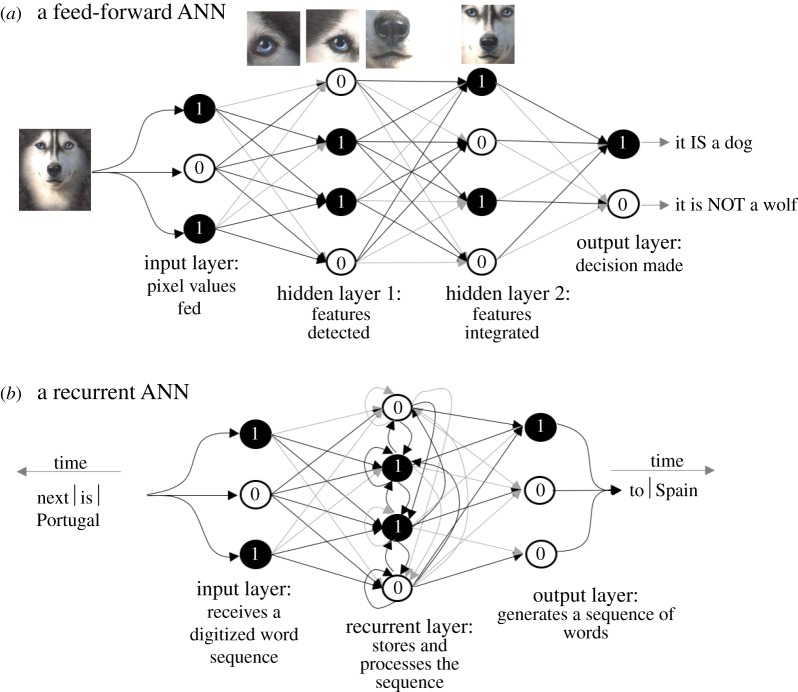
An ANN consists of a network of processing ‘units’ known as ‘neurons’ (figure 4). A unit typically follows a nonlinear threshold-like behaviour, where the ‘firing rate’ which depends on the firing rates of the input neurons follows an S-shape curve (that is, beyond a threshold total input, the output rises dramatically). Every ANN has an ‘input’ layer, zero or more ‘hidden’ (processing) layers and an ‘output’ layer. An ANN computes the output from the input information by processing it in the hidden layers. For example, a classifier-ANN might receive the pixels of the image of a dog in the input layer, and output a number representing the breed by processing various features of the image (size, colour, shapes of the ear flaps, etc.). A predictive-ANN, for example, might receive a sequence of words in the input layer over time, and output the words that it would predict to follow by processing it in the hidden layer (e.g. by drawing from a memory of exposure to past example word sequences).

Figure 4.

The two main types of artificial neural networks (ANNs). Schematics of ANNs, with the arrows representing connections between neurons, and the numbers 1 and 0 representing the possible binary states of the neurons (processing units). The grey level of the edges represents the associated weights. Panels show schematics of possible mechanisms by which: (a) a feed-forward ANN might distinguish huskies from wolves; and (b) a recurrent ANN might predict meaningful sequences of words from an input sequence. (Online version in colour.)

There are mainly two different types of ANN architectures, namely feed-forward and recurrent. Connections in the former flow in a unidirectional manner, whereas they can form cycles in the latter. The main consequence of the architectural difference in terms of functionality is that feed-forward ANNs cannot remember past inputs, whereas recurrent ANNs have the capability to do so by storing an encoding of them in the form of the so-called ‘internal states’ in the hidden layers. For this reason, the input in a feed-forward ANN is fixed, whereas the input in a recurrent ANN can vary over time. Likewise, the output of a feed-forward ANN is a fixed pattern, whereas recurrent ANNs can output dynamic patterns. In this sense, recurrent ANNs not only tend to be better models of the brain but also find better engineering applications [94].

ANNs can be trained to perform specific tasks through a process called ‘learning’ that typically involves adjustment of the connection ‘weights’ (modelled after synaptic weights). A common method of learning in ANNs is known as ‘backpropagation’ where the adjustments to the weights are calculated based on the relationship between the current weights and the output error: if increasing the weight increases the error, then it is decreased by a small amount; otherwise it is increased. A trained ANN that has learned to perform a certain task can be thought of as having a ‘static memory’ in the form of the configuration of connection weights. In comparison, the memory of input sequences in the internal states, as described above, can be thought of as a form of ‘dynamic memory’. Backpropagation is a form of ‘static learning’ where the ANN is trained offline before putting to test, and once trained the weights do not change. Another form of learning is known as ‘dynamic learning’, where the weights could change over time as the ANN is functioning. A classic biological analogue of dynamic learning is Hebbian learning, the principle that neurons that fire together wire together. An example of this type of ANN is presented in §3f.

(b). Information-theoretic approaches

Information theory (IT) offers a set of tools that can help analyse how the constituent parts of a system store, process and exchange information via processes like information acquisition, memory and recall [95]. Claude Shannon formulated mathematical theorems that describe how messages can be passed along noisy channels [95,96]. Measuring the channel capacity of neurons has been the object of active research [95], and it has been reported that the brain operates at an optimal capacity [97]. Remarkably, not just brains, but a plethora of biological systems ranging from GRNs to flocks of brains operate with near-optimal information transmission [97]. We next describe a few basic information-theoretic measures that biologists may find useful.

Entropy is defined as the amount of information gained, or the uncertainty reduced, by learning the answer to a question. For example, if a question can have four equally likely answers but only one of them is correct, then it takes a minimum of two questions to learn the correct answer, and the associated entropy is equal to 2 ‘bits’. If the answers have differing probabilities, then the entropy would be less than 2 bits; it takes fewer than two questions on average to determine the correct answer. Finally, if only one of the answers is possible, then entropy is 0 bits, since there is no uncertainty to begin with [39]. Mutual information (MI) between two variables X and Y is defined as the amount of uncertainty reduced in guessing the value of one by knowing the value of the other. For example, if X represents the state (ON/OFF) of a switch and Y the state (ON/OFF) of a light bulb, and if Y is ON if and only if X is ON, then there is maximum MI between them, since the state of one can be inferred from the state of the other with complete certainty.

The MI measure, as defined above, contains no reference to time, but time is an important feature of communication, since there is an inevitable time delay in the communication between the parts of a system. The transfer entropy (TE) between a source variable X and a target Y partly resolves this issue: it is defined as the reduction of uncertainty in the future state of Y provided by learning the current state of X beyond the uncertainty reduction offered by the past states of Y [98]. Thus, it measures how much ‘pure’ influence X has over Y, beyond what Y's past has. Active information of X is defined as the amount of uncertainty reduced in the future state of X by learning the past states of X. Various other dynamic extensions of MI have been proposed [99], some of which can quantify interdependencies at multiple spatial scales. One such measure, known as effective information, can be used to quantify the average uncertainty reduced by the global state of the system on the future global states, thus quantifying causality [100]. Other related measures are defined in the ‘integrated information theory’ framework [98,100].

One example of these techniques was the analysis of an artificial ‘agent’, driven by a continuous-time recurrent neural network, that solves a relational categorization problem [101]. A ball of some size falls vertically in a virtual space, followed by a ball that is either larger or smaller than the first. The agent is free to move horizontally, and it has sensors through which it can collect information about the features of the ball. The goal of the agent is to ‘catch’ the smaller ball and avoid the larger one. An ‘information flow’ analysis (capturing how information is transferred between the components) of the agent using the above information-theoretic measures, along with certain multivariate generalizations of the same, revealed various interesting features. For example, it was found that the agent performed ‘information offloading’, wherein the position of the agent partially encoded the size of the first ball. Furthermore, the agent was also found to perform ‘information self-structuring’, wherein the agent shapes its own interaction with the environment (in terms of movement) such that its position also encodes the relative size of the two balls [101]. For this analysis, the authors devised novel dynamic extensions of MI that measured the information content between variables at different times or how information was transferred between them [101]. These ideas of offloading and self-structuring, quantified by information-theoretic measures, are philosophically well-founded in the frameworks of embedded cognition [102,103] and embodied cognition [104], which argue for the central roles of the environment and the body of the cognitive agent aside from the brain.

A similar form of information flow analysis has also been performed on a realistic model of klinotaxis behaviour (attraction to salt) observed in Caenorhabditis elegans, revealing several interesting features [105,106]. Some of the findings include left/right information asymmetry between interneurons of the same type, gap junctions playing a critical role in giving rise to the above asymmetry and an ‘information gating’ mechanism where the state of the system determines how information is transferred [106]. Moreover, the above analysis was performed on an ensemble of models all of which reproduced observed klinotaxis with equal performance. The crucial finding was that even though the model parameters widely varied, thus resulting in different models, the emergent information flow architecture was unique [106]. This kind of analysis, complementing recent efforts to understand the signalling perception space of cells in vivo [107,108] will be indispensable to understand the decision-making of cells during development, regeneration and immune system function.

A recent analysis of the GRN controlling the yeast cell cycle [98] found that the TE between pairs of genes in the network was significantly larger compared with the TE measured in the associated null models (models of null hypotheses). This result suggests two key ideas: the operation of the network was selected for by natural selection, and the TE is likely optimized for the cell cycle function. Furthermore, it was found that the TE from global to local scales was much more that of the TE from the local to global scale, thus pointing to an inherent top-down control mechanism [98]. Other applications of IT involve the analysis of the effects of single-gene knockouts on the communication within the system [109], identification of optimal pathways in cell signalling [110] and identification of the mechanisms by which information translates into function [111]. It is clear that numerous opportunities await the application of these ideas to signalling across molecular, cellular and tissue-level agents in pattern regulation contexts.

There are strong parallels between DS and IT that are gradually being revealed [101]. Intuitively, a connection between them would be expected since ‘information is necessarily dynamical’ and ‘dynamics is necessarily informational’ [101, p. 29]. In general, the way in which information-theoretic quantities vary over time in a DS seems to coincide with the geometry of the phase space (see Glossary). For example, in a DS trained to differentiate between objects of different sizes, it was found that the entropy of environmental information (object size) and the MI between environmental and neuronal states coincide with the spread and shapes of the trajectory bundles in the dynamical phase space [101]. In the example described in §3f, we characterize a system in terms of both dynamical systems and simple information-theoretic measures.

(c). Least-action principles-based approaches

One of the hallmarks of biological systems is their obvious goal-directedness. While teleology is a hotly debated subject [6], cybernetics has shown how mechanisms can instantiate goal-seeking processes. In cognitive science, the pursuit of goals by animals is the focus of an active mainstream research programme, and ideas like active inference are only now beginning to be used to understand and manipulate non-neural systems, like organs and appendages which regenerate to a specific shape and then stop [2,112]. Interestingly, physics offers a set of powerful ideas with which to understand systems that attempt to reach a specific end state.

The principle of least action (LA) states that the course taken by a natural process is the one that globally minimizes ‘action’, mathematically defined as the integral of the ‘Lagrangian’ of the system (e.g. the difference between kinetic and potential energies). From this body of mathematical work various special natural laws, like Newton's Laws of motion, can be derived. For example, the path taken by a ball rolling down a frictionless ramp can be calculated using Newton's Laws of motion (a ‘bottom-up’ approach), or using Lagrangian mechanics (Hamilton's principle) simply by requiring that the ball reach the bottom by spending the least total amount of energy (a ‘top-down’ approach) [113]. These principles have begun to be applied to understanding biological complexity, collective behaviour, evolution and brain function [114–118].

Cognitive systems tend to be goal-directed [41], as an important component of cognition is choosing among multiple available options and constructing an efficient path to the goal. Information processing would especially be required to compute the most appropriate path from a set of multiple sub-optimal and perfectly optimal paths. In this sense, LA offers a suitable approach to characterize cognition where the Lagrangian would comprise the combination of how fast the system is and how far it is from the goal. In other words, cognition can be characterized as the set of LA steps taken by the system to attain the goal. On the other hand, we note that goal-directedness and LA are necessary but not sufficient for cognition, since non-living systems exhibit such properties as well (the example of the ball rolling down a plane described above). We next describe specific applications of LA in characterizing the mechanisms of certain cognitive systems.

Learning and inference in neural networks can be viewed as applications of the LA principle [119–122]. If the edge weights of an ANN represent an imaginary particle's coordinates, then the loss function (defined as the error between the observed output and the target) would represent the potential energy of the system of particles and the derivatives of the error with respect to the weights would represent the kinetic energies of the particles [120,121]. Thus, learning in the neural network involves transforming the potential energy (error) into kinetic energies (weight alteration), together constituting the ‘cognitive energy’. The principle of LA simply helps compute the ‘cognitive action’ (the learning trajectory), from the constraint that the least amount of cognitive energy is spent. Such a process is also at play in the case of a neuron becoming a target for a neurotrophic factor, or when a new synapse is generated [122]. Moreover, this view extends to aneural processes as well, like when bacteria display chemotaxis or when humans acquire more resources over time, both targeted at consuming energy in the least time [122].

The ‘free energy principle’ which states that biological systems strive to minimize surprise in their sensory states has foundations in LA. Models of ‘active inference’, based on the free energy principle, have been proposed as underlying embodied perception in neuroscience [123]. In these models, systems strive to infer the causes of their inputs and act to reduce the uncertainty (also referred to as free energy minimization) about those causes [112]. The ‘inference’ part of the model can be viewed as the perception of the system, while the ‘active’ part is its action. Being a model of perception and action, active inference is a model of cognition that helps generate perception–action loops in the most efficient way possible. The unique feature of the active inference framework is that it is very general, as it makes no assumptions about the actual mechanisms involved, thus leading to the hypothesis that free energy minimization is a fundamental property of biological systems [123]. According to this framework, neurons encode a generative model of the world in terms of the sensory signals they should expect at a given instance. The predictions are then compared with the actual sensory signals from which an error is computed. The prediction error is then used to align predictions to the actual signals, whereas the action strives to align the actual signals received to the predictions [124]. A specific mechanism of neural cognition based on active inference, known as ‘predictive coding’, has been proposed [19,125]. In this model, the brain is organized as a hierarchy where predictions are generated in a top-down fashion, whereas prediction errors are propagated bottom-up, thus constituting a form of ‘message passing’ [19].

We have suggested that this kind of process is applicable to biological systems at many levels; cells, tissues and whole organs need to refine internal models of their environments to better anticipate stressors and to properly react to developmental signals. One interpretation of somatic regeneration is that bodies strive to minimize the difference between the current anatomy and the target morphology; it remains to be seen whether the bioelectric and biochemical processes by which cells measure local and global properties to carry out regenerative repair fit the predictions of surprise minimization models. Being a generic model of cognition, active inference approaches have also motivated a variety of aneural contexts, including self-organization in a primordial soup [19], and morphogenesis in a biological model of the flat-worm [112]. Moreover, hierarchical forms of active inference have been proposed as models of specific forms of cognition such as associative learning, homeostasis and allostasis [125,126].

Language—arguably the epitome of cognition—has a unique statistical signature captured by ‘Zipf's Law’, which is a power-law distribution, which expresses the empirical fact that the frequency of a word is inversely proportional to its rank (the position of the word in a list ordered by frequency) [127]. For example, the most frequent word occurs about twice as frequently as the second most frequent word. Clearly, a language has many other features, and yet Zipf's Law is almost universal, since many languages have this property [127]. Of the various possible mechanisms that could generate a power-law [128], those based on the principle of LA constitute some. In one study, a combination of least effort principles and information theory was used to formulate a generative mechanism. In particular, an assumption that a language-generating mechanism minimized communication inefficiency and cost of producing symbols (formulated in terms of information-theoretic quantities) is sufficient to generate a power-law distribution of the symbols [129]. Though there was no rigorous formulation of ‘action’ (the integral of the Lagrangian) in that model, one can imagine it being implicit in the process of communication, as it requires effort. Power-laws, and in general long-tailed distributions, that are characteristic of underlying complexity have been observed in a variety of biological processes [130–133]. It is an open question as to whether LA-based mechanisms are at play in these processes.

(d). Algorithmic approaches

Algorithmic approaches are motivated by the view that all processes are deterministic in nature [134]. They are specifically distinct from the dynamical and informational approaches described above, in that they rely on Turing machines. A Turing machine, originally conceived by Alan Turing, is an abstract description of a general-purpose computer [135]. Modern digital computing devices are just customized physical instantiations of a Turing machine. Since a Turing machine is deterministic, all processes instantiated on it, known as ‘algorithms’, are also deterministic. Thus, the common goal of algorithmic approaches is to infer the simplest algorithm that can reproduce a given set of observations or data, and explain differences between different datasets (e.g. experimental versus control) using differences between the associated algorithms.

A well-established measure in this area is ‘algorithmic complexity’ (AC)—a measure of the length of the smallest Turing machine program that reproduces a set of observations. The measure of AC has helped throw some light on how humans memorize and recall information. Humans tend to use a process known as ‘chunking’ to memorize large sets of information. Essentially, they split the information into chunks of some size, memorize those chunks and attempt to find some way of organizing and relating the chunks to facilitate recall. It has been reported that humans tend to minimize the AC of chunks, which is also directly related to the idea of maximally compressed code [136,137]. AC has also been found to be useful in explaining how humans generate and perceive randomness [138]. The measure of AC has helped characterize certain emergent properties of dynamical systems, hence the link to cognition. For example, it helps predict that as a cell shifts from an undifferentiated to a differentiated state, the epigenetic landscape (in Waddington's terms [139, p. 36]) has fewer and deeper attractors, indicating that the latter states are more stable than the former [134]. Also, it helps characterize the emergence of persistent patterns in Conway's ‘Game of Life’, a type of cellular automaton (Glossary) [140].

(e). An example of cognitive perspective on a molecular developmental mechanism: associative learning in gene-regulatory networks

In this section, we consider the phenomenon of learning—a hallmark of cognition—to illustrate the utility of our toolkit and explore the deep consilience among diverse computational perspectives. Specifically, we show, using the tools of DS and IT, that: (1) two different models of learning show the same dynamical behaviour, and thereby that cognition is substrate-independent; (2) a simple higher-level learning rule emerges from the lower-level rules specified by the models, and (3) learning can be quantified by an increase in the information-level association between the components involved. Specifically, we present a simple GRN that displays associative learning (figure 5), then explicate the learning mechanism from a dynamical systems perspective using some of the tools described above (figure 6). Then, we present an ANN that performs the same function as the GRN, thus demonstrating similar learning capabilities of systems with different mechanisms (figure 7).

Figure 5.

A GRN model of associative learning. A GRN model adapted from [141]. The dynamics of w1, w2 and p follow the ‘Hill’ function, which is traditionally used to model gene activation and repression behaviour through a binding process. An application of conditioned stimulus (CS) alone initially does not evoke a response (concentration of p is close to zero). However, an application of CS following a joint application of US–CS stimuli manages to evoke a response. This is because CS is ‘associated’ with US (unconditioned stimulus) during the joint application, in the sense that the GRN learns to ‘think’ that CS is equivalent to US during subsequent applications of CS alone. (Online version in colour.)

Figure 6.

A cognitive view of associative learning as offered by the tools of dynamical systems. Each panel illustrates the flow together with the phase portrait of the GRN in the space of p and w2 (the w1 axis is ignored for conciseness, since it is not informative). Here, ‘response’ represents the concentration levels of p. The red and green curves in the top and bottom panels, respectively, depict representative trajectories. The red and green trajectories are each split over time across the horizontal panels in their respective rows, as depicted by grey dashed lines connecting the consecutive pieces whose endpoints are marked by colour filled circles. Note that the endpoint of one piece and the starting point of the following piece are of the same colour since they represent the same states. The overall initial state of the two trajectories (green filled circle) are the same. Also shown in each panel are the stable equilibrium and saddle points. The top panels show CS alone cannot evoke a response (red trajectory eventually reaches a low-response state in panel (c)). The bottom panels show that following an association of CS with US, CS alone can evoke a response (the green trajectory eventually reaches a high-response state in panel (f)). Notice that there are two attractors (hence two basins of attraction) when CS alone is applied (right panels). In the dynamical systems view, associative learning is about steering the internal state associated with CS (w2) into the basin of attraction associated with high value of p with the help of application of US. More specifically, a minimum value of w2 is necessary and sufficient to evoke a high response; this is termed the ‘learning threshold’ (the black dashed line in panels (a,c,f)). Here, associative learning is accomplished by w1 ‘shepherding’ w2 above the learning threshold.

Figure 7.

A neural network (NN) model of associative learning. A NN model that performs the same task as the GRN in figure 5. This NN was adapted from [139], but we supplied the appropriate model parameters (electronic supplementary material, Supplement 1). This model consists of the two stimuli, US and CS, and the response (p) just as described for the GRN model above. The main difference is that w1 and w2 in this case are not response neurons (they are molecules in the GRN) but the synaptic weights between US-p and CS-p respectively. Furthermore, this NN follows the Hebbian rewiring principle of ‘neurons that fire together wire together’. The dynamical portrait of the behaviour is very similar to the one for the GRN (electronic supplementary material, Supplement 1, figure S2). Finally, we show an example of how information theory can be used to quantify cognition. We show the normalized MI between the behaviours of w1 and w2 (both change with time, as described above), showing that it significantly increases during the learning step, and it remains higher after learning compared with the MI before learning. (a) Schematic of the NN. US, CS and p (response) represent the same as in the GRN above. The difference is that (1) the dynamics of p follow the sigmoidal activation which is traditionally used to model the integrate-and-fire behaviour of neurons and (2) the synaptic weights are influenced by the activities of the pre-synaptic and post-synaptic neurons following the Hebbian principle. (b) The behaviour (response p) of the NN before, during and after the association step (middle box). The normalized mutual information (MI) between the behaviours of w1 and w2 is also shown during the three phases. Clearly, the MI increases during and after learning, even though there is no direct connection between w1 and w2, thus demonstrating the power of information theoretic tools. (Online version in colour.)

The goal of associative learning, in general, is to pair a neutral stimulus that does not naturally evoke a response to a native stimulus that does, such that the neutral stimulus is sufficient to evoke a response following the association. The neutral stimulus is often referred to as the conditioned stimulus (CS), and the native stimulus as the unconditioned stimulus (US). The GRN presented in figure 5 was adapted from [141], with the only differences existing in the parameter values (electronic supplementary material, Supplement 1). This model consists of input molecules (enhancers, shown in yellow) that bind to certain repressor molecules (red) allowing transcription of memory proteins (brown) that in turn activate the transcription of the response protein (green). The ability of the US to naturally evoke a response (result in a high level of concentration of p) is attributed to the assumption that there is a small constant rate of generation of w1 but not w2. Associative learning in this model is initiated by the joint application of US and CS, which through the positive feedback of p (which is initially increased by the effect of US) and activation by r2, helps increase the level of w2 (figure 6d). Following that, both stimuli are removed, resulting in the lowering of p to zero (figure 6e). Finally, when CS alone is applied, the level of w2, which was raised during the association step, is sufficient to raise the level of p, thus evoking a response (figure 6f). The overall time-varying levels of p in response to the various stimulus are depicted in electronic supplementary material, Supplement 1, figure S1.

A dynamical-systems view of associative learning in this GRN model is shown in figure 6. First, we depict the flow of the GRN under both learning and no-learning conditions. We next observe that when only CS is applied, the system is bistable—two attractors exist (one corresponding to a low level of p and another corresponding to a high level of p), but when US and CS are jointly applied only one attractor exists (high p). When no stimulus is applied, naturally only one attractor exists (low p). Importantly, the separation between the two basins of attraction in the CS-only case is almost entirely determined by the value of w2 (a value of about 600—figure 6a,c,f). What the associative learning step (figure 6d) accomplishes is to guide the state of w2 from the lower basin into the upper basin associated with high p in which case the application of CS alone results in absorption into the upper attractor associated with a high p (thus evoking a response). In other words, associative learning is about placing the system's state in an appropriate context (basin) associated with a desired output. From a complementary point of view, DS analysis has revealed a separation between the learning and non-learning behaviours—the ‘learning threshold’—which must be crossed by w2 to evoke a high response. Specifically, w2 must be greater than about 600 (figure 6a,c,f) to reach the high-response attractor. This higher-level rule is an emergent outcome of the lower-level rules specified by the model, revealed only by DS analysis.

We also illustrate the parallelism between connectionist cognitive models and transcriptional regulatory networks by illustrating a neural network (NN) that performs the same task as the GRN above (figure 7a), and whose dynamical behaviour is akin to that of the GRN (figure 7b and electronic supplementary material, Supplement 1, figure S2). Furthermore, we quantify the increase in association between the stimuli (learning) using information–theoretic tools (figure 7b). Thus, DS analysis not only helps show that the behaviours of apparently different systems are equivalent at the dynamical level, but also reveals higher-level rules the model implicitly makes use of that are not themselves apparent in the model specification.

The Cognitive Lens perspective on workhorse concepts of molecular developmental biology, such as GRNs, is useful because it suggests novel approaches to the control of growth and form. Most contemporary work is currently focused on re-writing the circuits (topology) of the GRNs using transgenes and genomic editing. However, a view of GRNs as learning associations and classification tasks suggests the design of closed-loop stimulation protocols to stably change the behaviour of the GRN via experiences. Our laboratory is currently pursuing the strategy of altering the function of GRNs in disease states and developmental contexts by training and behaviour-shaping strategies taken from cognitive neuroscience.

4. Conclusion

Metazoan bodies harness individual cell activities toward maintenance and repair of a specific anatomical pattern. While the necessary molecular mechanisms of this remarkable process are beginning to be identified, the computational processes sufficient for the observed pattern memory and decision-making represent a fertile area for future research. Progress is stymied by thematic silos: cognitive-like processes and patterning mechanisms are dealt with by very different communities with limited overlap in conceptual approaches. Here, we introduced a variety of concepts from DST, information theory and physics, to help frame a cognitive perspective from which to view patterning and other decision-making mechanisms.

Molecular-genetic and behavioural analyses across taxa show that cognitive abilities arose early in evolution, and developed gradually, expanding from the control of unicellular behaviour and physiology, to metazoan embryogenesis and regeneration, to complex organisms' purposeful behaviour. Thus, we suggest a research programme to migrate tools heretofore used only for analysis of brain function (and machine learning) to other areas of biology—especially pattern control. Dynamic pattern remodelling includes both bottom-up, emergent features (ideally handled by molecular biology and complexity science) and top-down controls, for which new formalisms are only now being established. It is crucial for workers in bench biology to be aware of the deep synergy and consilience between concepts in disciplines like computer science, physics and cognitive science, as these represent extremely fertile sources of inspiration for tackling the next challenges of systems biology and biomedical control.

Fulfilling the promises of regenerative medicine and synthetic bioengineering will require unprecedented advances in manipulating systems-level outcomes (large-scale anatomy and function of complex processes like the immune system). We propose that the most efficient way is to understand and exploit the hierarchical, information-centred processes that organisms themselves use to implement dynamic plasticity and multi-level integration. Optimal outcomes in, for example, regeneration of whole human hands, will be greatly facilitated by understanding how cell behaviour is harnessed toward regeneration and how to exploit the ability of cells to build to a (re-writable) specification. Offloading the complexity onto the cells themselves (not micromanaging), using training and other ways to modify tissue self-models and goal-seeking behaviours will necessitate appropriating successful ideas from other disciplines about the flow of information and control.

Unifications of disparate-seeming concepts and discoveries of fundamental physical dualities have been some of the most powerful revelations in twentieth century science. The time is right for a deep consilience of ideas across several fields, to show that mechanism and meaning (molecular events and information-processing computations/representations) are two facets of the same biological processes. Advances in this emerging field will benefit biology (evolvability, origin of multicellularity), biomedicine (cancer, regenerative medicine) and engineering (custom living machines). As befits the interdisciplinary origin of this research programme, broader impacts can also be expected on artificial intelligence and philosophy of mind, as the physical bases of active cognitive information embodied in biological and synthetic substrates become clarified.

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests.

Funding

This research was supported by the Allen Discovery Center program through the Paul G. Allen Frontiers Group (12171). M.L. also gratefully acknowledges support from the Templeton World Charity Foundation (TWCF0089/AB55), the Barton Family Foundation, the Defense Advanced Research Projects Agency (DARPA) under Cooperative Agreement no. HR0011-18-2-0022, and the National Science Foundation (DBI-1152279 and Emergent Behaviors of Integrated Cellular Systems subaward CBET-0939511). The content of the information does not necessarily reflect the position or the policy of the Government, and no official endorsement should be inferred. Approved for public release.