Critical transitions in malaria transmission models are consistently generated by superinfection

Abstract

The history of modelling vector-borne infections essentially begins with the papers by Ross on malaria. His models assume that the dynamics of malaria can most simply be characterized by two equations that describe the prevalence of malaria in the human and mosquito hosts. This structure has formed the central core of models for malaria and most other vector-borne diseases for the past century, with additions acknowledging important aetiological details. We partially add to this tradition by describing a malaria model that provides for vital dynamics in the vector and the possibility of super-infection in the human host: reinfection of asymptomatic hosts before they have cleared a prior infection. These key features of malaria aetiology create the potential for break points in the prevalence of infected hosts, sudden transitions that seem to characterize malaria’s response to control in different locations. We show that this potential for critical transitions is a general and underappreciated feature of any model for vector-borne diseases with incomplete immunity, including the canonical Ross–McDonald model. Ignoring these details of the host’s immune response to infection can potentially lead to serious misunderstanding in the interpretation of malaria distribution patterns and the design of control schemes for other vector-borne diseases.

This article is part of the theme issue ‘Modelling infectious disease outbreaks in humans, animals and plants: approaches and important themes’. This issue is linked with the subsequent theme issue ‘Modelling infectious disease outbreaks in humans, animals and plants: epidemic forecasting and control’.

1. Introduction

Critical transitions occur when natural systems drastically shift from one state to another. They are currently receiving considerable attention in ecology, geophysics, hydrology and economics [1]. In epidemiology, critical transitions are of relevance to the emergence of new pathogens and the re-emergence of old ones. They may also be central to the within-host dynamics particularly when pathogens evolve or mutate in ways that allow them to escape control by the immune system. Critical transitions often underlie and potentially enhance (or undermine) attempts to control and eliminate infectious pathogens. Following an intervention, the trajectory of the host–pathogen systems may cross a critical transition where pathogen prevalence drops to apparent eradication, the robustness of which is strongly determined by the structure of the transition. Tipping points associated with the coexistence of alternative equilibria are of particular interest, as small changes in a driving parameter can lead to large shifts from low to high levels of prevalence (or vice versa). Continuous external pressure on critical transmission parameters, or seasonal variation in vector abundance, can also lead to hysteresis, whereby a delayed response of the system would effectively keep it trapped longer in either the endemic or disease-free state.

Evidence for the existence of alternative steady states in infectious disease dynamics remains limited [2–4], although they have been proposed as a possible explanation for the observation that malaria often fails to re-invade local regions that have achieved elimination. One potentially important pre-condition for the existence of alternative steady states in malaria is superinfection: the infection of a single host by concurrent multiple strains of the pathogen. Malaria infections are not fully immunizing, and multiplicity of infection (MOI) is common in endemic regions as a consequence of additional infectious bites by the vector before the host has cleared a prior infection. In endemic regions, a large fraction of the human population carries the malaria parasite asymptomatically in non-apparent infections that can contribute to transmission [5,6]. Under these conditions, significant levels of superinfection can create a positive feedback within the intensity of transmission that has the potential to generate multiple alternative equilibria and associated tipping points.

A large number of model formulations have been proposed to capture the complexity of malaria epidemiology [7,8]. The consequences of repeated infectious bites have been represented in models of re-infection by a formulation that only allows a host to re-acquire infection after it has cleared a previous exposure. Two such recent models suggest that this might cause malaria dynamics to exhibit alternative steady states [9,10]. Here, we develop a complementary, but more general, analysis that provides a formulation for superinfection that explicitly allows infections to occur concurrently without interfering with each other. We initially present a semi-analytical approach to identify alternative equilibria in models for vector-transmitted diseases. We then apply these methods to a vector-borne disease model that was used to understand the origins of environmentally driven fluctuations of malaria in epidemic regions [11]. We then broadly consider superinfection in a series of hierarchical formulations of increasing complexity (commencing with the original Ross–MacDonald equations [12–15]). We demonstrate that irrespective of the details, superinfection consistently creates tipping points that can generate hysteresis in responses to control efforts (as well as seasonal variation in vector abundance). We argue that because models for re-infection and superinfection effectively bracket a continuum of different assumptions about within-host dynamics with multiple concomitant infections, then models that include these vital details of malaria biology should consistently exhibit tipping points in their response to control regardless of model formulation. Models that fail to include these effects may be misleading, or of limited utility when used to examine transitions towards low rates of transmission in response to control of vectors or of the pathogen. Although the model is framed in the context of malaria in humans, the results should be more generally relevant to the dynamics of the disease in other, non-human, hosts and to other vector-borne diseases, when immunity is partial and parasite antigenic diversity allows repeated infection.

2. The model

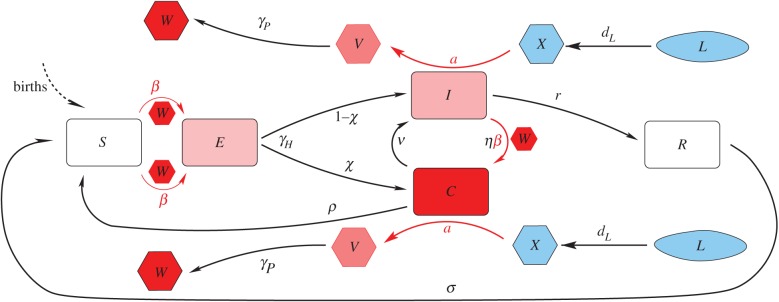
The model is formulated as a system of ordinary differential equations that describe the transmission of the disease between the mosquito vector and the human host. It differs from the standard Ross–McDonald model by explicitly considering the vital dynamics of the two populations. Figure 1 presents the flow diagram of the initial model whose equations are described in detail in the electronic supplementary material, §1. (Simplifications of this model are considered later in the paper.) The mosquito population is subdivided into larval and adult stages, and adult individuals can be susceptible, infected or infectious. The human population has a constant size and deaths are assumed to exactly balance the birth rate; infected hosts are subdivided into two classes to differentiate individuals whose clinical infection leads to treatment from those whose natural recovery leads to the acquisition of immunity. These two classes map, respectively, to symptomatic individuals who are detected by the health system and to symptomatic or asymptomatic individuals who are not. The latter are crucially important as clinical infections typically represent only a small fraction of the total incidence in endemic regions [16–18]. Dietz et al. [19] and Aron & May [20] scale the effective recovery rates, r by transmission intensity (the rate of infectious bites per human). Under the assumptions that (i) infectious bites arrive at a constant rate, (ii) the individual infections within a host proceed independently, and (iii) a constant period, 1/r₀, Dietz et al. [19] derived the following expression for the effective per capita recovery rate:

$$r(\mathit{\Lambda })=\frac{\mathit{\Lambda }}{\exp (\mathit{\Lambda }/r_0)-1},$$ 2.1

where Λ denotes the rate of infectious bites per human, and r₀ is the basal recovery rate when disease transmission is very low (more precisely, in the limit of the infectious mosquito population tending to zero). Thus, the higher the rate of infectious bites per human host, Λ, the slower the disease clearance rate. When this rate Λ is measured per year, it is usually called the entomological inoculation rate (EIR). Finally, we assume that once individuals recover naturally from malaria (including the superinfection state with multiple concurrent infections), they enter a refractory period during which they are transiently immune and cannot re-acquire infection until they return to the susceptible class. Those who receive treatment as a result of detected symptomatic infection either clear infection and move back to the susceptible class, or fail to clear the parasite and flow into the I class. All derived parameters such as the recovery rate and EIR whose expression is a function of basic parameters (and variables) of the model are summarized in table 1.

Figure 1.

The human–mosquito SECIR–LXVW coupled model. The human stages of infection ‘SECIR’ are depicted in the central part of the figure progressing from S to E to I from left to right. The different stages of the mosquito population, from larva (L) to infectious adult mosquito (W), are drawn in the upper and bottom of the figure progressing from uninfected L, larvae and adults (blue) to incubating (pink) and infected adults (red), from right to left (LXVW). Per capita death rates (respectively, δ_H and δ_M, and δ_L in the equations) affect all mosquito and human classes, and for simplicity are not included in the diagram. (Online version in colour.)

Table 1.

Derived parameters are those expressed as a function of basic parameters and variables of the SECIR–LXVW model (figure 1). Their definition is summarized here, together with their appearance in the electronic supplementary material or main text. The full list of basic model parameters with their definitions and symbols is given in table S1 (electronic supplementary material, §1.1).

mosquito parameters
rate of infectious bites per human	$\mathit{\Lambda }=a\frac{W}{N}$	EIR, when expressed as infectious bites per person per year
force of infection	$\lambda =c\hspace{0.17em}a\hspace{0.17em}\frac{I+C}{N}$	equation (2.2)
human parameters
fraction of infectious humans	$y=\frac{I+C}{N}$
loss of immunity rate	$\sigma =\frac{\mathit{\Lambda }}{\exp (\mathit{\Lambda }/{\sigma }_0)-1}$	equation (S7), electronic supplementary material (section 1.1)
recovery rate	$r=\frac{\mathit{\Lambda }}{\exp (\mathit{\Lambda }/r_0)-1}$	equation (S8), electronic supplementary material (section 1.1)
force of infection	β = bΛ + βe	equation (2.2) and equation (S10), electronic supplementary material (section 1.3)
human–mosquito parameters
basic reproduction ratio	R0	equation (S43), electronic supplementary material (section 2.2)
dominant period	T0	equation (S67), electronic supplementary material (section 4)

The couplings between human and mosquito dynamics are given by the force of infection β, the per capita rate at which a susceptible human contracts the disease from infectious bites, and by the per capita rate λ at which adult mosquitoes acquire the pathogen from infectious humans. Under reasonable assumptions [21], these two rates can be written as

$$\beta =b\frac{W}{N}a+{\beta }_e\lambda =c\hspace{0.17em}a\hspace{0.17em}y,$$ 2.2

where b and c are the respective probabilities that humans develop infection once bitten and that mosquitoes acquire the parasite from biting an infectious human host. Moreover, (W/N)a is the number of infectious bites per human host (see definition of Λ above), β_e is an external force of infection and y is the fraction of infectious humans (see electronic supplementary material, §§1.2 and 1.3, for details).

Our model can be seen as an extension of the classical formulation introduced by Ross [22] and MacDonald [23] (RM) (see also [7,21,24] for reviews). Although the original RM model has given rise to a multiplicity of malaria models [8] spanning different degrees of complexity that range from delayed ordinary differential equations (delayed ODEs) to SIR (Susceptible–Infected–Recovered)-like structures, we show that these models are all related to the RM formulation through a set of sequentially simplifying assumptions. In particular, all converge to the RM model, which is based on two strong simplifications: (1) constant mosquito (M) and human populations (N), and (2) only two classes (susceptible and infectious) representing vectors and humans (see electronic supplementary material §7 and appendix A1, for details). We start with the analysis of alternative steady states in the full model of figure 1, and end with the consideration of their more general existence in a suite of models of decreasing complexity. Model parameter space has been explored between maximum and minimum values (around two different parameter combinations—A and B; see electronic supplementary material, table S1 in §1) that provided a good fit to data in a previous study from an epidemic region [11].

3. Results

To identify the stationary points of the coupled system, we present a semi-analytical method that consists of first finding the equilibria of the two submodels, namely the expression for infectious mosquitoes as a function of infectious humans and vice versa. The fixed points are then obtained by calculating the intersection of these two curves (figure 2). The generality and feasibility of this method rest on the linearity of the human and mosquito submodels when considered separately. This means that, for a given number of infectious mosquitoes ($W^{\star }$), the human submodel becomes a linear ODE system. And, likewise, for a given fraction of infectious humans (y), the mosquito submodel becomes a linear ODE system as well. We summarize the main steps of the approach below (full details are given in electronic supplementary material, §3). Once the stationary points have been fully characterized, we can map several quantities of interest onto the parameter space, including the model reproductive number R₀, the expected number of secondary cases produced by an initial single infection in a completely susceptible population, and the dominant period, T₀, associated with the damped oscillations in the transients towards stationarity.

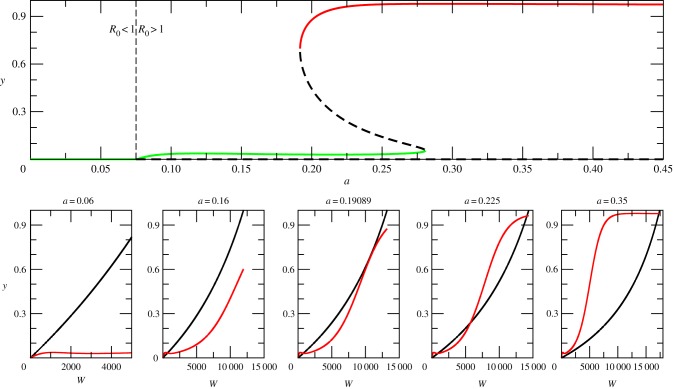
Figure 2.

Relationship between saddle-node bifurcation and mosquito biting rates. When biting rates are low, the curves intersect at zero and malaria fails to establish, resulting in a disease-free equilibrium (R₀ < 1). As the biting rate a increases, the two curves intersect initially at one single point (a = 0.16) corresponding to a stable endemic equilibrium. When the biting rate crosses a critical value (a_C = 0.19089), a tangential bifurcation arises. Further increases of the biting rate end up producing two alternative stable states corresponding to the coexistence of two endemic equilibria characterized by high and low malaria incidence (a_C < a < 0.28). Eventually, only the upper equilibrium is left (a > 0.28). The full bifurcation diagram shown in the upper plot is calculated with parameter combination A (but with β_e = 0; see electronic supplementary material, table S1). It represents a cross section of figure 4b following the horizontal broken line shown there (but here starting at a = 0 rather than at a = 0.15) for incremental increases in biting rate. (Online version in colour.)

(i). Mosquito submodel: stationary points

To obtain the expression for infectious mosquitoes at equilibrium, one first needs to calculate the fixed point for total mosquito abundance. It is easy to show that the mosquito population model has only one globally stable point (electronic supplementary material, §3):

$$\begin{array}{r}{M}^{\ast }=K_0\frac{d_L}{{\delta }_M}\frac{\hspace{0.17em}f-{\delta }_M(1+{\delta }_L/d_L)}{f}\text{and}\\ L^{\ast }=\frac{{\delta }_M}{d_L}\hspace{0.17em}{M}^{\star }=K_0\frac{\hspace{0.17em}f-{\delta }_M(1+{\delta }_L/d_L)}{f}\end{array}.$$ 3.1

A single condition controls when this point is a feasible stable point for the dynamics:

$$\frac{\hspace{0.17em}f}{{\delta }_M}\ge 1+\frac{{\delta }_L}{d_L}.$$ 3.2

Biologically, this condition means that the mosquito population will be locally maintained in a given area when the number of larvae recruited per female during their adult average life time compensates for the larval losses during their development stage. This threshold condition arises naturally in the full expression for R₀ (see electronic supplementary material, equations S28 and S43), whose value is positive only when M* is also positive.

(ii). Human–mosquito model: stationary points

The equilibrium number of infectious mosquitoes $W^{\star }$ is derived by solving the mosquito ODE subsystem at equilibrium when the fraction of infectious humans y (table 1) is considered as a fixed parameter. We obtain the curve

$$W^{\star }=\frac{ac{y}^{\star }}{{\delta }_M+ac{y}^{\star }}{\left[\frac{n_P{\gamma }_P}{n_P{\gamma }_P+{\delta }_M}\right]}^{n_P}{M}^{\star }.$$ 3.3

A second curve is then calculated by solving the human submodel at equilibrium for a given level of infectious mosquito population; this makes β a constant parameter (table 1). This curve for the stationary fraction of infectious humans is given by

$$\begin{array}{rl}y& \equiv \frac{I+C}{N}\\ & =\beta \frac{\nu +(1-\chi )(\rho +{\delta }_H)+\eta \beta +\chi (r+{\delta }_H)}{q(1+z)}{[{\theta }_H]}^{n_H},\end{array}$$ 3.4

where the total force of infection, β, depends on the number of infectious mosquitoes per human, with q and z standing for composite parameters. Full expressions for these parameters and fixed points are given in electronic supplementary material §3, equations (S61)–(S62).

(a). Coexistence of alternative stable states

Figure 2 shows that the intersection of the curves represented by equations (3.3) and (3.4) can produce more that one fixed point. When intersections are present, the corresponding stable points can be computationally calculated with a cobweb procedure (see electronic supplementary material, figure S2). Although this procedure cannot converge to the intermediate unstable equilibrium, this point can be calculated with a standard bisection method [25]. The pair $(W^{\star },y^{\star })$ defines the stationary state and the full solution can then be unfolded from it (see electronic supplementary material §3 for details). Figure 2 also shows that as the biting rate a increases, the system undergoes several bifurcations. Each of these represents the emergence of a new stationary point.

The first bifurcation is transcritical [26] and gives rise to a transition from a free-disease situation (R₀ < 1) to an endemic stable equilibrium (R₀ > 0). This kind of bifurcation is typical of infectious disease models and is found in Susceptible-Infectious-Susceptible (SIS), SIR and Susceptible-Exposed-Infectious-Recovered (SEIR) systems [27]. The second transition corresponds to a saddle node bifurcation (also called a tangential or fold bifurcation). The tangential intersection of the two curves defines a critical biting rate (a_C = 0.19089) at which a pair of resting points suddenly appears, consisting of a saddle node and a second stable point with higher disease incidence. The previous stable point remains for the lower incidence endemic equilibrium. As a result, two basins of attraction coexist, each consisting of initial conditions that lead to one of the two alternative stable states. These basins are separated by the intermediate unstable state. Thus, for the same parameter values and depending on initial conditions, the system can end up in one of two possible stable equilibria for high and low disease incidence, respectively.

The emergence of the first transition (from disease-free to endemic equilibrium) can be characterized by calculating the reproductive number R₀. The transcritical bifurcation corresponds to R₀ = 1 (see vertical broken line in the upper panel of figure 2, and thick broken line in figure 3a). We calculated this quantity as the dominant eigenvalue of the next-generation matrix [28] (see electronic supplementary material §2.2).

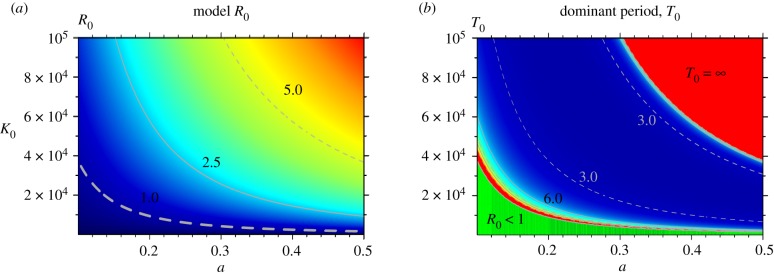
Figure 3.

(a) The reproductive number R₀ (see electronic supplementary material equation S43, §2.2.2) as a function of mosquito carrying capacity K₀ and biting rate a. Values increase from low (blue) to high (red) values. The contour line R₀ = 1 is the thickest broken line delimiting the region where R₀ < 1 on the bottom-left corner. (b) The dominant period of the damped epidemic oscillations T₀ in the same parameter plane (see electronic supplementary material §4). In the region where bi-stability is found, the natural period was calculated for the damped oscillations to the lower stable equilibrium. This period was computed from the complex eigenvalues of the Jacobian evaluated at this lower equilibrium. Within the whole area where damped oscillations are found, the colours go from blue (low values of T₀), in the centre of the region, towards red (high values of T₀), at the boundaries of the region. Selected contour lines representing periods of 3 and 6 years are also shown for guidance. The red region in the upper-right corner corresponds to stable endemic equilibria that are approached monotonically with no transient oscillations (T₀ = ∞). The region in green is the parameter space where the system exhibits global disease-free equilibria. For consistency, we have kept the same convention of red and green areas as in figure 4. In panel (a), χ = 0, and in (b), χ = 0.2. In both panels, other parameter values are those of parameter combination B, with β_e = 0 (see electronic supplementary material table S1, §1). (a) Model R₀, (b) dominant period, T₀.

In addition, we mapped R₀ onto the sub-parameter space defined by the carrying capacity of the vector K₀ and its biting rate a (figure 3a). These two parameters determine the intensity of transmission. The expression underlying R₀ is the same for the model with and without superinfection since this quantity depends only on the basal rates r₀ and σ₀ (see electronic supplementary material §2, equation S43). Moreover, for the regions where damped oscillations occur, the dominant period of those oscillations can be also calculated (see electronic supplementary material §4). In the region of the parameter space we studied (see electronic supplementary material, table S1, §1), we found dominant periods between about 2.5 and 11 years (figure 3b).

Identifying the different regimes of the system requires us to determine the local stability of the different fixed points. The Jacobian matrix J* is evaluated at the corresponding fixed points and its eigenvalues are obtained as the roots λ of the characteristic polynomial:

$$p_J(\lambda )=det(J^{\ast }-\lambda \hspace{0.17em}\mathbb{1})=0,$$ 3.5

where 1$\mathbb{1}$ is the identity matrix. Because this polynomial can have as many roots as the dimension of the dynamical system, a fixed point is asymptotically locally stable if and only if its associated eigenvalues λ_i have all strictly negative real parts. In that case, if the imaginary part of the dominant eigenvalue is not null, damped oscillations are observed in the approach to the fixed point. We determined different properties of the stationary state, such as the possibility of coexisting fixed points, parameter-induced bifurcations and the presence of endogenous (damped) oscillations. The resulting possible dynamical regimes are mapped onto different subregions of the parameter space in figure 4. Comparison of the upper and lower panels shows that the coexistence of alternative steady states critically depends on including superinfection in the model.

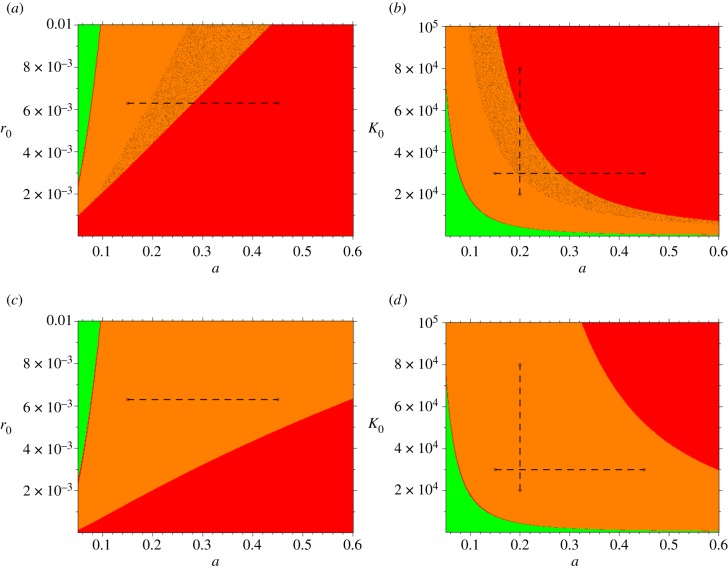
Figure 4.

Dynamic regimes. Relationship between key parameters in the model and the emergence of bifurcations. In all cases, the x-axis depicts the biting rate a and the y-axis, either the basal recovery rate r₀ (a,c) or the carrying capacity K₀ (b,d). The coloured regions delineate different domains of dynamics behaviour. The orange regions correspond to non-trivial disease equilibria that are locally stable and are approached with damped oscillations. Within these regions, two stable equilibria coexist in the shaded area (panels (a) and (b)). The red regions correspond to stable endemic equilibria that are approached with no oscillations. The green regions represent the region of parameter space where the system exhibits global disease-free equilibria. The fraction of infectious humans exhibits a bifurcation in the section illustrated by the broken lines in the upper panels. These lines cross a region where a single-stable equilibrium gives rise to two coexisting stable equilibria as the value of either of the bifurcation parameters increases (see also figure 5c and electronic supplementary material, figure S2, panel d). The lower panels present phase diagrams for the same model structure and parameter combinations but without superinfection (parameter combination A, with β_e = 0, from electronic supplementary material §1, table S1). These panels are representative of the more widely used model, whose rates of recovery (r = r₀) and loss of immunity (σ = σ₀) are constant. Clearly, these simplifications fail to capture the tipping points and multiple equilibria seen in the upper figures.

Our procedure to calculate fixed points is completely general and can be applied to any coupled vector–human model. It is independent of specific assumptions about the force of infection, including the existence of an external source of infection, as well as other possible ways in which both the mosquito and human submodels might be defined, as long as both of these are linear ODE systems when considered separately. In the electronic supplementary material (see §§1 and 7), we add further realism and apply the approach to a system where the exponential distribution of disease incubation times in both human and mosquito submodels has been replaced by the more general (gamma) distribution, which effectively reduces the variance of the incubation period without changing its average value [29]. The gamma distribution has lower variance than the exponential distribution. Here, these distributions are implemented for humans and vectors, respectively, with a chain of n_H and n_V compartments. The higher their number, the lower the variance of the resulting distribution. The stationary solution reduces to the case illustrated in figure 4 when n_H = n_V = 1 (see also, electronic supplementary material, table S1).

(i). Hysteresis

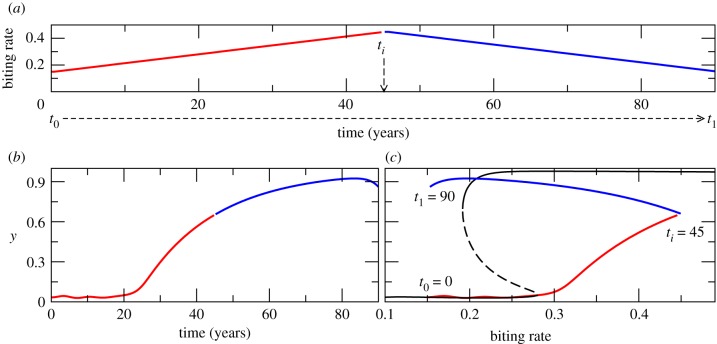
Coexistence of stable equilibria can underlie sharp transitions between levels of disease prevalence if a sufficient perturbation is applied to the system to move it from one basin of attraction to the other. The responses to more gradual changes in parameters can instead lead however to hysteresis [1], which is of key interest to malaria control, since the dynamic memory of the system can delay responses and allow the persistence of endemicity beyond the bifurcation point at which we would expect elimination to occur. A related further possible effect is an asymmetry in the temporal trajectories from endemicity to elimination, and from elimination to re-emergence. These hysteresis effects are illustrated in figure 5 for slow changes in the biting rate a; these might occur during the transition between dry and rainy seasons. We consider first changes from an initial biting rate a = 0.1 at t₀, to a value of 0.5 at the intermediate time t_i, and then back to its initial value at time t₁. The response of the system is illustrated for the fraction of infectious humans (y = (C + I)/N), a measure of disease incidence, where N is total human population (figure 5b,c). The response of the system to a linear increase of the biting rate is a nonlinear increase in disease incidence (figure 5c). This can be represented as a hysteresis cycle on the corresponding bifurcation diagrams (panel c). In fact, extensive initial increases in a leave disease levels almost unchanged up to a certain threshold. In addition, there is clear asymmetry in the two opposite control trajectories: the identical linear trajectory back to the initial low levels of the biting rate does not return the system to the same initial levels of disease incidence (figure 5). Beyond the threshold, the system has been pushed towards a higher incidence state from which it is hard to return. Although decreasing a back to its initial low values would eventually lead the system to settle down at the initial low incidence equilibrium determined by imported infections (for ${\beta }_e\ne 0$), the transient trajectory to this final state can be very long. Provided everything else remains constant, the amplitude of hysteresis cycles depends on how fast the driving parameter changes. The same behaviours can be illustrated by measuring system response in terms of the EIR (electronic supplementary material, figure S2 in §5).

Figure 5.

Hysteresis cycles. Response of the fraction of infectious humans to a slowly increasing biting rate a, from low to high values and back (a). Other parameter values are given by set A of electronic supplementary material, table S1. We plot the time evolution of the system when considering superinfection. The blue and red curves correspond to dynamics with a biting rate that increases and decreases respectively as a linear function of time. These diagrams takes us across changes in a given by the horizontal broken line in figure 4a. Because of the slowing-down effect, as biting rates go from low to high and back in a linear way (a), disease incidence (y) shows a highly nonlinear response (see panel b), which can also be represented as a hysteresis cycle in the bifurcation diagrams (see panel c). (Online version in colour.)

(ii). Model robustness

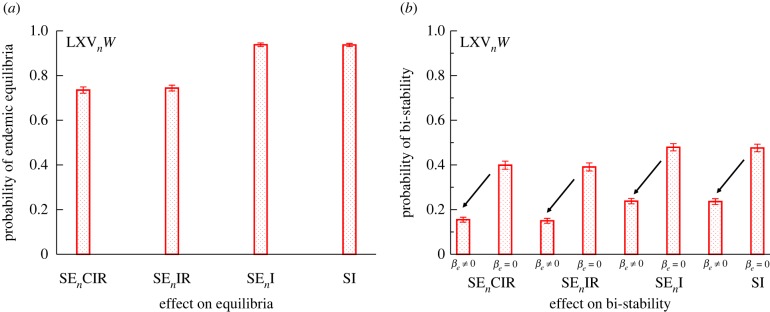
In order to quantify how the presence of bi-stability in malaria models depends on their degree of complexity, we evaluated the relative size of the region of parameter space where this behaviour arises for different formulations (figure 6). We specified 16 different human–mosquito coupled ODE models of increasing realism. The models are labelled according to the number of classes considered for the human and mosquito populations: four possibilities for the former (SE_nCIR, SE_nIR, SE_nI and SI), and four for the latter (LXV_nW, X_KV_nW, XV_nW and XW). Without exhausting possible variations, this scheme results in a total of 16 different combinations, which are labelled as SE_nCIR–LXV_nW, SE_nCIR–X_KV_nW (see electronic supplementary material, §7, for a detailed description of each model). When a model increases in complexity by the addition of new model parameters (encoding particular processes), the fraction of parameter space leading to a given dynamical regime can increase, remain unchanged or decrease. The fraction of parameter space where a given regime is found is calculated by randomly drawing parameter sets within minimum and maximum values (as given in electronic supplementary material, table S1) and evaluating the fraction of those draws leading to a given dynamic regime. Figure 6 compares models from the perspective of the relative size of regions with endemic equilibria or bi-stability. The exercise suggests that the coexistence of alternative stable states is robust to model simplification. This is shown here by representing the probability of bi-stability as model complexity decreases, from the SECIR–LXV_nW, a model with 21 parameters, to the SI–LXV_nW, a model with only 13 parameters (figure 6b). Even the simplest mosquito–human coupled model (SI–XW), with only eight parameters, corresponding to the RM formulation, exhibits this feature as long as the positive feedback introduced by the slowing down of the human recovery rate under repeated infectious bites is maintained (see electronic supplementary material, §6 and figure S4). For each of these model combinations, the removal of the slowing-down effect in the recovery rate that is produced by superinfection eliminates bi-stability (as shown in figure 4c,d). We also show the effect of one added parametric dimension, the introduction of an external force of infection, in models that combine the mosquito subcomponent LXV_nW with human submodels of decreasing model complexity (figure 6b). These ‘open models (${\beta }_e\ne 0$)’ show a relative decrease in the fraction of the parameter space showing bi-stability, mainly owing to the linearizing effect of external infections.

Figure 6.

Effect of model complexity resulting from the addition of human and mosquito classes (and the corresponding increase in the number of parameters) on the fraction of the full parameter space corresponding to either the existence of a single endemic equilibrium (a) or the presence of bi-stability (b). (a) Effect on equilibria and (b) effect on bi-stability. (Online version in colour.)

In summary, superinfection introduces a slowing-down effect on recovery rates as infectious bites increase, which is a necessary condition for the presence of bi-stability. Bi-stability only arises, however, in certain regions of parameter space. Under superinfection, further refined necessary conditions for a given parameter can be derived. The presence of bi-stability can be studied in any vector–human coupled model by comparing the slopes of the curves represented in figure 2 at the origin for W = 0. By using this strategy, for instance for the model SI–XW, we derived a necessary condition for the onset of bi-stability in terms of b, the probability of infection of a susceptible human upon receiving an infectious bite. This condition b_c < b < 0.5 indicates that b has to be lower than 50% but higher than a certain critical threshold b_c determined by the other model parameters (see derivation and threshold value in electronic supplementary material §6.1).

4. Discussion

The results described here demonstrate that superinfection introduces the possibility of alternative steady states of low and high prevalence, with important implications for malaria control programmes. These findings resonate with insights gained from studies of other pathogens whose population dynamics exhibit nonlinear regime shifts, for example in [30] for the hepatitis B virus (HBV). Mathematical models for vector-borne diseases have tended to adopt representations of immunity from classical SIR formulations and to assume that coinfection with different strains of the same pathogen is a rare or unusual event. Yet immunity to malaria clearly differs from that in standard epidemiological models assuming full protection upon recovery (classical SIR models), and MOI is common in endemic regions where antigenic diversity is extremely large. Naturally acquired immunity involves diverse immunity responses to the different phases of the parasite within humans [31], and the major antigen of the blood stage of infection (PfEMP) is encoded by a multicopy gene family exhibiting extreme variation [32–34]. The antigenic complexity of the parasite in high transmission regions underlies superinfection and goes hand-in-hand with the existence of a vast reservoir of asymptomatic infections in individuals of all ages [5,6,35,36].

Similar epidemiological patterns of high prevalence and widespread population immunity characterize other vector-borne infections of non-human hosts in tropical regions [37]. Here too, a high degree of antigenic variation underlies superinfection, as shown for Anaplasma marginale, the most globally prevalent vector-borne pathogen of livestock infecting both wild and domestic ruminants [37]. Thus, our results might apply to other complex pathogens transmitted by vectors in human and non-human hosts whose immune responses must contend with large repertoires of antigenic variants.

In falciparum malaria, the additional nonlinearities created by important details of acquired immunity mean that bi-stability may not be uncommon in its empirical dynamics. Its presence would most likely express itself when control pushes the prevalence of the disease to lower levels, or more disconcertingly when malaria is expanding its range and establishing or re-establishing in new areas. It may have been ignored in linear statistical analyses focused on the impact of climate change on vector dynamics, or the quality of data available may have been gathered at insufficient temporal resolution or extent to detect sudden transitions in levels of prevalence. A recent study of highland malaria using long-term data from Kericho in Kenya presents evidence for the critical slowing down in malaria dynamics in response to different control strategies (M Harris, S Hay S, J Drake 2019, personal communication).

Dynamical consequences of bi-stability are numerous for outcomes of intervention and emergence/re-emergence. Small changes in parameters (for instance, biting rate a or mosquitoes’ carrying capacity K) could give rise to large changes in incidence. Progressive control efforts may see no clear decrease of incidence until a sudden effect finally occurs. To achieve elimination, these efforts would require pushing transmission intensity to lower levels than under more standard transcritical transitions because of hysteresis. Drastic intervention may thus be required to move the system into the basin of attraction of the low prevalence equilibrium, and in so doing, avoid the transient effects of hysteresis with a protracted persistence of high prevalence. In the opposite direction, elimination states may be more robust than in the case of standard transcritical transitions. Empirical evidence for the plausible robustness of the elimination state has been discussed in [38,39]. Also, the progressive relaxation of control efforts in endemic regions could generate sudden transitions from low to high incidence. Similarly, the range expansion and invasion of disease-free regions will tend to achieve low or high prevalence in a discontinuous fashion depending on the local conditions determining transmission intensity. Only beyond the upper threshold for which a single equilibrium exists (for R₀ ≫ 1) will invasion establish high prevalence. For lower transmission intensity and R₀ > 1, the importation of cases would be trapped into the low prevalence equilibrium, even in areas where conditions previously allowed high prevalence. Finally, concerning variability, sudden shifts from low to large fluctuations in incidence may follow in epidemic regions from environmental conditions such as temperature warming driving the system across a critical threshold [11].

A positive feedback is the key ingredient for the strong nonlinearities that underlie regime shifts and associated alternative equilibria, as also illustrated by a number of ecological systems [1]. In our model, a positive feedback is introduced by the slowing-down effect of transmission intensity (rate of arrival of infectious bites) on the recovery rate (r) and therefore, the lengthening of the duration of infection. Thus, higher transmission intensity sustains and exacerbates higher transmission itself. Interestingly in HBV, higher prevalence of carriers leads through higher transmission rates to a younger age of infection, which in turn results in higher probability of carriage [30]. These are both examples of the reinforcement of transmission intensity through positive feedback. A second effect we considered in our model is on the lengthening of the duration of immunity (through σ). This effect is not sufficient for the occurrence of alternative steady states. This observation finds a clear explanation in the contrasting effects of the two assumptions: a lengthening of infectious periods produces a positive feedback on infection duration and transmission rate. With longer infections, a higher number of vectors acquire the parasite, increasing the rate of infectious bites, and concomitantly further slowing the recovery rate. By contrast, a deceleration of the loss of immunity slows down the return of resistant hosts to the susceptible class, and the resulting higher number of immune individuals decreases the number of infected vectors. In brief, this implements a negative feedback on transmission intensity.

Our derivation for the implications of superinfection for a critical transition is robust to consideration of a wide range of malaria models spanning different levels of complexity. Even the simple RM model exhibits bi-stability when the recovery rate slows down with increasing transmission intensity.

Previous malaria models showing bi-stability differ from ours in that they assume re-infection, and therefore only allow a host to re-acquire the parasite after complete clearance of infection and its return to the susceptible state [9,10]. When our findings are taken together with those of these earlier models, they underscore the broad generality of critical transitions in malaria models regardless of specific biological details on multiple infections and within-host dynamics. This generality follows from the observation that re-infection and superinfection (in the sense implemented here) effectively bracket a continuum of possible assumptions on the outcome of repeated exposure to infectious bites. In the former, repeated infections completely interfere with each other; in the latter, they do not ‘see’ each other at all. Neither complete interference (re-infection) nor a complete lack of interference (superinfection) is likely. Reality is likely to fall somewhere in between and closer to superinfection given that in endemic regions MOI is the rule rather than the exception, and that re-infection formulations cannot capture it.

A different kind of mechanism independent from repeated exposure has been proposed for alternative steady states in malaria dynamics. This mechanism combines density-dependent biting rates and disease-induced mortality [2]. This mechanism assumes that increasing disease levels would decrease total human population through disease-induced mortality, which then makes biting rates higher since they depend on the density of infectious mosquitoes per human, which, in turn, would raise infection levels in the human population. We believe this positive feedback is less important and considerably less general than the one described here, although it could work in conjunction with the main mechanism of repeated exposure described here, either through re-infection or superinfection.

Multiplicity of infection and the large antigenic diversity of the Plasmodium parasite in endemic regions complicate the acquisition of immunity in ways that can only be captured phenomenologically in standard transmission models. Whereas our abstraction is more suitable for the question addressed and the associated analytical approaches presented here, more complex representations could explore the generality of bi-stability. These representations include the explicit consideration of antigenic/strain variation and MOI in compartmental and individual-based models (e.g. [40–43]) and the age of hosts in age-structured (partial differential equations) models [44]. Stage-structured models could also be used to represent increasing levels of immunity acquired through repeated exposure, beyond the two-stage models considered so far [9,44]. Multiscale models representing both between-host and within-host dynamics (e.g. [45]) could investigate the consequences for critical transitions of relaxing our assumption of completely independent overlapping infections. We expect bi-stability to also occur in these more complex models depending on parameters.

An important next step is to confront these kinds of dynamics with data from surveillance efforts across changing control and environmental conditions (e.g. [44]). On-going developments in ecology and epidemiology include early warning systems related to critical transitions [46–49] and the prediction of bifurcations based on the monitoring of large perturbations [50]. These efforts should be brought together with sustained surveillance efforts over time and space, and with theoretical findings on the behaviour of mathematical models for the population dynamics of malaria and other vector-borne infections.

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests.

Funding

No funding has been received for this article.