Predicting plant disease epidemics from functionally represented weather series

Abstract

Epidemics are often triggered by specific weather patterns favouring the pathogen on susceptible hosts. For plant diseases, models predicting epidemics have therefore often emphasized the identification of early season weather patterns that are correlated with a disease outcome at some later point. Toward that end, window-pane analysis is an exhaustive search algorithm traditionally used in plant pathology for mining correlations in a weather series with respect to a disease endpoint. Here we show, with reference to Fusarium head blight (FHB) of wheat, that a functional approach is a more principled analytical method for understanding the relationship between disease epidemics and environmental conditions over an extended time series. We used scalar-on-function regression to model a binary outcome (FHB epidemic or non-epidemic) relative to weather time series spanning 140 days relative to flowering (when FHB infection primarily occurs). The functional models overall fit the data better than previously described standard logistic regression (lr) models. Periods much earlier than heretofore realized were associated with FHB epidemics. The findings were used to create novel weather summary variables which, when incorporated into lr models, yielded a new set of models that performed as well as existing lr models for real-time predictions of disease risk.

This article is part of the theme issue ‘Modelling infectious disease outbreaks in humans, animals and plants: approaches and important themes’. This issue is linked with the subsequent theme issue ‘Modelling infectious disease outbreaks in humans, animals and plants: epidemic forecasting and control’.

1. Introduction

One defining feature of epidemiology is the pursuit of successfully predicting epidemic outbreaks or disease occurrences before they are realized. Weather impacts diseases; many animal, plant and human diseases are driven by weather, and epidemiologists are often interested in understanding how disease outbreaks are correlated with weather patterns, especially in a changing climate [1,2]. Epidemiologists may be interested in a static endpoint (disease has occurred or not by a given time, or disease intensity has exceeded a threshold defined in terms of impact), or they may be interested in following the progression of disease occurrences over time in relation to weather, in which case the endpoint is now dynamic. These issues and different objectives have spawned several analytical methodologies, ranging from the use of time-series analysis [3] to distributed lag models [4]. The underlying goal is the same: does weather at some time s influence disease at another time t? In this article, we focus on plant diseases, but the concepts and methodology can be applied to many other disease systems.

All crops are susceptible to diseases caused by pathogens. Whether a plant disease epidemic is realized or not depends on a favourable combination of susceptible host (plant), the presence and abundance of disease-inducing pathogen propagules (inoculum) and environmental conditions that promote inoculum production, its dispersal, infection of the host, colonization and disease development [5]. A low level of disease is common in most crops, but sporadic epidemics can unacceptably reduce crop quality or yield. In some cases, plant disease epidemics can be prevented by genetic resistance in the host plant. In the absence of genetic resistance (an all too common situation), farmers must often depend on the judicious use of crop protection chemicals, preventing diseases from becoming severe enough to economically impact quality or yield. Such interventions are costly and should ideally coincide with an actual risk of disease outbreak (or the subsequent losses). For many crops, these management decisions are supported by predictive models that help farmers evaluate (forecast) disease risk and the need for intervention [5–7].

Human disease risk (operationally defined in different ways) may be connected to weather-related variables at different times [3,4,8]. Identifying suitable weather-based predictors of disease is a significant challenge within any modelling paradigm, for humans, animals or plants. Many plant disease forecast models or decision support systems are driven by weather variables reflecting conditions favouring the plant pathogen at critical crop developmental stages (e.g. [9,10]). In most cases, predictors are based on previous research linking weather conditions to different stages of plant disease development. When using empirical modelling, it is common for plant disease epidemiologists to mine a time series of weather variables with the objective of identifying time periods and variables correlated with a disease outcome [11]. One popular (logical) formalization of this approach in the field of plant pathology is a so-called window-pane analysis [12]. The algorithm divides a continuous time series (such as daily temperature) into discrete fixed-length ‘window-panes’ and then exhaustively searches for associations (e.g. statistical correlation) between summaries of conditions within a window (e.g. mean or sum) and a disease outcome (such as disease severity on a continuous scale or a binary categorization of disease into low and high levels). The starting and ending times over which windows are defined, as well as window length, can be set by the user, with typically many different window lengths and starting times considered. Many overlapping windows are created by sliding the start (end) points along the time series. Results from a window-pane analysis then inform the construction of fixed-time/fixed-window-length variables to be used in models.

From the statistical perspective, window-pane analysis can be criticized for being ‘data dredging’. It leads to the problem of selecting variables from a set of highly correlated predictors [13,14], the possibility of spurious large correlations with the outcome [15], and extreme multiplicity in testing correlations [16]. Multiplicity issues and p-value-based testing [17] of correlations are further compounded by trying several window lengths and many starting/ending times. Plant pathologists typically do not consider the multiplicity problem, with some exceptions [16]. Functional data analysis (FDA) is a refinement over the traditional window-pane approach [18]. In the functional paradigm, a continuous weather time series is represented by a mathematical curve, which is analysed in its entirety relative to an outcome. There is no discretization of the series into arbitrary window panes, and therefore no splitting of a potential signal across several windows. FDA is a rapidly growing field [19] that was only recently introduced to plant pathologists [20].

In this article, we investigate one form of FDA, namely scalar-on-function regression [21], as a means of identifying weather variables and time periods associated with epidemics of Fusarium head blight (FHB), arguably the most economically important wheat disease in many parts of the world [22,23]; and of great concern because of pathogen-produced mammalian toxins in affected grain. There are several different empirical models for FHB risk prediction [24], including the National FHB risk model (http://www.wheatscab.psu.edu/) that is routinely used in the USA. We show that FDA, by making full use of a weather-related time series, is effective for modelling the temporal relationship between weather and FHB epidemics. In so doing, FDA can lead to novel predictors which, when incorporated into existing model structures, can lead to similar or improved prediction accuracy relative to that of models currently used for FHB prediction.

2. Results

Altogether 26 different models for predicting FHB epidemics were fit (see electronic supplemental material, figure S1). Twelve models were built upon previously reported logistic regression (lr) models with variables summarizing weather in fixed-length windows near wheat anthesis (flowering) [14]. Six of these 12 lr models (1, 2, 3, 5, 15, 17) were focused on pre-anthesis conditions, whereas the other six models (7, 8, 9, 11, 12, 13) targeted post-anthesis conditions. Six penalized scalar-on-function regression (s-o-f) models (4, 6, 10, 14, 16, 18) were fit with inputs being weather times series from 120 days pre-anthesis to 20 days post-anthesis, a much longer time frame than the 30-day anthesis-centred period underlying the 12 lr models.

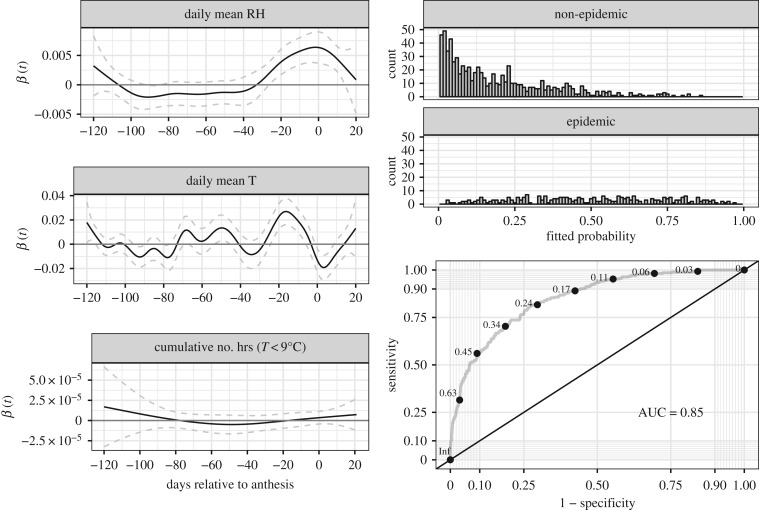
Figure 1 illustrates an s-o-f model fit to the data, in this case model 16. There were three weather series (120 days pre- to 20 days post-anthesis) in this model: daily mean relative humidity (RH; %), daily mean temperature (T;°C), and the cumulative number of hours in which T < 9°C. The β(t) curve for daily mean RH indicated a positive and consistent association between this condition and FHB epidemics from about 30 days pre-anthesis continuing into the post-anthesis period. Daily mean T exhibited its strongest positive association with FHB epidemics at about 15 days pre-anthesis, with the association turning negative in the 10-day post-anthesis window. The relatively flat β(t) curve for the cumulative number of hours in which T < 9°C indicated this variable was weakly associated with FHB epidemics (after adjusting for the other variables in the model). Model fitting returned the probability that an observation was an FHB epidemic. Distributions of fitted model probabilities showed much overlap between the two disease classes (epidemic and non-epidemic), though the non-epidemic class tended to have lower probabilities. The incomplete separation of the two classes by model-fitted probabilities highlights the difficulty in accurately predicting FHB epidemics from local environmental data. Nevertheless, the ROC plot in the lower right panel of figure 1 shows there is predictive value in relatively simple models (in the sense that model 16 uses only three weather series.).

Figure 1.

Scalar-on-function regression results for model 16. The left column of panels shows the fitted β(t) regression coefficient (see the code in the electronic supplementary material) for each of three weather series across 140 days (with 95% confidence intervals calculated from the estimated coefficient standard errors). Sections of the β(t) curves away from 0 indicate windows in the weather series positively (or negatively) associated with FHB epidemics. The upper two panels in the right column show the model-fitted probabilities for FHB epidemic and non-epidemic observations. The lowest panel in the right column shows the Receiver Operating Characteristic (ROC) curve; different cut-points are indicated along the curve. Sensitivity = proportion of FHB epidemics correctly classified. Specificity = proportion of FHB non-epidemics correctly classified; hence 1 – Specificity is the proportion of FHB non-epidemics incorrectly classified as FHB epidemics.

After examining the results from all six s-o-f models, another eight lr models (19–26) were formulated from newly derived predictor variables summarizing windows not considered previously [14]. Predictor inputs to four of the new lr models (21–24) covered pre-anthesis conditions. Two models (19, 20) were focused on post-anthesis conditions, and the last two (25, 26) covered conditions in windows spanning anthesis (see the electronic supplementary material).

Models with two scalar predictors, accounting for cultivar genetic resistance (resist) as well as for combinations of wheat type with maize residue presence/absence, overall fit the data better (mean AIC = 992) than models with resist as the only scalar (mean AIC = 1030). Twenty of the 26 models had three weather-based predictors. Generally, increasing the number of weather-based predictors in the model from one (mean AIC = 1058) to three (mean AIC = 1005) led to better model fit. The s-o-f models fit the data better on average (mean AIC = 932) than either the 12 original lr models (mean AIC = 1044) or the eight new lr models (mean AIC = 1035). However, this was not true for all pairwise comparisons of the models (e.g. s-o-f model 4 (AIC = 1043) compared with lr model 15 (AIC = 1024)). On average, the new pre-anthesis lr models (mean AIC = 1052) were as competitive as the original pre-anthesis lr models (mean AIC = 1057) in terms of model fit. However, the new post-anthesis lr models (19, 20) were no better (mean AIC = 1038) than the original post-anthesis lr models (mean AIC = 1032). The greatest improvement in model fit, from the lr perspective, came from the two new lr models (25, 26) in which the weather-based predictors summarized pre- and post-anthesis conditions in windows spanning anthesis (mean AIC = 999).

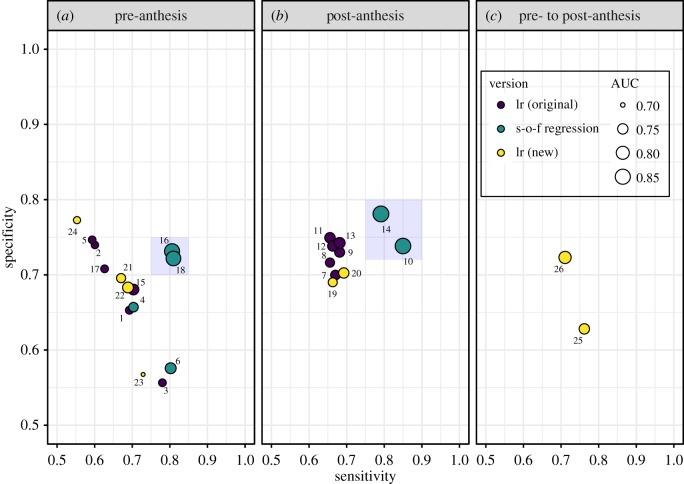
We were ultimately interested in how well the models predicted the occurrence of FHB epidemics. In terms of sensitivity and specificity, the new pre-anthesis lr models were as competitive as the original lr models (figure 2a) but could not match the performance of two s-o-f model versions (models 16 and 18; located in the light blue area of figure 2a). Similarly, none of the post-anthesis lr models were as good as the s-o-f versions (models 10 and 14; light blue area of figure 2b), bearing in mind that all the s-o-f functional predictors covered a period from 120 days pre- to 20 days post-anthesis. Model 26, with predictors summarizing conditions in windows beginning pre-anthesis and ending post-anthesis (thus including and spanning anthesis), offered one of the better overall balances between sensitivity and specificity from the lr perspective (figure 2c). Four s-o-f models (10, 14, 16, 18), all with three weather series, had the lowest misclassification rates (MR) overall (mean MR = 0.237), compared with the entire set of lr models (mean MR = 0.310).

Figure 2.

(a–c) Sensitivity and specificity for the models. The scalar-on-function regression models were not restricted by period relative to anthesis but were placed in the panels corresponding to their associated standard lr model versions. Points are labelled with the corresponding model.

3. Discussion

Scalar-on-function regression is applicable to any situation where interest lies in modelling a static outcome (binary or continuous) in relation to explanatory variables observed over time. Recent examples have included the modelling of myocardial infarction occurrences in relation to electrocardiographic traces [25], of lupus flares from daily stress levels [26] and of influenza rates from weather in the previous weeks [8]. We illustrated, via application to a pernicious disease of wheat [27], the utility of scalar-on-function regression in predicting a binary plant disease outcome. FHB epidemics have proved difficult to predict with high accuracy from local weather [28,29]. Part of the difficulty has to do with defining and identifying predictor variables that are correlated with FHB epidemics [30], and this is where window-pane-type analyses have in the past played a key role [16]. Practically, all FHB models to date have focused on relatively short windows around anthesis (not illogical, as infection occurs primarily during this growth stage), and our s-o-f results do support that notion. In an earlier analysis, we showed how function-on-scalar (f-o-s) regression (i.e. modelling of how a functionally represented weather series depends on a scalar representing FHB epidemic class) could be used to explore the relationship between FHB epidemics and weather. That analysis relied primarily on graphical assessments of associations and did not involve prediction of epidemic outcome (as epidemic class was not the response variable in the f-o-s models). Confirming those earlier findings [20], s-o-f modelling in the present article identified other longer windows that were associated with FHB within weather series (presumably accounting for pre-anthesis pathogen reproduction and dispersal, and post-anthesis colonization). However, functional modelling is not the panacea for FHB prediction; for instance, s-o-f model 4 with mean daily RH as the sole weather series predictor (see the electronic supplementary material) was no better than some of the lr models, which demonstrated that reliance on a single weather time series is not enough.

Functional models with up to three weather series fit the FHB data much better than lr models. Nevertheless, lr models are at this time more amenable for large-scale deployment and rapid real-time updating of predictions, as done for the publicly available forecaster of FHB in US wheat. For these reasons, our approach was to use FDA as a methodology for identifying which temporal regions of various weather series were most associated with FHB epidemics. Summaries of those latter windows were used to formulate new lr models that were competitive with existing models. One of the more significant findings was that summaries over windows which crossed anthesis were better input predictors than summaries that were restricted to either side of anthesis; our earlier modelling efforts generally focused on pre-anthesis weather with the objective of providing FHB predictions before anthesis so that fungicides could be applied [27]. However, post-anthesis fungicide applications against FHB may also be effective [31]. Functional modelling, as we have shown, can be useful in the process of developing simple (lr) models that are at least as good as existing models, that make use of novel predictors, and which add to the pool of existing models to choose from. Having a suite of simple, practical models opens the possibility of model averaging approaches to disease prediction [32].

For examining weather series in relation to epidemic outcomes, FDA [18] is a more principled methodology than window-pane analysis, a standard approach in plant disease epidemiology for decades [33]. The functional approach avoids the multiplicity issues in statistical testing that plague the window-pane technique [34]. We postulate that functional approaches to analysing other disease occurrences in relation to weather time series is a promising endeavour that may lead to more refined predictive models and novel insights into disease–weather relationships.

4. Methods

Field observations (999 total) of FHB epidemics (N = 273) and non-epidemics (N = 726) were linked to field-specific temperature (T), RH or combinations of T and RH conditions (TRH), and to cultivar resistance level (resist), wheat type (spring or winter wheat market class) and the presence or the absence of maize residue (a source of the pathogen inoculum) [20]. The FHB observations (Y_i, i = 1, … ,999) were binary; that is Y_i = 0 for FHB non-epidemics, and Y_i = 1 for FHB epidemics. The expected value of Y_i, E(Y_i), was modelled via standard lr:

$$g[E(Y_i)]=\mu +\hspace{0.17em}{\beta }_1{X}_{1i}+\dots +\hspace{0.17em}{\beta }_h{X}_{hi},$$ 4.1

where μ was the overall intercept, and the β_j were regression coefficients for each of the h predictors (which could be categorical, continuous or a mixture of both). The logit link function g(.) makes equation (4.1) linear with respect to the h predictors. The β_j are constants to be estimated by the model. Twelve lr models for predicting FHB epidemics were fit to the data (models 1, 2, 3, 5, 7, 8, 9, 11, 12, 13, 15, 17; fully described in the electronic supplementary material). They were versions of previously reported lr models [14]. Weather-based predictors (derived from T, RH and TRH) in these models summarized conditions in narrow windows (5–15 days before or after flowering), as previous analyses found correlations between FHB epidemics and weather in these short-length periods [16]. Flowering (anthesis) is the critical time for infection: inoculum production and dispersal take place in the pre-anthesis period, with spike colonization and toxin production occurring post-anthesis.

Penalized scalar-on-function (s-o-f) FDA regression models [21] were fit to the Y_i with scalar predictors for resist, wheat type and maize residue, and weather series for T, RH and TRH (from 120 days pre-anthesis to 20 days post-anthesis) as functional predictors. The s-o-f regression model was

$$\begin{array}{rl}g[E(Y_i)]& =\hspace{0.17em}\mu +\hspace{0.17em}{\alpha }_1{Z}_{1i}+\dots +{\alpha }_n{Z}_{ni}\\ & +\int {\beta }_1(t)X_{1i}(t)\hspace{0.17em}\mathrm{d}t+\dots +\int {\beta }_p(t)X_{\hspace{0.17em}pi}(t)\hspace{0.17em}\mathrm{d}t,\end{array}$$ 4.2

where E(Y_i) was modelled with respect to an intercept μ, n scalar covariates (Z) whose coefficients (α) did not vary with time (t), and p functional predictors (X) with time-varying functional coefficients β(t). The term ‘functional’ here means that the X(t) (as well as the β(t)) are smooth continuous curves (approximated by mathematical functions). Penalization finds a balance between β(t) that are too smooth (interesting features having been smoothed away) and β(t) curves that are too wiggly (risk of noise being modelled and hence leading to a lack of interpretability). Functional regression versions of model groups (1, 2, 3), (7, 8, 9) and (11, 12, 13) were the s-o-f models 4, 10 and 14, respectively. The functional versions of the lr models 5, 15 and 17 were the s-o-f models 6, 16 and 18, respectively. Functional regression models were fit with the pfr function in the refund package (v. 0.1-16) in R (v. 3.4.4).

After fitting s-o-f models, periods associated with FHB epidemics were identified from the magnitude of the estimated β(t) regression parameters. Twelve new variables (built from T, RH and TRH) were created as summaries over periods associated with FHB epidemics. These 12 variables formed the basis of eight new lr models (19–26), each with three weather-based predictors and scalar predictors representing resist, wheat type and maize residue.

Models were compared by way of the Akaike information criterion (AIC), area under the receiver operating characteristic curve (AUC), sensitivity (the proportion of FHB epidemics correctly classified as such), specificity (the proportion of FHB non-epidemics correctly classified as such) and misclassification rate (proportion of all observations that were incorrectly classified). The latter three statistics were derived after estimating the Youden Index (the classification cut-point which maximizes sensitivity + specificity − 1) from the fitted probabilities given by each model [35]. Detailed results for each model fit are given in the electronic supplementary material.

Data accessibility

The datasets supporting this article have been uploaded as part of the electronic supplementary material.

Authors' contributions

All authors participated in the conception of the project and its design. D.A.S. analysed the data and wrote the first draft of the article, with all authors contributing to revising and finishing the product.

Competing interests

We declare we have no competing interests.

Funding

This research was supported by the U.S. Wheat & Barley Scab Initiative (Agreement nos 59-0206-6-015 and 59-0206-4-018).