Abstract
An important step in data preparation involves dealing with incomplete datasets. In some cases, the missing values are unreported because they are characteristics of the domain and are known by practitioners. Due to this nature of the missing values, imputation and inference methods do not work and input from domain experts is required. A common method for experts to fill missing values is through rules. However, for large datasets with thousands of missing data points, it is laborious and time consuming for a user to make sense of the data and formulate effective completion rules. Thus, users need to be shown subsets of the data that will have the most impact in completing missing fields. Further, these subsets should provide the user with enough information to make an update. Choosing subsets that maximize the probability of filling in missing data from a large dataset is computationally expensive. To address these challenges, we present ICARUS, which uses a heuristic algorithm to show the user small subsets of the database in the form of a matrix. This allows the user to iteratively fill in data by applying suggested rules based on their direct edits to the matrix. The suggested rules amplify the users’ input to multiple missing fields by using the database schema to infer hierarchies. Simulations show ICARUS has an average improvement of 50% across three datasets over the baseline system. Further, in-person user studies demonstrate that naive users can fill in 68% of missing data within an hour, while manual rule specification spans weeks.
1. INTRODUCTION
Data used for analysis is often incomplete. Reasons for this can be broadly classified into two categories: 1) random missing data, which includes incomplete response, attrition, human error and 2) data that is not reported because it is known by practitioners. Traditional methods for dealing with missing data, such as imputation or learning, address the first category. These methods do not apply to the second category since imputation and machine learning are based on observed values. When the data is unreported because its values for specific instances are known, the observed data will not contain results for those instances. Thus, inferred values for unreported instances will be highly inaccurate. Our work addresses this second category of missing data. In the rest of this paper we use inputs, edits, updates and completions interchangeably to mean the user filling in a null field.
1.1. Motivating Example
To better illustrate our contributions, we consider a real-world clinical microbiology task [28] at the University’s medical center, where ICARUS has been deployed for biomedical researchers to use on real data for the past six months. Microbiology laboratories report sensitivities of antibiotics to infection-causing organisms in urine cultures. Each laboratory result contains an organism that grew in culture and whether certain antibiotics are effective against it. If an antibiotic is effective in killing the organism, the organism is said to be sensitive (S) to it, otherwise it is resistant (R). Depending on characteristics of the organism, antibiotic, and institutional preference, laboratories only do sensitivity testing for a subset of antibiotics. For example, if the organism Staphylococcus aureus is sensitive to the antibiotic Cefazolin, it is also sensitive to the antibiotic Cefepime. Hence, for Cefazolin sensitive Staphylococcus aureus, Cefepime is unreported and there is no evidence in the data to learn or impute from. For auxiliary use of this data, such as modeling risk of resistance to individual antibiotics [17,27,28], sensitivity information on all antibiotics is needed. For such cases, the unreported data has to be filled in by domain experts, such as physicians and microbiologists, whose time is expensive. Manually specifying rules is time consuming and can span multiple weeks. Hence, experts need to be able to effectively interact with the data.
A normalized database schema for this dataset might consist of the six tables shown in Figure 2A. In this example, the antibiotic table is self-referencing with nested classes. The organism table also has a hierarchical relation where an organism references the family it belongs to, which in turn references its gram_stain. The culture table links every culture to the organism it grew. The culture_antibiotic table is a many-to-many join between cultures and antibiotics, with the result field storing R/S/null indicating resistant, sensitive or unknown respectively. To complete null values in the result field, the culture, organism and antibiotic tables need to be joined with the culture_antibiotic table. However, this only shows organism and antibiotic pairs, which is not enough to complete all missing sensitivities. The user further needs to look at the sensitivities that have been tested for the antibiotics of the same family for that culture. This corresponds to a pivot on culture_id, so that each row represents a culture and each column an antibiotic (Figure 2B). In a many-to-many join, pivoting on one of the join values can create a very wide table, making it hard to reason about the data. Thus, there is a need to guide the user on which updates will have the most impact, and allow them to apply that update to multiple cells by expressing the edit as a rule.
While much work has been done in using rule-based systems to identify and correct errors, including HoloClean [44] and NADEEF [15], they have focused on using violations to known conditional functional dependencies (CFD) and integrity constraints. Interactive rule systems such as guided data repair [55] and Active-Clean [34] use a combination of machine learning and human input to learn rules. They select elements for user validation which are likely to increase the accuracy of their models, which is not applicable in our case when some user rules contradict the data. Further, these systems deal with cleaning dirty data, while our system addresses unreported data that is semantically knowable. He et al.’s Falcon [26] is the only system that we know of which addresses a similar problem of reducing user effort in an interactive cleaning system. Falcon iteratively asks the user multiple questions based on a single update, to find the most general update query but is unable to provide guidance on which updates will have the highest impact, i.e., will fix the most number of values. Further, Falcon generalizes updates by using attributes within one table, but does not use foreign-key relations among tables, which can apply to a larger number of values. Thus, previous works either do not allow direct updates and suggest rules based on violations to CFDs and knowledge bases [13,55], or if they allow updates [26,46], they do not provide guidance on useful updates. In summary, we need to address the following challenges:
Guiding Users on Impactful Completions
For wide databases containing sparse data, it is difficult for the user to write update queries to complete data if they do not know what information is present and hence, which queries will fill in the most cells. Consider a database containing country, city, temperature and precipitation. Suppose the user is filling in information for the temperature field, and they specify an update query setting null values of temperature to Below freezing whenever precipitation equals Snow. But if the precipitation attribute is mostly missing whenever temperature is missing, this update has a very low impact. Now, say the location attribute is present for most cases when temperature is missing. A better query would be to set temperature to Below freezing when city equals Reykjavik and month equals January. Thus, users need to be guided by seeing high impact fields together.
However, simply showing high impact fields is not enough if the information is not relevant. For example, showing temperature with traffic density is not helpful, even if traffic density is always present when temperature is missing. Hence, the subsets should contain attributes that are semantically relevant. However, this is computationally expensive in an interactive system. If the user has the capacity or screen size, to look at a 10 × 10 matrix at a time, then selecting an optimal 10 × 10 matrix from a dataset of 10, 000 rows and 50 columns gives 1035 subsets to choose from.
Generalizing Completion Updates:
Manually updating thousands of null values in a large database is infeasible, while writing rules a priori is ineffective. Thus, when the user updates a null value, the system needs to suggest general update rules that apply to a larger set of fields. Going back to the above example, once the user updates the temperature for Reykjavik, along with suggesting an update query of setting temperature to Below Freezing when city equals Reykjavik, the system can also suggest a generalized update of setting temperature to Below Freezing when country equals Iceland, since there is a hierarchical relation between country and city, denoted by a foreign-key in a normalized database.
1.2. Contributions
To address the above challenges, we designed ICARUS (Iterative Completion with RUles, Figure 1) which shows the user samples of the database containing missing cells in the form of a p × q matrix. Once the user fills in a data value, ICARUS suggests data specific update rules (i.e., english translations of update queries) based on the information present on the screen. It also presents general versions of these rules, by linking them to attributes in joined tables. If the user sees a correct rule in the list of suggested rules, they can immediately apply it to the entire dataset, thereby filling in all the null values where the rule is applicable. The user goes back and forth between editing the subset and picking rules until the desired amount of data is filled. If they are no longer able to update null values in the subset, they can choose to see a different sample. This approach effectively completes sparse datasets while minimizing the user input. Our contributions include:
Figure 1:
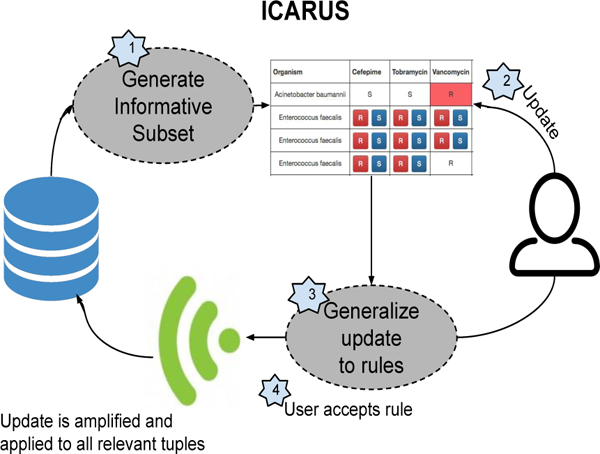
ICARUS Workflow: ICARUS uses its entropy based sampling algorithm to display a subset of the database containing missing data to show the user, in the form of a matrix. The user then updates a cell, based on which ICARUS generates multiple update statements, presented as rules. Users can then choose to apply correct rules, amplifying their single update to multiple tuples.
Algorithm for identifying and showing the user candidates for updates that are semantically relevant.
Minimization of user input by displaying high impact candidates whose updates can be applied to a large set of null values.
Amplifying the user’s input to a larger number of cells using foreign-key relations for rule generalization.
Implementation details and experimental evaluation of ICARUS, which allows users to efficiently update incomplete databases. Simulations show up to 70% reduction in human effort as compared to the state-of-the-art baseline system. user study results show that domain experts (who were naive users of the system) were able to fill in 68% of the missing values within an hour, while the manual rule formulation process took weeks.
2. PROBLEM FORMULATION
Let D be a normalized database schema, containing multiple relations. Each relation is defined over a set of attributes attr(A). Domain of an attribute is denoted by dom(X).
2.1. Update Language
The supported repair language can be expressed as standard SQL Update statements, where only null values are updated:
Where and can be a set of constants or a SELECT query pulling from other relations in D which are joinable with A. The where clause can be extended to constrain multiple attributes in A. For the rest of this paper, we use the terms “update queries” and “rules” interchangeably.
2.2. Multiple Relations for Rule Generation
When a user updates a null value given the context of a single relation, suggested rules would traditionally consider attributes of only that relation [26], But given a normalized database, we can leverage its structure to suggest more general rules to the user.
While normalized schemas are optimal for storing information, they are not ideal for data exploration. Consider a relation where C is a many-to-many join between A and B, and , are foreign-keys to A and B respectively. Suppose contains null values. Presenting C to the user with a_id, b_id is unhelpful, since they do not know what these keys mean. Instead, we should show them a meaningful attribute from the referenced relation. This can either be manually specified or be the most distinct attribute, i.e., whose distinct cardinality is closest to the cardinality of the relation. However, an advantage of a normalized schema is that the join relations often encode hierarchies in the form of many-to-one joins which we can use to reduce human effort.
In a many-to-one join, one can think of the relation in the many-side as belonging to, or being a subtype of the relation in the one-side. Thus, there is a hierarchy where the one-side relation is a parent of the many-side and rules on attributes of a relation can be generalized to attributes of the parent relation. For example, a rule about a city could apply to all cities in a state, or a rule about a book could generalize to all books written by that book’s author, etc. We define a parent relation as follows:
Definition 1. Consider relations R, X, and Y, where . Then Y is a parent of X if R is a many-to-one join between X,Y. Formally, Y = Parent(X) if :
Rules from one relation could be generalized to its parent. While generalization in databases traditionally refers to attributes and is defined with respect to addition/deletion of predicates [10], here we use it to mean rule generalization, i.e., a rule that applies to an attribute value can be generalized to the attribute’s parent value in the next level of the hierarchy.
Definition 2. For relations X, Y, if Y is a parent of X, then rules made on attributes of X can be generalized to attributes of Y. We use to denote “can be generalized”.
Generalization is transitive:
We refer to a parent’s parent as the relation’s grandparent and so on. In the example shown in Figure 2, rules about an organism can be generalized to the organism’s family and through the family to its gram stain. Similarly, rules about an antibiotic can be generalized to its parent class, its grandparent class, etc. If in Figure 2B, the user were to fill in S in the first null cell of the table, which corresponds to the result cell in the first row of the culture_antibiotic table in Figure 2A, the generated update queries (and the corresponding rules shown to the user) would include the following :
-
UPDATE culture_antibiotic SET result = S WHERE cult_id IN (SELECT id FROM culture WHERE org_id = 1)
AND anti_id = 1;
Translates to “Escherichia coli is Sensitive to Cefepime”
-
UPDATE culture_antibiotic SET result = S WHERE cult_id IN (SELECT culture_id FROM culture JOIN organism WHERE fam_id =1) AND anti_id = 1;
Translates to “Enterobacteriaceae are Sensitive to Cefepime”
-
UPDATE culture_antibiotic SET result = S WHERE cult_id IN (SELECT culture.id FROM culture JOIN organism JOIN family WHERE gram_id = 1) AND anti_id IN (SELECT antibiotic.id FROM antibiotic WHERE class = 4;
Translates to “Gram Negative organisms are Sensitive to 4th Generation Cephalosporins”
The where clauses of these rules are conditioned only on the join keys in the many-to-many relation and independent of other tuples in this relation. Hence, we refer to these as independent rules.
Figure 2:
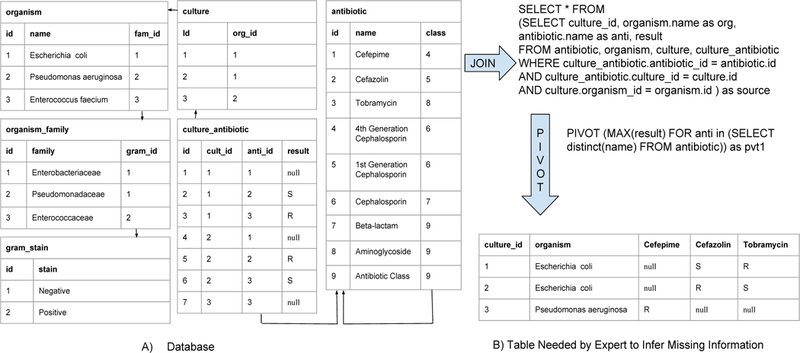
Motivating Example - Microbiology Culture Database: Missing data is in the culture_antibiotics table, which is a many-to-many join between the culture and antibiotic tables. To make any inferences on the missing values, atleast four tables need to be joined. Further, the culture’s sensitivity to other relevant antibiotics are also needed, hence the culture_antibiotic table needs to be pivoted on culture_id.
In addition to the above rules, since the attribute being updated already contains some data, the user could potentially use the information of tuples associated with the same foreign-keys to make update decisions. This would require a rotated view of the relation, constituting a pivot operation (Figure 2):
SELECT culture_id, organism.name as org, antibiotic.name as anti FROM antibiotic JOIN cult_anti JOIN culture JOIN organism PIVOT max(result) FOR anti IN (SELECT name FROM antibiotic)
A pivot operation creates a column for each value of the attribute specified in the pivot line (antibiotic), grouped by attributes in the outer select statement (organism,culture_id). Since each culture and antibiotic pair have one value for result, max is an appropriate aggregate. Going back to the above scenario of the user filling S in the first null cell, the following rule is also added to the list of possible rules:
-
UPDATE culture_antibiotic SET result = S WHERE cult_id IN (SELECT cult_id FROM culture_antibiotic WHERE anti_id = 2 AND result = S) AND anti_id = 1;
Translates to “Organisms Sensitive to Cefazolin are also Sensitive to Cefepime”
In this case, the where clause is dependent on other tuples in the relation being updated (i.e., where clause selects from culture_antibiotic relation). Hence, we refer to these as dependent rules. Dependent rules are only generated between attributes that have a similarity above a threshold. The attribute similarity measure can be user-defined, such as sharing a common foreign-key to the parent relation, in our case (both Cefepime and Cefazolin are Cephalosporins), or automated using the CORDS algorithm [30].
It should be noted that all of the update rules have an additional clause requiring result = null, i.e., the rules never update existing data that is known or has been filled in with a prior rule. Further, rules are not applied until the user accepts them. It is possible that a user defined rule conflicts with the original data, but this does not imply that the rule or the original data is incorrect. It is the nature of this dataset. For example, in Figure 2B, the Escherichia coli in culture 1 is sensitive to Cefazolin while the one in culture 2 is resistant (i.e. the organism that grows in each culture has different sensitivities), hence domain experts are required. Further, experts may first apply specific narrow rules and then later make broader generalizations that contradict with one of their earlier rules for the remaining cells. In our pilot studies we observed that rules selected in later passes were for rare cases and of lower confidence, hence should not overwrite prior rules.
2.3. Problem Statement
Now that we have explained how rules are generated from an edit, we are ready to formalize the data completion problem. As explained above, the normalized tables do not provide the user with enough information to make edits and have to be presented in a denormalized form, shown in Figure 2B. But the matrix in Figure 2B can be undigestible to humans due to its size (10, 000 × 50 in our case) and moreover, denormalization is expensive. Hence, the user needs to be shown subsets from the denormalized view. Subsets shown should maximize null values filled during user interaction. Without loss of generality, we assume that a relation contains only one attribute with null values.
Given a relation D that needs to be completed, let be the set of tuples containing null values in D. Let S = Powerset(D) be the set of potential subsets that can be shown to the user. Each subset contains null value tuples, which upon editing generates a set of rules - rules(si). Each rule , if accepted, in turn fills in a set of null values in . We refer to each subset shown to the user as one iteration. With these definitions, we formally define our problem as follows.
Iterative Data Completion Problem:
Given relation D and denoting the set of tuples containing null values in D, the iterative data completion problem (IDCP) is minimizing the number of iterations required to complete U by selecting subsets which maximize at each iteration.
2.4. Search Space
IDCP is an instance of the maximal weighted set cover problem (MWSCP), which is a well known NP-complete problem [23]. Given D, U, S as defined above and M = Powerset(U): Each potential subset which can be shown to the user in matrix form (Figure 2B), maps to one set . We define the mapping as follows. For every cell , let pc be the probability of the user updating it. Updating c generates rules(c). For each rule , let pr be the probability of the user accepting it. On showing si to the user, every cell thus has probability pc × pr of being updated. Each subset can then be mapped to where . The weight of mi is calculated as the number of cells si can fill divided by the probability of filling in each cell. Thus, those subsets with higher probability of filling have lower weights. We want to pick a set of minimum weight sets from M such that the maximum number of elements in U is covered, which is MWCSP.
In fact, calculating any optimization function to find an ideal subset is expected to be expensive. If the denormalized matrix is m × n, and we want to select subsets of size p × q, the number of ways to do this is equal to . This has a growth rate of . For our motivating example, there are about subsets to choose from. This calculation is expensive in an interactive system which has low latency requirements.
3. SYSTEM DESIGN
In this section we provide implementation details of ICARUS, a system that aims to minimize the user’s effort in filling in null values. It does this by showing digestible subsets of the dataset in the form of c = p × q matrix that fits on screen. c contains a combination of null and filled in cells. The user has the option to fill in one of the null values or choose to see a different subset if they feel they do not have enough information to make a decision. On filling in a null values, ICARUS suggests rules to generalize the edit on the rules pane as shown in Figure 3. If the user sees a correct rule, they can accept it, and it is immediately applied to the dataset. The user then continues filling in the subset and applying rules until they are unable to make any more updates. They can then ask for a different subset, ending an iteration. This process continues until the desired percentage of data is filled, which the user is able to track from a progress bar on top. Due to the computational challenges in choosing optimal subsets outlined in Section 2, we use sampling based techniques.
Figure 3:
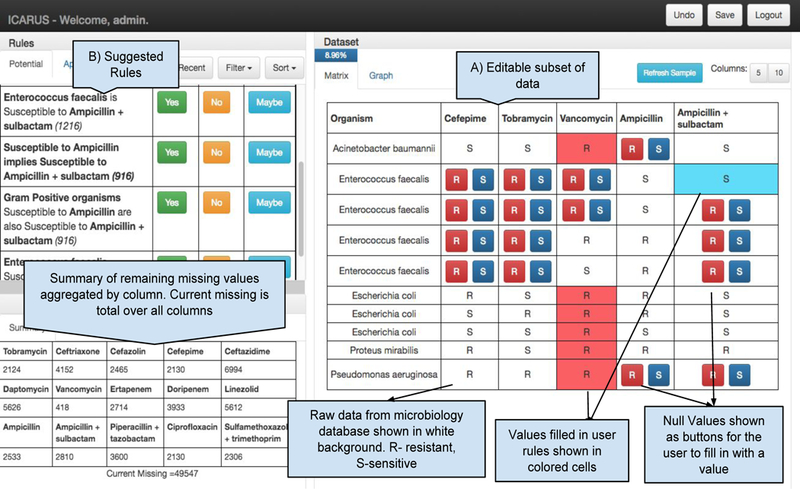
ICARUS Interface: A) Editable interface showing a subset of the missing data. In each iteration, the user fills in as many values as possible, based on the information present, and then proceeds to refresh. B) Once they update a cell with a value, generalized update rules, which can fill in a larger set of values, are suggested to the user.
Algorithm 1.
ICARUS Workflow
| C: dataset | |
| 1: | while Percentage of missing cells > threshold do |
| 2: | GENERATE_SUBSET(C) |
| 3: | while user can edit do |
| 4: | user edit |
| 5: | rules = GENERATE_INDEPENDENT_RULES(c,v,i) ∪ |
| 6: | GENERATE_DEPENDENT_RULES(c,v,i) |
| 7: | if user accepts rule ∈ rules then |
| 8: | apply rule to C |
| 9: | end if |
| 10: | end while |
| 11: | end while |
3.1. Subset Selection
Before we present our heuristic algorithms for choosing subsets, we provide some intuition. A row with all values missing is not very helpful because the user does not have any information to make a decision, and only independent rules can be generated from an edit. Similarly, having rows with only filled in values is a waste, since they do not contribute to completing the dataset. Hence, we would like to pick a subset with filled in and null values distributed in a manner that maximizes the probability of the user updating a null value. Clustering, machine learning and imputation methods do not work well as we will show in Section 4, since they do not account for the user’s information needs.
3.1.1. Optimization Function
The probability of a user updating a cell in the given subset depends on whether they have informative filled values. A filled cell is informative to a null cell if it has a common foreign-key, i.e., they belong to the same row in the denormalized matrix. Thus, given a denormalized matrix C = X × Y, with X denoting rows and Y denoting columns, we want to select c = x × y where, , that maximizes the probability of a null cell being updated and its impact. Impact, in this case, refers to number of values in the entire dataset that will be updated if the user accepts a rule generated by updating that cell. Formally, let denote the set of null cells and , denote cells that are filled in the matrix, be the similarity between column j and k, be the number of rows where column k is filled but j is missing. We want to maximize:
| (1) |
Subject to the following constraints:
where p, q are screen constraints
Equation 1 is maximizing the probability of a null cell being filled, which is proportional to the similarity between the columns of the filled cells and the null cell in that particular row. This is weighted by the number of cells that will be impacted if a rule based on these two columns is formulated. Thus, if there are many rows where j is filled and k is empty and the columns are correlated, then having the user specify a rule between the two will fill in a large number of cells. Column similarity can be user-defined with help of experts, using number of common parents through foreign-key relations, or for a single relation, CORDS [30] can be used.
3.1.2. Increasing Entropy for Subset Diversification
Similarity alone is not enough for completing the entire dataset. The independent rules described in Section 2, are based on characteristics of two relations that are not necessarily related. These rules could be generated by looking at row and column headers in the denormalized view, i.e., the user needs to see null cells in different row-column positions. To ensure that the null cells are distributed across rows and columns, we maximize the information entropy [35] for each row and column. Entropy of an item denotes the amount of uncertainty contained in it and is calculated as:
| (2) |
where X is the set of values in the row/column and P(x) is the probability with which each value occurs. A row/column with high entropy has a diverse set of values and hence provides more information. Initially, however, we want to show the user subsets with higher impact. The diversity of subsets has more importance towards the end of the session when there are fewer null cells which need to be filled in with specific rules and the user requires more information to make a decision. Keeping this in mind, we borrow ideas from simulated annealing techniques [3] and increase the weight of entropy as the temperature, i.e., iterations increase. Thus, our final optimization function is a modified version of Equation 1:
| (3) |
3.1.3. Two-stage Subset Sampling
Picking a subset with the above conditions is challenging, since we are optimizing for two different conditions along each dimension, i.e., similar columns but diverse row. Co-clustering techniques do not work since they cluster based on data, without accounting for external column similarity such as semantic similarity or foreign-key relationships. In fact, co-clustering does the opposite by selecting subsets that have the exact same values of rows and columns, instead of diversifying. Hence, we follow a two-stage sampling approach where we first sample rows with probability proportional to the row’s entropy and number of null cells and inversely proportional to number of prior iterations that the row has been selected. In the second stage, we choose a column to optimize for and select the remaining columns by maximizing Equation 3 with respect to the chosen column and rows sampled in the first stage. Subset selection pseudocode is presented in Algorithm 2.
3.2. Rule Generation
As explained in Section 2, the suggested rules are generalized based on many-to-one joins referenced by attributes of the denormalized table. Given C = A × B, suppose the user fills in a value which corresponds to for in the denormalized version. Suggested independent rules then include setting c = v when the foreign-keys a_id and b_id share parents with and , i.e., values of the updated tuple. Two items share a parent if they have the same foreign-key to a parent relation directly or transitively as defined in Section 2.2. Also, in the denormalized matrix, for every column y that shares a parent with column c and has a filled in value ti[y] in the row being updated, the suggested rules include setting c = v when y = ti[y]. The pseudocode for this is presented in Algorithm 3.
Algorithm 2.
Entropy based Subset Selection
| visx[i] : no. of iterations row i was selected | |
| iterations: no. of iterations user has gone through | |
| impact[i][j]: no. of times coli is filled but colj is missing | |
| entropyx[i]: entropy of row i | |
| : entropy of column i for {rows} | |
| I[x][i]: Indicator function = 1 if value is present in row x and column y, 0 otherwise {rows} | |
| 1: | procedure GENERATE_SUBSET(C) |
| 2: | X = C.rows, Y = C.columns |
| 3: | |
| 4: | for do |
| 5: | |
| 6: | end for |
| 7: | |
| 8: | select column to optimize for, with probability proportional to missing values |
| 9: | for do |
| 10: | |
| 11: | end for |
| 12: | columns = Top q indices from scoresy |
| 13: | return |
| 14: | end procedure |
3.3. User Interactions
The interactions available to the user on ICARUS interface include:
Update NULL Value:
The user can update a null value, represented as R/S buttons in the interface by clicking on the corresponding button. On an update, rules are generated on the top left pane.
Navigate Rules:
The rule pane is scrollable, with suggested rules ranked from broadest to narrowest impact. Rules can be filtered to display only independent or dependent ones.
Rule Application:
Once the user sees a correct rule, they can accept it by clicking on “Yes” or “Maybe” next to the rules. Both these buttons have the same effect - they apply the rule to the entire dataset, however the “Maybe” rules are noted as “low confidence” rules when stored. While this feedback is not used in Icarus, it is useful for uphill analysis when results of experts are compared. If the user selects “No” for a rule it is never generated again.
Refresh Sample:
The user can see a different subset by clicking the “refresh sample” button on top of the subset.
3.4. Optimizations
Even though we present a denormalized form of the database to the user, the complete database is never denormalized during implementation. We provide further details of this with respect to different components of our system below.
Algorithm 3.
Rule Generation
| c : updated column; v : updated value; i : tuple index | |
| C – A many-to-many join B | |
| 1: | procedure GENERATE_INDEPENDENT_RULES(c,v,i) |
| 2: | |
| 3: | while do |
| 4: | |
| 5: | while do |
| 6: | rules.append (UPDATE SET c = v WHERE a_id in (SELECT id from A WHERE ) AND b_id in (SELECT id from B WHERE )) |
| 7: | |
| 8: | |
| 9: | end while |
| 10: | |
| 11: | |
| 12: | end while |
| 13: | return rules |
| 14: | end procedure |
| 15: | procedure GENERATE_DEPENDENT_RULES(c,v,i) |
| 16: | |
| 17: | |
| 18: | for do |
| 19: | while do |
| 20: | rules.append (UPDATE SET c = v WHERE a_id in (SELECT id from A JOIN C WHERE AND C.b_id = b.id AND AND b_id = ti [b_id]) |
| 21: | |
| 22: | |
| 23: | end while |
| 24: | end for |
| 25: | return rules |
| 26: | end procedure |
Subset Selection:
Each of the components used during subset selection such as missing cells per row and column, row entropy, column entropy, column similarity, and impact of an edit is calculated and stored as a separate table prior to initialization of the system. In fact column entropy is only calculated over the rows that will be shown to the user, and hence can be calculated on the fly since p ≤ 10. As rows and columns are updated by rules, these numbers can be updated quickly for the affected rows and columns.
Rule generation and application:
Rule generation follows a depth-first search on parents (defined in Section 2.2) of the shown relations. In case a relation has a deep ancestry, the depth can be capped at a user defined k, or the Falcon dive algorithm [26] can be used for restricting rule suggestion. In each iteration this only needs to be done for the subset shown to the user, i.e., for p+q values. Thus, the rules are generated and cached, along with the tuple IDs of their result sets, for each missing cell in the subset (number of missing cells < p × q = 100), at the beginning of each iteration. As rules are applied, the result sets of the cached rules are updated as well, removing IDs that are no longer missing.
Number of suggested rules:
We show the user all the rules in a scrollable pane on the left of the interface Figure 3. The dependent rules suggested are limited to pairwise clauses. Let kx, ky be the depth of parents for rows and columns, respectively. So in the rare case that all q − 1 columns in a row are filled and have the same foreign-key value to the parent relation as the updated column, the number of rules suggested is dependent and kx × ky independent). The user is able to filter rows by type (dependent vs. independent), to narrow this set. This can further be reduced by sorting by impact (our default) or rarity and showing top n, or again by using techniques in [26].
3.5. Complexity Analysis
Consider the denormalized m × n table. At each iteration, if components of the optimization function are precomputed, then subset sampling is constant time, otherwise, sampling rows is and columns is . Let x be the percentage of cells that are missing. Then rule application will require to fill in all values. The entire session has complexity .
4. EXPERIMENTAL EVALUATION
In this section, we report results of experiments to (a) compare the effectiveness of subset selection algorithms in reducing user effort; (b) compare latency of these algorithms; (c) show contributions of components of our optimization function; (d) compare ICARUS to Falcon [26] and Holoclean [44]; and (e) report findings from an in-person user study with domain experts [31]. ICARUS is implemented using Python Django framework with MySQL database backend and Javascript frontend. We use the following datasets:
Microbiology:
This is the dataset from our motivating example, whose schema along with a few tuples is shown in Figure 2, and the interface for the user study is shown in Figure 3. It consists of culture results of patients admitted to the Ohio State Wexner Medical Center with urinary tract infection (UTI) between 2009 and 2014. The dataset contains around 10, 797 cultures (rows) and about 50 antibiotics (columns). Out of these we are only interested in filling in missing information for the 14 antibiotics which are used for empiric treatment. The UMLS Metathesaurus [8] was used to create the classification tables [42]. Around 55% of the data we are interested in is unreported, which is equivalent to around 83, 000 null cells. Before creating ICARUS, this dataset was filled in with rules created manually with consensus from four domain experts, which took around a month. It was a cumbersome process that involved looking at columns pairwise, trying to find dependencies that covered the maximum null cells, formulating rules, and then generating the pairwise frequencies again. These rules are used as “gold” standard. 89 of the rules are dependent and 80 are independent. Domain of null cells is binary: 1: sensitive, −1: resistant. This dataset has up to three levels of hierarchy, i.e., the base relation has a parent, grandparent and great grandparent along both dimensions (refer to Section 2 and schema in Figure 2).
IMDB:
The IMDB data [1] was collected using IMDbPy [2] to create a database. We selected the top 500 voted TV shows from the database. For each show, we found all actresses that appeared in them and then collected up to 10 episodes where the actress appeared. This was done to create rules of the form (actress, ). We generated rules by comparing episodes that appeared in the same show pairwise, as well as seeing if an actress had the same values for all episodes of a show. 7,496 of these rules were dependent while 23, 051 were independent. We removed any show that did not have any actresses that appeared in more than one episode. This left us with 73 shows, 504 episodes and 317 actresses, giving us 317×504 matrix with about 160, 000 cells. From this we removed 50% of the data based on the generated rules, giving us around 80, 000 missing cells. Missing values are binary: 1 : actress appeared in series, −1 : actress did not appear. This dataset has one level of hierarchy, where every episode has a parent series.
Hospital:
This dataset, adopted from US Department of Health and Human Services 1, contains 100, 000 rows and 17 columns. Out of these we non-randomly removed data from 7 attributes based on 45 manually created dependent rules, giving 517,134 missing cells, all text. To transform these for regression and clustering, word features were created for 10 out of the 17 columns. “State” was used as a proxy for geographic attributes like “address”, to limit feature size (139 features). Unlike the other two datasets, this does not have a many-to-many relation, with a hierarchy. Instead, it contains three relations and the attribute’s parent is the relation it belongs to, again giving a one level hierarchy.
4.1. Comparison of Subset Selection Algorithms
We compare our subset selection algorithms, in terms of how much information they allow the user to fill in incrementally over iterations, against the following algorithms:
Random:
At each iteration, this chooses a random subset.
Random_history:
Similar to random, except it inversely weights the probability of selection of rows and columns to the number of prior iterations in which it was selected.
Clustering:
At each iteration, this algorithm clusters rows based on their similarity, picks rows from the cluster proportional to missing values then selects columns using our optimization function.
Regression:
At each iteration, this algorithm selects the column with the most missing values to optimize for. It then trains a linear support vector machine (SVM) [48] on a maximum of 10, 000 rows (to limit compute time) that have results for the missing column and uses the weights of the model to choose the top q - 1 columns. In cases where no training information is available, it simulates random. Rows were then chosen based on those which had the most filled in values for the selected columns.
In order to simulate sessions, our algorithm generates a subset and if editing one of the cells generates a rule that is in the gold standard, that rule is applied. This is done for all applicable cells. Once no more edits can be made, a new subset is generated and the process continues for the given number of iterations. The number of iterations shown is based on the point after which most algorithms are stable. For each algorithm, we ran the simulation 50 times and picked the average to get the datapoint at each iteration. Since rules applied in the simulation are from a gold standard, there is no concept of accuracy since all applied rules are correct.
Figure 4 shows the results for the three datasets - regression and clustering are shown with dotted lines since they do not meet latency requirements (Section 4.2). ICARUS consistently performs well for all three datasets, achieving almost 80% in just 5 iterations for the microbiology dataset (Fig 4a), while maintaining low latency. The IMDB dataset requires a higher number of iterations due to its shallow one level hierarchy, which limits the amount that edits can be generalized. This is also reflected in the number of rules (approx. 30, 000 rules to fill in 80, 000 cells for IMDB as opposed to 169 rules to fill in 83, 000 cells for the microbiology dataset). The hospital dataset stabilizes in 20 iterations in spite of having a shallow hierarchy because it has a smaller number of attributes. ICARUS can thus work on datasets with different levels of hierarchies and number of attributes, however the savings in human effort vary accordingly.
Figure 4:
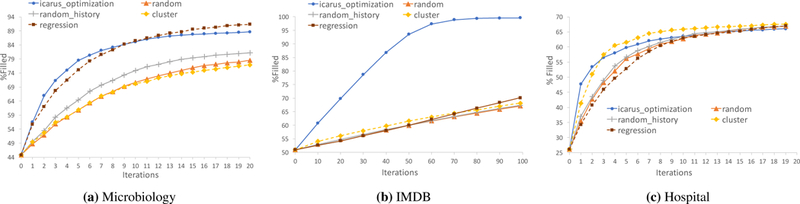
Iterations vs. Cumulative Percentage Filled over Entire Dataset: ICARUS consistently performs well across all three datasets. Dotted lines are used to represent baselines which violate latency requirements.
4.2. Latency
Table 1 shows the average latency over 50 simulations for each dataset for the subset selection algorithm. ICARUS maintains a latency of under 200ms across all three datasets; interaction latency is negligible (less than 100ms which is below the threshold of human perception [5] ). It is 6x faster than the other methods for the microbiology dataset and 800x faster for the hospital dataset. On the other hand, clustering latency increases as number of attributes (IMDB) and samples (hospital) grow, while regression is highly sensitive to number of samples and datatype. It performs fastest for IMDB which has 317 rows, so on average the training size is around a 100 for each attribute, compared to about 8, 000 for microbiology and 10, 000 for hospital. The large sample size along with the multi-class prediction makes regression especially slow for the hospital dataset.
Table 1:
Subset Generation Latency: Shaded cells violate latency constraints of 300ms, which Icarus meets in all datasets
 |
Subset generation has strict latency requirements. Since the user explicitly requests a new subset once they are done editing the current one, they are idle during the time that a subset is generated. Further, since the generated subset depends on the user’s edits in the current iteration, it cannot be precomputed. Hence, regression and clustering are unsuitable for use in its current form.
4.3. Components of the Optimization Function
In this section, we study the effect of each component of our weighted sum, namely, column similarity, entropy and impact. For this experiment, we modified our optimization function to only use one of the components for a set number of iterations and took the percentage filled at the end as its result. We then normalized this by the total percentage filled by all three. Further, we also studied each component’s effect when using only one type of rule (i.e. dependent vs. independent), except for the hospital dataset which only has dependent rules.
We can see in Figure 5, that all three components are equally important in most cases. Entropy does slightly better for independent rules while similarity does better for dependent rules, as expected (Section 3.1). The difference is noticeable in IMDB since the distribution of rules between dependent and independent is skewed, while for microbiology they are almost evenly split. Thus, based on the distribution of the rules, each component needs to be weighted accordingly. By increasing the weight of entropy with iterations we cover this entire spectrum, as demonstrated by results in Figure 4.
Figure 5:
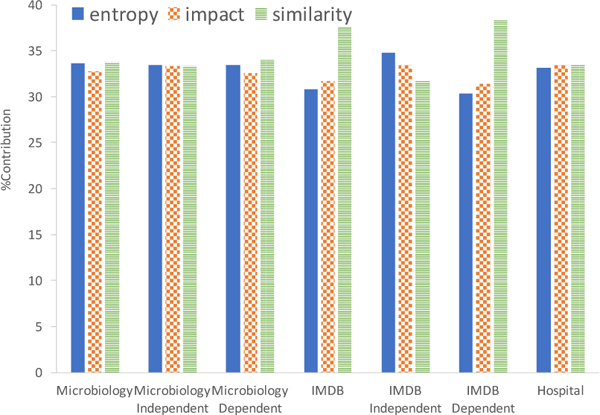
Percent contributed by each component of weighted sum for 50 simulations, grouped by rule type (hospital data only has dependent rules).
4.4. Comparison to Other Systems
Falcon:
The Falcon system [26] is the state-of-the-art system in reducing user effort in rule based updates. They perform better than systems such as guided data repair [55] and active learning approaches. While their contributions can be considered orthogonal to ours (since they use rules for error detection and correction), they are the closest work to our system.
Falcon algorithm:
Given a table and a user edit. Falcon’s goal is to find the most general update statement in terms of the number of attributes involved. The most specific update would contain all attributes in the WHERE clause, while the most general update would have an empty WHERE clause. It creates a lattice out of all possible subsets of attributes and iteratively asks the user to validate rules until it finds the most general one. Falcon chooses rules for validation are based on the user’s input (accept or reject) and then performs a binary search on the set of rules ordered by impact. We compare number of edits for ICARUS and Falcon.
Figure 6 shows the percentage filled against number of edits for 300 edits for the microbiology dataset. Note that Falcon operates on a single table and hence would not suggest broader rules based on relations. However, we compared a denormalized version that has the many-to-one join attributes on the table, encoding the hierarchy. This version performs better but still does not catch up to ICARUS. We also compared using semantic schema-based similarity as used by ICARUS against Falcon’s similarity metric which uses modified CORDS [30] for attribute sets.
Figure 6:
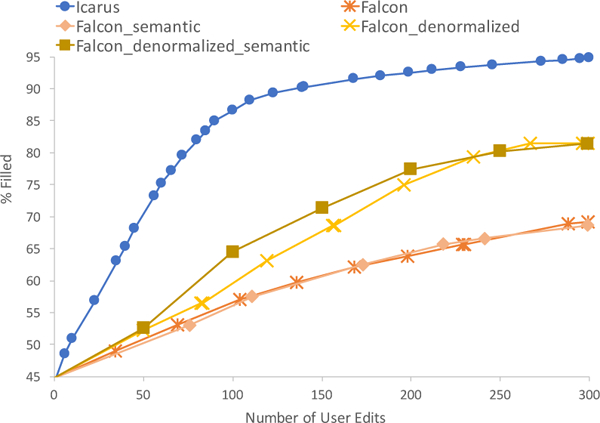
Iterations vs. Cumulative Percentage Filled for Microbiology dataset for ICARUS and Falcon, with different optimizations. ICARUS does significantly better.
The main benefits in using ICARUS over Falcon arise from the fact that ICARUS guides the user on which edits will be the most impactful. Further, ICARUS allows rule updates that affect multiple columns in the denormalized matrix, while Falcon only updates one column. The improvements for the other two datasets are comparable to the microbiology dataset and summarized in Figure 7, which shows the average number of edits saved over maximum number of edits. Even if we ignore the edits the user makes in rejecting rules, ICARUS provides significant improvement.
Figure 7:
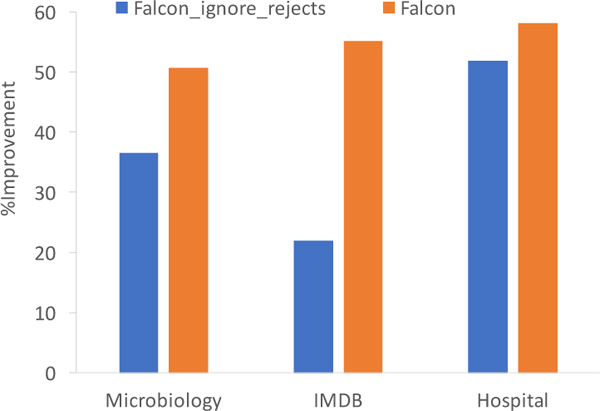
Percentage of Edits Saved when using ICARUS instead of Falcon for each dataset (out of 300 edits for microbiology and hospital, and 1000 for IMDB). The impact of ignoring rejects is significant for IMDB, since it has 500 attributes leading to a large Falcon lattice (i.e., more questions for the user to answer).
Holoclean:
Holoclean [44] is a system that allows users to specify “rules” in the form of denial constraints, which can be used to express integrity constraints and functional dependencies, and then combines signals from these with external vocabularies and quantitative statistics to perform error detection and repairs. As summarized in Table 4, Holoclean is not the most appropriate system for our use case, but can serve as a orthogonal and complementary component of ICARUS’s data preparation pipeline. In order to ascertain Holoclean’s capabilities on our datasets, we started by manually expressing our rules as denial constraints (a task that we do not expect our users to perform). We observed that Holoclean yielded the following precision, recall scores respectively for the microbiology data set: (.72, .24), IMDB (.99, .54), hospital (.21, .99) – which are high recall or high precision, but not both (a contrast ICARUS’s high recall / high precision performance shown in Figure 9). The results for microbiology are interesting – the highest results, which are reported here, were achieved when we manually defined constraints for the rules which could be expressed as functional dependencies. We consider this to be additional manual intervention. On adding conditional functional dependency rules, the precision went down to .5 with recall remaining the same. This is possibly due to there being circular dependence between rules, or because the rules sometimes contradicted the data, leading the system to incorrectly mark the original data as erroneous. From these observations, we can infer that Holoclean is not an ideal standalone tool in cases when rules are not true constraints. Moreover, the default denial constraint error detector has very low precision (.22) and a custom null detector had to be constructed by us, entailing data scientist intervention before end-users perform cleaning.
It should be noted that Holoclean takes as input denial constraints or the rules which ICARUS helps formulate. Holoclean thus solves an orthogonal and complementary problem of combining multiple signal types for error detection and repair; we report its results here to demonstrate that automatic repair systems by themselves are insufficient, and reducing human effort remains desirable when using them. Such systems are also hard to interpret, especially when it is unclear how different combinations of constraints conflict and what each fills in. For these reasons, a combination of Holoclean and ICARUS seems to be a promising area of future work.
4.5. User Study
We recruited 6 domain experts consisting of infectious disease physicians and pharmacists, separate from the ones who created the manual “gold” standard, to do a preliminary usability study on the microbiology dataset. All users were naive users of the system, but experts in their fields. The first user was used as a pilot and is not included in analysis. We met with each user individually for a 60 minute study session which consisted of the following:
Users are trained for 15 minutes during which they are shown how the system works and allowed to interact with it while we walk them through updating a cell and applying a rule.
They are then told to fill in as many of the missing cells correctly as possible in the next 45 minutes.
At the end of the hour, they stopped and were asked to fill out the System Usability Survey [9] anonymously.
We evaluate our system over the user effort required, the SUS score and agreement of the filled in dataset with the “gold”. Table 2 summarizes the results of the user study for the five domain experts.
Table 2:
User Study Results: On average, users were able to fill 56,000 cells in just 148 edits.
| User | %Null Cells Filled | #Cells Filled | Iterations | Edits |
|---|---|---|---|---|
| 1 | 70.6 | 58,672 | 19 | 246 |
| 2 | 35.3 | 29,299 | 3 | 46 |
| 3 | 68.8 | 57,104 | 4 | 155 |
| 4 | 95.76 | 79,480 | 13 | 126 |
| 5 | 68.8 | 57,104 | 35 | 147 |
4.5.1. Human Effort
Figure 8 shows the amount of information filled over iterations by each user. The performance of the user depends on their approach. Some worked more slowly, looking up antibiotic-organism coverage from literature. A user of this type would have low recall over the short time period but high precision. A user that was focused on task completion in the hour would have high recall but potentially low precision. Users went through different number of iterations in 45 minutes, hence the percentage filled flatlines over iterations. This plot lines up with our simulations in that users are able to see and make rules on high impact cells at the beginning.
Figure 8:
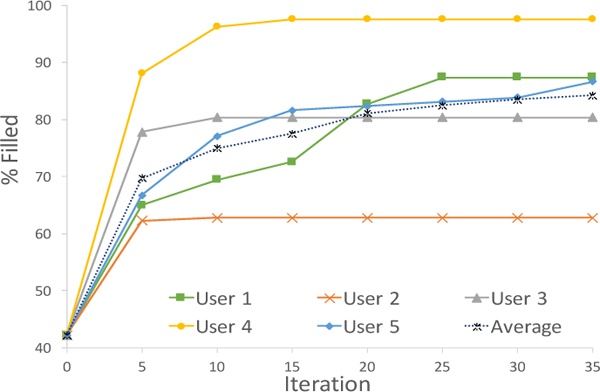
Percentage filled by each user over iteration. The results match our simulations.
4.5.2. System Usability Scale
At the end of the study, users were asked to fill the system usability scale (SUS) [9], an industry standard, robust and versatile scale [6] for measuring system usability. It consists of 10 Likert scale questions, paraphrased in Table 3, with each users Likert score. We can see that users found the system and its function useful (questions 1,3), albeit slightly complex (questions 6,7). Overall, ICARUS scored an average of 75 across the five users on the SUS scale (scoring details for SUS in [9]). Studies show that a score of 68 and above is considered good [6, 9],
Table 3:
Paraphrased questions from SUS and the Likert score for 5 users: 1- Srongly Disagree, 5 - Strongly Agree. Last column shows the average per question and its interpretation. The last row shows overall SUS scores per user (SUS scoring details in [9]): ICARUS scored an average of 75 (above 68 is considered good [6]).
| Question | A | B | C | D | E | Average |
|---|---|---|---|---|---|---|
| 1. I would like to use this frequently. | 4 | 3 | 5 | 5 | 5 | 4.4 - Agree |
| 2. The system was easy to use. | 2 | 4 | 5 | 4 | 5 | 4 - Agree |
| 3. The various functions in this system were well integrated. | 4 | 4 | 5 | 4 | 5 | 4.4 - Agree |
| 4. Most people would learn to use this system very quickly. | 3 | 3 | 4 | 4 | 5 | 3.8 - Agree |
| 5. I felt very confident using the system. | 2 | 3 | 3 | 4 | 5 | 3.4 - Neutral |
| 6. I found the system unnecessarily complex. | 4 | 3 | 1 | 2 | 2 | 2.4 - Disagree |
| 7. I would need the support of a technical person to use this. | 3 | 3 | 1 | 2 | 3 | 2.4 - Disagree |
| 8. There was too much inconsistency in this system. | 2 | 2 | 2 | 1 | 1 | 1.5 - Disagree |
| 9. The system is very cumbersome to use. | 3 | 2 | 1 | 1 | 1 | 1.75 - Disagree |
| 10. I needed to learn a lot of things before I could get going with this system. | 3 | 2 | 4 | 1 | 1 | 1.75 - Disagree |
| Score | 50 | 62.5 | 82.5 | 87.5 | 92.5 | 75 |
4.5.3. Agreement with Gold
Inferring antibiotic susceptibility is not a simple or traditional task for a domain expert and is somewhat subjective. Since the recruited users are new users of the system with limited time and training, the variability in their usage patterns is expected. Hence, we do not expect the user’s dataset to line up exactly with the “gold” which was formulated by a different set of experts who did not interact with the data using ICARUS. This does not imply that either set of experts are wrong but reflects the subjectivity of the task and motivates the need for human involvement. We compare the precision (number of correct cells out of those filled in) and recall (number of cells filled in out of total missing) of the five users against automatic imputation methods. The following methods are compared; all of which, except the first, are computed using Python’s fancyimpute package [45]: Single Imputation [18], Matrix Factorization [33], Multiple Imputations via Chained Imputation (MICE) [53], K-Nearest Neighbors (KNN) [20], and Soft Imputation [37], We also augmented each of the methods with hierarchical information used by ICARUS. This was done by transforming each value in a parent attribute into a binary feature. We see in Figure 9 that the automated methods perform poorly, with most of them having low precision, and the only one with high precision has very low recall of 16%. The augmented methods do better but do not catch up to experts using ICARUS. The low recall here is not a true metric, since they were given forty-five minutes for the usability test. In real usage scenarios, users would have more time.
Figure 9:
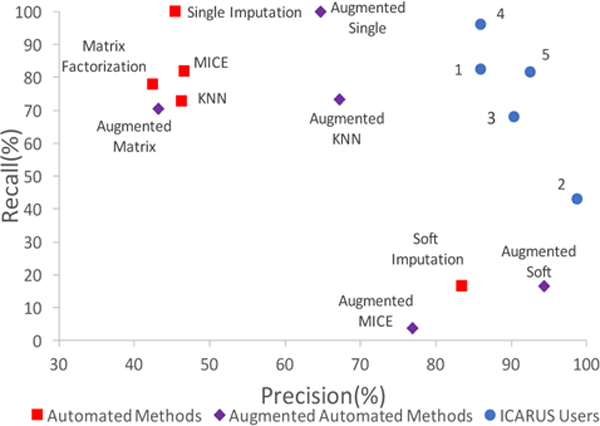
Agreement with Gold: Humans using ICARUS do better than automated imputation methods.
Imputation on partially filled dataset:
One can argue that automated methods could be used in conjunction with ICARUS, i.e., machine learned model could be trained after partially filling in data with ICARUS. This is true, if data is filled in randomly. However, with ICARUS, after the user makes an edit, they explicitly choose a rule that covers most cases where that edit applies. Hence, the machine learned areas for that edit are already filled in by the user. The alternative would be to have the user only make direct edits and automatically learn rules from those edits. This would take more user effort, since they would have to make more direct edits for the machine to learn one rule, while with ICARUS their ratio of edit to rule is almost 1:1. We demonstrate this in Figure 10, where we can see that random 17571 edits are required to achieve 90% precision from single imputation, which corresponds to 17571 edits. Conversely, while ICARUS allows the user to fill in 17571 cells in 23 edits, imputation has a precision of only 48% for cells filled in this manner.
Figure 10:
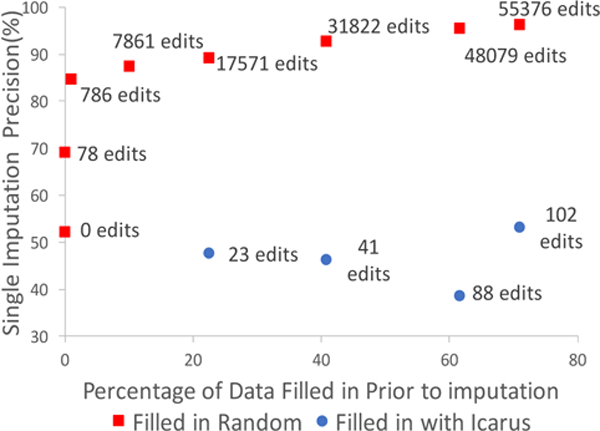
Ineffectiveness of imputation in conjunction with Icarus: Random edits lead to improvement in imputation, but ICARUS edits don’t because the user explicitly chooses rules to fill in data where the edit applies.
5. RELATED WORK
ICARUS addresses reducing human effort when input is required in filling in unreported data. While no prior work deals with this, there are many that appear to be similar. Table 4 summarizes how seemingly similar systems fail in user guided data completion.
Table 4:
Summary of limitations of prior work when applied towards the completion problem. ICARUS addresses all 3 features.
| System | Direct Edits |
Guides Edits |
Generalizes Edits |
Limitations with respect to Data Completion |
|---|---|---|---|---|
| Falcon | ✓ | × | ✓ | Does not guide the user on edits. |
| SampleClean | × | × | ✓ | Addresses duplication and value errors for aggregate queries only. Does not fill in incomplete datasets. |
| Data Imputation & Holoclean | × | × | × | Low precision or recall, as shown in Section 4.4 and 4.6.3, since limited evidence in the data for missing values. |
| Transformational Edits -Trifacta, Potter’s Wheel, Polaris | ✓ | × | ✓ | While these systems generalize edits based on transforms, they do not guide users on effective transforms. |
| Interactive Learning - ActiveClean, Guided Data Repair | × | ✓ | ✓ | Suggests rules based on underlying models, which is not applicable when specific data instances are missing. |
Interactive Data Cleaning:
As mentioned earlier, the Falcon system [26] is similar to ours in that it aims to reduce user effort by generalizing updates through relaxation of the where clause. However, since its rules are used for error detections as well as updates, the system cannot guide users on impactful updates. This is especially a problem in long and wide tables, where navigating the dataset is painful. In fact, the maximum number of attributes considered in Falcon’s test datasets was 15 attributes. Further, its rules do not generalize based on foreign-key relations. Due to these reasons, Falcon is not able to match the performance of ICARUS, as shown in Section 4.4.
Uguide [49] is a similar system that asks the user cell based edits. However, it uses experts for identifying functional dependencies (FDs) by choosing between asking the user cell-based question, tuple based question and FD rules. This is orthogonal to our work, since we need user feedback for correcting while they are trying to identify errors. In our case, we already know which values are missing. The Rudolf system [39] employs interactive rule refinement for fraud detection by clustering misclassifled tuples while Yakout et al’s Guided Data Repair [55] work shows users subsets of data to clean. Similarly, DataProf [52] generates Armstrong samples based on violations to business rules, and shows the users samples of these violations. However, both theses systems have a base set of rules that they know to be true, which they use to find dirty tuples that will have the most impact on cleaning the dataset. This is not applicable in our case since our system generates the rules based on the user’s edit.
On the other hand, DDLite [19], a framework for labeling data sets for machine learning algorithms, addresses a similar problem of finding large coverage rules for labeling data. However, data exploration is a manual process. The authors mention that users have difficulty finding high impact items to label. ICARUS addresses these problems to an extent.
Rule-Based Systems:
Rule-based systems for data cleaning, such as NADEEF [15], cleanse data by finding data violations to pre-specified rules, using a MAX-SAT algorithm. Other rule-based systems [11, 14, 21, 22, 24] are focused on discovering and using CFDs for finding data discrepancies. CFD based techniques assume a static database, hence techniques used there, such as association rule mining, are inefficient to run in our case where the database is constantly being updated. Finally, ERACER [36] uses statistical techniques to find dependencies, but the problem of showing impactful subsets to the user remains.
In fact, the need for ICARUS is motivated by Meduri et al. [38], where the authors make a case for users being involved in the rule discovery process as opposed to validating at the endpoints. Wang and Tang use fixing rules, as described in [51], which contain an evidence pattern used to match tuples, negative patterns that identify errors and a fact value that is used to correct a tuple. Their rule generation starts with known FDs and then employs user input to expand negative patterns. HoloClean and Holistic Data Repairing [12,44] aim to combine different modes of error detection such as integrity constraints, FDs, knowledge bases, and statistics, which is a very different goal from ours. Holoclean by itself is not effective in solving the data completion problem, as shown in Section 4.4. On a different note, DeepDive [16] uses user defined rules for knowledge base construction from literature. The main difference between the rule-based systems and ICARUS is that most of them do not rely on iterative human input and use data and knowledge bases to generate their rules. And for those that do rely on human input, they do not address guiding and optimizing the user’s input.
Data Imputation:
Missing data imputation [56] involves predicting trends based on given data, however is not applicable when domain expertise is needed to fill in the information, since the data is not missing at random. This is corroborated in Section 4.5.3, which shows imputation either has low recall or low precision.
Crowdsourced and Knowledge-Based Cleaning:
Systems such as Crowdfill [41] and Deco [40] use the crowd to fill in missing data, while AutoDetect [29] and Katara [13] employ knowledge bases. QOCO [7] and DANCE [4] addresses a similar problem of asking a minimum number of questions to the crowd to cleanse the database, but they do not allow direct edits or constraint creation. Hao et al. [25] match positive and negative signals of a dataset to a knowledge base for cleaning. Most of these systems lack an interactive, iterative component.
Transformational Edits and Spreadsheet Interfaces:
Systems such as Potter’s Wheel [43] use constraint violations transforms, while Polaris [47] infers rules from user edits. However, neither of these deal with showing a sample of the database to the user, and they assume rules are definite and can be inferred from columns. Specifically, they do not consider the benefit of looking at a variety of tuples to infer rules. Direct manipulation interfaces such as Wrangler, commercialized as Trifacta [32], suggest general transformational rules based on user edits, but they focus on attribute extraction as opposed to filling in missing data. Singh and Gulwani [46] deal in semantic transformations by learning and synthesizing all possible set of transformations from a set of input-output examples. All of these show the user the entire dataset and does not solve picking informative subsets.
Query-Based Cleaning:
Other approaches in data cleaning account for dirty data based on semantics of the query [50,54]. SampleClean [50], for example, uses a sample of the database to answer aggregate queries, and accounts for errors by generalizing the sample errors to the whole database. However, it deals with duplication error and value errors as opposed to missing data. Further, it addresses aggregate queries such as sum, average, etc. for numeric data while we deal with categorical. ICARUS is not comparable to SampleClean since we deal with different errors and datatypes. Similarly, ActiveClean [34] cleans subsets of the dataset that have the most impact in terms of improving accuracy of machine learning models that are being trained to clean the data. These systems deal with query-based data cleaning, which is very different from the problem we aim to solve, i.e., minimizing user effort in rule- based updates of null values.
6. CONCLUSION AND FUTURE WORK
In this paper we present ICARUS, an interactive system that iteratively allows the user to fill in missing data by making direct updates to a p × q matrix. Based on the update, ICARUS suggests general dependency rules using the database schema, which the user can immediately apply. They can keep making edits and applying rules iteratively until the desired number of cells are filled. The subset selection algorithm used by ICARUS maximizes the probability of the user making an update. Further, the subsets shown also maximize the probability of formulating high impact rules. This reduces the burden of finding related candidates that will fill in the most number of cells. Our experimental evaluations show that a user is, on average, able to fill in 68% of missing cells in an hour with each update filling in around 380 cells.
In terms of future work, we would like to draw the user’s attention to cases when they contradict themselves during rule formulation. In other words, we want to highlight when a new rule violates one of the prior rules or contradicts observed values. Presenting this information to the user concisely and quickly is an interesting problem. We are also working on visualizing disagreements in rules between experts and techniques for suggesting resolutions. Further, we could expand ICARUS to correct errors along with data completion. Using techniques mentioned [39, 49, 55], we can find suspected errors, after which ICARUS would need to select a subset of attributes to show the user that provide evidence for the tuple being incorrect. Finally, another direction we would like to explore is finding the minimum set of rules required to fill in a dataset. This can be done by comparing result sets as the user is specifying new rules, synthesizing them with previously accepted ones when results overlap.
Acknowledgment
Research reported in this publication was supported by the NIAID of the NIH under R01AI116975. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH. This work is supported by the NSF under awards IIS-1422977, IIS-1527779, CAREER IIS-1453582.
Footnotes
PVLDB Reference Format:
Protiva Rahman, Courtney Hebert, Arnab Nandi. Icarus: Minimizing Human Effort in Iterative Data Completion. PVLDB, 11 (13): 2263–2276, 2018.
Contributor Information
Protiva Rahman, Department of Computer Science & Engineering, The Ohio State University.
Courtney Hebert, Department of Biomedical Informatics, The Ohio State University.
Arnab Nandi, Department of Computer Science & Engineering, The Ohio State University.
7. REFERENCES
- [1].IMDB Dataset. http://www.imdb.com/interfaces/.
- [2].IMDB Python Script. http://imdbpy.sourceforge.net/.
- [3].Aarts E and Korst J. Simulated Annealing and Boltzmann Machines. 1988. [Google Scholar]
- [4].Assadi A, Milo T, and Novgorodov S. Cleaning Data with Constraints and Experts. In Proceedings of the 21st International Workshop on the Web and Databases, page 1 ACM, 2018. [Google Scholar]
- [5].Bailey BP, Konstan JA, and Carlis JV. The Effects of Interruptions on Task Performance, Annoyance, and Anxiety in the User Interface. In Interact, volume 1, pages 593–601, 2001. [Google Scholar]
- [6].Bangor A, Kortum PT, and Miller JT. An Empirical Evaluation of the System Usability Scale. Intl. Journal of Human-Computer Interaction, 24(6):574–594, 2008. [Google Scholar]
- [7].Bergman M, Milo T, Novgorodov S, and Tan W-C. Query-oriented Data Cleaning with Oracles. In ACM SIGMOD, 2015. [Google Scholar]
- [8].Bodenreider O. The Unified Medical Language System (UMLS): Integrating Biomedical Terminology. Nucleic acids research, 32(suppl_1):D267–D270, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Brooke J et al. SUS-A Quick and Dirty Usability Scale. Usability evaluation in industry, 189(194):4–7, 1996. [Google Scholar]
- [10].Cai Y. Attribute-oriented Induction in Relational Databases. PhD thesis, Theses (School of Computing Science)/Simon Fraser University, 1989. [Google Scholar]
- [11].Chiang F and Miller RJ. Discovering Data Quality Rules. PVLDB, 1(1):1166–1177, 2008. [Google Scholar]
- [12].Chu X, Ilyas IF, and Papotti P. Holistic Data Cleaning: Putting Violations into Context. In Data Engineering (ICDE), 2013 IEEE 29th International Conference on, pages 458–469. IEEE, 2013. [Google Scholar]
- [13].Chu X, Morcos J, Ilyas IF, Ouzzani M, Papotti P, Tang N, and Ye Y. Katara: A Data Cleaning System Powered by Knowledge Bases and Crowdsourcing. In ACM SIGMOD, 2015. [Google Scholar]
- [14].Cong G, Fan W, Geerts F, Jia X, and Ma S. Improving Data Quality: Consistency and Accuracy In PVLDB, pages 315–326. VLDB Endowment, 2007. [Google Scholar]
- [15].Dallachiesa M, Ebaid A, Eldawy A, Elmagarmid A, Ilyas IF, Ouzzani M, and Tang N. NADEEF: A Commodity Data Cleaning System. In ACM SIGMOD, 2013. [Google Scholar]
- [16].De Sa C, Ratner A, Ré C, Shin J, Wang F, Wu S, and Zhang C. Deepdive: Declarative Knowledge Base Construction. ACM SIGMOD Record, 45(1):60–67, 2016. [PMC free article] [PubMed] [Google Scholar]
- [17].Dewart CM, Gao Y, Rahman P, Mbodj A, Hade EM, Stevenson K, and Hebert CL. Penicillin Allergy and Association with Ciprofloxacin Coverage in Community-onset Urinary Tract Infection. Infection Control & Hospital Epidemiology, pages 1–2, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Donders ART, Van Der Heijden GJ, Stijnen T, and Moons KG. A Gentle Introduction to Imputation of Missing Values. Journal of clinical epidemiology, 59(10):1087–1091, 2006. [DOI] [PubMed] [Google Scholar]
- [19].Ehrenberg HR, Shin J, Ratner AJ, Fries JA, and Ré C. Data Programming with DDLite: Putting Humans in a Different Part of the Loop. In HILDA@ SIGMOD, 2016. [Google Scholar]
- [20].Falkowski MJ, Hudak AT, Crookston NL, Gessler PE, Uebler EH, and Smith AM. Landscape-scale Parameterization of a Tree-Level Forest Growth Model: A K-Nearest Neighbor Imputation Approach Incorporating LiDAR Data. Canadian Journal of Forest Research, 40(2):184–199, 2010. [Google Scholar]
- [21].Fan W and Geerts F. Foundations of Data Quality Management. Synthesis Lectures on Data Management, 2012. [Google Scholar]
- [22].Fan W, Geerts F, Li J, and Xiong M. Discovering Conditional Functional Dependencies. IEEE, 2011. [Google Scholar]
- [23].Garey MR and Johnson DS. Computers and Intractability, volume 29 wh freeman; New York, 2002. [Google Scholar]
- [24].Golab L, Karloff H, Korn F, Srivastava D, and Yu B. On Generating Near-optimal Tableaux for Conditional Functional Dependencies. PVLDB, 1(1):376–390, 2008. [Google Scholar]
- [25].Hao S, Tang N, Li G, and Li J. Cleaning Relations using Knowledge Bases. In Data Engineering (ICDE), 2017 IEEE 33rd International Conference on, pages 933–944. IEEE, 2017. [Google Scholar]
- [26].He J, Veltri E, Santoro D, Li G, Mecca G, Papotti P, and Tang N. Interactive and Deterministic Data Cleaning. In Proceedings of the 2016 International Conference on Management of Data, pages 893–907. ACM, 2016. [Google Scholar]
- [27].Hebert C, Hade E, Rahman P, Lustberg M, Stevenson K, and Pancholi P. Modeling Likelihood of Coverage for Narrow Spectrum Antibiotics in Patients Hospitalized with Urinary Tract Infections In Open forum infectious diseases, volume 4, page S281 Oxford University Press, 2017. [Google Scholar]
- [28].Hebert C, Ridgway J, Vekhter B, Brown EC, Weber SG, and Robicsek A. Demonstration of the Weighted-incidence Syndromic Combination Antibiogram: An Empiric Prescribing Decision Aid. Infection Control & Hospital Epidemiology, 33(4):381–388, 2012. [DOI] [PubMed] [Google Scholar]
- [29].Huang Z and He Y. Auto-Detect: Data-Driven Error Detection in Tables. In Proceedings of the 2018 International Conference on Management of Data, pages 1377–1392. ACM, 2018. [Google Scholar]
- [30].Ilyas IF, Markl V, Haas P, Brown P, and Aboulnaga A. CORDS: Automatic Discovery of Correlations and Soft Functional Dependencies. In Proceedings of the 2004 ACM SIGMOD international conference on Management of data, pages 647–658. ACM, 2004. [Google Scholar]
- [31].Jiang L, Rahman P, and Nandi A. Evaluating Interactive Data Systems: Workloads, Metrics, and Guidelines. In Proceedings of the 2018 International Conference on Management of Data, pages 1637–1644. ACM, 2018. [Google Scholar]
- [32].Kandel S, Paepcke A, Hellerstein J, and Heer J. Wrangler: Interactive Visual Specification of Data Transformation Scripts. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, pages 3363–3372. ACM, 2011. [Google Scholar]
- [33].Koren Y, Bell R, and Volinsky C. Matrix Factorization Techniques for Recommender Systems. Computer, 42(8), 2009. [Google Scholar]
- [34].Krishnan S, Wang J, Wu E, Franklin MJ, and Goldberg K. Activeclean: Interactive Data Cleaning while Learning Convex Loss Models. PVLDB, 9(12):948–959, 2016. [Google Scholar]
- [35].Lin J. Divergence Measures Based on the Shannon Entropy. IEEE Transactions on Information theory, 37(1):145–151, 1991. [Google Scholar]
- [36].Mayfield C, Neville J, and Prabhakar S. ERACER: A Database Approach for Statistical Inference and Data Cleaning In ACM SIGMOD, 2010. [Google Scholar]
- [37].Mazumder R, Hastie T, and Tibshirani R. Spectral Regularization Algorithms for Learning Large Incomplete Matrices. Journal of machine learning research, 11(Aug):2287–2322, 2010. [PMC free article] [PubMed] [Google Scholar]
- [38].Meduri VV and Papotti P. Towards User-Aware Rule Discovery In Information Search, Integration, and Personlization, pages 3–17. Springer, 2017. [Google Scholar]
- [39].Milo T, Novgorodov S, and Tan W-C. Rudolf: Interactive Rule Refinement System for Fraud Detection. PVLDB, 9(13):1465–1468, 2016. [Google Scholar]
- [40].Park H, Pang R, Parameswaran A, Garcia-Molina H, Polyzotis N, and Widom J. An Overview of the Deco System: Data Model and Query Language; Query Processing and Optimization. ACM SIGMOD Record, 2013. [Google Scholar]
- [41].Park H and Widom J. CrowdFill: Collecting Structured Data from the Crowd. In ACM SIGMOD, 2014. [Google Scholar]
- [42].Rahman P, Hebert CL, and Lai AM. Parsing Complex Microbiology Data for Secondary Use. In AMIA, 2016. [Google Scholar]
- [43].Raman V and Hellerstein J. Potter’s Wheel: An Interactive Framework for Data Cleaning. Technical report, Working Paper, 1999. http://www.cs.berkeley.edu/~rshankar/papers/pwheel.pdf, 2000.
- [44].Rekatsinas T, Chu X, Ilyas IF, and Ré C. Holoclean: Holistic Data Repairs with Probabilistic Inference. PVLDB, 10(11):1190–1201, 2017. [Google Scholar]
- [45].Rubinsteyn A, Feldman S, O’Donnell T, and Beaulieu-Jones B. Hammerlab/Fancyimpute: Version 0.2.0. September 2017. [Google Scholar]
- [46].Singh R and Gulwani S. Learning Semantic String Transformations from Examples. PVLDB, 5(8):740–751, 2012. [Google Scholar]
- [47].Stolte C, Tang D, and Hanrahan P. Polaris: A System for Query, Analysis, and Visualization of Multidimensional Relational Databases. IEEE Transactions on Visualization and Computer Graphics, 8(1):52–65, 2002. [Google Scholar]
- [48].Suykens JA and Vandewalle J. Least Squares Support Vector Machine Classifiers. Neural processing letters, 9(3):293–300, 1999. [Google Scholar]
- [49].Thirumuruganathan S, Berti-Equille L, Ouzzani M, Quiane-Ruiz J-A, and Tang N. Uguide: User-guided Discovery of FD-detectable Errors. In Proceedings of the 2017 ACM International Conference on Management of Data, pages 1385–1397. ACM, 2017. [Google Scholar]
- [50].Wang J, Krishnan S, Franklin MJ, Goldberg K, Kraska T, and Milo T. A Sample-and-clean Framework for Fast and Accurate Query Processing on Dirty Data. In ACM SIGMOD, 2014. [Google Scholar]
- [51].Wang J and Tang N. Dependable Data Repairing with Fixing Rules. Journal of Data and Information Quality (JDIQ), 8(3–4):16, 2017. [Google Scholar]
- [52].Wei Z and Link S. DataProf: Semantic Profiling for Iterative Data Cleansing and Business Rule Acquisition. In Proceedings of the 2018 International Conference on Management of Data, pages 1793–1796. ACM, 2018. [Google Scholar]
- [53].White IR, Royston P, and Wood AM. Multiple Imputation Using Chained Equations: Issues and Guidance for Practice. Statistics in medicine, 30(4):377–399, 2011. [DOI] [PubMed] [Google Scholar]
- [54].Xu J, Kalashnikov DV, and Mehrotra S. Query Aware Determinization of Uncertain Objects. IEEE Transactions on Knowledge and Data Engineering, 2015. [Google Scholar]
- [55].Yakout M, Elmagarmid AK, Neville J, Ouzzani M, and Ilyas IF. Guided Data Repair. PVLDB, 4(5):279–289, 2011. [Google Scholar]
- [56].Yucel RM, He Y, and Zaslavsky AM. Imputation of Categorical Variables using Gaussian-based Routines. Statistics in Medicine, 30(29):3447–3460, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]


