Water content, not stiffness, dominates Brillouin spectroscopy measurements in hydrated materials

To the Editor: Brillouin microscopy is an optical method to map the mechanical properties of materials^1–5. The first Brillouin micrographs with cellular resolution were reported in Nature Methods in 2015⁴ and inspired a growing number of applications in biomechanics and biophotonics. In these publications, Brillouin measurements were considered a proxy for stiffness. In contrast, we show here in hydrogels that water content dominates Brillouin signals in hydrated materials. Brillouin microscopy relies on the phenomenon of Brillouin scattering, whereby photons exchange energy with thermally driven acoustic waves, or phonons, leading to a frequency shift ω_b between the incident and scattered light, given by

$${\omega }_b=\frac{2n}{\gamma }\sqrt{\frac{M}{p}}\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}sin}\frac{\theta }{2}$$ (1)

where ρ and n are the density and refractive index of the material, and λ and θ are thein vacuo wavelength and angle between the incident and scattered wave vectors. M is the longitudinal elastic modulus and represents the compressibility of a material or, specifically, the mechanical stress necessary to compress or expand it in one direction without lateral strain.

Despite the fact that equation (1) depends on M, recent reports have interpreted Brillouin micrographs in terms of Young’s modulus E for cells and tissues^3–5.E represents the stiffness of a material, that is, how resistive it is to deformation, and describes the stress necessary to compress or extend a material in one directionwhile allowing lateral strain. As biological materials are composed mostly of water, which is relatively incompressible, M is several orders of magnitude greater than E. Further, Brillouin scattering is sensitive to gigahertz frequencies where, owing to viscoelastic effects, mechanical properties may diverge from those at biologically relevant strain rates, which typically occur over seconds. Nonetheless, empirical correlations between M and E for cells⁴, hydrogels^3,4 and other biological tissues³ have suggested that variations in M, as measured by Brillouin scattering, reflect variations in E.

We set out to examine the relationship between Brillouin measurements and Young’s modulus, accounting for the potential influence of water content ε, which can affect both M and E in hydrated materials. We used hydrogels as a simplified model of biological materials because both contain fluid interspersed within a flexible solid network that provides elasticity.

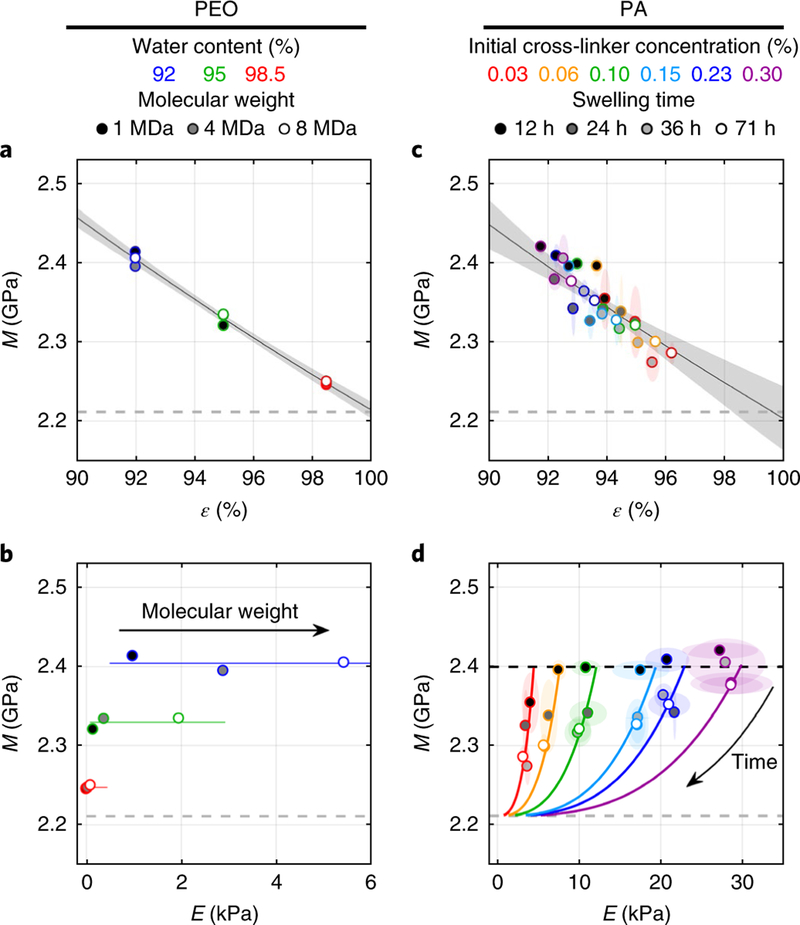
As the molecular weight of polyethylene oxide (PEO) increases, hydrogels change from a dilute suspension with zero Young’s modulus to a semi-dilute entangled network with finite E. When the molar concentration is decreased in proportion to the increase in molecular weight, water content ε can be fixed while E increases. Thus, we could vary E independently of ε while measuring M using a custom Brillouin microscope⁵ (Supplementary Methods). With increasing molecular weight, E measured by rheometry increased for a given ε. However, M was unaffected by the change in molecular weight, but decreased with ε (Fig. 1a and Supplementary Note). Thus, for PEO hydrogels, changes in E were uncorrelated with changes in M when controlling for water content (Fig. 1b and Supplementary Note).

Fig.1. Young’s modulus E, water content ε and longitudinal elastic modulus measured by Brillouin M for polyethylene oxide and polyacrylamide hydrogels.

a, M for PEO of the indicated molecular weight, measured at different ε. The fit to equation (2) is shown (R² =0.97; one hydrogel per data point).b, M is plotted versus E (color code as in a;one hydrogel per data point). Lines represent values of constant ε. c, M over all swelling times (shading within symbols) and cross-linker concentrations (colored symbols), plotted versus ε for PA. The fit to equation (2) is shown (R² =0.78; four hydrogels per data point, mean ±2 s. d.).d, Relationships between M and E at various PA hydrogel compositions. Changes in M and E during swelling were consistent with predictions of equations (2) and (3) using M_f =2.21 GPa and M_s =16.35 GPa (curves; four hydrogels per data point, mean ±2 s. d.). Dashed gray lines represent the value of M for pure water. The black dashed line in d represents the estimated initial value of M at the start of swelling when ε₀ =0.9 for all hydrogels. Elliptical regions surrounding data points in c and d represent 2 s.d. Shaded regions in a and c represent 95% confidence bounds on the fit by equation (2).

To understand the relationship between M and ε, we considered a biphasic model where the aggregate compressibility is equal to the sum of the individual fluid and solid compressibilities weighted by their respective volume fractions⁶,

$$\frac{1}{M}=\frac{\epsilon }{M_f}+\frac{1-\epsilon }{M_s}$$ (2)

where M_f and M_s are the longitudinal elastic moduli (inverse compressibilities) of the fluid and solid, respectively. Equation (2) captures the relationship between M and ε for PEO (Fig. 1a and Supplementary Note).

Previously reported correlations between M and E were based on polyacrylamide (PA) hydrogels^3,4, which swell over time (Supplementary Fig. 1). Using different concentrations of bis-acrylamide to vary PA stiffness, we measured M, E and ε during swelling (Supplementary Figs. 2–4). All values of M collapsed onto a single relationship with ε, consistent with equation (2), despite differences in E or the extent of swelling (Fig. 1c and Supplementary Note).

During swelling of PA, E measured by unconfined compression decreased according to

$$E=E_0{Q}^{-1/3}$$ (3)

where Q =(1–ε₀)/(1–ε) is the swelling ratio and E₀ is the estimated Young’s modulus immediately after gelation.

There was no clear relationship between M and E when considering all data. However, equations (2) and (3) predicted how M changed versus E for individual hydrogels as ε increased from ε₀ =0.9to 1These predicted trajectories (shown by solid curves in Fig. 1d and the Supplementary Note) explain how a correlation may arise owing to a mutual dependence on ε without an explicit relationship between M and E.

In conclusion, Brillouin measurements appear insensitive to Young’s modulus after accounting for the influence of water content in PEO and PA hydrogels. This suggests that Brillouin measurements applied to biological tissues may be similarly affected by water content, although differences in hydration between tissues and the role of bound water may have additional effects. This work cautions against the straightforward application of Brillouin microscopy, or Brillouin scattering in general, as a form of optical bioelastography and motivates further research into the factors influencing the Brillouin frequency shift in biological materials.