Coupling of Membrane Nanodomain Formation and Enhanced Electroporation near Phase Transition

Abstract

Biological cells are enveloped by a heterogeneous lipid bilayer that prevents the uncontrolled exchange of substances between the cell interior and its environment. In particular, membranes act as a continuous barrier for salt and macromolecules to ensure proper physiological functions within the cell. However, it has been shown that membrane permeability strongly depends on temperature and, for phospholipid bilayers, displays a maximum at the transition between the gel and fluid phase. Here, extensive molecular dynamics simulations of dipalmitoylphosphatidylcholine bilayers were employed to characterize the membrane structure and dynamics close to phase transition, as well as its stability with respect to an external electric field. Atomistic simulations revealed the dynamic appearance and disappearance of spatially related nanometer-sized thick ordered and thin interdigitating domains in a fluid-like bilayer close to the phase transition temperature (T_m). These structures likely represent metastable precursors of the ripple phase that vanished at increased temperatures. Similarly, a two-phase bilayer with coexisting gel and fluid domains featured a thickness minimum at the interface because of splaying and interdigitating lipids. For all systems, application of an external electric field revealed a reduced bilayer stability with respect to pore formation for temperatures close to T_m. Pore formation occurred exclusively in thin interdigitating membrane nanodomains. These findings provide a link between the increased membrane permeability and the structural heterogeneity close to phase transition.

Significance

The study characterizes the structure and dynamics of phospholipid bilayers close to phase transition employing atomistic molecular dynamics simulations. The simulations recover not only the well-studied first-order transition with discontinuities in the area per lipid or membrane thickness but the anomalous behavior for the isothermal compressibility and bending rigidity at phase transition previously reported from experiments, as well. To the best of our knowledge, the molecular dynamics simulations revealed, for the first time, the dynamic appearance and disappearance of both spatially related nanometer-sized thick ordered domains and thin interdigitating domains above the transition temperature that are reminiscent of the ripple phase. These thin membrane domains are related to the experimentally described increased permeability of membranes close to phase transition.

Introduction

Biomembranes are barriers that separate the cell exterior from the outer environment. They are semipermeable for water, small molecules, and to a lesser extent, also salt (1) but generally prevent the uncontrolled passage of salt and macromolecules in or out of the cell at ambient temperatures. The main components of membranes are phospholipids, sphingolipids, and sterols (2). The exact composition, however, is highly diverse and depends not only on the organism but also on the cell type, the membrane surrounding, and environmental factors such as temperature (3). Additionally, the lipid composition continuously changes as a result of lipid synthesis, degradation, or membrane fusion. The different lipid types vary in terms of their fatty acid chain length and degree of saturation, head/tail size ratio, and net charge. This feature of biomembranes allows them to fine-tune their structural characteristics, including their thickness, rigidity, and fluidity. Especially if the geometries of different lipids fit well together, local nano- to microdomains of high order (liquid-ordered, L_o) can develop in an otherwise fluid or liquid-disordered (L_d) environment (4, 5). These so-called rafts are thought to be important for physiological processes because they were, for instance, shown to be involved in protein trafficking from the endoplasmatic reticulum to the plasma membrane (5, 6). In general, “membrane (nano-)domains” are defined as dynamical membrane regions of “different chemical composition and/or physical properties compared to their surrounding lipid environment” (7).

Lateral membrane heterogeneity emerges not only because of an accumulation of certain lipid types, also single-component membranes can adopt different phases depending, for example, on the temperature. Below a critical main transition temperature T_m that is specific for the lipid type, lipids may arrange into the ordered crystalline (L_C), gel (L_β or L_β′), or ripple (P_β′) phase. In the ordered gel phase, lipid tails are stretched with preferentially all dihedral angles in trans conformation, and lipids with a PC headgroup additionally tilt with respect to the membrane normal (L_β′) (8, 9, 10, 11). The dense lipid packing within the ordered phase results in an increased membrane thickness with a heavily decreased diffusion coefficient (12, 13). Upon heating, small local seeds of fluid-state lipids develop that spread throughout the whole bilayer if the temperature is raised above T_m (14). In the fluid (L_α) phase at T > T_m, the dihedral angles of the lipid tails are predominantly in gauche conformation, rendering the membrane softer and more dynamic. The melting temperature T_m is typically determined via differential scanning calorimetry (15) and corresponds to the temperature at which the heat capacity of the system adopts a maximum.

Remarkably, the transition between the gel and fluid phase not only involves structural adaptations but also changes in membrane permeability (16, 17, 18, 19, 20, 21, 22, 23), also called soft perforation (20). Already in the early 70s, Papahadjopoulos et al. (16) demonstrated that sodium ions (Na⁺) diffuse spontaneously through the membrane of 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) vesicles, with a significant increase in permeability at temperatures close to the lipid’s T_m. Different from the narrow temperature interval of the main phase transition of pure lipid bilayers, an increased Na⁺ permeability was reported for a comparably broad temperature interval of ∼10 K. Importantly, unmodified DPPC vesicles were used in these experiments, i.e., the membrane was free of any ion channel, and the permeability could be altered simply by varying the temperature. Several experimental as well as computational studies followed (see, e.g., (17, 18, 22, 24, 25)) that addressed the permeability anomaly—also valid for water molecules (19), larger fluorescent dyes (21), and in mixed membranes (23)—in more detail. For example, currents through model membranes were observed to be quantized at temperatures close to T_m with distinct amplitudes (18, 20, 21, 22), and their lifetimes were similar to those measured in bilayers containing the ion channel gramicidin A (18). The former finding suggests the formation of lipid pores with characteristics similar to protein ion channels (18, 26, 27).

Two hypotheses evolved that aimed at explaining the permeability anomaly at the phase transition: 1) the authors of the original work concluded that leaky “regions of disorder” develop at the boundary between coexisting gel and fluid-phase lipids and that the area fraction of the boundary region is largest at the phase transition, explaining the increased permeability (16). The coexistence of ordered and disordered domains around T_m was further scrutinized in both experiments and simulations (14, 28, 29, 30, 31, 32), and the “leaky interface” hypothesis supported (17, 18, 28); 2) the second hypothesis uses thermodynamic arguments to relate membrane permeability to the lateral membrane compressibility (33). At phase transition, fluctuations in the lateral membrane density are high, thereby minimizing the energy for membrane pore formation (21, 22, 27, 33, 34, 35). Similarly, increased current fluctuation lifetimes at T_m were associated with the increased relaxation times of membranes at phase transition (22, 36, 37, 38). Of course, these hypotheses do not exclude each other because density fluctuations might be more pronounced at the phase boundaries.

Membrane stability may also be compromised by application of external electric fields, i.e., large transmembrane potentials may (transiently) disrupt the membrane, a process known as electroporation (39, 40). At a molecular level, the applied electric field triggers orientational changes of interfacial water molecules and lipids depending on their dipole moment. The tilting of lipids is eventually followed by spontaneous insertion of water molecules and a few lipid headgroups into the membrane hydrophobic core, followed by the formation of a toroidally shaped hydrophilic pore of similar size as compared to ion channels (41).

The underlying mechanisms for the increased passive ion permeability close to T_m and induced electroporation are likely closely related (20, 27): permeation mechanisms through lipid membranes in the absence of (protein) ion channels may include both ion-induced membrane deformation and the formation of transient pores (42, 43). At or close to phase transition, experiments by different groups showed quantized current fluctuations on comparably long timescales applying external fields (18, 20, 21, 22), which were absent below or above T_m. The field-induced permeability close to phase transition showed similar characteristics to experiments addressing the passive permeability of membranes close to T_m (16). Also, only small-to-moderate electric fields were sufficient to induce membrane pore formation at T_m (20). The amplitudes and lifetimes were similar as compared to protein ion channels (reviewed in (27)). We have shown before using simulations that electric fields induce such well-defined pores with a radius of ∼0.5 nm, in excellent agreement with findings from conductance experiments (41). This suggests that the formation of pores of well-defined size rather than membrane defects causes the increased ion permeability at T_m.

Furthermore, combined data from swelling experiments and MD simulations of membranes in the fluid phase at various electric field strengths E could be combined by assuming that the pore formation time t follows a simple exponential, t ∝ exp(−ΔμE/k_BT), with the activation dipole moment upon pore formation Δμ (41). This implies that pores with similar characteristics to electropores appear as well at vanishing electric fields. Taken together, experiments and simulations hint at an important role of lipid pore formation as a source for the increased permeability of membranes close to phase transition. A different underlying mechanism for the observed permeability increase of membranes close to T_m appears unlikely but cannot be ruled out.

Both of these methods to transiently decrease membrane stability, i.e., electroporation and soft perforation, are widely applied in medicine and molecular biology (44, 45, 46): in electrochemotherapy for the transfer of nonpermeant chemotherapeutics into tumor cells (47), electrogene transfer for the delivery of genes into cells (48), and in drug delivery via temperature-sensitive liposomes releasing their content upon local mild hyperthermia (49, 50, 51), to mention a few.

Besides temperature, membrane phase behavior may also be altered by pressure (52), addition of calcium (53), changes in pH (54), application of electric fields (55, 56), or addition of anesthetics (21). The latter change the membrane characteristics—e.g., broaden the lateral pressure profile within the hydrophobic/hydrophilic membrane interface—by binding to phospholipids (57, 58). Likewise, all resting cells are subjected to an inherent membrane potential on the order of 100 mV formed in part by an asymmetric distribution of ions between the cell interior and exterior. Temporary variations in the ion composition induce changes and, during an action potential, even an inversion of the membrane potential. For instance, the calcium concentration is locally raised in the presynapse before synaptic vesicle release to trigger the formation of the fusion pore (59).

The observations that 1) the phase transition temperatures of different biological membranes are slightly below physiological temperatures (60, 61, 62), 2) biological membranes compartmentalize dynamically and laterally into functional nano- and microdomains with differing protein affinities (6, 63), and 3) the phase transition temperature strongly depends on the environmental conditions and the membrane composition suggest an important physiological role of membrane phase transitions for living organisms.

Here, we addressed the formation and coexistence of ordered and disordered nanodomains in fluid DPPC bilayers at different temperatures close to and above phase transition using atomistic molecular dynamics (MD) simulations. DPPC was chosen as a prototypical phospholipid used in numerous experimental and simulation studies addressing structural and dynamical characteristics of lipid bilayers and was also frequently used in experimental studies addressing the temperature-dependent permeability anomaly (16, 20, 21).

We observed both nanometer-sized ordered domains and strongly interdigitating, thin domains coexisting close to phase transition. The results were corroborated by studies on a preformed two-phase system with gel and fluid domains that revealed a thinned interdigitated region at the domain interface. The occurrence of thin interdigitated membrane domains suggested as precursors of the interdigitated domains observed during ripple-phase formation (64) could be related to the experimentally observed permeability anomaly close to phase transition: Pore formation induced by an external electric field was significantly pronounced close to phase transition, with pores preferentially developing within the thin membrane domains. Both the increased electric field across thin membrane domains in conjunction with defects in the integrity of the surrounding membrane cause an enhanced pore formation at T_m.

Methods

Simulation systems

The following systems were set up to study the coexistence of ordered and disordered domains of varying thickness in lipid bilayers and the coupling between membranes close to phase transition and enhanced ion permeability.

• 1)A two-phase system (gel-fluid) consisting of, in total, 1280 DPPC lipids was used to study the phase transition temperature of DPPC, the phase boundary, and electropore formation at the phase boundary (DPPC^gf system).
• 2)The temperature-dependent spontaneous formation of differently ordered nanodomains was addressed in simulations of a large membrane in the fluid phase (1280 DPPC lipids, DPPC^f system).
• 3)A smaller membrane in the fluid phase (640 DPPC lipids) was used to study temperature-dependent electropore formation rates (${\text{DPPC}}_s^f$ system).

An overview of all performed simulations is provided in Table 1.

Table 1.

Overview of Conducted Simulations

System	Purpose	Replicas per Temperature	Length	Temperatures	Total Number
DPPCgf	Gel-fluid interface	1	100 ns	280/360 K	1
DPPCgf	Determination of Tm	1	100 ns	314–330 K (ΔT = 2 K)	9
DPPCgf	Electroporation	3 × 10a	≤100 nsb	321 K (= Tm)	30
DPPCgf	Pore closure	1	100 ns	321 K (= Tm)	1
DPPCf	Nanodomain formation	1	500 ns	322, 326, 330, 335, 340 K	5
${\text{DPPC}}_s^f$	Electroporation	3 × 10a	≤100 nsb	322, 330, 335, 340 K	120
DPPCf	Electroporation	3 × 10a	≤100 nsb	322, 335 K	60

^a10 replica simulations were performed each starting from three different configurations.

^bSimulations were conducted until 100 ns or stopped after an electropore formed.

DPPC^gf system

Initially, a small coarse-grained (CG) DPPC lipid bilayer (640 lipids) was created with the tool insane (65), minimized (500 steps), and equilibrated for 50 ns at a temperature of 280 K (lipids) and 305 K (water) with the parameters of the standard MARTINI 2 force field (66, 67). The insane tool allows for the generation of sophisticated membranes (68) and, in conjunction with the initram workflow (69), for the fast and efficient setup of pre-equilibrated membranes of almost arbitrary composition at atomistic resolution (AA). After conversion to atomistic resolution using initram (69), the system was duplicated in the x-direction to yield a system with the lateral dimensions of ∼27 × 11 nm. During a subsequent 100 ns AA simulation (CHARMM36 force field (70)), the first membrane duplicate was coupled to a temperature of 280 K and the second to 360 K, resulting in a bilayer with one gel and one fluid-phase stripe (both infinite in the y-direction; see Fig. S1 for the evolution of the area per lipid [APL]). The temperature of the solvent was maintained at 310 K. A fully hydrated bilayer was used, i.e., 40 water molecules per lipid were added to the system to avoid effects on the lipid phase behavior due to dehydration (71). The system covered, in total, 1280 DPPC lipids and ∼50,500 water molecules (in total, ∼320,000 atoms).

The melting temperature T_m was determined by starting a series of 100-ns-long AA simulations with the equilibrated two-phase structure as starting structure. In each simulation, the whole system (i.e., bilayer and solvent) was coupled to a temperature between 314 and 330 K (nine simulations, 2 K steps). T_m was defined by the temperature at which the mean dihedral angle of the lipid tails, expressed as the fraction of gauche dihedrals, remained unchanged (T_m = 321 K; see Results) (72, 73). An additional 20-ns-long simulation proceeding the 100 ns long simulation at T = 320 K from above was carried out at T = T_m, yielding an equilibrated (metastable) two-phase gel-fluid lipid bilayer system at T_m (Fig. S2).

The structures at t = 10, 15, and 20 ns of the follow-up simulation were used as starting structures for 10 replica simulations, each with different starting velocities (in total 30 simulations), in which an external electric field (40, 41) of 0.2 V/nm was applied normal to the membrane while maintaining the temperature of the system at T = T_m. All starting structures thus contained the DPPC bilayer in a gel-fluid coexistence phase with box dimensions of ∼30 × 11 × 8.6 nm (see Fig. 1 B; Fig. S3). The simulations were run for 100 ns or stopped after an electropore formed. After initial pore formation (pore of 2 nm in diameter), one simulation was continued with the field switched off and simulated for additional 100 ns. A stable pore with a diameter of 1 nm (see also (41)) developed that did not close during these 100 ns.

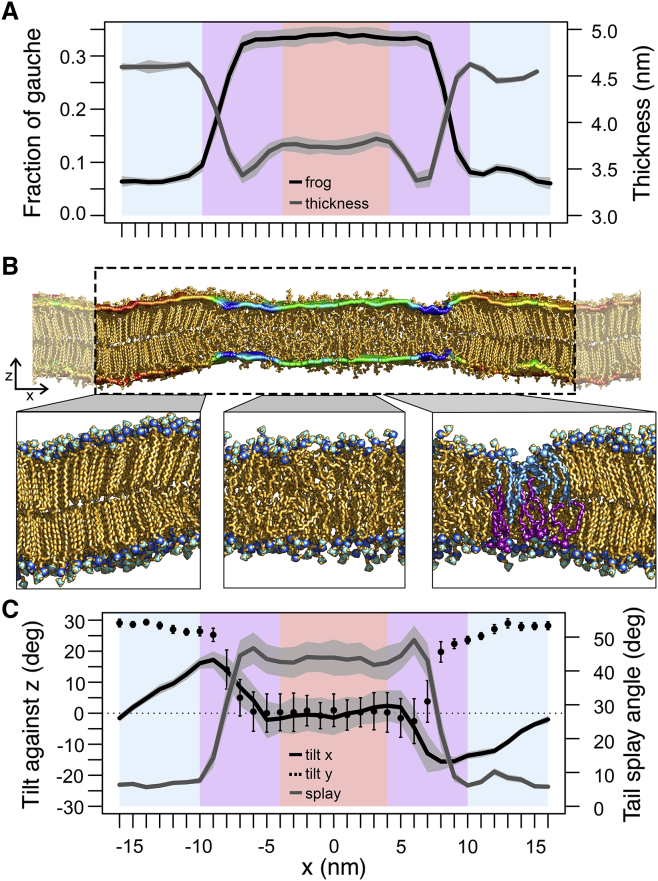
Figure 1.

Structural characteristics of a DPPC bilayer with coexisting fluid and gel phase domains (DPPC^gf system). (A) Fraction of gauche (black line) and thickness (gray line) profiles across the interface (along the x axis) are shown. The blue, purple, and red backgrounds correspond to the gel, interface, and fluid domains, respectively. (B) A snapshot of the two-phase bilayer at the end of the simulation (100 ns) is shown. The bilayer thickness is superimposed on the headgroup region as a rainbow-colored surface, the colors ranging from blue (thickness of 3 nm) to red (5 nm). (C) Profiles of lipid tilt angle against z axis (black lines) are shown. The tilt in the x-direction (i.e., projection of the lipid tails on the xz-plane; see Fig. S1C) is given as a solid line, the tilt in the y-direction (i.e., projection of the lipid tails on the yz-plane) as dotted line (see also Fig. S1B). The gray line represents the lipid tail splay angle profile. All profile values were averaged over the final 50 ns. The SD is given as shaded area for all profiles except for the tilt in the y-direction, where it is represented as error bars. To see this figure in color, go online.

DPPC^f system

Ordered and disordered nanodomain formation in fluid-like phase membranes was investigated in 500-ns-long atomistic MD simulations of large DPPC bilayers (1280 lipids, 64,000 water molecules) at temperatures of 322, 326, 330, 335, and 340 K, i.e., above the computationally determined T_m. All starting structures were equivalent and based on a fluid bilayer obtained by backmapping (69) the last structure of a corresponding 50 ns CG simulation (at 335 K). The water layer between two periodic images of the bilayer in the normal direction ranged between ∼4.52 nm at 322 K and ∼4.42 nm at 340 K. The layer thickness was calculated based on the distance of the choline headgroup density (data not shown).

${\text{DPPC}}_s^f$ system

A small fluid bilayer (640 DPPC lipids, 33,000 water molecules) was employed to study the temperature dependency of electropore formation rates. This smaller system effectively yields the same area as compared to the fluid domain of the mixed DPPC^gf system. The system was setup in CG representation (see above) and simulated at 335 K for 50 ns, which was followed by conversion to all-atom representation (69). The starting structures for electroporation (E_ext = 0.2 V/nm) were extracted from a following all-atom equilibration simulation (snapshots taken at t = 10, 15, and 20 ns), with the systems coupled to a temperature bath (see below) at 322, 330, 335, and 340 K. The system dimension normal to the membrane was similar (∼8.6 nm) among all poration simulations to ensure similar potential differences of ∼1.7 V across the box. 10 replicas for each temperature and starting configuration were run until 100 ns or stopped after pore formation. Equilibration was monitored by the APL (Fig. S10 A). Pore formation was not biased by the starting structures as the formed pores formed were well distributed across the membrane (Fig. S10 B).

In total, ∼230 all-atom MD simulations were conducted with a total simulation length of ∼9 μs (Table 1).

All CG standard MARTINI simulations were conducted with the GROMACS 5.1 simulation software (74) with the commonly used simulation parameters (66, 67, 75) and an integration time step of 20 fs. Atomistic simulations were performed with the GROMACS 2018 software suite together with the CHARMM36 force field (70). Simulation parameters were equivalent to those described in our previously published force-field comparison study (76), except that the recommended force-based switch (1.0–1.2 nm) was used for the van der Waals interactions (77). Long-range Coulomb interactions were calculated using the particle mesh Ewald method (78) with a real-space cutoff of 1.2 nm. The temperature was controlled every 1 ps with the Nosé-Hoover thermostat (79, 80), and pressure was maintained semi-isotropically at 1 bar with τ_p = 5 ps and a compressibility of 4.5 × 10⁻⁵ bar⁻¹ employing the Parrinello-Rahman barostat (81). The integration time step was set to 2 fs, and bonds to hydrogens were constrained with the LINCS algorithm (82). The CHARMM TIP3P model was used for water (83). Because in the two-phase system, half of the lipid bilayer was present in gel and the other half in fluid phase (striped in the x-direction), here, anisotropic pressure coupling was applied, with all off-diagonal compressibilities set to zero to maintain the rectangular shape of the box. This allowed for an independent equilibration of the x and y axis. The relative change of the x- and y-box vectors during the 280/360 K simulation by 16 and 5%, respectively, confirmed the necessity for anisotropic pressure coupling in the DPPC^gf system instead of the generally used semi-isotropic pressure coupling for lipid bilayers.

Data analysis

Lipid diffusion, APL, and membrane thickness

The lateral lipid diffusion coefficient D_l was calculated by a linear fit to the mean-squared displacement of the lipids’ centers of masses in the DPPC^f simulations (84). The center-of-mass motion was removed separately for the two monolayers. The 500-ns-long simulations were split into 40 ns intervals to calculate the mean and standard error, and the fitting was done between 2 and 6 ns (Fig. S4). The first 20 ns of each simulation were discarded for equilibration purposes.

The APL and the membrane thickness were analyzed using the g_lomepro tool with a grid spacing of ∼1 Å (85) and phosphate atoms as reference and given as averages over 1 ns time intervals with a sliding window of 500 ps length.

Thin and thick membrane domains

Membrane domains of varying thickness were identified as follows: first, all grid points with a 1-ns-average thickness of ≤3.5 nm (thin domains) or ≥4.5 nm (thick domains) were extracted. The lower value of 3.5 nm was determined from the local thickness minimum of ∼3.4 nm for the DPPC^gf system (two-phase system). Also, electropores were seen to predominantly occur within membrane domains thinner than ∼3.5 nm (see also Fig. 9). The upper cutoff of 4.5 nm was chosen according to the thickness of the gel phase (4.55 nm) in the DPPC^gf system. Note that the typical lipid tilt of 30° within the DPPC gel phase was absent in the thick, ordered nanodomains observed also above phase transition (DPPC^f system), resulting in a thickness even larger than for the gel phase. Subsequently, domains were identified by grouping all grid points (separately for thin and thick membrane domains) that were found within a distance of 2 Å to each other. The domain size was estimated by the number of grid points forming the domain (1 grid point $\stackrel{\wedge}{=}$ 1 Å²). For the analysis, we only included domains larger than 2 nm² corresponding to ∼3 DPPC lipids per monolayer. The domain lifetimes were estimated by following the centers of mass (COMs) of the domains. Domains were allowed to move <2 nm between subsequent time intervals (0.5 ns) and were assigned an individual ID if the criterion was satisfied.

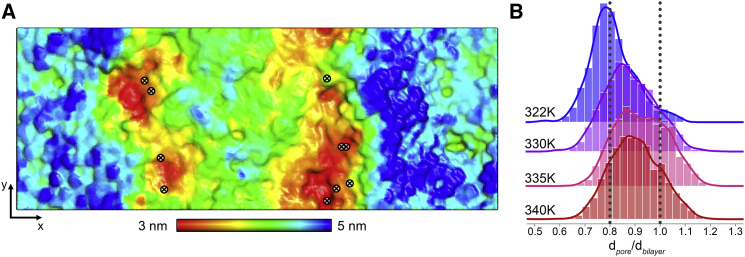
Figure 9.

Relation between pore location and membrane thickness. (A) 2D membrane thickness map of the DPPC^gf (two-phase) system before application of the external field and positions where pores formed in individual simulations (circles and crosses; 10 replica simulations starting from the same initial configuration, T = T_m = 321 K). (B) Ratio between the local thickness of pore-forming nanodomains (0.5 nm around the future water wires) and the overall membrane thickness of the small fluid DPPC^f_s systems at the respective temperature is shown (30 replicas for each temperature, three different initial configurations; see Methods). The local thickness was extracted 5–0.5 ns before the water wire formed across the membrane. In the 322 K system, pores formed in domains with a local thickness of ∼3.2 nm; in the 340 K system, the membrane was ∼3.5 nm thick. To see this figure in color, go online.

Lipid tail overlap

To calculate the lipid tail overlap, grids were separately defined for the lower and upper leaflets of the membrane using a 1 Å spacing. The terminal carbon atoms of the DPPC acyl chains (C16_sn1, C16_sn2) were chosen as reference positions for the lipid tail insertion depth. Each grid point was assigned the z-coordinate of the nearest reference atom (in lateral direction) of the respective monolayer. The tail overlap was then estimated as the difference between the z-coordinates of the upper and the lower monolayer grid points, i.e., a negative overlap is obtained for interdigitating lipid tails. Also here, the tail overlaps were averaged over 1 ns intervals.

Lipid tail angle

For analysis, the membrane was divided along the x axis in 1 nm slabs (DPPC^gf system). Individual lipids were assigned to the respective slabs according to their headgroup phosphate position with an update frequency of 100 ps. All reported lipid tail angles were calculated based on vectors connecting the C2 and C16 atoms of the fatty acid chains and the membrane normal (z-direction; see Fig. S1 C for further details). The lipid splay angle was computed as the angle between the two tail vectors (Fig. S1 C).

Pore formation rate

Pore formation rates were obtained by linearly least-square fitting the logarithm of the probability function P(t) ∝ exp(−λt), describing the probability that pore formation is initiated at times larger than t, to the simulation data using R (86). The pore initiation time was defined as the time at which a water column formed across the bilayer that developed subsequently in a hydrophilic pore (41).

Results

The aim of this study was to analyze the characteristics of a planar DPPC bilayer for temperatures at and above the main phase transition temperature T_m, in particular the formation and dynamics of membrane (nano)domains differing in lipid order and packing, as well as to provide a mechanistic link to experimentally observed enhanced ion permeation rates close to T_m. To this aim, we first characterized a lipid bilayer system with stable coexisting fluid- and gel-phase domains and a well-defined interface. The domains were initially enforced by coupling of the corresponding membrane halves to different temperatures (see next section). The determination of the melting temperature for this system in the second section is followed by analysis of a corresponding DPPC bilayer within the fluid-like phase for different temperatures T > T_m, with a focus on spontaneously and transiently formed membrane nanodomains of divergent structural characteristics. The last section addresses membrane poration at and above T_m by application of an external electric field, enabling a coupling between membrane permeation and membrane phase behavior.

Structural properties of the DPPC gel-fluid interface

The interface of a fluid phospholipid bilayer between coexisting gel and fluid phases (DPPC^gf system) was analyzed for a fully hydrated two-phase bilayer consisting of one fluid (L_α) and one gel (L_β′) phase domain. The phase separation was artificially initiated and stabilized in a 100 ns simulation by the coupling of two membrane halves (each 640 DPPC lipids) to temperatures well below (280 K) and above (360 K) the main phase transition temperature. Employing this procedure, a well-defined gel-fluid interface developed that allowed to pinpoint the main physical characteristics of this phase crossing. Importantly, the lipid acyl chain orientation within the gel phase and at the interface (described below) could develop in an unbiased fashion. Obtained results were corroborated in a subsequent MD simulation (for 120 ns) of the above pre-equilibrated two-phase system coupled to one temperature at and close to the main phase transition temperature T_m (Fig. S3; see next section for determination of T_m). The interface structure was largely retained at T_m.

A representative snapshot at the end of the simulation (280/360 K) is given in Fig. 1 B. The interface (normal to the plane in Fig. 1 B, i.e., along the y axis) was scrutinized below based on the final 50 ns of the simulation. In general, lipids within the gel phase adopt a stretched conformation, with the dihedral angles of the lipid tails preferentially in trans conformation, whereas lipids within the fluid phase display more disordered tails with a significantly increased fraction of dihedral angles in gauche conformation. The average fraction of gauche (frog) per acyl chain, i.e., the fraction of dihedral angles between −120° and +120°, was recently shown to be a good structural measure for phase transition (14). In experiments, frog values of 1–2% in the gel and 30% in the fluid phase were reported (87, 88, 89). During the 100 ns simulation of the DPPC^gf system, the average frog distribution of all lipids developed from an unimodal distribution to a distribution with two maxima at 5 and 33%, indicating that lipids transformed to either the gel or fluid state depending on the temperature at which they were maintained (Fig. S1, A and D). Fig. 1 A (black line) shows the frog profile along the x axis averaged over the last 50 ns of the simulation. A clear separation of fluid domain lipids from lipids within the gel domain is seen, with frog values of 0.34 within the disordered, fluid domain and of 0.07 within the ordered gel domain, in very good agreement with experiment (87, 88, 89).

The central fluid membrane domain adopted an average thickness of 3.76 nm (Fig. 1 A, gray line), which is in excellent agreement with the thickness of ∼3.8 nm measured experimentally for a fluid bilayer at 323 K (90). In turn, the ordered gel domain was on average 4.55 nm thick being also in line with experiments (4.3 nm at 298 K (91)). Remarkably, the interface region between the fluid and thick domain shows a minimum in membrane thickness of ∼3.40 nm. This transition region is rather broad because it has a width of 6 nm. The thickness minimum between membrane domains adopting different phases was recently reported by Cordeiro (92) as well, based on atomistic simulations of two-phase DPPC bilayers preassembled from membranes in either fluid or gel phase, and was suggested to be driven by the membrane bending rigidity. Here, the induced phase separation by coupling to different temperature baths allowed the unbiased study in particular of lipid tilting at the phase boundary.

The locally decreased thickness at the boundary region was accompanied by a decrease in lipid tilt from the gel domain (15–30°; see below) to the fluid domain (0°; Fig. 1, B and C, black lines). The lipid tilt is distinguished with respect to the z axis within the xz-plane (tilt x, plane of Fig. 1 B) and the yz-plane (tilt y, see also Fig. S1 B). The typical tilt of phosphatidylcholine (PC) lipids within the gel phase of ∼30° that arises because of the head/tail size ratio and allows for better chain packing (8, 91, 93, 94) developed exclusively perpendicular to the membrane plane shown in Fig. 1 B, i.e., in direction of the domain interface (tilt y). In contrast, the tilt within the xz-plane vanishes in the center of the gel domain and increases to ∼16° within the interface toward the fluid domain with, however, opposing directions at the boundaries at the left and the right. This collective lipid inclination is different from the characteristic tilt of ∼30° in the L_β′ phase. Already the tilting of the lipids of both monolayers in the same direction results in a slight thickness decrease. Additionally, the tail ends are shifted with respect to the lipid headgroups, resulting in an hourglass-like shape at the boundary (Fig. 1 B). To fill the wedge-like volume between the two leaflets that are tilting to each other, adjacent fluid-phase lipids splay their fatty acyl chains slightly more (48°) as compared to the lipids in the bulk fluid phase (43°, Fig. 1 C, gray line). This, together with lipid interdigitation of opposing leaflets (Fig. 1 B), resulted in an interfacial domain between the gel and fluid phase where the membrane is thinned by ∼0.4 nm as compared to the fluid phase.

Determination of the melting temperature T_m

To determine the main transition temperature T_m used for further analysis of the gel-fluid-phase system, we followed the phase growth procedure applied before for phospholipid bilayers (72) or pentadecane (73). Starting from the equilibrated gel-fluid DPPC^gf system coupled to different temperatures as described above, a series of simulations was conducted in which the growth of either phase was traced while coupling the whole system, i.e., bilayer and solvent, to one temperature ranging between 314 and 330 K in 2 K increments (i.e., nine simulations).

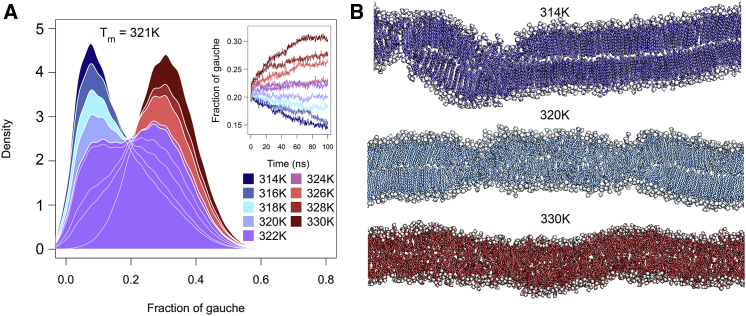
The phase growth was investigated by tracking the average fraction of acyl chain dihedrals in gauche state (frog) of all lipids over time (Fig. 2 A, inset). The temporal evolution of the APL is additionally shown in Fig. S2 and displays a similar behavior. For low temperatures, the frog declined from 0.20 to ∼0.15, indicating that the metastable state of the two coexisting phases collapsed and the gel state spread over the whole bilayer. In fact, the membranes formed a structure that was reminiscent of the ripple phase P_β′, the intermediate state between the L_β′ and L_α phase in DPPC bilayers (Fig. 2 B, top). In the P_β′ phase, two highly ordered domains were built with one of them fully interdigitating, resulting in a periodic ripple pattern of thin and thick structures (64, 94, 95). Recently, Khakbaz and Klauda (95) characterized in detail the P_β′ phase of DPPC and DMPC bilayers in atomistic simulations using the CHARMM36 force field and showed good agreement to x-ray diffraction data (96). Although the experimental main transition temperature of DPPC was determined to be 314 K (97), the bilayers showed a drift toward lower frog values for temperatures up to ∼320 K (Fig. 2 A, inset). In contrast, the two-phase systems simulated at temperatures above 324 K displayed a slow transformation to a fluid-phase bilayer. A full transition to the fluid phase at this timescale was only observed at the highest simulated temperature of 330 K, which reached a frog of 0.30 after 70 ns. At intermediate temperatures, the half-gel, half-fluid system remained (meta)stable. Fig. 2 A displays the frog distribution analyzed over the last 20 ns, in which a tendency to either lower or higher frog values is visible. We thus determined T_m to be 321 ± 1 K, i.e., 7 K above the experimentally determined value (97).

Figure 2.

Determination of T_m. (A) Distribution of fraction of gauche values (frog) over the last 20 ns for DPPC bilayers at different temperatures is shown. Inset: Individual frog values over time are shown. The different temperatures are colored from blue (314 K) to dark red (330 K). (B) Snapshots after t = 100 ns of DPPC bilayers simulated at 314 K (top), 320 K (middle), and 330 K (bottom) are given. To see this figure in color, go online.

The bilayer structure at the end of the 320 K simulation (Fig. 2 B, middle) was then further simulated for 20 ns at 321 K for analysis of the phase boundary (Fig. S3) at T_m and for a subsequent electroporation study (see below). One of the two interfacial domains was slightly distorted during these 120 ns (100 ns at 320 K plus 20 ns at 321 K, Fig. S2), but the overall structure detailed above remained stable, with only minor changes to the thickness profiles as compared to the 280/360 K system (Fig. S3).

Domain formation in fluid-phase-like lipid bilayers

The observation of thinned membrane domains in the L_α/L_β′ coexistence system at the main phase transition temperature led us to revisit the structural and dynamical properties of fluid-phase like membranes at or above T_m.

It is well-known that the membrane structure changes with changes in temperature. An increase in temperature of fluid-phase membranes results in a decrease in membrane thickness, as well as an increase in the APL and vice versa. These overall changes during a temperature change can also be employed to determine the main phase transition temperature T_m (14). Most studies report on these and other overall structural changes obtained by averaging over time and space, thereby simplifying the comparison of in silico results to experimental observables. Some earlier Monte Carlo and MD studies focused also on local properties of single-component membranes at varying temperature (28, 29, 30, 98). One main result of these studies was that near T_m, transient local domains of high order and increased thickness (“thick domains”) may form in an otherwise disordered bilayer and vice versa, resulting in a laterally heterogeneous membrane. In turn, a peristaltic undulation in membrane thickness was reported in an atomistic study of a DPPC bilayer with 360 lipids at T_m, possibly reflecting a first step in ripple-phase formation. The undulation was stable on the 100 ns timescale (92). As compared to thick ordered and fluid membrane domains, surprisingly little is known about the formation of thin, interdigitating membrane nanodomains and their dynamics.

Here, we aimed at investigating the local characteristics of bilayers, in particular the dynamic formation of thin and thick domains, at varying temperatures close to and above T_m. For length scales of simulation systems on the order of the membrane thickness, metastable undulatory states may occur. Therefore, we here investigated comparably large lipid bilayers consisting of 1280 DPPC lipids (lateral size of 32 × 12 nm) that were simulated for 500 ns each at T = 322, 326, 330, 335, and 340 K. For completeness, we also calculated the overall thickness and APL and summarized the data in Table 2 (see also Fig. S4). The APL of 60.05 Å² found in our simulation at 322 K is slightly lower than the experimental value of 63.0 Å² at 323 K (99), as also reported from earlier simulations (77). Note, however, that the experimental T_m is 7 K below the computationally determined T_m. The averaged bilayer properties showed the expected behavior, i.e., with an increase in temperature, the APL increased while the thickness decreased.

Table 2.

Mean APL, Thickness, and Diffusion Coefficients for Membranes at Various Temperatures Averaged over 20–500 ns of each Simulation and Experimental Values

T (K)	APL (Å2)		Thickness (nm)		D1 (× 10−8 cm2/s)
	Simulation	Experiment	Simulation	Experiment	Simulation	Experiment
322	60.05 (0.57)	63.0 325 K (99)	4.03 (0.03)	3.9323 K (99)	17.46 (0.92)	14323 K (142)
326	61.11 (0.50)		3.98 (0.02)		20.86 (1.52)	16.5325 K (142)
330	61.78 (0.54)		3.96 (0.03)		23.95 (1.36)	20330 K (142)
335	62.70 (0.52)	65.0333 K (143)	3.93 (0.02)	3.81333 K (143)	28.21 (2.78)	23333 K (142)
340	63.42 (0.57)	69.5338 K (144)	3.90 (0.02)		33.72 (1.63)

Values in parentheses represent the SD. See also Fig. S4.

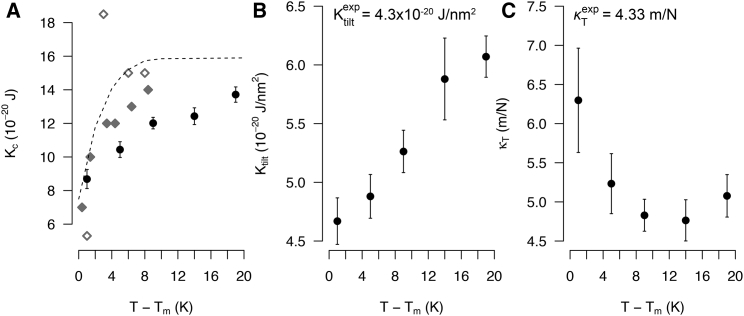
In addition to the structural characteristics of membranes close to T_m, the membrane elastic constants K_c (bending modulus), K_tilt (tilt modulus), and κ_T (isothermal area compressibility) have been described as indicators of membrane phase transition. In detail, K_c and K_tilt of PC bilayers were shown to adopt a minimum (100, 101, 102, 103, 104) and κ_T to display a maximum (33, 102, 105) at T_m. Both the temperature dependency as well as the magnitude of these observables are well described by atomistic simulations (Fig. 3; see Supporting Materials and Methods for further details).

Figure 3.

Temperature dependency of membrane elastic constants determined from simulations of a DPPC lipid bilayer system (320 lipids; see Supporting Materials and Methods for further details on system construction, determination of elastic constants, and errors). The dependency is given as a function of the reduced temperature, i.e., as difference to T_m, for better comparison between simulations and experiments. (A) Bending modulus obtained from simulations (black dots) and from experiments measuring membrane deformation via differential confocal microscopy (gray closed diamonds) (101) and thermal shape fluctuations of DPPC vesicles (gray open diamonds) (100) is shown. The black dashed line presents a theoretical prediction using a kinetic nucleation model (130). (B) Tilt modulus determined from simulations is shown. The experimental value was obtained 9 K above T_m (145). (C) Area compressibility of simulated DPPC membranes is shown. The experimental value was determined at 9 K above T_m (146).

Overall bilayer structure

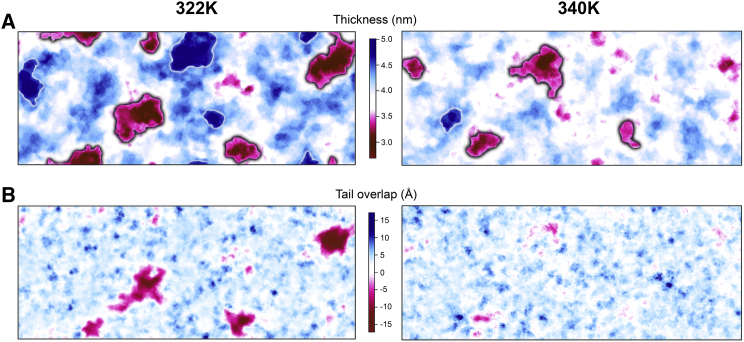
Fig. 4 A shows representative two-dimensional (2D) thickness maps of the bilayers simulated at 322 K (left) and 340 K (right), respectively. Because of the pronounced dynamics of the membrane thickness, all other frames and temperatures are provided as Videos S1, S2, S3, S4, S5, and S6. As can be seen in Fig. 4 A, local nanodomains with an increased thickness are formed (colored blue). These domains are built by lipids that are in a stretched conformation (Fig. 5 A), similar to a previous MD study on transiently ordered domains (30). Different from the lipid tilt angle of ∼30° in the L_β′ phase, the lipids were approximately aligned with the membrane normal.

Figure 4.

Local membrane thickness and lipid tail overlap analyzed for representative snapshots of a DPPC bilayer simulated close to T_m (322 K, left column) and well above T_m (340 K, right column). The properties were averaged over a selected 1 ns interval. (A) Bilayer thickness, calculated as the distance between the phosphate atoms, is shown. Thin and thick domains further analyzed (domain size, lifetime) are surrounded by a black and white line, respectively. The largest thick, ordered domain (top middle in the map) in the 322 K simulation had a size of ∼12 nm². (B) Lipid tail overlap expressed as the difference between the tail end atoms (C16_sn1, C16_sn2) of the upper monolayer and the lipid tail end atoms of the lower monolayer is shown. A negative value corresponds to lipid tail interdigitation. To see this figure in color, go online.

Figure 5.

Snapshots of transient thick and thin nanodomains in a fluid bilayer simulated at a temperature close to T_m. (A) A thick domain is formed by lipids in a stretched conformation. The average thickness, APL, and tail-tail distance are 4.71 nm, 57.4, and 4.01 Å. (B) A thin domain is formed by interdigitating lipids of opposing monolayers. The average thickness, APL, and tail-to-tail distance are 3.23 nm, 56.9, and −3.34 Å, respectively. (C) In a few cases, a strong interdigitation of up to −7 Å was observed, and the bilayer structure was slightly reminiscent of the ripple phase (64, 95). The fatty acid tails are shown as sticks and the phosphorus and nitrogen atoms of the lipid headgroup as spheres. To see this figure in color, go online.

Video S1. DPPC Bilayer Thickness at 322K

(lateral size approx. 31nm x 12nm, window 10ns–500ns)

Video S2. DPPC Bilayer Thickness at 326K

(lateral size approx. 31nm x 12nm, window 10ns–500ns)

Video S3. DPPC Bilayer Thickness at 330K

(lateral size approx. 31nm x 12nm, window 10ns–500ns)

Video S4. DPPC Bilayer Thickness at 335K

(lateral size approx. 31nm x 12nm, window 10ns–500ns)

Video S5. DPPC Bilayer Thickness at 340K

(lateral size approx. 31nm x 12nm, window 10ns–500ns)

Video S6. DPPC Bilayer Thickness at 310K

(lateral size approx. 18.5nm x 18.5nm, window 50ns–300ns) taken from (107).

In addition, we observed nanodomains with a significantly decreased thickness at both temperatures (Fig. 4 A, colored magenta). Two distinctly different types of thin membrane domains emerged: close to T_m, thin domains consisted of strongly interdigitating lipids of the opposing leaflets, resulting in exceptionally thin regions (Fig. 4 B, left; Fig. 5 B). These structures are probably precursors of the ripple P_β′ phase formed below T_m (106), where the minor side is formed by completely interdigitating lipids (64, 95). Interdigitated lipids and surrounding lipids showed a high order in previous studies of the P_β′ phase (64, 95). This was rarely the case in our simulations and indicates that the bilayer is close to but still above T_m. However, in some minor cases, the bilayer structure was slightly reminiscent of the P_β′ phase (Fig. 5 C). Considering interdigitation, the predominant structure of thin domains was similar to the structure of the interfacial lipids in the two-phase system. However, the collective tilt arising because of a gel phase domain was only weakly pronounced, and only a few lipids tilted toward the thin domain (Fig. 5 B). Additionally, thick ordered domains (≥4.3 nm) but also rather fluid-like domains were found in their environment, similar to the two-phase DPPC^gf system, although no well-defined interface developed because of the size and dynamics of the nanodomains. The heterogeneity in membrane thickness and interdigitation affected membrane integrity (Fig. S5). Similar to the kink region of the P_β′ phase (64, 95), lipids partially showed a high disorder that resulted in a reduced membrane density (Fig. S5).

Differently, at 340 K, the thickness reduction of thin membrane domains was coupled to an increase in the lipid area, i.e., lipids increased their area at the cost of their height as a consequence of lipid volume incompressibility. For instance, the largest of these temperature-induced thin membrane domains in the bilayer simulated at 340 K shown in Fig. 4 A had a mean thickness of 3.32 nm. Although the lipids only slightly interdigitated (0.95 Å; Fig. 4 B), the APL was increased to 67.1 Å².

The domain properties are analyzed in more detail in the following sections.

Domain occurrence and domain size

The different membrane domains were defined based on their thickness, ≤3.5 nm for thin and ≥4.5 nm for the thick domains. Additionally, the minimal area of a membrane nanodomain was set to 2 nm², corresponding to ∼3 lipid molecules per monolayer (see also Fig. 4 A for accepted and discarded domains). This approach allowed us to calculate the average domain number and size for each time frame and temperature (Fig. S6). With increasing temperature, the number of thin and thick domains decreased. On average, ∼4.1 thin domains were found at a temperature of 322 and 326 K, decreasing for higher temperatures to 3.6 (330 and 335 K) and 3.3 (340 K) (Fig. S6 A). Additionally, the size distributions narrowed (Fig. S6 C) and shifted to smaller average areas (from 5.4 nm² at 322 K to 4.2 nm² at 340 K). The occurrence of ordered thick domains drastically decreased for increasing temperatures, ranging from 3.4 to 1.4 domains within the 322 K and the 326 K systems to only 0.03 at 340 K (Fig. S6 B). A similar effect of temperature was observed for the average area of ordered domains, which decreased from 5.1 nm² at 322 K to 2.8 nm² at 340 K. To sum up, both thin as well as thick ordered nanodomains preferentially occurred close to the phase transition temperature.

Lipid characteristics within membrane nanodomains

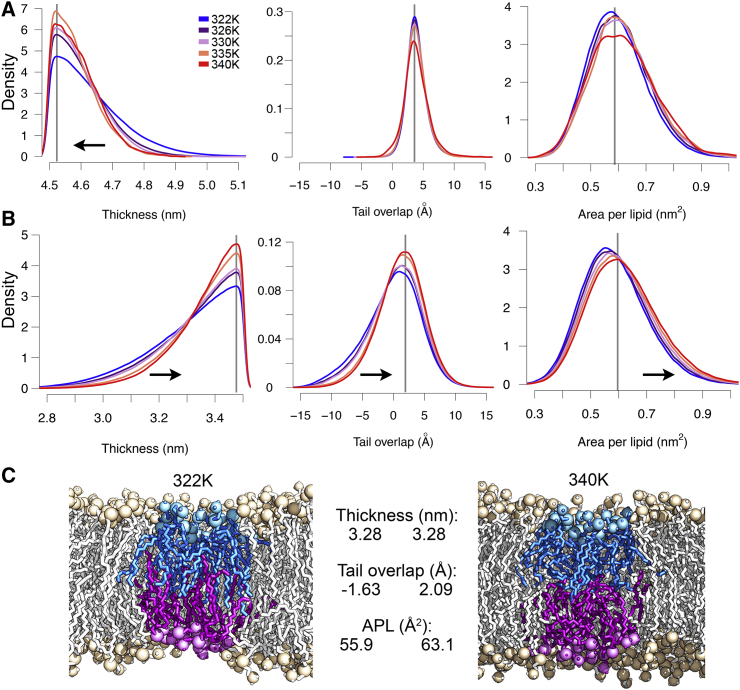
Fig. 6 shows the distributions of the thickness, tail overlap, and APL within the thick ordered (Fig. 6 A) and the thin domains (Fig. 6 B). For the ordered domains, the membrane thickness was shifted to slightly larger values for temperatures closer to phase transition (see also Fig. S7 A), and lipids showed no interdigitation as their tail-to-tail distance was centered around 3.5 Å between 322 and 340 K (Fig. 6 A, middle) with an APL of ∼58 Å². Positive values for the average tail overlap reflect the dip observed in the membrane electron density within the membrane center both in x-ray scattering and MD simulations (76). Overall, ordered domains showed similar structural characteristics over the studied temperature range (322–340 K).

Figure 6.

Structural characteristics of thin and thick membrane nanodomains. The arrows indicate the direction of structural changes if the system is heated up. The gray lines highlight the distribution maxima of the 340 K system. (A) Thickness, tail overlap, and APL of the ordered, thick membrane domains are shown. (B) Thickness, tail overlap, and APL of thin membrane domains are shown. (C) Representative configurations of thin membrane domains close to T_m (322 K, left panel) and at 340 K (right). Both domains are, on average, 3.28 nm thick; however, the average APL and tail overlap was 55.9 and −1.63 Å at 322 K and 63.1 and 2.09 Å at 340 K. To see this figure in color, go online.

On the contrary, for the thin membrane nanodomains, the average thickness was shifted to smaller values close to T_m, and the lipid tail interdigitation was much more pronounced (Fig. 6 B; Fig. S7 B). Additionally, the APL was decreased as compared to higher temperatures (see also Fig. S7). As discussed above, a thin membrane nanodomain may be formed either by an increase in lipid interdigitation or an increase in the APL. Fig. 6 C exemplarily shows two snapshots of thin nanodomains with the same average thickness of 3.28 nm. In one domain (left), lipids remarkably interdigitated (−1.63 Å) but had a small APL (55.9 Å²), whereas lipids in the second domain (right) barely overlapped (2.09 Å) but occupied more space (APL = 63.1 Å²). Interestingly, both thin and thick membrane nanodomains showed similar small APL values at T_m: for thin domains, the small APL is caused by partial interdigitation and related differences in lipid insertion depths (compare Fig. 6 C), whereas the increased lipid tail order has a condensing effect on the thick membrane domains, resulting in an increased packing density within the monolayers.

Domain stability

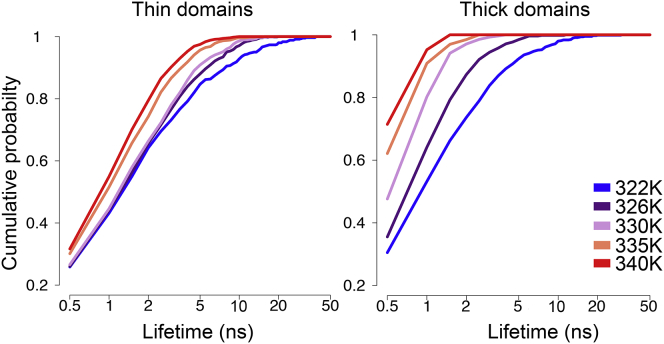
The domain stability was assessed by the domain lifetime assuming a maximal domain center-of-mass displacement of <2 nm within 500 ps. The lifetimes both of the thin and thick membrane nanodomains were significantly larger close to T_m (Fig. 7) and decreased for increasing temperatures: in the 322 K system, thin domains existed for far longer (up to 39 ns) as compared to the 340 K system (<10 ns). The number of thin, short-lived domains increased for increasing temperatures (Fig. 7, left). Also, the lateral lipid diffusion coefficient increases with temperature (Fig. S4 B; Table 2), resulting in a highly dynamic membrane that, together with the decreased interdigitation at higher temperatures, likely contributes to the reduced lifetimes of the thin nanodomains. A slight domain movement within the membrane plane was observed with a center-of-mass displacement of only 0.2–0.3 nm within 500 ps (Fig. S6 D). The displacement was larger at higher temperatures. Similarly, the thick domains were more stable close to T_m, with lifetimes between 31 ns (322 K) and 2 ns (340 K).

Figure 7.

Cumulative probability of lifetimes of thin (left panel) and thick (right) membrane nanodomains at different temperatures. The y axis shows the fraction of domains with a lifetime lower or equal than the given lifetime. To see this figure in color, go online.

The dynamics of membrane nanodomains was visualized in videos displaying the laterally resolved membrane thickness as a function of simulation time (Supporting Material). The highly dynamic formation of thin and thick nanodomains was also observed in a reanalysis of a recent simulation study of a DPPC bilayer close to phase transition by Javanainen et al. (107) with a different force field (Slipids (108, 109)): The simulation trajectory (provided online by the authors) demonstrated similar bilayer characteristics as detailed in Fig. S9 and Video S6, suggesting that the coexistence of the described ordered, thick domains and of the interdigitated thin membrane domains is a force-field-independent effect.

Electropore formation and its dependency on temperature

The experimentally reported enhanced ion permeability of lipid membranes close to T_m was recently ascribed to the reduced thickness between ordered and disordered phases using umbrella sampling free-energy calculations on single permeating ions in a two-phase atomistic (united-atom) system (92). Because an increased ion permeability was experimentally observed for a rather broad temperature range around T_m (22) and because the phase boundary may only contribute a small fraction of the overall membrane area even at phase transition (110), we studied here the spontaneous pore formation in fluid-like lipid bilayers at different temperatures between 322 and 340 K, employing external electric fields (electroporation). Electroporation was used here as a measure for the stability and thus also permeability of membranes. It does not require the a priori localization of the ion permeation sites like in free-energy calculations and thus enables the determination of membrane pore formation rates at a moderate computational effort.

This section follows a twofold aim: first, it addresses the temperature dependency of electropore formation close to T_m, based on atomistic MD simulations of a DPPC bilayer in a fluid-like phase with in total 640 lipids (${\text{DPPC}}_s^f$ system). Second, it takes up the previous MD-based permeability study by Cordeiro (92) and investigates the favorable localization of permeation events in a two-phase setup (DPPC^gf system).

Computational methods for electropore formation rely on two different well-established approaches that basically lead to similar results (40, 111). In the first approach, an external field E_ext is applied by adding an additional force F = E_ext × q on all particles with a nonzero partial charge q (112). The second method mimics the physiological conditions more closely: an ionic charge imbalance is induced between two water compartments that are separated by two bilayers in a single simulation cell (double bilayer setup; see also Fig. S11) (113, 114). The former approach was employed here because the focus of this study was on the onset and localization of pore formation as a stochastic process and less on the development of stable hydrophilic electropores. For comparison, however, the localization of electropores was additionally addressed for a double bilayer system (Fig. S12). Results were comparable to those for external electric fields and are reported in the Supporting Materials and Methods.

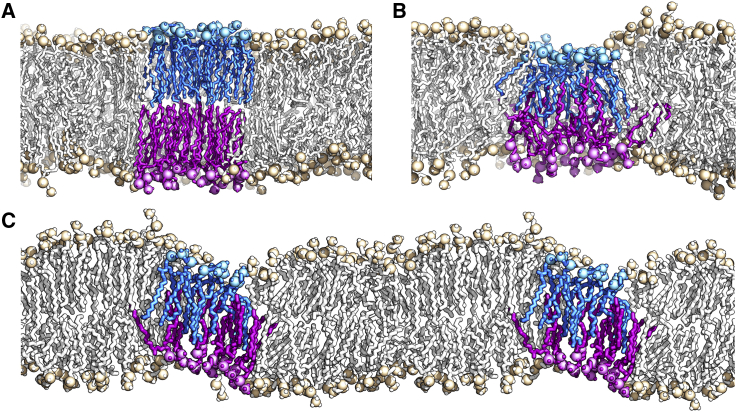
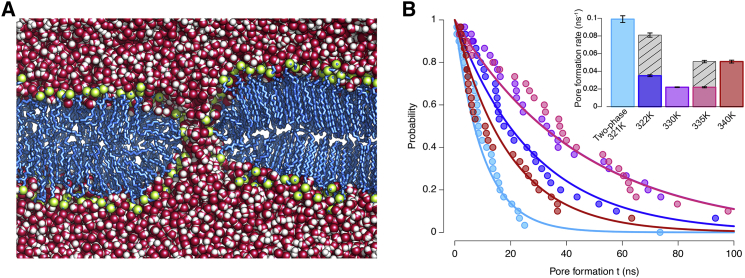
Pore formation rates were systematically determined for the ${\text{DPPC}}_s^f$ system for an external electric field of E_ext = 0.2 V/nm and temperatures of 322, 330, 335, and 340 K, as well as for the equilibrated DPPC^gf two-phase system at 321 K (= T_m). In all simulations, pore formation proceeded as described earlier: application of an electric field results in the reorientation of water and lipid dipole moments at the membrane-water interface, resulting in membrane defects and increased water permeation into the hydrophobic bilayer core. Eventually, a water column is formed across the bilayer, connecting the opposing water reservoirs. The initial hydrophobic pore quickly grows and develops into a hydrophilic pore with lipid headgroups lining the pore wall (Fig. 8 A) (41, 112, 115, 116, 117, 118, 119, 120).

Figure 8.

Electropore formation at an external electric field of 0.2 V/nm. (A) Snapshot of an equilibrated hydrophilic pore, obtained after 100 ns of MD simulation with electric field switched off, is shown. The pore formed at the interface between the fluid (left) and gel (right) lipid phase (DPPC^gf system). The pore diameter decreased from 2 to ∼1 nm (see also (41)). Lipid tails are colored in blue, the phosphate and nitrogen atoms in green, and water is shown as red and white spheres. (B) Probability of pore formation after time t is shown. Solid lines are fits of the exponential (Eq. 1) to the simulation data (dots). The two-phase system is colored in light blue, and the small systems (DPPC^f_s system) simulated at T = 322, 330, 335, and 340 K in dark blue, purple, pink, and red, respectively. Note that the fits for 330 and 335 K are undistinguishable. Inset: Pore formation rates λ for the different temperatures obtained by exponential fit are shown (see main text). The gray bars correspond to the rates obtained for the 1280 lipid systems (DPPC^f system). The error of the fit is given by black bars. To see this figure in color, go online.

The large number of replicas for each system/temperature (30 per system) allowed us to estimate the pore formation rate λ from the pore formation times, which were determined visually as the time at which a closed water wire was formed. The probability P(t) that pore formation is initiated at times larger than t can be described by the exponential function

$$P\left(t\right)\propto e^{-\lambda t}.$$ (1)

Fig. 8 B displays the empirical probability obtained from the simulations (dots) and the corresponding exponential fits (solid lines), together with the deduced pore formation rates (inset) for different temperatures. The two-phase system at 321 K clearly showed the largest pore formation rate: almost all pores were formed within less than 30 ns, and λ was determined to be 0.1 ns⁻¹. Thereby, the pores never formed within the gel phase, i.e., only the membrane domain in fluid phase contributed to pore formation. This observation prompted us to set up the smaller fluid membrane (${\text{DPPC}}_s^f$ system, 640 lipids) with a similar area of fluid lipids as compared to the two-phase system (1280 lipids in total) to allow for a better comparison among the systems. That the pore formation rates are indeed linked to the total area is reflected by the approximately doubled rates computed for two additional DPPC^f systems of twice the size (both in fluid-like phase, studied for 322 and 335 K; gray versus colored bars in Fig. 8 B, inset).

Overall, a strong dependency of the pore formation rate on the system temperature was observed: the DPPC bilayers at 330 and 335 K reflected the largest stability (pore formation rate of 0.022 ns⁻¹). Both, for a decreased temperature (322 K) toward T_m as well as for an increased temperature (340 K), pore formation was significantly enhanced, with a rate of 0.035 ns⁻¹ at 322 K and of 0.051 ns⁻¹ at 340 K (Fig. 8 B). Both trends are in good agreement with experiment: a permeability increase close to the phase transition was reported in different studies (16, 17, 19, 20, 21, 22), and Papahadjopoulos et al. observed increased sodium self-diffusion through vesicles for higher temperatures above T_m already in 1973 (16). Pore closure could not be observed in an additional 100 ns simulation (without external field) of the two-phase system with a pore formed at the gel-fluid interface (Fig. 8 A). Simulations of the two-phase system DPPC^gf with an external electric field covered, in total, 370 ns without pore formation within the gel domain. This allows to estimate that the pore formation rate for gel phase membranes is at least 13 times smaller than for a corresponding fluid-phase system of similar size at 322 K.

The finding that pore formation was significantly enhanced within the two-phase system at T_m as compared to the fluid-like phase system at 322 K—with the pore formation rate for the former system being ∼3 times larger—suggests a pronounced role of the domain interface for pore formation. Fig. 9 A displays the initial thickness pattern of the two-phase system together with positions of the formed electropores (10 replicas from the same initial configuration; see Methods). All pores formed within the thin membrane domains (≤3.5 nm) at the phase interface. A connection between membrane thickness and pore location could also be drawn by analysis of the relative membrane thickness of the pore-forming domains with respect to the average bilayer thickness (shown in Fig. 9 B; 30 replicas for each temperature of the DPPC^f_s system). Overall, the pore-forming nanodomains were ∼10–20% thinner as compared to the surrounding membrane, i.e., pores preferentially formed in the pre-existing thin membrane domains.

Pore formation within these regions is facilitated for three reasons: first, the comparably low membrane thickness facilitates formation of water wires across the membrane. Second, lipids surrounding thin domains partly showed a collective tilt toward the thin domain, thus creating a precursor of a pore (see above), which was more pronounced for the two-phase system. Finally, the constant potential drop across the membrane results in enhanced electric fields (normal to the membrane) across thin membrane domains.

Discussion

In the past, several experiments demonstrated an increased permeability of lipid membranes for ions and small molecules at or close to the gel-fluid phase transition (16, 17, 19, 20, 21, 22). Here, we addressed the characteristics of fluid-phase DPPC membranes close to the melting temperature and their stability with respect to external electric fields by means of atomistic MD simulations. The latter is thereby thought to be related to the permeability of membranes. Structural analysis of a metastable gel-fluid interface revealed a nonmonotonous progression of the membrane thickness between a thick gel (L_β′) and a thin, fluid, liquid-disordered (L_α) domain close to phase transition. The gel and fluid phases were shown to be separated by comparably thin membrane domains, similar to recent findings (92). In addition, transiently ordered (L_o) and fluid domains were also found to be connected in fluid-like bilayers by nanometer-sized, very thin domains that were hallmarked by a pronounced lipid tail interdigitation between the opposing monolayers and an increased lipid density (sketched in Fig. 10). The formation of these nanodomains was shown to result in increased electroporation rates close to phase transition.

Figure 10.

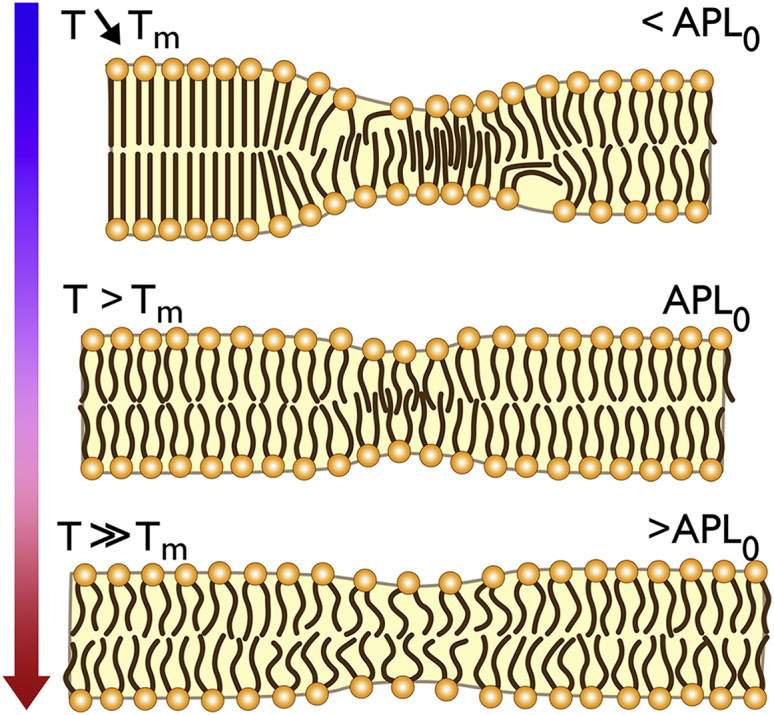
Sketch of temperature-dependent structural features of fluid-like DPPC bilayers observed in atomistic MD simulations. Top: Close to T_m, exceptionally thin nanodomains are formed by interdigitating lipids that are frequently surrounded by thick domains consisting of lipids with high or enhanced order. Both lipid interdigitation as well as stretching results in a dense packing of lipids (small APL). Lipid tilting is observed at the transition from thick ordered to thin nanodomains, which may be accompanied by a disturbance of membrane integrity (Fig. S5B). These membrane structures likely represent precursors of the P_β′ phase. Middle: An increase in temperature suppresses the formation of highly ordered domains and decreases lipid interdigitation within thin domains. Bottom: At temperatures well above T_m, the lipid membrane shows an overall increased APL. The formation of thin nanodomains of decreased stability can be attributed to highly disordered lipids with a large APL. To see this figure in color, go online.

The coupling of membrane regions to different temperatures allowed for the unbiased study of the interface characteristics of a metastable L_β′-L_α two-phase membrane. The thin interfacial region is likely tightly coupled to the DPPC structure; because of the large PC headgroup, gel phase DPPC lipids characteristically tilt their hydrophobic tails along one direction by ≈30° with respect to the membrane normal, thereby allowing for an optimal packing of both headgroup and lipid tails (8, 91, 93, 94). In the two-phase system studied here and different from Cordeiro, who composed a two-phase system from two systems either in gel and in fluid phase (92), the characteristic acyl chain tilting developed spontaneously in an unbiased fashion parallel to the gel-fluid interface. In addition, interfacial gel phase lipids adopted a collective tilt toward the phase interface, resulting in a wedge-like void between the monolayers (Fig. 1 B). Adjacent fluid lipids then splayed to fill the void, which together with lipid interdigitation ultimately resulted in local membrane thinning. Omitting the molecular details, the formation of the constriction region at the L_β′/L_α interface was discussed and attributed previously (92) to the interplay between the phase thickness mismatch and membrane elasticity (121, 122, 123), similar to the characteristics of the hydrophobic mismatch between membrane proteins and the surrounding lipids (124, 125, 126, 127).

The stability as well as the size of coexisting membrane domains in the gel and liquid-crystalline phases is difficult to assess. Also, it is not clear whether L_β′ and L_α do indeed coexist at phase transition or whether, upon melting from the L_β′ or the P_β′ phase, another intermediate state occurs that could not be captured in simulations yet (14). Therefore, we additionally studied fluid-like membranes above but close to the main phase transition in unbiased all-atom simulations on the 500 ns timescale. We report the coupled formation of both ordered thick domains (L_o phase) and thin, interdigitating membrane domains. The appearance and disappearance of these nanodomains is highly dynamic (see Videos S1, S2, S3, S4, S5, and S6). Although the transient formation of ordered domains was reported earlier on a timescale of a few tens of nanoseconds by Murtola et al. (30) for a fluid DPPC bilayer above the melting temperature or by Leekumjorn et al. (31), who reported the formation of a “mixed phase” below T_m with ordered and fluid-like domains, no accompanying thin interdigitating domains were characterized before. These thin domains are suggested to reflect precursors of the ripple phase P_β′ of DPPC (64, 95).

Additionally, we investigated the stability of the nanodomains present at all temperatures and found that their lifetime and size were strongly dependent on the temperature. Close to phase transition, domains existed for several tens of nanoseconds, whereas an increase in temperature resulted in decreased lifetimes. Visual inspection of 2D thickness maps (Supporting Material) indicated that thin interdigitated domains are partly surrounded by clusters of stretched lipids. Interestingly, such peristaltic thickness fluctuations on the order of 100 ns have recently also been observed by neutron spin echo spectroscopy (128) and have already earlier been suggested as a plausible mechanism to explain the increased membrane permeability close to phase transition (35). To what degree domain formation and domain stability depend also on structural lipid properties (e.g., smaller headgroup) remains an important open question to be resolved. Interestingly, in a previous simulation study of a preassembled two-phase system with a smaller lipid headgroup (1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine, DPPE), thin domains hardly developed (92).

Atomistic simulations were shown here to recover not only the well-studied first-order transition with discontinuities in the APL, membrane thickness, or enthalpy (see (14)) but for the first time, to our knowledge, the anomalous behavior for the isothermal compressibility at phase transition previously reported from experiments as well, i.e., the in-plane area fluctuations are significantly increased at phase transition. Note, however, that the limited system size and periodicity likely affect long-range fluctuations, e.g., in the density, line tension, or lipid ordering that were not addressed in this study. The compressibility anomaly at phase transition and related ones such as a decreased bending rigidity and increased undulations (see also Fig. 3) were described within the framework of a kinetic nucleation model by Kharakoz et al. (129, 130), based on earlier work by Frenkel (131). This model suggests the occurrence of small unstable nuclei above phase transition reflecting the solid state, i.e., the gel or the ripple phase of a membrane. This concept is supported by our data: we observe both ordered domains that might be interpreted as nuclei for the gel domain as well as thin interdigitated membrane domains occurring within the ripple phase. Additionally, the size of the described domains (eight lipids), the size distribution (Fig. S6 C) with exponentially decreasing probabilities for larger clusters, and the shift toward larger clusters for the temperature approaching the transition temperature fit excellently to the nuclei sizes predicted by Kharakoz and Shlyapnikova (130).

In a second step, temperature-dependent electropore formation rates and pore localization were analyzed both for fluid-like membranes close to T_m and for a membrane with coexisting gel and fluid DPPC domains at T_m. The electroporation rate was drastically increased in the two-phase system at T_m and preferentially occurred within the thin membrane domain at the interface between the gel and fluid domains. However, fluid-like membranes also exhibited a high poration rate near T_m, which fell off with rising temperature and then increased again. Also, here, pores were mainly formed in pre-existing thin membrane regions, either in interdigitated thin domains close to phase transition or in thin domains well above phase transition (T_m + 19 K). In our simulations, lipid interdigitation was accompanied by a disturbance of membrane integrity in the surroundings. Additionally, the membrane thickness was locally small, and thus, the hydrophobic barrier decreased. Both of these factors most likely contribute to a facilitated water permeation at the constriction regions and allow for the formation of pores. In particular, the drastically enhanced pore formation rate observed for the two-phase system is likely coupled to these factors. To conclude, results of our MD study support the original hypothesis explaining the permeability anomaly with a leaky interface between coexisting gel-fluid phases, extended by an increased permeability in proximity of highly dynamic thin, interdigitated domains close to T_m. Our study cannot, however, resolve the relative importance of both factors as the stability of the gel-fluid-phase separation, and the relative contribution of the interface area to the total membrane area could not be addressed here.

The nonmonotonous pore formation rates for the fluid-like, equilibrated DPPC bilayer close to and above T_m clearly cannot be described by a pure Arrhenius-like behavior, with rates k changing with temperature according to k ∝ exp(−ΔG/k_BT), where ΔG is the activation energy for pore formation (39) and k_B the Boltzmann constant. This was suggested by an earlier MD study that addressed pore opening rates at different temperatures well above T_m (132). ΔG was assumed in this study to be independent of the temperature, which might be a valid assumption well above T_m as well as within the gel phase but does not hold true at temperatures close to T_m, at which the membrane has significantly different structural properties such as, e.g., long-lasting thin domains that may be coupled to disturbed lipids. Also, Majhi et al. did not observe an enhanced electropore formation close to phase transition, possibly related to the enhanced field strengths employed (132).

Instead, the free-energy change associated with pore formation is proportional to the fluctuations in lateral area, i.e., proportional to the thermal compressibility κ_T (33). The latter adopts a maximum at phase transition, as also indicated in our simulations. Furthermore, previous studies demonstrated that the free-energy barrier for pore formation is reduced for lipids with shorter acyl chains, i.e., a thin bilayer is easier to porate than a thick bilayer (92, 133, 134, 135). Accordingly, the minimal electric field required to porate a bilayer as well as the barrier for water permeation was shown to increase with bilayer thickness (117, 136). Our data revealed an increased lifetime of thin nanodomains close to T_m, and pore formation preferentially occurred in these thin areas. In summary, the simulations demonstrate a coupling of temperature with membrane domain thickness and domain lifetime and thereby with the free-energy barrier for pore formation.

To the best of our knowledge, currently only one MD study addressed electropore formation in a laterally heterogeneous membrane (120). The multicomponent membrane (1,2-dioleoyl-sn-glycero-3-phosphocholine, DOPC; 1,2-distearoyl-sn-glycero-3-phosphocholine, DSPC; cholesterol) consisted of a central round patch in either the liquid-ordered (L_o) or disordered (L_d) phase surrounded by the opposite phase. Seemingly contradictory to our results, application of an electric field triggered pore formation exclusively in the L_d phase, and pore formation was never observed at the boundary region. Also, no thickness minimum developed in the transition region. However, the largest simulated system in this study had a lateral size of ∼9 nm, and the transition between the L_o and L_d phase was observed over ∼2 nm. In our simulations using a one-component DPPC membrane with gel-fluid coexistence, the transition region was thrice as large. Possibly the small system size in the latter study prevents formation of a constriction region. The recent work of Cordeira supports this assumption because a thickness minimum (∼5 nm wide) developed in a raft-forming membrane (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine, POPC; DPPC; cholesterol) (92).

Conclusion

In summary, atomistic simulations close to phase transition conclusively revealed for the first time, to our knowledge, the existence of thin, nanometer-sized domains in DPPC bilayers characterized by a high level of interdigitation of the acyl chains of the opposing lipid leaflets. These domains not only appeared at the interface of metastable configurations with coexisting large gel and fluid lipid domains (92) but also in conjunction with nanometer-sized ordered domains in dominantly fluid-like lipid domains close to the main phase transition temperature.

We unambiguously show that the occurrence of these thin membrane domains is at least partly responsible for the increased permeability of membranes close to T_m. One may hypothesize the existence of similar domains in biological membranes that are probably stabilized by transmembrane proteins with specific domain preference.

Author Contributions

R.A.B. designed and directed research. S.A.K. set up the simulations and performed the analysis. Both authors wrote the manuscript.

Editor: Alemayehu Gorfe.

Supporting Citations

References (137, 138, 139, 140, 141) appear in the Supporting Material.