Abstract
The sequence of events leading to an eye movement to a target begins the moment visual information has reached the brain, well in advance of the eye movement itself. The process by which visual information is encoded and used to generate a motor plan has been the focus of substantial interest partly because of the rapid and reproducible nature of saccadic eye movements, and the key role that they play in primate behavior. Signals related to eye movements are present in much of the primate brain, yet most neurophysiological studies of the transition from vision to eye movements have measured the activity of one neuron at a time. Less is known about how the coordinated action of populations of neurons contribute to the initiation of eye movements. One cortical area of particular interest in this process is the frontal eye fields, a region of prefrontal cortex that has descending projections to oculomotor control centers. We recorded from populations of frontal eye field neurons in macaque monkeys engaged in a memory-guided saccade task. We found a variety of neurons with visually evoked responses, saccade-aligned responses, and mixtures of both. We took advantage of the simultaneous nature of the recordings to measure variability in individual neurons and pairs of neurons from trial-to-trial, as well as the moment-to-moment population activity structure. We found that these measures were related to saccadic reaction times, suggesting that the population-level organization of frontal eye field activity is important for the transition from perception to movement.
SIGNIFICANCE STATEMENT The transition from perception to action involves coordination among neurons across the brain. In the case of eye movements, visual and motor signals coexist in individual neurons as well as in neighboring neurons. We used a task designed to compartmentalize the visual and motor aspects of this transition and studied populations of neurons in the frontal eye fields, a key cortical area containing neurons that are implicated in the transition from vision to eye movements. We found that the time required for subjects to produce an eye movement could be predicted from the statistics of the neuronal response of populations of frontal eye field neurons, suggesting that these neurons coordinate their activity to optimize the transition from perception to action.
Keywords: correlation, eye movements, FEF, saccade
Introduction
The process of identifying salient elements in the world and moving the eyes to foveate those elements is central to primate behavior. The coordination of visual input and motor output involves neural circuits that are woven throughout the cerebral cortex and subcortical regions (Wurtz, 2008). One of the key players in this visuomotor transformation is the frontal eye fields (FEFs), located in the anterior bank of the arcuate sulcus. While FEF's role in both visual processing and saccade generation is well studied at the level of neurons recorded one at a time, there has been relatively less attention paid at the population level to how groups of FEF neurons coordinate from moment to moment during vision and eye movements.
For the brain to produce a fast and accurate eye movement, commands from an oculomotor control area, such as FEF, would ideally need to be robust. FEF contains neurons that respond exclusively to visual stimuli or eye movements, but most exhibit some degree of response to both (Bruce and Goldberg, 1985; Lawrence et al., 2005). These responses can take the form of persistent activity after a visual stimulus that remains elevated until an eye movement is made (Bruce and Goldberg, 1985). Behaviorally, single-neuron firing rates to target stimuli (vs distractors) are correlated with reaction time (Thompson et al., 1996), and eye movements are difficult to cancel once firing rate exceeds a certain threshold (Brown et al., 2008). The functional properties of FEF neurons and their relationship to behavior, combined with their anatomical connections to visual cortex (Schall et al., 1995) and the superior colliculus (SC) (Stanton et al., 1988; Sommer and Wurtz, 1998, 2000; Helminski and Segraves, 2003), make FEF neurons ideal candidates to mediate the visual to motor transformation in an eye-centered coordinate frame (Sajad et al., 2015).
To generate consistent, repeatable eye movements, the ideal oculomotor command signal should be reliable. At the single-neuron level, reliability, as measured by Fano factor, decreases after stimulus presentation in a wide variety of visual and motor areas (Churchland et al., 2010), including FEF. Fano factor in FEF neurons is lowest before saccade initiation (Purcell et al., 2012) and reductions in Fano factor are driven by visual stimulation independent of the saccade plan (Chang et al., 2012). Although trial-to-trial correlated variability among pairs of neurons (also known as “spike count correlation,” or rsc) has been widely studied in visual cortex (for review, see Cohen and Kohn, 2011) and linked to shifts in visual attention (Cohen and Maunsell, 2009; Mitchell et al., 2009; Herrero et al., 2013; Snyder et al., 2016), there has been much less investigation of the role of correlated variability in movement planning and initiation.
The neural code by which FEF neurons signal an eye movement was initially described by relating presaccadic activity to saccade reaction time using a fixed rise to threshold model (Hanes and Schall, 1996). What is less clear is whether activity well before the saccade (e.g., early in the delay period of a memory-guided saccade task), particularly at the pairwise and population level, is important for saccade preparation. This question has been recently addressed in the SC, where Jagadisan and Gandhi (2017) proposed that stability in the time-varying responses of individual neurons in SC was a key factor in determining whether SC activity leads to an eye movement. Kaufman et al. (2014) posed a similar question in the skeletomotor system, asking why population average delay activity in motor cortex did not appear to appreciably rise or change to signal the onset of a reach. They proposed a “potent” and “null” space for movement generation signals in the population, through which a linear readout could use specific activity patterns, or mixtures of neural responses, to signal movement. Together, these results suggest that the rapid generation of a motor action is not just about having an elevated firing rate at the single-neuron level but also can be influenced by interactions at the pairwise (or population) level.
To determine the population-level signatures of eye movement preparation, we recorded simultaneously from groups of FEF neurons in three rhesus macaque monkeys using linear microelectrode arrays while the animals performed a memory-guided saccade task. We found that the generation of an eye movement depended on activity changes at the single-neuron, pairwise, and population levels. In particular, the speed at which a saccade was generated depended not only on the overall firing rate of a group of neurons, but also the level of variability across neurons and over time, and the particular pattern of activity observed in the population as a whole. We observed that variability at the single-neuron (Fano factor) and pairwise (trial to trial fluctuations in responsivity, or correlated variability) levels decreased for the FEF neuronal population once the saccade target appeared, and variability was lowest on trials with the fastest reaction time. Furthermore, low-dimensional representations of population activity were also correlated with reaction time, with the relationship often persisting throughout the entire delay epoch. These results suggest that FEF activity and its fluctuations from trial to trial, across numerous levels (single-neuron, pairwise, and population), are coordinated in a way that contributes to an optimal state for the rapid transition from preparation to execution of an eye movement.
Materials and Methods
Neuronal recordings
Surgical preparation.
Three adult male rhesus macaque monkeys (Macaca mulatta; Monkeys B, R, and W) were surgically implanted with titanium headposts and FEF recording chambers (centered at stereotaxic coordinates: 25 anterior, 20 lateral) using sterile surgical techniques under isoflurane anesthesia. All procedures were approved by the Institutional Animal Care and Use Committee of the University of Pittsburgh and complied with guidelines set forth in the National Institute of Health's Guide for the care and use of laboratory animals.
Electrophysiological methods.
Extracellular activity was recorded with a 16-channel linear microelectrode array (U-Probe, Plexon), with contacts spaced 150 μm (Monkeys R and W) or 200 μm (Monkey B), spanning a distance of 2.25 mm or 3.0 mm, respectively. Electrodes were lowered into cortex using a custom-designed mechanical microdrive (Laboratory for Sensorimotor Research, Bethesda, MD), inserted through a plastic grid with 1 mm spacing. The location of FEF within the chamber was identified first by the functional properties of recorded neurons and then confirmed by identifying sites where saccades could reliably (>50%) be evoked using low-amplitude microstimulation (≤50 μA, 0.25 ms pulse duration, 70 ms pulse train duration, 350 Hz stimulation frequency) (Bruce et al., 1985). We mapped out the recording chamber using microstimulation at multiple locations and then considered successful stimulation sites and their immediate neighbors (1 mm away) as FEF.
Data collection.
Stimuli were displayed on a 21 inch cathode ray tube monitor with a resolution of 1024 × 768 pixels and a refresh rate of 100 Hz at a viewing distance of 36 cm. Stimuli were generated with custom software written in MATLAB (The MathWorks) using the Psychophysics Toolbox extensions (Brainard, 1997; Pelli, 1997; Kleiner et al., 2007). Eye position was monitored monocularly via infrared tracking at a 1000 Hz rate (EyeLink 1000, SR Research), and neural and behavioral data were recorded with a Grapevine recording system (Ripple). For each electrode, waveform segments that exceeded a threshold (set as a multiple of the root mean square noise on each channel) were saved and stored for offline analysis and sorting. Waveforms were automatically sorted using a competitive mixture decomposition method (Shoham et al., 2003) and manually refined based on waveform shape and interspike interval using custom time amplitude window discrimination software written in MATLAB (Kelly et al., 2007, available at https://github.com/smithlabvi-sion/spikesort).
Following the offline sorting procedure, the signal-to-noise ratio (SNR) was calculated for each identified unit as the ratio of the average waveform amplitude to the SD of the waveform noise (Kelly et al., 2007). We considered only candidate units with a signal-to-noise ratio of 2.5, and then eliminated 162 units whose delay period response was not >1 sp/s for at least one condition. This resulted in a total of 976 units (230, 232, and 514 units in 14, 25, and 36 sessions from Monkeys W, B, and R, respectively), from which we analyzed 7656 pairs of simultaneously recorded neurons (2038 from Monkey W, 1199 from Monkey B, and 4419 from Monkey R, same-channel pairs were excluded).
Experimental design and statistical analysis
Behavioral task.
Monkeys performed a conventional memory-guided saccade task (see Fig. 1) (Hikosaka and Wurtz, 1983). The trial began when the monkey was required to fixate a small blue circle (0.5° diameter). After maintaining fixation within a 1.8° diameter window for 200 ms, a circular peripheral target (0.8° diameter, 11° eccentric) was briefly flashed (50 ms duration) at 1 of 8 locations (cardinal and oblique directions). The animal was required to maintain fixation for 550 or 600 ms (held constant within a session) until the fixation point was extinguished, which signaled the monkey to make a saccade to the remembered location of the stimulus. The monkey had 500 ms to initiate a saccade, as defined by the eye position leaving a window 1.8° in diameter around the fixation point. Once the saccade had been initiated, the monkey's eye position had to reach the saccade target within 200 ms and maintain gaze within 2.7° of the location for 150 ms to receive a liquid reward. Each block consisted of pseudorandomized presentations of all eight directions, with at least 50 blocks gathered per session (mean = 132 blocks). On a subset of days, after the fixation point was extinguished and the monkey began its saccade, the target was reilluminated to aid in saccade completion. The analysis presented here is not affected by this target because it appeared after the analysis window.
Figure 1.
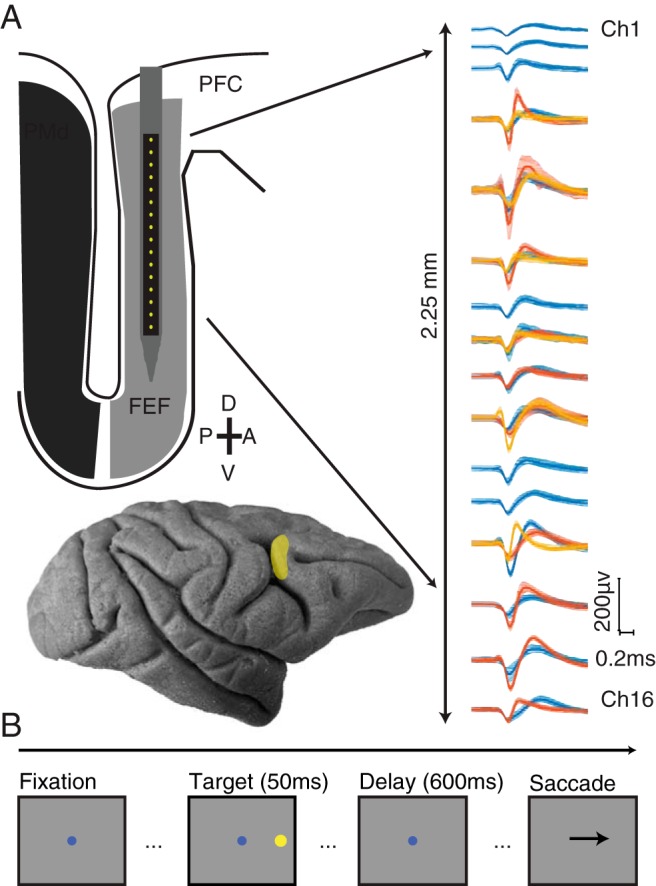
Experimental methods. A, Top, Schematic of 16 channel linear microelectrode array. Contacts were spaced at either 150 or 200 μm (total length of electrode shank 85 mm). Sample waveforms (mean ± SEM) recorded after manual spike sorting. Bottom, Lateral view of the macaque brain. FEF is highlighted and located along the bank of the arcuate sulcus (PMd indicates dorsal premotor cortex, PFC indicates prefrontal cortex). B, Memory-guided saccade task. Each trial began with the subject fixating on a central dot. After the subject fixated the central dot, a peripheral stimulus briefly appeared at 1 of 8 locations equidistant from fixation and 45 degrees in angle apart. The subject was required to maintain fixation on the central dot while remembering the location of the peripheral stimulus. When the central fixation point was extinguished, this signaled the subject to make a saccade to the remembered location of the peripheral stimulus.
General statistical analysis.
For pairwise analyses (correlated variability and covariance), degrees of freedom were across pairs of neurons (n = 7656 pairs unless stated differently in Results). For single-neuron measurements (firing rate, variance, correlation between firing rate, and reaction time), degrees of freedom were across the number of single neurons (n = 976 neurons). Detailed information for the specific statistical tests used for each figure can be found in the results.
For statistically testing the time course of variability (see Fig. 5A–C), a running one-sample t test was computed for each condition after baseline (200 ms before target onset) subtraction. To compare conditions to each other, an independent samples t test was used. Both statistical tests were Bonferroni-corrected. For statistical tests on the Fano factor time course, see the section below.
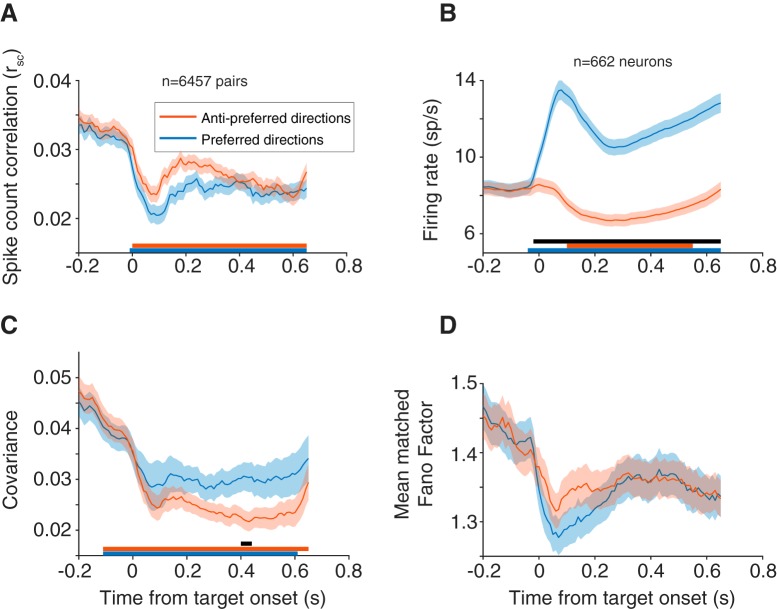
Figure 5.
Time course of rsc starting at fixation (t = −0.2) through stimulus presentation (t = 0.0 to t = 0.05) until fixation offset (t = 0.65). rsc was calculated in overlapping 100 ms bins, with a sliding window of 10 ms. Each time point corresponds to the leftmost point of the bin (t = 0 for example corresponds to rsc in a window from 0 to 100 ms). All panels use this window analysis. A, rsc time course for preferred and antipreferred directions. Both conditions showed a decrease in rsc after stimulus onset, lower for the preferred direction, that was persistent throughout the delay epoch. B, Same time course as in A, but with individual neuron firing rate. C, Covariance across pairs for preferred and antipreferred directions. Covariance decreased after stimulus onset and was higher in preferred compared with antipreferred directions. A–C, Statistical data points for are plotted as lines under each subplot. Lines corresponding to the colors in the plot represent each condition relative to baseline (baseline = average in 200 ms after fixation but before stimulus onset). Black line indicates differences between the two conditions (see Materials and Methods). D, Mean matched Fano factor followed the same time course as rsc: a decrease after stimulus onset (more in the preferred direction) that was persistent throughout the entire period. Pairs from a small number of sessions (n = 1199 pairs, 24 sessions), where the time course varied (delay epoch = 550 ms or stimulus duration = 100 ms) were removed from this analysis.
Calculation of preferred direction and tuning selectivity.
The preferred direction and selectivity of each FEF neuron, calculated during the delay period, were determined by a vector average similar to that used for preferred orientation (Smith et al., 2002). Preferred direction is given by the circular mean angle as follows:
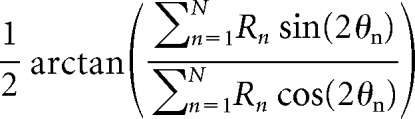 |
Where Rn is the response magnitude during the delay period, θn is the stimulus location, and n is an index from 1 to the number of points, 8, in the tuning curve.
To measure the selectivity of each neuron's tuning curve, we calculated the complex summed response vector (where i = ) as follows:
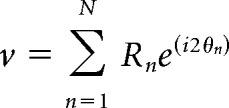 |
And normalized the magnitude by the summed magnitude of all the response vectors:
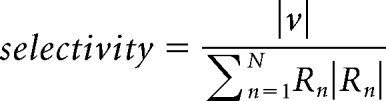 |
A selectivity of 0 corresponds to a neuron that fires equally for all conditions, and a selectivity of 1 would be for a neuron that responds exclusively to one condition. The preferred direction of a pair of neurons was the preferred direction of the neuron with a higher selectivity.
Measurement of correlated variability.
The methods used to compute rsc (also known as “spike count correlation” or “noise correlation”) have been presented in detail in previous publications (Kohn and Smith, 2005; Smith and Kohn, 2008). Briefly, correlated variability was measured by calculating spike count correlation (rsc, also known as noise correlation). The rsc of a given pair of neurons is the Pearson correlation coefficient of the evoked spike responses to a repeated stimulus. For most of the results in this paper, rsc was calculated during the memory epoch (550 or 600 ms in duration), and thus did not include the time period when the stimulus was on. When an rsc value was calculated across multiple directions, we normalized each neuron's response for each direction by z scoring it, and then calculated the rsc by combining responses across directions. For calculating the “preferred” and “antipreferred” direction of the pair of neurons, we first identified the eye movement direction closest to the preferred direction of the most selective neuron in the pair. That direction, along with the two directions flanking it on either side were combined to yield the “preferred” direction. The three directions 180 degrees opposite the directions used for the preferred direction were combined to yield the “antipreferred” direction. We combined conditions in this way to increase our statistical power—results using the preferred and antipreferred directions alone (without the flankers) were qualitatively similar. We also defined the preferred direction of the pair by using the geometric mean of the two neuron's tuning curves instead of the more selective neuron. Instances where these two methods would differ would only result from pairs with disparate tuning; and even for these pairs, results were nearly indistinguishable. We chose to use the method of defining based on the more selective neuron as it guaranteed that the direction chosen was in the preferred direction of at least one neuron in the pair (while centering on the geometric mean of the pair can be more likely to identify compromise directions that are not at the peak response of either neuron).
Visuomotor response properties.
To classify units as visual, motor, or visuomotor, the relative strength of the response to the visual stimulus was compared with that around the time of the eye movement. The visual response was defined as the spike count from 50 to 150 ms after stimulus onset, whereas the motor response was defined as the spike count from 50 ms before to 50 ms after the onset time of the saccade. We computed a standard d′ metric for each neuron comparing the distributions of its responses to the visual and motor epochs (differences in the means of the distributions divided by the square root of the product of their variances). We arbitrarily assigned positive d′ to neurons that responded most in the visual epoch and negative d′ to those that responded most in the motor epoch. d′ values that were close to zero represented neurons that had nearly identical visual and motor responses.
rsc and reaction time analysis.
To relate rsc to reaction time on a trial-by-trial basis, rsc was calculated on subsets of trials sorted by their reaction time. For a given recording session, within each saccade direction, trials were sorted according to reaction time. rsc was calculated in a 40-trial sliding window, such that the first bin would correspond to rsc in the 40 trials with the fastest reaction times and the last bin would correspond to rsc in the 40 trials with the slowest reaction times. For a session with 100 repeats, the number of rsc bins would total 60. Three sessions that did not have sufficient trials for 10 reaction time bins (50 repeats) were omitted. To compare measurements across sessions (as the number of repeats varied day-to-day), the rsc bins, still sorted by reaction time, were then combined into deciles in each session. This ensured that each neuronal pair had 10 rsc measurements across a range of reaction times that could be averaged across sessions. The same process was also used to compare pairwise covariance and single-neuron mean firing rate and variance with reaction time bin. For rsc, statistical testing was done by implementing a linear mixed-effects model (MATLAB function fitlme) with fixed effects for reaction time and summed d′ of a pair (and an interaction term), a random effect term for neuron pair, and a correlated random effect term for pair and reaction time. For other measures (covariance, variance, firing rate), the summed d′ term was excluded. This model was fit separately for preferred and antipreferred conditions.
Mean matching.
To account for any differences in the relationship between d′ and rsc due to firing rate (see Fig. 7A,B), we performed a mean matching procedure as follows. A population mean firing rate was calculated as the average rsc across all d′ values and reaction time deciles. Then, within each d′ group, pairs were removed until the average geometric mean firing across pairs and reaction time deciles was within 5% of the population mean. Upon removing these pairs, all trends in Figure 7A, B were preserved (mean matching procedure was performed separately for preferred and antipreferred directions).
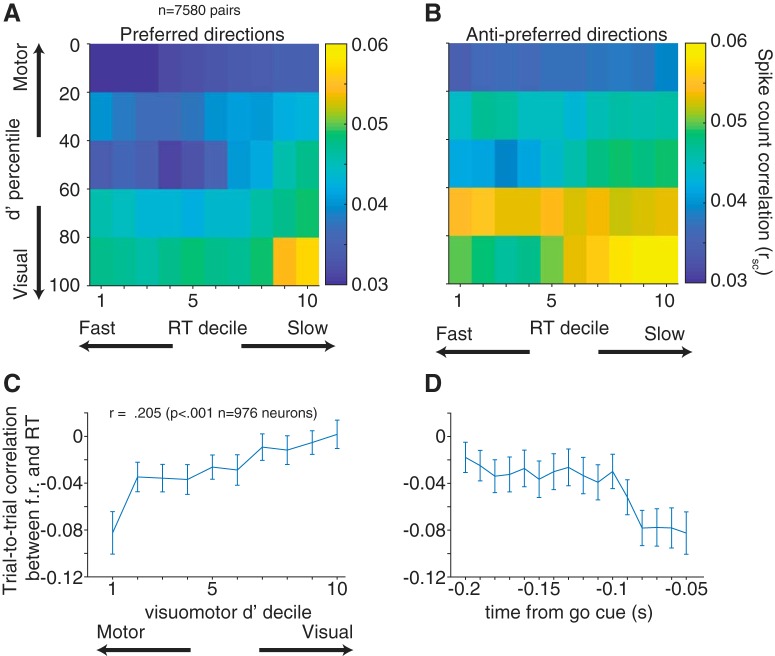
Figure 7.
Variability and reaction time in visual and motor subpopulations. rsc with reaction time, grouped by visuomotor d′ for preferred (A) and antipreferred (B) directions. rsc was lower for motor-motor pairs, and the relationship between rsc and reaction time decile was weaker, however not significant (preferred: p = 0.298; antipreferred: p = 0.254). C, Trial-to-trial correlation between firing rate in the last 50 ms of the delay period and reaction time. Neurons are divided by visuomotor strength (d′ decile). D, Time course of correlation between firing rate and reaction time for neurons with the strongest motor responses (see first decile in C). x axis value marks the beginning of each point's time window (first value is −0.2 s to −0.15 s).
Fano factor.
Fano factor was calculated using methods and code previously published (Churchland et al., 2010). Data were aligned on stimulus onset, and Fano factor and mean rate were computed using a 100 ms sliding window. Analysis included only the preferred and antipreferred directions (flanker directions included for increased statistical power). Fano factor was computed after mean matching the firing rate, to rule out any possibility that changes in Fano factor were trivially due to changes in firing rate. The statistical significance of the Fano factor decrease was assessed by comparing the Fano factor 100 ms before target onset to the Fano factor 200 ms after stimulus onset. Significance was computed based on sampling distributions from the 95% CIs calculated by the least-squares regression used when calculating the Fano factor (Churchland et al., 2010). The decline was significant for both preferred and antipreferred directions (both p < 0.0001).
Microsaccade detection.
Microsaccades were identified using a velocity criterion based on a previously published detection algorithm (Engbert and Kliegl, 2003). The criterion, η, was based on a multiple of the SD of the velocity distribution and calculated separately for the x and y velocity components as follows:
Where λ is a multiplier and σx, y is a median estimator of the velocity time series defined as follows:
Where v represents the velocity and 〈v〉 denotes the median estimator. We used a value of λ = 10, and any potential microsaccades must have had a minimum duration of 6 ms and minimum amplitude of 0.05 degrees. Trials that contained at least one microsaccade were removed from the rsc calculation. To maximize statistical power in calculating rsc after the microsaccade trial removal, we z-scored both the spike counts and the reaction times for the preferred direction and its two flankers and combined them to calculate one rsc value for the preferred direction (and one for the antipreferred). On the full set of trials, using this z-scoring procedure did not appreciably change the results from computing the rsc separately for each condition.
Factor analysis (FA).
FA was used to characterize neural activity at a population level (Santhanam et al., 2009; Churchland et al., 2010; Everett, 2013; Williamson et al., 2016). FA allows for the partitioning of spiking variability into a component shared by the neural population and a component independent across neurons (Churchland et al., 2010). For a given session, condition, and trial repeat, spike counts were binned across the delay period for each simultaneously recorded neuron (as for the spike count correlation analysis, above). The mean spike counts, loading matrix, and independent variances for each neuron were estimated using the expectation-maximization algorithm (Dempster et al., 1977). Only sessions with ≥10 neurons were included (this excluded 30 sessions, leaving 41 that met this criterion). For the analysis of shared variance on fast versus slow trials, an additional criterion of a minimum number of repeats (100 trials) was used to minimize the overlap of trials used to calculate shared variance for fast and slow reaction times (5 additional sessions were removed in addition to neuron criterion, leaving 36 sessions).
We determined the latent dimensionality (which could range from 1 to N − 1, with N being the number of simultaneously recorded neurons) using a two-stage process previously described (for a more detailed explanation, see Williamson et al., 2016). First, we found the dimensionality that maximized the cross-validated data likelihood. Having fit an FA model with this dimensionality, we then defined the optimal dimensionality, dshared, as the number of dimensions needed to explain at least 95% of the shared covariance of the model. The value of dshared is more reliable than the dimensionality that produces the peak data likelihood in situations where some dimensions explain small amounts of covariance. dshared was calculated individually for each condition and session (see Fig. 8A). Because the majority of dshared values were 1 with this procedure, we set the latent dimensionality to 1 for all sessions to simplify the comparison.
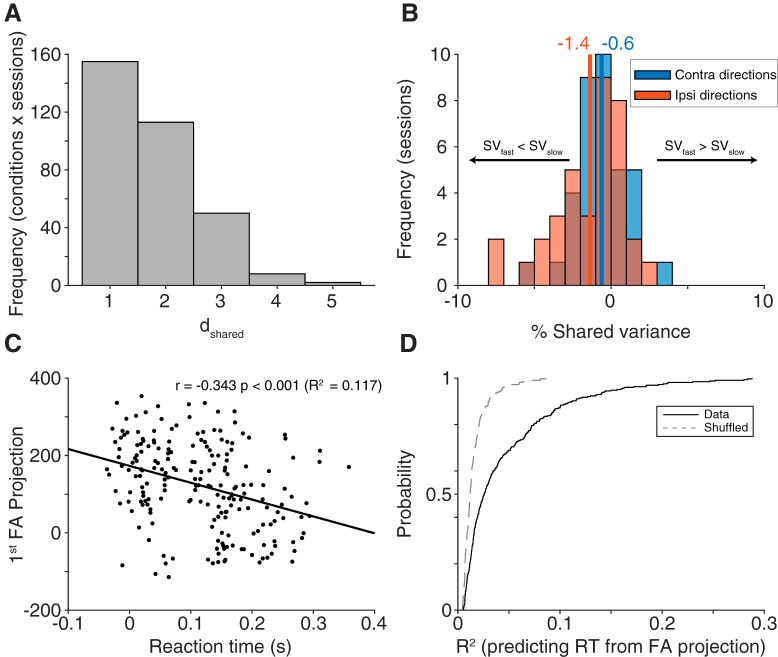
Figure 8.
FA. A, Dimensionality (dshared) calculated for each condition in each session separately (n = 328, 8 conditions each from 41 session). Most conditions had an optimal dimensionality of 1. B, Change in shared variance (SV, fast trials-slow trials) for each session, separated into contralateral and ipsilateral directions (n = 36 for each direction). For both directions, shared variance was lower in fast trials compared slow trials, with a stronger effect in ipsilateral directions, consistent with our correlated variability findings. C, Example condition from one session (n = 205 trials, Monkey Wi, session 109) demonstrating a strong relationship between the first FA dimension's projection value and reaction time. D, Population summary (n = 41 sessions) of R2 values from a linear fit between the first FA dimension's projection value and reaction time (fit to each condition separately, all session and conditions shown with the solid black line). The relationship between projection value and reaction time was significantly stronger compared with a shuffled distribution shown with a gray dashed line (p < 0.001, Wilcoxon sign rank test).
As a complement to our analysis of the time course of correlated variability across the delay period, we also wanted to understand how population activity evolved over the course of the trial. As stated above, with FA we used data binned across the entire delay period, which did not consider spike timing within the delay. Gaussian process factor analysis (GPFA), an extension of FA, leverages spike timing information to produce a low dimensional estimate of activity that can be calculated at different time points (for a more detailed explanation, see Yu et al., 2009). The same neuron criterion used in the FA was applied here for GPFA, with only sessions with ≥10 neurons included (41 sessions). The time series used for GPFA began at fixation and ended 1.5 s after fixation to guarantee the time course included all saccades made on every trial, but further analyses were restricted to data from fixation to saccade onset. For a given neuron and trial, the data structure used by the GPFA model was formed by first binning the neuron's spike counts into 1 ms bins corresponding to the time series chosen (0–1.5 s after fixation), creating a peristimulus time histogram (PSTH) with 1 ms resolution. This was done for all simultaneously recorded neurons in a session. To increase our statistical power, all trials were combined after first subtracting the mean PSTH for a given neuron and condition from each single trial spike count vector. Thus, the final data structure input to GPFA for each neuron was a residual spike count for each trial, with each millisecond bin mean subtracted by the corresponding value from the average PSTH for that condition, concatenated into a matrix containing all simultaneously recorded neurons. This method was then applied to each session separately. Because of the mean subtraction, the data structure could have values <0, which precluded the use of the square root transform in GPFA.
As in FA, a two-stage process was used to calculate the optimal dimensionality of the model, dshared. For each session, the model was fit to the dimensionality that maximized the data likelihood. After the model was fit, dshared was calculated, which determined how many of the latent dimensions were included in the subsequent analysis of reaction time. For example, for a session with 15 simultaneously recorded neurons, the maximum cross-validated likelihood might occur for a 12-dimensional model. The GPFA model would then be fit to 12 dimensions, and the dshared calculated. If the dshared was 8, only the first 8 dimensions would be used for the reaction time analysis for that session. Finally, neural trajectories were orthonormalized to provide a more intuitive specification of the trajectories in low dimensional space (for more detailed explanation, see Yu et al., 2009).
Ordering of latent dimensions with reaction time.
A secondary effect of the orthonormalization process was that dimensions were ordered based on the amount of data covariance explained. When calculating the R2 fit between GPFA dimensions and reaction time, it was not necessarily the case that the dimensions with the highest amount of data covariance explained had the highest R2 (although this was usually the case). To order the dimensions based on R2 for a given session, we first split the data into even and odd trials. Then, for a given dimension and time point during the trial, the R2 value resulting from a linear fit between the dimension's projection value and reaction time was calculated separately for even and odd trials. Using the R2 values obtained from the even trials, the R2 values were averaged across the 7 time points and sorted according to highest average R2. By using the average R2 across time points, we prioritized dimensions which consistently predicted reaction time across the entire trial. We then used this ordering to sort the dimensions and R2 values obtained from the odd trials. Because the datasets were independent, this removed any bias caused by sorting. Ordering the dimensions by data covariance explained (i.e., not performing the R2 sorting procedure) did not qualitatively change any of the results.
To determine whether the R2 values observed were statistically significant, we used a shuffling procedure as follows. In each session, for each dimension and time point, the reaction time values were randomly shuffled relative to the dimension's projection value. This was done for all sessions, with a Wilcoxon rank signed test used to compare the shuffled and real R2 values for each time point and dimension, across all sessions. To account for multiple comparisons, a p value of 0.0003 was used (Bonferroni correction to maintain a p value of 0.05 given a statistical test for 22 dimensions × 7 time points).
Results
We recorded from 976 neurons (see Materials and Methods) in FEF across 75 recording sessions in 3 macaque monkeys. This resulted in 7656 pairs of neurons recorded while the animals performed a memory-guided saccade task (Fig. 1). The focus of our analyses was on how the population activity structure evolved during the delay period before saccade execution.
Trial-to-trial correlated variability
To understand how changes in correlated variability could affect eye movement preparation, we first characterized its overall structure in FEF. Correlated variability (spike count correlation, or rsc), has been extensively studied in visual areas, such as V1(Kohn and Smith, 2005; Smith and Kohn, 2008), V4 (Cohen and Maunsell, 2009; Smith and Sommer, 2013), and MT (Zohary et al., 1994; Ruff and Cohen, 2014a,b), but much less in oculomotor areas, such as FEF (but see Cohen et al., 2010; Zirnsak et al., 2014; Astrand et al., 2016; Dehaqani et al., 2018). We calculated rsc for each saccade direction (and combined across directions in some cases, see Materials and Methods) for each pair of neurons (Fig. 2). To understand the structure of rsc with respect to basic functional properties and how that structure compares with findings in other cortical areas, we examined rsc as a function of physical distance, tuning similarity, and visuomotor preference.
Figure 2.
Correlated variability. A, For a given pair of FEF neurons, firing rates during the delay period (0–600 ms after target offset) to a repeated stimulus were used to calculate the Pearson's correlation, representing the correlated variability (rsc) of the pair. B, rsc was calculated separately for each of the 8 conditions.
We first grouped pairs of neurons by electrode contact distance and calculated rsc during the delay period of the task for all pairs of neurons (Fig. 3A). The magnitude of rsc decreased with increasing electrode separation (Pearson's r = −0.070, p < 0.0001). This finding is consistent with findings of the distance dependence of rsc in numerous previous studies (Smith and Kohn, 2008; Leavitt et al., 2013; Smith and Sommer, 2013; Zirnsak et al., 2014; Snyder et al., 2018).
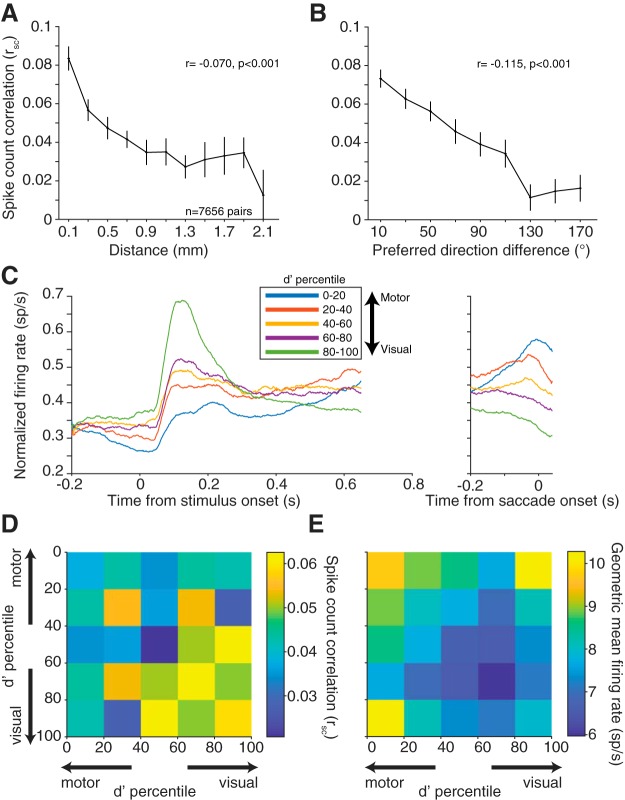
Figure 3.
Correlated variability with basic response properties. A, Mean ± SEM rsc for pairs of neurons as a function of distance. Neuronal pairs were grouped by distance with bin centers starting at 0.100 mm and bin edges spanning ±0.100 mm. Bins with <100 pairs were removed. B, Average rsc for pairs of neurons as a function of preferred direction difference (tuning similarity). Neuronal pairs were grouped in 20° bins starting at 10°. rsc decreased with increasing neuronal distance and tuning dissimilarity. Both panels show binned data, but statistical analyses were performed on 7656 total pairs. C, Average PSTH across neurons for one condition at each d′ quintile. Conditions were chosen separately for each neuron as the condition that elicited the highest firing rate during the delay period. Each neuron's PSTH was normalized to the maximum firing rate in either the visual/delay or saccade window. The d′ prime statistic reliably differentiated visual, motor, and visuomotor subpopulations. D, rsc for pairs based on visuomotor response properties. Each pair was binned based on the visuomotor d′ ranking of each neuron in the pair relative to all neurons recorded. E, Same binning in C but geometric mean firing rate during the delay epoch. Visual-visual pairs had significantly higher rsc compared with motor-motor or visuomotor pairs, despite having lower geometric mean firing rate.
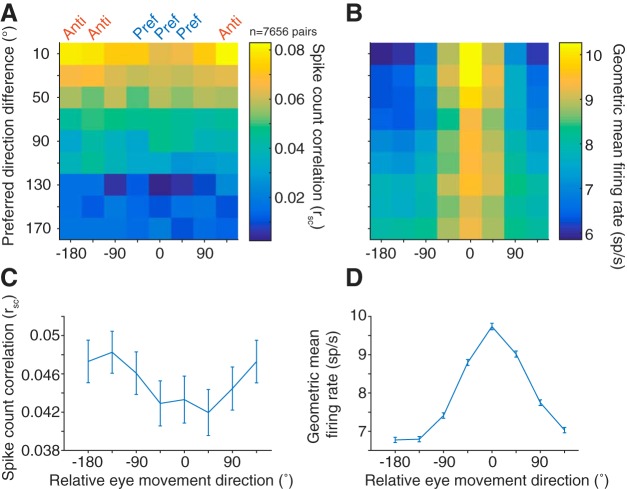
Tuning similarity between pairs of neurons has also been shown to affect correlated spiking (Zohary et al., 1994; Bair et al., 2001; Smith and Kohn, 2008; Cohen and Maunsell, 2009; Cohen et al., 2010; Smith and Sommer, 2013), with the overarching finding being that similarly tuned neurons exhibit larger levels of correlated variability. As a measure of tuning similarity, we calculated the difference in preferred direction for each neuron in a pair (0 degrees for pairs with identical tuning, to 180 degrees for pairs that had opposite tuning). The firing rate window to determine the preferred direction was the entire memory delay period (from stimulus offset to fixation offset) to incorporate all possible tuning information. Thus, the delay period would include visual responses from the stimulus as well as any preparatory motor activity before the “go” cue. For visual neurons, the preferred direction represents the location of a classical RF of the neuron, whereas for motor neurons it is often described as a movement field. For rsc, as the difference in preferred direction between the pair increased, the magnitude decreased (Pearson's r = −0.115, p < 0.0001; n = 7656 pairs).
Finally, given the variety of visuomotor response properties observed in FEF (Bruce and Goldberg, 1985), we wanted to determine whether similarly tuned visual or motor neurons had higher correlated variability. To perform the memory-guided saccade task, a visual stimulus must be processed and transformed into a motor command. The convergence of these response properties in FEF neurons with the demands of the task suggested to us that correlated variability might depend on the role of individual neurons in the visuomotor transformation. To examine this possibility, we calculated a visuomotor d′ for each neuron based on our ability to differentiate between the stimulus-aligned and the saccade-aligned responses in that neuron (see Materials and Methods). Neurons with a negative d′ can be considered motor neurons (fire preferentially for the saccade compared with the visual stimulus), positive d′ visual (fire preferentially for the visual stimulus compared with the saccade), and near zero d′ visuomotor (fire equally for visual stimulus and saccade) (Fig. 3C). We then divided neurons into quintiles based on this d′ measure and focused on interactions between visual-visual (VV), visuomotor (VM), and motor-motor (MM) pairs. The decision to use d′, a continuous measure, was based on our observation that the visuomotor spectrum seemed more of a continuum than 3 distinct groups. If we divided our groupings into smaller bins (deciles, for example), the same trends were observed. The decision to use quintiles was based on having enough bins to visualize the continuum but also maintain a large sample of pairs within each bin. VV were pairs of neurons where both d′ measures were positive, MM were pairs of neurons where both were negative, and VM were pairs that had one of each. Given the results above that pairs that are spatially closer and more similarly tuned have higher rsc, if visual and motor tuning similarity followed the same trend, we would expect VM pairs to have the lowest rsc compared with more similarly “tuned” VV and MM pairs. VM pairs did have significantly lower rsc than VV pairs; however, VM pairs were not significantly different from MM pairs (Fig. 3D; two sample t test, VV to VM, p = 0.0025; VV to MM, p = 0.0002; MM to VM, p = 0.2602). This result suggests that the level of correlated variability that is characteristic of one subpopulation (e.g., VV pairs) may not necessarily be characteristic of another (MM pairs).
It has been previously shown that the level of correlated variability is positively correlated with firing rate (de la Rocha et al., 2007). This effect cannot underlie our findings because we observed the highest firing rates in groups with the lowest rsc (VM, MM) (Fig. 3E). Despite their differences in absolute rsc level, all three groups (VV, VM, MM) had significant trends with respect to electrode distance (Pearson's r = −0.129, p < 0.0001; r = −0.045, p = 0.007; r = −0.063, p = 0.003 for VV, VM, and MM, respectively) and preferred direction (r = −0.119, p < 0.0001; r = −0.106, p < 0.0001; r = −0.123, p < 0.0001 for VV, VM, and MM, respectively). To maximize our statistical power, in later analyses in this paper, all neuronal pairs were pooled unless stated otherwise. To summarize, correlated variability in FEF was higher in visual populations compared with motor or visuomotor, and the patterns we observed in FEF were largely consistent with other brain regions with respect to the basic properties of distance and receptive field location.
Tuning similarity and eye movement direction
In trying to understand how the population of FEF neurons contributed to planning and executing an eye movement, the analyses so far have considered mean rsc across all directions. We were next interested in how rsc changes as animals plan different eye movements. Because the population of FEF neurons contains a range of direction preferences, we aligned the eye movement conditions relative to the preferred direction of each pair of neurons. This allowed us to consider the population variability structure in FEF neurons that were presumably involved in an eye movement (when the stimulus aligned well with their preferences) versus neurons that had less involvement (when the stimulus was not aligned with their preference).
Correlated variability in the spiking activity of pairs of neurons was lowest when saccades were made toward the pair's preferred direction (chosen as the preference of the more selective of the two neurons) and highest in the antipreferred direction, particularly for pairs of neurons with similar tuning (Fig. 4A,C). The decrease in rsc as a function of proximity to preferred direction was also present, albeit weaker, in pairs with dissimilar tuning. The geometric firing rate computed within the same conditions (Fig. 4B,D) demonstrated that the rsc trend was opposite that predicted if the changes in rsc were purely due to an increase in firing rate (de la Rocha et al., 2007).
Figure 4.
Correlated variability and eye movement direction. A, Average rsc in each of the 8 conditions binned by preferred direction difference. B, Same binning as in A, but with geometric mean firing rate. Across all preferred direction differences, though more prominent for pairs with similar tuning, rsc was lower in the preferred directions (Pref) of a pair compared with antipreferred directions (Anti), despite the higher firing rate in the preferred directions. C, Average rsc across all pairs for each of the 8 conditions, relative to the preferred direction of each pair. D, Same as in C, but with geometric mean firing rate.
The time course of correlated variability
Our analyses up to this point have considered the delay epoch (550 or 600 ms in duration) in aggregate. If correlated variability in FEF is an important factor in the sequence of events leading up to a saccade, we would expect changes in correlated variability to manifest some time after the visual target appears. We used a sliding analysis window (100 ms windows sliding in 10 ms increments) to determine the time scale on which the neuronal population structure shifted as a target appeared and an eventual saccade took place. We first considered how rsc and firing rate changed over time for different eye movements by grouping the preferred eye movement direction and its flankers with the 180 degree opposite direction and its flankers. It is possible a decrease in rsc observed in a pair's preferred direction could be driven merely by the recent presence of the visual stimulus in or near the RF as observed in previous studies in visual cortex (Smith and Kohn, 2008; Smith and Sommer, 2013; Snyder et al., 2014), with rsc returning to baseline levels as the delay period continues. If a low correlated variability level contributed to a high-fidelity stimulus encoding and reliable motor preparation, we would predict the low level to be persistent across the entire delay epoch. After stimulus onset (time = 0 s), mean firing rate increased (Fig. 5B), whereas rsc decreased (Fig. 5A) for both preferred and antipreferred directions, with a sharper decrease in preferred directions. This decrease persisted throughout the entire delay period, consistent with our prediction that FEF population variability could be meaningful for both encoding the stimulus and preparing an eye movement. Toward the end of the delay period, rsc in the preferred and antipreferred directions overlapped, meaning that the variability structure while preparing to make an eye movement was broadly tuned, even for directions in the ipsilateral hemifield.
Because of how rsc is measured (from the covariance of a pair of neurons normalized by the product of the individual variances), it is affected by both the both joint and individual neuronal variability, and both components could drive changes in the overall rsc level. Thus, a decrease in rsc could be due to a decrease in covariance, increase in individual variance, or both. We further investigated the time course of individual neuronal variability and correlated variability through the delay period to determine what components drive the changes observed in rsc. The covariance, like rsc, decreased immediately after stimulus presentation and maintained a low level throughout the delay period (Fig. 5C). This decrease in covariance drove rsc downward for both the preferred and antipreferred directions. Contrary to rsc, the covariance was higher in the preferred direction compared with the antipreferred, and the difference appeared later in the memory period. The inversion between rsc and covariance with respect to saccade direction is explained by the difference in variances, an effect driven largely by the substantial differences in firing rate in the two directions. To measure individual neuron variability in a way that was not impacted by the mean firing rate, we calculated Fano factor using a mean matching method (see Materials and Methods). Consistent with previously reported findings (Churchland et al., 2010), Fano factor for both conditions decreased after stimulus onset and remained at a low level (relative to baseline) throughout the memory period (Fig. 5D).
In summary, variability at the single-neuron and pairwise level decreased relative to baseline when preparing to make an eye movement, even in antipreferred directions. This implies that bilateral populations of neurons are involved in eye movement preparation. We next sought to understand how correlated variability, a measure calculated across groups of trials, could vary with behavior on a trial-by-trial basis.
The role of population variability in reaction time
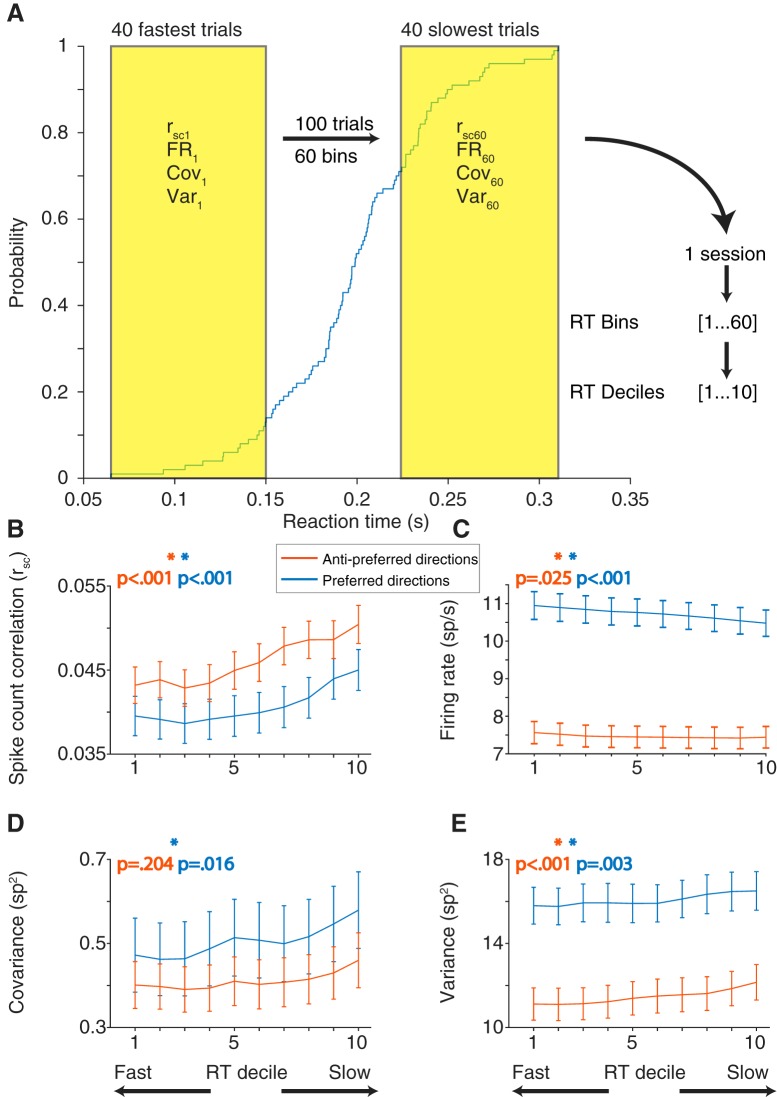
Although the memory-guided saccade task we used was easy for our subjects, they did vary in their behavior from trial to trial. A primary source of that variation was their reaction time: the difference in time between the “go cue” (fixation offset) and the onset of their eye movement toward the remembered target location. Comparing a trial-to-trial measure of variability (rsc) with a single-trial measure of behavior presented a problem. To solve this, we grouped the trials to calculate rsc separately based on reaction time. We used a group of 40 trials because smaller numbers of trials produced less reliable estimates of rsc and larger numbers of trials impaired our ability to measure differences in reaction time. For each condition, rsc was calculated on a sliding group of 40 trials that were ranked based on the reaction time of the subject (Fig. 6A; see Materials and Methods). Our hypothesis was that, if the low correlated variability levels observed provide some benefit to eye movement planning, rsc calculated with fast reaction time trials should be lower than that calculated with slow reaction time trials. We found that this was true for saccades in both the preferred and antipreferred directions (Fig. 6B). To statistically test the relationship between rsc and reaction time, we constructed a linear mixed-effects model. The model was fit to the reaction times and corresponding rsc bins separately for preferred and antipreferred directions. We found a significant trend (linear mixed-effects model, p < 0.001) across the population for both directions, indicating that a low rsc value was associated with fast reaction times.
Figure 6.
rsc calculated in subsets of trials based on saccade reaction time rank, for both preferred and antipreferred directions. A, Blue trace represents the cumulative distribution function of reaction time for a given session and saccade direction. For a given saccade direction, trials were sorted from slowest to fastest reaction time. A sliding window 40 trials long was then used to calculate rsc, firing rate (FR), covariance (Cov), or variance (Var) in subsets of trials. For this example session, the result is 60 measures of rsc calculated across fast, slow, and intermediate reaction times. To average across sessions that may have different numbers of repeats, rsc measures in each session were divided into deciles. The reaction time decile (RT decile) binning applies to all panels. B, rsc plotted against reaction time decile for preferred and antipreferred directions. For both directions, rsc was lowest when calculated for fast reaction time trials, compared with slow reaction time trials. C, Firing rate decreased (preferred) or stayed the same (antipreferred) with reaction time decile. D, Covariance followed the same trends as rsc for both preferred and antipreferred directions (low covariance for fast reaction time bins, high covariance for slow reaction time bins). E, Single-neuron variance followed the same trend with reaction time decile as rsc does, when it would be expected to follow the opposite if the rsc trends were being driven by single-neuron variability.
To ensure that our results were not biased due to fluctuations in behavior during the delay period, we performed two additional control analyses. First, we analyzed the first and last 200 ms of the delay epoch and found in both cases that the results were qualitatively similar to those reported here for the entire epoch. This makes it unlikely that simple firing rate effects due to visual or motor transients could account for our results. Second, to ensure that the changes in correlation with reaction time were not due to the presence of small eye movements during the delay period, we used a microsaccade detection algorithm (see Materials and Methods). After removing trials that contained one or more microsaccades, there was still a significant relationship between rsc and reaction time for both preferred and antipreferred directions (linear mixed-effects model, preferred, p = 0.003; antipreferred, p = 0.001).
In the same manner, we analyzed single-neuron firing rates to determine their association with reaction time (Fig. 6C). We found that, for saccades in the antipreferred direction, firing rate was relatively constant (linear mixed-effects model, p = 0.025). However, for saccades in the preferred direction, a high firing rate was associated with faster reaction times (linear mixed-effects model, p < 0.001), consistent with previous findings in FEF (Everling and Munoz, 2000) and SC (Dorris et al., 1997). In addition to overall rsc, we broke down this measure of correlated trial-to-trial variability into its constituent statistics: covariance and variance. Covariance (Fig. 6D) followed the same trends as rsc in that it was lowest for fast reaction time trials; however, the result was not significant in our model for the antipreferred direction (linear mixed-effects model, preferred: p = 0.016; antipreferred: p = 0.204). Variance (Fig. 6E) was also lowest on fast reaction time trials (Fig. 6E; linear mixed-effects model, preferred: p < 0.001; antipreferred: p = 0.003). Because a lower variance would tend to increase rsc, we conclude that correlated variability (and not single-neuron variability) is the primary change associated with fast reaction times.
Visual and motor subpopulations and reaction time
While the relationship between rsc and saccade reaction time was observed across the entire population, one might suspect differences between visual and motor subgroups. We have already shown that rsc for MM pairs is lower than that of VV pairs, but does this persist for the rsc relationship with reaction time? The linear mixed-effects model previously used was fit with an additional parameter, the sum of the visuomotor d′ of each pair. As expected, based on the previous d′ rsc result, there was a main effect of d′ on rsc for both preferred and antipreferred directions (linear mixed-effects model, preferred: p = 0.011; antipreferred: p = 0.002), meaning that VV pairs had significantly higher rsc compared with MM pairs. It appeared the relationship between rsc and reaction time was also stronger in VV pairs compared with MM pairs (Fig. 7A,B), but the interaction term between reaction time and sum d′ was not statistically significant (linear mixed-effects model, preferred: p = 0.143; antipreferred: p = 0.061). To account for any differences in rsc due to firing rate, we mean matched the geometric firing rate of each d′ group (see Materials and Methods). The mean matching procedure yielded qualitatively similar results (data not shown). It should be noted that the weaker relationship between rsc and reaction time in MM and VM pairs could be due to a floor effect, as these pairs of neurons overall had lower rsc compared with VV pairs. Together, our analyses indicate that substantial shifts in correlated trial-to-trial variability in the delay epoch activity accompany eye movement preparation.
While decreases in rsc across the entire population, particularly among visual neurons, may underlie efficient motor preparation, we also observed that increases in firing rate were associated with fast reaction times (Fig. 6B). Previous studies have related the firing rate of single neurons to saccade initiation in FEF (Hanes and Schall, 1996; Ding and Gold, 2012; Hauser et al., 2018). While we found a relatively weak (albeit highly statistically significant) relationship over the entire delay epoch, the firing rate signals for saccades would be expected to be more tightly coupled with the timing of the saccade itself.
To relate FEF firing rate to saccade reaction time on an individual neuron basis, we correlated on a trial-by-trial basis the firing rate of each neuron in its preferred direction for the last 50 ms before the go cue with the reaction time of the animal for that trial. Previous research on firing rate correlations with reaction time split FEF neurons into motor and visuomotor populations (Ray et al., 2009; Jantz et al., 2013); however, none has divided groups based on the strength of the motor or visuomotor response within these populations. We ranked each neuron based on our visuomotor d′ metric (see Materials and Methods), and then compared the relationship between firing rate and reaction time in each of the deciles transitioning from motor to visuomotor to visual neurons. The 10% of neurons with the relatively strongest motor responses had, on average an ∼−0.08 correlation between their firing rates and the animal's reaction time. That is, higher firing in those neurons led to small (fast) reaction times. As we considered progressively less strong motor neurons, the magnitude of correlation decreased between firing rate and saccade reaction time, such that activity in the strongest visual neurons had nearly zero correlation with reaction time (Fig. 7C; Pearson's r = 0.205, p < 0.001). Not only was this firing rate signal strongest in the motor neurons, but it was strongest close to the “go” cue (Fig. 7D), indicating a tight coupling with the eventual saccade. Together, our results support a role of both single-neuron firing rates and pairwise correlated variability in saccade preparation.
Population-level variability structure
While our analysis of variability at the level of pairs of neurons showed a relationship with reaction time, it is challenging to determine the mechanistic relationship between these quantities. One approach to resolve this is dimensionality reduction, which attempts to distill the key relationships among neurons from the larger set of possible interactions. For this, we used FA, a method that parcels the variability observed in neurons into shared and private components. We fit FA models to binned spike counts during the delay period for each session and condition separately (excluding any sessions with <10 simultaneously recorded neurons, leaving us with 41 viable sessions), with the resulting shared variance matrix being N × D, where N indicates the number of neurons and D indicates the latent dimensionality of the model. To determine the optimal dimensionality, the FA model was first fit to the dimensionality with the highest cross-validated likelihood. Having fit the model with this dimensionality, the optimal dimensionality, dshared, was calculated as the number of dimensions needed to account for 95% of the shared covariance (see Materials and Methods). Many conditions (47%) had a dshared of 1, meaning that most of the shared variance could be attributed to a single dimension in the neural population space (Fig. 8A). We thus used a one-dimensional latent model to keep our methods constant across all sessions and because it provided a good fit to the data. Using this model, we calculated the percent shared variance for each neuron as an indication of how much its activity covaried with the other recorded neurons.
If our pairwise results were an indication of a connection between shared variability and reaction time, then a similar finding would be predicted in the context of the FA model. We first fit the FA model to fast and slow trials, calculating the percent shared variance using the 60 fastest trials and the 60 slowest trials, for each condition. To minimize the number of overlapping trials in the two models, any sessions with <100 repeats per condition were excluded (leaving 36 sessions for this analysis). Percent shared variance was then averaged across neurons in a session, resulting in one value per condition and session. To increase our statistical power, we then averaged the three contralateral directions together (and separately, the three ipsilateral directions), akin to the preferred and antipreferred division in the correlated variability results. Congruent with our results in correlated variability, percent shared variance was lower in fast trials compared with slow trials for both contralateral and ipsilateral directions (one-sample t test, ipsilateral: p = 0.0015; contralateral: p = 0.0302; Fig. 8B).
The second FA comparison we made expanded upon our previous finding that single-neuron activity was correlated with reaction time. We predicted that, if this were true at the single-neuron level, population activity in a low dimensional space should correlate with reaction time as well. To test this, we fit the FA model using one latent dimension (see Materials and Methods) for each condition of each session. An example condition from one session is shown, where the value along the first FA dimension was negatively correlated with reaction time (Fig. 8C; r = −0.343, p < 0.001). Because the FA model was fit separately for each condition and session, the factor space from condition to condition (and session to session) can lie along a different low dimensional axis, leading to sometimes positive and other times negative correlations with reaction time. To compare the FA projection value-reaction time correlation across sessions and conditions, we used a metric agnostic to the direction of the relationship: the R2 of the linear fit between reaction time and FA projection value. To compare these R2 values against what would be expected by chance, for each condition within a session, we randomly shuffled the reaction times with respect to their FA projection values and calculated the R2 from the resulting linear fit. The resulting shuffled distribution was compared with the R2 distribution from the data across conditions and sessions. The relationship between FA projection value and reaction time was significantly stronger for the data compared with the shuffled distribution (Fig. 8D; two-sided Wilcoxon signed rank test, p < 0.001). These analyses demonstrate that both the overall level of shared variability (% shared variance on fast and slow trials) as well as the particular configuration of population activity (the projection along the first FA dimension) were related to the speed at which a saccade is generated.
Temporal evolution of population activity leading up to a saccade
Using FA to reduce the dimensionality of population data provided a snapshot confined to a single moment in time in which the spikes are binned. We report above that correlated variability decreased after stimulus onset and that this decrease persisted throughout the entire delay period. This led us to ask whether the relationship between low dimensional population activity and reaction time was present earlier in the trial, and to ask how this relationship evolved over time within the trial leading up to the eye movement. To achieve this, we used GPFA, an expansion upon FA, which allowed us to examine how low dimensional trajectories evolved across time (Yu et al., 2009).
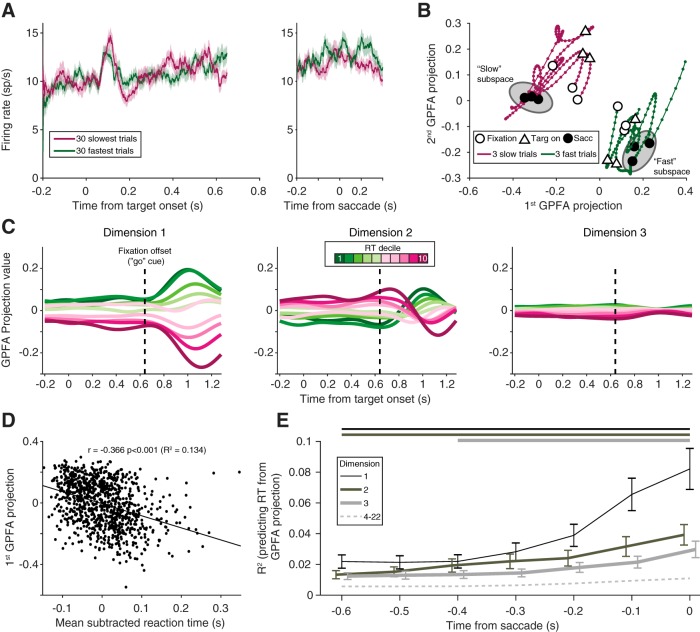
At first glance, a simple population-level analysis to examine the time course of activity across the trial would be to average the responses of all simultaneously recorded neurons. By averaging across neurons, however, subtle differences across the population can be masked. We found that the population PSTHs for fast and slow trials exhibited no salient differences in population activity (one representative session is shown in Fig. 9A). GPFA, like FA, leverages dimensionality-reducing techniques to define low dimensional spaces, which account for shared variability across the population of neurons. Using the same example session, we applied GPFA to the population activity. To increase our statistical power when fitting the GPFA model, we combined all conditions (after subtracting the average PSTH for each condition), and the latent dimensionality, dshared, was chosen using the same two-stage process as in the FA model (see Materials and Methods). We expected, based on our FA results, that GPFA would reveal neural trajectories that were clearly separable for fast and slow reaction time trials (6 example trials shown in Fig. 9B).
Figure 9.
GPFA. A, Population PSTH for an example session (Monkey Ro, session 123) for the 30 fastest (green) and 30 slowest (purple) trials, aligned to the stimulus and the saccade. Shading represents SE across trials. No systematic difference was observed in the average firing rate of the population. B, Example trajectories from the same session as in A, plotted in GPFA space for 3 trials in the first reaction time decile (fast trials, green) and the 10th reaction time decile (slow trials, purple). Throughout the course of the trial, fast and slow trials occupied different neural spaces, despite their average PSTHs overlapping. Gray ellipses represent the concept of an “optimal subspace” for movement generation (Churchland et al., 2006; Afshar et al., 2011). C, Neural trajectories from the first three orthonormalized dimensions for the same session, averaged across subsets of trials based on reaction time. For each dimension, projection values were easily differentiated by reaction time, even during the delay period. Dashed vertical line indicates fixation offset. D, Relationship between the first GPFA dimension's value at the time of the saccade and reaction time for all trials in the same session. This dimension had a strong relationship with reaction time. E, R2 between GPFA dimension projection value and reaction time, averaged across sessions. Dimensions within each session were ordered using a sorting procedure (see Materials and Methods). The first three GPFA dimensions (darker, solid lines) had a significant relationship with reaction time (Wilcoxon signed rank test compared with shuffled data), that persisted throughout the delay period. Horizontal lines above the subplot indicate significant time points. This relationship was weaker for the remaining dimensions (dashed line, average of dimensions 4–22) and only significant for a few of the remaining dimensions around the time of the saccade.
To visualize the resulting trajectories from the GPFA model and how they varied with reaction time, we binned trajectories into deciles based on reaction time. Because the GPFA model was fit with trials combined across conditions, to account for any differences in reaction time between conditions, each trial's reaction time was subtracted by the mean reaction time of that condition. Neural trajectories were clearly differentiated when arranged by reaction time, and this order was frequently preserved throughout the trial's time course, for multiple dimensions (Fig. 9C). To make the comparison between dimensions more intuitive, each dimension was orthonormalized, which also resulted in the dimensions being ordered according to the amount of covariance they explained (see Materials and Methods and Yu et al., 2009). To quantify the relationship between a given GPFA dimension's projection value and reaction time, we calculated the R2 (as in the FA results), using the trajectory's value at the time of the saccade (Fig. 9D). Using GPFA in this way, we demonstrated (as in Fig. 8C using FA) that the population activity structure in a low-dimensional subspace was related to the reaction time of the animal.
Because GPFA leverages the time course of neural activity to calculate trajectories through a low-dimensional subspace, we were able to assess how the population activity was structured leading up to the saccade. Our analysis of a single session (Fig. 9C) indicated that the configuration of population activity very early in the trial could impact the reaction time much later on, and this effect was not confined to a single dimension of the subspace. Our use of GPFA sorted the dimensions by their ability to explain shared variability in the population (from greatest to least). Although in general the dimensions that explained the largest amounts of shared variance were the ones that were able to account for reaction time, this was not strictly true in every session. Therefore, to make comparison across sessions, we sought a method that would sort each session's dimensions by their ability to explain the reaction time of the animal. To do this, we ran GPFA on all of the trials, but then split them in half (even and odd). We used the first half of the trials to measure the relationship (i.e., R2) with reaction time, averaged across the delay period, and resorted the dimensions based on this R2 value. Then, in the other half of the trials, we measured the R2 with reaction time in time windows ending at saccade onset and proceeding back by 100 ms steps. In this way, we guaranteed that our sorting of dimensions based on their ability to explain reaction time would not necessarily lead to an effect if it were driven purely by noise. Whether using this method or leaving the dimensions sorted by shared variance explained, our overall effects were qualitatively similar.
We found that several dimensions had a statistically significant relationship with reaction time, which persisted throughout the delay period (Fig. 9E, solid lines; Wilcoxon Sign Rank test at each time point, corrected for multiple comparisons), consistent with our result in a single session (Fig. 9C). While some additional higher dimensions had a significant relationship with reaction time, it was largely at time points close to the saccade (Fig. 9E, dashed line). In summary, population activity was correlated with reaction time, consistent with our findings for pairwise correlated variability. We conclude that the rapid execution of a saccadic eye movement is enabled by particular configurations of neural activity, revealed in our analysis at both pairwise and population levels.
Discussion
Preparation for a saccade involves signals in a diverse population of FEF neurons. We found that two aspects of FEF activity were associated with efficient oculomotor preparation as measured by a fast saccadic response. The first was that variability among single neurons, pairs of neurons, and in the population decreased during the delay epoch and was related to the generation of fast reaction times (for both preferred and antipreferred saccade directions). The second was that certain patterns of neural activity, identified in a low dimensional space using FA and GPFA, were also related to reaction time. Both of these findings were evident across the entire delay period, and not confined to the immediate presaccadic period. Together, these findings suggest that population-level signatures of FEF activity are important in the generation of eye movements.
Correlated variability in FEF and other visual areas
Despite being documented in many other visual areas (Kohn and Smith, 2005; Smith and Kohn, 2008; Cohen and Maunsell, 2009; Smith and Sommer, 2013; Ruff and Cohen, 2014a), the structure of correlated variability with respect to basic functional properties has been less investigated in movement-related areas, such as FEF and motor cortex (with the exception of Lee et al., 1998; Cohen et al., 2010; Zirnsak et al., 2014; Astrand et al., 2016; Dehaqani et al., 2018). We observed that rsc decreased with interneuronal distance and increased with tuning similarity, traits that match previous findings in other cortical areas (Kohn and Smith, 2005; Smith and Kohn, 2008; Cohen and Maunsell, 2009; Leavitt et al., 2013; Smith and Sommer, 2013; Ruff and Cohen, 2014a; Snyder et al., 2018). This is consistent with a conserved structure of correlated variability across multiple cortical regions in the visual hierarchy. It is possible that this conserved computational feature is driven by similarly conserved anatomical structures across cortex, such as laminar (Barbas and Pandya, 1989; Felleman and Van Essen, 1991; Anderson et al., 2011) and local circuit architecture (Stanton et al., 1989; Kritzer and Goldman-Rakic, 1995).
We further examined rsc as a function of visuomotor response properties. Motor-motor pairs had lower rsc compared with visual-visual pairs, in agreement with some previous results that demonstrated very low rsc values in motor cortex compared with visual areas (for review, see Cohen and Kohn, 2011). In a system in which the initiation of movement was in part driven by the response magnitude in a subset of “motor” neurons, the presence of high correlated variability in the trial-to-trial responses of that population would be particularly influential in driving trial-to-trial behavioral variability. In the extreme, large correlations among such movement-generating neurons could effectively amplify noisy fluctuations in a few neurons, leading to errant movements. Visual populations, on the other hand, may have higher correlated variability due to fluctuations of internal states (e.g., attention and motivation) which affect neuronal responses. This comparison hints at potential fundamental differences in the neural code for sensory signals and motor control; the contrast in correlated variability between visual and motor populations may reflect a sort of insulation of the motor signal against fluctuating cognitive signals. Ultimately, the difference in correlated variability between pairs of neurons based on visuomotor response properties adds to the evidence that these subpopulations are separate and play distinct roles in eye movement generation (Sato and Schall, 2003; Thompson et al., 2005; Gregoriou et al., 2012).
Role of variability in planning eye movements across space
FEF neurons encode both visual stimuli and eye movements across the entire visual field. In FEF, the synergistic activity of ensembles of neurons can represent regions of visual space that are poorly encoded by single neurons (Dehaqani et al., 2018). Compared with baseline measures, we found that a decrease in both correlated variability of pairs of neurons and in the variability of individual neurons was associated with movement preparation. It occurred rapidly after target onset and was maintained throughout the delay period. This is reminiscent of the decrease in correlated variability in visual neurons that occurs after visual stimulus onset (Smith and Kohn, 2008; Smith and Sommer, 2013; Snyder et al., 2014), as well as the broad finding across cortex of a reduction in variability after stimulus onset (Churchland et al., 2010). In FEF, the Fano factor decrease after visual stimulation has been shown to be broadly tuned, occurring for targets inside and outside the response field (Chang et al., 2012). In agreement with our time course findings, rsc in FEF drops and remains low after a cue during an attention task (Astrand et al., 2016). Similarly, in an attention task in V4, shifts in correlated variability coincide with the time of likely target presentations (Snyder et al., 2016). Comparing correlated variability across saccade directions, our result that correlated variability was lowest in the preferred direction differed somewhat from a previous study (Cohen et al., 2010). This may be due to their focus on faster time scale interactions using a different (but related) statistical approach, as well as a different experimental paradigm (visual search in their study). Overall, our observation of a link between rsc and the reaction time reinforces the importance of this pairwise variability structure in the control of eye movements.
In oculomotor areas, such as FEF, saccade initiation has often been linked to increases in activity of oculomotor neurons whose movement fields correspond to the saccade direction. Linear accumulator models have been used to describe how neuronal activity in FEF relates to movement preparation and execution, with movement initiation governed by the time at which a threshold is reached (Hanes and Schall, 1996; Heitz and Schall, 2012, 2013; Jantz et al., 2013). Additionally, baseline firing rates have been related to movement initiation (Hauser et al., 2018). Downstream from FEF, the role of SC in movement generation incorporates both a preparatory buildup to movement and a release from fixation (Dorris et al., 1997), whereas low-frequency SC preparatory activity can trigger a movement if inhibitory networks downstream are removed (Jagadisan and Gandhi, 2017). Together, these studies point to an important role in the overall firing rate of individual neurons and selected populations in initiating eye movements. However, it has remained unclear whether a full accounting of eye movement generation can rely on intuition and models built from single-neuron or even paired recordings.
Movement preparation in neuronal populations
With the increasing availability of technologies that allow simultaneous recordings of multiple neurons, it has become possible to consider how populations of neurons act in concert to plan and initiate movements. In prefrontal cortex, for example, population activity remains in a stable low dimensional subspace during the memory period of a working memory task ending in an eye movement, despite the responses of single neurons varying in both tuning and latency (Murray et al., 2017). In primary motor cortex (M1), even when neural responses are complex and difficult to relate to specific movement parameters, low dimensional representations of population activity during the movement epoch have predictable trajectories when indexed by activity during the preparatory epoch (Churchland et al., 2012). Additionally, the relative contributions of neurons to the population signal can index task epoch (preparation vs execution) (Kaufman et al., 2014; Elsayed et al., 2016), preparatory state to one of two targets (Ames et al., 2014), and the decision making process between two reaches (Kaufman et al., 2015). The power of these studies, considered together, has been their collective demonstration that population-level coordination of neural activity, combined with simple linear readout mechanisms, can explain the transition from planning to execution of a motor act.
Our results extend the existing literature in two key ways. First, we found that variability, across single neurons, pairs of neurons, and at the population level, was a key signature in the sequence leading up to a movement. That is, to prepare a short-latency rightward eye movement, it is important (1) rightward-preferring FEF neurons have a low correlated variability; (2) rightward-preferring FEF motor neurons fire vigorously before saccade execution; (3) leftward-preferring FEF motor have low correlated variability; and (4) shared variance across the population of FEF neurons decreases. One way to think about this is that, while a group of neurons plans the eye movement, all the others must also be sure to avoid contaminating the planning signal (but for caution in interpreting the role of correlated variability, see Moreno-Bote et al., 2014; Arandia-Romero et al., 2016; Kohn et al., 2016). Another interpretation comes from the skeletomotor system, where mixtures of population activity can be categorized as either “potent” or “null” with respect to the generation of a motor output (Kaufman et al., 2014; Elsayed et al., 2016). Instead of constraining the decodability of the neuronal population, the shifts in pairwise variability and shared variance exhibited across the population may instead point to the importance of particular configurations of population activity (in the “potent” space) in triggering movement initiation.
Our second main finding was that, at the population level, different mixtures of neural activity can result in shorter or longer-latency eye movements. In motor cortex (Afshar et al., 2011) and parietal cortex (Michaels et al., 2015), the moment-by-moment firing rate of the neuronal population has been shown to predict reaction time in reaching and grasping tasks, respectively. This has been interpreted as evidence for a theoretical framework in which there is an “optimal subspace” for movement generation, and that the initial conditions within that subspace affect the eventual movement. Our prediction of reaction time (a peak R2 of ∼8% in the best GPFA dimension averaged across sessions) is comparable with (but slightly smaller than) the values reported in those studies, although our neuronal population sizes were also smaller. Our findings extend the potential applicability of these subspace theories to the oculomotor domain, pointing to potentially common mechanisms across distinct modes of movement generation. The separation of neural trajectories did not occur only around the time of the eye movement, but often began early in the trial and persisted across the entire delay period. This further emphasizes that the mixture of activity is not just related to executing the eye movement but also to prior processes, such as encoding the stimulus, holding it in memory, and preparing to generate the eye movement, all of which could impact the eventual reaction time. Considering our results together, it could be the case that high variability from trial to trial “pushes” the mixture of neural activity from populations of neurons away from the optimal configuration for saccade preparation, and thus results in a longer reaction time.
An important future direction will be to better link changes in the activity of FEF populations to the signals in their downstream targets in the SC and, in turn, to eye movement initiation. While the firing rates of individually recorded neurons clearly can explain some of the variance in behavior given the correlations with reaction time, our study points to the importance of population-level activity structure in generating eye movements. To further test the importance of variability at the population level, one future direction would be to disrupt this structure causally, by using microstimulation, and observing the effects on behavior. One such study in the skeletomotor system demonstrated that microstimulation during the preparatory period of a movement influences reaction time, dependent on the cortical area that was stimulated (Churchland and Shenoy, 2007). Further extensions of this work could help answer whether similar approaches are used by the oculomotor and skeletomotor systems to separate movement preparation from execution. While simultaneous population recordings have been relatively less common in eye movement-related structures because of their relative inaccessibility, new recording approaches can reveal the way populations of neurons give rise to fast and accurate eye movements.
Footnotes
M.A.S. was supported by National Institutes of Health Grants R00EY018894, R01EY022928, R01EB026953, R01MH118929, and P30EY008098, National Science Foundation Grant NCS 1734901, a career development grant and an unrestricted award from Research to Prevent Blindness, and the Eye and Ear Foundation of Pittsburgh. S.B.K. was supported by National Institutes of Health Grant T32 EY07271 to the University of Pittsburgh. A.C.S. was supported by National Institutes of Health Grant K99025768. We thank Neeraj Gandhi, Udaya Jagadisan, Ryan Williamson, and Akash Umakantha for helpful advice and discussion; Amie DiTomasso and Christina Mangiaracina for technical assistance; Natalie Klein for help with statistics; and Patrick Mayo for comments on earlier drafts of this manuscript.
The authors declare no competing financial interests.
References
- Afshar A, Santhanam G, Yu BM, Ryu SI, Sahani M, Shenoy KV (2011) Single-trial neural correlates of arm movement preparation. Neuron 71:555–564. 10.1016/j.neuron.2011.05.047 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ames KC, Ryu SI, Shenoy KV (2014) Neural dynamics of reaching following incorrect or absent motor preparation. Neuron 81:438–451. 10.1016/j.neuron.2013.11.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson JC, Kennedy H, Martin KA (2011) Pathways of attention: synaptic relationships of frontal eye field to V4, lateral intraparietal cortex, and area 46 in macaque monkey. J Neurosci 31:10872–10881. 10.1523/JNEUROSCI.0622-11.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arandia-Romero I, Tanabe S, Drugowitsch J, Kohn A, Moreno-Bote R (2016) Multiplicative and additive modulation of neuronal tuning with population activity affects encoded information. Neuron 89:1305–1316. 10.1016/j.neuron.2016.01.044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Astrand E, Wardak C, Baraduc P, Ben Hamed S (2016) Direct two-dimensional access to the spatial location of covert attention in macaque prefrontal cortex. Curr Biol 26:1699–1704. 10.1016/j.cub.2016.04.054 [DOI] [PubMed] [Google Scholar]
- Bair W, Zohary E, Newsome WT (2001) Correlated firing in macaque visual area MT: time scales and relationship to behavior. J Neurosci 21:1676–1697. 10.1523/JNEUROSCI.21-05-01676.2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbas H, Pandya DN (1989) Architecture and intrinsic connections of the prefrontal cortex in the rhesus monkey. J Comp Neurol 286:353–375. 10.1002/cne.902860306 [DOI] [PubMed] [Google Scholar]
- Brainard DH. (1997) The psychophysics toolbox. Spat Vis 10:433–436. 10.1163/156856897X00357 [DOI] [PubMed] [Google Scholar]
- Brown JW, Hanes DP, Schall JD, Stuphorn V (2008) Relation of frontal eye field activity to saccade initiation during a countermanding task. Exp Brain Res 190:135–151. 10.1007/s00221-008-1455-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruce CJ, Goldberg ME (1985) Primate frontal eye fields: I. Single neurons discharging before saccades. J Neurophysiol 53:603–635. 10.1152/jn.1985.53.3.603 [DOI] [PubMed] [Google Scholar]
- Bruce CJ, Goldberg ME, Bushnell MC, Stanton GB (1985) Primate frontal eye fields: II. Physiological and anatomical correlates of electrically evoked eye movements. J Neurophysiol 54:714–734. 10.1152/jn.1985.54.3.714 [DOI] [PubMed] [Google Scholar]
- Chang MH, Armstrong KM, Moore T (2012) Dissociation of response variability from firing rate effects in frontal eye field neurons during visual stimulation, working memory, and attention. J Neurosci 32:2204–2216. 10.1523/JNEUROSCI.2967-11.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchland MM, Shenoy KV (2007) Delay of movement caused by disruption of cortical preparatory activity. J Neurophysiol 97:348–359. 10.1152/jn.00808.2006 [DOI] [PubMed] [Google Scholar]
- Churchland MM, Yu BM, Ryu SI, Santhanam G, Shenoy KV (2006) Neural variability in premotor cortex provides a signature of motor preparation. J Neurosci 26:3697–3712. 10.1523/JNEUROSCI.3762-05.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchland MM, Yu BM, Cunningham JP, Sugrue LP, Cohen MR, Corrado GS, Newsome WT, Clark AM, Hosseini P, Scott BB, Bradley DC, Smith MA, Kohn A, Movshon JA, Armstrong KM, Moore T, Chang SW, Snyder LH, Lisberger SG, Priebe NJ, et al. (2010) Stimulus onset quenches neural variability: a widespread cortical phenomenon. Nat Neurosci 13:369–378. 10.1038/nn.2501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchland MM, Cunningham JP, Kaufman MT, Foster JD, Nuyujukian P, Ryu SI, Shenoy KV (2012) Neural population dynamics during reaching. Nature 487:51–56. 10.1038/nature11129 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen JY, Crowder EA, Heitz RP, Subraveti CR, Thompson KG, Woodman GF, Schall JD (2010) Cooperation and competition among frontal eye field neurons during visual target selection. J Neurosci 30:3227–3238. 10.1523/JNEUROSCI.4600-09.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MR, Kohn A (2011) Measuring and interpreting neuronal correlations. Nat Neurosci 14:811–819. 10.1038/nn.2842 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MR, Maunsell JH (2009) Attention improves performance primarily by reducing interneuronal correlations. Nat Neurosci 12:1594–1600. 10.1038/nn.2439 [DOI] [PMC free article] [PubMed] [Google Scholar]
- de la Rocha J, Doiron B, Shea-Brown E, Josić K, Reyes A (2007) Correlation between neural spike trains increases with firing rate. Nature 448:802–806. 10.1038/nature06028 [DOI] [PubMed] [Google Scholar]
- Dehaqani MA, Vahabie AH, Parsa M, Noudoost B, Soltani A (2018) Selective changes in noise correlations contribute to an enhanced representation of saccadic targets in prefrontal neuronal ensembles. Cereb Cortex 28:3046–3063. 10.1093/cercor/bhy141 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dempster AP, Laird NM, Rubin DB (1977) Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc B 39:1–38. [Google Scholar]
- Ding L, Gold JI (2012) Neural correlates of perceptual decision making before, during, and after decision commitment in monkey frontal eye field. Cereb Cortex 22:1052–1067. 10.1093/cercor/bhr178 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dorris MC, Paré M, Munoz DP (1997) Neuronal activity in monkey superior colliculus related to the initiation of saccadic eye movements. J Neurosci 17:8566–8579. 10.1523/JNEUROSCI.17-21-08566.1997 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elsayed GF, Lara AH, Kaufman MT, Churchland MM, Cunningham JP (2016) Reorganization between preparatory and movement population responses in motor cortex. Nat Commun 7:13239. 10.1038/ncomms13239 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engbert R, Kliegl R (2003) Microsaccades uncover the orientation of covert attention. Vision Res 43:1035–1045. 10.1016/S0042-6989(03)00084-1 [DOI] [PubMed] [Google Scholar]
- Everett B. (2013) An introduction to latent variable models. New York: Springer. [Google Scholar]
- Everling S, Munoz DP (2000) Neuronal correlates for preparatory set associated with pro-saccades and anti-saccades in the primate frontal eye field. J Neurosci 20:387–400. 10.1523/JNEUROSCI.20-01-00387.2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felleman DJ, Van Essen DC (1991) Distributed hierarchical processing in the primate cerebral cortex. Cereb Cortex 1:1–47. 10.1093/cercor/1.1.1 [DOI] [PubMed] [Google Scholar]
- Gregoriou GG, Gotts SJ, Desimone R (2012) Cell-type-specific synchronization of neural activity in FEF with V4 during attention. Neuron 73:581–594. 10.1016/j.neuron.2011.12.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanes DP, Schall JD (1996) Neural control of voluntary movement initiation. Science 274:427–430. 10.1126/science.274.5286.427 [DOI] [PubMed] [Google Scholar]
- Hauser CK, Zhu D, Stanford TR, Salinas E (2018) Motor selection dynamics in FEF explain the reaction time variance of saccades to single targets. Elife 7:33456. 10.7554/eLife.33456 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heitz RP, Schall JD (2012) Neural mechanisms of speed-accuracy tradeoff. Neuron 76:616–628. 10.1016/j.neuron.2012.08.030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heitz RP, Schall JD (2013) Neural chronometry and coherency across speed-accuracy demands reveal lack of homomorphism between computational and neural mechanisms of evidence accumulation. Philos Trans R Soc Lond B Biol Sci 368:20130071. 10.1098/rstb.2013.0071 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Helminski JO, Segraves MA (2003) Macaque frontal eye field input to saccade-related neurons in the superior colliculus. J Neurophysiol 90:1046–1062. 10.1152/jn.00072.2003 [DOI] [PubMed] [Google Scholar]
- Herrero JL, Gieselmann MA, Sanayei M, Thiele A (2013) Attention-induced variance and noise correlation reduction in macaque V1 is mediated by NMDA receptors. Neuron 78:729–739. 10.1016/j.neuron.2013.03.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hikosaka O, Wurtz RH (1983) Visual and oculomotor functions of monkey substantia nigra pars reticulata: III. Memory-contingent visual and saccade responses. J Neurophysiol 49:1268–1284. 10.1152/jn.1983.49.5.1268 [DOI] [PubMed] [Google Scholar]
- Jagadisan UK, Gandhi NJ (2017) Removal of inhibition uncovers latent movement potential during preparation. Elife 6:e29648. 10.7554/eLife.29648 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jantz JJ, Watanabe M, Everling S, Munoz DP (2013) Threshold mechanism for saccade initiation in frontal eye field and superior colliculus. J Neurophysiol 109:2767–2780. 10.1152/jn.00611.2012 [DOI] [PubMed] [Google Scholar]
- Kaufman MT, Churchland MM, Ryu SI, Shenoy KV (2014) Cortical activity in the null space: permitting preparation without movement. Nat Neurosci 17:440–448. 10.1038/nn.3643 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufman MT, Churchland MM, Ryu SI, Shenoy KV (2015) Vacillation, indecision and hesitation in moment-by-moment decoding of monkey motor cortex. Elife 4:e04677. 10.7554/eLife.04677 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly RC, Smith MA, Samonds JM, Kohn A, Bonds AB, Movshon JA, Lee TS (2007) Comparison of recordings from microelectrode arrays and single electrodes in the visual cortex. J Neurosci 27:261–264. 10.1523/JNEUROSCI.4906-06.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kleiner M, Brainard D, Pelli D, Ingling A, Murray R, Broussard C (2007) What's new in psychtoolbox-3. Perception 36:1. 10.1068/p3601ed [DOI] [Google Scholar]
- Kohn A, Smith MA (2005) Stimulus dependence of neuronal correlation in primary visual cortex of the macaque. J Neurosci 25:3661–3673. 10.1523/JNEUROSCI.5106-04.2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohn A, Coen-Cagli R, Kanitscheider I, Pouget A (2016) Correlations and neuronal population information. Annu Rev Neurosci 39:237–256. 10.1146/annurev-neuro-070815-013851 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kritzer MF, Goldman-Rakic PS (1995) Intrinsic circuit organization of the major layers and sublayers of the dorsolateral prefrontal cortex in the rhesus monkey. J Comp Neurol 359:131–143. 10.1002/cne.903590109 [DOI] [PubMed] [Google Scholar]
- Lawrence BM, White RL 3rd, Snyder LH (2005) Delay-period activity in visual, visuomovement, and movement neurons in the frontal eye field. J Neurophysiol 94:1498–1508. 10.1152/jn.00214.2005 [DOI] [PubMed] [Google Scholar]
- Leavitt ML, Pieper F, Sachs A, Joober R, Martinez-Trujillo JC (2013) Structure of spike count correlations reveals functional interactions between neurons in dorsolateral prefrontal cortex area 8a of behaving primates. PLoS One 8:e61503. 10.1371/journal.pone.0061503 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee D, Port NL, Kruse W, Georgopoulos AP (1998) Variability and correlated noise in the discharge of neurons in motor and parietal areas of the primate cortex. J Neurosci 18:1161–1170. 10.1523/JNEUROSCI.18-03-01161.1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michaels JA, Dann B, Intveld RW, Scherberger H (2015) Predicting reaction time from the neural state space of the premotor and parietal grasping network. J Neurosci 35:11415–11432. 10.1523/JNEUROSCI.1714-15.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell JF, Sundberg KA, Reynolds JH (2009) Spatial attention decorrelates intrinsic activity fluctuations in macaque area V4. Neuron 63:879–888. 10.1016/j.neuron.2009.09.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moreno-Bote R, Beck J, Kanitscheider I, Pitkow X, Latham P, Pouget A (2014) Information-limiting correlations. Nat Neurosci 17:1410–1417. 10.1038/nn.3807 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray JD, Bernacchia A, Roy NA, Constantinidis C, Romo R, Wang XJ (2017) Stable population coding for working memory coexists with heterogeneous neural dynamics in prefrontal cortex. Proc Natl Acad Sci U S A 114:394–399. 10.1073/pnas.1619449114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pelli DG. (1997) The VideoToolbox software for visual psychophysics: transforming numbers into movies. Spat Vis 10:437–442. 10.1163/156856897X00366 [DOI] [PubMed] [Google Scholar]
- Purcell BA, Heitz RP, Cohen JY, Schall JD (2012) Response variability of frontal eye field neurons modulates with sensory input and saccade preparation but not visual search salience. J Neurophysiol 108:2737–2750. 10.1152/jn.00613.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ray S, Pouget P, Schall JD (2009) Functional distinction between visuomovement and movement neurons in macaque frontal eye field during saccade countermanding. J Neurophysiol 102:3091–3100. 10.1152/jn.00270.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruff DA, Cohen MR (2014a) Attention can either increase or decrease spike count correlations in visual cortex. Nat Neurosci 17:1591–1597. 10.1038/nn.3835 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruff DA, Cohen MR (2014b) Global cognitive factors modulate correlated response variability between V4 neurons. J Neurosci 34:16408–16416. 10.1523/JNEUROSCI.2750-14.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sajad A, Sadeh M, Keith GP, Yan X, Wang H, Crawford JD (2015) Visuomotor transformations within frontal eye fields during head-unrestrained gaze shifts in the monkey. Cereb Cortex 25:3932–3952. 10.1093/cercor/bhu279 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santhanam G, Yu BM, Gilja V, Ryu SI, Afshar A, Sahani M, Shenoy KV (2009) Factor-analysis methods for higher-performance neural prostheses. J Neurophysiol 102:1315–1330. 10.1152/jn.00097.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato TR, Schall JD (2003) Effects of stimulus-response compatibility on neural selection in frontal eye field. Neuron 38:637–648. 10.1016/S0896-6273(03)00237-X [DOI] [PubMed] [Google Scholar]
- Schall JD, Morel A, King DJ, Bullier J (1995) Topography of visual cortex connections with frontal eye field in macaque: convergence and segregation of processing streams. J Neurosci 15:4464–4487. 10.1523/JNEUROSCI.15-06-04464.1995 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shoham S, Fellows MR, Normann RA (2003) Robust, automatic spike sorting using mixtures of multivariate t-distributions. J Neurosci Methods 127:111–122. 10.1016/S0165-0270(03)00120-1 [DOI] [PubMed] [Google Scholar]
- Smith MA, Kohn A (2008) Spatial and temporal scales of neuronal correlation in primary visual cortex. J Neurosci 28:12591–12603. 10.1523/JNEUROSCI.2929-08.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith MA, Sommer MA (2013) Spatial and temporal scales of neuronal correlation in visual area V4. J Neurosci 33:5422–5432. 10.1523/JNEUROSCI.4782-12.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith MA, Bair W, Movshon JA (2002) Signals in macaque striate cortical neurons that support the perception of glass patterns. J Neurosci 22:8334–8345. 10.1523/JNEUROSCI.22-18-08334.2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snyder AC, Morais MJ, Kohn A, Smith MA (2014) Correlations in V1 are reduced by stimulation outside the receptive field. J Neurosci 34:11222–11227. 10.1523/JNEUROSCI.0762-14.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snyder AC, Morais MJ, Smith MA (2016) Dynamics of excitatory and inhibitory networks are differentially altered by selective attention. J Neurophysiol 116:1807–1820. 10.1152/jn.00343.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snyder AC, Issar D, Smith MA (2018) What does scalp electroencephalogram coherence tell us about long-range cortical networks? Eur J Neurosci 48:2466–2481. 10.1111/ejn.13840 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sommer MA, Wurtz RH (1998) Frontal eye field neurons orthodromically activated from the superior colliculus. J Neurophysiol 80:3331–3335. 10.1152/jn.1998.80.6.3331 [DOI] [PubMed] [Google Scholar]
- Sommer MA, Wurtz RH (2000) Composition and topographic organization of signals sent from the frontal eye field to the superior colliculus. J Neurophysiol 83:1979–2001. 10.1152/jn.2000.83.4.1979 [DOI] [PubMed] [Google Scholar]
- Stanton GB, Goldberg ME, Bruce CJ (1988) Frontal eye field efferents in the macaque monkey: II. Topography of terminal fields in midbrain and pons. J Comp Neurol 271:493–506. 10.1002/cne.902710403 [DOI] [PubMed] [Google Scholar]
- Stanton GB, Deng SY, Goldberg ME, McMullen NT (1989) Cytoarchitectural characteristic of the frontal eye fields in macaque monkeys. J Comp Neurol 282:415–427. 10.1002/cne.902820308 [DOI] [PubMed] [Google Scholar]
- Thompson KG, Hanes DP, Bichot NP, Schall JD (1996) Perceptual and motor processing stages identified in the activity of macaque frontal eye field neurons during visual search. J Neurophysiol 76:4040–4055. 10.1152/jn.1996.76.6.4040 [DOI] [PubMed] [Google Scholar]
- Thompson KG, Biscoe KL, Sato TR (2005) Neuronal basis of covert spatial attention in the frontal eye field. J Neurosci 25:9479–9487. 10.1523/JNEUROSCI.0741-05.2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williamson RC, Cowley BR, Litwin-Kumar A, Doiron B, Kohn A, Smith MA, Yu BM (2016) Scaling properties of dimensionality reduction for neural populations and network models. PLoS Comput Biol 12:e1005141. 10.1371/journal.pcbi.1005141 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wurtz RH. (2008) Neuronal mechanisms of visual stability. Vision Res 48:2070–2089. 10.1016/j.visres.2008.03.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu BM, Cunningham JP, Santhanam G, Ryu SI, Shenoy KV, Sahani M (2009) Gaussian-process factor analysis for low-dimensional single-trial analysis of neural population activity. J Neurophysiol 102:614–635. 10.1152/jn.90941.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zirnsak M, Steinmetz NA, Noudoost B, Xu KZ, Moore T (2014) Visual space is compressed in prefrontal cortex before eye movements. Nature 507:504–507. 10.1038/nature13149 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zohary E, Shadlen MN, Newsome WT (1994) Correlated neuronal discharge rate and its implications for psychophysical performance. Nature 370:140–143. 10.1038/370140a0 [DOI] [PubMed] [Google Scholar]