Predicting catalytic proton donors and nucleophiles in enzymes: how adding dynamics helps elucidate the structure-function relationships

Abstract

Despite the relevance for understanding structure-function relationships, robust prediction of proton donors and nucleophiles in enzyme active sites remains challenging. Here we tested three types of state-of-the-art computational methods to calculate the pK_a’s of the buried and hydrogen bonded catalytic dyads in five enzymes. We asked the question what determines the pK_a order, i.e., what makes a residue proton donor vs. nucleophile. The continuous constant pH molecular dynamics simulations captured the experimental pK_a orders and revealed that the negative nucleophile is stabilized by increased hydrogen bonding and solvent exposure as compared to the proton donor. Surprisingly, this simple trend is not apparent from crystal structures and the static structure-based calculations. While the generality of the findings awaits further testing via a larger set of data, they underscores the role of dynamics in bridging enzyme structures and functions.

Catalytic functions of enzymes are often carried out by titratable groups that can act as proton donors (acids) and nucleophiles (bases).¹ Thus, accurate prediction of the relative order of active-site pK_a’s helps establish the structure-function relationships.^1–3 Over the past two decades, tremendous progress has been made in the development of computational methods for pK_a calculations;^4–7 however, reliable identification of proton donor and nucleophile remains challenging. This is because most enzyme active sites are deeply buried, giving rise to large pK_a shifts relative to the solution (or model) pK_a’s, and site-specific protonation/deprotonation can be highly coupled to each other due to hydrogen bonding and electrostatics. Accurate calculation of these balancing forces is non-trivial.^6,8,9 Structure-based calculations are further complicated by the ionization induced conformational reorganization and water penetration which are not readily accounted for.¹⁰ Current empirical methods lack of rules for establishing the pK_a order for coupled sites.

Commonly used computational approaches for pK_a predictions can be grouped into three classes:⁶ methods based on empirical functions, macroscopic methods based on solving the Poisson-Boltzmann (PB) equation, and microscopic methods based on constant pH molecular dynamics (MD). A popular empirical method PropKa estimates the contributions to pK_a shifts using structure-based energy calculations for desolvation, hydrogen bonding and Coulomb interactions.^11,12 In the PB-based methods, electrostatic potential is computed using the continuum model, in which the protein is considered as a low dielectric cavity embedded in a high dielectric medium. Popular tools include the MCCE program¹³ and DelPhiPKa which employs a smooth Gaussian dielectric function.¹⁴ Several web servers are also available, for example, APBS-PDB2PQR,^15,16 H++,¹⁷ and DelPhiPKa.¹⁸ Unlike the empirical and PB-based macroscopic methods, constant pH MD determines pK_a’s using the Henderson-Hasselbalch equation, where the ratio of the protonated and deprotonated states is estimated by simulations at different pH.^19–25 Thus, in addition to pK_a values, constant pH MD also reports on the details of pH-dependent conformational dynamics.

Recently, we became interested in the pH-dependent catalysis and inhibition of the aspartic protease BACE1 β-secretase 1 (BACE1), which is a major drug target for Alzheimer’s disease.²⁶ Correct assignment of the proton donor (higher pK_a) and nucleophile (lower pK_a) is a pre-requisite for studying pH-dependent enzyme dynamics and its relationship to substrate and inhibitor binding.^26,27 In this work, we asked the question, what is the molecular determinant of the microscopic pK_a order of the aspartyl dyad in BACE1 and two close homologs, β-secretase 2 (BACE2) and cathepsin D (CatD)? In all three structures, the catalytic dyad is completely buried and hydrogen bonded to each other. As comparison and control, we also examined two classic enzymes with abundant experimental data, hen egg white lysozyme (HEWL) and staphylococcal nuclease (SNase). In these enzymes the catalytic residues are partially buried, and in one of them (HEWL), the dyad carboxylates are spatially separated (titration is not coupled). We tested the empirical PropKa,^11,12 the PB solver APBS,^15,16 and the hybrid-solvent²² as well as the all-atom²³ continuous constant pH MD (CpHMD) methods. CpHMD simulations reproduced the experimental pK_a orders, and revealed that the negative nucleophile is more stabilized by hydrogen bonding and solvent exposure as compared to the proton donor. Surprisingly, this simple trend is not apparent from the crystal structures (and therefore the static structure-based calculations).

Five enzymes are considered here (Fig. 1), BACE1, BACE2, CatD, HEWL and SNase. BACE1 is an aspartyl protease which catalyzes the β-site cleavage of the amyloid precursor protein.²⁸ Kinetic experiments gave the pK_a’s of 5.2 and 3.5 for Asp32 and Asp228, which act as the general acid and base, respectively.²⁹ BACE2 and CatD are two close homologs of BACE1 with the respective catalytic dyads Asp48/Asp241 and Asp33/Asp231. HEWL is a glycoside hydrolase that catalyzes the hydrolysis of the glycosidic bond in polysaccharides comprising the cell wall.³⁰ The catalytic dyad is comprised of Glu35 (proton donor) and Asp52 (nucleophile), which have NMR-derived pK_a of 6.1 and 3.6, respectively.³¹ SNase is a phosphodiesterase which catalyzes the cleavage of the phosphodiester bond in DNA and RNA hydrolysis.³² The active site of SNase involves Asp19, Asp21, Asp40 and Glu43.³² Here we focus on the hydrogen bonded residues Asp19 and Asp21, with the respective NMR-derived pK_a’s of 2.2 and 6.5.³³ For simplicity in discussion, we will refer to Asp19 with the lower pK_a as the nucleophile component of the “dyad”.

Figure 1.

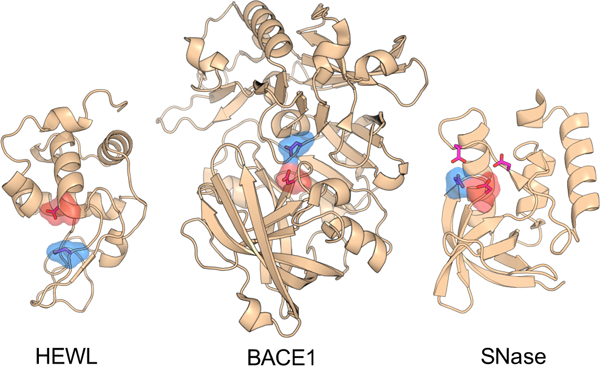
Crystal structures of HEWL (PDB ID 2LZT), BACE1 (PDB ID 1SGZ) and SNase (PDB ID 3BDC). The structures of BACE2 and CatD are very similar to BACE1 and not shown here. The active-site residues are represented by the stick model. The catalytic dyads in HEWL and BACE1 as well as the two hydrogen bonded catalytic residues in SNase are highlighted by surface rendering. The proton donor and nucleophile are colored blue and red, respectively.

To calculate the catalytic pK_a’s, we employed the empirical method PropKa,^11,12 the PB solver APBS,^15,16 and the hybrid-solvent²² as well as all-atom CpHMD.²³ The hybrid-solvent CpHMD is the most validated CpHMD method,⁷ and makes use of explicit solvent for accurate conformational sampling and generalized Born (GB) model for rapid calculation of solvation forces affecting protonation states. The recently developed all-atom CpHMD with particle mesh Ewald (PME) for long-range electrostatics²³ and titratable water for charge neutrality^36,37 is most rigorous but requires much longer simulation time²³ (see later discussion). Thus, it was not applied to BACE2 and CatD.

Table 1 lists the calculated pK_a’s of the five enzymes using the empirical, PB and CpHMD methods in comparison to experimental data. The catalytic pK_a’s of BACE1/BACE2/CatD are most challenging to predict, as the dyads are completely buried and hydrogen bonded to each other (i.e. coupled). Since PropKa cannot determine the order of coupled residues, it offers two alternative sets of pK_a’s. As to the PB results, the two pK_a’s are too similar to be assigned to the proton donor and nucleophile. In contrast, both CpHMD methods reproduce the experimental pK_a orders. Note, in the absence of experimental data for BACE2, the pK_a order is expected to be the same as the homologous BACE1. We also note that, the CpHMD titration data was fit to the Hill equation (Eq. 1) and the two-proton model (Eq. 2). The former yields the microscopic site-specific pK_a’s, while the latter yields the macroscopic stepwise pK_a’s, which can be directly compared to experiment. If the titration of two residues is highly coupled, i.e., involving shared protons, the two site-specific pK_a’s are similar, while the stepwise pK_a’s are split (see an example in our recent study of a salt-bridge triad³⁸). This is however not the case for the enzymes studied here. The site-specific and stepwise pK_a’s are nearly identical for HEWL and SNase, and are only slightly different for BACE1/BACE2/CatD (up to 0.3 pH units). This suggests that, despite hydrogen bonding between the dyad, titration can be assigned to a specific residue, consistent with the NMR experiments.^31,33

Table 1.

Experimental and calculated pKa’s of the catalytic residues in BACE1/BACE2/CatD, HEWL and SNase^a

	Expt	PropKa	APBS	Hybr	All-atom
BACE1
Asp32	5.2	8.0/4.4	5.5/5.4	4.1/4.2	3.7/4.1
Asp228	3.5	4.3/7.9	5.2/5.1	1.9/1.8	−0.4/−0.6
BACE2
Asp48	n/d	6.9/5.2	6.3/5.6	3.5/3.7	n/d
Asp241	n/d	5.2/6.9	6.2/5.7	2.2/1.9	n/d
CatD
Asp33	>5	8.4/4.6	10.5/6.2	4.4/4.7	n/d
Asp231	4.1	3.1/8.3	11.9/6.6	3.2/2.9	n/d
HEWL
Glu35	6.1	6.5	4.9/3.5	5.9/5.9	7.7/7.8
Asp52	3.6	3.9	−0.3/2.3	3.7/3.7	5.7/5.6
SNase
Asp19	2.2	4.2/2.9	7.5/5.0	1.6/1.5	3.5/3.3
Asp21	6.5	2.3/3.7	7.1/4.7	4.3/4.4	5.8/6.0

^aThe nucleophile (lower experimental pK_a or by homology to BACE1) is highlighted in italics. The experimental pK_a’s of HEWL and SNase are taken from NMR data,^31,33 while those of BACE1 and CatD are inferred from kinetic experiments.^29,34 The same structures with missing residues added were used in all calculations. The empirical calculations (PropKa 3.1^11,12 ) returned two sets of pK_a’s for the coupled dyads in BACE1/BACE2/CatD and SNase. For the APBS calculations (version 1.4.1^15,16), two pK_a’s are listed corresponding to the use of an effective protein dielectric constant of 4 or 20. The van der Waals surface based on the CHARMM radii was used. For the CpHMD simulations, the first pK_a corresponds to the microscopic residue-specific pK_a, while the second one corresponds to the macroscopic stepwise pK_a. The hybrid-solvent CpHMD data for BACE1 and CatD were taken from our previous work.^26,35

Although the correct pK_a orders are predicted by the CpHMD methods, there are deviations between the calculated and experimental pK_a’s. For the hybrid-solvent method, both dyad pK_a’s in BACE1 series and SNase are too low by up to 1.5 pH units, as the major source of error is the underestimation of desolvation penalty ^22,26 by the GBSW implicit-solvent model.³⁹ For the PME-based allatom CpHMD, however, the pK_a error can be either positive or negative due to the balance of two opposing factors. The desolvation penalty is too high, which overly upshifts the pK_a’s of buried carboxylic groups, while the attractive electrostatics (e.g., hydrogen bonding) in the interior is too strong, which overly downshifts the pK_a’s of these groups. Both factors are related to the lack of polarizability in the protein interior represented by the additive force field (dielectric constant is too low⁴⁰). These errors are also exacerbated by limited sampling; estimation of free energies in explicit solvent converges much slower than in the GB solvent. Asp228 of BACE1 shows the largest pK_a error, as it is subject to the strongest hydrogen bonding in the largest protein among all.

We turn to HEWL, which is the “easiest” case among the test set of enzymes, as the two carboxyl groups are spatially well separated (by about 7 Å in the crystal structure) and only partially buried. All four methods correctly predicted the experimental pK_a order of the catalytic dyad. In fact, a correct pK_a order was also predicted by other PB methods such as MCCE¹³ and DelPhiPKa.¹⁴ As to the hydrogen bonded and partially buried active-site residues in SNase, the four methods perform similarly as for BACE1 homologs. PropKa cannot assign the pK_a order; PB method give very similar pK_a’s; and the two CpHMD methods correctly predict the pK_a order. Taken together, these data suggests that CpHMD can reliably differentiate the proton donor and nucleophile components of coupled carboxyl dyads.

The distinct performance of CpHMD prompted us to investigate the physical origin of the pK_a order. We considered hydrogen bonding and desolvation, which are the major contributors to the pK_a shifts of the catalytic residues relative to the model values. Coulomb interactions with other residues are not considered here, as they are negligible for the carboxyl dyads in BACE1 series,^26,35 which is typical for buried and coupled catalytic dyads. Since catalytic dyads are subject to a similar degree of hydrophobic burial, we first examined the hydrogen bond patterns of dyad residues in the five enzymes. Surprisingly, in all five enzymes, the calculated occupancy of hydrogen bonds formed by the nucleophile carboxylate in the titration pH range is always larger than the proton donor, and its pH dependence is well correlated with the pH profile of deprotonation (Fig. 2, Fig. S8 and S9). The hybrid-solvent CpHMD results (Fig. 2) are in agreement with the all-atom CpHMD results (Fig. S6). Interestingly, the carboxyl sidechains are always hydrogen bond acceptors, which suggests that hydrogen bonding stabilizes the deprotonated form and explains the match between the pH profiles of carboxylate hydrogen bonding and deprotonation (Fig. 2, compare curves in the left and right panels).

Figure 2. Deprotonated state of the nucleophile is stabilized by hydrogen bonding.

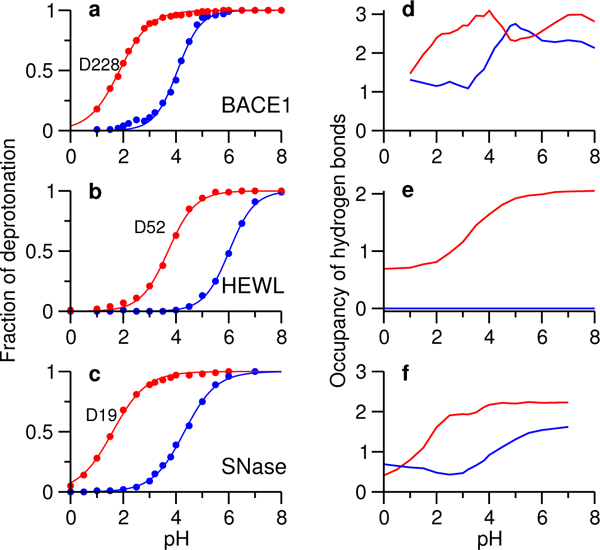
The fraction of deprotonation at different pH for Asp32/Asp228 in BACE1 (a), Glu35/Asp52 in HEWL (b), and Asp19/Asp21 in SNase (c) in the hybrid-solvent CpHMD simulations. Total occupancy of hydrogen bonds formed by the proton donor (blue) and nucleophile (red) carboxylates in BACE1 (d), HEWL (e) and SNase (f) at different simulation pH.

We were curious as to whether the difference in hydrogen bonding between the two carboxyl groups is present in the crystal structures. In BACE1 and its homologs BACE2 and CatD, the aspartyl dyad are hydrogen bonded to each other. Additionally, the BACE1 proton donor Asp32 forms hydrogen bonds with Gly34 and Ser35, while the nucleophile Asp228 forms hydrogen bonds with Gly230 and Thr231. PropKa calculation showed that these hydrogen bonds (two for each carboxyl group) make nearly identical contributions to the pK_a down shifts: −1.58 for Asp32 and −1.53 for Asp228. The hydrogen bond patterns in the homologous BACE2 and CatD are very similar to BACE1. The proton donor forms hydrogen bonds with a serine and a glycine, while the nucleophile forms hydrogen bonds with a threonine and a glycine. PropKa calculation gave identical contributions (about −1.4 units) to the pK_a down shifts. The hydrogen bond environment of the carboxyl dyads in the CpHMD simulations is similar to the crystal structures, except that the catalytic nucleophile can form (accept) a hydrogen bond with not only the sidechain but also the backbone of the aforementioned threonine: Thr231 in BACE1 (Fig. 3d), Thr244 in BACE2 (Fig. S8), and Thr234 in CatD (Fig. S9). Interestingly, the occupancies of the carboxylate–threonine hydrogen bonds increase with pH (Fig. 3a and Fig. S8 and S9), consistent the pH profiles of the total occupancy of hydrogen bonds. The all-atom CpHMD simulations confirmed these trends (Fig. S6).

Figure 3. pH-dependent hydrogen bonding of the nucleophiles in HEWL, BACE1 and SNase.

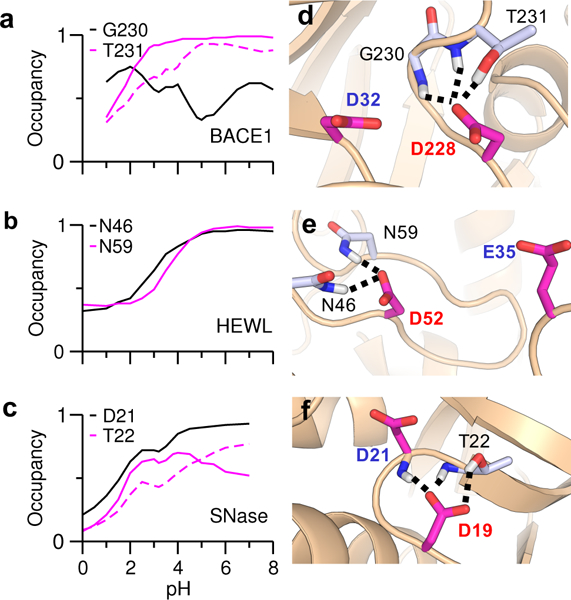
Occupancy of individual hydrogen bonds at different simulation pH for the dyad nucleophiles, Asp228 in BACE1 (a), Asp52 in HEWL (b), and Asp 19 in SNase (c) in the hybrid-solvent CpHMD simulations. The carboxylate–backbone hydrogen bond not present in the crystal structure is indicated by the dashed lines. The residues forming hydrogen bonds with the dyad nucleophile are indicated. Representative snapshots showing the hydrogen bonds formed by the nucleophile in BACE1 (d), HEWL (e), and SNase (f). The proton donor and nucleophiles are labeled in blue and red, respectively.

In the crystal structure of HEWL, the proton donor Glu35 forms a hydrogen bond with Ala110, while the nucleophile Asp52 forms hydrogen bonds with Asn44, Asn46 and Asn59. Based on these hydrogen bonds, PropKa calculation gave the pK_a shifts of −0.6 for Glu35 and −1.92 for Asp52. These results are largely in agreement with the CpHMD simulations, although in the simulations, Glu35 does not form any hydrogen bond, while Asp52 forms hydrogen bonds with Asn46 and Asn59 only (Fig. 3b and e, Fig. S7). The occupancies of the two hydrogen bonds increase with pH, matching the profile of Asp52 deprotonation. Consistently, hydrogen bonding is the major energetic factor that lowers the pK_a of Asp52 in the PropKa calculation. This agreement is likely the reason for the same pK_a order calculated by PropKa and CpHMD simulations.

In the crystal structure of SNase, Asp19 and Asp21 are hydrogen bonded to each other. The nucleophile Asp19 forms a hydrogen bond with the sidechain of Thr22, while Asp21 forms hydrogen bond with both the sidechain and backbone of Thr41. These hydrogen bonds result in similar pK_a shifts for the dyad residues (−1.33 for Asp19 and −1.4 for Asp21). These hydrogen bonds are present in the CpHMD simulations; however, Asp19 can form an additional hydrogen bond with the backbone of Thr22 in the simulations (Fig. 3c and f, Fig. S7). Considering the five enzymes together, we can see that for a coupled carboxyl dyad, crystal structure shows no hydrogen bonding difference, while CpHMD simulation reveals one additional hydrogen bond that stabilizes the charged nucleophile. For a non-coupled carboxyl dyad, both crystal structure and simulation show more hydrogen bonding for the charged nucleophile. Thus, we hypothesize that hydrogen bonding is the molecular determinant for the pK_a order of the carboxyl dyads.

Desolvation is another major contributor to the pK_a shifts of catalytic dyads. In contrast to hydrogen bonding, which stabilizes the charged form and hence shifts the carboxylate pK_a down, desolvation favors the neutral state and shifts the carboxylate pK_a up. We previously mentioned that it is expected that the dyad residues are buried to a similar degree. We test whether it is indeed the case for the five enzymes. For BACE1, BACE2 and CatD, the PropKa calculations gave 100% burial for the carboxyl dyads, which is consistent with the CpHMD simulations showing below 10% fractional solvent accessible surface area. (SASA). Interestingly, in the titration pH range of the nucleophile, it is slightly more exposed to solvent than the proton donor for all three enzymes (Fig. 4a and Fig. S10). For HEWL, the PropKa calculation showed that Glu35 and Asp52 are 66%) and 50%) buried, respectively. Consistently, CpHMD simulations showed about 20% fractional SASA values for the two carboxylates, and in the titration pH range of the nucleophile Asp52, its solvent exposure is slightly higher than the proton donor Glu35 (Fig. 4b). For SNase, the PropKa. calculation gave 60%) and 86%) burial for the coupled carboxylates Aspl9 and Asp21, respectively, which is in agreement with the CpHMD simulations which showed 20–25%) and 10%) fractional SASA values for the two residues, respectively (Fig. 4c). The same trends are seen in the all-atom CpHMD simulations (Fig. S11). Taken together, the above analysis suggests that the catalytic dyads have similar solvent exposure based on both CpHMD simulations and crystal structures; however, the nucleophile is always slightly more exposed than the proton donor during dynamics even if they are both 100%) buried in the crystal structure.

Figure 4. Solvent exposure of the carboxyl dyads in HEWL, BACE1 and SNase.

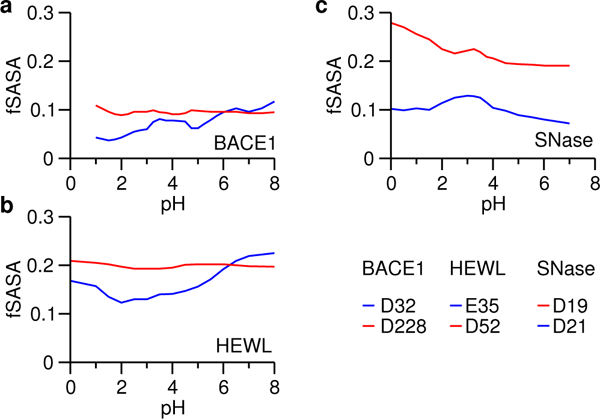
Fractional SASA (fSASA) refers to the solvent accessible surface area of the carboxy late oxygens in the protein environment relative to that in solution. Data for the nucleophiles are shown in red.

In summary, CpHMD simulations recapitulated the experimental pK_a orders of coupled and buried carboxyl dyads in enzyme active sites, which presents a challenge for the commonly used empirical calculations and PB electrostatic calculations. Intriguingly, CpHMD data revealed that the negative nucleophile is stabilized by a higher occupancy of hydrogen bonds than the proton donor in both spatially separated and hydrogen bonded (coupled) carboxyl dyads. For the latter, the higher occupancy is captured in the CpHMD simulations but not PropKa calculations based on the crystal structures. Additionally, simulations showed a consistently, slightly higher solvent exposure for the negative nucleophile than the proton donor even if the dyad is 100%) buried according to the crystal structure. Although these findings are initially surprising, increased hydrogen bonding and solvent exposure stabilize the charged state, consistent with the lower pK_a of the nucleophile. Increased solvent exposure also makes it easier for the general base (one form of nucleophile) to engage in the deprotonation of a nearby water, which initiates the catalytic process. While the generality of the findings emerged from the study awaits further testing using a larger set of data, they demonstrate how adding dynamics helps advance our understanding of the structure-function relationships. As such, molecular dynamics based pK_a prediction approaches hold a unique potential.

Methods and Protocols.

Five enzymes, BACE1 (PDB ID 1SGZ), BACE2 (PDB ID 3ZKQ), CatD (PDB ID ILYA), HEWL (PDB ID 2LZT) and the hyperstable Δ+PHS SNase (PDB ID 3BDC) were studied in this work. While all five proteins were subject to the hybrid-solvent CpHMD titration simulations,²² three of them, BACE1, HEWL and SNase were subject to the PME-based a.ll-atom CpHMD simulations.²³ The carboxyl dyad pK_a’s were also calculated by the empirical PropKa method (version 3.1)^11,12 and the PB method APBS (version 1.4.1)^15,16 based on the same crystal structures with missing residues added.

All CpHMD simulations were carried out using the CHAR.MM package (version c36a.6).⁴¹ CHAR.MM22/CMAP force field was used to represent proteins.^42,43 and the CHAR.MM modified TIP3P model⁴¹ was used to represent water. pH replica-exchange protocol was used in all CpHMD simulations.²² In the hybrid-solvent CpHMD titration of BACE1, BACE2 and CatD, the simulations lasted 20, 20 and 30 ns per replica, corresponding to an aggregate sampling time of 480 ns, 400 ns, 720 ns, respectively. For the smaller HEWL and SNase, 5 ns per replica was used, corresponding to an aggregate sampling time of 80 ns. In the all-atom PME CpHMD titration of BACE1, HEWL and SNase, 30 ns per replica was used, corresponding to an aggregate sampling time of 720 ns, 700 ns, and 660 ns, respectively.

To verify structural stability at different pH, the backbone root-mean-square deviation (RMSD) from the starting structure was calculated (Fig. S1–2 for HEWL and SNase; pH-dependent conformational dynamics of BACE1 was discussed previously²⁶). As expected, the backbone RMSD for the hyper-stable SNase was about 1 Å with a small fluctuation throughout the pH range, while for HEWL, the RMSD remained below 2 Å with larger fluctuation at pH below 2. The latter is likely a result of the acid-induced structural change, consistent with the simulations using Monte-Carlo based constant pH method.⁴⁴ To verify sampling convergence, time series of the pH-dependent unprotonated fractions of the dyads and the pK_a values were calculated (Fig. S3–S5). We note that pH replica exchange enhances the sampling of both protonation and conformational states, allowing a significant reduction of the convergence time per replica (by at least one order of magnitude in our experience) relative to the single pH constant pH simulations. ²²

The fraction of unprotonated states was calculated using the following definition: λ < 0.1 for the protonated state and λ > 0.9 for the deprotonated state. The microscopic site-specific pK_a’s were calculated by fitting the fraction of unprotonated states S at different pH to the modified Hill equation,

$$S\text{=}\frac{\text{1}}{{\text{1}\text{+}\text{10}}^n\text{(p}{K}_a\text{-pH)}},$$ (1)

where n is the Hill coefficient. We also calculated the macroscopic stepwise pK_a’s by fitting the total number of bound protons to the dyad, N_prot, to the following model based on statistical mechanics,^33,36,45,46

$$N_{\text{prot}}\text{=}\frac{{10}^{{\text{p}}^{K_2}-\text{p}\text{H}}+2\times {\text{10}}^{\text{p}{K}_{\text{1}}+\text{p}{K}_{\text{2}}-2\text{pH}}}{{1+10}^{\text{p}{K}_{\text{2}}-\text{pH}}{+10}^{\text{p}{K}_{\text{1}}+\text{p}{K}_{\text{2}}-2\text{pH}}},$$ (2)

where pK₁ and pK₂ are the two macroscopic pK_a’s, and the denominator represents the partition function.