Abstract
An obstacle to establishing widely useful data acceptance criteria for U.S. Environmental Protection Agency (EPA) qPCR methods has been the unavailability of standardized reference materials. Earlier versions of EPA Methods 1609 and 1611 for enterococci used cellular reference materials for quantifying enterococci in unknown test samples, however, EPA updates to these fundamentally DNA-based analysis methods have shifted toward the use of DNA standards. This report describes the application of droplet digital PCR (ddPCR) analysis for the quantification of a set of synthetic plasmid DNA standards that have been made available for updated EPA Methods 1609.1 and 1611.1 as well as for EPA Draft Method C for Escherichia coli. To obtain the most accurate concentration estimates possible, part of this effort was to develop a data analysis model for determining the fluorescence thresholds that distinguish positive from negative droplets produced by the ddPCR reactions. Versions of this model are described for applications with individual reactions, multiple reactions within a ddPCR system run, and multiple reactions within and across different system runs. The latter version was applied toward determinations of error in the concentration estimates of the standards from replicate analyses of each standard in multiple ddPCR system runs. Mean concentration estimates for the five standards from the ddPCR analyses were 4.356, 3.381, 2.371, 1.641 and 1.071 log10 copies/5 μL with associated standard deviations of 0.074, 0.082, 0.108, 0.131 and 0.188, respectively. These estimates contrasted with expected log10 concentrations of 4.6, 3.6, 2.6, 1.9 and 1.3 copies/5 μL, respectively, based on the yield of the plasmid reported by the vendor and spectrophotometric analysis of the initial stock solution of this material. These results illustrate how the analyses of original stocks may lead to potential bias(es) in the concentration estimates of final DNA standards and subsequently in the estimates of unknown test samples determined from these standards in qPCR analyses.
Keywords: QPCR, DNA standards, EPA Methods 1609.1 and 1611.1, digital droplet PCR
1. Introduction
Quantitative polymerase chain reaction (qPCR) methods are now widely used for absolute quantification of RNA and DNA target sequence copies in widely varying test matrices for numerous applications (Bustin, 2000; Kubista et al., 2006). One of the most common approaches for obtaining these quantitative target sequence copy estimates is from the use of standard curves generated from qPCR cycle threshold (Ct) measurements of nucleic acid reference materials, e.g. DNA standards (Sivaganesan et al., 2010). Growing interest in rapid qPCR methods for fecal indicator bacteria (FIB) to determine recreational water quality underscores the need for developing standard reference materials for these methods to facilitate comparison of analysis results with EPA water quality criteria values and within and between laboratories (Haugland et al, 2014). Recent emphasis has shifted towards encouraging the use of centralized sources of DNA standards in U.S. Environmental Protection Agency (EPA) qPCR methods for FIB’s (U.S.EPA, 2015a,b; Shanks et al., 2016). Genomic DNA isolated from the FIB target organisms is one obvious source of such standards, however, in some instances the targeted organisms have not been identified or are not readily culturable. Even when the target organisms are available, the standardization of different genomic DNA preparations can remain difficult (Haugland et al, 2014). This has led to the use by the EPA of de novo synthesized DNA constructs that can either be cloned into plasmids for large scale production or used directly (e.g. gBlocks®, Integrated DNA Technologies, Coralville IA) as standards. Another advantage of such constructs is that target sequences for multiple assays can be concatenated into a single target DNA molecule.
EPA has provided sets of five different concentrations of such a multi-purpose plasmid DNA construct to laboratories upon request for use as standards with enterococci qPCR Methods 1609.1 and 1611.1 (U.S.EPA, 2015a,b). These standards are also applicable for EPA Draft Method C for Escherichia coli FIB (modified from Chern et al. 2011) and for EPA Method B for total Bacteroidales (U.S.EPA, 2010). The procedures used to initially prepare and quantify these plasmid DNA standards are described in this report.
The cornerstone of the quantitative analysis in this study was the use of droplet digital PCR (ddPCR) technology. This rapidly emerging technique can quantify the number of target sequence copies in DNA samples containing from approximately 1 up to approximately 50,000 copies of the sequence – an ideal dynamic range for analysis of the plasmid DNA standards prepared for the EPA qPCR methods. The Bio-Rad droplet digital PCR (ddPCR) system used in this study can generate up to 20,000 droplets in oil emulsions from an initial reaction volume of 25 μL. Nanoscale PCR reactions using TaqMan™ sequence detection chemistry are performed in each droplet after which flow cytometry is used to classify each droplet as positive or negative for the presence of target sequences based on the amplitude of the reporter dye fluorescence signal. The number of target DNA sequences present can be calculated from the fraction of positive end-point reactions using Poisson statistics (Cochran, 1949, Hindson et al., 2011).
Another way of stating this calculation is that the estimated proportion (p) of negative droplets is equated to the probability that the sample is free of target sequences, where the target sequence concentration is assumed to have a Poisson distribution. Thus -ln(p) provides an estimate for the target sequence concentration. As the proportion of negative droplets determines the concentration, it is important that the digital PCR correctly classifies the droplets as negative and positive. The ddPCR system software will automatically set a threshold amplitude value to cluster the droplets and classify them as positive or negative. If there is a clear separation between amplitude values of negative and positive droplets, then the threshold value can be any amplitude value between the range of the highest amplitude of negative droplets and the lowest amplitude of positive droplets and the proportion of negative droplets does not change with the selected threshold value. But, for several possible reasons, clear separation of amplitudes is often not seen. In such cases, there is no well-defined process or method provided by the ddPCR system manufacturer to determine the threshold value for distinguishing positive from negative droplets.
In this study, a model was developed and used for estimating positive droplet threshold values for each ddPCR analysis. A further goal of this effort was to characterize the uncertainty of the ddPCR-estimated target sequence quantities in each of the five EPA plasmid DNA standards. Therefore, variations of this model were also developed and used to estimate the variability in target sequence copy estimates from replicate analyses of each of the standards performed in multiple ddPCR system runs. The application of this model in conjunction with ddPCR quantification is recommended for any laboratories wishing to create their own DNA standards with comparable concentration estimates and uncertainty to the EPA-provided standards.
2. Material and Methods
2.1. Plasmid DNA starting material and preparation of standards.
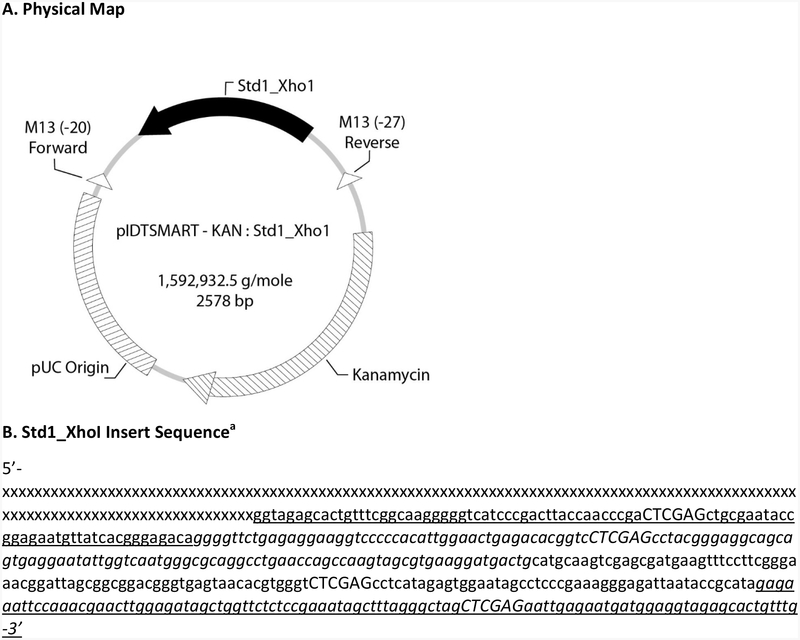
Concatenated target sequences for the Enterococcus and several other qPCR assays (Std1_Xho1) were custom-synthesized de novo and inserted into the plasmid vector pIDTSMART-KAN by a commercial vendor (Integrated DNA Technologies, Coralville IA). The recombinant plasmid was cloned into Escherichia coli and subsequently recovered, purified and lyophilized by the vendor. A map of the IDTSMART-KAN_Std1_Xho1 recombinant plasmid construct and the annotated base sequence of the Std1_Xho1 insert are shown in Figure 1. The lyophilized material was suspended in AE buffer (Qiagen, Valencia, CA) to give an expected gravimetric concentration of 20 ng/μL based on the vendors estimate of yield and incubated at room temperature for 30 min to fully dissolve. The concentrations of four, 2 μL aliquots of the dissolved plasmids were determined by A260 absorbance in a Nanodrop™ spectrophotometer (Thermo Fisher Scientific, Life Technologies, Grand Island, NY) against an AE buffer blank and the mean concentration and standard deviation determined.
Figure 1.
A) Physical map of the IDTSMART-KAN_Std1_Xho1 recombinant plasmid construct with position and reverse orientation of Std1_Xho1 insert sequence indicated by solid, bold arrow and B) annotated Std1_Xho1 insert sequence. a Capital letters indicate inserted Xho1 restriction sites. x’s denote a proprietary sequence. Underlined bases denote EC23S587 assay target sequence for EPA Draft Method C. Italicized bases denote GenBac3 assay target sequence for EPA Method B. Underlined and italicized bases denote Entero1A assay target sequence for EPA Methods 1609.1 and 1611.1. Other bases correspond to the target sequence (not currently in use) for an additional assay.
The plasmid was linearized to facilitate PCR amplification of the target sequences as follows. First an aliquot of the plasmid stock solution containing 200 ng based on the vendors yield estimate (corroborated by Nanodrop™ analysis as described in sections 3.1 and 4.1) was diluted with PCR-grade water, 10× NE buffer 3 and 20 units of Pvu I restriction enzyme (New England BioLabs, Ipswich, MA) to give a final volume of 50 μL with final concentrations of 1× NE buffer, 0.4 units/μL Pvu I enzyme and 40 ng/μL plasmid DNA. The Pvu I enzyme recognizes only one site in the plasmid vector according to sequence information provided by the vendor. The solution was incubated at 37° C for 1 hr and then at 80° C for 30 min to inactivate the restriction enzyme.
Concentrations of the linearized plasmid DNA stock solution were converted from gravimetric units (ng/μL) to copies/μL based on the vendor-reported molecular weight of the plasmid (1592932.5) and dilutions of the linearized plasmid DNA stock solution were made in AE buffer to prepare standards with expected concentrations of ~40000, 4000, 400, 80 and 20 copies per 5 μL (log10 concentrations: 4.6, 3.6, 2.6, 1.9 and 1.3 copies/5 μL). Aliquots of each standard as well as the remaining undigested and linearized plasmid stock solutions were prepared in low retention micro-centrifuge tubes (VWR, Radnor, PA) for storage at −80° C.
2.2. ddPCR analysis
The sequences of the probe and forward and reverse primers for the Entero1 assay used for all ddPCR analyses in this study have been described (U.S.EPA, 2015a,b). For ddPCR analyses with the Entero1 assay, the TaqMan® hydrolysis probe (Eurofins, Louisville, KY) was 5’-labeled with a 6-FAM reporter dye and 3’ labeled with a Blackhole, non-fluorescent quencher (BHQ-1). The simplex reaction mixes contained 12.5 μL of ddPCR Supermix™ for probes with no dUTP (BioRad, Hercules, CA #1863024), 1.25 μL of primer-probe mix (for a final concentration of 375 nM of each primer and 100 nM of probe in the reactions), 6.25 μL of PCR-grade water and 5 μL of the DNA samples for a total reaction volume of 25 μL. Aqueous droplet emulsions were prepared in droplet generation oil for probes (BioRad, #1863005) using a manual droplet generator, PCR amplifications were performed in a C1000 Touch Thermal Cycler with 96-Deep Well Reaction Module and reactions were analyzed in a QX200 Droplet Reader with QuantaSoft™, version 1.4.0 software (collectively referred to as the QX200 ddPCR system, BioRad, Hercules, CA) following the manufacturer’s protocols. Thermal cycling conditions for the PCR amplifications were: 95°C for 5 min, followed by 40 cycles of 95°C for 30 seconds, 60°C for 1 min, and then 98°C for 5 min, and finally hold at 12°C. A total of five ddPCR system runs of different frozen aliquots (tubes) of the standards, each consisting of eight replicate analyses of each of the five standards plus eight negative control reactions containing AE buffer in place of the standards, were performed within approximately one month of the time the standards were prepared, aliquoted and frozen. The fluorescence amplitudes of the droplets in each reaction well of each plate run were visually inspected for wells with substantial shifts from the norm (indicative of defective reactions most probably caused by defects in the manual droplet generation process). Data from these reactions were excluded from further analysis. Accepted partitions (droplets) in the accepted reactions ranged from 6066 to 16943 (median: 11883). Mean volume of the droplet partitions, used for calculating plasmid concentrations, was 0.00085 μL.
2.3. ddPCR data analysis: Mixture Model
Raw fluorescence amplitude and positive/negative clustering data for each droplet from each ddPCR analysis reaction of the five plasmid DNA standards were determined by the QX200 system software and exported as .cvs files. Further analysis of the droplet amplitude data was performed in Winbugs (https://www.mrc-bsu.cam.ac.uk/software/bugs/the-bugs-project-winbugs/) using a mixture model as detailed below.
In the mixture model, amplitude value Yi (I = 1,…N) is assumed to come from either the negative droplet group G1 or from the positive droplet group G2, where group Gj (j = 1,2) has a normal distribution with mean λj and variance Supposing P is the (unknown) fraction of Yi ‘s in group G1, the mixture model of two normal distributions can be expressed as:
| (1) |
As the amplitude values for positive droplets are always greater than negative droplets, it is assumed that λ2 > λ1, and λ2 can be re-parameterized as:
| (2) |
As no prior information is available, the following prior distributions were used to estimate the five model parameters λ1, θ, , and P:
| (3) |
where the term I(0, ) in the prior distribution of θ restricts the normal distribution to positive values and U(0,1) is the uniform distribution. A Monte Carlo Markov Chain (MCMC) simulation method was used to generate posterior distributions of the model parameters. Supposing the average volume of a droplet is v μL, the posterior distribution of
| (4) |
can be used to obtain summary statistics, such as mean, median and the 95% Bayesian Credible Interval (BCI), for the plasmid concentration × per unit reaction volume. The threshold which separates the negative droplets group from positive droplets group, is the Y value where the densities of the two normal distributions N(λ1, ) and N(λ2, )intersect. Thus, solving the following equation for Y for given values of λ1, λ2, and gives the threshold value:
| (5) |
The estimated threshold value T is given by:
| (6) |
where
| (7) |
and ,, and are posterior means of the corresponding model parameters described in equation (1). Note that if σ12 = σ22 (i.e. both droplet groups have the same variance) then the estimated threshold value T is simply the average of , and .
2.4. ddPCR data analysis: Pooled Mixture Model
For each ddPCR system run, eight replicate analysis reactions were performed for each standard. Pooled data from all replicate analyses in the run giving similar negative droplet fluorescence amplitudes were used to account for variability in the plasmid concentration estimates using a pooled mixture model. Equation (1) was modified in this model to:
| (8) |
where λ1j, θj, , and Pj are model parameters, vj is a known reaction volume and Xj is the concentration per unit volume for the jth replicate, m is the number of replicate analyses, μ and σ2 are the mean (DNA concentration in log10 base) and variance parameters, combining information from all replicate analyses of the given ddPCR system run. The following prior distributions were used to estimate the model parameters:
| (9) |
Using the above (non-informative) priors would lead to posteriors dominated by the likelihood (i.e. data). As the percentage of positive droplets is negligible compared to the negative droplets at plasmid concentrations of ~ 10 and 40 copies per reaction (the approximate numbers of copies for standards 4 and 5), the positive droplet group from standard 3 (~400 copies per reaction) was used to estimate an informative prior distribution for . The following informative prior was used for standards 4 & 5:
| (10) |
where, the constants α and β were chosen so that the mean (= α/β) and variance (= α/β2) of a Gamma (α, β) distribution are the estimated mean and variance of the posterior distribution of the average of , j=1,2,…m of the positive droplet group for standard 3. For example, if the estimated posterior mean and variance are m0 and v0, then α = m02 /v0 and β = m0 /v0. Adding a subscript j to all the terms in equations (6) and (7) gives the threshold Tj for jth reaction. The overall threshold was defined as the average of all Tj’s and is given by:
| (11) |
2.5. ddPCR data analysis: Master Mixture Model
A total of five independent ddPCR system runs were performed on different frozen aliquots (tubes) of each dilution (concentration) of the standards to determine the initial concentrations of the standards in this study. Both run-to-run and within-run variability were accounted in a master mixed model. The pooled mixture model provided in equation (8) was modified to include the between run variability in this model as:
| (12) |
where , θjk, , and Pjk are model parameters, vjk is a known reaction volume and Xjk is the concentration per unit volume for the jth replicate of kth system run, μk and σk2 are the mean (DNA concentration in log10 base) and variance parameters, combining information from all replicates of kth system run, and are overall mean and variance of the plasmid DNA concentration incorporating between system run variability. Within system run variability was estimated as the average of the all posterior mean estimates of σk2. Thus, the estimated total variance is given as:
| (13) |
Following prior distributions were used to estimate the model parameters:
| (14) |
As discussed in the pooled mixture model section, the following informative prior was used for standards 4 and 5:
| (15) |
Where αk and βk are known constants correspond to kth run.
2.6. Adjusting plasmid DNA concentrations for false positive results
Negative control samples were occasionally observed to give small quantities of positive droplets in these analyses, presumably due to contamination of the reagents with target sequences. Thus, adjustments for false positive results were made in estimating the plasmid DNA concentrations. The threshold T defined by equation (4) was estimated for the pooled data from all of the negative control replicate samples and the posterior mean estimate of T was used to classify the droplets as positive or negative. Supposing that Yo is the total number of droplets and M0 is the number of negative droplets for the pooled data (note that for uncontaminated pooled samples, M0 = Yo, otherwise, M0 < Yo), equation (4) was modified to provide the necessary adjustment for the number of target sequences with the modified equation given as:
| (16) |
where, M0 and P0 (the fraction of negative droplets of a negative control) are assumed to have the following distribution:
| (17) |
For the pooled mixture model, Pj in equation (8) for Xj is replaced by Pj /P0. Similarly, for master mixture model and kth system run, Pjk in equation (12) for Xjk is replaced by Pjk /P0k, where P0k is the fraction of negative droplets of a negative control for the kth system run. Subscript k is added to all the variables in equation (17) to get the distributions for kth system run and is given as:
| (18) |
3. Results
3.1. Spectrophotometric concentration estimates of the plasmid DNA stock solution.
The original lyophilized IDTSMART-KAN_Std1_Xho1 recombinant plasmid DNA material provided by the vendor was dissolved to give an expected concentration of 20 ng/μL based on the vendor’s yield estimate. A260 readings of this stock solution in a Nanodrop™ spectrophotometer gave a mean concentration estimate of 23.87 ng/μL (standard deviation: 12.36). Further processing and dilutions of this material to make the standards as described in section 2.1 were based on the vendor’s yield estimate following the rationale discussed in section 4.1.
3.2. ddPCR positive droplet threshold determination and estimates of standards concentrations.
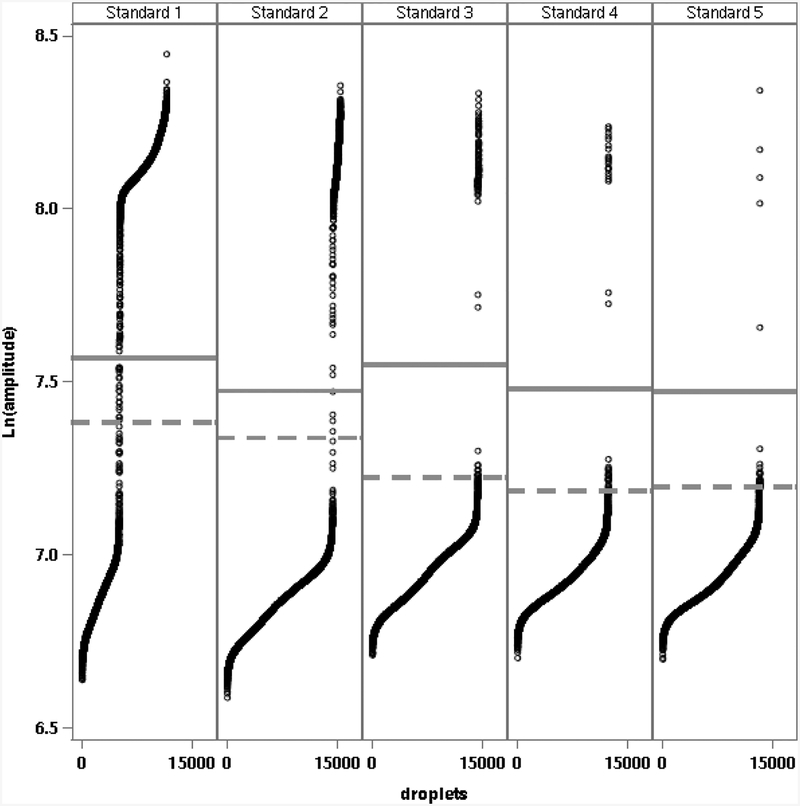
Figure 2 shows the fluorescence amplitude of droplets in natural logarithm (log base e) scale and the estimated threshold T (solid line) using equation (6) from analyses of the five standards in one representative ddPCR system run. These results illustrate that each of the standards concentrations were well within the dynamic range of the ddPCR system. Figure 2 also shows the estimated threshold (dashed line) from default analysis by the ddPCR system software. Droplets with amplitudes between the two lines were classified as positive by the system software threshold and negative by the mixture model threshold. Negative and positive droplets from both thresholds are shown below the lower and above and upper lines, respectively. Estimated log10 copies per 5 μL for the five standards from this run were 4.379, 3.313, 2.370, 1.699 and 1.047 from the mixture model and 4.381, 3.314, 2.413, 2.030 and 1.810 from the system software thresholds, respectively.
Figure 2.
Natural logarithm (Ln) fluorescence amplitudes of droplets (ordered from lowest to highest amplitude on x-axis) for a single set of analyses of the five plasmid standards (Standards 1 to 5). Solid and dashed horizontal lines denote fluorescence amplitude threshold values used for clustering negative and positive droplets from the pooled mixture model and from the default analysis by the ddPCR system software, respectively.
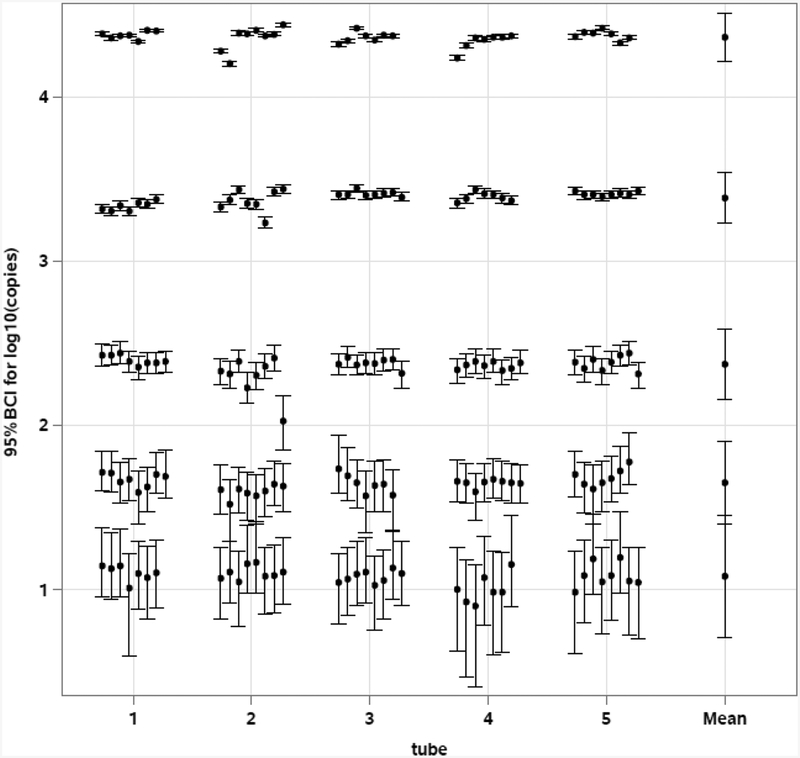
Figure 3 shows the estimated mean log10 copies and 95% BCIs from the replicate analyses of the five standards from each of the five ddPCR system runs as determined from the pooled mixture model. It also shows the overall mean log10 copies and 95% BCI’s for the five standards from the five system runs as determined from the master mixture model. Table 1 gives the overall posterior means and standard deviations of the concentration estimates of the five standards.
Figure 3.
Estimated 95% BCI of log10 copies/5 μL for each of the accepted replicate analyses of the five plasmid standards from five system runs of different frozen aliquots (tubes), as well as for the overall mean. Within and between run variabilities are incorporated in the BCI for overall mean.
Table 1.
Expected and ddPCR-estimated posterior mean log10 copies/5 μL and standard deviation (SD) of the five standards.
| Standard | Expected mean | Estimated mean | SD |
|---|---|---|---|
| 1 | 4.6 | 4.356 | 0.0739 |
| 2 | 3.6 | 3.381 | 0.0819 |
| 3 | 2.6 | 2.371 | 0.1081 |
| 4 | 1.9 | 1.641 | 0.1309 |
| 5 | 1.3 | 1.071 | 0.1885 |
3.3. Stability of plasmid DNA standards during freezer storage
The uncertainties of the initial ddPCR log10 copies/5 μL concentration estimates of the five standards, expressed as mean ± 2 and 3 standard deviations, were used as acceptance bounds for evaluating the stability of different aliquot tubes of the standards over a period of about 40 months from the time of their initial analyses. During this time, 15 tubes of each standard were analyzed at intervals of roughly three months. Only three of the 75 tubes analyzed gave estimates below the 2 standard deviation acceptance bound in greater than 25% of replicate ddPCR analyses (N = 8) and none of the tubes failed this criterion using the 3 standard deviation bound. Two of the three failed tube analyses using the 2 standard deviation bound were of the lowest concentration standard 5, however, no trends towards higher failure rates with longer storage time were observed with any of the standards (data not shown).
4. Discussion:
4.1. Vendor vs. spectrophotometric estimates of original plasmid DNA stock solution concentration.
Spectrophotometric analysis is a standard, conventional technique for the measurement of nucleic acid concentrations in solution (Kline et al., 2009). Nanodrop™ spectrophotometers are widely used in many laboratories for this purpose due to their relatively low cost, ease of use and particularly because of their ability to analyze small sample volumes. Procedures followed for the Nanodrop™ analysis of the plasmid DNA stock solution in this study were in accordance with the instrument manufacturer’s guidelines including making up the stock solution to an expected concentration within the reported dynamic range of the instrument (https://www.thermofisher.com/order/catalog/product/ND-2000). Despite the unexplained low precision of concentration estimates from replicate analyses of the plasmid DNA stock solution by this technique in this study (CV: 52%), the mean concentration estimate from these analyses was considered sufficiently close to the expected concentration from the vendors estimate of yield (vendors yield estimation method not disclosed) to use the vendor’s value for determining the expected concentrations of plasmid copies in the standards.
4.2. Selection of ddPCR positive droplet fluorescence amplitude thresholds
As shown in Fig. 1, the default thresholds established by the ddPCR system software were clearly within the negative droplet cluster for the lowest three concentrations of standards and thus would overestimate the corresponding concentrations of these standards. These results suggest that a certain unknown minimum number of positive droplets are required for the default system software to accurately perform cluster analysis. The system software also allows for threshold setting based on combined analysis of multiple wells with different samples in a reaction plate, however, the validity of this potential option was not further explored in the initial analyses of the standards described in this report.
The mixture model for setting thresholds described in this report does not rely on the system software and should be applicable for the entire dynamic range of the ddPCR system. Amplitudes from all droplets and from all reactions are considered in this model. Limitations to this approach are that it is computationally intensive and there is no universal threshold value that can be applied to all concentrations. Threshold values would need to be re-estimated for future batches of standards. Advantages to this approach are that variability between replicate runs is accounted for in setting the threshold and within and between run variabilities are accounted for in estimating the standard concentrations. Several other approaches have been described recently that also do not rely on the system software for threshold setting in ddPCR reaction analysis (Dreo et al., 2014; Jones et al. 2014; Strain et al., 2013; Trypsteen et al., 2015). Strain et al. (2013) and Jones et al. (2014) described robust approaches for automated threshold setting. These methods use clustering algorithms to identify positive and negative droplet groups with 90 or 95% confidence intervals and droplets that are not in either group are not used in estimating the proportion of negative droplets. This approach thus may over or under estimate the target sequence densities. Dreo et al. (2014) used a standardized manual threshold which is the average fluorescence amplitude in the no template controls (NTCs) plus six times the standard deviation. Trypsteen et. al (2015) proposed a method for threshold setting based on extreme value theory that does not assume any specific distribution for the amplitudes of droplet populations in no template control (NTC) samples. This latter approach uses results from single or multiple NTC sample analyses to estimate a single threshold value and applies it to all test samples to classify droplets as positive or negative. Even though it does not exclude any droplets, the amplitude values of the droplets in the actual test samples are not considered in this approach.
4.3. ddPCR vs. conventional estimation of plasmid DNA standards concentrations.
Expected log10 concentrations per 5 μL of the plasmid standards from the spectrophotometrically corroborated yield estimate of the vendor and extrapolations based on the dilutions were higher than the mean log10 concentrations estimates from ddPCR analysis by an average of 0.236, corresponding to about a 1.7-fold difference. The mean differences among the five individual standards ranged from 0.219 to 0.259 suggesting that the serial dilutions used to go from the highest to lowest concentration standards were relatively consistent. Consequently, the greatest source of the differences appeared to be from either the dilutions and other manipulations going from the original non-linearized stock solution of the vendor’s material to the highest concentration standard or with the freezer storage and thawing of the aliquoted materials for analysis. Subsequent analyses of a thawed aliquot of the linearized plasmid DNA stock solution with a Qubit fluorometric quantitation system (Thermo Fisher Scientific, Life Technologies) led to expected concentration estimates for the standards that were lower than but also in closer agreement with the ddPCR estimates (average log10 difference of 0.15). These results tended to corroborate the ddPCR estimates and again suggested that the difference between the original vendor/spectrophotometric concentration estimate and the ddPCR/Qubit estimates were either associated with the initial manipulations of the plasmid stock solution including restriction enzyme digestion or with freezing and thawing. As discussed in section 3.3, little evidence was seen that extended storage of the standards at −80° C had a significant effect on the effective concentrations of the standards in ddPCR analyses. It may be noteworthy that the extrapolated vendor/spectrophotometric concentration estimates were outside the approximate 95% confidence ranges (±2 standard deviations) of the ddPCR estimates for only standards 1 and 2 owing to the higher variability of the ddPCR estimates for the other three standards. Nevertheless, use in this instance of the original vendor/spectrophotometric concentration estimates in place of the mean ddPCR estimates in standard curves for qPCR analyses would be expected to produce a substantial (~70%) difference in subsequent unknown test sample target sequence copy density estimates.
4.4. Applications of EPA plasmid DNA standards
The originally published EPA Methods 1611 and 1609 for enterococci (U.S.EPA, 2012b, 2013), Method B for total Bacteroidales (U.S.EPA, 2010) and unpublished Draft Method C for E. coli, used cellular reference materials for quantifying the target organisms in unknown test samples which, in the case of the enterococci methods, were associated with published EPA recreational water quality criteria in units of CCE or calibrator cell equivalents (U.S.EPA, 2012b). With possible exception of Method C, an economically viable standardized source of cellular reference materials is still not available for these methods. Subsequent studies have however, illustrated that the use of different cultured cell preparations can give substantially different CCE estimates (Cao et al., 2012; Sivaganesan et al., 2011). These observations, combined with the recognition that qPCR is a DNA-based analytical technique, led to a call for the standardization of these methods based on the use of DNA reference materials (Haugland et al., 2014). The outcome of this recommendation was the publication of EPA Methods 1611.1 and 1609.1 for enterococci (U.S.EPA, 2015a,b, available at: http://www2.epa.gov/cwa-methods/other-clean-water-act-test-methods-microbiological) and the drafting of a similar, as yet unpublished, modification of EPA Draft Method C for E. coli. These updated methods call for the use of accurately quantified DNA standards in the quantification model. For enterococci, they also provide a means of translating target sequence copy estimates determined from this model to the CCE units in the EPA recreational water quality criteria. These standards also were used in a recent multi-laboratory study of EPA draft Method C for E. coli (Sivaganesan et al., Unpublished results). An effort is currently underway to develop similar multi-assay reference DNA standards for a wide array of EPA water quality testing qPCR methods that would be available from a commercial source.
4.5. Conclusions
To support the generation of data from different laboratories that can be compared with the national recreational water quality criteria that are now established for EPA Methods 1611 and 1609 for enterococci (U.S. EPA, 2012a), the EPA has prepared DNA standards that can be used in these methods as well as in EPA Draft Methods B & C for E. coli and Bacteroidales, respectively. Procedures used for the quantification of these standards, including models for determining fluorescence thresholds for assigning positive droplets from ddPCR analysis are described in this report. While the use of EPA-provided or recommended standards for performing these methods is encouraged, the procedures described can be used by laboratories wishing to create their own DNA standards in order to obtain comparable target gene copy concentration estimates of unknown samples.
Acknowledgements
The authors thank Drs. Kevin Oshima and Eric Villegas (EPA, Office of Research and Development) and Drs. Lemuel Walker and John Ravenscroft (EPA, Office of Water) for their critical review of this manuscript.
References
- Bustin SA 2000. Absolute quantification of mRNA using real-time reverse transcription polymerase chain reaction assays. J. Mol. Endocrinol 25(2), 169–193. [DOI] [PubMed] [Google Scholar]
- Cao Y, Sivaganesan M, Kinzelman J, Blackwood AD, Noble RT, Haugland RA, Griffith JF, Weisberg SB 2013. Effect of platform, reference material, and quantification model on enumeration of Enterococcus by quantitative PCR methods. Water Res. 47(1), 233–241. [DOI] [PubMed] [Google Scholar]
- Chern EC, Siefring S, Paar J, Doolittle M, Haugland RA 2011. Comparison of quantitative PCR assays for Escherichia coli targeting ribosomal RNA and single copy genes. Lett. Appl. Microbiol 52(3), 298–306. [DOI] [PubMed] [Google Scholar]
- Cochran WG 1950. Estimation of bacterial densities by means of the “most probable number”. Biometrics 6(2), 105–116. [PubMed] [Google Scholar]
- Dreo T, Pirc M, Ramsak Z, Pavsic J, Milavec M, Zel J, Gruden K 2014. Optimising droplet digital PCR analysis approaches for detection and quantification of bacteria: a case study of fire blight and potato brown rot. Anal. Bioanal. Chem 406(26), 6513–6528. [DOI] [PubMed] [Google Scholar]
- Haugland RA, Siefring SD, Varma M, Dufour AP, Brenner KP, Wade TJ, Sams E, Cochran S, Braun S, Sivaganesan M (2014). Standardization of enterococci density estimates by EPA qPCR methods and comparison of beach action value exceedances in river waters with culture methods. J. Microbiol. Methods 105: 59–66. [DOI] [PubMed] [Google Scholar]
- Hindson BJ, Ness KD Masquelier DA, Belgrader P, Heredia NJ, Makarewicz AJ, Bright IJ, Lucero MY, Hiddessen AL, Legler TC, Kitano TK, Hodel MR, Petersen JF, Wyatt PW, Steenblock ER, Shah PH, Bousse LJ, Troup CB, Mellen JC, Wittmann DK, Erndt NG, Cauley TH, Koehler RT, So AP, Dube S, Rose KA, Montesclaros L, Wang S, Stumbo DP, Hodges SP, Romine S, Milanovich FP, White HE, Regan JF, Karlin-Neumann GA, Hindson CM, Saxonov S, Colston BW 2011. High-throughput droplet digital PCR system for absolute quantitation of DNA copy number. Anal. Chem 83(22), 8604–8610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones M, Williams J, Gartner K, Phillips R, Hurst J, Frater J 2014. Low copy target detection by Droplet Digital PCR through application of a novel open access bioinformatic pipeline, ‘definetherain’. J. Virol. Methods 202, 46–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kline MC, Duewer DL, Travis JC, Smith MV, Redman JW, Vallone PM, Decker AE, Butler JM 2009. Production and certification of NIST Standard Reference Material 2372 Human DNA Quantitation Standard. Anal. Bioanal. Chem 394(4), 1183–1192. [DOI] [PubMed] [Google Scholar]
- Kubista M, Andrade JM, Bengtsson M, Forootan A, Jonak J, Lind K, Sindelka R, Sjoback R, Sjogreen B, Strombom L, Stahlberg A, Zoric N 2006. The real-time polymerase chain reaction. Mol. Aspects Med 27(2–3), 95–125. [DOI] [PubMed] [Google Scholar]
- Shanks OC, Kelty CA, Oshiro R, Haugland RA, Madi T, Brooks L, Field KG, Sivaganesan M 2016. Data Acceptance Criteria for Standardized Human-Associated Fecal Source Identification Quantitative Real-Time PCR Methods. Appl. Environ. Microbiol 82(9), 2773–2782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sivaganesan M, Haugland RA, Chern EC, Shanks OC 2010. Improved strategies and optimization of calibration models for real-time PCR absolute quantification. Water Res. 44(16), 4726–4735. [DOI] [PubMed] [Google Scholar]
- Sivaganesan M, Siefring S, Varma M, Haugland RA 2011. MPN estimation of qPCR target sequence recoveries from whole cell calibrator samples. J. Microbiol. Methods 87(3), 343–349. [DOI] [PubMed] [Google Scholar]
- Strain MC, Lada SM, Luong T, Rought SE, Gianella S, Terry VH, Spina CA, Woelk CH, Richman DD 2013. Highly precise measurement of HIV DNA by droplet digital PCR. PLoS One 8(4), e55943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trypsteen W, Vynck M, De Neve J, Bonczkowski P, Kiselinova M, Malatinkova E, Vervisch K, Thas O, Vandekerckhove L, De Spiegelaere W 2015. ddpcRquant: threshold determination for single channel droplet digital PCR experiments. Anal. Bioanal. Chem 407(19), 5827–5834. [DOI] [PubMed] [Google Scholar]
- U.S. EPA, 2010. Method B: Bacteroidales in Water by TaqMan® Quantitative Polymerase Chain Reaction (qPCR) Assay. EPA-822-R-10-003. United States Environmental Protection Agency, Office of Water: Washington, DC. [Google Scholar]
- U.S. EPA, 2012a. Recreational Water Quality Criteria. EPA-820-F-12-058. United States Environmental Protection Agency, Office of Water: Washington, DC. [Google Scholar]
- U.S. EPA, 2012b. Method 1611: Enterococci in water by TaqMan® quantitative polymerase chain reaction (qPCR) assay. EPA-821-R-12-008. US Environmental Protection Agency, Office of Water, Washington, D.C. [Google Scholar]
- U.S. EPA, 2013. Method 1609: Enterococci in water by TaqMan® quantitative polymerase chain reaction (qPCR) assay with internal amplification control (IAC) assay. EPA-820-R-13-005. US Environmental Protection Agency, Office of Water, Washington, D.C. [Google Scholar]
- U.S. EPA, 2015a. Method 1609.1: Enterococci in water by TaqMan® quantitative polymerase chain reaction (qPCR) assay with internal amplification control (IAC) assay. EPA-820-R-15-009. US Environmental Protection Agency, Office of Water, Washington, D.C. [Google Scholar]
- U.S. EPA, 2015b. Method 1611.1: Enterococci in water by TaqMan® quantitative polymerase chain reaction (qPCR) assay. EPA-820-R-12-008. US Environmental Protection Agency, Office of Water, Washington, D.C. [Google Scholar]