Energetics of Storage and Diffusion of Water and Cyclo-Octasulfur for a Nonpolar Cavity of RHCC Tetrabrachion by Molecular Dynamics Simulations

Abstract

Tetrabrachion forms the key component of the S-layer of Staphylothermus marinus. Molecular dynamics simulations have been used to study the energetics of occupancy of cavity 3 of the right-handed coiled-coil stalk of tetrabrachion by both water molecules and cyclooctasulfur S₈ crowns, as well as to determine possible pathways and free energy barriers for the diffusion of both water and cyclooctasulfur through the peptide walls of RHCC tetrabrachion between cavity 3 and bulk solvent. Calculations of the transfer free energy from solvent to cavity show that clusters of six, seven and eight water molecules are marginally stable in cavity 3, but that occupancy of the cavity by a cyclooctasulfur ring is favoured significantly over water clusters of all sizes. Thermal activation simulations at T = 400K revealed that water molecules diffusing through the wall pass through a sequence of metastable configurations where they are temporarily immobilized by forming networks of hydrogen bonds with specific wall residues. Calculations of the free energy of these metastable configurations using multi-configurational thermodynamic integration yielded a free energy profile with a principal free energy maximum ∆G~50 kJ/mol and a slight activation asymmetry in favour of the direction from cavity to solvent. Potential exit pathways for cyclooctasulfur were investigated with the methods of steered molecular dynamics and umbrella sampling. The cyclooctasulfur was steered through a gap in the tetrabrachion wall along a linear path from cavity 3 into the solvent and the resulting trajectory was subdivided into 22 sampling windows. The free energy profile created for the trajectory by umbrella sampling showed a sharp principal maximum as a function of the reaction coordinate with asymmetric free energy barriers ∆G_exit~220 kJ/mol and ∆G_entrance~100 kJ/mol for cavity exit and entrance, respectively.

Graphical Abstract

1. Introduction

Sulfur is an essential element for life. Staphylothermus marinus [1,2] is a hyperthermophilic, strict anaerobic reducing archaeon, isolated from the periphery of black smoker vents, that reduces S⁰ to H₂S. It utilizes peptides as a carbon source and grows at temperatures up to T = 98^°C [3]. Most known hyperthermophilic archaea depend on elemental sulfur (S0) as the terminal electron acceptor (TEA) in a number of unique and not yet fully understood metabolic pathways that typically use either H₂ or organic compounds as electron donors [[4], [5], [6]].

Structurally, Staphylothermus marinus has a proteinaceous S-layer composed of tetrabrachion units which consist of a 70-nm stalk that branches into four arms, each 24 nm in length [1,7,8]. The branches coat the surface of the archeon in a monolayer. The stalk contains a tetrameric parallel right-handed coiled-coil (RHCC) that is associated with two subtilisin-like proteases [3]. A narrow, continuous channel connects four unusually large hydrophobic cavities located along its axis [7]. The second and third cavities along the RHCC tetrabrachion axis are the largest of the four, with volumes V = 380 ų for cavity 2 and V = 354 ų for cavity 3. Fig. 1 shows the overall structure of RHCC tetrabrachion along with the locations of the 4 cavities. X-ray crystallography measurements performed on the apo-RHCC tetrabrachion structure at T~100K and P = 1 atm after crystallization at T = 298K in an aqueous environment (PDB 1FE6) have shown [7] that all cavities were filled with water molecules with occupancies of 2, 9, 5, and 1 in cavities 1 through 4, respectively. The nine water molecules in cavity 2 are arranged in a non-planar clathrate-like ring conformation. Molecular dynamics calculations [9] of the free energy of transfer of water molecules from the bulk solvent into the interior of cavity 2 in the PDB 1FE6 structure of archaeal tetrabrachion using the AMBER force field parm94 and the TIP3P water model showed that clusters of N water molecules with 6 ≤ N ≤ 9 are marginally favourable in cavity 2 at P = 1 atm and temperatures up to T = 365K, with a minimum free energy for an occupancy N = 8 at T = 298K, consistent with the measured occupancy N = 9.

Fig. 1.

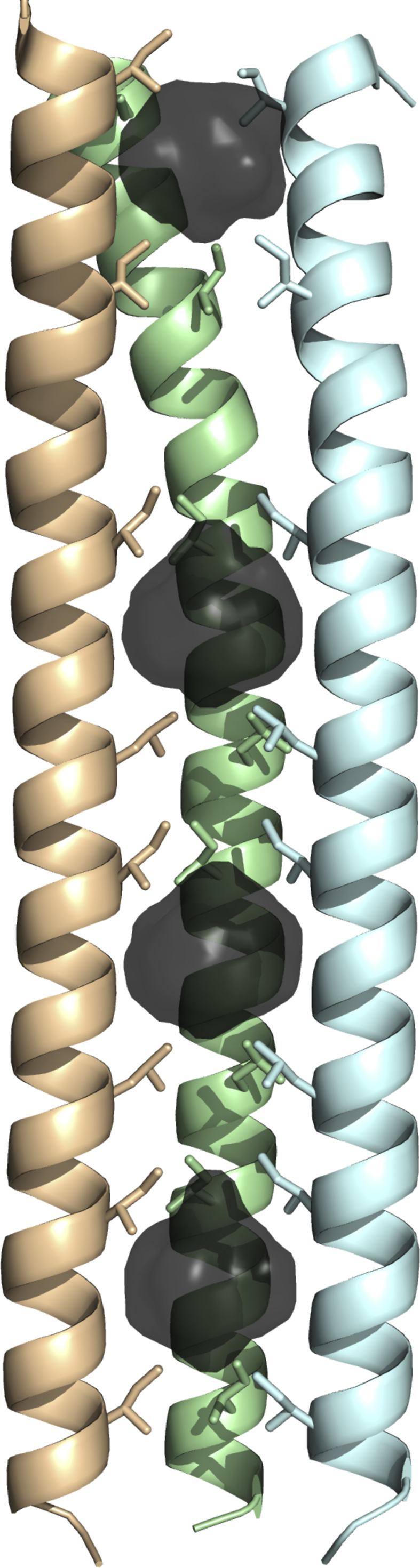
The RHCC homotetramer (pdb 1YBK) with the helices represented as cartoons. The frontmost helix is omitted for clarity. Interior hydrophobic surfaces bound by the internally facing Ile, Leu, and Val residues are depicted. The cavities are numbered 1 to 4 from top to bottom.

Hyperthermophilic archaea like Staphylothermus marinus thrive in extreme environments, such as submarine hydrothermal systems, hot springs, or terrestrial solfataric fields, where sulfur is produced in high concentrations over different temperature ranges [10]. However, the extreme hydrophobicity and poor solubility of sulfur in water (5 μg L⁻¹ at T = 25⁰C) make it a poor substrate for bacterial sulfur respiration. Recent X-ray crystallography, dynamic light scattering and molecular dynamic simulations [11] performed on crystallized RHCC tetrabrachion after immersing it in a sulfur-rich environment for an extended period of time at an elevated temperature T = 353K (PDB structure 5JR5) have indicated that it is highly likely that the larger cavities 2 and 3 of RHCC tetrabrachion in its native environment do not contain water clusters but instead contain crowns of cyclooctasulfur S₈, the most common allotrope of sulfur. This expectation is further reinforced by the remarkable similarity between the geometries of the clathrate water ring and the α − S₈ sulfur crown. Free energy calculations based on these MD simulations showed that the S₈ sulfur crown is preferred in cavity 2 over all favourable water conformations [9]. The dynamic light scattering measurements showed that RHCC tetrabrachion exhibits a marginal increase in hydrodynamic radius at the elevated temperatures that were used to incorporate S₈ in the channel. However, due to the large size of the sulfur crown, and its spectroscopic inactivity, it is unknown precisely how S₈ diffuses into the protein channel. This raises the question of what pathways the S₈ crown might follow as it moves between the solvent and the RHCC tetrabrachion cavities and of the free energy barriers that control this diffusion process.

In the current investigation, MD simulations are used to perform a comprehensive study of the energetics of occupancy of cavity 3 of RHCC tetrabrachion by both water molecules and cyclooctasulfur S₈ crowns, as well as to determine and compare possible pathways and free energy barriers for the diffusion of both water and cyclooctasulfur through the peptide walls of RHCC tetrabrachion between cavity 3 and bulk solvent.

2. Systems and Methods

2.1. Systems

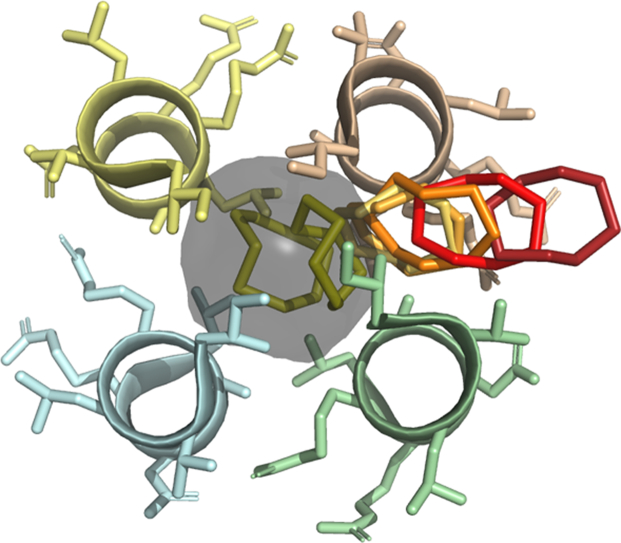
All molecular dynamics simulations of RHCC − water complexes were based on a higher pressure structure PDB 1YBK which was crystallized at P = 15 atm and T = 273K, and which contained clusters of 13 water molecules in cavity 2 and 8 water molecules in cavity 3. All simulations of the RHCC − cyclo − octasulfur complex were based on the structure PDB 5JR5 [11] which was crystallized at T = 277K and which contained a single crown-shaped S₈ ring in cavity 2 with a geometry similar to crystalline α − S₈ and two competing equal-occupancy conformations in cavity 3, one similar to the twisted-ring S₈ arrangement and one in the exo − endo − S₈ arrangement. For both complexes, this investigation was focused exclusively on cavity 3 and its contents and the twisted-ring conformation of S₈ was selected for analysis.

2.2. Molecular Dynamics Setup

Molecular dynamics simulations were performed with the GROMACS molecular dynamics simulation package [12] using the AMBER force field parm94, and the TIP3P water model. Amber topologies for S₈ were generated with ACPYPE [13]. In order to obtain good agreement with the measured solvation free energy of S₈, it was necessary to modify the non-bonded LJ parameters of S₈ obtained from ACPYPE. These modifications are discussed in more detail under point 3 below. Each RHCC complex was solvated in an identical rectangular box with dimensions 5.2 nm × 5.2 nm × 9.8 nm containing 7900 SPC solvent water molecules and a set of 16 charge neutralizing Na + ions. The closest distance between any point on the RHCC complex and the surface of the simulation box was 1.2 nm. Long-range electrostatic interactions were treated with the particle mesh Ewald method. The cut-off radius for all non-bonded interactions was taken to be 1.0 nm and the neighbour list for all non-bonded interactions was updated every 10 time steps. The measured structure was initially energy minimized to 1000 kJ/mol using the method of steepest descent and then re-minimized for decreasing values of the energy until convergence was achieved typically around 40 − 50 kJ/mol.

The energy minimized system was first heated gradually from 0 K to 50 K and stabilized for a period of 20 ps while position-restraining the non-hydrogen atoms, using velocities chosen randomly from a Maxwell-Boltzmann distribution. Heating and stabilization was repeated at 150 K and 300 K over the same period of 20 ps, with initial velocities at each new temperature chosen from the final frame of the equilibrated trajectory at the previous temperature. During the production run, the entire system (RHCC tetrabrachion plus cavity contents plus solvent bath) was maintained at a pressure of 15 atm to conform to the high-pressure measurement conditions and a temperature of 300 K using Berendsen barostats and thermostats, respectively, with time constants of 0.1 ps. Production runs were performed for 1 ns in time steps of 1 fs using temperature and pressure scaling.

2.3. Transfer Free Energies

The incremental free energy required to create a cluster of n water molecules (W_n) in cavity 3 of RHCC tetrabrachion from a pre-existing cavity cluster of n − 1 water molecules (W_n−1) by transferring a single water molecule from the solvent into the cavity was calculated by the method of double-decoupling for cavity occupancies 1 ≤ n ≤ 8. The free energy ΔG_trans^(n−1)→n for creating cluster W_n from cluster W_n−1 is given by

$$\mathrm{\Delta }{G}_{\mathit{trans}}^{\left(n-1\right)\to n}=\mathrm{\Delta }{G}_{\mathit{sol}}^{1\to 0}-\left(\mathrm{\Delta }{G}_{\mathit{cav}}^{n\to \left(n-1\right)}+\mathrm{\Delta }{G}_r^0\right)$$ (1)

ΔG_sol^1→0 is the free energy to remove a single, unrestrained, fully-interacting water molecule from solvent to the gas phase. ΔG_cav^n→(n−1) is the free energy to remove a single water molecule from a cavity containing a pre-existing, fully-interacting cluster of n water molecules to the gas phase in the presence of a flat bottom harmonic well (FBHW) restraint potential [11] U_FBHW(r < r₀) = 0; U_FBHW(r > r₀) = k(r − r₀)² that restricts the water molecules to the volume of the cavity, where k = 1000 kJ mol⁻¹nm⁻² and r₀ = 0.55 nm. ΔG_r⁰ is the free energy cost of removing the constraint from a single water molecule, which includes a correction for the standard concentration. All pre-existing clusters used in the current simulations were created from the measured W₈ clathrate ring by removing the appropriate number of water molecules from the ring. The cumulative free energy ΔG_n for building an n−water cluster W_n by transferring n water molecules one at a time from solvent into an initially empty cavity is then given by the sum of the incremental free energies in Eq. (1):

$$\mathrm{\Delta }{G}_n=\sum _{i=1}^n\mathrm{\Delta }{G}_{\mathit{trans}}^{\left(i-1\right)\to i}$$ (2)

The free energy for transferring one sulfur molecule S₈ into cavity 3 from the solvent was adapted from Eq. (1) by setting n = 1. In order to obtain a calculated solvation free energy for S₈ which matched the measured solvation free energy ΔG_sol^exp(S₈) =  + 15.5 kJ/mol [11], it was necessary to increase the repulsive van der Waals parameter C₁₂ for atomic sulfur by a factor of 1.25, leading to a modified set of non-bonded LJ parameters σ = (1.25)^1/6σ₀ and ε = (1.25)⁻¹ε₀ relative to the values (σ₀ = 0.356359 nm, ε₀ = 1.04600 kJ/mol) generated by ACPYPE. This yielded a calculated solvation free energy for S₈ of ΔG_sol^cal(S₈) =  − ΔG_sol^1→0(S₈) =  + 13.4 ± 1.4 kJ/mol.

ΔG_sol^1→0 and ΔG_cav^n→n−1 are computed using the method of multi-configurational thermodynamic integration (MCTI) [[14], [15], [16], [17]] which employs a hybrid potential energy function U = (1 − λ) U_initial(λ) + λ U_final(λ) for the non-bonded electrostatic and van der Waals interactions with a coupling parameter 0 ≤ λ ≤ 1 which allows U to be varied incrementally from an initial state U_initial(λ = 0) in which the target molecule to be decoupled is fully interacting with the rest of the system to a final state U_final(λ = 1) in which the target molecule is free and, in the case of the cavity, interacts only with the restraint potential. The current investigation employed approximately 20 values of the non-bonded coupling parameters λ_e and λ_vdW. The restraint free energy ΔG_r⁰ was calculated analytically [11] using ΔG_r⁰ =  + RTln(V_FBHW/V₀) where V_FBHW = ∫₀^∞ exp (−U_FBHW(r)/RT)d³r = (4/3)πr₀³ + 4πr₀²(πRT/k)^1/2 + 2πr₀(πRT/k) + (πRT/k)^3/2 is the effective FBHW simulation volume and V₀ is the standard state volume (V₀ = 0.030 nm³ for water and V₀ = 1.660 nm³ for sulfur).

The energy minimization and thermal equilibration procedures were repeated for each value of λ before generating production runs for 1 ns. Structures were saved for analysis every 0.5 ps during the production runs and the resulting set of 4000 structures was used to determine 〈dG/dλ〉 for each value of λ. The mean value 〈dG/dλ〉 was calculated using g_analyze of the Gromacs MD simulation package and the errors were computed by block averaging. The statistical error in 〈dG/dλ〉 was determined from the autocorrelation of the data over the 1 ns trajectory. Soft-core interactions were incorporated into all simulations presented in this paper in order to remove the discontinuity in the non-bonded parameters as the interactions are turned off and to allow for proper convergence. A soft-core parameter α = 0.1 was found to produce the smoothest free energy curves and the best convergence. The sampling of configuration space during end-state removals (in the non-interacting limit λ → 1) is believed to be sufficiently extensive based on the low statistical error in 〈dG/dλ〉, which is typically between 0.5% and 3%. For all λ steps, the values of 〈dG/dλ〉 converged to a time-independent constant within the first 2 ps of each 1 ns trajectory and the derivative dG/dλ varied smoothly with λ, both of which are indicative of convergence.

Test simulations were run to determine the sensitivity of the calculated mean values 〈dG/dλ〉 and free energies ΔG_cav^n→(n−1) to the precise choice of the n water molecules used to construct the water clusters W_n from the original measured clathrate ring, as well as to the specific choice of the water molecule to be removed to the gas phase. All such comparisons showed agreement to within the calculated block averaging errors.

2.4. Exit Pathways for Water

The allowed exit pathways for water molecules out of cavity 3 into the solvent were determined by a thermal activation MD simulation. Since thermal activation at ambient temperature T = 300K is slow, the process was artificially accelerated by heating the measured RHCC − W₈ complex and solvent to T = 400K and the trajectories of selected water molecules were tracked as a function of time during a 2ns production run at constant pressure P = 15 atm. The structural distortions of RHCC − tetrabrachion were determined to be minimal in the neighbourhood of the cavity by monitoring the rmsd of the structure throughout the simulation. The molecules typically followed a zig-zag trajectory consisting of approximately linear segments of rapid motion which terminate in six transient, metastable configurations where the molecule executes small amplitude vibrations and rotations. Each metastable configuration corresponded to multiple frames of the simulation trajectory. Six frames were chosen from the original simulation, each representative of one of the six metastable configurations, and these were taken as the starting structures for MCTI calculations of the free energy required to place a single fully-interacting water molecule at each metastable location at ambient temperature T = 300K starting from the non-interacting gas phase state in the presence of a harmonic restraint potential U_HW(r) = (k/2)(r − r₀)² with k = 1000 kJ mol⁻¹nm⁻² to prevent the CM of the water molecule from diffusing away. These calculated free energies, when corrected for restraint effects and the solvation free energy, yielded a free energy profile for the exit pathway as a function of the total distance traveled.

2.5. Exit pathways for Cyclooctasulfur

The expulsion of a molecule of cyclooctasulfur from cavity 3 of the RHCC − S₈ complex by thermal activation on time scales t ≤ 10ns requires temperatures in excess of T = 800K, well above the nominal unfolding temperature T~400K. At these temperatures, RHCC − tetrabrachion loses much of its structural integrity, except in the vicinity of the two largest cavities, and the S₈ molecule escapes by moving down the channel and then out through large, thermally-induced gaps between neighbouring coiled strands.

Consequently, it was necessary to use the method of steered molecular dynamics (SMD) [[18], [19], [20], [21], [22]] to identify potential exit pathways. The van der Waals representation of the RHCC − S₈ complex was observed in Pymol in order to identify channels in the RHCC wall through which the S₈ crown was visible from the solvent, and a pulling direction through the channel was defined for the centre of mass (CM) of S₈ starting from its initial location in cavity 3 and terminating in the solvent. The largest channel identified by this process was bounded by five residues, isoleucine 30, threonine 31, alanine 34 from coil A and leucine 29 and arginine 33 from neighbouring coil D. A moving harmonic constraint, anchored on an arginine 33 residue on coil B, was applied to the CM of the S₈ molecule and the molecule was pulled through the wall at a speed of 0.01 nm/ps. A relatively small moving force constant k = 200 kJ mol⁻¹nm⁻² was deliberately chosen so as to allow the S₈ molecule freedom to respond to the local environment and to deviate from the nominal pulling direction. The CM of the anchor residue (and the entire coil B to which it belonged) was held immobile with a stationary harmonic constraint with a large force constant =10,000 kJ mol⁻¹nm⁻².

An MD simulation of the pulling process was used to identify 22, approximately equally spaced, reference locations x_{CM, i}^ref of the CM along the exit trajectory of the S₈ molecule and the free energy along the exit path as a function of the position x_CM of the CM was constructed by the method of Umbrella Sampling (US) [[23], [24], [25]]. At each of the chosen locations, an initial equilibration was performed for t = 50 ps, during which the motion of the S₈ molecule was constrained to the vicinity of the reference point by a harmonic bias potential ω_i(x_CM) = (k/2)(x_CM − x_{CM, i}^ref)² applied to the CM of the S₈ molecule. This was followed by an MD production run for t = 1 ns which yielded a biased probability distribution P_i^b(d) for finding the S₈ molecule in sampling window i at a distance d = x_CM − x_CM^Arg from the CM of the anchor residue, from which the free energy G_i(d) in each window was computed. Two harmonic force constants k = 1000 kJ mol⁻¹nm⁻² and k = 5000 kJ mol⁻¹nm⁻² were employed in the current investigation.

The umbrella sampling technique produced distributions P_i^b(d) which overlapped with those in neighbouring windows and the individual results were combined using the weighted histogram analysis method (WHAM) [26,27] to generate a global free energy G(d). Errors were estimated using the bootstrapping technique [28,29].

3. Results

• 1.Transfer free energies

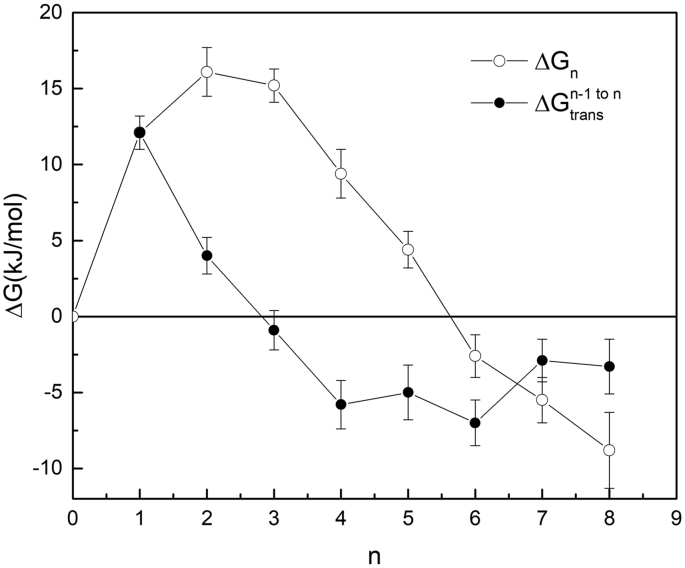
Table 1 summarizes the calculated values of all three contributions to the incremental transfer free energy ΔG_trans^(n−1)→n in Eq. (1) required to create a cluster of n water molecules in cavity 3 of RHCC tetrabrachion by transferring a single water molecule from the solvent into a cavity containing a pre-existing cluster of n − 1 water molecules for all values of n between 1 ≤ n ≤ 8, as well as the cumulative free energy ΔG_n in Eq. (2) for building an n−water cluster by transferring n water molecules one at a time into an initially empty cavity. The FBHW radius r₀ = 0.55 nm corresponded to a simulation volume V_FBHW = 0.90 nm³ and this yielded a restraint free energy ΔG_r⁰ =  + RTln(V_FBHW/V₀) =  + 8.5 kJ/mol for the removal of one water molecule from the cavity to the gas phase. The calculated self-solvation free energy for water ΔG_solvation =  − ΔG_sol^1→0 =  − 26.7 ± 2.0 kJ/mol agrees well with the experimental value of ΔG_solvation^exp =  − 26.8 kJ/mol. Fig. 2 shows plots of the incremental and cumulative free energies as a function of cluster size n. An inspection of Fig. 2 and Table 1 shows that the incremental transfer free energy ΔG_trans^(n−1)→n becomes negative for all pre-existing cluster sizes n − 1 ≥ 2, indicating that the local environment in cavity 3 is more favourable for the addition of a single water molecule than the solvent bath. The free energy of formation ΔG_n of an n−water cluster initially increases from n = 1 to n = 2 and then decreases monotonically, becoming negative for n ≥ 6, with cluster W₈ being the most stable, consistent with the experimentally measured occupancy.

Table 1.

Standard hydration free energies in kJ/mol for cavity 3 of RHCC tetrabrachion at P = 15 atm.

n	ΔGcavn→(n−1)	ΔGr0	ΔGsol1→0	ΔGtrans(n−1)→n	ΔGn
1	+6.1 ± 0.6	+8.5	+26.7 ± 0.4	+12.1 ± 1.1	+12.1 ± 1.1
2	+14.2 ± 0.8	+8.5	+26.7 ± 0.4	+4.0 ± 1.2	+16.1 ± 1.6
3	+19.1 ± 1.0	+8.5	+26.7 ± 0.4	−0.9 ± 1.3	+15.2 ± 1.1
4	+24.0 ± 1.3	+8.5	+26.7 ± 0.4	−5.8 ± 1.6	+9.4 ± 1.6
5	+23.2 ± 1.6	+8.5	+26.7 ± 0.4	−5.0 ± 1.8	+4.4 ± 1.2
6	+25.2 ± 1.4	+8.5	+26.7 ± 0.4	−7.0 ± 1.5	−2.6 ± 1.4
7	+21.1 ± 1.2	+8.5	+26.7 ± 0.4	−2.9 ± 1.4	−5.5 ± 1.3
8	+21.5 ± 1.6	+8.5	+26.7 ± 0.4	−3.3 ± 1.8	−8.8 ± 2.5

Fig. 2.

The incremental free energy ΔG_trans^(n−1)→n required to create a cluster of n water molecules in cavity 3 of RHCC tetrabrachion from a pre-existing cavity cluster of n − 1 water molecules by transferring a single water molecule from the solvent into the cavity and the cumulative free energy ΔG_n for building an n−water cluster by transferring n water molecules one at a time from solvent into an initially empty cavity.

Visual examination of the MD trajectories using Pymol showed that no water molecules entered cavity 3 from the solvent throughout the entire 2ns production runs for all cluster sizes n and for all values of the coupling parameter λ. The same visual inspection reveals that, for all cluster sizes n, the water molecules in the cavity are all highly mobile and each molecule explores the entire cavity during the course of the simulation independent of the initial cluster conformation. Quantitative support for this observation is provided by calculations of the time-averaged position of the cavity waters performed over the complete 2ns trajectories, which show that the average positions of the individual cavity water molecules are tightly clustered around the centre of the cavity. Individual water molecules are observed to form temporary hydrogen bonds preferentially with the carbonyl oxygens of the four isoleucine residues (Ile 30) in the walls of cavity 3 [9], with an equal contact probability for each of the four chains. The cavity waters are also observed to form transient hydrogen bonds with other water molecules in the cavity and these intra-cluster bonds have the effect of systematically reducing the frequency of water-isoleucine contacts as the cluster size increases.

Table 2 shows the calculated contributions to the free energy for transferring one cyclo − octasulfur S₈ molecule from the solvent bath into cavity 3 for the same applied pressure P = 15 atm. Not surprisingly, the non-polar cavity 3 of RHCC − tetrabrachion provides a highly favourable environment for the uncharged S₈ ring relative to the water bath. A comparison of the calculated transfer free energies for water molecules and cyclooctasulfur rings in Tables 1 and 2, respectively, shows that the cyclooctasulfur ring is much more favoured energetically (relative to the solvent) in cavity 3 than are all water clusters 1 ≤ n ≤ 8 (compare ΔG_trans^0→n(W) ≥  − 8.8 kJ/mol with ΔG_trans^0→1(S₈) =  − 74.5 kJ/mol).

• 2.Exit pathways for water

Table 2.

Standard free energy in kJ/mol to transfer S₈ from solvent to cavity 3 of RHCC tetrabrachion at P = 15 atm.

ΔGcav→gas	ΔGr0	ΔGsol→gas	ΔGtrans = ΔGsol→gas − ΔGcav→gas − ∆GSS
+62.6 ± 3.0	−1.5	−13.4 ± 1.4	−74.5 ± 4.4

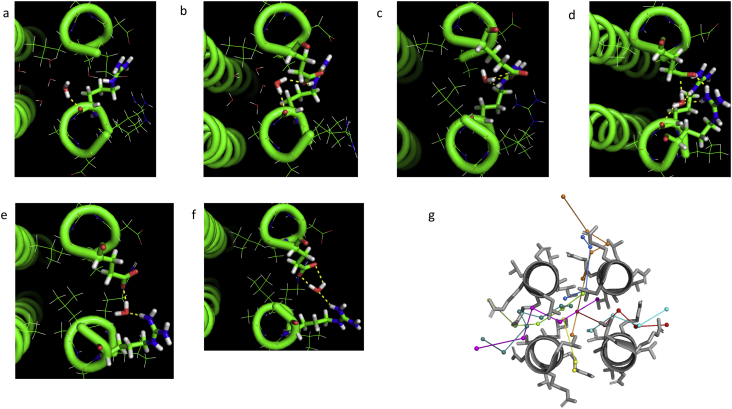
Fig. 3 shows a sequence of Pymol images of a typical thermally activated water molecule in each of its six metastable configurations where the molecule pauses temporarily as it passes along its exit trajectory from the interior of cavity 3 through the walls of RHCC tetrabrachion and into the solvent bath. The duration of the trajectory shown in Fig. 3 was 1550 ps. Over the interval 0 ≤ t < 90 ps, the water molecule remained relatively mobile and confined to the volume of the cavity (position 1 in Fig. 3(a)). Between 90 ps < t < 950 ps, the water molecule rapidly penetrated the interior surface of the protein wall and became trapped in a volume centred roughly at the midpoint of the wall, where it was observed to fluctuate between several different positions while simultaneously adjusting its orientation (positions 2, 3 and 4 in Fig. 3(b), (c) and (d)). Between 950 ps < t < 1550 ps, the water molecule shifted to another metastable region located closer to the outer surface of the wall (positions 5 and 6 in Fig. 3(e) and (f)), before moving rapidly into the solvent for t > 1550 ps. Fig. 3(g) summarizes the exit pathways of all 8 water molecules in cavity 3 in a cross sectional view of RHCC tetrabrachion through cavity 3.

Fig. 3.

A sequence of Pymol images of a typical thermally activated water molecule in six representative metastable configurations where the molecule pauses temporarily as it passes along its exit trajectory from the interior of cavity 3 through the walls of RHCC tetrabrachion and into the solvent bath. The dotted lines are hydrogen bonds to coil residues. The image times and bonding residues are (a) 86 ps, arginine 33 A,

(b) 118.5 ps, arginine 33 A, glutamate 38 B, (c) 853.5 ps, arginine 33 A, glutamate 38 B,

(d) 877.5 ps, arginine 33 A, arginine 36 A, glutamate 38 B,

(e) 1403 ps, arginine 36 A, glutamate 38 B, (f) 1420.5 ps, arginine 36 A, glutamate 38 B.

(g) A cross section of RHCC immediately above cavity 3 showing the exit pathways of all 8 waters initially in the cavity. Each water is individually coloured, with straight lines approximating the trajectory between metastable configurations.

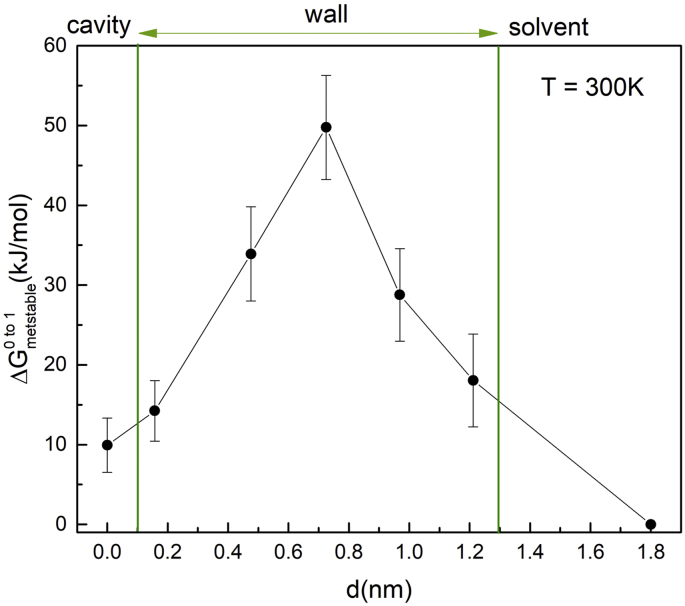
Fig. 4 shows a plot of the calculated free energy ∆G_metastable^0→1(d) required to create a fully interacting water molecule in each of these metastable configurations as a function of the total zigzag path length d traveled by the water molecule. Table 3 summarizes the various contributions to the calculated free energy ∆G_metastable^0→1(d) =  − ∆G_MCTI^1→0 − ΔG_r⁰ + ΔG_sol^1→0, where ΔG_sol^1→0 is the free energy to remove a single, unrestrained, fully-interacting water molecule from solvent to the gas phase, ∆G_MCTI^1→0 is the free energy to remove a single water molecule from its instantaneous metastable location by gradually turning off the non-bonded interactions using MCTI, and ΔG_r⁰ =  + RTln(V_HW/V₀) =  − 6.8 kJ mol⁻¹ corrects for the restraint, where V_HW = (2πRT/k)^3/2 = 0.00196 nm³ for an harmonic well with k = 1000 kJ mol⁻¹nm⁻² and V₀ = 0.030 nm³. The remaining seven water molecules in cavity 3 were collectively restrained to the cavity by a FBHW with spring constant where k = 1000 kJ mol⁻¹nm⁻² and radius r₀ = 0.55 nm centred on cavity 3.

Fig. 4.

A plot of the calculated free energy ∆G_metastable^0→1(d) required to place a fully interacting water molecule at each of the metastable locations in Fig. 2 by transferring the molecule from the solvent bath, as a function of the total zigzag path length d measured from the starting location in cavity 3. The vertical lines mark the approximate locations of the interior and exterior surfaces of the protein wall.

Table 3.

calculated free energy in kJ/mol to place a single fully interacting water molecule (W54) at various points along the thermally induced exit trajectory from cavity 3 at P = 15 atm.

point	d(nm)	∆GMCTI1→0	ΔGr0	ΔGsol1→0	∆Gmetastable0→1
1	0	23.6 ± 3.4	−6.8	+26.7 ± 0.4	9.9±3.8
2	1.57	19.3 ± 3.8	−6.8	+26.7 ± 0.4	14.2 ± 4.2
3	4.76	−0.4 ± 4.9	−6.8	+26.7 ± 0.4	33.9 ± 5.3
4	7.25	−16.3 ± 5.5	−6.8	+26.7 ± 0.4	49.8 ± 5.9
5	9.69	4.7 ± 3.8	−6.8	+26.7 ± 0.4	28.8 ± 4.2
6	12.12	15.5 ± 5.8	−6.8	+26.7 ± 0.4	18.1 ± 6.2

A frame-by-frame examination of the complete exit trajectories of the water molecules showed that the metastable configurations identified earlier appear to coincide with regions in the wall where the water molecules become trapped in a local network of hydrogen bonds with specific wall residues. For the particular water molecule shown in Fig. 3 for which the exit pathway is bounded by coils A and B of the RHCC structure, the configuration in (a), where the water adheres to the inner surface of the cavity, is associated with a bond to a carbonyl oxygen of a polar-charged arginine 33 residue belonging to coil A. Configurations (b), (c) and (d), where the water occupies the region in the centre of the wall, are associated with two bonds for each of configurations (b) and (c), one to the carbonyl oxygen of the same arginine 33 A residue and the other to the carboxylic oxygen of a polar-charged glutamate 38 residue in coil B, and with a triplet of bonds to arginine 33 A, the amine group of a polar-charged arginine 36A and glutamate 38 B for configuration (c). The configurations (e) and (f) which are located close to outer periphery of the wall are each stabilized by two bonds to arginine 36A and glutamate 38 B. While the free energies of these metastable configurations are all highly unfavourable relative to the solvent, particularly in the region near the centre of the wall, as shown in Fig. 4, these local networks of bonds capture the water molecules in local free energy minima surrounded by free energy barriers which are temporarily able to impede the progress of the water molecule as it diffuses out of the cavity.

While the free energy profiles for all the water molecules were very similar in shape and magnitude, some waters were observed to spend the majority of their trajectory time within the cavity (0 ≤ t < 1460 ps) and to pass through the wall essentially unimpeded, with very short cavity-to-solvent transfer times ~40 ps. These residues were observed to follow trajectories which brought them into contact almost exclusively with nonpolar residues including leucine 29, isoleucine 30, threonine 31 and alanine 34, and encountered the polar-charged arginine 33 residue only when they are on the verge of emerging from the wall and entering the solvent (see Fig. 3(g)). Thus the progress of these water molecules did not suffer the same impedance to diffusion due to local free energy minima created by hydrogen bond networks.

• 3.Exit pathways for cyclooctasulfur

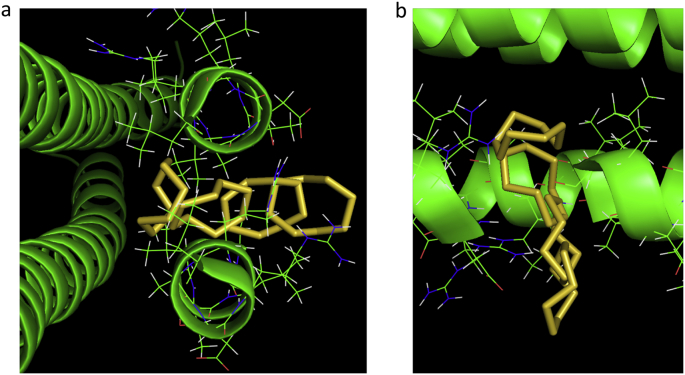
Fig. 5 shows a sequence of Pymol images of the cyclooctasulfur ring S₈ at a selected subset of sampling windows along its exit trajectory as the molecule is steered by a weak, moving harmonic constraint (k = 200 kJ mol⁻¹nm⁻²) directed along a line from a point in the interior of cavity 3 through a gap in the walls of RHCC tetrabrachion between coils A and D and into the solvent bath. The duration of the trajectory shown in Fig. 5 was 1125 ps. Over the interval 0 ≤ t < 595 ps, the S₈ ring remained relatively mobile and confined to the volume of the cavity. Between 595 ps < t < 985 ps, the ring adhered to a region on the inside surface of the cavity, where the surface intersected with the direction of steering, before making a relatively sudden transition to a region centred roughly at the midpoint of the wall, where the ring remained trapped over the interval 985 ps < t < 1123 ps. The ring then moved rapidly out of the wall and into the solvent within the last 2 ps.

Fig. 5.

A sequence of Pymol images of the cyclooctasulfur ring S₈ at a selected subset of sampling windows along its exit trajectory from the interior of cavity 3 through the walls of RHCC tetrabrachion and into the solvent bath. For the umbrella sampling analysis, the molecule was restrained at each selected location by an harmonic umbrella bias potential. (a) channel view (b) top view.

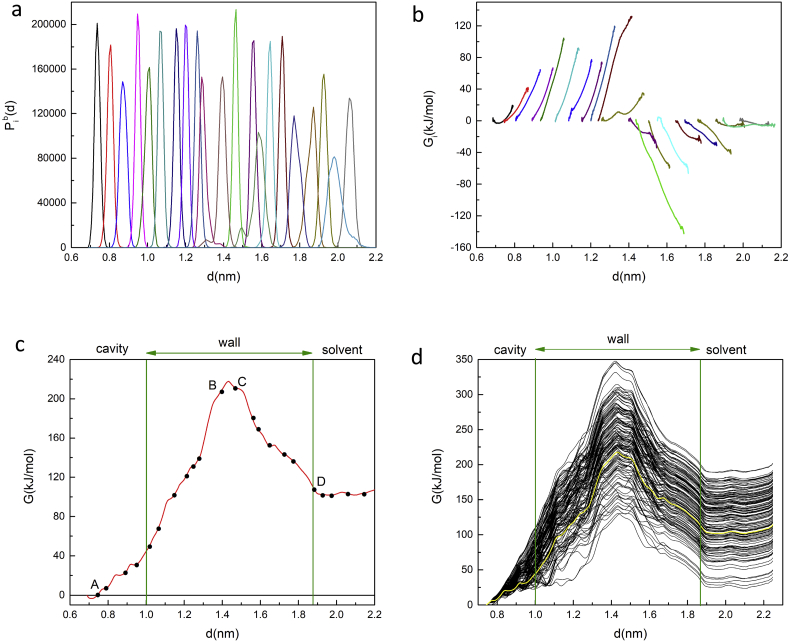
Fig. 6(a) shows the individual biased distributions (histograms) of CM locations P_i^b(d) generated by umbrella sampling for all of the 22 selected sampling windows along the steered MD trajectory of the cyclooctasulfur molecule S₈ as a function of the distance d = x_CM − x_CM^Arg between the CM of S₈ in the i^thwindow and the CM of the harmonically restrained anchor residue arginine 33, and Fig. 6(b) shows the individual free energy profiles G_i(d) for all sampling windows. Two harmonic force constants are represented in these figs. A set of histograms and free energy profiles was first generated with a moderate force constant k = 1000 kJ mol⁻¹nm⁻². Those windows for which the force constant was too weak to prevent excessive wandering of the S₈ molecule away from the set point produced gaps in the histogram spectrum that were filled by repeating the analysis [25] with a larger force constant k = 5000 kJ mol⁻¹nm⁻², which was typically sufficient to provide a stable, single-peaked distribution.

Fig. 6.

(a) The complete set of biased probability distributions of CM locations P_i^b(d) generated by umbrella sampling in all of the selected sampling windows along the exit trajectory of the cyclooctasulfur molecule S₈ as a function of the reaction coordinate defined as the distance d of the CM of S₈ relative to the location of the CM of the harmonically restrained anchor residue arginine 33 B. (b) The complete set of free energy profiles G_i(d) for all sampling windows. (c) A plot of the global free energy G(d) generated from the set of biased distributions in (a) by a simple application of WHAM. The dots show the equilibrated CM locations for all 22 sampling windows. The vertical lines mark the approximate locations of the interior and exterior surfaces of the protein wall. (d) WHAM free energy profiles generated with bootstrapping. The curve from Figure (c) is included in solid yellow. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. 6(c) shows a plot of the global free energy G(d) of the RHCC − S₈ complex generated from the individual distributions by a simple application of WHAM, as a function of the distance d, and Fig. 6(d) shows the WHAM free energy profiles generated with bootstrapping. Since the S₈ crown is known to be energetically less stable in the solvent than it is in the cavity based on the double-decoupling MCTI analysis (see Table 2), the auxiliary condition G(d = 2.25nm) > 0 was imposed on the bootstrapping analysis [29]. The solid circles in Fig. 6(c) mark the locations of the centres of the sampling windows and the vertical lines mark the approximate locations of the inner and outer surfaces of the protein wall in the vicinity of cavity 3. Starting from sampling point A located in the centre of cavity 3, G(d) initially increases with d and passes through a relatively sharp peak between sampling points B and C, both located roughly at the midpoint of the wall of RHCC − tetrabrachion, before decreasing to a plateau region at sampling point D just outside the outer surface of the protein, beyond which the cyclooctasulfur molecule lies entirely in the solvent and the free energy is essentially flat. According to transition state theory, a free-energy barrier ∆G = 100 kJ/mol at a temperature T = 298 K would correspond to a rate constant k_r = (kT/h) exp (−∆G/RT) = 1.95 × 10⁻⁵M⁻¹s⁻¹. The bootstrapping analysis in Fig. 6(d) shows a dark band which captures the single profile in Fig. 6(c) obtained without bootstrapping. The physical implications of the free energy profiles in Fig. 6 are clear; thermal shuttling of the cyclooctasulfur ring in and out of cavity 3 requires activation over an asymmetric system of energy barriers between two global free energy minima, one located in the centre of the cavity and the other located in the solvent, with capture from the solvent being energetically favoured over release from the cavity. In order to further confirm the details of the structure of the free energy profile in Fig. 6, a series of MD simulations were performed in which the cyclooctasulfur ring was placed at all the selected sampling locations along the trajectory without a harmonic position restraint and then released. For all sampling points below the peak in Fig. 6, the sulfur ring moved rapidly and irreversibly back into the cavity, while for all points above the peak, the sulfur ring moved rapidly and irreversibly into the solvent.

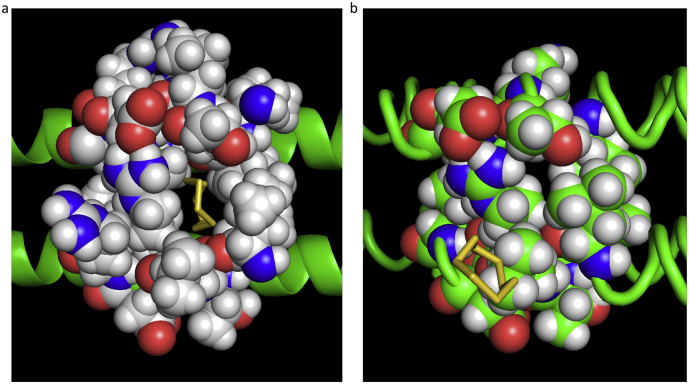
A frame-by-frame inspection of the steered MD trajectory of the cyclooctasulfur ring showed that, during the time interval when the S₈ ring adhered to the inside surface of the cavity, its orientation was such that the plane of the ring was predominantly transverse to the pulling direction and to the axis of the exit channel. By contrast, the sudden transition from the inside surface of the cavity to the centre of the wall appeared to be coincident with a rotation of the ring plane from a transverse to a parallel orientation which provided a better match to the geometry of the exit portal. Immediately prior to the release of the ring into the solvent, a distortion was observed to occur in the configuration of the five residues surrounding the exit portal (isoleucine 30, threonine 31, alanine 34 from coil A and leucine 29 and arginine 33 from coil D), which had the effect of expanding the width of the portal by about ~50%. The distortion relaxed immediately following release. Fig. 7(a) and (b) show a comparison of the exit portal during and after release.

Fig. 7.

A comparison of the configuration of the exit portal (a) during and (b) immediately after release of the sulfur ring into the solvent.

A comparison of the two free energy profiles in Fig. 4 and Fig. 6(c) for the shuttling of water molecules and cyclooctasulfur rings, respectively, between cavity 3 of RHCC tetrabrachion and the aqueous solvent bath, shows that the free energy barrier for the diffusion of a single water molecule out of cavity 3 through the walls of RHCC tetrabrachion into the solvent ΔG_{cavity−solvent}(W)~ + 40 kJ/mol is lower than that for the diffusion of a single cyclooctasulfur ring into cavity 3 from the solvent ΔG_{solvent−cavity}(S₈)~ + 100 kJ/mol.

4. Discussion

There are several elements of the current investigation that require further comment in light of other related methodologies that have appeared in the literature and commonly expressed concerns regarding the limitations of MD-based analyses arising from insufficient sampling times. Computationally intensive methods have been developed for mapping entire networks of entry/exit channels in biomolecules based on a detailed reconstruction of the landscape of local metastable free energy traps (pockets) which characterize such complex systems using a variety of enhanced sampling techniques [[30], [31], [32]]. Many of these approaches are concerned primarily with active site binding and unbinding events of ligands that might adversely affect the biological functionality of the enzyme, where a detailed knowledge of ligand migration routes can aid in the formulation of novel design strategies. In the current investigation, where the emphasis is on ligand diffusion for the purposes of simple storage rather than chemical transformation, and where the pathways between the solvent and the cavities tend to lack the diversity and complexity of those in other systems, a more heuristic approach has been adopted which depends, where feasible, on simple thermal activation or, where not feasible, on direct steering through gaps in the protein walls. In the accelerated thermal activation simulations of the diffusion of water molecules out of cavity 3, the exit pathways are expected to be not only reflective of the conditions that both inhibit and accelerate diffusion in real systems, but also “optimal” or “highly probable” since they are the product of an unbiased exploration of configuration space, and thus potentially closely related to minimum free energy pathways (MFEPs) identified by steepest descent techniques in other systems. The application of steered MD with umbrella sampling to cyclooctasulfur is, by contrast, a considerably more biased process, limited to generating free energy profiles along specific predetermined directions, although it is not strictly linear and does allow some flexibility for the molecule to wander off the pulling direction. The advantage of the method is that it is capable of yielding free energy profiles with only a modest number of relatively short simulations; however, such steered trajectories cannot conclusively be identified as MFEPs. In both cases, however, it is noteworthy that the current analysis also proceeds through the identification of a sequence of metastable binding pockets that form a conduit to guide ligand diffusion. These pockets are observed directly in the thermal activation analysis of water and indirectly in the PMF analysis of cyclooctasulfur through the forced abolition of local barriers.

The simulation time of 1 ns which was employed in the current investigation raises the question of whether sufficient time was allowed to achieve equilibration perpendicular to the reaction coordinate, particularly among rotameric states of side chains. Several recent publications have directly addressed the difficulties associated with extending simulation runs to achieve sufficient sampling of rotameric transitions which, in principle, can involve timescales ranging from ps to several hundred ns depending on the local environment [33,34]. Given this broad spectrum of potential equilibration times and the consequent uncertainty in defining an appropriate simulation time, these investigations applied PMF methods to calculate corrections to the free energy arising from rotamer transitions by pulling the side chain between its stable rotameric orientations. This requires advance knowledge in the form of measured crystallographic structures for each of the relevant rotameric states. While the authors of the current work do not have the necessary crystallographic evidence for their system, we note that the magnitude of the corrections performed on a model protein system T4 lysozyme for a series of different ligands ranged between 8 and 16 kJ/mol, which amounts to about a 10% of the diffusion free energy barrier calculated for cyclooctasulfur in the current analysis, and which lies well within the bootstrapping error.

Future work will concentrate on the role of mutations in enhancing or inhibiting the flow of cyclooctasulfur, with a particular focus on mutations of Arg 33, as well as on a reconstruction of the corresponding free energy profiles and diffusion pathways of water and cyclooctasulfur between cavity 2 and solvent.

5. Conclusion

Elemental sulfur is the most prominent terminal electron acceptor (TEA) for energy production in living organisms. However, two questions remain open in this regard. First, how is the S₈ allotrope of elemental sulfur, with its low solubility in water, stored in a proteinaceous environment? Second, how is it made accessible as a TEA? The large-sized cavities of RHCC tetrabrachion are strictly hydrophobic in nature and its ability to store sulfur compounds in the cavities is an attractive concept, taking into consideration that S. marinus is a strict anaerobic hyperthermophilic archeon that uses S⁰ as a TEA [35]. Our findings presented here clearly suggest that cyclooctasulfur rings can diffuse through a gap in the tetrabrachion wall making elemental sulfur accessible for redox-reactions. It has been shown by Hao et al. [35] that S. marinus is an S⁰-reducing archaeon with sulfur reductase activity comparable to those in other sulfur-reducing prokaryotes. Our results suggest the possibility of a mechanism whereby reducing equivalents are generated by the oxidation of amino acids from STABLE -catalyzed (STalk Associated archaea-BacteriaL Endo-protease [36]) peptidolysis, which then reduce S⁰ and protons to H₂S and H₂, respectively.

Declaration of Interest

There is no conflict of interest to declare.