Abstract
There is growing interest in genetic arrhythmia since mutations in gene which encodes the ion channel underlie numerous arrhythmias. Hasegawa et al reported that G229D mutation in KCNQ1 underlies atrial fibrillation due to significant shortening of action potential duration (APD) in atrial cells. Here, we predicted whether KCNQ1 G229D mutation affects ventricular fibrillation generation, although it shortens APD slightly compared with the atrial cell. We analyzed the effects of G229D mutation on electrical and mechanical ventricle behaviors (not considered in previous studies). We compared action potential shapes under wild-type and mutant conditions. Electrical wave propagations through ventricles were analyzed during sinus rhythm and reentrant conditions. IKs enhancement due to G229D mutation shortened the APD in the ventricular cells (6%, 0.3%, and 8% for endo, M, and epi-cells, respectively). The shortened APD contributed to 7% shortening of QT intervals, 29% shortening of wavelengths, 20% decrease in intraventricular pressure, and increase in end-systolic volume 17%, end-diastolic volume 7%, and end-diastolic pressure 11%, which further resulted in reduction in stroke volume as well as cardiac output (28%), ejection fraction 33% stroke work 44%, and ATP consumption 28%. In short, using computational model of the ventricle, we predicted that G229D mutation decreased cardiac pumping efficacy and increased the vulnerability of ventricular fibrillation.
Keywords: arrhythmia, computational model, KCNQ1 G229D, mutation
1 |. INTRODUCTION
Over the last decade, the mutations in ion channel genes have been shown to underlie a number of arrhythmias.2 Several studies have reported that gain-of-function mutations in KCNQ1 are linked to familial atrial fibrillation (AF).3–8 KCNQ1, a gene encoding potassium channel, assembles with KCNE1, forming a slow delayed rectifier current (IKs), which is crucial for proper repolarization of cardiac action potential (AP).9 Alteration of IKs may lead to serious arrhythmias, ventricular fibrillation, and cardiac arrest.9
First report by Chen et al in 20133 identified that gain-of-function of IKs in KCNQ1 (S140G) was linked to the inherited AF in a 4-generation family in China. Later, Bellocq et al4 revealed that a noticeable shift of the half-activation potential and an acceleration of the activation kinetics lead to a gain-of-function of IKs under V307L KCNQ1 mutation. Recent studies with other mutant variants, including R231H,10 V241F,5,6 and G229D,7,8 also discovered that the gain-of-function of IKs underlies AF by shortening the AP duration (APD) and promoting reentry in the atria.
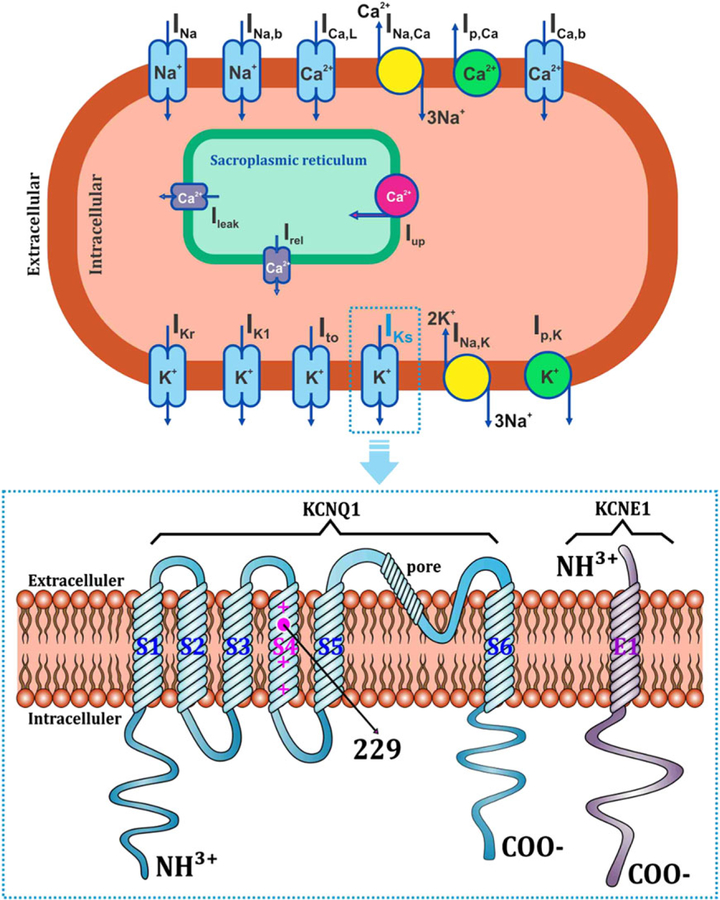
A novel study by Hasegawa et al7 revealed that mutation caused by an amino acid change from glycine to aspartic acid at position 229 in transmembrane segment 4 of KCNQ1 (see G229D topology in Figure 1) significantly shortened the APD in the atria, but only slightly in the ventricles. Here, we hypothesized that, despite small APD shortening, KCNQ1 G229D mutation also has the possibility to generate ventricular arrhythmia. Moreover, although several computational studies have carried out cardiac electrophysiological simulation of KCNQ1 mutation, none of these take into account the mechanism by which the mutation promotes the alteration in the mechanical behavior of the heart. Therefore, in this study, we predict the effects of KCNQ1 G229D mutation on cardiac pumping efficacy and reentrant dynamics in the ventricle through computational simulation.
FIGURE 1.
Topology of the KCNQ1 G229D mutation. (top) Ventricular cell model together with the ionic channels (blue rectangles), pumps (green circles), and exchangers (yellow circles). INa is the rapid inward Na+ current, INa,b is the background Na+ current, ICa,L is the L- type Ca2+ current, INa,Ca is the Na+-Ca2+ exchanger current, Ip,Ca is the Ca2+ pump current, ICa,b is the background Ca2+ current, Ileak is the current of Ca2+ release from the sarcoplasmic reticulum (SR), Iup is the SR Ca2+ uptake current, Irel is the Ca2+-induced Ca2+release, IKr is the rapid delayed rectifier K+ current, IK1 is the inward rectifier K+ current, Ito is the transient outward K+ current, IKs is the slow delayed rectifier K+ current, INa,K is the Na+-K+ pump current, and Ip,K is the K + pump current. (bottom) Location of the G229D mutation within the transmembrane topology of the KCNQ1 (blue) assembly with KCNE1 (purple), which comprise the IKs channel. S1 to S6 are the transmembrane segments of the α-subunit in KCNQ1; E1 is the transmembrane domain of the ®-subunit in KCNE1
2 |. METHODS
2.1 |. Hardware and software
To run the simulation in this study, we used custom code developed and run by using Microsoft Visual C++ 2008 Express Edition on a Windows 10 LG desktop PC, with a 64-bit Intel Core i7 processor. We also used custom C++ code run on a TERATEC, Intel cluster, consisting of 12 cores with 32 GB RAM and Intel Xeon processors, running Linux and Grid Engine (Sun Microsystems). Execution scripts were also written in C++ and compiled by using GCC 4.1.2. To reconstruct the 3D finite element ventricular mesh, we used Hypermesh software. To analyze the results, we used Paraview 4.0 to visualize the 3D ventricle and Origin Pro 8 to plot the graphs.
2.2 |. Description of computational model
We used a finite element electromechanical model of ventricles combined with a lumped parameter model of the circulatory system, as developed in previous studies,11–13 to achieve the goals of this study. The novel G229D mutation was found in a 16-year-old patient7; hence, in our study, we used the geometry of canine failing ventricle which has bigger size than a normal canine heart and smaller than normal adult heart. However, the myocyte properties were constructed based on human ventricular model proposed by O’Hara et al,1 and the mutation equations were fit to the model proposed by Hasegawa et al.7
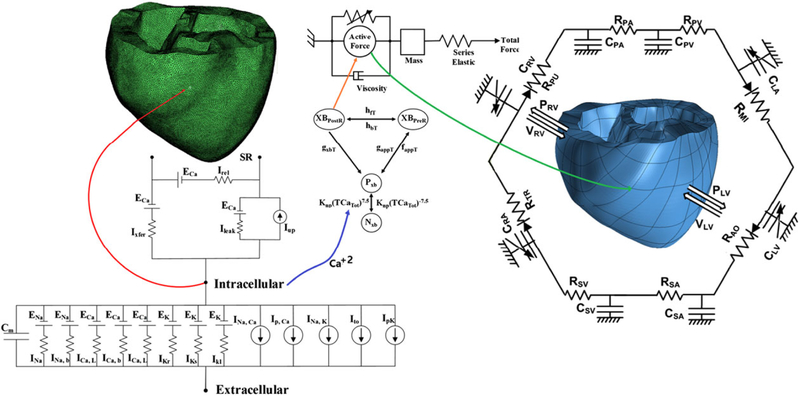
The model is shown schematically in Figure 2. The electrical components (left) consist of cell membrane Cm as a capacitive component connected in parallel with variable resistances and batteries, representing the ionic currents and pumps. INa is the rapid inward sodium current; INa,b and ICa,b are the background sodium and calcium currents, respectively; ICa,L is the L-type calcium current; IKr is the rapid delayed rectifier potassium current; IKs is the slow delayed rectifier potassium current; IK1 is the inward rectifier potassium current; INa,Ca is the sodium-calcium exchanger current; Ip,Ca is the calcium pump current; INa,K is the sodium-potassium pump current; Ito is the transient outward potassium current; Ip,K is the potassium pump current; Ileak is the current of calcium release from the sarcoplasmic reticulum; Iup is the sarcoplasmic reticulum calcium uptake current; Irel is the calcium induced-calcium release current; ENa is the potential equilibrium of sodium; ECa is the potential equilibrium of calcium; and EK is the potential equilibrium of potassium. The mechanical component (right) is represented by the myofilament model. NxB and PxB are the nonpermissive and permissive confirmation of regulatory proteins, respectively; XBPreR and XBPostR are the prerotated and postrotated states of myosin head binding, respectively. The circulatory system is represented by a lumped parameter of electrical circuits surrounding the mechanical mesh. PRV is the right ventricular pressure, VRV is the right ventricular volume, PLV is the left ventricular pressure, VLV is the left ventricular volume, RPA is the pulmonary artery resistance, CPA is the pulmonary artery compliance, RPV is the pulmonary vein resistance, CPV is the pulmonary vein compliance, RMI is the mitral valve resistance, CLA is the left atrium compliance, RAO is the aortic valve resistance, RSA is the systemic artery resistance, CSA is the systemic artery compliance, RSV is the systemic vein resistance, CSV is the systemic vein compliance, RTR is the tricuspid valve resistance, CRA is the right atrium compliance, and RPU is the pulmonary valve resistance.
FIGURE 2.
Schematic diagram of the finite-element ventricular electromechanical model coupled with the circulatory system model. The electrical (green) and mechanical (blue) meshes replicated from a diffusion tensor-magnetic resonance imaging scan of the ventricle are coupled with the intracellular calcium transient (Ca+2)
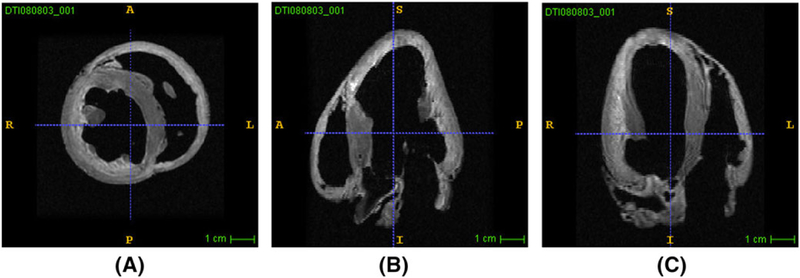
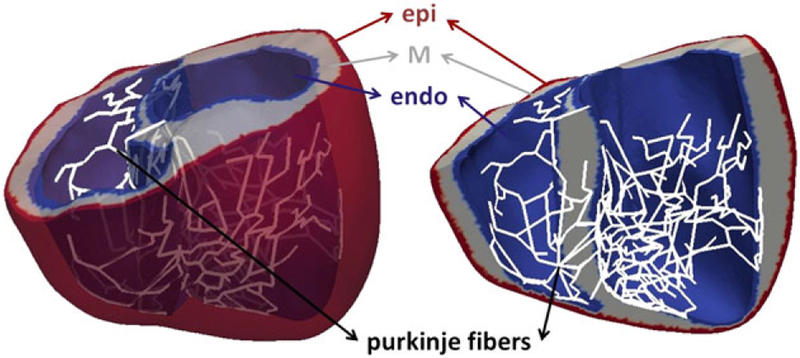
High-resolution magnetic resonance imaging and diffusion tensor magnetic resonance imaging scans of ventricles (see Figure 3) were used to construct the ventricular geometry, fibers, and laminar sheet architecture of the model. The ventricular wall consists of 3 compartments, ie, endocardium, midmyocardium, and epicardium. To account for sinus pacing activation simulation, 2D Purkinje fibers were incorporated into the endocardial surface of the ventricles by mapping the 2D line mesh onto the 3D ventricular mesh (see Figure 4).
FIGURE 3.
Magnetic resonance imaging scans of canine ventricle under conditions of heart failure. A, Short axis view of the right and left ventricles. B, Long axis view of the right ventricle. C, Long axis view of the left ventricle
FIGURE 4.
Three-dimensional model of ventricular tissue. Heterogeneity characteristics of the ventricle are shown with endo (blue), M (gray), and epi (red) cells, as well as Purkinje fibers (white)
The electromechanical model was implemented in electrophysiology and mechanical contraction of myofilaments. Two components are functionally coupled via intracellular calcium transient, which is derived from the electrophysiological model, and assigned to the contractile myofilament dynamic model. Distributions of the Ca2+ transient were obtained from the electrical properties of the model, which later serves as the input to the cellular myofilament model. The myofilament model represents the generation of active tension within each myocyte. For this, a set of ordinary differential equations and algebraic equations describes Ca2+ binding to troponin C, cooperativity between regulatory proteins, and cross-bridge cycling.14
We represent the electrical propagation through the conduction space by using the Hodgkin-Huxley equation, as follows:
| (1) |
where Vm is the transmembrane potential (mV), t is time (ms), Cm is cell membrane (pF), and Itot is total transmembrane current described by the following equation:
| (2) |
where ICa,t is the total Ca2+ current, INa,t is the total Na+ current, IK,t is the total K+ current, and ICLt is the total Cl− current. Detail equations for these currents and the model are specified in original publication of O’Hara et al.1
To explore the role of KCNQ1 G229D mutation, the IKs equation in the O’Hara et al1 cell model was modified with the formulation from Hasegawa et al7 to simulate the mutant (G229D) and wild-type (WT) condition. For both WT and G229D mutation,
| (3) |
| (4) |
| (5) |
For WT,
| (6) |
| (7) |
| (8) |
For G229D,
| (9) |
| (10) |
| (11) |
where GKs is the maximum conductance of IKs; [Ca2+]i is the intracellular Ca2+ concentration; and xs1 and xs2 are the activation and deactivation gates of IKs, respectively; Vm is the membrane potential; EKs is the reversal potential for IKs; xs1,∞ and xs2,∞ are the steady-state value of xs1 and xs2, respectively; and τx,s1 and τx,s2 are the time constant of xs1 and xs2, respectively. The values of GKs for the atrial and ventricular models were 0.0136 and 0.0034 ms/μF, respectively.
The mechanical properties illustrate the active contraction and deformation of the ventricles. Ventricular contraction resulted from the development of active tension, represented by the myofilament dynamics model of Rice et al.14 The ventricular deformation was described by the stress equilibrium equations of passive cardiac mechanics, with the myocardium assumed as an orthotropic, incompressible, and hyperelastic material, with passive properties defined by an exponential strain energy function.15
The mechanical model of Rice et al allows for calculation of adenosine triphosphate (ATP) consumption rate. We calculated the ATP consumption rates in 3D during 1 cycle of contraction of the ventricle by integrating the ATP consumption of each node. The ATP consumption rate was the product of cross-bridge detachment rate (gxbT) and single overlap fraction of the thick filaments (SOVFThick):
| (12) |
To simulate the interaction between the blood and the ventricles (ie, hemodynamic responses), the finite element electromechanical model was coupled with a circulatory model, following the coupling method of Gurev et al.16 The intraventricular pressures were added to the endocardial surfaces as additional unknown variables in the nonlinear system of equations, and the ventricular volumes were expressed as functions of the degrees of freedom of the endocardial surface nodes by using the divergence theorem. The initial conditions of the circulatory model were determined from the elastic model of ventricular contraction.17
2.3 |. Simulation protocol
The single cell simulations were carried out by using a standard S1-S2 protocol.18 Initially, the stimuli were applied at a constant basic cycle length (BCL) of 1 second. After 30 stimuli were applied at this BCL, the pacing was stopped and APD90 (ie, the APD at 90% repolarized from the peak potential) was obtained from the last AP. The BCL was then reduced, and APD90 from last AP was calculated after the stimuli were reapplied 30 times at the new BCL. The BCL was decreased at intervals of 20 ms until it reached 300 ms, and then decreased in 2 ms intervals for BCLs of <300 ms. The APD restitution curves were generated by plotting APD90 against BCL and diastolic interval (DI).
In the 3D tissue mode, the propagation waves were analyzed by applying 2 pace activation scenarios: during normal sinus rhythm and during reentry. For the simulation during sinus rhythm pacing, the electrical impulse was initiated at the Purkinje fibers, which were integrated at the endocardial surface of the ventricle (see Figure 4). In this study, we incorporated the Purkinje fibers model based on Berenfeld and Jalife19 by mapping the 2D line mesh onto the 3D ventricular mesh, which has been adjusted to generate a normal excitation sequence with CV of 200 cm s−1, consistent with the experimental results of Durrer et al,20 for both WT and G229D mutation conditions. We assumed the same CV for the WT and G229D conditions because there have been no previous studies differentiating the CV of Purkinje fibers in relation to the G229D mutation condition. Moreover, we wished to confirm our hypothesis that despite the electrical stimulus being the same (ie, originating from Purkinje fibers with the same CV) for the WT and G229D conditions, the repolarization response could be different for both cases, indicating an effect of G229D mutation. In contrast, a standard S1-S2 protocol was used for the reentry. Two S1 stimuli were applied in the apex of the ventricle with the same BCL of 600 ms; these stimuli produced waves propagating in all directions. When the refractory tail of this wave reached the middle of the medium, the S2 stimulus was applied parallel to the S1 stimulus, but for only three-quarters of the medium length. This produced a second wave front with a curly tip, generating a spiral wave (reentry).
Next, the results from the electrical simulation were coupled with the intracellular Ca2+ transient, which served as the inputs for the mechanical simulation. The mechanical simulation was carried out up to 12 seconds for the sinus pacing and reentrant conditions, to obtain the steady-state responses. For both cases, we used a BCL of 600 ms. For sinus pacing, we used only the last rhythmic cycle, which was from 11.4 to 12 seconds. For reentry, we used the whole cycles, which were from 0 to 12 seconds. These data were used to analyze the ventricular mechanical responses, such as pressure, volume, cardiac output, and contractile ATP consumption rate.
3 |. RESULTS
3.1 |. Model comparison
To confirm the electrophysiology properties in our study, we compared the shape of AP in single cell from our simulation with the previous studies.1,7 For the WT condition, we compared the AP shape of endo, M, and epi cells with the model proposed by O’Hara et al,1 which is based on experimental study from Gluckhov et al.21 Whereas for the G229D condition, we compared our AP shape (endo cell) with Hasegawa’s simulated AP,7 which is based on their own experimental study. The simulated AP shapes in our model are similar with the shape of AP in the O’Hara et al1 and Hasegawa et al7 as shown in Figure 5. Meanwhile, to validate the mechanical results under WT condition, we compared with the normal value of healthy ventricles from the reference literatures as provided in Table 1.
FIGURE 5.
Comparison of action potential (AP) shapes taken from the reference studies and recent simulation. A, AP shape for wild type condition with 3 cell types (red is endo, green is M-cell, and blue is epi) from previous simulation study of O’Hara et al1 (left) and our simulation (right); B, AP shape for G229D mutation condition with endo cell from previous simulation of Hasegawa et al7 (left) and our simulation (right). The basic cycle length is 1000 ms.
TABLE 1.
Numerical mechanical results for the WT and G229D mutation conditions under 3D sinus rhythm simulation
| Parameter | Value From Reference | WT | G229D | Difference |
|---|---|---|---|---|
| LVPP (mmHg) | 98-132[1] | 110 | 105 | 5% |
| Aortic SP (mmHg) | 100-140[1] | 107 | 104 | 3% |
| Aortic DP (mmHgg) | 60-90[1] | 64 | 60 | 6% |
| ESV (mL) | 37-57[2] | 39 | 48 | 23% |
| EDV (mL) | 121-163[2] | 88 | 96 | 9% |
| SV (mL) | 60-100 | 49 | 48 | 2% |
| EF (%) | 55-68 | 56 | 50 | 11% |
| LV CO (L/min) | 4.0-8.0[3] | 6.9 | 4.8 | 2% |
| LV SW (mmHgmL) | Not available | 3.7 × 103 | 3.48 × 103 | 7% |
| LV ATP consumption rate (s−1) | Not available | 105 | 86 | 18% |
LVPP, left ventricle peak pressure; ASP, aortic systolic pressure (systolic blood pressure); ADP, aortic diastolic pressure (diastolic blood pressure); ESV, end systolic volume; EDV, end-diastolic volume; SV, stroke volume; EF, ejection fraction; CO, cardiac output; SW, stroke work; ATP, adenosine triphosphate; WT, wild-type condition.
3.2 |. Single cell responses
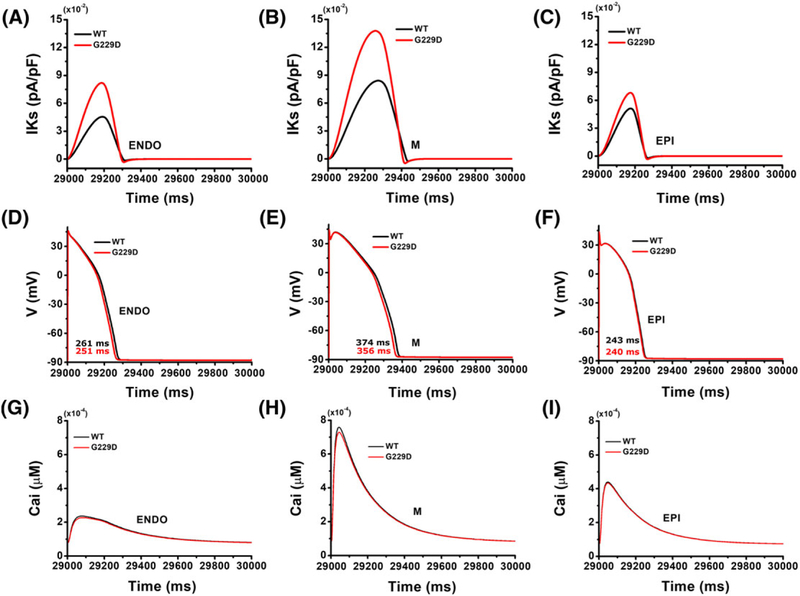
Figure 6 presents a comparison of the cellular responses for 3 cell types under the WT and G229D mutation conditions with 1000 ms of BCL. Compared with WT, the G229D mutation significantly increased the IKs density (Figure 6A–C). This enhancement in IKs due to G229D mutation slightly shortened the ventricular APD90 (Figure 6D–F). The APD90 measured under the WT condition were 261, 374, and 243 ms for the endo, M, and epi cells, respectively. Under the G229D mutation, the APD90 was slightly shortened by approximately 3%, 5%, and 1% for endo, M, and epi cells, respectively. Figure 6G to I shows the intracellular Ca2+ transients under WT and G229D mutation conditions. The concentration of Ca2+ transient was not markedly altered by G229D mutation.
FIGURE 6.
Single-cell simulation results for different myocardial cell types for wild type (black line) and the G229D (red line) mutation with basic cycle length of 1000 ms. A to C, Steady-state amplitude of slow delayed rectifier K+ current (IKs); D to F, profiles of action potential; G to I, profiles of calcium transient
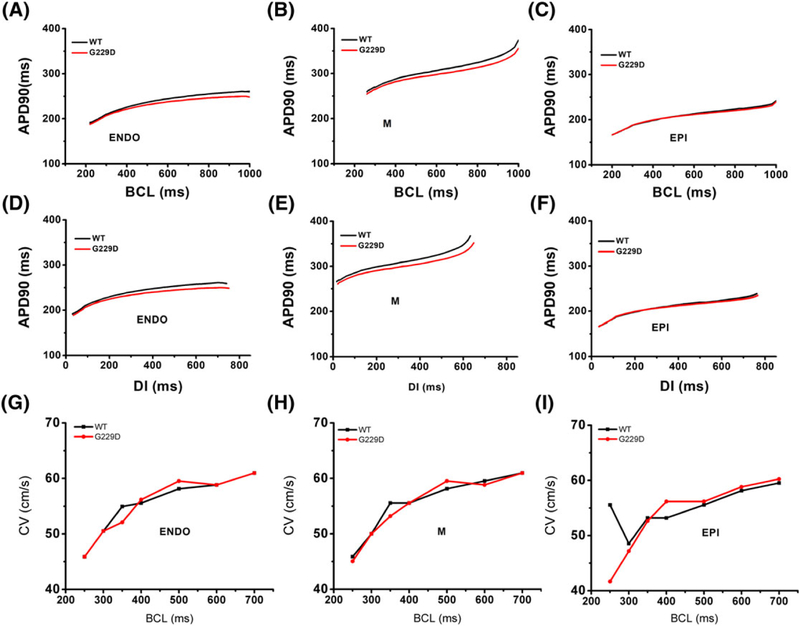
The APD90 restitution curves are shown in Figure 7A to C (APD90 vs BCL) and Figure 7D to F (APD90 vs DI). The data shown in these figures indicated that the G229D mutation maintained shorter APD90 for all BCL and DI ranges compared with the WT condition. The alternans or steep restitution was observed under both WT and G229D mutation conditions in this study. Figure 7G to I shows the comparison of the conduction velocity restitution curves under WT and G229D mutation conditions in endo, M, and epicardium cells. The simulation was conducted in the “cable” shape mesh with 10 cm × 0.02 cm with BCL of 250, 300, 350, 400, 500, 600, and 700 ms.
FIGURE 7.
A to C, APD90 restitution curves as a function of basic cycle length (BCL); D to F, APD90 restitution curves as a function of diastolic interval (DI). APD90 is the action potential duration at 90% repolarization, BCL is the basic cycle length, and DI is the diastolic interval; G to I, conduction velocity restitution curves simulated in cable mesh for endo, M-cell, and epicardium cell
3.3 |. 3D ventricular responses during sinus pacing
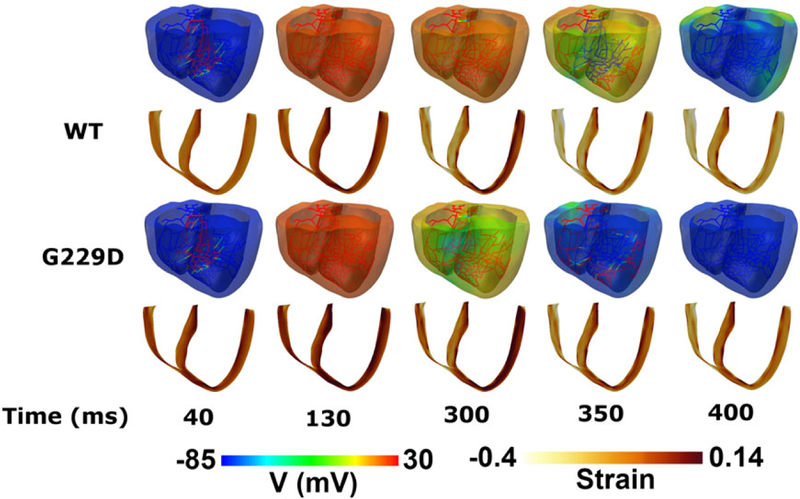
Figure 8 shows the maps of transmembrane potential (first and third rows) along with strain (second and fourth rows) in the 3D ventricular model during 1 cycle of sinus pacing. The membrane potential scale was set from −85 to 30 mV (ie, blue to red, respectively). The strain scale was set from −0.4 to 0.14 (ie, white to brown, respectively). Although the Purkinje fibers initiated at the same time (see the snapshot at 40 ms), the repolarization phase was faster with the G229D mutation than in the WT. The snapshot at 40 ms shows that the Purkinje fibers initiated an electrical stimulus at the same time for both the WT and G229D mutation conditions. At 130 ms, the ventricle was fully depolarized in both cases. The snapshot at 300 ms shows that in the G229D mutation, the ventricular tissue was already at the end of the repolarization state, indicated in green-blue, while for WT, some of the ventricular tissues were still excited, indicated in orange-yellow. The snapshot at 350 ms shows that the ventricle was in the repolarization state for the WT, but the ventricular tissue was already in the resting state for the G229D mutation condition. At 400 ms, under the G229D conditions, the ventricle was completely in the resting state (indicated in blue in the whole ventricle), while under the WT condition, some of the ventricular tissues were still in the repolarization state (indicated in green at the basal part of the ventricle). Meanwhile, the snapshots of the strain maps show that the strain increased slightly with the mutation, indicating less contractility under G229D mutation conditions. For both cases, the strain was darker at times less than 300 ms because the ventricle had not yet contracted.
FIGURE 8.
Snapshots of transmural distribution of membrane potential (top) and strain (bottom) during 1 cycle of sinus pacing for wild type and G229D conditions in the 3D ventricular tissue model
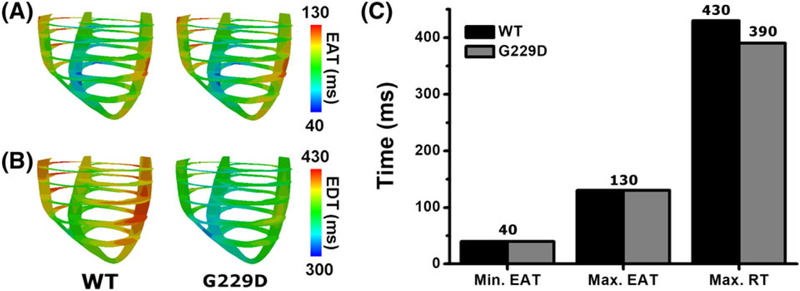
Figure 9 shows maps of electrical activation time (EAT) (Figure 9A) and repolarization time (RT) (Figure 9B), as well as a comparison among the minimum EAT, maximum EAT, and maximum RT (Figure 9C), for WT and the G229D mutation during 1 cycle of sinus pacing. The minimum EAT is the initial electrical impulse in the ventricles (ie, Q wave in electrocardiogram [ECG]), while the maximum EAT is the time at which all of the tissues are activated (ie, S wave in ECG). The maximum RT is the time at which all of the tissues are repolarized (ie, T wave in ECG).
FIGURE 9.
EAT and RT during 1 cycle of sinus pacing for wild type and G229D. A, Maps of EAT; B, maps of RT; C, comparison of minimum EAT, maximum EAT, and maximum RT. EAT denotes the electrical activation time; RT denotes the repolarization time
The EAT maps were similar for both cases (see Figure 9A), with the maximum EAT at the left ventricle (LV) free wall (ie, approximately 130 ms, indicated in red). This was consistent with the maximum EAT value in Figure 9C for the WT and G229D mutation conditions. The minimum EAT value was 40 ms, because the Purkinje terminal node was activated at an average at 40 ms for both cases. However, the RT maps were significantly different (see Figure 9B) between the WT and mutation conditions. Under the WT condition, the color for all ventricular regions tended to be red, whereas with the G229D mutation, the color tended to be blue, indicating faster repolarization under the G229D mutation condition. This is also explained in Figure 9C, which shows that the presence of mutation decreased the maximum RT by approximately 40 ms (ie, from 430 ms under WT to 390 ms under the G229D mutation condition).
In addition, we estimated the QT interval and QRS width of the ECG for the WT and G229D mutation conditions, based on the EAT and RT values shown in Figure 9C. Table 2 shows the results of the QT interval and QRS width calculation for both cases. The QT interval was shortened by 10% with the G229D mutation (ie, from 390 ms under WT to 350 ms under the G229D mutation), although the QRS width was the same in both cases (ie, 90 ms).
TABLE 2.
Estimated QT interval and QRS width (in ms) for the WT and G229D mutation conditions
| Condition | QRS Width (Max. EAT-Min. EAT) | QT Interval (Max. RT-Min. EAT) |
|---|---|---|
| WT | 90 | 390 |
| G229D | 90 | 350 |
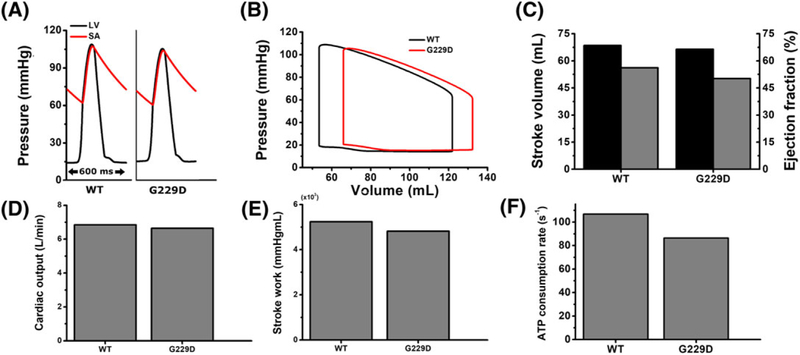
Figure 10 shows the ventricular mechanical responses during sinus pacing for the WT and G229D mutation conditions, including LV pressure waveforms (Figure 10A), LV pressure-volume (PV) curves (Figure 10B), stroke volume (SV), and the ejection fraction (EF) (Figure 10C), stroke work (SW) (Figure 10D), cardiac output (Figure 10E), and the average ATP consumption rate (Figure 10F). The responses were observed for only 1 cycle (ie, from the last rhythmic cycle, 11.4-12 s). Examination of the simulated pressure waveforms in Figure 10A showed that the WT condition generated an LV peak pressure of 110 mmHg with systolic and diastolic aortic pressures of 107 and 64 mmHg, respectively. With the G229D mutation, the LV peak pressure was slightly reduced, by approximately 5% (ie, to 105 mmHg), with systolic and diastolic aortic pressures of 104 and 60 mmHg, respectively.
FIGURE 10.
Ventricular mechanical responses for 1 cycle during sinus pacing for WT and the G229D mutation. A, Pressure waveforms of LV (black line) and SA (red line) over time; B, LV pressure-volume curves (black line, WT; red line, G229D); C, stroke volume (black bar) and ejection fraction (gray bar) of LV; D, LV stroke work; E, cardiac output; F, energy consumption rate of LV in the form of adenosine triphosphate (ATP). LV, left ventricle; SA, systemic artery; WT, wild type
In the PV relationship of LV shown in Figure 10B, the curve was shifted to the right with the G229D mutation, indicating increases in LV end systolic volume (ESV) and end diastolic volume (EDV). Under the WT condition, the ESV and EDV were 54 and 122 mL, respectively. With the G229D mutation, ESV and EDV were increased by approximately 23% (to 66 mL) and 9% (to 132 mL), respectively, forming a curve that tended to lean toward the right. End systolic volume and EDV determine the SV, ie, the amount of blood pumped out of the ventricles during a single phase of the cardiac cycle. The SV was calculated by subtracting the EDV from the ESV. Ejection fraction, which indicates the ratio of the blood ejected from LV in each contraction, was calculated by dividing SV by EDV.22 With the G229D mutation, SV and EF were decreased by approximately 2% and 11%, respectively, compared with the WT condition (Figure 10C, black bar). Consequently, LV cardiac output was also decreased, following reduction of the SV, by approximately 2% under the G229D mutation condition (see Figure 10D). Cardiac output was calculated as the product of blood pumped by each heart beat (ie, SV) and the heart rate. Here, we assumed a heart rate of 100 beats per minute based on a BCL of 600 ms.
Stroke work (Figure 10E), the internal area within the PV curve, is calculated by integrating the pressures and volumes in the PV curves (Figure 10B). Stroke work indicates the amount of work performed during 1 cycle of ventricular contraction. In the case of the G229D mutation, SW was decreased by approximately 7% compared with the WT condition. Furthermore, the contractile energy consumption rate, in the form of ATP, was also decreased in the presence of the G229D mutation (Figure 10F). Compared with the WT condition, the contractile ATP consumption was decreased by 18% with the G229D mutation. Details of these mechanical numerical results are provided in Table 1.
In summary, the G229D mutation did not markedly affect the heart pumping ability during sinus rhythm simulation. Although the mechanical responses were reduced under the G229D mutation condition, the ventricular performance was still normal, as indicated by normal pressure, SV, EF, CO, and SW values.
3.4 |. 3D ventricular responses during reentry
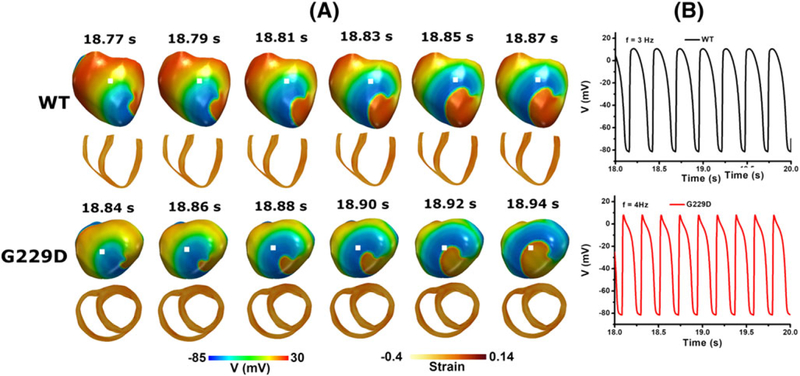
Figure 11 shows snapshots of reentrant spiral waves for the WT and G229D mutation conditions. The center of rotation of the spiral waves under the WT and mutation conditions was located in different regions in the ventricles. Reentry was sustained until the end of the simulation for both the WT and G229D mutation conditions. However, the wavelength generated under the mutation condition was slightly shorter than that under the WT condition (see Figure 11), resulting in a 1-Hz higher frequency of excitation (see Figure 11B); ie, the frequency of excitation was 3 and 4 Hz under WT and mutation conditions, respectively.
FIGURE 11.
Reentrant dynamics wave in the 3D ventricular tissue model for the wild type and G229D mutation conditions. A, Snapshot of the transmural distribution of membrane potential (top) and strain (bottom). B, Time traces of action potentials at the center of the ventricle (white dot). (top) WT condition and (bottom) G229D condition
Figure 12 illustrates the ventricular hemodynamic responses during reentry, including LV pressure waveforms (Figure 12A), LV volume waveforms (Figure 12B), LV PV curves (Figure 12C), and the overall ATP consumption rate of the ventricles (Figure 12D). Instead of evaluating the response over only 1 cycle, we used the response over the total simulation time (ie, 0-10 s) because the phenomena varied during reentry. The WT and mutation cycles were different (see the extended view of the steady-state responses on the right side of Figure 12). The ventricular beating rate was higher in the mutation condition than in WT (ie, 300 and 225 bpm, respectively). This was due to the shorter wavelength in the mutation condition, which generates a higher reentrant rate in the ventricle area. Moreover, transient responses were observed at the initial simulation time (ie, 0-4 s). These responses occurred due to the initial conditions used in our computational model. However, these transient responses did not influence the responses under the steady-state conditions.
FIGURE 12.
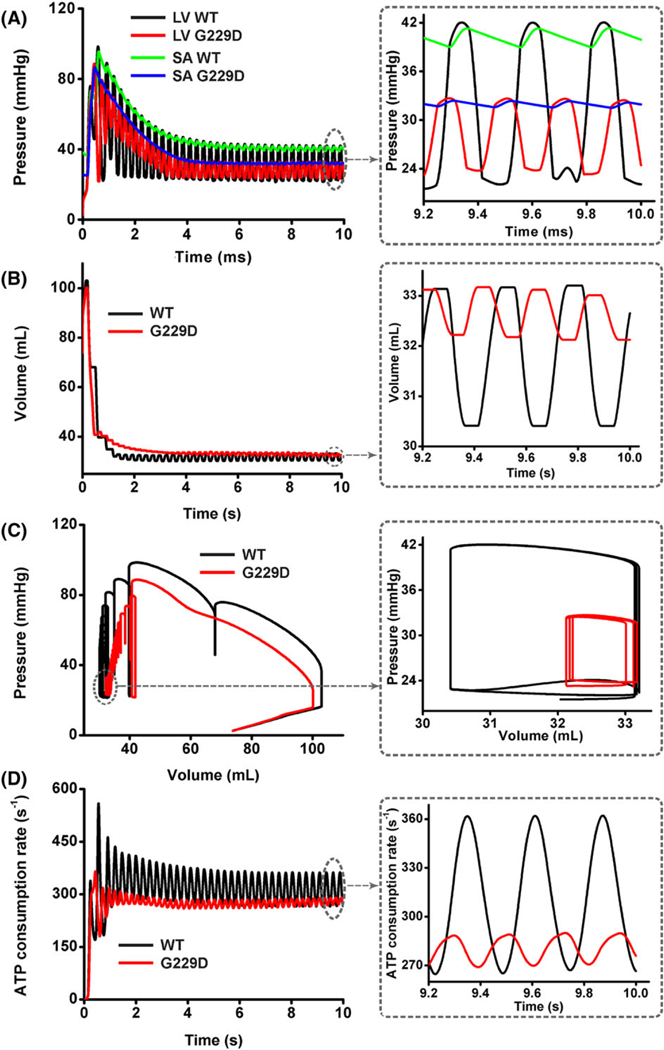
Ventricular mechanical responses of reentrant dynamics wave in the 3D ventricular tissue model for wild type (WT) and G229D. A, Left ventricular (LV) pressure waveforms; B, LV volume waveforms; C, LV pressure-volume curves; D, adenosine triphosphate P curves for WT and G229D mutation conditions
The pressure waveforms during reentry under G229D mutation converged to lower value compared with that of the WT condition, indicating a reduction with G229D mutation (Figure 12A). The average LV peak pressure of the last 3 constitutive waves was 42 mmHg under the WT condition. As the mutation was applied, the average of LV peak pressure, which is related to the pumping strength, decreased approximately 21% to 33 mmHg. The pressure in the aorta also decreased with the presence of mutation. The average systolic and diastolic aortic pressures were 41 and 39 mmHg, respectively, under the WT condition. Under the mutation, the systolic and diastolic aortic pressures were reduced to 32 and 31 mmHg, respectively. For both the WT and mutation conditions, the blood was still ejected successfully to the circulatory system, because the LV pressure was higher than aortic pressure during systole. The average of LV and aortic pressure, ATP consumption rate, and LV volume is shown in Table 3.
TABLE 3.
Average LV pressure, SA pressure, ATP consumption rate, and LV volume for WT and G229D mutation conditions under 3D reentrant dynamic simulation
| Condition | Avg. of LV Pressure | Avg. of SA Pressure | Avg. of ATP Rate | Avg. of LV Volume |
|---|---|---|---|---|
| WT | 42 mmHg | 34 mmHg | 319 s−1 | 34 mL |
| G229D | 34 mmHg | 40 mmHg | 270 s−1 | 46 mL |
Hidetsugu Asanoi, Tomoki Kameyama, Shinji Ishizaka, Takashi Nozawa, and H. Inoue, Circulation, 93:67-73, 1996.
A. Maceira, S. Prasad, M. Khan, and D. Pennell, “Normalized left ventricular systolic and diastolic function by steady state free precession cardiovascular magnetic resonance,” Journal of Cardiovascular Magnetic Resonance, 8:417-426, 2006.
J. Kabal, “Noninvasive hemodynamic analyzer alterable to a continuous invasive hemodynamic monitor,” Google Patents, 1996.
Based on the LV volume waveforms (Figure 12B), EDV was similar for both the WT and G229D mutation conditions, namely, 33 mL. However, the ESV increased by approximately 7% under mutation (ie, the ESV was 30 mL on WT and 32 mL on mutation). The ESV indicates the residual volume of blood remaining in the ventricle after ejection. Thus, an increase in ESV under constant EDV indicates that SV decreased under mutation.
The relationship between the pressure and volume shown in Figure 12A and B can be described by the PV curves in Figure 12C. As shown in the magnified viewpoint, the PV curves under mutation form smaller loops than those under the WT condition, where the ESV is shifted to the right and end systolic pressure decreased rapidly. Under the WT condition, the end-systolic pressure was approximately 42 mmHg. Under mutation, this value was reduced by 21% to 33 mmHg, although the EDV was the same (ie, 33 mL). This causes smaller SW (ie, area enclosed by the PV loop) under mutation than that under the WT condition. The smaller SW indicates less ventricle contractility and pumping efficacy under the mutation.
Figure 12D shows the overall ATP consumption rate during reentry for both the WT and G229D mutation conditions. The ATP consumption rate decreased significantly in the presence of mutation. In comparison with the WT condition, the contractile ATP consumption decreased by 21% under the G229D mutation condition.
4 |. DISCUSSION
4.1 |. Review of the results
Our study using an image-based electromechanical model is a new approach to understand the roles of G229D mutation on cardiac performance, particularly regarding ventricular hemodynamics. This study was conducted to investigate the effect of alteration of ion channels due to KCNQ1 G229D mutation on cardiac pumping functions and the relationship between G229D mutation and ventricular fibrillation. The major findings of this work are as follows:
KCNQ1 G229D mutation increased the IKs density and led to slight abbreviation of ventricular APD.
During sinus rhythm simulation, G229D mutation shortened QT interval but maintained normal hemodynamic responses.
During reentrant dynamic condition, G229D mutation worsened the ventricular contractility and energetic by decreasing intraventricular pressure, increasing ESV and preload, and reducing ATP consumption rate.
KCNQ1 G229D mutation, which is widely linked to AF, alters the IKs function in cardiac AP. IKs plays a prominent role in repolarization and termination of cardiac AP. Therefore, the rise in IKs resulting in the early repolarization of AP led to abbreviate APD. However, the shortened APD due to G229D mutation was not markedly seen in the ventricular cells, with only 3% decrease in endocardium, 5% in midmyocardium, and 1% in epicardium, with 1000 ms of BCL. This result is similar to the findings from the preliminary study of Hasegawa et al7 that gain-of-function of IKs caused only 3% shortening of APD in ventricular cell (ie, from 263 ms under WT condition to 254 ms under G229D mutation condition), whereas in atrial cell, APD shortened up to 20% (ie, from 294 to 232 ms).
Alternans, a condition where repetitive beat-to-beat oscillation occurs between subsequent APs, is widely linked to ventricular arrhythmia and fibrillation.23 However, alternans was not observed in this study because the slope of APD90 restitution curves for both WT and G229D mutation conditions were less than 1. Nolasco and Dahlen24 reported that alternans usually occurs when the APD90 restitution curves slope ≥1. Conversely, for APD90 restitution curves with slopes <1, disturbances in APD90 decrease, resulting in more stable activation. In addition, consistent with our results, a simulation study by 10 Tusscher et al25 indicated that the slope of the restitution curve is not the main parameter determining wave instability. In this study, a steep of restitution curve was not observed. However, the electrical wave instabilities were observed by using 3D simulation under reentrant dynamic condition.
QT interval reflects the activation-recovery cycle of the ventricular myocardium, measured from the beginning of the QRS complex wave (ie, minimum EAT) to the end of the T-wave (ie, maximum EDT). Thus, in the present study, QT interval was calculated by subtracting the maximum EDT from the maximum EAT, based on Figure 10C. Based on our 3D sinus rhythm simulation with 600-ms BCL, stronger IKs due to G229D mutation could facilitate in 10% shortening of QT intervals (see Table 2). This result is contradicted to what has been reported by Hasegawa et al7 with the proband (a 16-year-old boy diagnosed AF), which he showed a borderline of QT prolongation (QT/ATc 380/429 ms), instead of short QT. We believe this is because the repolarization (plateau) of AP is regulated not only by IKs but also by IKr and ICa,L. The previous study from Zhou et al26 has been identified that if the reduction of IKr was dominant compared with the increment of IKs, the overall repolarization strength would decrease, resulting in longer APD. And under longer BCL, IKr activity will increase, whereas the IKs activity decreases. Because our 3D simulation was conducted at lower BCL (ie, 600 ms), therefore, the repolarization was fastened, and QT interval was shortened. Furthermore, even though the mechanical responses were lowered in G229D mutation, the ventricular function was still normal, represented by normal pressure, volumes, EF, and SW (Figure 10 and Table 1). This is similar to what has been reported by Hasegawa et al7 that the cardiovascular and blood examination of the proband (a 16-year-old boy with AF) were all normal. But the sinus rhythm of the proband was failed to maintain.
Later, to investigate the instability of electrical wave, we conducted 3D simulation under reentrant dynamic conditions. Our simulation results showed that G229D mutation worsens the condition during reentrant dynamics. The wave-lengths were slightly shortened with the application of G229D mutation (Figure 8A). Wavelength is strongly correlated to CV and APD. The wavelengths (ie, the distance between the activation wavefront and the repolarization waveback) were calculated as the product of CV (ie, speed of electrical excitation) and APD (ie, duration of electrical excitation).8,27 Thus, for the same CV, the G229D mutation produced shorter wavelengths than the WT condition due to shorter APD. This shortening of wavelengths allows G229D mutation to generate higher reentrant rates than the WT condition, thus allowing G229D mutation to increase the probability of sustaining ventricular fibrillation.
For the LV hemodynamic response under reentry condition, there was a 20% reduction in LV and aortic peak pressure (ie, pressure unloading) due to G229D mutation. This indicates that the pumping strength of the ventricle decreased with the presence of G229D mutation.
As shown in the Figure 8, the wavelength under G229D mutation was shortened moderately compared with the normal case. This implied shorter Ca transient activation in the 3-dimensional space in the ventricle. Ca is the main factor for the myofilament sliding or the cross-bridge. Reduction in the Ca activation would decrease the performance of the contraction. That is why the LV and aortic pressure were reduced, thus the SV and the EF under the pure G229D mutation.
The pumping strength is the ultimate force required to eject an appropriate amount of blood to the circulation. Because LV did not have sufficient force, the residual volume of blood within the ventricle after ejection increased owing to incomplete ventricular emptying. Therefore, ESV increased by 17% under G229D mutation. This extra residual volume was added to the incoming venous return and led to an increase in preload (ie, the “load” imposed on the ventricle at the end of diastole). This is represented by the 7% increase in EDV and 11% in EDP. The reduction in LV pressure with increasing ESV, EDV, and EDP is shown in the PV relationship graphs, where the curves shifted to the right and down-ward, respectively (Figure 10B). This indicates a loss in ventricle contractility under G229D mutation. This loss resulted in a 28% reduction in SV (Figure 10C) and, consequently, cardiac output (Figure 10E). In addition, as shown, the increment in EDV (preload) was not as much as that in ESV. This is because the increment in preload is compensatory according to the Frank-Starling’s mechanism, to help maintain SV despite the loss of contractility. If the preload did not increase, the reduction in SV would be even greater for a given loss of contractility. Because SV decreased and EDV increased, there was a significant reduction of approximately 33% in EF (Figure 10C) under G229D mutation. Likewise, SW (ie, area within the PV loop) also decreased by approximately 44% (Figure 10D). This indicates that the work performance of LV decreased dramatically with the presence of G229D mutation.
This study further found that contractile energy consumption rate in the form of ATP decreased by approximately 28% under G229D mutation. It is well known that ATP was the main energy for the cell, including myocardium, to perform any work. Because of impaired ventricle contraction under G229D mutation, the ventricle work decreased; consequently, the ATP consumption rate also decreased.
4.2 |. Limitations in the study
The present study had several limitations. First, no experimental data were obtained in this study. Instead, we used a validated cell model7,14,25 and methodologies11–13 from previous studies. To further validate the model, studies using statistical methods in patients with ventricular fibrillation induced by the KCNQ1 G229D mutation are required. Second, we did not implement strong coupling of the mechanoelectrical feedback in this study, to avoid complexity of the model. Instead, we implemented 1-way excitation-contraction coupling, where only the electrophysiological behavior induced cardiac mechanics. Another important thing is that the APD90 difference from the single cell and 3D simulation results is highly possible due to tissue coupling problem.28 Moreover, further studies are necessary to investigate the roles of the G229D mutation in slower pacing rates (BCL > 600 ms) and to examine the subtle interactions of IKs and IKr.
5 |. CONCLUSIONS
This paper presents a summary of recent studies regarding the effects of G229D gene mutation on cardiac performance using computational simulation. We have expanded the preliminary study on G229D mutation, which only considered the electrophysiological responses, up to mechanical contraction, particularly regarding ventricular hemodynamics and energy. Our numerical studies identified that the augmented IKs channel due to G229D mutation caused a slight shortening of ventricular APD; this is consistent with the findings of Hasegawa et al. However, the shortened QT interval in this study is contradictive with the phenomenon on the proband with borderline of QT prolongation. Therefore, considering other ionic currents like IKr and ICa,L should be addressed to improve the modeling. The mechanical contraction was normal under sinus rhythm simulation but worsened under reentrant dynamic simulation.
ACKNOWLEDGEMENTS
This research was supported by the MSIP, under the CITRC support program (IITP-2017-2014-0-00639) supervised by the IITP, and basic engineering research project (2016R1D1A1B0101440) and the EDISON Program (NRF-2011-0020576) supervised by NRF.
Funding information
NRF, Grant/Award Number: NRF-2011-0020576 2016R1D1A1B0101440; IITP, Grant/Award Number: IITP-2017-2014-0-00639
REFERENCES
- 1.O’Hara T, Virág L, Varró A, Rudy Y. Simulation of the undiseased human cardiac ventricular action potential: model formulation and experimental validation. PLoS Comput Biol 2011;7(5):e1002061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wilde AA, Bezzina CR. Genetics of cardiac arrhythmias. Heart 2005;91(10):1352–1358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chen YH, Xu SJ, Bendahhou S, et al. KCNQ1 gain-of-function mutation in familial atrial fibrillation. Science 2003;299(5604):251–254. [DOI] [PubMed] [Google Scholar]
- 4.Bellocq C, van Ginneken A, Bezzina CR, et al. Mutation in the KCNQ1 gene leading to the short QT-interval syndrome. Circulation 2004;109(20):2394–2397. [DOI] [PubMed] [Google Scholar]
- 5.Ki CS, Jung CL, Kim HJ, et al. A KCNQ1 mutation causes age-dependant bradycardia and persistent atrial fibrillation. Pflugers Arch 2014;466(3):529–540. [DOI] [PubMed] [Google Scholar]
- 6.Imaniastuti R, Lee HS, Kim N, Youm JB, Shim EB, Lim KM. Computational prediction of proarrhythmogenic effect of the V241F KCNQ1 mutation in human atrium. Prog Biophys Mol Biol 2014;116(1):70–75. [DOI] [PubMed] [Google Scholar]
- 7.Hasegawa K, Ohno S, Ashihara T, et al. A novel KCNQ1 missense mutation identified in a patient with juvenile-onset atrial fibrillation causes constitutively open IKs channels. Heart Rhythm 2014;11(1):67–75. [DOI] [PubMed] [Google Scholar]
- 8.Zulfa I, Shim EB, Song KS, Lim KM. Computational simulations of the effects of the G229D KCNQ1 mutation on human atrial fibrillation. J Physiol Sci 2016;66(5):407–415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jespersen T, Grunnet M, Olesen SP. The KCNQ1 potassium channel: from gene to physiological function. Physiology (Bethesda) 2005;20:408–416. [DOI] [PubMed] [Google Scholar]
- 10.Bartos DC, Anderson JB, Bastiaenen R, et al. A KCNQ1 mutation causes a high penetrance for familial atrial fibrillation. J Cardiovasc Electrophysiol 2013;24(5):562–569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lim KM, Constantino J, Gurev V, Zhu R, Shim EB, Trayanova NA. Comparison of the effects of continuous and pulsatile left ventricular-assist devices on ventricular unloading using a cardiac electromechanics model. J Physiol Sci 2012;62(1):11–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lim KM, Hong SB, Lee BK, Shim EB, Trayanova N. Computational analysis of the effect of valvular regurgitation on ventricular mechanics using a 3D electromechanics model. J Physiol Sci 2015;65(2):159–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Trayanova NA, Constantino J, Gurev V. Electromechanical models of the ventricles. Am J Physiol Heart Circ Physiol 2011;301(2):H279–H286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rice JJ, Wang F, Bers DM, de Tombe PP. Approximate model of cooperative activation and crossbridge cycling in cardiac muscle using ordinary differential equations. Biophys J 2008;95(5):2368–2390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Holzapfel GA, Ogden RW. Constitutive modelling of passive myocardium: a structurally based framework for material characterization. Philos Trans Royal Soc Lond A Math Phys Eng Sci 2009;367(1902):3445–3475. [DOI] [PubMed] [Google Scholar]
- 16.Gurev V, Lee T, Constantino J, Arevalo H, Trayanova NA. Models of cardiac electromechanics based on individual hearts imaging data. Biomech Model Mechanobiol 2011;10(3):295–306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kerckhoffs RC, Neal ML, Gu Q, Bassingthwaighte JB, Omens JH, McCulloch AD. Coupling of a 3D finite element model of cardiac ventricular mechanics to lumped systems models of the systemic and pulmonic circulation. Ann Biomed Eng 2007;35(1):1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Koller ML, Riccio ML, Gilmour RF Jr. Dynamic restitution of action potential duration during electrical alternans and ventricular fibrillation. Am J Physiol 1998;275(5 Pt 2):H1635-H1642. [DOI] [PubMed] [Google Scholar]
- 19.Berenfeld O, Jalife J. Purkinje-muscle reentry as a mechanism of polymorphic ventricular arrhythmias in a 3-dimensional model of the ventricles. Circ Res 1998;82(10):1063–1077. [DOI] [PubMed] [Google Scholar]
- 20.Durrer D et al. Total excitation of the isolated human heart. Circulation 1970;41(6):899–912. [DOI] [PubMed] [Google Scholar]
- 21.Glukhov AV, Fedorov VV, Lou Q, et al. Transmural dispersion of repolarization in failing and nonfailing human ventricle. Circ Res 2010;106(5):981–991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Amstrong W, Ryan T, Feigenbaum H. Feigenbaum’s Echocardiography Lippincott Williams & Wilkins; 2010. [Google Scholar]
- 23.Rosenbaum DS, Jackson LE, Smith JM, Garan H, Ruskin JN, Cohen RJ. Electrical alternans and vulnerability to ventricular arrhythmias. N Engl J Med 1994;330(4):235–241. [DOI] [PubMed] [Google Scholar]
- 24.Nolasco JB, Dahlen RW. A graphic method for the study of alternation in cardiac action potentials. J Appl Physiol 1968;25(2):191–196. [DOI] [PubMed] [Google Scholar]
- 25.ten Tusscher KH, Panfilov AV. Alternans and spiral breakup in a human ventricular tissue model. Am J Physiol Heart Circ Physiol 2006;291(3):H1088–H1100. [DOI] [PubMed] [Google Scholar]
- 26.Zhou X, Harmer S, Bueno-Orovio A, Burrage K, Tinker A, Rodriguez B. How can a gain-of-function mutation in KCNQ1 lead to action potential prolongation? Europace 2016;18(suppl_1):i167. [Google Scholar]
- 27.Adeniran I, el Harchi A, Hancox JC, Zhang H. Proarrhythmia in KCNJ2-linked short QT syndrome: insights from modelling. Cardiovasc Res 2012;94(1):66–76. [DOI] [PubMed] [Google Scholar]
- 28.Kaur J, Nygren A, Vigmond EJ. Fitting membrane resistance along with action potential shape in cardiac myocytes improves convergence: application of a multi-objective parallel genetic algorithm. PLoS One 2014;9(9):e107984. [DOI] [PMC free article] [PubMed] [Google Scholar]