The Curve of Optimal Sample Size (COSS): a Graphical Representation of the Optimal Sample Size from a Value of Information Analysis

Abstract

Value of information (VOI) analysis quantifies the opportunity cost associated with decision uncertainty, and thus informs the value of collecting further information to avoid this cost. VOI can inform study design, optimal sample size selection, and research prioritization. Recent methodological advances have reduced the computational burden of conducting VOI and have made it easier to evaluate the expected value of sample information, the expected net benefit of sampling, and the optimal sample size of a study design (n*). The volume of VOI analyses being published is increasing, and there is now a need for VOI studies to conduct sensitivity analyses on VOI-specific parameters. In this practical application, we introduce the curve of optimal sample size (COSS), which is a graphical representation of n* over a range of willingness-to-pay thresholds and VOI parameters (example data and R code are provided). In a single figure, the COSS presents summary data for decision makers to determine the sample size that optimizes research funding given their operating characteristics. The COSS also presents variation in the optimal sample size given variability or uncertainty in VOI parameters. The COSS represents an efficient and additional approach for summarizing results from a VOI analysis.

Introduction

Value of information (VOI) analysis quantifies the value of reducing decision uncertainty regarding the choice between competing strategies and can inform research prioritization and inform future data collection efforts [1]. Recent methodological advances have reduced computational burdens associated with conducting VOI analyses [2–7]. With improved efficiency, the use of VOI to inform decision-making and research prioritization has increased [8–13].

Findings from a VOI analysis are generally reported via several summary measures described in detail below. The expected value of perfect information (EVPI) and the expected value of partial perfect information (EVPPI) are normally graphically presented over a range of willingness-to-pay (WTP) thresholds. In contrast, VOI analyses typically only report point estimates of measures of the expected value of sample information (EVSI), the expected net benefit of sampling (ENBS), and the optimal sample size (n*), which is the sample size that maximizes the ENBS of a data collection process (i.e., research study) that aims to reduce decision uncertainty (i.e., n* at a single WTP) [14–17]. However, as we illustrate below, n* can be sensitive to a decision maker’s WTP threshold. To increase the utility of VOI analyses, researchers should not only report point estimates for all VOI measures but should report n* over a range of WTP thresholds and variation in n* in VOI parameters (e.g., cost of research).

Our objective is to help analysts report n* over a relevant set of sensitivity analyses on VOI-specific parameters that can help decision makers better understand findings from VOI analyses. We introduce the curve of optimal sample size (COSS), which is a graphical representation of n* over a range of WTP thresholds and can also be used to show how n* changes based on VOI-specific parameters. The COSS shows n* in a single figure for a range of decision maker operating characteristics and it represents an additional graphical approach to summarize results from a VOI.

Review of VOI Measures

VOI analysis typically follows an economic evaluation and the core data used to inform a VOI are derived from a probabilistic sensitivity analysis (PSA) of an economic evaluation [2, 7, 3]. Detailed methodological [18–20] and applied [8, 21, 22] VOI studies have been published, so we present only a brief overview of five key VOI measures that are typically used to inform a research prioritization framework. In addition, VOI analyses require many assumptions. As our objective is to introduce the COSS as a method for summarizing findings, we refer the reader to relevant literature that discuss in detail the analytical assumptions that must be made.

The first VOI measure is EVPI, which represents the maximum amount a decision maker should be willing to pay to reduce all sources of uncertainty in the model’s parameters.

The second measure is EVPPI, which estimates the value of eliminating uncertainty (within the context of the decision problem) for specific model inputs (e.g., effectiveness of treatment) or sets of inputs [2, 23, 24]. Results from an EVPPI analysis can be used to inform the upper threshold that a decision maker should be willing to pay for a data collection process (e.g., randomized trial) to collect data to eliminate uncertainty for a single input or sets of inputs. In practical terms, the actual data collection process is driven by the nature of the input(s). For example, inputs related to treatment effect typically imply a randomized trial. A key assumption of VOI is that any data collection process will result in an unbiased sample estimate of the input of interest. Thus far, the only requirements to the VOI analysis are the PSA dataset and the WTP threshold.

Up to now, we have discussed reporting EVPI and EVPPI on an individual level. To extrapolate results to a population level, several assumptions need to be made regarding the discount rate that should be applied to the future benefit of information, the decision lifetime, the number of current prevalent cases that could benefit from the decision and the number of future incidence cases that could benefit from the decision during the decision lifetime [18, 19, 25].

The third and fourth VOI measures are the population expected value of sample information (pEVSI) and the expected net benefit of sampling (ENBS). pEVSI represents the value of reducing uncertainty by a data collection process for a single input or sets of inputs by collecting data from a finite sample size of n individuals for a given WTP threshold [2, 26, 27]. Recent methodological advances support the computation of pEVSI [2, 7, 3, 6] for different sets of inputs, which can represent various data collection processes, using economic models of high complexity [28] and over different WTP threshold values [8].

There is a cost to collecting data. ENBS provides an estimate of the marginal population benefit of an additional sample collected in a specific data collection process accounting for the cost of collecting the data. To calculate ENBS, a study cost function is required. Cost functions can be simple or complex and depend on the study design and setting (e.g., single site or multicenter study). Basic cost functions typically include a fixed cost of conducting the research study and a variable or per-person cost of conducting the research study [18, 19]. For randomized trials, the variable cost of research can also include the loss of benefit from randomizing a portion of the patients to an inferior arm, the time it takes to conduct the trial, and imperfect implementation of the intervention into practice [29, 30].

A fifth measure in a VOI analysis is the optimal sample size (n*), which is the sample size that maximizes the ENBS of pEVSI. ENBS can be computed for multiple data collection processes. From a research prioritization perspective, the data collection process with the highest ENBS is optimal. Again, selecting the WTP threshold and making VOI analytical assumptions are not trivial and detailed methodological approaches are extensively described elsewhere [18–20].

VOI Parameters

In summary, six main parameters inform a VOI analysis that can be categorized into three groups: decision maker parameters: 1) WTP threshold, 2) discount rate, 3) decision lifetime; epidemiological parameters: 4) number of prevalent cases, 5) number of incident cases; study design parameters: 6) costs function of study design separated into relevant components (e.g., fixed costs and variable costs) (Table 1). Parameters 1 and 2 affect the weight placed on the effective population’s health gains. Parameters 3–5 directly affect the size of the effective population or number of individuals who can benefit from the information. Parameter 6 is a cost function.

Table 1.

VOI Inputs, Potential Data Sources, and Ranges for Sensitivity Analysis

VOI Parameter	Potential Data Sources	Examples of Potential Ranges to Test in Sensitivity Analysis
Decision Maker Parameters
1. Willingness-to-pay threshold	Cost-effectiveness acceptability curve and frontier, or decision makers revealed threshold ranges	Based on decision makers’ revealed threshold ranges or identified from the cost-effectiveness acceptability curves and frontier where there is competition regarding optimal strategy.
2. Discount rate	Expert opinion or literature (gray or published)	3% based on recommendation in Cost-Effectiveness in Health and Medicine 2nd Ed [32].
3. Decision lifetime	Expert opinion or patent data	High/low estimates from experts or external sources such as patent data.
Epidemiological Parameters
4. Prevalent cases	Epidemiological data	High/low ranges from data or from the literature.
5. Incident cases	Epidemiological data	High/low ranges from data or from the literature.
Study Design Parametersa
6. Cost functionb	Expert opinion or literature (gray or published)	High/low estimates from experts, the literature, or data.

^aProposed study designs can be hypothesized from a review of the expected value of partial perfect information for individual or groups of parameters.

^bcosts function of study design should be separated into relevant components (e.g., fixed costs and variable costs).

VOI value of information

Decision makers often have a range of values over which they evaluate VOI parameters (e.g., range of WTP thresholds). In addition, there is often heterogeneity between decision makers and contexts that impact the values selected for VOI parameters. Finally, for some VOI parameters there is uncertainty in the value of the parameter (e.g., number of prevalent cases).

Curve of Optimal Sample Size (COSS)

To determine variability in n* over a range of WTP values and VOI parameters, results can be visualized. The curve of optimal sample size (COSS) graphically presents the change in n* (y-axis) for each data collection process over a range of WTP thresholds (x-axis). Results are graphed over a range of WTP values and can also be presented for variation in select VOI parameters (e.g., cost of research), multiple select VOI parameters, or as best-case and worst-case scenarios where all VOI parameters are set to their extreme values. By graphing n* over a range of WTP values and VOI parameters, decision makers can identify if further data collection is warranted given their operating characteristics (Table 2 for COSS algorithm).

Table 2.

Curve of Optimal Sample Size (COSS) Algorithm

Step 1:	Generate a probabilistic sensitivity analysis dataset from an economic evaluation.
Step 2:	For each willingness-to-pay threshold, calculate the expected value of sample information for a set of parameters or a proposed study design.
Step 3:	For each willingness-to-pay threshold, calculate the expected net benefit of sampling as the difference between the expected value of sample information and cost of research for a study of size n.
Step 4:	Compute the optimal sample size (n*) that maximizes the expected net benefit of sampling.
Step 5:	Plot n* across willingness-to-pay thresholds.

Applied COSS Example

Below we provide a simplified VOI example and corresponding R code (eStatistical Code; eTable 1 data dictionary) to generate the COSS. The data and R code are based on our prior cost-effectiveness analysis and VOI evaluation of nine urate-lowering treatment strategies for the management of gout [8]. From these analyses, we obtained the data from the PSA (eData 1). The emphasis of this example is on the application of the COSS; as such, the original study and data have been simplified for pedagogical purposes. Three strategies (allopurinol only dose-escalation, allopurinol-febuxostat sequential therapy dose-escalation, and febuxostat-allopurinol sequential therapy dose-escalation) were optimal across a range of WTP thresholds. We report the VOI analyses based on these three optimal strategies and select model inputs related to treatment effectiveness of allopurinol dose-escalation and health utilities.

We first identified values for the VOI parameters for the WTP threshold (input #1), discount rate (input #2), decision lifetime (input #3), number of prevalent gout cases that could benefit from the decision (input #4), and number of future incident gout cases that could benefit from the decision (input #5). We adopted a WTP range of $US0-$US150,000 per QALY based on recommended decision thresholds (eTable 2 assumptions of VOI analysis). Without an a-priori decision threshold, we could also identify the range of WTP values for use in the VOI by identifying regions on the cost-effectiveness acceptability curve and frontier derived from the PSA where there is meaningful uncertainty regarding the optimal strategy (eFigure 1). We chose a discount rate of 3% which corresponds with guidelines for discounting in cost-effectiveness analyses and a decision lifetime of 5 years, which corresponds with the remaining lifetime of the patent for febuxostat [31, 32]. The number of prevalent and incident gout patients that could benefit from the decision regarding the cost-effectiveness of urate-lowering treatment strategies were obtained from epidemiological data [33–36].

Using the PSA data (eData 1) generated from the cost-effectiveness analysis, we calculated population EVPI (eFigure 2). We then calculated population EVPPI (eFigure 3) separately for model parameters related to the effectiveness of allopurinol dose-escalation and health utilities. Population EVPPI indicates there is potential value in reducing uncertainty on the parameters informing the effectiveness of allopurinol dose-escalation and health utilities.

To inform the cost-effectiveness of model inputs related to treatment effectiveness and health utilities, we hypothesized two distinct data collection processes (i.e., study designs) could be conducted. First, a randomized controlled trial in which allopurinol dose-escalation is compared against placebo. Second, an observational study to elicit health utilities of gout patients. Utilities would be obtained that correspond with the model states of controlled on treatment, uncontrolled on treatment, and uncontrolled off treatment. In a more detailed VOI evaluation, additional study designs could be hypothesized.

For pedagogical purposes, we assumed our cost function only had a fixed and variable cost (input #6). The cost of conducting a randomized trial also included the loss of benefit for patients randomized to placebo compared to allopurinol dose-escalation (i.e., incremental net benefit). In a more detailed evaluation we could also include costs that capture the time it takes to conduct the study and implement findings [29, 30]. We obtained data on the cost of research from studies reporting the total and average per participant cost of conducting a randomized trial [37, 38]. We separately estimated the cost of conducting an observational study. To be consistent with our prior analyses, we report all costs in 2013 US dollars.

We used a published method to calculate pEVSI that is based on adopting a Gaussian approximation of the Bayesian updating and a linear regression meta-modeling of the relations between the model inputs and the expected opportunity cost [2].

We graphically reported n* over a range of WTP using the COSS (Figure 1), and we graphically reported n* for a randomized controlled trial comparing allopurinol dose-escalation to placebo over a range of WTP given variation in the cost of research (Figure 2).

Figure 1.

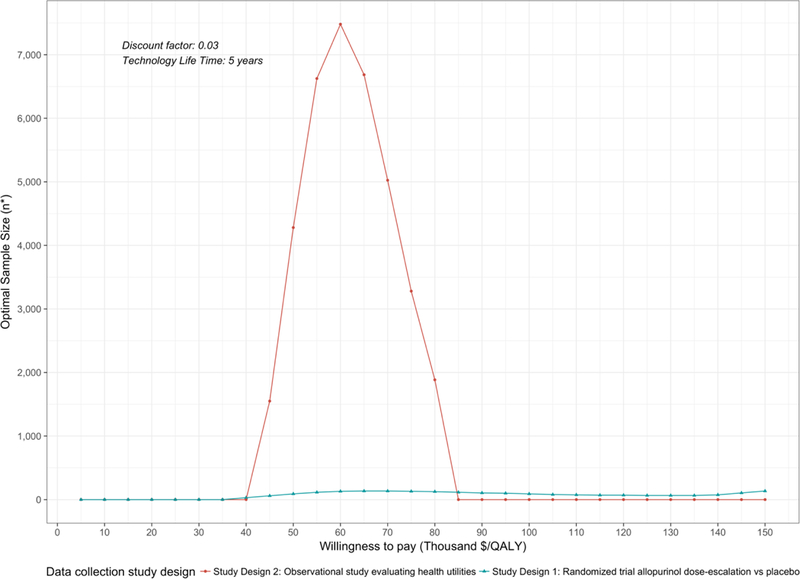
Curve of Optimal Sample Size n* is reported as the total sample size. For a two-arm randomized trial, n*/2 represents the optimal sample size per study arm.

Figure 2.

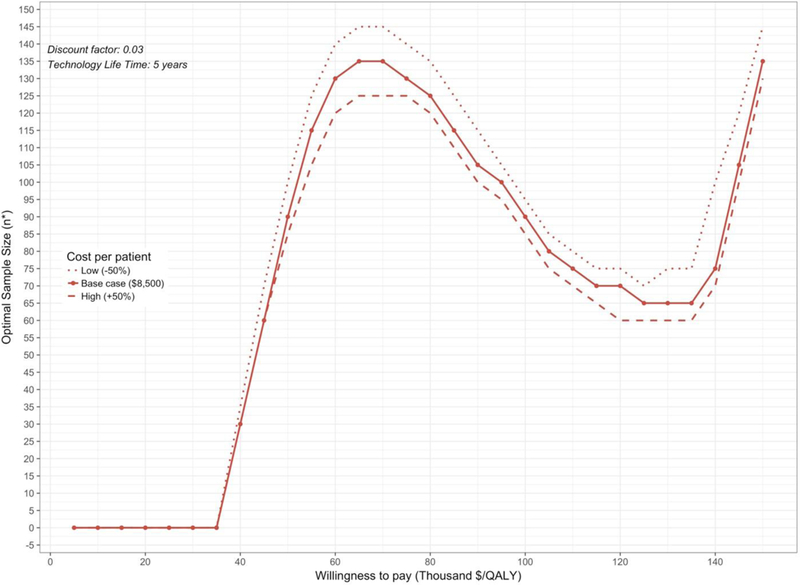
Curve of Optimal Sample Size (COSS) for Study Design 1 (RCT) with Sensitivity Analysis on Variable Cost of Research n* is reported as the total sample size. For a two-arm randomized trial, n*/2 represents the optimal sample size per study arm.

From the COSS, a decision maker is able to determine the optimal sample size for a study design given their a-priori WTP threshold. For example, given a decision maker’s WTP is $US50,000 per QALY, an observational study collecting data on health utilities should enroll 4,300 subjects (rounded to nearest 25^th) and a randomized trial on the effectiveness of allopurinol dose-escalation should enroll 100 subjects or 50 per arm. From a research prioritization perspective, the decision maker must also evaluate the ENBS of the proposed study designs to determine which study generates the largest benefit (eFigure 4). While the optimal sample size of the randomized trial is less than the observational study, the ENBS of the randomized trial is greater indicating it will generate a larger reduction in uncertainty.

DISCUSSION/CONCLUSION

VOI should be used beyond just informing value of eliminating uncertainty and can and should inform future research funding and study design. Recent methodological developments allow researchers to quickly and efficiently calculate VOI measures. Similar to cost-effectiveness analyses, sensitivity analyses in VOI analysis should become the norm. To support the reporting of sensitivity analysis of parameters and assumptions, we propose the COSS as a standard for graphically representing n* over a range of WTP values and VOI parameters.

The COSS graphically displays n* for all study designs over a range of WTP threshold values and VOI parameters as these vary by agency and setting. The COSS can also show variation and uncertainty in multiple or select VOI parameters (e.g., cost of research) on n*. To facilitate research prioritization, ENBS and n* should be evaluated concurrently. As our example illustrated, the study design with the highest optimal sample size is not necessarily the design that yields the largest benefit (eFigure 4).

Since a decision maker’s WTP is given a-priori, the COSS should not be used to determine the cost-effectiveness threshold required to provide an optimal sample size. That is, the COSS should be used to determine the optimal study design and n* given an a-priori WTP threshold.

Graphically presenting n* in the COSS efficiently summarizes a key measure of a VOI analysis and allows decision makers with different WTP thresholds and operating characteristics to identify if further research is in fact needed and the size of such research studies.

Key Points for Decision Makers.

• We introduce the curve of optimal sample size (COSS), which is a graphical representation of the optimal sample size of a study design over a range of willingness-to-pay thresholds.

• The COSS presents summary data for decision makers to determine the sample size that optimizes research funding given their operating characteristics (e.g., willingness-to-pay threshold).