AFNMR: Automated Fragmentation Quantum mechanical Calculation of NMR Chemical shifts for Biomolecules

Abstract

We evaluate the performance of the automated fragmentation quantum mechanics/molecular mechanics approach (AF-QM/MM) on the calculation of protein and nucleic acid NMR chemical shifts. The AF-QM/MM approach models solvent effects implicitly through a set of surface charges computed using the Poisson-Boltzmann equation, and it can also be combined with an explicit solvent model through the placement of water molecules in the first solvation shell around the solute; the latter substantially improves the accuracy of chemical shift prediction of protons involved in hydrogen bonding with solvent. We also compare the performance of AF-QM/MM on proteins and nucleic acids with two leading empirical chemical shift prediction programs SHIFTS and SHIFTX2. Although the empirical programs outperform AF-QM/MM in predicting chemical shifts, the differences are in some cases small, and the latter can be applied to chemical shifts on biomolecules which are outside the training set employed by the empirical programs, such as structures containing ligands, metal centers, and non-standard residues. The AF-QM/MM described here is implemented in version 5 of the SHIFTS software, and is fully automated, so that only a structure in PDB format is required as input.

Introduction

NMR spectroscopy is widely used to study the structure, dynamics, and interactions of proteins and nucleic acids. The chemical shift is one of the most abundant and precise outputs of an NMR experiment, and there has been significant progress in using chemical shifts to directly obtain structural and dynamic information of biomolecules (Cavalli et al, 2007,Sahakyan et al, 2011,Shen et al, 2008,Shen et al, 2009). However, a detailed interpretation of these NMR parameters is still a significant challenge due to the inherently complex dependence of chemical shifts on geometric, dynamic, and electronic properties.

Chemical shift calculations for proteins have matured far more quickly than calculations for nucleic acids due in part to the larger volume of NMR experiments performed on proteins. The most common models used to compute chemical shifts of biomolecules utilize empirical formulae whose parameters are derived by fitting to databases of experimental chemical shifts, such as those models implemented by SHIFTX2 (Han et al, 2011), the proton chemical shift predictor in SHIFTS (Xu et al, 2001), CAMSHIFT (Kohlhoff et al, 2009), PROSHIFT (Meiler et al, 2003), SHIFTCALC (Williamson et al, 2009), etc. While empirical models for chemical shifts of nucleic acids are far less mature than those for proteins, developments in the programs SHIFTS (Xu et al, 2001), NUCHEMICS (Cromsigt et al, 2001,Wijmenga et al, 1997), PPM (Li et al, 2012) and RAMSEY (Frank et al, 2013)—spurred by increased availability of more reliable experimental data—demonstrate promise in the field of DNA and RNA chemical shift prediction. These methods make use of empirical or semi-empirical equations to account for the effects arising from non-neighboring residues, and most of them rely on experimental data from a limited set of high-quality structures. These empirical methods are usually quite successful in predicting backbone chemical shifts which are primarily determined by the local secondary structure, but they are not well suited to handle proteins with nonstandard residues, metal cofactors, protein-ligand complexes, or non-canonical structures in the case of nucleic acid systems.

The fact that empirical models are trained to fit experimental shifts is both a strength and a potential weakness: the models may understate the sensitivity of shifts to small changes in structure. Ochsenfeld and co-workers (Sumowski et al, 2014) have compared the sensitivity of ab initio versus empirical approaches in computing structural effects on NMR chemical shifts. They found that the chemical shifts predicted by many empirical methods were often insensitive to protein structural changes—in particular CAMSHIFT, PROSHIFT, SHIFTS, SHIFTX, SHIFTX2, and SPARTA+.

In the past two decades, several research groups have applied quantum mechanical (QM) methods to accurately predict NMR chemical shifts in proteins. (Arnold et al, 2000,de Dios et al, 1993,Flaig et al, 2014,Hartman et al, 2014,Moon et al, 2006,Sitkoff et al, 1997) However, due to the poor scaling of ab initio methods, it has not been practical to apply standard, all-electron quantum chemistry methods to macromolecules of common biological interest. Full quantum mechanical computations on structures with thousands of atoms are not currently feasible. Fortunately, nuclear shielding is fundamentally a local physical property and many previous studies have found that there is no need to include all protein or nucleic acid atoms in the QM calculations of NMR shielding tensors (de Dios et al, 1993). Cui et al. proposed a method for calculating protein NMR chemical shifts in the QM/MM framework (Cui et al, 2000), and concluded that the QM/MM method can provide good descriptions of the environmental effect on chemical shifts. Scheurer and co-workers used DFT calculations on manually-generated fragments to compute chemical shielding anisotropy tensors (Scheurer et al, 1999). Exner and co-workers calculated the chemical shifts using the fragment based adjustable density matrix assembler (ADMA) method (Dracinsky et al, 2013,Exner et al, 2012,Frank et al, 2011,Victora et al, 2014). Gao et al. also have used the fragment molecular orbital (FMO) method for protein NMR chemical shift calculations. (Gao et al, 2010,Gao et al, 2007)

Here, we present results for an efficient automated fragmentation quantum mechanics/molecular mechanics approach (AF-QM/MM), which is applicable to routine ab initio NMR chemical shift calculation for protein or nucleic acid systems of any size (Case 2013, He et al, 2009, He et al, 2014, Salomon-Ferrer et al, 2013,Tang et al, 2011,Wang et al, 2013, Zhu et al, 2012, Zhu et al, 2013, Zhu et al, 2014). In this approach, the entire system is divided into individual fragments, and residues within a certain buffer region surrounding each fragment are included in the QM calculation to preserve the local chemical environment around the fragment. The remainder of the system outside the buffer regions is described using standard molecular mechanics. Solvation effects have also been included in the AF-QM/MM calculation with implicit and explicit solvent models (Zhu et al, 2012,Zhu et al, 2013). In this work, new developments and applications of AF-QM/MM will be discussed and compared with the latest semi-empirical models for computing chemical shifts in proteins and nucleic acids.

Methods

Figure 1 depicts the workflow of the AFNMR program which implements the AF-QM/MM approach. Prior to calculating the shielding tensor, the starting structure is optimized using sander from the AMBER program suite (Case et al, 2014,Salomon-Ferrer et al, 2013) in order to remove bad contacts and to regularize bond lengths and angles prior to subsequent computations. The atomic charges in the MM region can be estimated in several ways. Some earlier work²³ has used the linear-scaling divide-and-conquer semi-empirical algorithm DivCon (Wang et al, 2004), constructing PM3/CM2 charges. Other charge models such as polarized protein-specific charges (PPC) (Ji et al, 2008,Song et al, 2013) or AMBER94 charges can also be used. Most molecular mechanical force fields use charge models that differ little in the assigned partial atomic charges, and since these charges are by construction far away from the atom whose shift is being computed, the effects of these differences on predicted chemical shifts, through their representation as point charges in the DFT calculation or through their effect on the computed induced surface charges, are small.

Figure 1.

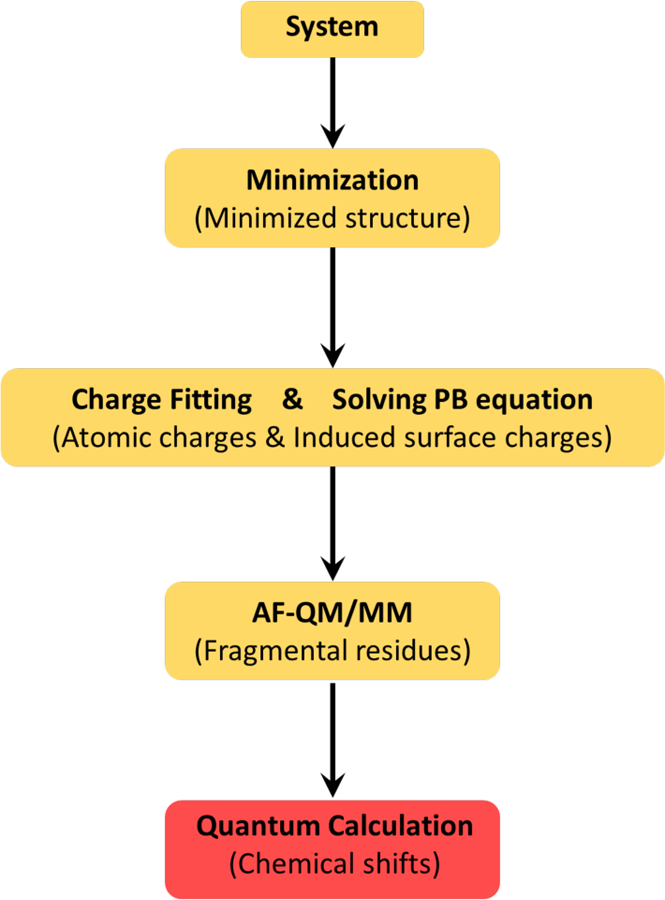
A flowchart showing the design of the AFNMR program based on the AF-QM/MM method.

After the atomic charge model for the target system is selected, a set of induced charges on the biomolecule surface which represents the reaction field of solvent on the solute is calculated by solving the Poisson-Boltzmann (PB) equation. By adding these surface charges in the AF-QM/MM calculation, solvent effects can be treated implicitly (see Figure 2). Alternatively, the surface charges can be computed by solving the PB equation using a 3 dielectric model. The solinprot program from the MEAD package can be used to set the dielectric constants inside the QM region to 1, inside the solute but outside the QM region to 4, and outside the solute to 80. Setting the dielectric constant inside the solute (but outside the QM region) to 4 allows the effects of electronic polarization to be taken into account implicitly when computing the NMR shielding tensors. This procedure is illustrated in Figure 2. While the choice of partial atomic charges will influence the induced surface charges, similarity between popular charge models will keep the influence of this choice small on the computed chemical shift (for example, the charges differ between the Amber and CHARMM force fields by an average of only 0.05 atomic charge units for standard biopolymer residues).

Figure 2.

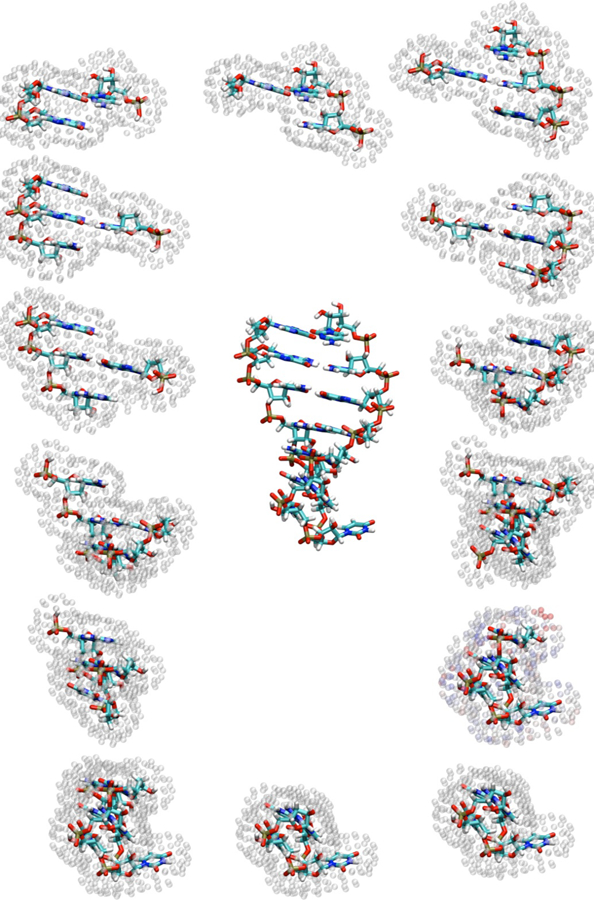
Hairpin structure shown alongside the 14 fragments (one for each nucleotide) used to compute chemical shifts. Surface charge positions representing the reaction field are shown as translucent spheres around each fragment.

Our previous study of amide protons has shown remarkable improvement in the accuracy of NMR chemical shift predictions when the explicit solvent molecules in the first solvation shell are treated by quantum mechanics (Zhu et al, 2013). The main obstacle to include explicit solvent molecules in the AF-QM/MM calculation is that an algorithm that can accurately predict the positions and orientations of solvent molecules around biomolecules is still unavailable. There are occasionally some crystallographic water molecules present in X-ray structures, but they just represent a small fraction of the water molecules around the proteins. Owing to the inefficiency of sampling, using standard MD simulation to locate the solvent positions is also a formidable task, since long simulation times are needed to converge the water distribution.

In the AF-QM/MM approach used here, the distribution of explicit solvent molecules is determined using the PLACEVENT program developed by Hirata and co-workers. (Sindhikara et al, 2012) PLACEVENT is based on the 3D reference interaction site model (3D-RISM), a method based on statistical mechanics that has been shown to accurately reproduce water distributions at a reduced computational cost (Sindhikara et al, 2012). Previous studies have demonstrated that this program places the water molecules on the highest likelihood location and gives excellent agreement with experimental data (Imai et al, 2007, Yoshida et al, 2006, Zhu et al, 2013). Only the water molecules in the first solvation shell (within 3.5 Å from any atom in the protein) are regarded as part of the entire system in our approach. The implicit solvent model is used to represent the bulk solvent effect beyond the first solvent shell.

The fragmentation scheme used in the AF-QM/MM approach is shown in Figure 3. In AF-QM/MM, the entire protein is divided into non-overlapping residues termed core regions. The residues within a certain distance cutoff from the core region are assigned as the buffer region. Both the core region and its buffer region are treated by QM calculation, whereas the rest of the system is described by the point charge model. The aim of using buffer area is to include the local QM effects on the shielding tensors. Each residue-centric QM/MM calculation is carried out separately. Only the total isotropic shielding constants of the atoms in the core region are extracted from the individual QM/MM calculation.

Figure 3.

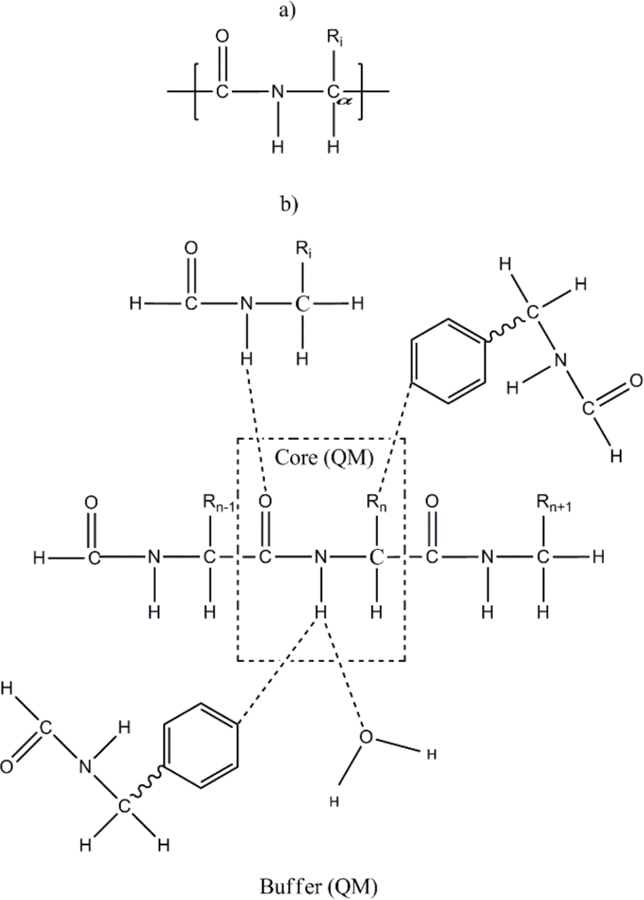
a) Definition of a “residue” used by AF-NMR to preserve electron delocalization across a peptide bond in protein systems. b) Graphical representation of the distance-dependent criteria used to define the buffer region of each core residue (see the text for further details).

In the AF-QM/MM approach, we use a different definition of the residue in proteins, which consists of the −CO−NH−CHR− group to preserve the electron delocalization across the peptide bond (Figure 3a). A generalized molecular cap was also introduced to take into account the QM polarization effect and charge transfer within the first shell from the residue of interest, as shown in Figure 3b. The following distance-dependent criteria is used to include residues within the buffer region of each core residue: (1) if one atom of the residue outside the core region is less than 4 Å away from any atom in the core region and at least one of the two atoms is a non-hydrogen atom or (2) if the distance between one hydrogen atom in the core region and the other hydrogen atom outside the core region is less than 3 Å. Of course, other distance-dependent criteria could be used to further optimize the choice of the buffer region, but our approach appears to strike an acceptable balance between accuracy and efficiency. The non-neighboring residues in the buffer region are simply capped by hydrogen atoms to complete the closed-shell fragment.

The remaining atoms beyond the buffer region are treated by atomic charges which account for the electrostatic field outside the QM region. Alternatively, when the 3-dielectric model is used—as in this study—the partial charges of the atoms outside the QM region are used when solving the PB equation to compute the surface charges used to reproduce the reaction field at the boundary. By using a general criterion to assign a buffer zone to each residue, we can reduce the size of each fragment in order to make the QM calculation as small as possible until we strike a compromise between the desired accuracy and the computational cost. In the AF-QM/MM calculation of protein NMR chemical shift with the explicit solvent model, all the water molecules within the 3.5 Å from any atom of each core region are included in each fragment QM calculation, while the remaining water molecules are represented by point charges. Although the total number of residue pairs is proportional to the square of the number of residues, the size of each fragment is independent of the overall protein size because each residue can have only a limited number of residues in its vicinity. Hence, the largest fragment normally contains less than 300 atoms consisting of C, H, O, N, and S, which is an affordable calculation at the HF and DFT levels. According to the recent work of Ochsenfeld and co-workers (Flaig et al, 2012), the buffer size utilized in the current AF-QM/MM approach is sufficiently large.

In this work, most of the NMR calculations were performed using the GIAO method with the TZVP basis set. Previous studies on small organic molecules have demonstrated that at least a triple-zeta basis set with diffuse basis functions should be utilized to accurately reproduce the experimental amide hydrogen chemical shift (Helgaker et al, 1999,Zhang et al, 2006). Because the computational cost is very demanding to apply large basis sets on the entire QM region, the use of locally dense basis sets, i.e. the combination of two basis sets where the larger one is used for the atoms of interest and the smaller one for all the other atoms, is adopted. The TZVP//4–31G* basis set was employed for protein amide hydrogen by combining with the explicit solvent model. The AFNMR program itself allows the user to choose basis sets and functional, as well as the program to be used for the molecular electronic structure calculations. For the nucleic acid and implicit solvent protein examples shown below, a mixed basis of TZVP/DZVP (Schafer et al, 1994) was used. The shielding tensors for the protein and nucleic acid systems presented here were computed using the OLYP density functional with GIAO basis functions implemented in the deMon3k program. The calculated chemical shifts were referenced to the the ¹H, ¹³C and ¹⁵N isotropic shielding constants computed for the NMR structure of Ubiquitin (PDB id: 1d3z) taken from the first model and minimized using the Amber FF99SB molecular mechanical force field at the same level used in this study (OLYP/TZVP: ¹H: 32.0 ppm; ¹³C: 182.5 ppm; ¹⁵N: 237.8 ppm). The DFT calculation on the amide proton in explicit solvent was performed using the Gaussian09 package (Frisch 2010). The quantum chemistry packages Q-Chem (Krylov et al, 2013,Shao et al, 2006) and ORCA (Neese 2012) are also interfaced with the AF-QM/MM program, but were not used for the results reported here. For a given basis set and density functional, the results for the four quantum chemistry programs are nearly indistinguishable.

Finally, we compare the performance of the AF-QM/MM method presented here with semi-empirical and classical chemical shift prediction models for protons. The shifts program—a chemical shift predictor built on a classical model—is distributed alongside the AF-QM/MM program and was used to compute the proton chemical shifts of the protein and nucleic acid systems. We further compared the performance of SHIFTX2, which uses a sequence-based semi-empirical model combined with a structure-based classical model to predict protein chemical shifts with remarkable accuracy. Since SHIFTX2 does not currently support nucleic acid systems, it was just used to compute the chemical shifts of the protein nuclei. One advantage that shifts has is that its classical equations used to predict the secondary chemical shifts are based only on the system conformation and utilize a simple, analytically-differentiable equation that makes it suitable for use as restraints in molecular dynamics simulations that rely on gradients to compute forces.

Results and Discussion

A. Fragmentation calculation vs. full system calculation

To check the performance of the AF-QM/MM method, we first use it to compute the ¹H, ¹³C and ¹⁵N absolute chemical shieldings of a small protein (30 residues, PDB entry: 2RTY) in the gas phase. The results are compared with the conventional full system calculation as shown in Figure 4. In the full system calculation, the protein is computed as an intact molecule (without any partition). The root mean square errors (RMSEs) for the ¹H, ¹³C and ¹⁵N are only 0.18, 0.80 and 1.16 ppm, respectively. These errors are small—less than 1% of the absolute chemical shieldings—and the correlation coefficients are above 0.99. The results show that, as expected, the AF-QM/MM calculated chemical shifts accurately reproduce the QM calculation of the full protein. It is worth noting that the calculation for each residue-centric QM/MM takes about 1-3 hours of computer time on a single node Intel Xeon 3.0 GHz processor (8 cores), using the current definition of the buffer region.

Figure 4.

Three-dimensional structure of 2RTY (441 atoms) and the correlation between AF-QM/MM and full system B3LYP/6–31G** calculations (in the gas phase) for ¹H, ¹³C, and ¹⁵N chemical shieldings.

B. AF-QM/MM with implicit solvent model

We also calculated the ¹H, ¹³C and ¹⁵N chemical shifts for three small proteins (PDB codes 2MC5, 1AIL and 1C44, with BMRB accession numbers 19428 (Liu et al, 2014), 4317 (Chien et al, 1997) and 4438 (Garcia et al, 2000), respectively) with a 3-dielectric implicit solvent model. Results are shown in Figs. 5–7. The utility of these computations clearly depends on the use that will be made of them. The chemical shifts plotted in Figures 5 to 7 are divided into separate colors based on the chemical environment of each proton. The differences in the chemical shifts of related nuclei that share a similar chemical environment results from so-called secondary chemical shifts caused by differences in the secondary and tertiary structures surrounding the nuclei. Discriminating between chemically similar nuclei is a more challenging problem than discriminating between nuclei whose chemical environments are drastically different. The prediction of secondary chemical shifts is discussed more thoroughly in section F.

Figure 5.

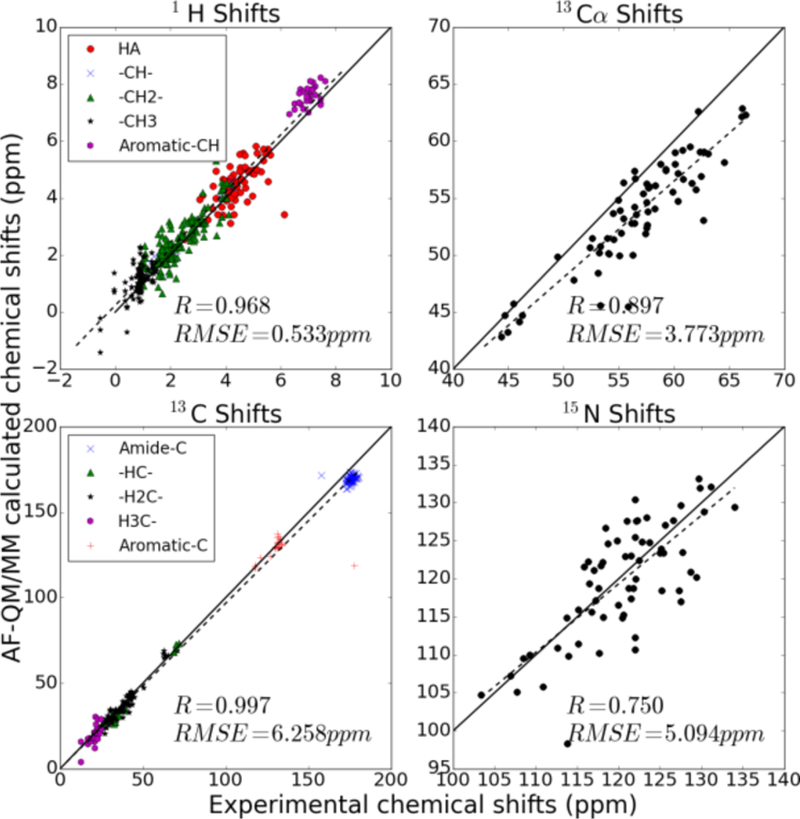
Correlation between experimental ¹H, ¹³C, ¹³C_α and ¹⁵N NMR chemical shifts and calculated chemical shifts of 2MC5 using the AF-QM/MM-PB method. (The amide hydrogen atoms (¹H_N) and ¹⁵N atoms on the side chain were excluded.)

Figure 7.

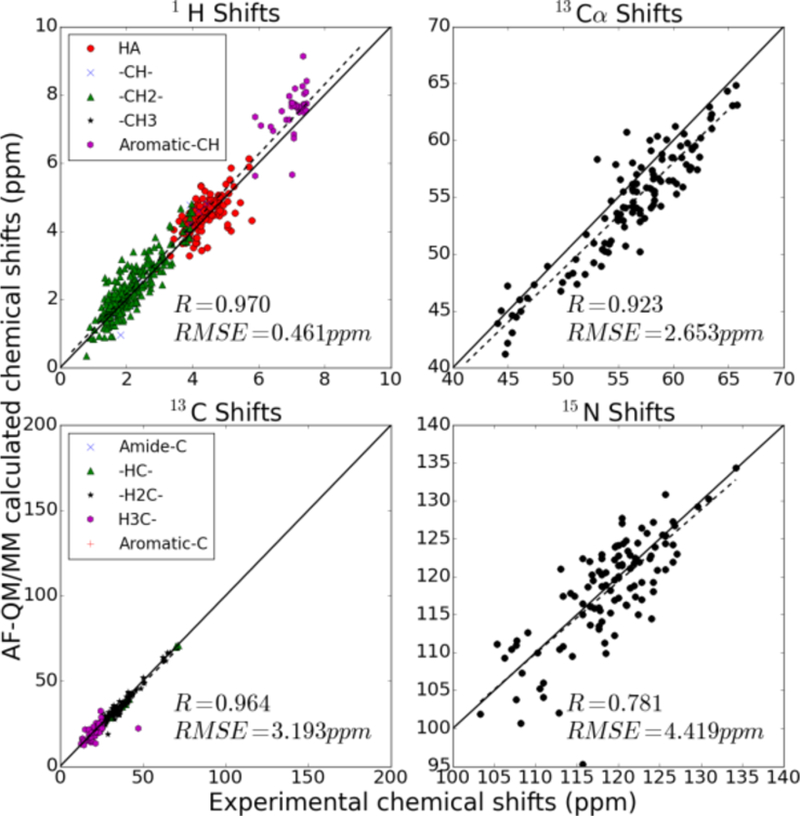
Same as Fig. 5 for PDB code 1C44.

C. AF-QM/MM for RNA

We computed the ¹H, ¹³C, and ¹⁵N chemical shifts of a UUCG hairpin RNA (Nozinovic et al, 2010) (14 residues, PDB entry: 2KOC) with the 3-dielectric implicit solvent model (solinprot), shown schematically in Figure 2. The PB equation was solved separately for each of the 14 fragments, leading to 14 distinct sets of surface charges surrounding the QM region.

Chemical shifts of all nuclei were computed as an average of the chemical shift for that nucleus over each of the 20 solved structures. The RMSE of the average ¹H chemical shifts computed for all protons in the structure for which experimental assignments were made is 1.12 ppm with a correlation coefficient of 0.852 (Figure 8). However, experimental assignments were made for numerous labile protons for which hydrogen bonding with solvent molecules is very important for accurate calculation of the shielding tensor. Even the 3-dielectric model used to model solvent effects implicitly seems unable to account for the effects of solvent on protons bonded to nitrogen.

Figure 8.

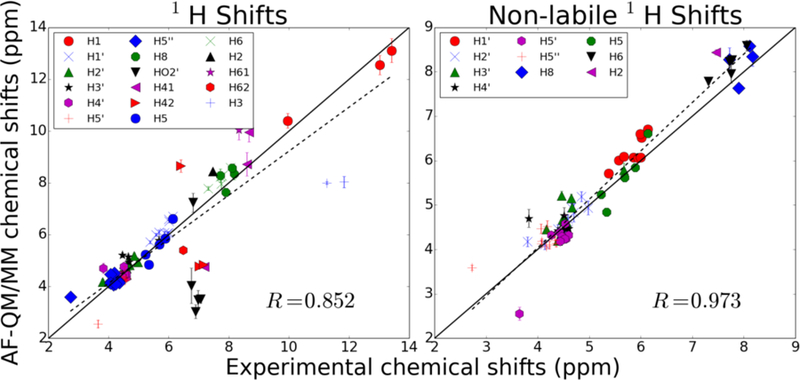
Proton shifts computed for all solved hairpin structures in 2KOC. Markers represent average shifts and error bars show the size of the standard deviation of the shifts. The plot on the left represents every proton with an assigned experimental shift. The plot on the right shows only shifts of non-labile protons.

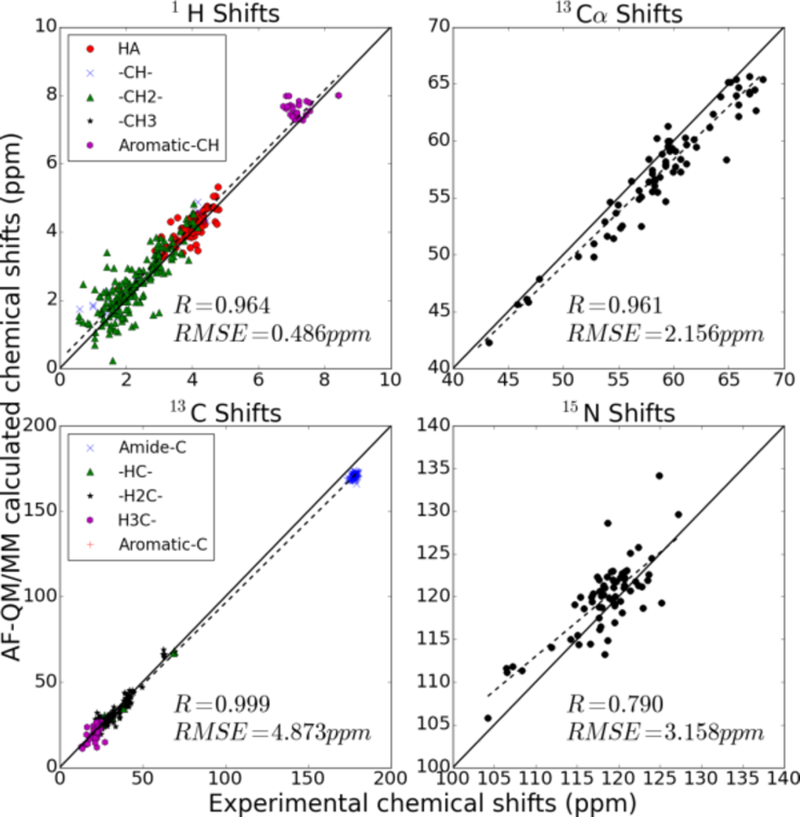
When ¹H atoms attached to nitrogen are omitted from the analysis, the chemical shift RMSE from experiment drops to 0.38 ppm, which is comparable in magnitude to empirical models (nuchemics and shifts). The ¹³C and ¹⁵N chemical shifts were predicted with a RMSE of 3.59 ppm and 7.80 ppm compared to experiment, respectively. The predicted chemical shifts correlate quite well with experimental measurements, having correlation coefficients of 0.999 and 0.998 for ¹³C and ¹⁵N chemical shifts, respectively. By contrast, no meaningful correlation was observed for phosphorus shifts using this model. We suspect that, as with labile protons, solvent effects may be very important for the accurate calculation of phosphorus chemical shifts. These results are summarized in Figure 9.

Figure 9.

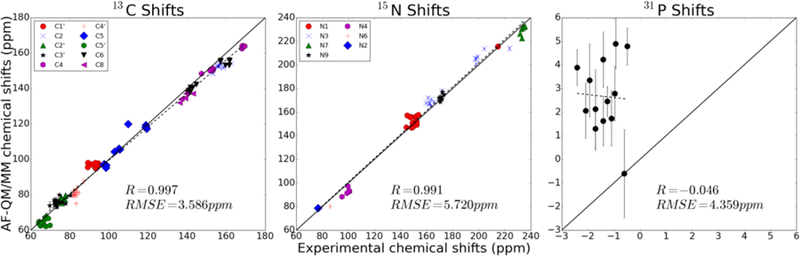
Heavy atom chemical shifts for 2KOC.

D. AF-QM/MM with DNA

We computed the ¹H chemical shifts of the self-complementary Dickerson dodecamer using the same 3-dielectric model implicit solvent model (solinprot) we used for the hairpin RNA structure. Like with hairpin structure, surface charges were computed from the reaction field calculated via the PB equation for all 24 fragments.

We used both the ensemble of NMR-derived structures solved in PDB id 1NAJ and the structure solved using X-ray refinement in PDB id 1BNA to compute chemical shifts for the non-labile protons of the dodecamer. The shifts—summarized in Figure 10—yield similar results for both families of structures, with RMSEs of 0.59 ppm and 0.52 ppm for the NMR and X-ray structures, respectively. While the calculated chemical shifts agree worse with experimental measurements and assignments than those reported for the RNA hairpin, the correlation is still quite strong (correlation coefficients near 0.97 for both sets of structures).

Figure 10.

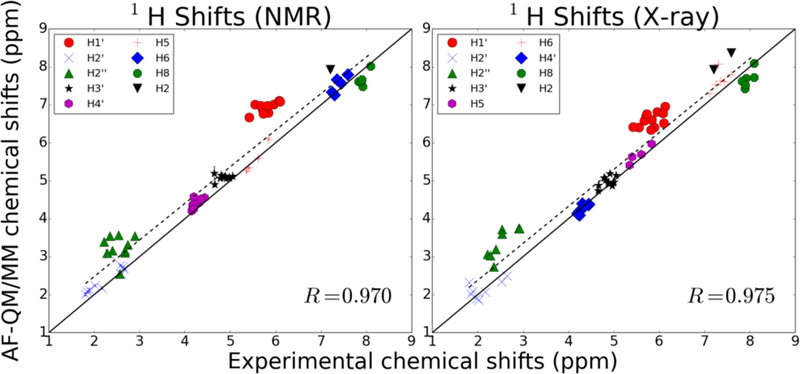
Proton chemical shifts for the Dickerson dodecamer. The plot on the left represents the predicted chemical shifts based on using the NMR-solved structures from PDB 1NAJ. The plot on the right is the shifts derived using the structure solved with X-ray crystallography in PDB 1BNA.

Of particular note in Figure 10 are the two groups of assignments whose calculated shifts are systematically downfield from their experimentally determined shift. The H1’ protons, measured between 5 and 6 ppm, have shielding tensors that are underestimated by AF-NMR, resulting in predicted shifts that are about 1 ppm downfield from their experimental shifts. There is a similar systematic underestimation of the shielding tensors for H2’ protons whose experimental assignments fall between 2 and 3 ppm, although the magnitude of the downfield shift error is smaller than for H1’ protons. Interestingly, the predicted chemical shifts for H1’ and H2’ protons are modestly improved when using the crystal structure instead of the NMR structures, suggesting that the AF-NMR chemical shift prediction may be improved compared to experiment if better structures are used.

E. AF-QM/MM with explicit solvent model

In the previous calculations, the chemical shifts of amide hydrogen atoms (1HN) were excluded. However, the 1HN chemical shifts play key roles in NMR signal assignments and are the most precise NMR parameters that can be measured. Thus, a QM model that can accurately predict their chemical shift is in demand. Previous studies (Zhu et al, 2013) have found that the main reason for the inaccuracy in predicting 1HN chemical shifts originates from the improper treatment of the solvation effect, especially the specific solvent-solute hydrogen bond effect. To include these effects in the calculation, explicit inclusion of solvent molecules is introduced in the AF-QM/MM method (see Figure 11). The NMR structure of protein basic pancreatic trypsin inhibitor (BPTI) mutant A16V (first structure from PDB entry 1LD5, BMRB accession number 5381) is taken as the initial geometry. About 300 water molecules were added by the PLACEVENT program to mimic the first solvent shell. As shown in Figure 12, the predicted 1HN NMR chemical shifts in explicit solvent show remarkable improvement over those calculated with the implicit solvation model. The correlation coefficient (R) between the theoretical and experimental values is improved from 0.44 to 0.61. Although this is an encouraging improvement over the implicit solvent model, it is clear that there is still much room for improvement. The interaction between protein and water is essentially a dynamical phenomenon. It is also difficult to predict the accurate location and distribution of water molecules on the surface of a protein. Further studies in this area are ongoing.

Figure 11.

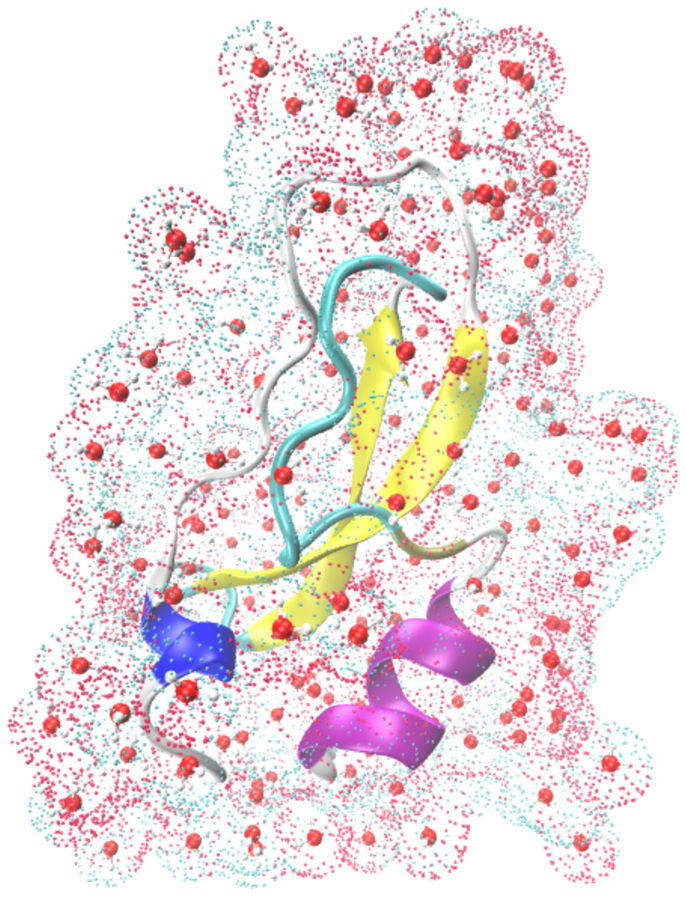
Graphical representation of a small protein (PDB entry: 1LD5) together with the first solvation shells and surface charges calculated by DivCon program (colored dots represent the surface charges).

Figure 12.

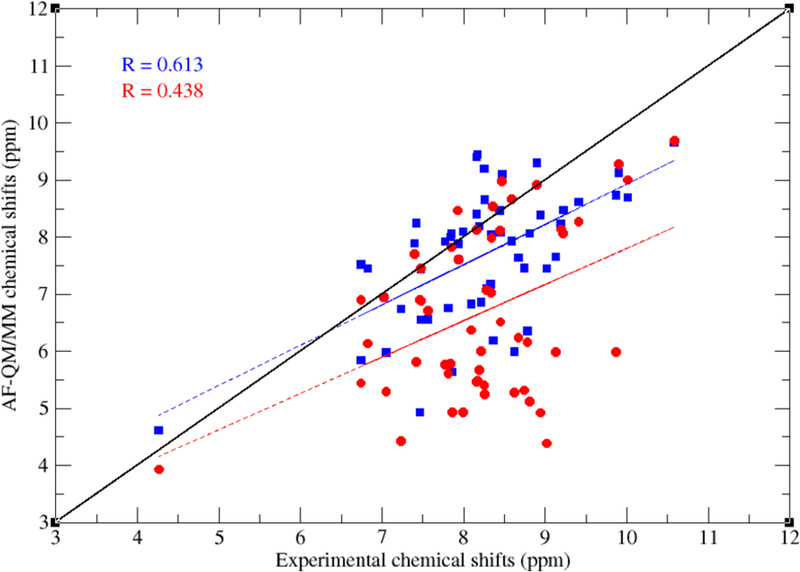
Correlation between experimental and calculated ¹H_N chemical shifts of BPTI mutant A16V (PDB entry:1LD5) using the AF-QM/MM method (the QM level is at OLYP/TZVP//4–31G*). Red and blue dots represent the results using the implicit and explicit solvent models, respectively.

F. Comparison with classical and semi-empirical models

In this section, the performance of the AF-QM/MM is compared to that of commonly-used semi-empirical and classical chemical shift predictors for proton signals. Chemical shifts for the protein systems (PDB IDs 1ail, 1c44, 2mc5, and 1dz3) were computed using both the shifts and SHIFTX2 programs, which utilize a structure-based and combined structure and sequence-based prediction algorithm, respectively, while the nucleic acid chemical shifts were only computed with the shifts program. The results for the chemical shifts of the protein protons are summarized in Figure 13, while those for the heavy atoms ¹³C and ¹⁵N are shown in Figure 14 and 15, respectively.

Figure 13.

Comparison of proton chemical shifts for all protons in the structures with PDB IDs 1c44, 2mc5, 1ail, and 1d3z predicted using the AF-QM/MM model, shifts classical model, and SHIFTX2 semi-empirical/classical model. The chart on top shows the correlation coefficient, R, between the predicted and observed chemical shifts. The chart on bottom shows the average signed chemical shift deviation compared to experiment with the error bars indicating the standard deviation of the computed errors. The HA protons are those attached to the Cα of each amino acid. The rest are shown in their local chemical environment.

Figure 14.

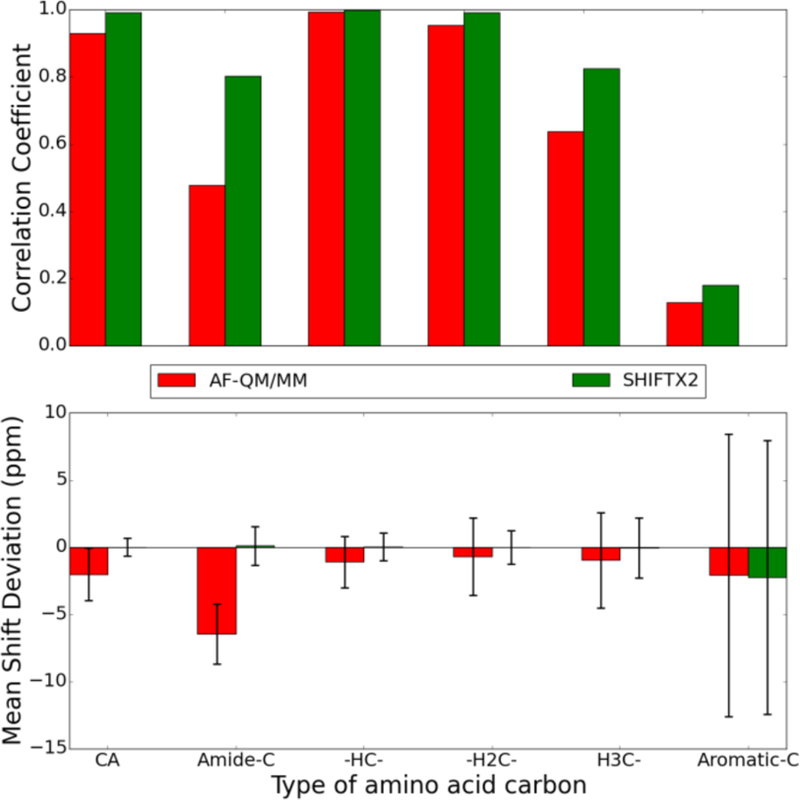
Comparison of ¹³C chemical shifts for all carbons in the structures with PDB IDs 1c44, 2mc5, 1ail, and 1d3z predicted using the AF-QM/MM model and SHIFTX2 semi-empirical/classical model. The chart on top shows the correlation coefficient, R, between the predicted and observed chemical shifts. The chart on bottom shows the average signed chemical shift deviation compared to experiment with the error bars indicating the standard deviation of the computed errors. The CA carbons are the Cα of each amino acid. The rest are classified by their local environment.

Figure 15.

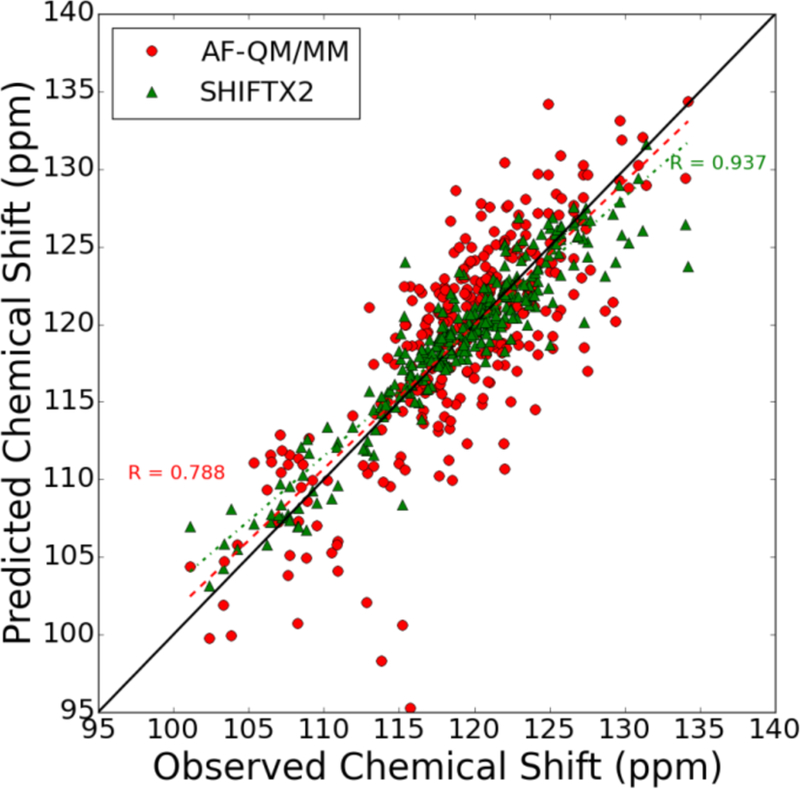
Comparison of amide ¹⁵N chemical shifts in the structures with PDB IDs 1c44, 2mc5, 1ail, and 1d3z predicted using the AF-QM/MM model and SHIFTX2 semi-empirical/classical model. The correlation coefficient for the SHIFTX2 model is shown in the upper right (0.947) while that for the AF-QM/MM model is shown in the lower-left (0.788). The best-fit line for each data set is shown alongside the raw data.

The AF-QM/MM model with implicit solvent performs poorly for protons bonded to nitrogen compared to those bonded to carbon. This behavior is not surprising, though, given that the effect of hydrogen bonding with solvent frequently contributes to deshielding nitrogen. Using an explicit solvent model with AF-QM/MM yields some improved agreement with experiment (as shown in Fig. 12), but also increases the computational cost of the calculations.

The AF-QM/MM model yields similar accuracy for the nucleic acid structures surveyed here compared to those computed for non-labile protons on proteins. However, the mean signed deviation of the AF-QM/MM predicted shifts to experiment is larger for many of the non-labile protons in RNA and DNA compared to the proteins. This is not completely surprising, though, given that nucleic acids carry a much larger net charge than proteins and each residue contains at least one aromatic ring, making them more challenging targets for chemical shift prediction.

The correlation coefficients for the various types of protons, related to the secondary chemical shifts (i.e., the structure-dependent contribution to the chemical shift relative to a “random coil” shift), are greater than 0.5 for most protons, and closer to 0.8 for many of them (see Figure 16 and 17). With the exception of the H4’ proton in the 2KOC structure, these correlation coefficients are very similar to those obtained using the classical model implemented in shifts. This means that AF-QM/MM is as good at distinguishing between two different protons of the same type as shifts is for the nucleic acid structures considered in this study.

Figure 16.

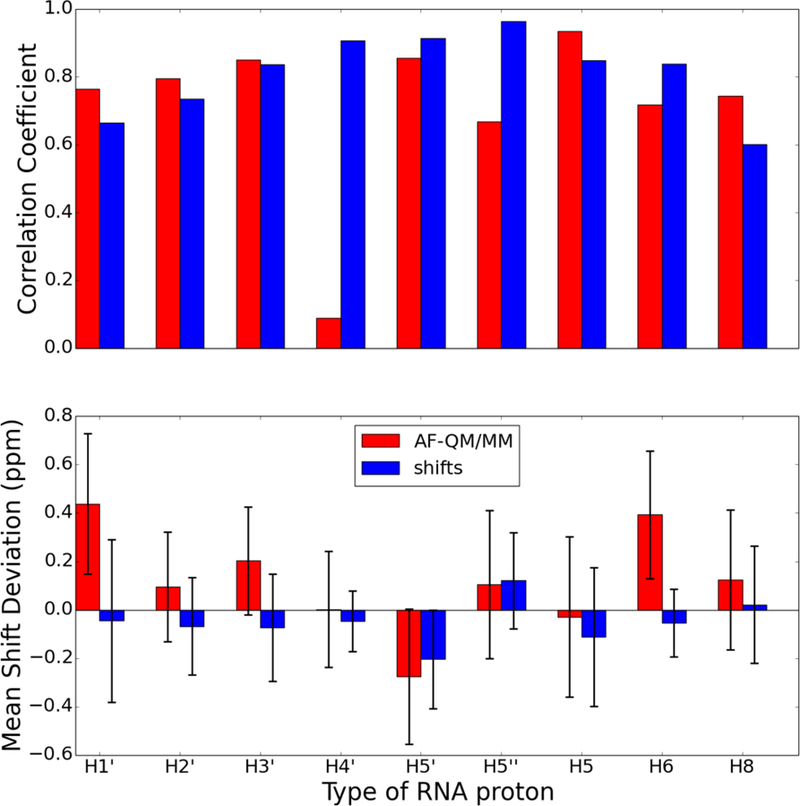
Comparison of proton chemical shifts for all protons in the UUCG RNA hairpin (PDB id 2KOC) predicted using the AF-QM/MM model and shifts classical model. The chart on top shows the correlation coefficient, R, between the predicted and observed chemical shifts. The chart on bottom shows the average signed chemical shift deviation compared to experiment with the error bars indicating the standard deviation of the computed errors. The proton types correspond to the PDB naming convention (e.g., H1’ is the proton attached to C1’ of the ribose).

Figure 17.

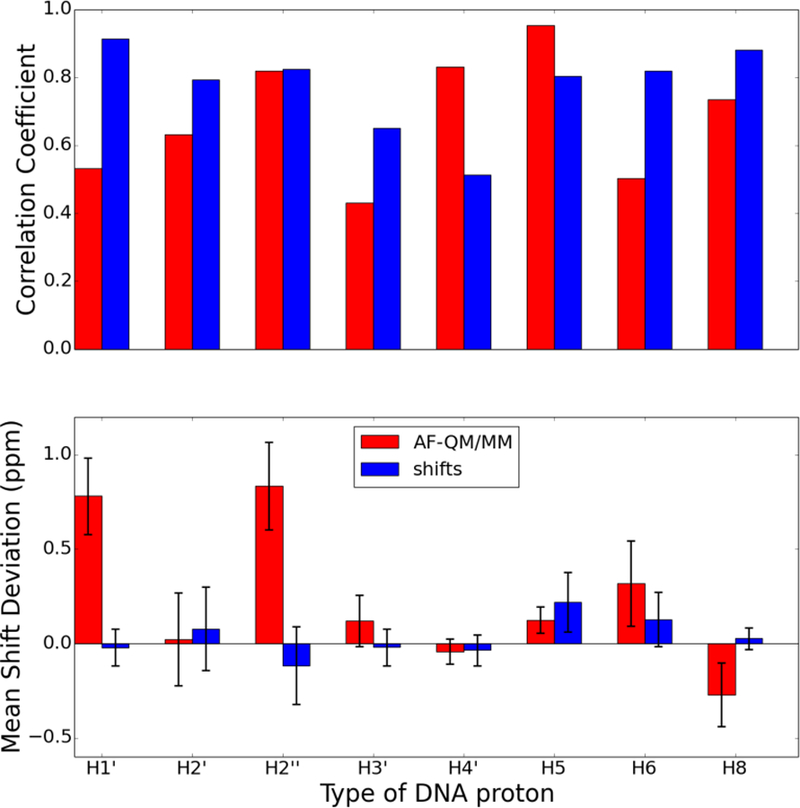
Comparison of proton chemical shifts for all protons in the Dickerson dodecamer (PDB id 1BNA) predicted using the AF-QM/MM model and shifts classical model. The chart on top shows the correlation coefficient, R, between the predicted and observed chemical shifts. The chart on bottom shows the average signed chemical shift deviation compared to experiment with the error bars indicating the standard deviation of the computed errors. The proton types correspond to the PDB naming convention (e.g., H1’ is the proton attached to C1’ of the ribose).

Conclusion

In this work, we evaluated a density functional theory (DFT)-based chemical shift prediction model based on an automated fragment hybrid quantum mechanical-molecular mechanical (AF-QM/MM) approach to predict ¹H, ¹³C, and ¹⁵N chemical shifts for proteins and nucleic acids. We then compared the performance of this model to the performance of other leading programs for computing classical and/or empirical chemical shifts—shifts and SHIFTX2.

The AF-QM/MM approach can either model solvent effects implicitly through a set of surface charges computed using the Poisson-Boltzmann equation or explicitly through the placement of water molecules in the first solvation shell around the solute. While adding explicit solvent molecules to the system can significantly increase the cost of the DFT calculations, it substantially improves the prediction of the chemical shifts of protons involved in hydrogen bonding with solvent, like the amide protons in proteins. For non-labile protons, the explicit solvent model offers little if any improvement in accuracy over the implicit solvent models.

While the correlation between the AF-QM/MM shift predictions and experiment is often strong—with R² values between 0.9 and 1—for non-labile ¹H and ¹³C nuclei, chemical shift prediction models are the most helpful when they can differentiate between two nuclei in the same general chemical environment in two different parts of a biomolecule. The differences between the chemical shifts of two nuclei in the same environment arises from the different local conformation around each nucleus, and it is these so-called “secondary” chemical shifts that are the most difficult to predict. The correlation between experimental and calculated secondary shifts is substantially worse for several of the families of nuclei surveyed here than the overall correlation coefficients reported for all ¹H or ¹³C nuclei. However, for many types of nuclei—specifically non-labile protons and aliphatic carbons—the AF-QM/MM correlation coefficients computed for those families of nuclei were still larger than 0.9 for both protons and carbons.

By comparison, several of the classical and semi-empirical chemical shift predictors significantly outperform AF-QM/MM both in predicting absolute chemical shifts as well secondary chemical shifts, at least for globular proteins. This trend is particularly pronounced for labile protons, although it holds for almost every type of nucleus. However, there are still advantages to using the AF-QM/MM model: the classical and semi-empirical models are heavily parameterized, and as a result can only effectively predict chemical shifts accurately for the subset of amino acid and nucleic acid residues and structural motifs that make up the original training set. For example, neither SHIFTX2 nor shifts will even attempt to predict the chemical shifts of nuclei belonging to non-standard amino or nucleic acid residues. By contrast, AF-QM/MM takes as input only the elements and starting positions of the atoms, in addition to a set of force-field charges that are frequently derived through QM calculations. As a result, AF-QM/MM can more readily be applied to structures containing non-standard residues, whether they are modified amino or nucleic acids or some ligand or cofactor. Furthermore, given that the parameters used in AF-QM/MM calculations are not fit to a training set of experimental chemical shift data, an accurate prediction of chemical shifts likely reflects a proper treatment of the underlying physics behind NMR measurements.

The AF-QM/MM method presented here can be a useful tool to probe primary and secondary chemical shifts for NMR-active nuclei, in particular non-labile protons and aliphatic carbons. Nuclei that interact more strongly with solvent molecules tend to be predicted more poorly than other nuclei. These nuclei would likely benefit from an improved treatment of solvent effects. Furthermore, chemical shifts are inherently an ensemble property, and they are highly sensitive to small changes in local conformation like bond lengths, angles, and torsional angles. As a result, AF-QM/MM chemical shift predictions can also likely be improved by using “better” starting structures as well as averaging over more representative structures of the ensemble such as those derived from a molecular dynamics simulation with a high-quality force field.

As with all shifts prediction routines, errors can arise both from uncertainties in the input structures and from limitations of the quantum chemistry and implicit solvent models that are used. (Errors arising from the fragmentation procedure itself are most likely quite small, as illustrated in Fig. 4.) The results shown here only provide examples of typical behavior. It is likely that better input structures would give improved results; some evidence for this comes from studies of ubiquitin, where extensively-refined NMR solution structures are available. The AF-QM/MM results reported for ubiquitin (Case 2013) are in closer agreement with experiment than those shown here in Fig. 5–7. More experience with this method will be required to better understand the sources of errors with respect to experimental values.

The AFNMR program is available with the shifts classical chemical shift prediction software at http://casegroup.rutgers.edu/shifts.html. We have attempted to automate the process as much as possible, so that default calculations require only a PDB file as input. The preliminary processing creates fragment input files for the Gaussian, ORCA, Q-Chem or deMon2k programs; analysis programs parse the quantum chemistry output files to create tables of computed shifts and to make comparisons with experimental data if it is available. Optional parameters control the level of calculation and basis set, and the type of explicit or implicit solvent model that is used.

Figure 6.

Same as Fig. 5, for PDB code 1AIL.