Disease prediction by cell-free DNA methylation

Abstract

Disease diagnosis using cell-free DNA (cfDNA) has been an active research field recently. Most existing approaches perform diagnosis based on the detection of sequence variants on cfDNA; thus, their applications are limited to diseases associated with high mutation rate such as cancer. Recent developments start to exploit the epigenetic information on cfDNA, which could have substantially wider applications. In this work, we provide thorough reviews and discussions on the statistical method developments and data analysis strategies for using cfDNA epigenetic profiles, in particular DNA methylation, to construct disease diagnostic models. We focus on two important aspects: marker selection and prediction model construction, under different scenarios. We perform simulations and real data analysis to compare different approaches, and provide recommendations for data analysis.

Introduction

Prognosis and diagnosis play vital roles in the prevention and treatment of diseases. Traditionally, various types of surgical biopsies such as bone marrow or needle biopsies are performed in clinical setting, especially for cancer diagnosis [1]. However, because of the invasive nature of the procedure and the potential sampling bias of tumor biopsy, surgical biopsy is often not a preferred choice. As an alternative to surgical biopsy, researchers and clinicians have been looking for molecular biomarkers for disease diagnosis. These biomarkers, either genetic or epigenetic, carry various indicative features for biological or disease states. They help achieve disease state detection, subtypes classification, progression prediction and response-to-treatment characterization [2]. The scope of molecular biomarker discovery has been greatly expanded during the past two decades, because of the advances of high-throughput genomics technologies such as microarray and next-generation sequencing. For example, based on gene expression microarray data, Prediction Analysis for Microarrays (PAM) identified a subset of gene biomarkers for cancer class prediction [3]. The PAM50 panel, which tests a group of 50 selected genes, has become the de facto gold standard for breast cancer subtype classification and metastasis prediction [4]. Zilliox et al. [5] created the ‘gene expression barcode’, which was trained on public gene expression microarray data, and can predict for a number of diseases given a new microarray data set.

In recent years, disease diagnosis based on molecular biomarkers in specimen, including blood, urine and cerebral spinal fluid, has gain tremendous attention. For example, the practice to look for traces of cancer DNA by interrogating biomarkers on plasma-isolated cell-free DNA (cfDNA) or circulating tumor DNA (ctDNA) is known as ‘liquid biopsy’ [6]. As a safer, cheaper and quicker alternative to surgical biopsy, the liquid biopsy has great potential in clinical practice. cfDNAs are short DNA fragments (∼160–180 base pairs) existing in plasma. When normal cells undergo apoptosis in a healthy individual, DNA fragments from the cells are shredded and released to blood stream. Thus, cfDNA is a mixture of DNA fragments from different cell types. In cancer patients, the cfDNA includes some ctDNA, which are DNA fragments released from cancer cells [7]. As a hallmark of cancer, the ctDNA carries tumor-specific genetic variants such as copy number variation and point mutations. After capturing and sequencing the cfDNA, ctDNA can be distinguished from normal cfDNA by tumor-specific genetic variants. Presence of nontrivial amount of ctDNA is an indication of cancer.

The essence of using cfDNA for cancer diagnosis is to detect ‘abnormal’ cfDNA segments. Here, the abnormality is defined as the presents of unusual genetic variants. This principal, however, is only applicable to ‘mutation-rich’ diseases—the ones with high rate of genetic alteration such as cancer. For many ‘mutation-poor’ diseases and disorders not associated with high level of genetic alteration, other approaches are needed. Recently, researchers start to explore the cfDNA epigenetics information such as DNA methylation or nucleosome position to look for biomarkers for diagnosis [8–11]. In analogous to the liquid biopsy, these approaches try to define abnormality based on the epigenetic profiles, and then construct model for disease prediction.

In this work, we focus on cfDNA methylation and explore how they can be used for disease prediction. We systematically review the existing publications and investigate the statistical methods for cfDNA methylation study. We discuss two important aspects: marker selection and prediction model construction, under different scenarios. We conduct extensive simulation and real data analysis, and provide some recommendations for data analysis strategies based on the results.

The cause of alteration of cfDNA methylation in disease

DNA methylation is an epigenetic modification on the DNA molecule. It plays an important role in cell development and gene regulation, and is associated with many diseases [12–14]. DNA methylation is known to be highly tissue-specific [15], which is an important basis for cfDNA methylation data analysis. Even though different tissues share exactly the same DNA sequence, the differences in their methylomes allow one to trace the tissue of origins of cfDNA, and subsequently use that information for disease prediction.

Considering cfDNA as a mixture of DNA segments from different tissues, the differences in cfDNA methylation between patients and healthy people could be from two sources. The first one is the alteration in one particular tissue type in disease, for example the methylation level changes in certain cell types between breast carcinoma versus normal [16]. The second is the change in mixing proportions in the composition of cfDNA, for example hepatocellular carcinoma (HCC) patients have an increasing proportion of cfDNA fragments originates from apoptotic liver cells [17]. It is important to note that both changes are usually not reflected in the methylation profiles in the blood sample; thus, one cannot construct disease prediction model from blood data but have to rely on cfDNA.

It is well known that DNA methylation is highly tissue-specific [8, 18–20]. Thus, both of these changes will lead to the marginal cfDNA methylation changes between cases and controls. For disease prediction, the most straightforward idea is to detect differentially methylated loci (DML) or regions (DMRs) between cases and controls from the cfDNA methylation data, and use the methylation levels in those regions as predictors for diagnosis [10, 11]. Another family of approaches is to first trace the tissue-of-origin of cfDNA and estimate the mixing proportions, and then construct a model to predict disease status based on the estimated proportions. This type of methods takes advantage of the tissue specificity of epigenetic profiles such as DNA methylation or nucleosome position, and uses signal deconvolution methods for proportion estimation [8, 17, 21]. We conduct detailed simulation studies to compare these two types of approaches under different scenarios (detailed in later section).

Existing works

Table 1 lists the existing publications for using cfDNA epigenetic profiles in disease diagnosis [8–11, 15, 17, 21–30]. As discussed before, the prediction model construction can be roughly categorized into two classes: (1) using the marginal cfDNA epigenetic profile as predictors or (2) using the mixing proportions as predictors. The first class includes [9–11, 15, 22, 23, 26, 27, 30]. For example, Xu et al. [9] used 10 cfDNA methylation markers for diagnosis of HCC using logistic regression. Another example is using Random Forest (RF) on a set of regions to classify cancer types [10]. The second class includes [8, 17, 28]. For example, Kang et al. [8] modeled proportion of tumor-derived cfDNA and used a probabilistic model to predict tumor burden and tumor type. Sun et al. [17] used an external thousands-marker reference panel to solve for tissue proportions in HCC patients and healthy controls. The estimated proportions can potentially be used for disease diagnosis.

Table 1.

List of publications of using cfDNA epigenetics information to infer disease

Disease	Epigenetic profile used	Data type	Sample size	Prediction method	Publication
Lung cancer, HCC, pancreatic cancer, glioblastoma, gastric cancer, colorectal cancer, breast cancer patients	5hmC	hMe-Seal	49	RF, Mclust	Song et al. [10]
Colorectal cancer, gastric cancer, pancreatic cancer, liver cancer, thyroid cancer	5hmC	hMe-Seal	350	Logistic regression	Li et al. [11]
HCC	5mC	BS-seq	1933	Logistic regression	Xu et al. [9]
Pregnant/nonpregnant plasma	5mC	BS-seq	27	NA	Jensen et al. [22]
General cancer	5mC	Methylation 450k microarray/BS-seq	87	Probalistic model for tumor burden	Kang et al. [8]
Diabetes, multiple sclerosis, traumatic or ischemic brain damage, pancreatic cancer or pancreatitis	5mC	Methylation 450k microarray	218	NA	Lehmann-Werman et al. [23]
General disease	5mC	Methylation 450k microarray/BS-seq	NA	NA	Tanic et al. [24]
Colorectal, breast, lung, pancreatic and ovarian cancers	5mC	Methylation 450k microarray/BS-seq	NA	NA	Warton et al. [25]
General disease-related pathogenic mechanisms	5mC	Methylation 450k microarray	N=4 (17 tissues)	NA	Lokk et al. [26]
Colon, prostate, breast, lung cancer	Nucleosome positioning	DNA sequencing	179	Coverage depth	Ulz et al. [21]
Pregnancies/nonpregnancies	5mC	Methylation 450k microarray	22	NA	Hatt et al. [27]
Lung, colorectal cancer	5mC	BS-seq	59	NA	Guo et al. [28]
Tissue-specific methylation	5mC	MethylC-seq	N= 4 (18 tissues)	NA	Schultz et al. [15]
General cell types contribution	Nucleosome positioning	DNA sequencing	60	Coverage depth	Snyder et al. [29]
Prenatal, cancer and transplantation assessments	5mC	BS-seq	83	QP	Sun et al. [17]
Metastatic breast cancer	5mC	BS-seq	120	NA	Legendre et al. [30]

Note: The epigenetics information used is either DNA methylation (5mC), DNA hydroxymethylation (5hmC) or nucleosome position.

In addition to DNA methylation, there is attempt to use other cfDNA epigenetic information such as nucleosome position for disease prediction [29]. Snyder et al. found that during apoptosis, genomic DNA protected by nucleosomes will be released to bloodstream, and the unprotected naked DNA will be degraded. The tissue-specific nucleosome positioning causes different fragmentation pattern in cfDNA, thus allows one to trace the tissue of origin, which could be helpful for conducting disease prediction. However, because of the limited number of researches and data available, using cfDNA nucleosome position to predict disease will not be included in this review.

Methods

Marker selection

Marker selection is the first step in disease prediction model construction. In cfDNA methylation studies, both the whole-genome bisulfite sequencing (WGBS) and the human 450k/27k methylation array profile large number of CpG sites. A majority of these CpG sites are either irrelevant, noisy or redundant for distinguishing the underlying disease status. Including all CpG sites as features in the model will have harmful impacts on traditional machine learning algorithms such as support vector machine (SVM) [31]. Therefore, marker selection is an important step to alleviate problem caused by bad markers. Typically, researchers select tens to thousands of markers based on data from all CpGs. These makers could be CpG sites, CpG clusters [8] or fixed-size genomic bins [17]. The selection criteria are typically based on the differentiating power of the markers, that is, selecting features showing significant differences among different tissues [17] or wide between-group methylation ranges [8]. All existing publications use their own approach for selecting CpG sites. These approaches generally take following three aspects into consideration. First, some studies use DML as predictive markers. For example, Xu et al. [9] used 10 highly selective CpGs as the informative markers in diagnosis of HCC. It is a direct and reasonable approach because selected markers are discriminative for disease status. Second, some studies use regions instead of single CpG markers as features for prediction. For example, Song et al. [10] used 5hmC signal within the gene body, Kang et al. [8] used 100 bp upstream and downstream CpG sites as regions and Lehmann-Werman et al. [23] used several adjacent CpG sites as the basic unit for features. The underlying assumption of choosing region instead of single CpG site as the feature is that adjacent CpG sites have similar methylation level, and pooling information from nearby CpG sites together can stabilize and enhance signals. Third, some studies borrow biological information from external data to select markers. For example, Xu et al. [9] used solid tumor samples from The Cancer Genome Atlas (TCGA) to conduct preliminary marker selection. The intuition behind such approach is that features differ significantly between solid tumor and normal tissue would also be likely to demonstrate detectable methylation differences in the cfDNA of the same disease.

To select informative and discriminative markers for disease prediction, we suggest detecting DML from training data first. The criteria for selecting markers from this step can be relatively loose, to retain relatively large number of markers. Next, when external biological information such as markers from tissue-specific methylation is available, one can use these locations to filter the markers from the previous step. Furthermore, one should consider pooling nearby CpG sites together to create regions if possible, instead of using single CpG site. This will help boost and stabilize the methylation signals. Finally, to determine the number of markers allowed in the final statistical model, one needs to conduct cross-validation to select the optimal number that minimize the prediction error. After all these steps above, data of the selected markers for all samples can be used either directly as features for disease prediction or for signal deconvolution (more details in ‘Disease prediction approach’ subsection).

Data generative model

Once the markers are selected, the next step is to build statistical model to predict the disease status. The training data include the cfDNA methylation profiles (denoted as Y, could be from the WGBS or the 450k/27k methylation array) for the selected markers, and disease status (denoted as Z) for N subjects including N₀ patients and N₁ healthy people (N = N₀+ N₁). Y is a matrix of M by N, where M is the number of preselected biomarkers (CpG sites or regions). Z is a binary vector of length N (1 for case and 0 for control). The goal of the problem is to use cfDNA methylation data (Y) to predict disease status (Z).

Suppose there are T tissues releasing DNA fragments into the cfDNA pool in plasma. Denote the methylation profiles for the M biomarkers in these T tissues as matrix R. R is of dimension M by T, where each column represents the methylation levels of the M biomarkers from one tissue. It is important to note that because of biological variation, the R matrices are not exactly the same from different people. However, the marker selection step guarantees that the variation among individual for the same tissue is significantly lower than the difference among different tissues. Moreover, as there could be differential methylation in certain tissue types between cases and controls, R in cases can be potentially different from the R in controls. In some situation, R can be obtained from methylomes of specific tissues or purified cell types [17]. R could also be unknown or unavailable if we do not have external information about those biomarkers or the tissues of interests.

As described earlier, cfDNA is a pool of mixing DNA fragments from each of the T tissues. For each individual, the tissue proportion is a vector of length T. Each element in the vector is a number between 0 and 1, and all elements from the vector will sum up to 1. For these N individuals, the tissue proportions are represented as a T by N matrix $\Pi$, where ${\pi }_{ij}$ is the tissue proportion of the $i^{th}$ tissue in the $j^{th}$ individual, and $i=1,\dots , T;j=1, \dots , N.$ It has the restriction of ${\sum }_{i=1}^T{\pi }_{ij}=1$ and each ${\pi }_{ij}\in [0, 1]$.

Following the above notations, the expected values of the cfDNA methylation (Y) are a mixture of the tissue-specific methylation (R):$E\left(Y\right)=R\Pi$. We use the expectation notation $E(.)$ here because the observed cfDNA methylation data Y contains random noises. For modeling and computational convenience, it is commonly assumed the random errors following normal distribution with mean 0. From this model, it is clear that the differences in either R or $\Pi$ will cause $E\left(Y\right)$ to differ between two groups. In the next section, we will discuss the possible statistical methods for using cfDNA methylation data Y to predict the disease.

Disease prediction approach

With training data, several methods can be applied for disease status prediction:

Directly using marker methylation to predict

As the most straightforward approach, one can directly use the observed cfDNA methylation (Y) to predict disease status Z, using an off-the-shelf machine learning [9–11] or model-based approach [8]. The trained model can be evaluated using test data, and eventually used as a panel to diagnose new patients. This approach is easy and intuitive, and widely used in many existing publications [8–11]. As differences in either R or $\Pi$ will cause $E\left(Y\right)$ to differ between case and control, one does not need to know exactly the source of changes as long as Y can predict Z.

Prediction based on tissue mixing proportions

To take a step further than using marker data directly, there are some researches to first estimate the mixing proportion $\Pi$, and then using $\Pi$ as predictor for diagnosis. The underlying assumption is that the disease is associated with the change of mixing proportions (which is related to cell death rates). The proportions estimation can be viewed as a dimension reduction step, which can potentially improve the signal-to-noise ratio in the data and lead to better prediction accuracy. An added benefit of this approach is that the results are more interpretable: disease is associated with the proportion change of certain cell type, which could be related to the cell death rate for that tissue.

The estimation of the mixing proportions can be achieved by using following two different procedures.

• 1. Reference-based method

When external reference panel R is available, the estimation can be done by regressing the mixed signal Y to purified tissue reference R. As the regression coefficients are not totally free parameters and have to satisfy some constraints (between 0 and 1, sum up to 1 in each individual), the problem is a constrained linear regression in the following form:

$$\left\{\begin{array}{c}E\left(\mathit{Y}\right)=R\Pi \\ {\sum }_{i=1}^T{\pi }_{ij}=1\\ 0{\le \pi }_{ij}\le 1\end{array}\right..$$

This can be converted into an optimization problem to minimize the residual sum of squares. The optimization problem has a quadratic loss function and linear constraints, and thus can be solved by quadratic programming (QP) algorithm.

With estimated proportions, we can train a SVM to predict Z from $\widehat{\Pi }$ from training data. When a new patient coming in, one can use the reference panel R to solve for new individual’s tissue proportion $\widehat{\pi }$ using QP, and then apply the trained SVM on $\widehat{\pi }$ to predict disease status.

This approach is easy, intuitive and computationally efficient. The only shortcoming is the requirement of R. One can look for R in public data but has to assume that it is not significantly different from the reference methylome of the population under study, which could be a strong assumption.

• 2. Reference-free method

When external reference panel R is unavailable, one can use nonnegative matrix factorization (NMF) algorithm to jointly solve for R and $\Pi .$ Briefly speaking, NMF is an algorithm that factorizes a matrix, say V, into two matrices W and H, such that: $V=WH$, where all three matrices contain nonnegative elements. Because W and H are both unknown, the factorization is solved by numerical approximation methods [32]. To be specific, the estimator of W and H follows:

$${argmin}_{W,H}{\left|\left|\mathit{V}-\mathit{W}\mathit{H}\right|\right|}^2,$$

where $0\le W\le 1$, $0\le H\le 1$ and ${\sum }_i{H}_{ij}=1$ for any j. After initialization of W and H, a procedure is taken to estimate W given fixed H, and then estimate H given fixed W, iteratively, until it converges. NMF was traditionally used on chemometrics, signal processing and image processing [33, 34]. Recently, NMF is gaining popularity among computation biological research community, especially in analyzing data from highly heterogeneous samples [35–37]. One major reason for this popularity is that the factorized matrices are in reduced dimensions and have better biological interpretation.

In estimating mixing proportions from cfDNA methylation, we factorize methylation matrix Y into two nonnegative matrices W and H, while constraining each cell in matrix H takes value within [0, 1] and each column in matrix H sum up to 1. To be noticed, the original version of NMF only requires W and H to be nonnegative but does not have those added constrains. The algorithm was specifically customized by adding these new constraints to solve for W and H for DNA methylation study [36, 38, 39]. Then, W can be interpreted as a sudo-reference matrix comparable with the external reference matrix R, and H can be interpreted as a sudo-tissue-proportion matrix similar to the tissue proportion matrix $\Pi$. Matrix H can then be used for disease status prediction, resembling using QP-solved proportion matrix $\Pi$.

NMF provides a flexible way to solve for tissue proportions when the external tissue reference information is unavailable. Under the context of cfDNA methylation study, assume we have training data for N individuals (with known disease status) and new patients (with cfDNA methylation data but disease status is unknown). Reference-free NMF-based approach is the following. First, we apply NMF on training data Y to factorize it into two matrices W and H. As the columns from H represent individuals with known disease status Z, we train an SVM using H to predict Z. Then, we regress new patients’ data ($Y^b$) on W using a constrained linear regression to get testing data’s tissue proportions ($H^b$). Finally, we apply the trained SVM on $H^b$ to predict disease status for new patients.

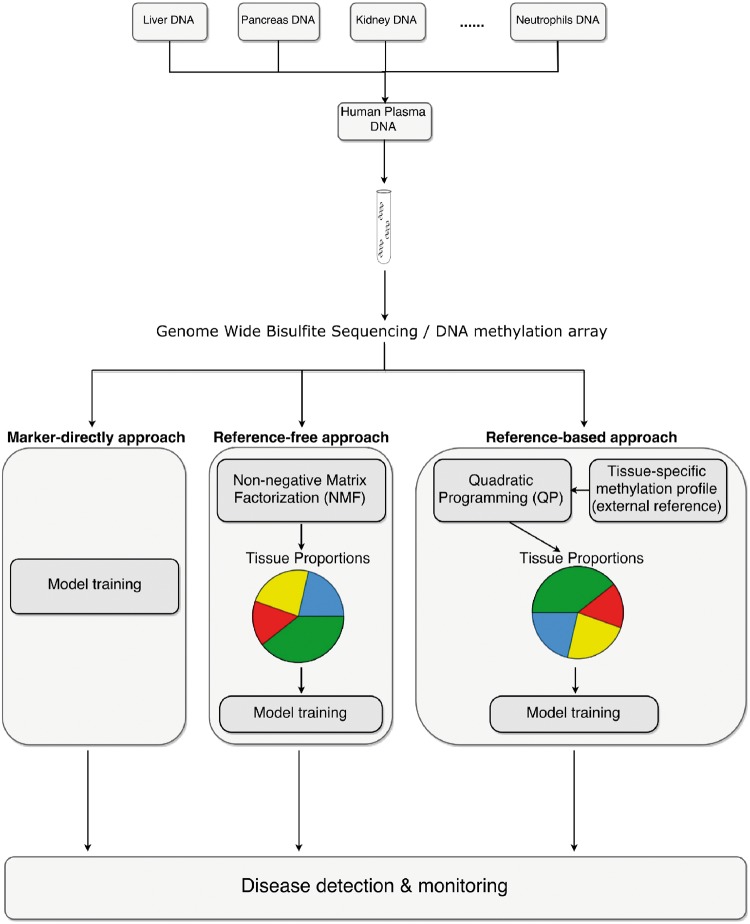
To summarize the methods described above, a schematic illustration of plasma cfDNA methylation mixing procedure and deconvolution methods for disease detection and monitoring is shown in Figure 1. Besides directly using markers to for disease predication and monitoring, signal deconvolution methods can be categorized into either the ‘reference-based approach’ when the tissue-specific reference profiles are known, or ‘reference-free approach’ when the tissue-specific methylation reference profiles are unavailable.

Figure 1.

Schematic overview of plasma cfDNA methylation mixing procedure and deconvolution methods for disease detection and monitoring. One straightforward approach is to use marker directly for disease detection. Besides using biomarkers directly, signal deconvolution methods can be categorized into either the ‘reference-free approach’ when the external tissue-specific methylation reference in unavailable, or the ‘reference-based approach’ when the tissue-specific profile is known.

Simulation

To evaluate and compare the aforementioned prediction approaches under different scenarios, we performed a series of simulations. In all simulations, data are generated to mimic the real data characteristics. The main simulation procedures are as following. We obtain the cfDNA WGBS methylation data of 32 healthy people as control samples and 29 HCC patients as case samples from a previous study [17]. Then, we take the methylation levels for 1013 CpG clusters (500 bp, each) from 14 different tissues as the reference panel R, which are reported by the authors and chosen based on tissue-specific methylation profiles. We further obtained the cfDNA methylation levels for all samples in these 1013 regions as the methylation data of interest, and applied QP on the methylation data and reference panel to solve for tissue proportions for each patient. Next, we assume 32 healthy people’s tissue proportions come from a common Dirichlet distribution Dir(${\alpha }_0$), and 29 HCC cancer patient’s proportions from another common Dirichlet distribution Dir(${\alpha }_1$). We obtain the MLE of ${\alpha }_0$ and ${\alpha }_1$, as $\widehat{{\alpha }_0}$ and $\widehat{{\alpha }_1}$, respectively.

Using $\widehat{{\alpha }_0}$ and $\widehat{{\alpha }_1}$, we generate 50 controls’ tissue proportions P₀ from Dir($\widehat{{\alpha }_0}$), and 100 cases’ proportions P₁ from Dir($\widehat{{\alpha }_1}$). To mimic the biological variation in reference panel for different person, we generate the noise-added reference panel R_i for each sample i base on the original reference panel R. To be specific, we use the original reference R as the mean parameter in beta distribution, and then adjust the dispersion level based on simulation setting to control the noise level. Using higher dispersion will generate noisier reference panel R_i. Then for each sample, we multiply R_i with the simulated mixing proportion to obtain the expected values for this individual’s cfDNA methylation levels. The next step in simulation is adding noise to the simulated cfDNA methylation level, which is again based on beta distribution. We reparametrize the beta distribution $Beta (\alpha ,\beta )$ into the following form:

$$Beta(\mu ,\mathrm{ }\varphi ),$$

where $\mu =\frac{\alpha }{\alpha +\beta }$ is the mean, and $\varphi =\frac{1}{\alpha +\beta +1}$ is the dispersion. Here, we take R_i P_i as the mean $\mu$ of beta distribution, and use different values for the dispersion $\varphi$ to investigate the effect of noise levels on the performance of prediction.

Simulation results

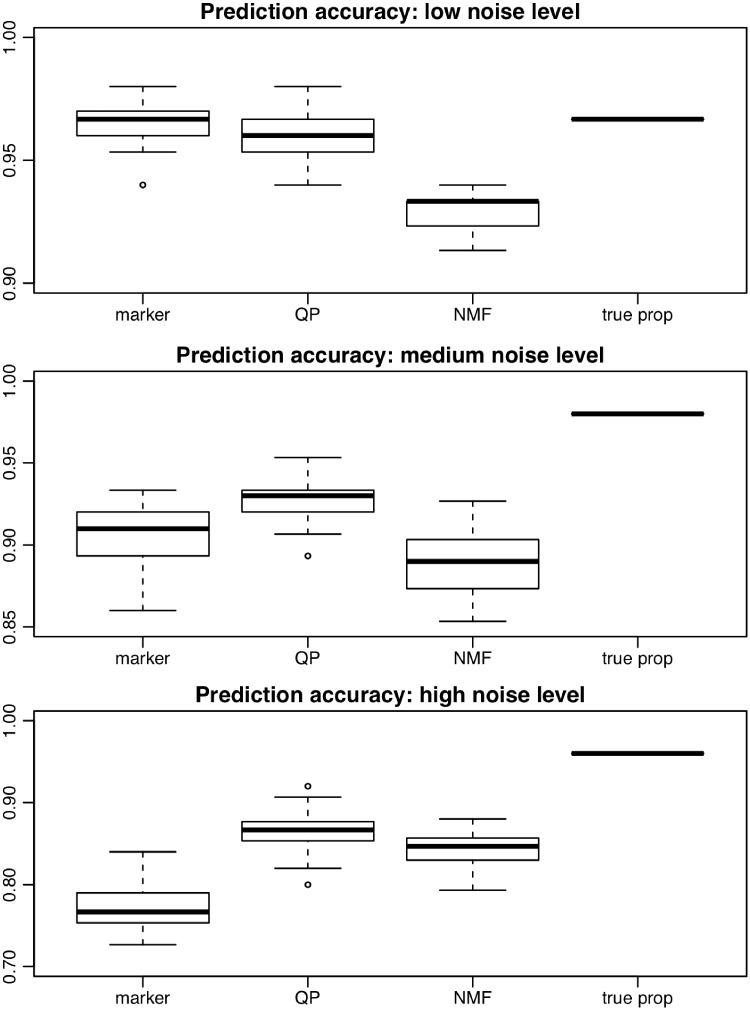
After obtaining the simulation data, we use leave-one-out cross-validation (LOOCV) to evaluate and compare the classification accuracies from different methods. The classification accuracies from all simulations are summarized by the boxplots in Figure 2. Simulations are conducted under low ($\varphi =0.17$, Figure 2A), medium ($\varphi =0.5$, Figure 2B) and high ($\varphi =0.67$, Figure 2C) noise levels. Each simulation is repeated for 20 times. The methods under comparison include marker-directly predict approach (presented as ‘marker’), estimate tissue proportion approach using QP (‘QP’) and the reference-free NMF approach (‘NMF’). As a benchmark, we also include the results from using the true proportions as predictor (‘true prop’).

Figure 2.

Boxplot of classification accuracies for multiple methods in simulations. Marker: Marker directly predict approach. QP: using tissue proportions solved from QP procedure for prediction. NMF approach. True Prop: using simulated true proportion in classification. A total number of 20 simulations are conducted. (A) Low noise level; (B) medium noise level; (C) high noise level.

As shown in Figure 2, using the true proportions as predictors achieves the highest accuracy in all simulation settings, as expected. When the noise level is low (Figure 2A), the prediction accuracies of all methods are reasonably good, with NMF’s accuracy lower than the others. When the noise level increases, the three methods under comparison start to differ. At medium noise level, using marker directly to predict performs worse than QP (P = 10⁻⁴, one-sided t-test) but better than NMF (P = 10⁻³, one-sided t-test). At high noise level, using marker directly to predict performs worse than the other two methods (P = 10⁻¹² and 10⁻¹⁰ high; one-sided t-test). In particular, at high noise level (Figure 2C), directly using marker to predict performs rather poorly. This is because under our simulation setting, the methylation differences come from the differences in mixing proportions between cases and controls. The proportion estimation serves as a signal filtering step to extract better prediction features, which subsequently improves prediction. Across all noise levels, QP performs better than NMF (P = 10⁻¹² low; 10⁻⁸ medium; 10⁻² high; one-sided t-test). This is expected because QP uses external information to help disease status prediction, which is supposed to outperform reference-free method NMF.

We then conduct the following simulations to further investigate the QP and NMF methods from other aspects.

Sample size consideration

As the simulation above contains rather small sample size (150), we investigate how the size of training data will affect the results by increasing the sample size to 750 and 1500. Supplementary Figure S1 shows that the total sample size has dramatic effect on prediction accuracy. As the sample size increase, the accuracies of all methods increase, across all noise levels. However, when the noise level is not low, NMF performs better than QP under larger sample size. This is because that when the noise level is high, the reference panel used for QP is noisy. In this case, it is suitable to use NMF for reference-free decomposition when the sample size allows. These results also provide some hints for sample size selection. For NMF, the gain of accuracy from 150 to 750 is dramatic, and then plateaued from 750 to 1500. It is therefore advisable to have at least several hundreds of samples to start using the NMF approach.

Other aspects in solving proportion

In either QP or NMF-based method, the estimated proportions are coordinates when projecting the original data into a lower-dimensional space. The improvement in prediction accuracy using estimated proportions suggests that the coordinates contain cleaner signals for the outcome. We investigate how much impact the direction of the projection will have on prediction. We conduct simulations under different external reference R, to see how the choice of reference will affect the classification results. We use a ‘high variance reference’ in QP estimate tissue proportion approach to solve for tissue proportions. That is, more noise is added to the R used in QP. This mimics the situation that there is significant bias for the reference panel being used. We also try to use a ‘random’ reference by randomly shuffling the entire R used in QP. This mimics the extreme situation where the reference R is completely off. Results in Supplementary Figure S2 indicate that using the ‘high variance reference’ (‘QP high var’) and ‘randomly shuffled reference’ (‘QP random’) both lead to a decrease of accuracy, where using random reference is much worse than all other methods (P = 0.0159, analysis of variance). Both QP and NMF project a matrix into lower-dimensional space with either known or unknown coordinates. Whether the projection has predictive power for the outcome is important for the performance of the method. The results in Supplementary Figure S2 illustrate that a bad projection direction leads to unfavorable prediction accuracy, and that using a more accurate external reference R will benefit the classification.

We also explore if directly solving proportions in ordinary least squares (OLS) without any constraint will affect the prediction accuracy. Results in Supplementary Figure S2 indicate that OLS has comparable performance with QP. Of course, the OLS results will lose biological interpretation, as without constraints, the regression coefficients cannot be interpreted as mixing proportions anymore. Thus, the QP is still a preferred method than OLS. When adopting reference-based approaches, we also compare QP with two other newly designed methods: Cibersort (CBS) [40] and EpiDISH [41]. CBS uses support vector regression, and EpiDISH uses robust partial correlations (RPCs). Results in Supplementary Figure S3 indicate that CBS performs better than QP in high noise level, whereas RPC and QP are comparable overall. This indicates the reference-based algorithms that specifically designed for gene expression or DNA methylation data, where solved proportions constraint can be implemented a posteriori, can provide alternative means for QP.

Validation of NMF results

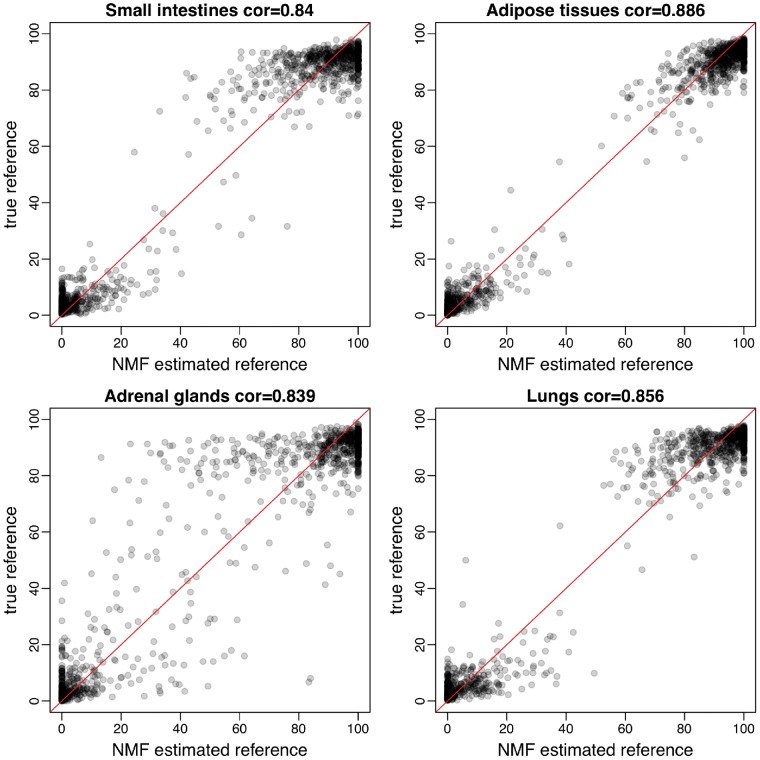
To validate if the NMF-solved reference matrix W is a good approximation to the true reference panel, we investigate the NMF results in simulation. As the column orders of W is randomly generated from NMF, we first need to ‘assign’ tissue types to the columns of W. To do so, we find matches based on pairwise correlations of the columns of W and the true references. In these two matrices, two columns with highest correlation are regarded to represent the same tissue. After this, we exclude these two matched columns and use the highest correlation on the remaining data to identify the second matched tissue. We iterate this procedure until all tissue types are determined. We found that overall the estimations of the reference are accurate. The average correlation between estimated and true reference is >0.83. Figure 3 shows the scatterplot for NMF-solved reference methylation versus the truth for 4 (of 14) tissues. Such scatterplots for all tissues are available in Supplementary Figure S4.

Figure 3.

Scatterplots of NMF estimated reference methylation levels versus true reference methylation levels in four tissues. (A) Small intestines; (B) adipose tissues; (C) adrenal glands; (D) lungs. Relatively strong correlations are observed. Spearman’s correlation is shown in each panel.

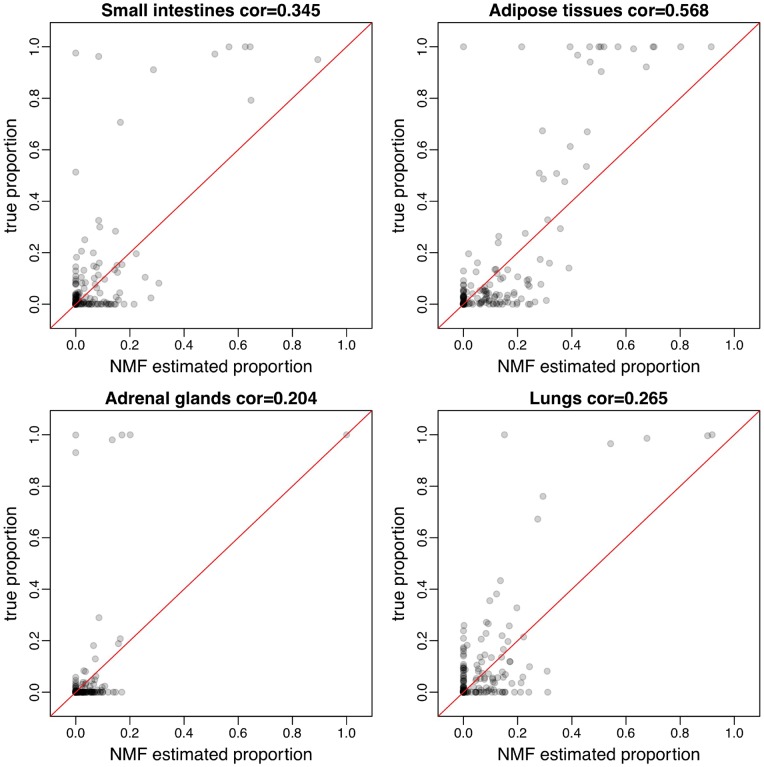
We further compare the NMF-solved proportion matrix H with the true proportions in simulation. Figure 4 shows the scatterplots of NMF-solved tissue proportions versus true proportions for the four tissues. In general, NMF-solved proportions correlate with true proportion well in most estimations, although in some tissues this relationship is weak. Possible reason for the inaccurate estimation in some cases is that the low abundance of certain tissue makes them difficult to estimate. The scatterplot for all tissues solved proportion versus true proportions are available in Supplementary Figure S5. Overall, reference-free approach has the capacity to elucidate compositions of heterogeneous cfDNA samples pertaining to their constituent homogeneous tissue types.

Figure 4.

Scatterplots of NMF estimated tissue proportions versus true tissue proportions in four tissues. (A) Small intestines; (B) adipose tissues; (C) adrenal glands; (D) lungs. Relatively strong correlations are observed. Spearman’s correlation is shown in each panel.

Real data results

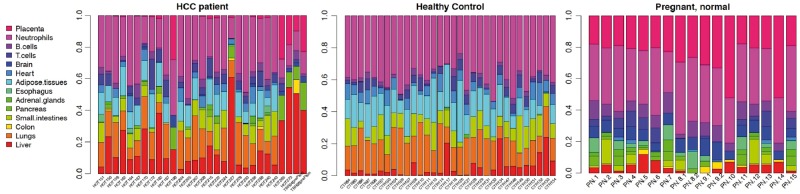
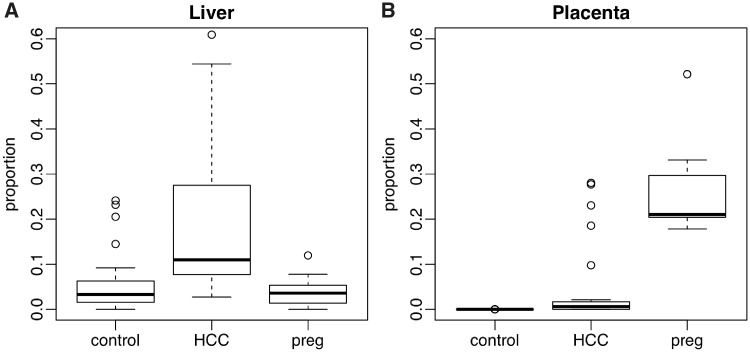
We further evaluate and compare the methods in real data. We obtain and process the cfDNA WGBS data for 27 HCC patients, 32 healthy unpregnant control subjects and 17 healthy pregnant subjects from [17]. This data set is referred to as the WGBS data set thereafter. The external reference panel is obtained from the same study, with reference data from the Roadmap Epigenomics Consortium [42] included. With this external reference panel known, we first apply QP to solve for tissue proportions. For each individual among HCC patients, healthy controls and pregnant subjects, the bar plots for estimated tissue proportions are shown in Figure 5. Each bar represents one person. To take a close look at the tissue proportions in a tissue-specific manner, the boxplot for liver and placenta tissue proportions among these three groups (HCC, control and pregnant) are shown in Figure 6. It demonstrates that HCC patients have an increased proportion of cfDNA originating from liver, which is consistent with the original study (Figure 7 in [17]) and suggests that the cell death rates in liver are higher among HCC patients. Similarly, pregnant women show an increased proportion of cfDNA originating from placenta. The marked differences in these proportions indicate that the proportions will be predictive for the outcome.

Figure 5.

Barplot for the estimated 14 tissue proportions from real data for HCC patients, healthy controls and pregnant subjects, using QP with external reference available. HCC patients showed an increased proportion of cfDNA originating from liver, while pregnant controls showed an increased proportion of cfDNA originating from placenta.

Figure 6.

Boxplot of real data solved tissue proportions for liver and placenta, respectively, among three groups. (A) Tissue proportions for liver among three groups; (B) tissue proportions for placenta among three groups.

The boxplots for all 14 tissue-type proportions, with one panel for each tissue type, are shown in Supplementary Figure S6. We then apply NMF on real data to see if the NMF-solved result is similar to the truth. Although on average the correlation is not as ideal as in simulation, Supplementary Figure S7 shows that NMF-solved reference correlates true reference well. NMF is effective for obtaining the underlying reference panel from real data.

We then apply three different methods to classify the HCC, control and pregnant subjects. The classification confusion matrices from LOOCV are shown in Table 2.

Table 2.

Classification confusion matrices for the WGBS data

Method		Marker predict			NMF proportion predict			QP proportion predict
		HCC	Control	Preg	HCC	Control	Preg	HCC	Control	Preg
Truth	HCC	11	12	4	8	15	4	14	13	0
	Control	3	29	0	4	28	0	3	29	0
	Preg	0	0	17	0	0	17	0	0	17

Note: Control: healthy, unpregnant control people. Preg: healthy pregnant women. Marker predict accuracy: 0.75. NMF predict accuracy: 0.70. QP predicted accuracy: 0.79.

As shown in Table 2, QP-based method has the highest classification accuracy (79%). It is because QP takes advantage of accurate external reference information, which helps to extract the proportion used in classification. Directly using markers for predication also yield satisfying predication accuracy and performs better than NMF approach. This is because when sample size is relatively small, NMF-solved reference and proportions are not as accurate as in relatively large samples. QP-based method can outperform NMF approach under small sample size setting. We also applied two other reference-based algorithms, CBS and RPC here. Supplementary Table S1 indicates that all three reference-based methods (CBS, RPC and QP) perform similarly.

The results show that the pregnant subjects can be easily separated with other groups, while separating HCC patients with healthy controls yields more misclassification. It is because pregnant subjects show a more profound change in estimated proportions for placenta (∼20% in proportion change on average) compared with the rest groups; thus, the signal-to-noise ratio is high. For HCC patients, even though the proportion from liver is significantly higher in liver, there is still nontrivial overlap in proportions between HCC and normal control, leading to the misclassifications. Overall, as a noninvasive prescreening procedure, the real data results are reasonably good and show promises that cfDNA methylation can potentially be used for disease diagnosis.

We also analyze a set of reference-free real data for further comparison. We obtain and process cfDNA hydroxymethylation data for 15 healthy controls and 18 colorectal cancer patients from [11]. The data were generated from capture sequencing technology known as 5hmC-Seal, which has similar data characteristics as MeDIP-seq. This data set is referred to as the 5hmC-seq data set thereafter. As there is no external reference panel available for this data set, we can only apply either marker-directly approach or NMF approach for disease prediction. We summarize the sequencing read counts on each 2 kb regions along the genome, and then use the counts as inputs for disease prediction. During each round of LOOCV, top 1000 DMRs are first identified in the training samples using DSS [43]. We then use the log-transformed read counts from the top 1000 DMRs as the input data for both marker-directly approach and NMF approach. The model is trained using top 1000 DMRs or deconvoluted proportions, respectively, for marker-directly approach and NMF approach. The prediction result from LOOCV is shown in Table 3. Overall, using marker and NMF yields similar prediction accuracies, although using marker performs slightly better (one more correct prediction). Based on our observation, the signal-to-noise ratio in this data set is reasonably high. Thus, the DMR markers themselves already have good differential power to detect the cancer–normal difference. Therefore, using marker-directly approach yields decent accuracy.

Table 3.

Classification confusion matrices for the 5hmC-seq data

Method		Marker predict		NMF proportion predict
		Cancer	Normal	Cancer	Normal
Truth	Cancer	11	4	10	5
	Normal	0	18	0	18

Note: Cancer: colorectal cancer patients. Normal: healthy controls. Marker predict accuracy: 0.88. NMF predict accuracy: 0.85.

Discussion and conclusion

Recent studies have reported that cfDNA contains rich information of disease status and can be used to extract biomarkers and construct disease prediction model [8, 24, 28]. As a noninvasive alternative to surgical biopsy, cfDNA-based assay has great potential in disease diagnosis. The highly promising and sought-after liquid biopsy in cancer diagnosis depends on cfDNA sequence variants, and thus can only be applied on diseases with high mutation rate such as cancer. Using cfDNA methylation overcomes such limitation and has much wider application. In this study, we review the published works of using cfDNA in disease diagnosis. We focus on the strategies for statistical method and data analysis and conduct simulations to investigate several potential methods for cfDNA methylation deconvolution and prediction for disease. The advantages and disadvantages for the three general approaches are summarized in Table 4.cfDNA is a mixture of DNA fragments from multiple tissues, and the mixing proportions are potentially associated with disease status. The difference in proportions will lead to some marginal cfDNA methylation changes because of the tissue specificity of the methylomes. The disease prediction can be achieved by either using methylation levels or estimated mixing proportions as predictors, with an off-the-shelf machine learning algorithm. Regardless of the downstream prediction approach, marker selection is a important first step. We review the approaches for selecting marker in existing works and make some recommendation. In general, we recommend selecting markers based on the training data as well as external biological information.

Table 4.

Advantages and disadvantages of three cfDNA methylation disease predicting approaches

Method	Advantages	Disadvantages
Marker-directly	Straightforward and easy to apply Applicable on disease with no cfDNA tissue proportion change	Results lack direct biological interpretation Results contain no tissue proportion information
Reference-based	Can estimate tissue proportions Tissue proportions have biological interpretation	Require external reference panel from pure tissues
Reference-free	Does not require external reference panel from pure tissues Can estimate reference panel and tissue proportions Tissue proportions have biological interpretation	Computationally more intensive

When there is no profound change in cell-type-specific methylomes between cases and controls, it is generally assumed that the changes of tissue proportions in the mixing pool of cfDNA are associated with disease status. If the reference methylome are available, reference-based methods like QP can produce reliable tissue proportion estimation. Simulation studies show that the accuracy of using estimated tissue proportions to predict disease status is higher than that of using marker directly. As an added advantage, the estimated proportions also provide more interpretable result. In contrast, the reference methylome could be unavailable under certain circumstances. For example, the subpopulation under this study is different from the previous one. Under this situation that the reference panel is different from the original one, NMF is a viable solution. NMF-based method provides a reference-free approach for solving both tissue proportion and tissue reference simultaneously. Simulation studies demonstrate that this method provide comparable results to reference-based approach.

Although the disease prediction accuracy in real data is reasonable, there could be complications in real practice. The prediction can be influenced by biological and/or technical artifacts such as genetic background, demographics or batch effects, which is a difficulty faced by many other genome-based predictive assays. For example, it has been shown that batch effect or different data normalization methods can negatively affect the prognosis in cancer using gene expression data [44]. To alleviate these problems, the training and test sample first need to be consistent: they must be from the same population and experimental platform. If significant batch effects were observed, one needs to first perform data normalization using approaches such as ComBat [45], or consider using alternative rank-based methods to stabilize the signal. Furthermore, there will be room for improving the results. First, larger training samples size can contribute to the improvement in prediction accuracy. We recommend to start with at least several hundred samples to construct a prediction model. We believe that with advances of experimental technologies and data analysis method, more cfDNA methylation data will be generated from larger-scale studies, which will greatly improve the model. We also envision that if the sample size increased significantly (e.g. doubled or tripled), we should retrain the model to improve accuracy. It is possible that with the retrained model, some diagnoses for existing patients could be different. In that case, the ethical issues have to be carefully addressed. However, this is the nature of clinical research: with accumulation of data and evidence, diagnosis criteria could evolve. Second, both reference-based and reference-free methods are dimension reduction approach to project data into lower-dimensional space: reference-based method projects the data matrix onto the known reference, and reference-free method jointly solves the reference and projection. The prediction accuracy will be related to the reference used (as we showed in our simulation study). It will be interesting to develop novel statistical method to identify the optimal low-dimension space to project to that can produce the best prediction accuracy.

Key Points

• cfDNA is a mixture of DNA fragments from multiple tissues, and the mixing proportions could potentially be associated with disease status. cfDNA screening has great potential to be a noninvasive procedure for disease testing.

• Prediction based on cfDNA methylation can be applied to diseases not associated with significant DNA sequence changes.

• One can predict disease based on cfDNA methylation levels, or the estimated mixing proportions.

• Marker selection is important for disease prediction using cfDNA methylation. It should be done using both the training data as well as external biological information.

• Mixing proportion estimation can be performed with or without reference methylomes.

Methods availability

The R scripts implementing the methods discussed in this work are available online at: https://github.com/haoharryfeng/cfDNAmethy, with instructions and an example data set.

Funding

This work was partially supported by the National Institutes of Health (grant numbers R01GM122083 to H.W., NS051630 and NS097206 to P.J.).

Hao Feng is a PhD Student in the Department of Biostatistics and Bioinformatics at Emory University, Rollins School of Public Health. His research interest is to develop methods and tools for high-throughput epigenetics data.

Peng Jin is a Professor and Vice Chair in the Department of Human Genetics at Emory University, School of Medicine. His research interests are the functions and mechanisms of epigenetics and noncoding RNAs in neural development and brain disorders.

Hao Wu is an Associate Professor in the Department of Biostatistics and Bioinformatics at Emory University, Rollins School of Public Health. His main research interest is to develop statistical methods and computational tools for analyzing large-scale biomedical data, in particular different types of high-throughput omics data.