Comparing the Diagnostics Accuracy of CD4+ T-Lymphocyte Count and Percent as a Surrogate Markers of Pediatric HIV Disease

Abstract

The percentage CD4+ T-lymphocytes is used to monitor pediatric HIV disease. However, in resource-limited settings, enumerating the percentage of CD4+ T-lymphocytes is hampered by the lack of laboratory infrastructure and trained technicians. In this paper, we investigated the performances of the percentage and absolute CD4+ T-lymphocytes as markers of pediatric HIV disease progression using data from HIV-infected children enrolled through the Yale Prospective Longitudinal Pediatric Cohort study. A Lehmann family of Receiver Operating Characteristic (ROC) curves were used to estimate and compare the performance of the two biomarkers in monitoring pediatric HIV disease progression. The area under the ROC (AUC) curve and its empirical estimator have previously been used to assess the performance of biomarkers for a cross-sectional data. However, there is a paucity of literature on the AUC for correlated longitudinal biomarkers. Previous works on the estimation and inference of the AUC for longitudinal biomarkers have largely focused on independent biomarkers or failed to consider the effect of covariates. The Lehmann approach allowed us to estimate the AUC of the aforementioned correlated longitudinal biomarkers as functions of explanatory variables. We found that the overall performance of the two biomarkers was comparable. The area under the ROC curves for CD4+ T cell count and percentage were 0.681 [SE = 0.029; 95% CI: 0.624–0.737] and 0.678 [SE = 0.024; 95% CI:0.630–0.725], respectively. Our results suggest that absolute CD4+ T-lymphocyte counts could be used as a proxy for percentage of CD4+ T-lymphocytes in monitoring pediatric HIV in resource-limited settings.

Introduction

HIV infects CD4+ T cells and leads to cell death and subsequent depletion of CD4 cells. The progressive depletion of CD4+ T cells results in an increased risk for the development of opportunistic infections, Acquired Immune Deficiency Syndrome (AIDS) and death (Nishanian et al., 1998; Pantaleo et al., 1993; Vlahov et al., 1998). Antiretroviral therapy (ART) suppresses HIV viral replication and leads to maintenance or increase in CD4+ T cells, thereby restoring immune function. In resource-rich countries, the standard of care for monitoring ART is the routine laboratory monitoring of CD4+ T cell count and HIV viral load (Hammer et al., 2006; Mellors et al., 1997). In the US, CD4+ T cell count and HIV viral load are measured at the time of diagnosis and at least every 3–4 months on ART. These laboratory services and frequency of measurements are not routinely available in many resource-limited settings (Diagbouga et al., 2003). The WHO recommendation for ART monitoring in low and middle income countries has evolved from CD4+ T cell monitoring every six months and viral load testing only when the capacity exists to routine viral load monitoring being the preferred monitoring approach to diagnose and confirm treatment failure (WHO, 2010; 2015). There is a preponderance of evidence to suggest that viral load monitoring is more sensitive in detecting patients with ART failure than clinical or immunological (CD4+ T cells) monitoring (Hosseinipour et al., 2009; Rawizza et al., 2011; Reynolds et al., 2009). However, if viral load is not routinely available, the WHO recommends that CD4+ T count and clinical monitoring should be used to diagnose treatment failure (WHO, 2015). This later recommendation is based on the fact that routine laboratory monitoring, particularly viral load determination, is not feasible in most resource-limited countries due to cost, lack of technical expertise and lack of infrastructure (Taiwo and Murphy, 2008). Moreover, there are instances where patients on ART may have suppressed viral load without CD4+ T cell recovery. Hence, CD4+ T cell assessment is the most popular ART monitoring tool and will continue to play an important role in ART monitoring, particularly, where viral load monitoring is not available (Ford et al., 2015).

Due to the well-known large natural decline and variation in absolute CD4+ T cell numbers during early childhood (Stein et al., 1992; Wade and Ades, 1998), the percentage of these cells is used in children, particularly in those less than 5 years of age (Hughes et al., 1994). We previously reported that in a pediatric HIV cohort, the changes in percentage CD4+ T cells with treatment were similar to that of absolute CD4+ T cell count, regardless of age (Paintsil et al., 2008). In many resource-limited settings, clinicians rely on clinical and immunologic criteria to identify children failing first-line therapy (Jittamala et al., 2009; Ruel et al., 2011). CD4+ T cells are enumerated with flow cytometry technique based on either dual or single platform technologies (Mandy et al., 2003). The dual-platform technology determines absolute T-lymphocyte numbers using two different instruments (a hematology analyzer and a flow cytometer). The absolute CD4+ T cell number is the product of three laboratory measurements: The white blood cell count, the percentage of white blood cells that are lymphocytes (determined by hematology analyzer) and the percentage of lymphocytes that are CD4+ (determined by flow cytometry). The single-platform technology is designed to determine both absolute and percentage lymphocyte subset values using a single tube. Because of the high cost of equipment, reagents and maintenance of the single and dual platform technologies, most resource-limited settings use relatively less expensive and technically less complex devices for CD4 enumeration (Lyamuya et al., 1996; Taiwo and Murphy, 2008). However, most of these devices provide the absolute CD4+ T cell counts and not the percentage of CD4+ T cells, thus they are not pediatric friendly (Diagbouga et al., 2003). There is a need for further research to determine whether absolute CD4+ T cell count can be used in place of percentage CD4+ T cells in managing HIV-infected children of all ages especially in areas where available devices for CD4 enumeration do not measure percentage CD4+ T cells (Diagbouga et al., 2003).

The objective of our study was two-fold: (1) To estimate the predictive accuracy of absolute CD4+ T count and CD4+ T percentage in monitoring pediatric HIV disease progression and (2) compare performances of the two markers. HIV disease progression was assessed by the proportion of detectable viremia defined as any detectable viral load above the limit of detection offered by the assay (Paintsil et al., 2016). We analyzed longitudinal data from HIV-infected children enrolled in the Yale Prospective Longitudinal Pediatric HIV Cohort study comprising of children born to HIV infected mothers in the greater New Haven area, since 1985. We assessed the performance of the two markers in a longer follow-up duration period spanning different treatment strategy eras (i.e., pre-highly active antiretroviral therapy (HAART) and HAART) and also provide evidence to support the use of absolute CD4+ T cell count in HIV-infected children, regardless of age.

Statistical Methods

Receiver Operating Curve (ROC) and Area Under ROC

Let D_i denotes the detectable viremia status for the ith subject. D is a binary random variable and takes the values 0 or 1 depending on the frequency of detectable viremia episodes. D=0 for individuals who had detectable viremia during less than or equal to 50% of their clinic visits (infrequent episodes of detectable viremia). For individuals who had detectable viremia during more than 50% of their clinic visits (frequent episodes of detectable viremia), D takes the value 1. Suppose Y¹ and Y² are continuous positive random variables and represent the absolute CD4+ T cell count and percent of an individual, respectively. Let $S_{y^1}$ and $S_{y^2}$ denote the survival functions for Y¹ and Y² in individuals with frequent episodes of detectable viremia; and $G_{y^1}$ and $G_{y^2}$ are the corresponding functions for the group with infrequent episodes of detectable viremia. The sensitivity (true positive rate) and 1-specificity (false positive rate) of the k^th (k = 1, 2) marker at cut-off t are given by $\mathbb{P}\left[Y^k\ge t|D=1\right]=S_{y^k}(t)$ and $1-\mathbb{P}\left[Y^k<t|D=0\right]=\mathbb{P}\left[Y^k\ge t|D=0\right]=G_{y^k}(t)$. The Receiver Operating Curve (ROC) is a plot of $G_{y^k}(t)$ (x-coordinate) versus $S_{y^k}(t)$ (y-coordinate) for every possible threshold t. That is, the ROC curve is the entire set of possible values of $G_{y^k}$ and $S_{y^k}$ obtained by dichotomizing Y^k with different values of t ϵ(−∞, +∞).

The ROC curve has many advantages over single measurements of sensitivity and specificity. ROC curve incorporates both of these measures and gives a full picture of the performance of the classifier marker at different thresholds. Furthermore, ROC curves show the trade-offs between these two measures as the threshold changes. While the ROC curve gives a full picture of the performance of the classifier at different thresholds, a quantitative summary index frequently used as an overall assessment of classifier performance is the area under the ROC curve (AUC) which is given by ${\int }_0^{1}ROC(u)du$. The area under the ROC curve is interpreted as the average value of sensitivity (specificity) for all possible values of specificity (sensitivity) and corresponds to the probability of correctly identifying subjects with frequent (+) and infrequent (−) episodes of detectable viremia. That is, AUC is equal to the probability $\mathbb{P}\left(Y_{+}^k>Y_{-}^k\right)$. For a given threshold t, the sensitivity which corresponds to specificity $z_0=1-G_{y^k}(t)$ is $S_{y^k}(t)=S_{y^k}\left(G_{y_k}^{-1}\left(1-z_0\right)\right)$. From this, we can write the AUC as ${\int }_0^1{S}_{y^k}\left(G_{y^k}^{-1}\left(1-z_0\right)\right)d{z}_0={\int }_{-\infty }^{\infty }-S_{y^k}(t)d{G}_{y^k}(t)=\mathbb{P}\left(Y_{+}^k>Y_{-}^k\right)$. Thus, the AUC is a measure of the separation in location between $S_{y^k}$ and $G_{y^k}$.

ROC Curves for Correlated Longitudinal Markers

The area under the ROC (AUC) and its empirical estimator have previously been studied for a cross-sectional data (Hanley and McNeil, 1982; Venkatraman and Begg, 1996). However, there is a paucity of literature on the AUC for correlated longitudinal markers. Obuchowski proposed a nonparametric approach for the estimation and inference of AUC of two correlated longitudinal markers (Obuchowski, 1997). However, her approach did not consider the effect of covariates. Covariates should be incorporated in the ROC curve analyses as they affect the performance of diagnostic markers (Pepe, 2003). In this paper, we used the Lehmann model (referred as the proportional hazards model) (Gönen and Heller, 2010; Holling et al., 2012) to estimate and compare the performance of absolute CD4 count and CD4 percentage as markers of pediatric HIV disease progression. Using the Lehman approach, the association between sensitivity and 1-specificity can be modeled as:

$$S_{y^k}(t)=G_{y^k}{(t)}^{\theta }$$ (1)

where, 0 < θ ≤ 1 is measure of marker performance with values close to zero indicating higher diagnostic accuracy. Thus, the Lehmann family of ROC curve can be written using the equation y = x^θ and the corresponding AUC is ${\int }_0^1{x}^{\theta }dx=\frac{1}{1+\theta }$. Moreover, from Equation (1), $\frac{\log S_{y^k}(t)}{\log G_{y^k}(t)}=\theta$ which is equivalent to the Cox Proportional Hazards (Cox PH) model used in survival analyses (Cox, 1972). The connection between the Lehmann and Cox model will enable us to estimate θ which in turn allows us to obtain the corresponding ROC and AUC. The Cox PH model states that covariates have proportional effect on the hazard function of failure time distribution. That is, if h_i(t) denotes the hazard for the ith individual at time t, the Cox PH model can be written as $h_i(t)=h_0(t)e^{{\beta }_1{x}_{i1}+\dots +{\beta }_p{x}_{ip}}$. h₀ denotes the hazard function for an individual whose covariates all have values of 0 and (x_i1,…, x_ip) are set of p covariates.

Let $Y_{ij}^k$ denotes values of the kth marker (k = 1, 2) for the ith (i = 1, 2,…,n) patient at the jth (j = 1, 2,…, n_i) time. The response vector for the kth marker is $Y^k=\left(Y_{11}^k,Y_{12}^k,\dots ,Y_{1n_1}^k,Y_{21}^k,Y_{22}^k,\dots ,Y_{2n_2}^k,\dots ,Y_{n1}^k,Y_{n2}^k,\dots ,Y_{n{n}_n}^k\right)$. Y^k is the kth marker values of all individuals stacked into a single response vector. The hazard functions for Y^k are defined as $h_s(y)=li{m}_{\mathrm{\Delta }y\to 0}\frac{P[y<Y<y+\mathrm{\Delta }y|Y\ge y,D=s]}{\mathrm{\Delta }y}$, for s = 0, 1. To estimate the area under the ROC curve of each longitudinal marker, Cox PH model was used with the marker values Y^k as dependent variable and the detectable viremia status indicator D as independent variable:

$$h_1(y|D)=h_0(y)e^{{\beta }_{1}D}.$$ (2)

Note that $\frac{h_1(y,D=1)}{h_1(y,D=0)}=e^{{\beta }_1}$ and using Lehmann model (1) the marker performance measure $\theta =e_1^{\beta }$. An estimate of ${\widehat{\beta }}_1$ can be obtained using Cox’s partial maximum likelihood estimation procedure available in many statistical software packages (Cox, 1975). By the invariance property of maximum likelihood estimators θ is estimated by $\widehat{\theta }=e^{{\widehat{\beta }}_1}$. Repeated marker measurements made on the same individual are correlated. Thus, we used the robust sandwich variance estimator in order to obtain the correct inferences and variance of ${\widehat{\beta }}_1$ (Wei et al., 1989). We then used the Delta method to obtain approximate variance for $\widehat{\theta }$. That is, we approximated variance of $\widehat{\theta }$ by ${\widehat{\theta }}^2{\sigma }_{{\widehat{\beta }}_1}^2$, where ${\sigma }_{{\widehat{\beta }}_1}^2$ is variance of ${\widehat{\beta }}_1$. Similarly, the variance for the AUC was estimated by ${\widehat{\theta }}^2{\sigma }_{{\widehat{\beta }}_1}^2{(1+\widehat{\theta })}^{-4}$.

The Lehmann (Cox PH) model can be also used to obtain covariate-adjusted ROC curves. We present here the effect of a single covariate but the model can be easily extended to include multiple covariates. Suppose X₂ denotes a covariate that may affect the performance of each marker and β₂ denotes the corresponding regression coefficient. Then the adjusted Cox PH model is:

$$h_1\left(y|D,X_2\right)=h_0(y)e^{{\beta }_{1}D+{\beta }_2{X}_2+{\beta }_{3}D{X}_2}$$ (3)

In the above model, covariate effect is assessed using the regression coefficient of the interaction term. Using the connection between the Lehman (1) and Cox (3) models, the covariate-adjusted marker performance parameter is $\theta \left(x_2\right)=e^{{\beta }_1+{\beta }_3{x}_2}$ (note that $\frac{h_1\left(y,D=1,x_2\right)}{h_1\left(y,D=0,x_2\right)}=e^{{\beta }_1+{\beta }_3{x}_2}$). Thus, the covariate-adjusted ROC curve is $y\left(x,x_2\right)=x^{\theta \left(x_2\right)}$.

The objective of our study was twofold: Estimate and compare the performance of the two biomarkers of HIV disease progression. As described above, Cox PH models were used in assessing the performance of each longitudinal biomarker in the absence or presence of covariates. In this section, we evaluate the performance of the two markers by comparing their corresponding ROC curves. Let Y = (Y¹, Y²) be the combined marker values, i.e., the absolute and percent CD4+ T cells of all patients are stacked into a single response vector. Let C define a dummy variable with C = 0 for k = 1 (CD4+ T cells absolute count) and C = 1 for k = 2 (CD4+ T cells percent). Then, using the combined marker values, the Cox PH model can be written as:

$$h_1(y|D,C)=h_0(y)e^{{\beta }_{1}D+{\beta }_{2}C+{\beta }_{3}CD}.$$ (4)

For the first marker, $\frac{h_1(y,D=1,C=0)}{h_1(y,D=0,C=0)}=e^{{\beta }_1}$ and for the second marker $\frac{h_1(y,D=1,C=1)}{h_1(y,D=0,C=1)}=e^{{\beta }_1+{\beta }_3}$. These show that the ROC curves of the two markers are the same when β₃ = 0. Thus, the performance of the two markers can be compared by testing the null hypotheses H_o: β₃ = 0. The statistic for testing H_o is computed as $T={\widehat{\beta }}_3^2/{\sigma }_{{\widehat{\beta }}_3}^2$, where ${\sigma }_{{\widehat{\beta }}_3}^2$ is the robust sandwich variance of ${\widehat{\beta }}_3$. Under H_o, T has an asymptotic chi-squared distribution with one degree of freedom (Wald chi-squared statistic).

Simulation Study

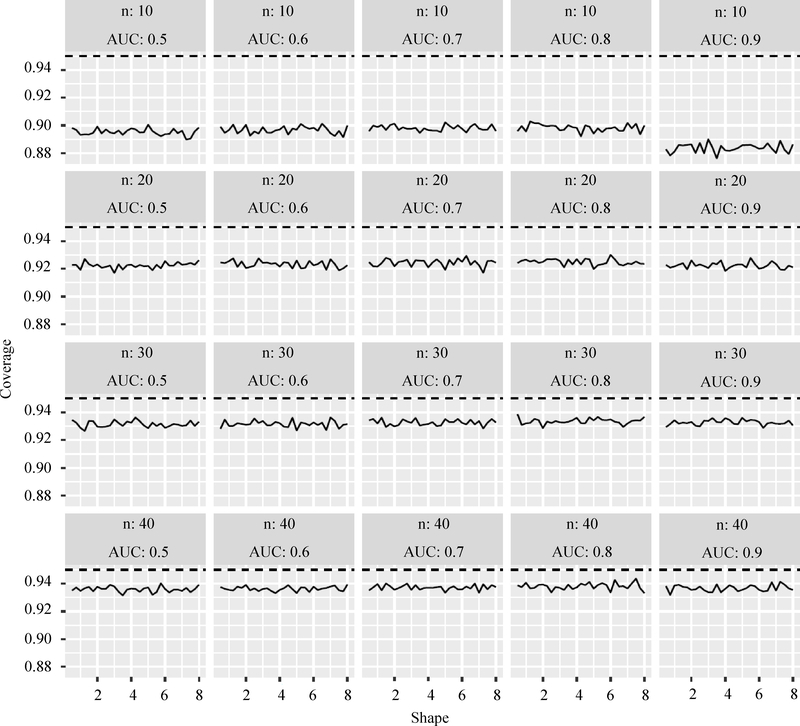
We ran a large set of simulation studies to evaluate the performance of the Lehmann model. In each simulation, the response for the ith (i = 1, 2,…, n) patient at the jth (j = 1, 2,…, n) time (i.e., Y_ij) was generated from a Weibull distribution with scale parameter 1 for the population with infrequent episodes of detectable viremia. For the population with frequent episodes of detectable viremia, Y_ij followed a Weibull distribution with scale parameter $1/{\theta }^{1/s}$ for a given choice of shape parameter s. We have considered various values of the Weibull shape parameter s. The Clayton copula with dependence parameter c was used to model the correlation structure of the ith patient response vector $Y_i=\left(Y_{i1},Y_{i2},\dots ,Y_{i{n}_i}\right)$. We generated 5,000 independent data sets and model 2 was applied to the generated 5,000 independent data sets to obtain ${\widehat{\beta }}_1$ and ${\sigma }_{{\widehat{\beta }}_3}^2$. For each data set, the asymptotic confidence interval of β₁(β₁ = log(θ)) was constructed using $\left({\widehat{\beta }}_1-q{\sigma }_{{\widehat{\beta }}_1},{\widehat{\beta }}_1+q{\sigma }_{{\widehat{\beta }}_1}\right)$, where q = Φ⁻¹(1-α/2) and Φ is the standard normal cumulative distribution function. A significance level α = 0.05 corresponding to the nominal confidence level 0.95 was considered. The empirical coverage probability was obtained by computing the proportion of times the confidence interval contained the true β₁.

The results presented here are representative of the many simulations performed. Figure 1 presents results for n_i = 5 (i = 1, 2,…,n) and c = 2, i.e., five repeated observations per person with Clayton copula dependence parameter = 2. Various sample sizes, values of the Weibull shape parameter and values of β₁ were considered. The true AUC value was obtained from β₁ using Equation (1), i.e., $AUC=\frac{1}{1+\theta }$ where $\theta =e_1^{\beta }$. The results in Figure 1 show that the empirical coverage rates of the nominal 1-α = 0.95 confidence intervals improve from approximately 0.9 when the sample size is 10 to approximately 0.94 when the sample size is 40. When the sample size is small, the coverage is somewhat poorer for higher true AUC values. The shape parameter does not appear to affect strongly the coverage in this design.

Fig. 1:

Coverage probabilities for the AUC obtained by the Lehman model

Data Analyses

Study Population and Measures

The study population was comprised of HIV-infected children enrolled through the Yale Prospective Longitudinal Pediatric Cohort study at Yale-New Haven Hospital. All the children either had mothers already known to be HIV-1 seropositive during pregnancy or at the time of delivery or were discovered to be infected with HIV-1 after presenting with an AIDS defining illness. In the analyses contained herein, we used longitudinal data collected from 104 HIV-infected children from January 1996, when plasma HIV-1 RNA quantification became available, to November 2013. The study participants were seen and examined at the pediatric clinic every 2–3 months and more frequently as necessary. Routine blood tests, HIV-1 RNA quantification and CD4+ T-lymphocyte counts and percentages were done every 2–3 months to follow HIV disease progression. HIV-1 RNA quantification was done using the Amplicor Monitor test (Roche Diagnostic Systems, Inc., Branchburg, New Jersey, USA). CD4+ T-lymphocyte levels were quantified using a standard dualplatform flow cytometry technology. The study protocol was reviewed and approved by Institutional Review Board at the Yale School of Medicine.

The outcome variable was viral blip defined as any detectable viral load above the limit of detection offered by the assay (Paintsil et al., 2008). The children were categorized into two groups based on the frequency of detectable viral load episodes: (1) Infrequent episodes of detectable viremia (children who had detectable viremia during less than 50% of their clinic visits) and (2). frequent episodes of detectable viremia (children who had detectable viremia during more than 50% of their clinic visits). The predictor variables included time varying (absolute CD4+ T-lymphocyte count and CD4+ T-lymphocyte percentage) and time-invariant (e.g., gender, race, age at study entry, age at HIV diagnosis, caregiver type, history of AIDS defining illness, time since HIV diagnosis, antiretroviral treatment status and CDC clinical staging of HIV infection) covariates.

Results

The demographic and HIV disease characteristics of the study participants are described in Table 1. Continuous characteristics were summarized using median and Inter Quartile Range (IQR); categorical characteristics were summarized using frequency and percent (%). Wilcoxon rank sum and Fisher’s exact tests were used to compare continuous and categorical patients characteristics, respectively, between subjects with infrequent and frequent episodes of detectable viremia. The median age of the study participants at study entry and the time of diagnosis were 7.83 (IQR = 5.02–11.98) and 1.79 (0.44–4.91) years, respectively. Majority of the participants (81%, n = 86) had frequent episodes of detectable viremia. Fifty four percent were males, 59% were African Americans and 57% had biological parents as caregivers. The majority of the participants had congenital HIV (93%), moderate to severe CDC classification (65%) and other comorbidities (55%). As previously reported (Paintsil et al., 2016), there were no statistically significant differences in patient characteristics between patients with frequent and infrequent episodes of detectable viremia.

Table 1:

Characteristics of study participants stratified by frequency of detectable viremia

		Detectable viremia
Study covariates	All (N = 104)	Infrequent (N = 18)	Frequent (N = 86)	P-value
Baseline CD4/mm3	436 (125–725)	550 (26–820)	420 (140–663)	0.48
Baseline VL (Log10)	4.79 (4.13–5.32)	4.60 (2.60–5.50)	4.79 (4.20–5.18)	0.85
Age at study entry (years)	7.83 (5.02–11.98)	7.74 (3.70–13.07)	7.83 (5.20–11.76)	0.92
Age at diagnosis (years)	1.79 (0.44–4.91)	2.04 (0.21–5.32)	1.79 (0.52–4.91)	0.82
Time since Diagnosis (years)	5.14 (2.32–7.35)	3.03 (0.60–8.88)	5.42 (2.52–7.32)	0.40
Gender				1.00
Female	48 (46%)	8 (44%)	40 (47%)
Male	56 (54%)	10 (56%)	46 (53%)
Race/Ethnicity				0.80
Black	61 (59%)	10 (56%)	51 (59%)
Other	43 (41%)	8 (44%)	35 (41%)
Other Illness				1.00
No	43 (45%)	7 (47%)	36 (44%)
Yes	53 (55%)	8 (53%)	45 (56%)
Caregiver				0.79
Parent	59 (57%)	11 (61%)	48 (56%)
Other	44 (43%)	7 (39%)	37 (44%)

Source: Paintsil et al., J AIDS Clin Res. 2016 Apr; 7(4). pii: 565

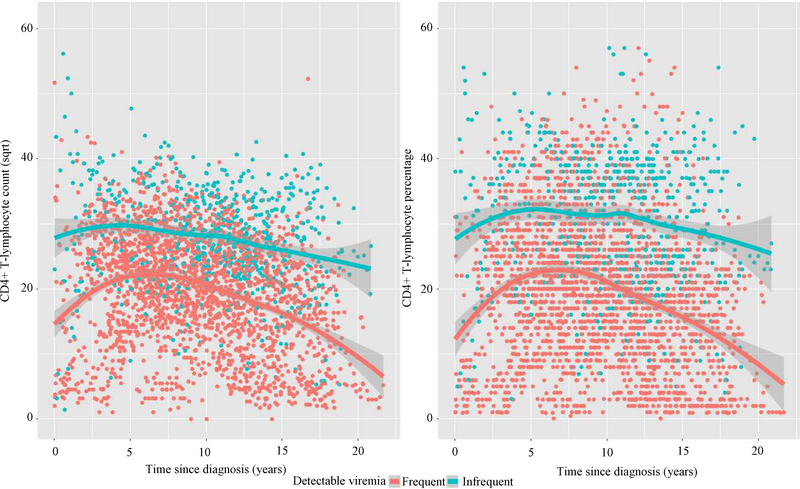
Figure 2 displays CD4+ T cell count and percentage trajectories by frequency of detectable viremia status. The average trend lines in Figure 2 show that CD4+ T cell count and percentage values for both groups slowly increased from baseline values and decreased at later time points over the study period. Moreover, Fig. 2 shows that children with infrequent episodes of detectable viremia had higher CD4+ T-cell counts and percentage over time compared with those with frequent episodes of detectable viremia.

Fig. 2:

Trajectories of CD4+ T Cell lymphocytes by Frequency of Detectable Viremia Status (LOESS Lines): Absolute CD4+ T-cells (Left), Percent CD4+ T-cells (Right)

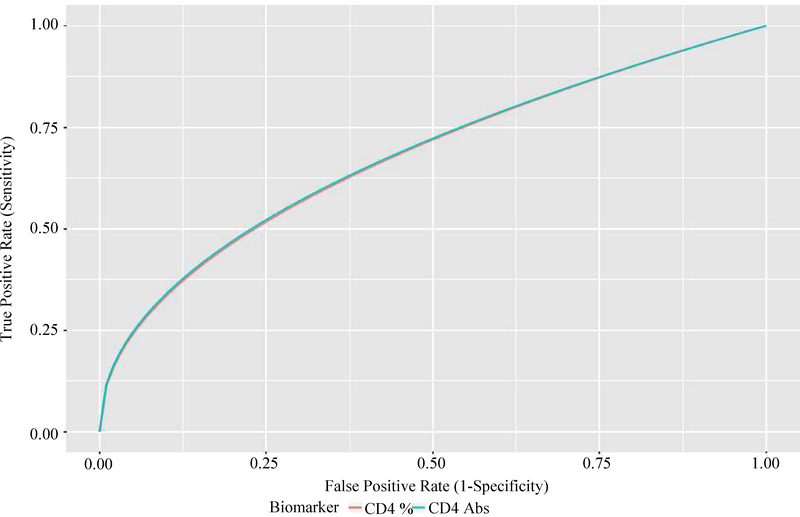
The association between episodes of detectable viremia and the two longitudinal biomarkers of interest was examined using model (2). More specifically, the model was used to construct the ROC curves of the two markers and compute the corresponding areas under the ROC curves. Figure 3 displays the ROC curves for the two biomarkers. The overall diagnostic accuracy of the two biomarkers were comparable. Both biomarkers had about a 68% probability of correctly distinguishing a frequent from an infrequent episodes of detectable viremia patient. The area under the ROC curves for CD4+ T cell count and percentage were 0.681 [SE = 0.029; 95% CI: 0.624–0.737] and 0.678 [SE = 0.024; 95% CI:0.630–0.725], respectively. We compared the two ROC curves by testing the null hypotheses H_o: β₃ = 0 against H_a: β₃ ≠ 0 in model 4. The two-sided Wald P-value was 0.59 and this shows that there was no statistically significant difference between the ROC curves of the two biomarkers.

Fig. 3:

ROC curves for absolute and percent CD4+ T cells

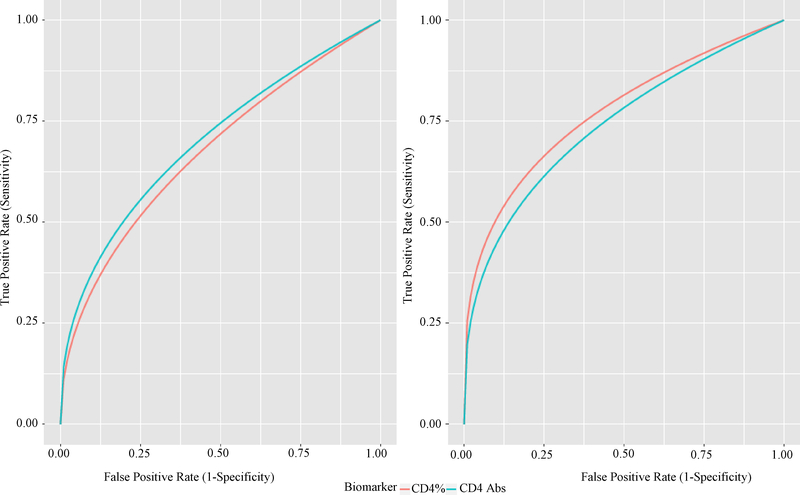
Given the greater variability of absolute CD4+ T-lymphocyte counts compared with percentage among children under 5 years of age (Paintsil et al., 2008), we investigated whether the performance of the two biomarkers will vary by age. Using model (3), we have shown that the performance of each biomarker did not change with age although there was a slight improvement in older patients. The area under the ROC curve for CD4+ T cell absolute count in younger (≤5 years) and older patients (5+ years) were 0.702 [95% CI: 0.647–0.757] and 0.739 [95% CI: 0.606–0.873], respectively; and the corresponding two sided Wald P-value was 0.650. Similarly, the area under the ROC curve for CD4+ T cell percent in younger and older patients were 0.677 [95% CI: 0.624–0.729] and 0.772 [95% CI: 0.706–0.837], respectively; and the corresponding two-sided Wald P-value was 0.097. Figure 4 display the ROC curves of the two biomarkers for the two age groups.

Fig. 4:

ROC Curves for Absolute and Percent CD4+ T Cells: Younger Patients (Left), Older Patients (Right)

Conclusion

In this paper, we developed model based AUC to estimate and compare the performance of absolute CD4+ T-lymphocyte count and CD4+ T-lymphocyte percentage. We found that the cross validated AUC for CD4+ T-lymphocyte count and percentage were approximately 0.681 (0.678) with the corresponding 95% confidence intervals [0.624–0.737] ([0.630–0.725]). Furthermore, there was no statistically significant difference between the AUC of the two biomarkers. This finding is of special interest with regard to the control of pediatric HIV in resource-limited settings where HIV prevalence is highest. Due to the variations in CD4+ T-lymphocyte numbers, the CD4+ T-lymphocyte percentage is traditionally used to monitor HIV disease progression and the effects of HAART in children (Paintsil et al., 2016). However, due to the high cost of equipment and lack of adequate laboratory infrastructure, most laboratories in resource-limited settings use simple protocols that enumerate only the absolute CD4+ T-lymphocyte counts. Our findings demonstrate that absolute CD4+ T-lymphocyte count could be as useful as the percentage CD4+ T-lymphocytes in monitoring pediatric HIV in resource-limited settings regardless of age.