Neurophysiological Muscle Activation Scheme for Controlling Vocal Fold Models

Abstract

A physiologically-based scheme that incorporates inherent neurological fluctuations in the activation of intrinsic laryngeal muscles into a lumped-element vocal fold model is proposed. Herein, muscles are activated through a combination of neural firing rate and recruitment of additional motor units, both of which have stochastic components. The mathematical framework and underlying physiological assumptions are described, and the effects of the fluctuations are tested via a parametric analysis using a body-cover model of the vocal folds for steady-state sustained vowels. The inherent muscle activation fluctuations have a bandwidth that varies with the firing rate, yielding both low and high frequency components. When applying the proposed fluctuation scheme to the voice production model, changes in the dynamics of the system can be observed, ranging from fluctuations in the fundamental frequency to unstable behavior near bifurcation regions. The resulting coefficient of variation of the model parameters is not uniform with muscle activation. The stochastic components of muscle activation influence both the fine structure variability and the ability to achieve a target value for pitch control. These components can have a significant impact on the vocal fold parameters, as well as the outputs of the voice production model. Good agreement was found when contrasting the proposed scheme with prior experimental studies accounting for variability in vocal fold posturing and spectral characteristics of the muscle activation signal. The proposed scheme constitutes a novel and physiologically-based approach for controlling lumped-element models for normal voice production and can be extended to explore neuropathological conditions.

I. Introduction

Phonation is the primary physiological process of speech production, in which the coordinated activation of breathing and laryngeal muscles controls the interaction of airflow, the vibratory activity of the vocal folds (VF), and sound. Phonation determines distinctive features of speech production, defining the fundamental frequency (f_o), amplitude, quality, and temporal patterns of vocalization.

A significant amount of data describing voice production from research and clinical perspectives have been collected in the past few decades using imaging and acoustic signal recording techniques. These efforts have resulted in mathematical models able to reproduce different aspects of the phonatory process in normal physiological conditions. Of particular value has been the development of lumped-element models of the VFs, since they can efficiently represent a wide range of gestures and voice qualities, including the self-oscillating modal response of the vibrating VFs [1] [2] [3]. These lumped-element models can be coupled with models of aerodynamic interactions and acoustical features, thus forming a complete framework able to simulate the transmission and propagation of acoustic waves within the vocal tract, the subglottal system, and the VF tissue. Reduced order VF models can also mimic complex pathological phenomena, including incomplete glottal closure [4] and nerve paralysis [5], which opens the possibility of using these models in the diagnosis and treatment of VF pathologies [6], [7]. However, a number of gaps need to be filled before VF modeling can be established as a viable and robust clinical tool. Although efforts to accurately represent an individual patient in a modeling framework have been performed recently [8], [9], [10], a reliable representation of the inter-subject variability inherent in the clinical population has not yet been achieved.

Titze and Story 11] proposed a set of rules to unfold the physiological relationship between laryngeal muscle activation and VF configuration for reduced order models of the VFs [11]. However, there are numerous assumptions in that relevant study that need to be revisited. For instance, the effect of antagonistic muscles is overly simplified and the number of intrinsic laryngeal muscles that the scheme effectively controls is reduced to the thyroarytenoid (TA) and cricothyroid (CT) muscles. Their assumption of simplifying the effect of lateral cricoarytenoid (LCA) and posterior cricoarytenoid (PCA) muscles in a single activation signal reduces the neurological relevance of the adduction process of the VFs. More importantly for the present study, the method by which the muscles are activated does not have a neural basis, which in turn results in fixed, deterministic muscle activation values. These limitations reduce the physiological and clinical relevance of lumped-element VF models, making it difficult to correctly replicate gestures that depend on muscle activation, like phonation onset and offset, among others. Also, disordered speech motor control (e.g., Parkinson’s disease, spasmodic dysphonia) cannot be properly represented with fixed muscle activation.

Several mathematical representations have been developed to describe the neural basis of force output during muscle activation, using the electrical and contractile properties of the muscle fibers in combination with the spatio-temporal electrical pattern of the neural population innervating the muscle. These representations mimic several physiological processes in a generic muscle [12] [13] [14], as well as the behavior of specific muscles [15] [16], including the laryngeal musculature [17]. In the latter, the variability of laryngeal muscle activity was explored assuming a linear relationship between the muscular force and f_o. Without using a VF model, it was shown that perturbations in f_o (coefficient of variation, CV, and jitter) were highly dependent on the contractile dynamics of the TA muscle. In spite of being a pioneering study, there are various limitations in [17] that need to be resolved, including: the disregard of the intricate relationships between the driving forces, VF configuration, and vibration patterns that leads to an overly simplified relationship between force and perturbation in f_o; the lack of muscle recruitment that is known to control muscle contraction [18]; and the absence of interactions between laryngeal muscles.

The connection between modeling and experimental realms in laryngeal neural control remains largely unexplored. Recordings of electromyography (EMG) of laryngeal muscles in human subjects have allowed for characterizing vocal fold posturing during running speech [19], and during steady-state under the presence of voice tremors [20]. Studies of in vivo canine phonation [21], [22] showed that a graded nerve stimulation procedure (i.e., electrical stimulation of the laryngeal muscles) can be used to achieve appropriate glottal configurations to produce normal phonation. This type of stimulation uses regular uniform 0.1 ms cathodic pulses at 100 Hz and has also been used to explore VF posturing and the effect on fundamental frequency and vibratory stability, among others [23], [24]. It is also relevant to note that these types of experiments have shown that acoustic perturbations (e.g., jitter, shimmer) can be present even in the absence of a neural drive in the laryngeal muscles [25], [26]. In fact, acoustic perturbations can be affected by acoustical [27], aerodynamic [28], biomechanical [29], and neural [30] [17] components, and thus are not useful to identify the source of abnormal behavior. Even though acoustic perturbations have limitations for diagnostic purposes, they continue to be used in the clinic as an overall measure of vocal function, and normative values have been provided by several authors [31] [32] [33].

In this study, a new neurophysiological modeling paradigm for laryngeal muscle activation is proposed. This approach significantly extends prior efforts with the aim of introducing a neurophysiological description in the control of muscle behavior for a reduced order model of the VFs. The scheme features inter-spike interval variability [34], interactions between different types of muscle fibers, muscle recruitment [35] [36] using motor units (MU) [37], and electro-physiologically relevant parameters measured in laryngeal muscles [38]. The proposed approach intends to capture more faithfully the main characteristics of the muscles, and therefore generate a more realistic representation of the activation signal.

In an effort to extend existing rules that relate muscle activation to VF parameters for low order models [11], the proposed scheme will be used to jointly study the TA and CT intrinsic laryngeal muscles. The models for TA and CT will be combined with a body-cover model (BCM) [2] of the VFs. By introducing neurophysiological fluctuations in the muscle activation with the proposed scheme, we aim to move away from the current fixed deterministic muscle activations and capture intrinsic fluctuations in the VF parameters. We hypothesize that the resulting fluctuations in the muscle activation signals will affect the VF dynamics in a physiologically meaningful way that differs from a simple addition of noise in the VF parameters. We relate our results with the proposed scheme to prior experimental studies in laryngeal neural control. To evaluate the impact of the muscle activation fluctuations, vocal fold posturing changes and spectral characteristics in the muscle activation signal will be computed and compared with prior in vivo canine measurements and intramuscular EMG recordings in human subjects. Contrast with other studies will be discussed.

II. Methods

A. Physiological and Morphological Aspects of Muscle Activation

Activation of the laryngeal muscles comprises two major physiological processes responsible for muscle force production, namely, the temporal and the spatial summations of the muscle contraction [39], [37]. Temporal summation is at the level of individual MUs, which are composed of an alpha motor neuron and the muscle fibers that it innervates [40], [39]. The spatial summation is the successive activation of additional MUs with increasing strength of voluntary muscle contraction; i.e., MU recruitment [37] [41].

Fibers forming an individual MU respond synchronously to every action potential (AP) arriving at the neuronal pre-synaptic terminal, producing a motor unit action potential (MUAP). In turn, MUAPs lead to muscle contraction, the extent of which depends on the firing rate of the MU. A single MUAP leads to a simple twitch (single contraction), allowing the fibers to return to a relaxed baseline before a subsequent contraction is elicited. Typically, the first MUs to fire are those that generate the slowest and the smallest twitches, producing relatively small and slow contractions (type I MUs). As more considerable force is required, high threshold MUs generating faster and larger twitches begin to respond (type IIa and IIb MUs) [35] [36]. Figure 1 shows a sketch of the time course of slow and fast twitches, highlighting the differences in both timescale and amplitude of the responses.

Fig. 1:

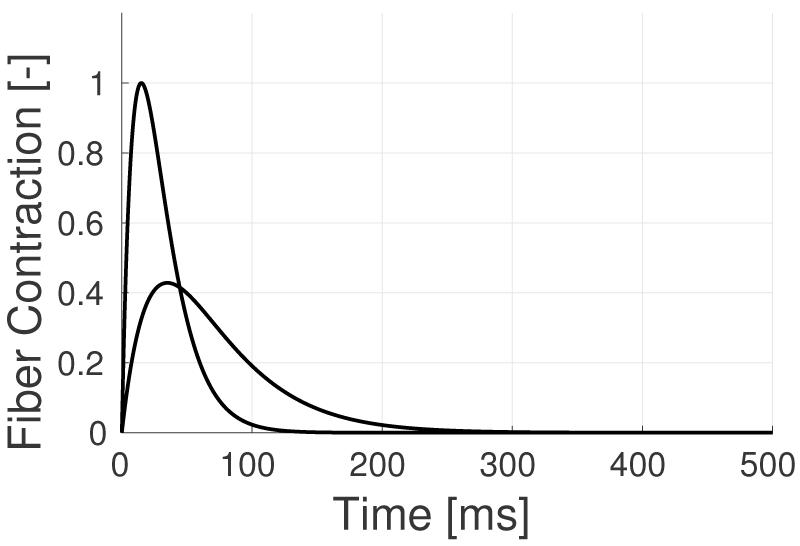
Examples of fast and slow twitch waveforms. Slow and fast twitches are normalized by the area under the curve, so the contribution in terms of energy is the same for both fiber types [42].

Twitches superimpose as the discharge rate increases, leading to stronger muscle contraction. Linear superposition is referred to as the wave summation model [39]. Figure 2 shows the contractile force as a function of MUAP firing rate for a single MU. At low firing rates, a given twitch almost completely relaxes before the next twitch occurs, leading to low frequency undulations and a low net force of contraction. Conversely, at high firing rates the superposition of twitches leads to a fast rise and larger “steady state” contractile force magnitude, with small high frequency fluctuations. At a sufficiently high firing rate, a MU will cease to increase its contractile force with further increases in firing rate, referred to as tetanus.

Fig. 2:

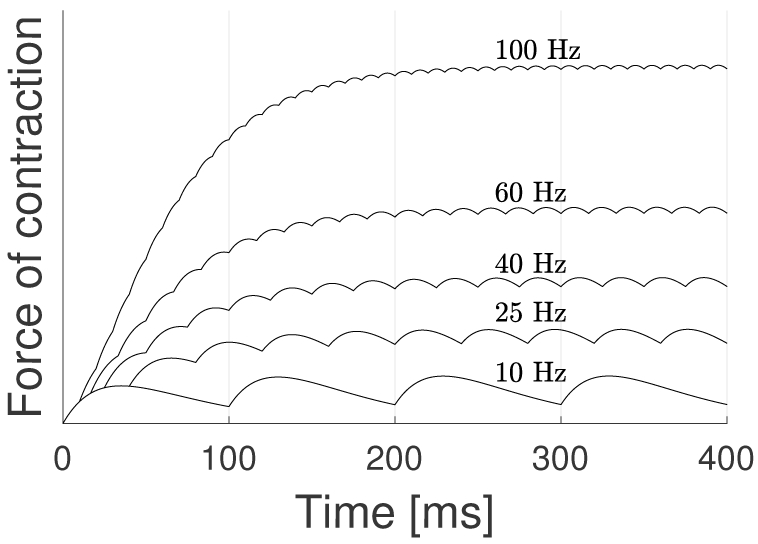
Wave summation model for different neuron firing rates. Each time a MU fires, a twitch is generated. The sum of successive twitches is the basis of the wave summation model [39].

Figure 2 is an idealized representation of the wave summation process, wherein the MUAP interval is a constant (deterministic) value. In actuality, biological systems exhibit some stochasticity, with the inter-spike intervals (ISI) for MUAPs being no exception. In addition, recruitment of subsequent MUs, while exhibiting an overarching structure, also demonstrates some randomness in the process.

B. Muscle Activation Scheme

Human skeletal muscles typically comprise hundreds of MUs, with both the MUAP frequency and the number of recruited MUs dictating the total contractile force of the muscle. According to Roth and van Rossum [42], a single MU contraction (twitch) can be described using

$$\ddot{\alpha }(t)+\frac{2}{\tau }\stackrel{.}{\alpha }(t)+\frac{1}{{\tau }^2}=u(t),$$ (1)

where u(t) represents the input MUAP, τ is the time constant of the contraction, and α(t) denotes the resulting contraction force of the fibers. Consequently, the impulse response of the system is represented by:

$$\alpha (t)=\frac{t}{\tau }{e}^{-(t-\tau )∕\tau },t\ge 0$$ (2)

which characterizes how a MU responds to an electric impulse (spike). Equation 2 is known as the alpha synapse function [42]. Herein, type I and II fibers can be differentiated by their time constants τ_s (slow) and τ_f (fast). All MUs for a given muscle are assumed to have the same number of fibers, independent of their type. Equation 2 should be scaled according to the magnitude of the response of the different fibers. However, due to the lack of available data on the laryngeal muscle fibers, a normalization by the area is performed to approximate the differences in amplitude of the slow and fast fibers. The normalized version of the alpha function [42], corresponds to

$${\alpha }_{\tau }(t)=\frac{t}{{\tau }^2}{e}^{-t∕\tau },t\ge 0$$ (3)

Figure 1 presents a plot of Equation 3 for both slow and fast twitch fibers. This waveform will serve as the foundation for the muscle activation scheme proposed herein to capture both the temporal and spatial summation processes.

To describe the spatial summation, MU recruitment is modeled via the rule of five (ROF), wherein additional MUs are recruited when currently activated MUs experience an approximately 5 Hz increase in MUAP firing rate [43]. To facilitate modeling of the recruitment of MUs, we assume the MUs to be functionally bundled into clusters, herein referred to as a group of motor units (GMU). GMUs can consist of both fast and slow MUs, the proportions of which will dictate the overall contraction speed of the GMU. GMUs are assumed to follow the ROF for recruitment.

GMUs are composed as follows: A fixed number of GMUs N is first defined for a given muscle. Slow-fiber MUs are assigned to the first GMUs, until all slow MUs are assigned. Fast-fiber MUs are then assigned to the remaining GMUs. Note that depending on the proportion of slow and fast fibers in a muscle, there could be a GMU with mixed fibers. GMUs then are recruited by the ROF from first to last (slow fibers to fast fibers), allowing for the recruitment of all slow fibers first.

To implement the ROF, we employ a parameter F to control the firing rate of the GMUs. The firing rate for a given GMU j ∈ {1,…, N} is governed by

$${\mathit{F}}_j=\text{min}\{\max \{F-5(j-1)+\eta ,0\},F_{\max }\},$$ (4)

where F_max is the maximum firing rate that a GMU can physically sustain, i.e., the firing rate at which the GMU tetanizes. The parameter $\eta ~\mathcal{N}$ (0, σ_F)is a random noise term to capture the inherent variability in the ROF; that is, subsequent MUs may not be recruited at exactly a 5 Hz increase in F. Herein, bold font is used to indicate stochastic parameters and functions.

The stochasticity inherent in the arrival of a MUAP is captured in the temporal summation process by incorporating a random component into the inter-spike interval (the interval between any two subsequent AP spikes). For a given GMU j with firing rate F_j sampled from Equation 4, we construct an impulse train III_i(t, F_j) with inter-spike interval drawn from $\mathcal{N}(1∕F_j,{\text{CV}}_e(F_j)∕F_j)$ for each MU i. The coefficient of variation (i.e., standard deviation divided by the mean value), CV_e(F_j), derived from the experimental data of Mortiz [34], is given as

$${\text{CV}}_e(F_j)=\left(1+e^{-F_j∕50}\right)∕10,$$ (5)

which captures the observed change in behavior across firing rates. This implementation implies that the CV_e ranges from 0.2 for lower activation frequencies to 0.1 at higher firing rates.

The pulse train comprising the time series of twitches is given by

$$\mathit{p}(t,F_j)=\frac{1}{M}\sum _{i=1}^M({\mathbf{III}}_i(t,F_j)\ast {\alpha }_{\tau })(t),$$ (6)

where M is the number of MUs in the GMU. We note that care must be taken in Equation 6 for GMUs comprising both slow and fast fibers, as α_τ differs for the two fiber types, as shown in Figure 1.

Finally, muscle activation, which is a normalized representation of the contractile force exerted by a given muscle [11], is given by

$${\mathit{a}}_m(t)=\frac{{\sum }_{j=1}^N\mathit{p}(t,F_j)}{\mathrm{E}\{{\sum }_{j=1}^N\mathit{p}(t,F_{\text{tet}})\}}$$ (7)

where E{·} is the expectation operator as t → ∞ and

$$F_{\text{tet}}=F_{\max }+5(N-1)$$ (8)

is the firing rate for a fully tetanized muscle (all GMUs fully activated). In this manner, a fully tetanized muscle is given by E{a_m} = 1, whereas E{a_m} = 0 represents a fully relaxed muscle. We highlight the fact that a_m is a function of our firing rate control parameter F introduced in Equation 4. The nonlinear mapping between these parameters will be discussed in subsequent sections.

C. Laryngeal Muscle Parameters

Two intrinsic laryngeal muscles are considered in this study due to their importance in pitch control during phonation [44] and the VF model used in the study: TA and CT. Table I presents the laryngeal muscle parameters employed in the proposed scheme. This includes experimental data on muscle morphology [45] [46] [38], as well as modeling assumptions, such as the number of GMUs per muscle and the number of MUs per GMU. Similar model parameters have been used recently in a experimental study of the dynamics of intrinsic laryngeal muscle contraction [47].

TABLE I:

Muscle parameters for CT and TA muscles [45], [46], [38].

Muscle	TA	CT
GMU per muscle (N)	10	10
MU per GMU (M)	35	44
Fibers per MU	10	20
Percentage of slow fibers	35%	47%
Percentage of fast fibers	65%	53%
Slow fibers time constant (τs)	35 ms
Fast fibers time constant (τf)	15 ms
Maximum firing rate for GMU (Fmax)	150 Hz
Standard deviation for ROF (η)	2 Hz

For this study, the body-cover model developed by Titze and Story [2] was employed. This low-dimensional model was chosen due to its simplicity and the physiologically-based relationship between model parameters and muscle activations established in [11]. Glottal aerodynamics were modeled following [48], and no vocal tract was included to facilitate comparisons with results presented in [11].

III. Results

A. Muscle Activation Description

Figure 3 shows examples of TA muscle activation signals obtained using the proposed stochastic muscle activation scheme for the same set of firing rates shown in Figure 2. At the lowest firing rate, only the first 2 GMUs are nominally recruited, while for the remaining firing rates all 10 GMUs may be active. In all cases shown, none of the GMUs are tetanized. The time series shown in the figure have transient portions that last for approximately 0.2 s, which represents the time required for the muscle to transition from the fully relaxed to a contracted state. In comparison with the traditional wave summation model shown in Figure 2, we observe that the muscle activation signal generated using the stochastic scheme lacks a periodic structure, thus more closely resembling actual muscle behavior [34].

Fig. 3:

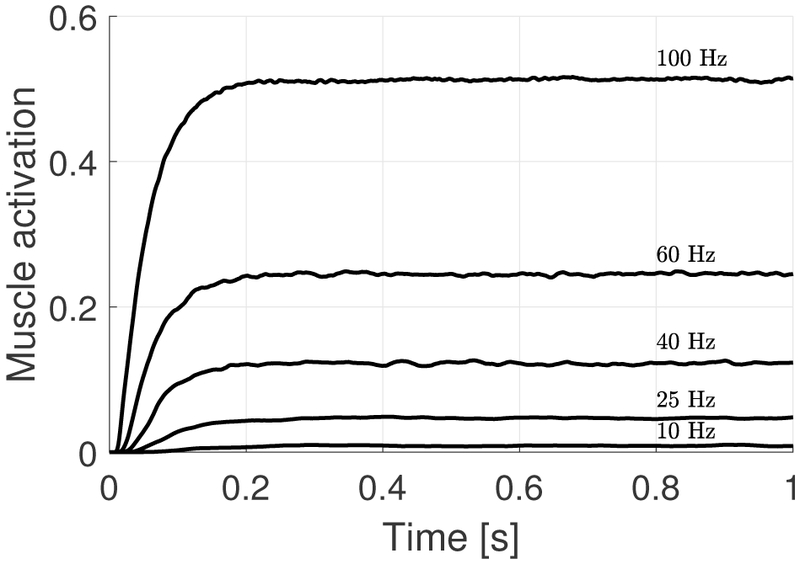
Examples of muscle activation for the TA muscle for a range of firing rates using the proposed stochastic activation scheme.

Note that Figure 3 was constructed with only one realization of the proposed stochastic muscle activation scheme. In order to characterize its general behavior we need to run statistics on many realizations of the signal. Therefore, 40 simulations of the activation signal were computed for each value of the firing rate, which spans from 10 Hz to 250 Hz, in steps of 10 Hz for a total of 10000 simulations. Note that F_max is set at 150 Hz, so the tetanization frequency F_tet is approximately 200 Hz by the ROF. At this frequency, nominally all 10 GMUs should be firing at F_max, barring stochastic variability in the ROF in Equation 4. Simulations are performed up to 250 Hz to account for the latter.

The average CV of the 40 signal realizations for each firing rate F for both the TA and CT muscles is shown in Figure 4. The average CV is an estimate of the variability within the activation signals across firing rate. The larger variability in low firing rates is a result of Equation 5 and the different responses between muscles is a product of the morphological construction of the muscles, as shown in Table I. Specifically, the differences between the two muscles is confined to lower firing rates due to the different proportion of slow-small fibers, which changes the properties of the temporal filtering in the muscles. We note that CV is essentially constant for F > 180 Hz as more and more GMUs become tetanized, and thus no longer change their behavior with increasing firing rate.

Fig. 4:

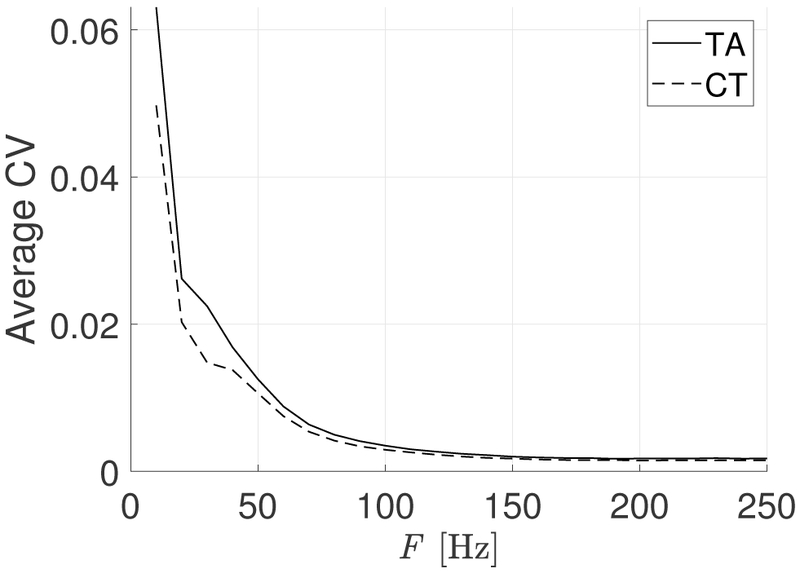
Average CV for CT and TA muscles versus firing rate F. Note that signal variability is higher at lower levels of muscle activation.

In addition to differences in signal variability between individual realizations, the mean of the signal can also change. That is, each realization may have a different steady state mean muscle activation value due to the stochastic nature of the scheme. To capture this, we present the average muscle activation (average of the mean signal values for all realizations) and coefficient of variation of the mean (standard deviation of the mean values divided by the average muscle activation) in Figure 5 for the TA muscle at each firing rate. We note that in the range of 40 Hz ≤ F ≤ 180 Hz the relationship between firing rate and mean activation is linear. Below 40 Hz there are inactive GMUs, while above 180 Hz the effect of saturated GMUs begins to be noticeable. Typical values of muscle activation employed in reduced order models range between approximately 0.1 and 0.5, which falls within the linear region of the mapping and is thus amenable to simple control strategies.

Fig. 5:

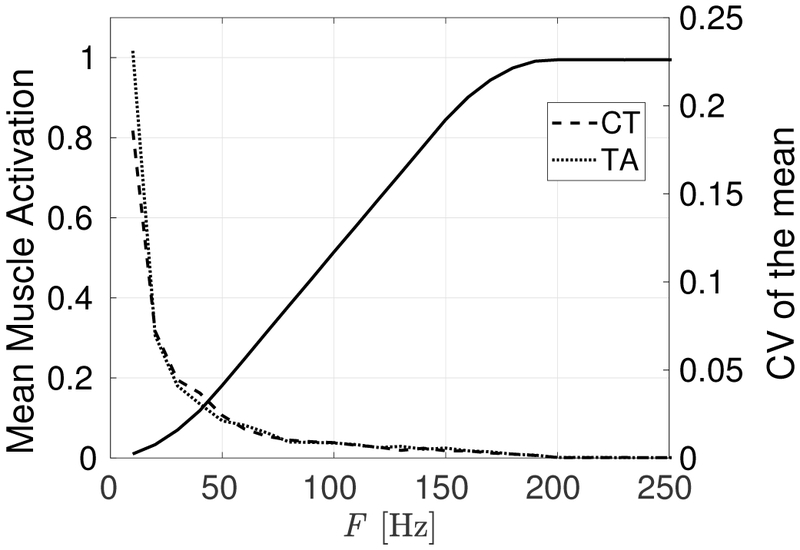
Mean activation (left axis, solid line, both muscles) and CV of the mean (right axis, dashed line, see legend for muscles) versus firing rate for CT and TA muscles. The mean muscle activation saturates at a value of 1 during tetanus, as expected.

Comparing the CV of the mean in Figure 5 with the average CV in Figure 4 shows that the variability of the mean is on the order of the variability of an individual realization, which has implications for pitch control. To begin to establish a relationship between the mean activation behavior and pitch control, we posit that mean activation represents a neurological target. Therefore, the standard deviation of the mean is associated with the target variability. The CV of the mean decreases exponentially with the firing rate due largely to the increasing mean; the standard deviation of the means remains relatively constant with firing rate, except at very low firing rates. Neurologically, this translates into a better pitch control at higher muscle activations.

The behavior of the average CV and the CV of the mean support the idea that variability in discharge rates influences force fluctuations at lower levels of activation. This is consistent with previous findings [49], which report that variability at lower levels is due to low-pass filtering of the neuronal drive. Most of the higher frequency components that are present in the input signal are damped out, leading to low-frequency oscillations manifesting in the muscle activation output. It is uncertain if low-frequency variations are due to ISI variability or low-frequency oscillations in MU discharge [50]; this is particularly true in the specific case of laryngeal muscles, for which information is scarce.

B. Spectral Analysis

To further characterize the properties of the muscle activation scheme, we analyze its spectral content as a function of firing rate. The power spectral density (PSD) is computed as the average periodogram of the 40 signal realizations. Figure 6 presents the resulting PSD for the TA muscle as a function of firing rate. A strong energy band is centered around the firing rate, which has a slope of 1 and saturates at a firing rate of 150 Hz due to tetanization (see Table I). The width of the high energy band is approximately 50 Hz that arises due to the ROF distributing energy between GMUs. Higher harmonics are present due to the quasi-periodic content in the signals. We note that when η = 0 in Equation 4 and CV_e = 0 in Equation 5, the muscle activation scheme is completely deterministic. In this case, the PSD has a similar structure, but with the high energy bands resolved into clear tonal components.

Fig. 6:

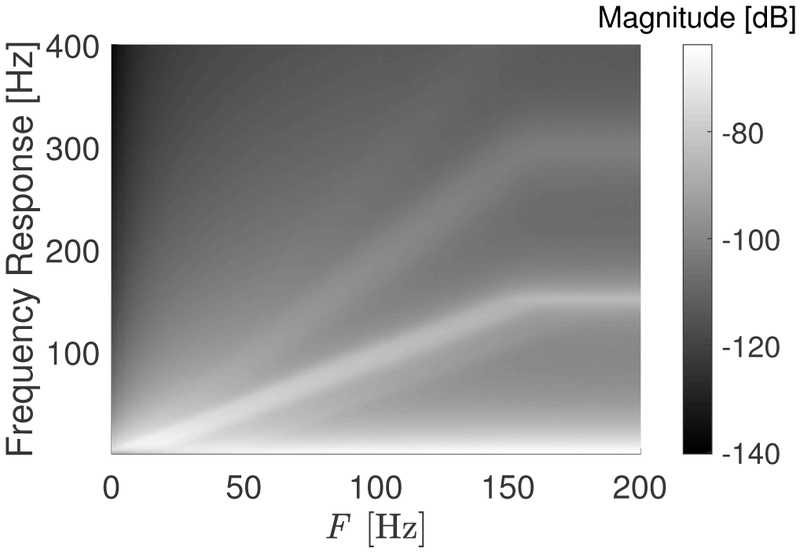
PSD of the stochastic muscle activation scheme versus firing rate for the TA muscle. Strong frequency components can be observed in the range in which active GMUs are firing. Low frequency components are present at any level of activation.

The other salient feature in Figure 6 is a low frequency component in the response below approximately 20 Hz. This arises from a cross-spectral DC component that is inversely proportional to the standard deviation of the random variable that models the ISI in the activation signal [51]. This is directly related to the non-zero CV of the mean observed in Figure 5; that is, there is variability in the mean muscle activation that arises as a direct result of the ISI variability. Low-frequency components are essential for the resulting activation profile (or force output), as they have been related to force steadiness at low activation values [49]. In the deterministic case, there is no variability in the ISI, thus the DC component does not appear and the mean muscle activation parameter is independent of realization, as expected.

To further characterize the low-frequency components, we examined the spectral tilt (slope) that the PSD exhibits between 2 Hz and 60 Hz according to Kuda and Ludlow [20]. This spectral slope was computed with a filtered version of the muscle activation signal in which the mean value was removed. The spectral slope was computed between the peak and a point 15 Hz higher. Figure 7 presents the spectral slopes for CT and TA muscles at different levels of activation.

Fig. 7:

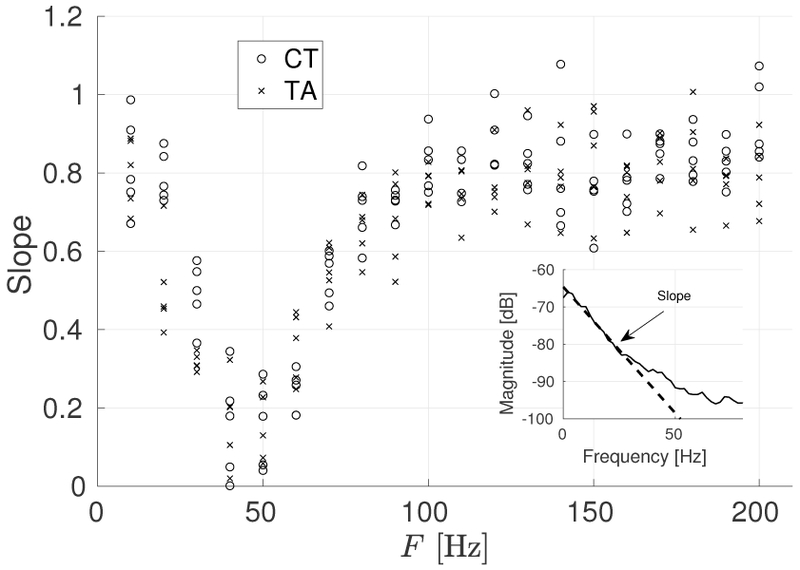
Spectral slope for CT (o) and TA (x) muscles at different firing rates. Inset: Example of spectral tilt calculation method. The spectral slope is computed between the peak frequency in the PSD and a 15 Hz point above it.

Previous studies show that normal voices that do not exhibit tremor have spectral slope values between 0 than 1, whereas voices with tremor have spectral slopes between 1 and 2 [20]. Figure 7 illustrates that the activation signal resulting from the proposed stochastic scheme for normal conditions has slopes between 0 and 1, which is in agreement with the expected normal behavior.

C. Body-Cover Model Integration

The BCM of the VFs is typically configured using physiological rules of muscle activation [11] that allow for a meaningful construction of the model parameters. The BCM model parameters are functions of the TA, CT, and LCA muscle activations, and as such, the output of the BCM accounts for the complex interactions between these muscles. By itself, a standard simulation of the model presents no stochastic or random behavior, although sources of perturbation can be included (i.e., aerodynamic turbulence [28]). We explore the impact of the proposed stochastic muscle activation scheme by implementing it into the BCM. The proposed stochastic variability is incorporated into the muscle activation input of rules of muscle activation [11] and will thus propagate through the BCM in a non-trivial manner, being the only stochastic source in the whole model in our implementation. Note that in this study we only looked at steady-state phonation and we did not explore the role of phonation onset, phonation threshold pressure, or pre-phonatory conditions for achieving self-sustained phonation [52], [19].

Figure 8 shows an example of how the proposed stochastic muscle activation scheme produces variability in the lower cover layer mass and spring constant in the BCM with time. This specific realization employs a firing rate for the TA muscle of 70 Hz with the CT and LCA activations assumed fixed at 0.2 and 0.5, respectively. Temporal variations in the BCM model parameters in Figure 8 arise due to the stochasticity embedded in the TA muscle activation by the proposed model. The mean (standard deviation) are 6.53 × 10⁻² (9.21 × 10⁻⁵) g and 8.78 × 10⁴ (67.3)dyn/cm for the mass and spring constant, respectively.

Fig. 8:

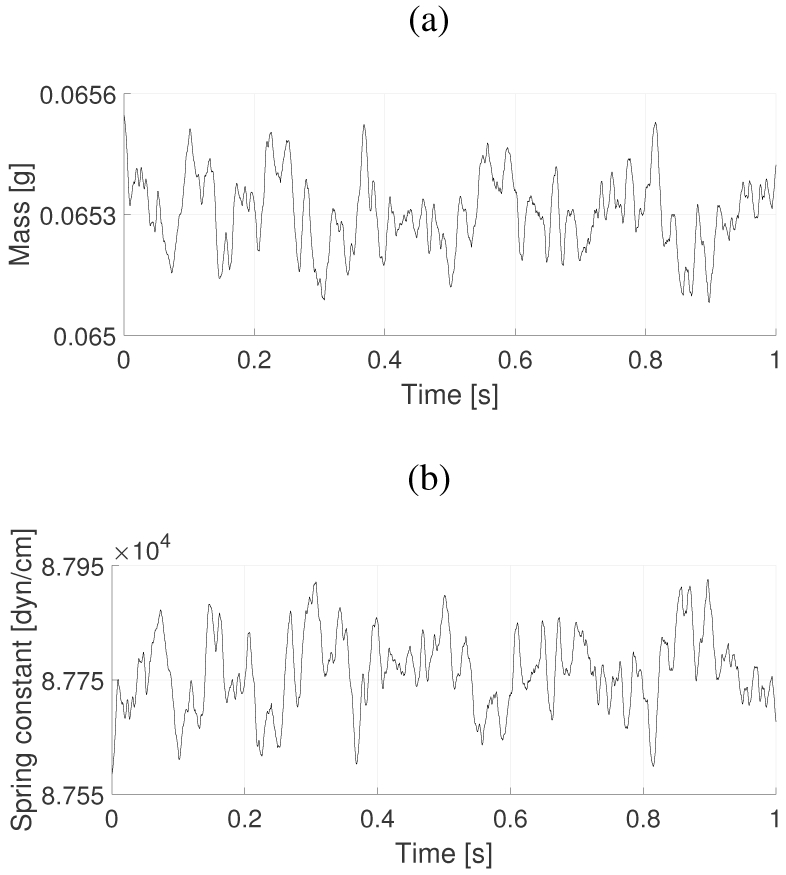
Effect of the proposed stochastic TA muscle activation scheme on the (a) lower cover mass m₁, and (b) lower cover spring k₁ of the BCM. Both parameters vary in time due to the temporal variability in the TA muscle activation parameter.

To more thoroughly evaluate the impact of the proposed stochastic muscle activation scheme, we perform a parametric analysis of CT and TA activations. An evenly spaced grid of 20 × 20 firing rates for CT and TA muscles, ranging from 0 to 200 Hz, was utilized with 40 simulations performed for each parameter combination. To facilitate comparison with the deterministic muscle activation rules established by Titze and Story [11], we extendws their Muscle Activation Plots (MAPs) to include variability in BCM output from our stochastic representation. MAPs now allow for an explicit representation of the BCM parameters as a function of firing rate for each muscle.

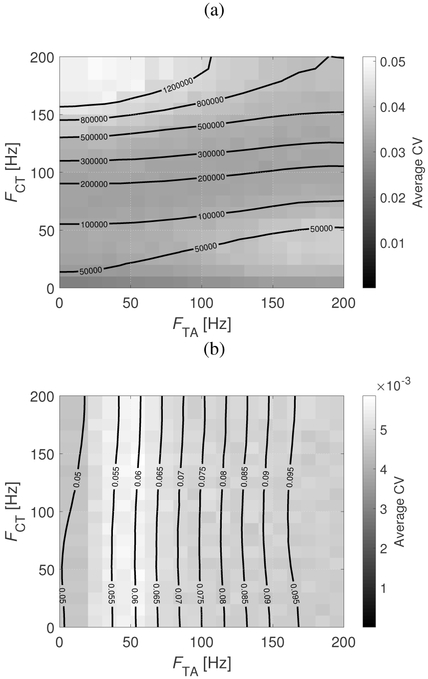
Figure 9 shows a contour MAP of fundamental frequency as a function of CT and TA firing rates. The estimation of f_o was obtained using the RAPT algorithm [53] on the glottal area waveform. The contour lines in Figure 9 display the mean value of f_o, while the flood contour indicates the average CV of the realizations. The range of displayed firing rates nominally corresponds to mean muscle activation parameters ranging from 0 to 1, barring the mapping presented in Figure 5. With this in mind, we note that the distribution of f_o with muscle activation parameters displays similarities to the MAP presented by Titze and Story [11]. Specifically, f_o generally increases with increasing CT and decreasing TA firing rates and vice versa. The CV distribution is somewhat more complex, with the highest variability occurring at high f_o, when F_CT is high and F_TA is low. A slight increase is also observed when F_TA is high and F_CT is low. Interestingly, CV is not elevated when both firing rates are high. Thus, there is not a direct relationship between the variability in f_o and that of a particular muscle. This is in contrast with the results from the simpler mathematical description presented in [17] that ascribed all f_o variation to the TA muscle. In addition, we highlight that the average CV of the fundamental frequency in Figure 9 provides information of target values for pitch control. That is, high pitch frequencies (high CT, low TA) are subject to the highest variability, meaning that it is more difficult to hit a pitch target in that scenario. In contrast, intermediate pitch frequencies (intermediate CT and TA) exhibit the lowest variability, meaning that it is easier to hit a pitch target in that condition.

Fig. 9:

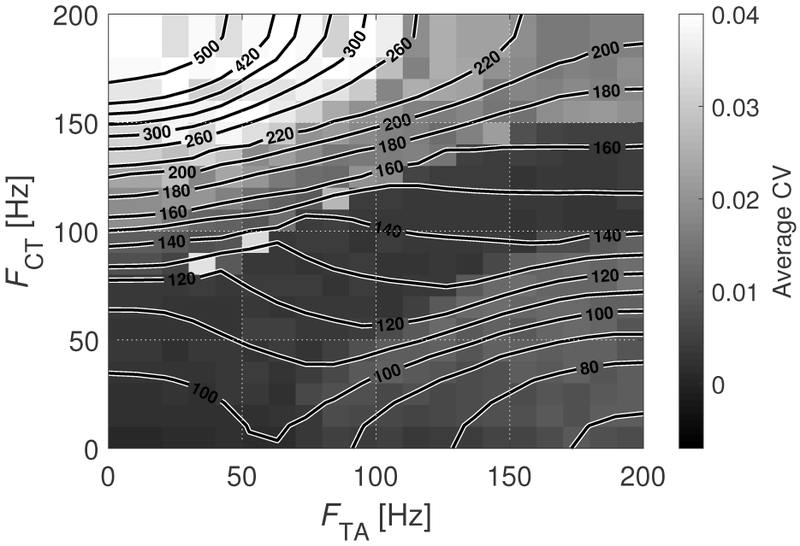
Mean fundamental frequency (iso-lines) and average CV (flood contour) for the BCM as functions of TA and CT firing rates. All units are in Hz.

To further investigate the trends observed in Figure 9, we explore the details of the principal BCM parameters influencing f_o, namely the lower cover spring k₁ and mass m₁. A sample time series for a specific case was previously presented in Figure 8. Figure 10(a) presents the mean spring stiffness and average CV for the full range of CT and TA firing rates. In general, the mean value of k₁ is a strong function of CT, increasing rapidly as F_CT increases. It is a much weaker function of F_TA. The opposite is true for m₁, shown in Figure 10(b), which increases with F_TA while remaining virtually unchanged with F_CT. The average CV distribution for k₁ shows relatively higher values for the extremes of F_CT, whereas the density for m₁ is highest at low values of F_TA and relatively invariant otherwise. The combination of these two average CV distributions largely explains the average CV map for f_o in Figure 9.

Fig. 10:

Mean BCM parameters (iso-lines) and average CV (flood contour) as functions of TA and CT muscle firing rates. (a) Lower cover spring constant k₁ (in dyn/cm); and (b) lower cover mass m₁ (in g) of the BCM.

One parameter of great importance in the BCM is the VF length, as the resulting f_o directly depends on it. It has been shown that small variations in VF length affect the pitch regularity [30]. Variations of VF length were obtained across all the possible combinations of activations. We contrast our results with experimental VF length measurements obtained from in vivo canine larynges that were excited using electrical stimulation [26]. Hirano’s four laryngeal adjustments were reproduced using the BCM with the proposed stochastic muscle activation scheme, and changes in the VF length were obtained with respect to its nominal length L₀. The results of this comparison are shown in Table II.

TABLE II:

VF length changes in % with respect to nominal length for Hirano’s four laryngeal adjustments [26].

	Vahabzadeh et al. 2017	BCM Simulations
Low TA/Low CT	+6% ± 1.5%	+ 10% ± 0.05%
High TA/Low CT	−2.5% ± 3%	−20% ± 0.06%
TA Slight >CT	0% ± 2%	0% ± 0.08%
CT >>TA	+8.4% ± 0.5%	+30% ± 0.1%

General agreement is observed in the trends in Table II, although it is necessary to point out the fundamental differences between the original experiment and our simulations, to understand the observed discrepancies. First, the experimental study of Vahabzadeh et al. [26] uses a canine larynx, whereas our representation is designed for human phonation. Naturally, the nominal values for the VF lengths and its variability are different. In addition, the type of graded nerve stimulation procedure in [26] and the experimental nature of the protocol introduce larger differences in the standard deviations.

To place the previous discussions on the output variability in a more clinical context, we computed common acoustic perturbations, i.e., jitter and shimmer [54]. While we acknowledge that these measures have limitations for diagnostic purposes since they are not capable of identifying the source of abnormal behavior (acoustic, aerodynamic, biomechanical, and neurological), they do enable comparisons with prior studies on the impact of muscle activation variability [30], [17], and have been widely reported in human subjects [31], [32] and speech synthesis studies [33]. Herein, jitter and shimmer were computed from the simulations previously described using PRAAT scripts [55]. Simulations of 3 s of duration were performed to accurately calculate both measures. 20 simulations were carried out for each activation combination, considering the same 20 × 20 spaced grid mentioned earlier. Once computed for the whole range of possible activation combinations, jitter was found to always be below 0.2% and shimmer below 0.7%, which is typical of a normal voice [31], [32], [33]. Therefore, it can be inferred that although the proposed scheme only introduces neuronal fluctuations, the resulting acoustic perturbations are within the “normal” range. In addition, it is worth noticing that articulatory speech synthesizers [33], [4] use fluctuations in the voice source (similar to jitter) that linearly increase with fundamental frequency, to make the synthesized speech more natural. This behavior is in agreement with our scheme, as observed in the flood contour in Figugre 9, although with more a complex pattern that depends on muscle configuration.

Finally, one additional simulation was conducted to illustrate the effects of the muscle variability near bifurcation zones in the BCM model. For this purpose, we included the effect of the LCA muscle, which is a very sensitive parameter for achieving self-sustained oscillations with the BCM, thus having a significant impact on the vibratory stability near bifurcation zones. Figure 11 shows an example in which the variability in the LCA muscle (with a mean value close to 0.5) causes a great instability in the area waveform. Jitter for this particular case was above 1%, with a spectral slope also above 2, which suggest abnormal behavior [32], [20]. The large sensitivity of the BCM model dynamics to LCA illustrates a weakness of the current rules for relating muscle activation to model parameters [11] and its inability to represent antagonist muscle action to regulate glottal adduction.

Fig. 11:

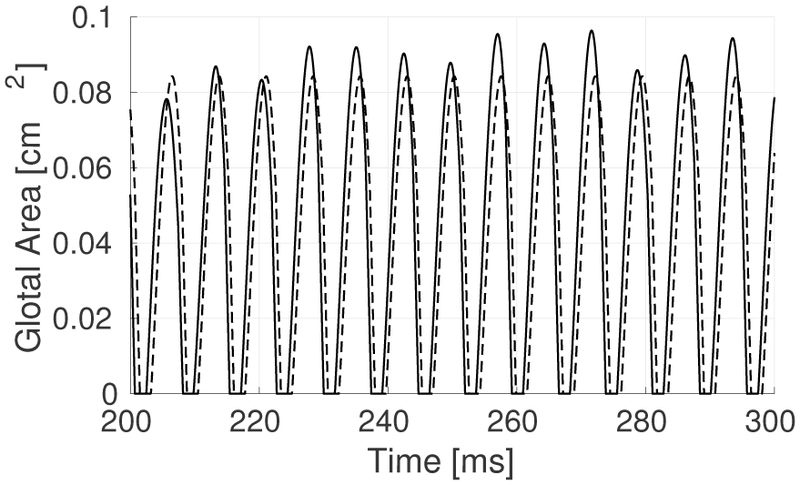
BCM simulation with stochastic LCA activation, with a mean activation around 0.5. Activation values for CT and TA were fixed at 0.5 and 0.25, respectively.

IV. Discussion

The proposed muscle activation scheme includes several assumptions regarding muscle morphology and functionality, including linear summation of muscle twitches, the “rule of five” for MU recruitment, and the collection of MUs into groups that are simultaneously recruited. Although linear twitch summation is well established in the literature [17], [39], a non-linear summation framework could be explored. We further note that other muscle recruitment models exist [12] and may warrant future examination. In this regard, the proposed morphology for the GMUs could be further revised. We acknowledge that the selection of the number GMU can have an effect on partial frequency components of the muscle activation signals, although the resulting VF model kinematics remain largely unaffected.

We contrasted the proposed muscle activation scheme with prior studies reporting vocal fold posturing changes during in vivo canine measurements and spectral characteristics during intramuscular EMG recordings in human subjects, obtaining general agreement in both cases. In addition, we provided contrast with studies assessing acoustic perturbations, where resulting jitter and shimmer from the BCM output were in the normal range and had an increasing behavior with frequency, matching prior observations [33], [4]. All these comparisons have limitations that need to be pointed out. The in vivo canine experiments from Vahabzadeh et al. [26] do not exactly match the anatomical conditions and type of nerve stimulation procedure in our human model, thus affecting mean values and their variability. In terms of the acoustic perturbations, we acknowledge that changes in the neural drive are not the only source that induces variability. Other factors (acoustic, aerodynamic, biomechanical) can result in significant changes in these measures. Furthermore, experiments with excised larynx phonation in neurally dead specimens indicate that vocal perturbation is present without fluctuations in the neural drive [22], [25]. It is interesting to note that the graded artificial stimulation used in these studies does not generate a voice pattern that corresponds to unnatural voice. We could hypothesize that the graded electrical input introduced to the laryngeal nerves in these canine experiments could be described through a deterministic (periodic) MU firing rate contracting the laryngeal muscles using a similar framework as the one proposed in this study, although further research would be needed to relate the electrical nerve activation to the MU constriction.

On the other hand, there is evidence in which twitch variations affect perturbations in the voice [30], particularly in the fundamental frequency. The simulations presented in this study support the idea that small variations in muscular activity can yield perturbations in the voice. One aspect that remains to be explored is how these fluctuations affect phonation stability near bifurcation zones, information that could be useful for modeling voice breaks or tremors. It is important to emphasize that our simulations were obtained for steady state vowels, given that previous studies have illustrated that the neural drive of the muscle activation changes during phonation onset but not in the same way than the resulting acoustic perturbations [52], [19], [47]. Phonation onset has added complexity given the inertial effects in the muscle dynamics [56] that are not captured by the current rules of reduced order models [11], and measures such as the relative fundamental frequency [57] may be more appropriate to assess the variability in pitch than traditional acoustic perturbations.

Future efforts will be devoted to exploring the neural effects of antagonistic muscles and extending the rules for controlling a triangular body-cover model [7]. In addition, a long-term goal of this work is to replicate the neural variability of common muscle-related pathologies like Parkinson’s disease. In the case of Parkinson’s disease, neurons exhibit an intricate pattern of inhibition and excitation, which leads to altered firing rate patterns [58]. The proposed scheme could potentially replicate this behavior and therefore serve as a starting point to construct a physiologically-relevant model of Parkinson voices, which is currently lacking. There are also other applications of the proposed muscle activation scheme, e.g., a model of the vocal tract that inherent neural fluctuations. Finally, it would be of value to design a comprehensive validation framework of the proposed stochastic muscle activation scheme with intramuscular EMG measurements of intrinsic laryngeal muscle activity of human subjects during phonation, though it could be quite invasive and complex.

V. Conclusion

The present study introduces a neurophysiological muscle activation scheme for intrinsic laryngeal muscles. It is designed to capture the essential characteristics of muscle control, providing an activation signal for use in numerical models of the vocal folds. The resulting muscle activation is controlled by the neural firing rate of the different MUs, therefore establishing a link between the nervous system and laryngeal muscle control. Synaptic stochasticity present in the neuronal input of the MU arises from the temporal and spatial summations that govern superposition of muscle twitches and MU recruitment, respectively. As a result, the muscle response has frequency content centered around both the firing rate and its harmonics, as well as a low-frequency DC component. These components influence both the fine structure variability of the signal, as well as the ability to achieve a target mean activation value for pitch control. The proposed scheme is integrated into a body-cover model of the vocal folds to assess the impact of muscle activation variability on overall laryngeal control. Along with muscle activation rules, neural firing rate becomes a novel control parameter that offers a natural, physiologically-based, framework to govern vocal fold properties. Fluctuations arise in the vocal fold model parameters, which in turn result in measurable changes in the model output. These changes are in agreement with prior experimental studies accounting for changes in vocal fold posturing, spectral characteristics of the muscle activation signal, and perturbations in the fundamental frequency. The variability in the resulting output is not a simple function of one muscle, but exhibits complex interactions between intrinsic laryngeal muscles.