Dethroning the Fano Factor: A Flexible, Model-Based Approach to Partitioning Neural Variability

Abstract

Neurons in many brain areas exhibit high trial-to-trial variability, with spike counts that are overdispersed relative to a Poisson distribution. Recent work (Goris, Movshon, & Simoncelli, 2014) has proposed to explain this variability in terms of a multiplicative interaction between a stochastic gain variable and a stimulus-dependent Poisson firing rate, which produces quadratic relationships between spike count mean and variance. Here we examine this quadratic assumption and propose a more flexible family of models that can account for a more diverse set of mean-variance relationships. Our model contains additive gaussian noise that is transformed nonlinearly to produce a Poisson spike rate. Different choices of the nonlinear function can give rise to qualitatively different mean-variance relationships, ranging from sublinear to linear to quadratic. Intriguingly, a rectified squaring nonlinearity produces a linear mean-variance function, corresponding to responses with a constant Fano factor. We describe a computationally efficient method for fitting this model to data and demonstrate that a majority of neurons in a V1 population are better described by a model with a nonquadratic relationship between mean and variance. Finally, we demonstrate a practical use of our model via an application to Bayesian adaptive stimulus selection in closed-loop neurophysiology experiments, which shows that accounting for overdispersion can lead to dramatic improvements in adaptive tuning curve estimation.

1. Introduction

Quantifying neural variability is crucial for understanding how neurons process and transmit information. This has motivated a large body of work that seeks to characterize the signal and noise governing neural responses to sensory stimuli. A simple but popular approach to this problem models neural spike counts using the Poisson distribution. Under this model, spike count mean and variance are equal. Deviations from this relationship are often characterized by the Fano factor, defined as the ratio of the spike count variance to the mean (Geisler & Albrecht, 1997; Eden & Kramer, 2010; Shadlen & Newsome, 1998). The Fano factor for a Poisson neuron is therefore equal to one. A Fano factor less than one indicates sub-Poisson variability, a condition referred to as underdispersion; a Fano factor greater than one indicates greater-than-Poisson variability, commonly known as overdispersion. A substantial literature has shown that Fano factors in a variety of brain areas differ substantially from one (Shadlen & Newsome, 1998; Gur, Beylin, & Snodderly, 1997; Barberini, Horwitz, & Newsome, 2001; Baddeley et al., 1997; Gershon, Wiener, Latham, & Richmond, 1998). Recent work has shown that not only do neural responses not obey a Poisson distribution; the overall mean-variance relationship is often not well characterized by a line, meaning the data are not consistent with a single Fano factor (Pillow & Scott, 2012b; Gao, Busing, Shenoy, & Cunningham, 2015; Stevenson, 2016; Goris, Movshon, & Simoncelli, 2014; Wiener & Richmond, 2003; Moshitch & Nelken, 2014). Rather, the spike count variance changes nonlinearly with the mean.

Here we develop a flexible model for overdispersed spike count data that captures a variety of different nonlinear mean-variance relationships. Our approach extends recent work from Goris et al. (2014), which described overdispersed spike responses in the early visual pathway using a Poisson model with multiplicative noise affecting the trial-to-trial spike rate. This produces a quadratic relationship between mean and variance, so the Fano factor increases linearly with mean spike count.

By contrast, our model seeks to describe a more diverse range of mean-variance relationships while maintaining tractability for simulation and fitting. Our model, which we refer to as the flexible overdispersion model, consists of a stimulus-dependent term, additive gaussian noise, a point nonlinearity, and conditionally Poisson spiking (see Figure 1). This framework includes the multiplicative Goris model as a special case when the nonlinearity is exponential but includes the flexibility to exhibit other behaviors as well—for example, Fano factors that decrease with increasing spike rate, which arises for a rectified-linear nonlinearity, and constant slope linear relationships, corresponding to a constant Fano factor, which arises for a rectified squaring nonlinearity. We show that the model can be tractably fit to data using the Laplace approximation to compute likelihoods and requires fewer parameters than other models for non-Poisson spike count data such as the modulated binomial or generalized count models (Gao et al., 2015; Stevenson, 2016). We apply our model to the V1 data set presented in Goris et al. (2014) and show that a rectified power law nonlinearity provides a better description of most individual neurons than a purely multiplicative model.

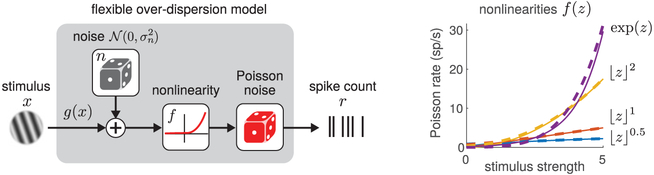
Figure 1:

Illustration of the flexible overdispersion model. (Left) Model diagram. A stimulus-dependent term g(x) plus a latent zero-mean gaussian random variable with variance ${\sigma }_n^2$ is transformed by a rectifying nonlinearity f(·), whose output drives Poisson spiking. (Right) The nonlinearity controls the relationship between the stimulus strength and firing rate and allows different forms of overdispersion. Example nonlinearities include hard rectification raised to a power and the exponential function, which can all be approximated with soft-rectification function raised to a power (see equation 3.7). Soft-rectification versions are shown as dashed lines, with the power p = 3 used to approximate the exponential nonlinearity.

In addition to exploring the properties of our model, as fit to spiking data from V1 recordings, we also explore the practical use of our model. As an example, we use our flexible overdispersion model to develop an application to adaptive stimulus selection in closed-loop experiments, also known as active learning, for characterizing multidimensional tuning curves. These methods seek to minimize the amount of time required to estimate tuning curves by selecting stimuli that are as useful or informative as possible about the tuning curve. We use the flexible overdispersion model in place of the standard Poisson model and demonstrate a marked improvement for tuning curve estimation for both simulated experiments and color-tuning maps in awake fixating monkeys.

2. Background: Fano Factor and the modulated Poisson Model

A popular model of neural responses uses the Poisson distribution to describe stimulus-evoked spike counts (Brillinger, 1988; Chichilnisky, 2001; Simoncelli, Pillow, Paninski, & Schwartz, 2004; Paninski, 2004). The basic model specifies a stimulus-dependent spike rate λ(x) that drives Poisson firing. If we express λ(x) in units of spikes per bin, the probability of observing r spikes in a bin is given by

$$P(r\mid \mathbf{x})=\frac{1}{r!}\lambda {(\mathbf{x})}^r{e}^{-\lambda (\mathbf{x})}.$$ (2.1)

This model makes the strong assumption that the mean and variance are equal: $\text{var}[r]=\mathbb{E}[r]=\lambda (\mathbf{x})$, for any stimulus x. A sizable literature has shown that that assumption is often inaccurate, as spike counts in many brain areas exhibit overdispersion relative to the Poisson distribution, meaning that variance exceeds the mean (Shadlen & Newsome, 1998; Gur et al., 1997; Barberini et al., 2001; Pillow & Scott, 2012b; Gao et al., 2015; Goris et al., 2014; Stevenson, 2016; Baddeley et al., 1997; Gershon et al., 1998; Tolhurst, Movshon, & Dean, 1983; Buracas, Zador, DeWeese, & Albright, 1998; Carandini, 2004).

A common approach to the phenomenon of overdispersion is to regard the Fano factor, $F=\text{var}[r]∕\mathbb{E}[r]$, as a constant that characterizes the generic degree of overdispersion in neural firing (Geisler & Albrecht, 1997; Shadlen & Newsome, 1998). However, this description is adequate only if spike count variance scales linearly with the mean. Recent work has shown that spike responses in four different early visual areas exhibit variance that grows superlinearly with the mean, meaning that overdispersion (and the Fano factor) increase with the firing rate, inconsistent with a single Fano factor (Goris et al., 2014). Moreover, the Fano factor falls short of providing a complete description of neural spike count statistics, as it does not specify a full probability distribution over spike counts. Such a description is necessary for quantifying information in neural population codes. In light of these shortcomings, we feel that the Fano factor should be set aside as the default statistic for characterizing neural overdispersion; rather, researchers should consider the full curve describing how variance changes as a function of mean.

A recently proposed model for overdispersed spike counts in the early visual pathway is the modulated Poisson model, in which the stimulus-dependent Poisson spike rate is modulated by a multiplicative stochastic gain variable on each trial (Goris et al., 2014). The model can be written as¹

$$G~P_G(G),$$ (2.2)

$$r\mid G,\mathbf{x}~\text{Poiss}(G\lambda (\mathbf{x})),$$ (2.3)

where P_G is the distribution of a (unobserved) stochastic gain variable G, which is assumed to have mean $\mathbb{E}[G]=1$, and variance $\text{var}(G)={\sigma }_G^2$. The conditional distribution of the response given the stimulus requires marginalizing over G,

$$P(r\mid \mathbf{x})={\int }_0^{\infty }\text{Poiss}(G\lambda (\mathbf{x}))P_G(G)dG,$$ (2.4)

where Poiss(·) denotes the Poisson distribution (see equation 2.1). When G has a gamma distribution, this integral can be evaluated in closed form and results in a negative binomial distribution, a popular model for overdispersed spike counts (Pillow & Scott, 2012b; Goris et al., 2014; Linderman, Adams, & Pillow, 2016). (See appendix A for a derivation of this relationship.)

For any choice of P_G, the constraint $\mathbb{E}[G]=1$ ensures that the gain variable has no effect on the marginal mean spike count, meaning that $\mathbb{E}[r\mid \mathbf{x}]=\lambda (\mathbf{x})$ as in the pure Poisson model. However, the variance exhibits a quadratic dependence on the spike rate, which can be derived using the law of total variance:

$$\text{var}[r\mid z]=\lambda (\mathbf{x})+{\sigma }_G^2{\left[\lambda (\mathbf{x})\right]}^2.$$ (2.5)

If the gain variable variance ${\sigma }_G^2=0$, meaning the gain variable is constant (G = 1), the model reverts to Poisson. However, for ${\sigma }_G^2>0$, it exhibits overdispersion that increases with firing rate, with the Fano factor given by

$$F=\frac{\lambda (\mathbf{x})+{\sigma }_G^2{\left[\lambda (\mathbf{x})\right]}^2}{\lambda (\mathbf{x})}=1+{\sigma }_G^2\lambda (\mathbf{x}).$$ (2.6)

Goris et al. (2014) showed that this model provides a more accurate description of mean-variance relationships than the Poisson model for neurons from multiple visual areas (LGN, V1, V4, and MT). However, as we will show in the following, the quadratic relationship between variance and mean imposed by the Goris model does not accurately apply to all neurons.

3. The Flexible Overdispersion Model

Our flexible overdispersion model for overdispersed spike counts consists of a stimulus-dependent term g(x), additive gaussian noise n, and a nonlinear function f that transforms (g(x) + n) to a firing rate, followed by Poisson firing. Mathematically it can be written as

$$r\mid \mathbf{x},n~\text{Poiss}(f(g(\mathbf{x})+n)),n~\mathcal{N}(0,{\sigma }_n^2),$$ (3.1)

where f is a nonnegative, monotonically increasing nonlinearity that ensures nonnegative firing rates. The joint distribution over spike count and latent noise is therefore a product of Poisson and gaussian distributions,

$$P(r,n\mid \mathbf{x})=P(r\mid n,\mathbf{x})P(n)=\frac{1}{r!}f{(g(\mathbf{x})+n)}^r{e}^{-f(g(\mathbf{x})+n)}\frac{1}{\sqrt{2\pi }{\sigma }_n}{e}^{\frac{-n^2}{2{\sigma }_n^2}}dn.$$ (3.2)

This flexible overdispersion model can be interpreted in terms of a noisy subthreshold membrane potential that is transformed by an output nonlinearity to drive Poisson spiking (cf. Carandini, 2004). In this interpretation, g(x) is the stimulus tuning curve of the membrane potential, ${\sigma }_n^2$ is the variance of noise affecting the membrane potential, and f(·) is a rectifying output nonlinearity that converts membrane potential to firing rate.

To obtain the probability of a spike count given the stimulus, we marginalize this distribution over the unobserved noise n:

$$P(r\mid \mathbf{x})={\int }_{\infty }^{\infty }P(r,n\mid \mathbf{x})dn.$$ (3.3)

Figure 1 shows a diagram illustrating the model and several example choices for the nonlinearity f(·).

The choice of nonlinearity f(·) allows the model the flexibility to produce different forms of overdispersion, that is, mean-variance curves with different shapes. When f(·) is exponential, we recover the Goris model framework with multiplicative noise, since exp(g(x) + n) = exp(g(x)) · exp(n), meaning the noise multiplicatively modulates with the stimulus-induced Poisson firing rate exp(g(x)). However, as we will show, other choices of f(·) lead to different overdispersion curves from the quadratic mean-variance curve implied by multiplicative noise, as depicted in Figure 2.

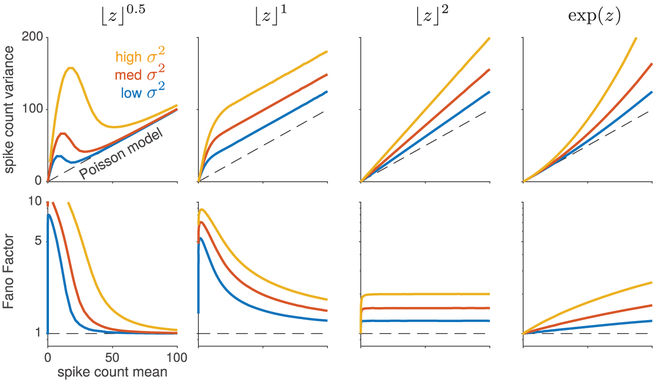
Figure 2:

Variance-mean curves for four different choices of nonlinearity f, each at three different levels of noise variance ${\sigma }_n^2$. The top row shows variance as a function of mean, while the bottom row shows Fano factor versus mean. Note that only the squaring nonlinearity (third column) produces responses of (approximately) constant Fano factor, that is, constant-slope variance-mean curves that pass through the origin. The exponential nonlinearity (fourth column) exhibits variance that grows quadratically with the mean, as shown in Goris et al. (2014), and thus has monotonically increasing Fano factor.

3.1. Spike Count Mean and Variance.

To characterize the overdispersion quantitatively, we need to compute the spike count mean and variance as a function of the stimulus drive, or stimulus-induced membrane potential, which we denote z = g(x) for notational convenience. The mean spike count, which we denote λ(z), can be computed via the law of iterated expectations,

$$\lambda (z)=\mathbb{E}[r\mid z]=\mathbb{E}[f(z+n)]={\int }_{-\infty }^{\infty }f(z+n)P_n(n)dn,$$ (3.4)

where $P_n=\mathcal{N}(0,{\sigma }_n^2)$ is the gaussian distribution of the noise variable n.

The spike count variance, denoted ${\sigma }_r^2(z)$, can be calculated using the law of total variance as

$$\begin{gathered} {\sigma }_r^2(z)=\mathbb{E}\left[\text{var}[r\mid z,n]\right]+\text{var}\left[\mathbb{E}[r\mid z,n]\right] \\ =\mathbb{E}[f(z+n)]+\text{var}[f(z+n)] \\ =\lambda (z)+\mathbb{E}[f^2(z+n)]-\lambda {(z)}^2, \end{gathered}$$ (3.5)

where the expectation in the last line is taken with respect to the gaussian noise distribution $\mathcal{N}(0,{\sigma }_n^2)$. When ${\sigma }_n^2=0$, the last two terms cancel, and the model reverts to Poisson, with variance equal to the mean λ(z).

For arbitrary choices of f, the spike count mean and variance have no closed-form expression and must be computed by numerical integration. However, for several simple choices for f, we can evaluate these quantities analytically or approximate them closely using the delta method (see Table 1).

Table 1:

Spike Count Mean and Variance for Specified Nonlinearities.

Nonlinearity	Mean λ(z)	Variance ${\sigma }_r^2$
$f(z)={\lfloor z\rfloor }^{\frac{1}{2}}$	$\frac{\sqrt{\pi }}{2{\sigma }_n\sqrt{-2z}}\text{exp}(-\frac{z^2}{2{\sigma }_n^2})\mathrm{{\rm Y}}(z,{\sigma }_n^2)$	$\approx \lambda (z)+{\sigma }_n^2\frac{1}{\lambda {(z)}^2}$
f(z) = ⌊z⌋	$\frac{{\sigma }_n}{\sqrt{2\pi }}\text{exp}(-\frac{z^2}{2{\sigma }_n^2})+z\mathrm{\Phi }\left(\frac{z}{{\sigma }_n}\right)$	$\approx \lambda (z)+{\sigma }_n^2$
f(z) = ⌊z⌋2	$\frac{{\sigma }_{n}z}{\sqrt{2\pi }}\text{exp}(-\frac{z^2}{2{\sigma }_n^2})+(z^2+{\sigma }_n^2)\mathrm{\Phi }\left(\frac{z}{{\sigma }_n}\right)$	$\approx (1+4{\sigma }_n^2)\lambda (z)$
f(z) = exp(z)	$\text{exp}(z+\frac{1}{2}{\sigma }_n^2)$	$\lambda (z)+(\text{exp}({\sigma }_n^2)-1)\lambda {(z)}^2$

Notes: Here Φ(·) denotes the normal cumulative density function and $\mathrm{{\rm Y}}(z,{\sigma }_n^2)={\sum }_{i=0}^3{a}_i(z)B_I(\frac{2i-1}{4},\frac{z}{4{\sigma }_n^2})$ with B_I(·, ·) denoting the modified Bessel function of the first kind and weighting coefficients a₀ = −z², $a_1=z^2+2{\sigma }_n^2$, a₂ = z², a₃ = 1. To calculate the approximate variances for f(z) = ⌊z⌋^p, we used the delta method (valid for small ${\sigma }_n^2$) to obtain a general approximation: $\text{var}[r\mid z]\approx \lambda (z)+{\sigma }_n^2{f}^{\prime }{(z)}^2$.

3.2. Capturing Different Forms of Overdispersion.

To illustrate the model’s flexibility, we consider several specific choices for f, namely, exponential, and rectified power functions, f(z) = ⌊z⌋^p for p = {1/2, 1, 2}, where ⌊z⌋ = max(z, 0). Figure 2 shows the different mean-variance relationships produced by these four different choices for f, at three different values of noise level ${\sigma }_n^2$. This demonstrates that simple nonlinear transforms that grow at different rates can capture important classes of behavior.

For concave nonlinearities like the rectified square root, f(z) = ⌊z⌋^0.5, the spike count variance is actually larger at low spike rates than at high spike rates, and the Fano factor drops rapidly to 1 with increasing spike rate (see Figure 2, column 1). Such responses are thus highly overdispersed at low spike counts but indistinguishable from Poisson at high spike counts. A linear-rectified nonlinearity, f(z) = ⌊z⌋, on the other hand, produces linear variance-mean curves with unit slope but with a positive intercept that grows with noise variance ${\sigma }_n^2$. Although they exhibit a constant degree of overdispersion relative to Poisson, such neurons have a falling Fano factor because the ratio of variance to mean is smaller at high firing rates (see Figure 2, column 2). Interestingly, a rectified squaring nonlinearity, f(z) = ⌊z⌋², gives rise to linear variance-mean curves with slopes that vary as a function of noise variance σ². This is the only model of the four considered that generates a constant Fano factor across spike rates (see Figure 2, column 3).

For the exponential nonlinearity, f(z) = exp(z), both the spike count mean and variance can be calculated analytically by exploiting the fact that exp(n) has a log-normal distribution (see Table 1). As noted above, this corresponds to the multiplicative noise setting considered by Goris et al. (2014) and exhibits variance that grows quadratically as a function of mean (see Figure 2, column 4). However, we will show in section 5 that this model behaves very differently from the multiplicative model with a gamma-distributed gain variable (i.e., which produces negative-binomial distributed spike counts discussed in Goris et al., 2014). This indicates that all multiplicative noise models are not equal; differences in the distribution of the multiplicative noise variable can give rise to major differences in higher-order moments, which in turn can produce very different fits to data.

It is also worth noting that a model with latent gaussian noise and exponential nonlinearity is also the default model considered in an extensive literature on factor or latent linear dynamical system models for multivariate spike count data (Macke et al., 2011; Buesing, Macke, & Sahani, 2012; Archer, Koster, Pillow, & Macke, 2014; Rabinowitz, Goris, Cohen, & Simoncelli, 2015; Ecker, Denfield, Bethge, & Tolias, 2016; Gao, Archer, Paninski, & Cunningham, 2016; Zhao & Park, 2017). The majority of this literature, however, has focused on capturing covariance across time or across neurons and has devoted less attention to the issue of how count variance grows with mean for single neurons.

While solutions given in Table 1 and Figure 2 are useful for building intuition, in practice it makes sense to choose a parameterized function whose parameters can be adapted to capture a variety of behaviors. For the general case f(z) = ⌊z⌋^p, p > 0, p ≠ 1 we can use the delta method to derive the approximate variance as

$$\text{var}[r\mid z]\approx \left(1+p^2{\sigma }_n^2\frac{\lambda (z)}{z^2}\right)\lambda (z).$$ (3.6)

Note that when $p^2{\sigma }_n^2{z}^{-1}\approx e^{{\sigma }_n^2}-1$, this expression for the variance mimics the mean-variance relation achieved by the exponential nonlinearity (see Table 1). Thus, for larger powers of p > 2, the rectification nonlinearity can reasonably approximate superlinear mean-variance relationships.

In addition, as optimizing these parameters to fit neuron firing counts will require calculating various derivatives, a smooth function is also beneficial for stability in the fitting process. We find that a useful alternative to the rectified power function given above is the soft-rectification power function—a soft rectification raised to a power p:

$$f(z)={(\log (1+\text{exp}(z)))}^p.$$ (3.7)

By fitting both p and the unknown latent variance ${\sigma }_n^2$, we find that this model is rich enough to capture a wide variety of overdispersion behaviors.

Finally, we note that despite λ(z) and ${\sigma }_r^2(z)$ often requiring numerical integration to obtain, we can guarantee certain properties on the parametric curve, as parameterized by z. First, we can guarantee that both λ(z) and ${\sigma }_r^2(z)$ are smooth functions of z (although the derivatives may be discontinuous). Second, so long as the function f(·) is positive and monotonically increasing, λ(z) is also a monotonically increasing function of z. This indicates that ${\sigma }_r^2(z)$ can truly be considered a function of λ(z) since each value of λ(z) maps onto only one value of ${\sigma }_r^2(z)$. No similar guarantee could be made for ${\sigma }_r^2(z)$, however, indicating that local minima can exist in the mean-variance relation. Local minima occur when the function f(·) has regions that are concave and have small derivatives, as occurs for f(z) = ⌊z⌋^p (see Figure 2). In fact, if f(·) were constructed to have multiple concave regions with small derivatives, multiple local minima and maxima could be present in the mean-variance relationship. Finally, we note that since $\mathbb{E}[f^2(z+n)]\ge \mathbb{E}{[f(z+n)]}^2$, we always have ${\sigma }_r^2(z)\ge \lambda (z)$, indicating that while the amount of overdispersion may vary significantly, our model always produces greater-than-Poisson spike count variance.

4. Model Fitting

In order to apply the flexible overdispersion model to neural data, we need a tractable method for fitting the model parameters. Consider a data set composed of a set of stimuli X = {x_i} and the measured spike counts of a single neuron R = {r_ij} where r_ij denotes the jth response of the neuron to stimulus x_i, for i ∈ {1, …, N}. The model parameters θ consist of a stimulus-dependent term for each stimulus, denoted z_i = g(x_i), the noise variance ${\sigma }_n^2$, and (optionally) the exponent p governing the soft-rectification power nonlinearity. (We consider the variable p to stand for any parameters governing the nonlinearity, although for the exponential nonlinearity, there are no additional parameters to fit.)

The likelihood is given by a product of conditionally independent terms, one for each spike count:

$$P(R\mid X,\theta )=\prod _{i,j}P(r_{ij}\mid z_i,{\sigma }_n^2,p)=\prod _{i,j}\left({\int }_{\infty }^{\infty }P(r_{ij},n_{ij}\mid z_i,{\sigma }_n^2,p)d{n}_{ij}\right),$$ (4.1)

where θ = {{z_i}, σ, p} is the full set of model parameters, and $P(r_{ij},n_{ij}\mid z_i,{\sigma }_n^2,p\}$ is the joint distribution of the spike count r_ij and latent noise n_ij for the jth response to stimulis x_i, which is given by a product of Poisson and gaussian distributions (see equation 3.2).

Because the integral over the latent noise n is intractable, we compute the likelihood using the Laplace approximation. This method uses a surrogate gaussian distribution to approximate the posterior of each n given r around its mode,

$$P(n\mid r,\theta )\approx P_{lapl}(n\mid r,\theta )=\frac{1}{\sqrt{2\pi {\widehat{\sigma }}^2}}\text{exp}\left(-\frac{{(n-\widehat{n})}^2}{2{\widehat{\sigma }}^2}\right),$$ (4.2)

where mean $\widehat{n}$ is the mode of P(n∣r, θ), which we find via a numerical optimization of log P(r, n∣θ) for n, and variance ${\widehat{\sigma }}^2$ is the inverse of the Hessian (second derivative) of the negative posterior log likelihood,

$$\begin{gathered} \frac{1}{{\widehat{\sigma }}^2}=\frac{{\partial }^2}{\partial n^2}\left[-\log (P(r,n\mid z,\theta ))\right] \\ =\frac{1}{{\sigma }_n^2}+\frac{{\partial }^2}{\partial n^2}\left[-r\log f(z+n)+f(z+n)\right], \end{gathered}$$ (4.3)

evaluated at mode $n=\widehat{n}$. If f is exponential, equation 4.3 simplifies to ${\widehat{\sigma }}^2={\sigma }_n^2∕(1+{\sigma }_n^2\text{exp}(z+\widehat{n}))$.

To evaluate the likelihood, we can replace the true posterior with the Laplace approximation to obtain a tractable form for the joint distribution, P(r, n ∣ θ) ≈ P(r ∣ θ) · P_lapl(n ∣ r, θ). We can then solve this expression for the desired likelihood, yielding

$$P(r\mid \theta )\approx \frac{P(r,n\mid \theta )}{P_{lapl}(n\mid r,\theta )},$$ (4.4)

where the numerator is the exact joint probability of r and n given θ, and the denominator is the approximation to the posterior over n given r. Evaluating the right-hand side at $n=\widehat{n}$ (where the Laplace approximation is most accurate) gives the following expression for the likelihood:

$$P(r\mid \theta )\approx \frac{1}{r!}f{(z+\widehat{n})}^r{e}^{-f(z+\widehat{n})}\frac{\widehat{\sigma }}{{\sigma }_n}{e}^{-{\widehat{n}}^2∕2{\sigma }_n^2}.$$ (4.5)

Note that the parameters of the Laplace approximation, $\widehat{n}$ and ${\widehat{\sigma }}^2$, are functions of θ, since they depend on numerical optimization of P(n, r∣θ) for n at a given θ. Thus, maximum likelihood parameter estimation, which involves maximizing the log of equation 4.1 for θ, requires that we update these per response parameters defining the gaussian distribution for each noise term n_ij given r_ij and θ every time we change θ.

To demonstrate that this method yields an accurate approximation to the log likelihood, we compare the true computed log likelihood (via numerical integration) with the Laplace approximation. Figure 3 depicts the log-likelihood landscapes for different spike counts (r ∈ {0, 2, 10, 50}) for both the numerically integrated log likelihood and the Laplace approximation. The ratio between numerically computed and Laplace-based log likelihoods (right-most column) demonstrates that errors are greatest at small spike counts (where the Poisson likelihood deviates most severely from the gaussian), but is negligible even in this regime for the exponential nonlinearity.

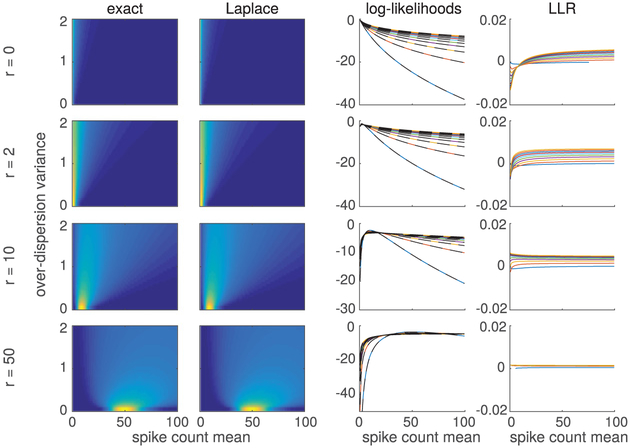
Figure 3:

Comparison of exact and Laplace approximation-based evaluation of model likelihood function under exponential nonlinearity. Left two columns: Image plots show log-likelihood function $\log p(r\mid z,{\sigma }_n^2)$ for spike counts r = 0, 2, 10, and 50 as a function of transformed parameters $e^{z+0.5{\sigma }_n^2}$ (mean spike count) and ($e^{{\sigma }_n^2}-1$) (overdispersion variance for Goris model). The third column shows horizontal slices through the two surfaces at different overdispersion levels (colored traces for exact; black dashed traces for Laplace), showing the two surfaces are virtually indistinguishable on the scale of the log-likelihood values. The last column shows the ratio between the true (numerically computed) and Laplace-based log likelihood, showing there is less than a 0.01% error in the approximation across the entire range of parameter settings at these spike counts. We note that the approximation error is greatest at low spike counts, where the Poisson log likelihood is most nongaussian.

We can use the above methodology to address the particular case where f(·) is the soft rectification raised to a power $(\theta =\{z_i,{\sigma }_n^2,p\})$ or an exponential function (θ = {z_i, σ²}). Full details about evaluating and maximizing the log-likelihood using the Laplace approximation are provided in appendix B.

5. Results: V1 Spike Counts

To test the ability of the flexible overdispersion model to capture the variability of real neurons, we fit to data collected from macaque primary visual cortex V1 (Graf, Kohn, Jazayeri, & Movshon, 2011), one of the data sets considered in Goris et al. (2014). This data set contained five recording sessions with multielectrode array recordings of neural population responses to 72 distinct visual grating orientations. A total of 654 neurons were recorded, and each orientation was presented 50 times. Trials consisted of drifting grating stimulus presentations for 1280 ms, with a 1280 ms rest period in between. From this data set, we chose the 112 well-tuned neurons for model fitting. Well-tuned neurons were determined as in previous studies by applying a threshold to the difference between the minimum and maximum mean firing rate over all stimuli orientations (Graf et al., 2011).

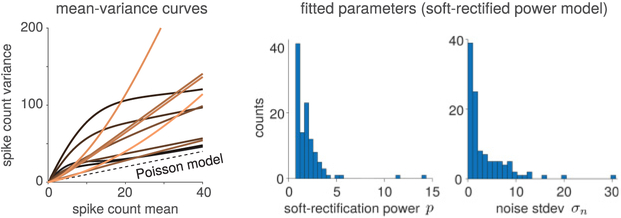
We fit the model parameters using the Laplace-approximation-based method described in section 4 for both the soft-rectification-power function (soft-rect-p; see equation 3.7) and the exponential nonlinearity. For comparison, we also fit the data with the negative-binomial (NB) model from Goris et al. (2014). All model fits had 72 parameters {z_i} to describe the stimulus drive for each orientation and a noise variance parameter ${\sigma }_n^2$, and one extra parameter p for the model with the soft-rect-p nonlinearity. Example mean-variance curves (as well as example draws from the model with the inferred parameters) are plotted against the true data in Figure 4. While for some neurons the negative binomial model and our model resulted in near-identical mean-variance curves, for other neurons, the flexibility of the soft-rectification function produced better qualitative fits. The fact that our model is a log-likelihood fit means that the justification for the mean-variance curves might not be completely apparent from the means and variances of the data. This quality is apparent in neurons 3 and 4 in Figure 4, where the data plotted as mean-variance plots seem ambiguous as to what model parameters might be appropriate, but the mean Fano factor plots below indicate that the model should capture the trend of the data to have lower Fano factors at higher firing rates, a property that our model cap-tures. Figure 5 depicts the range of mean-variance relationships inferred for a sampling of neurons in the data set. The range of curves observed for even this single data set implies that a single mean-variance relationship is insufficient to capture the entire range of neural variability. Figure 5 further emphasizes this point by showing histograms of the inferred parameters (in the case of soft rectification, this includes the latent noise standard deviation σ_n and the soft-rectification power p).

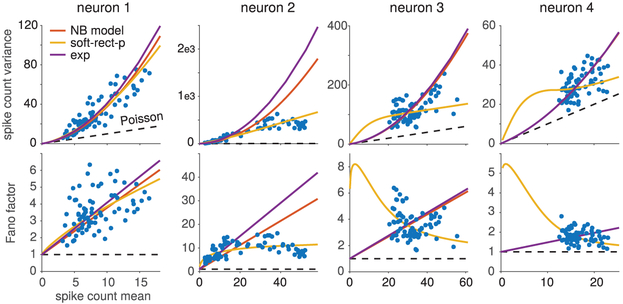
Figure 4:

Example fits to V1 neurons. Each column shows data from a single neuron, with the upper plot showing variance versus mean and the lower plot showing the Fano factor versus mean. Empirical spike count mean and variances (blue dots) were computed for over 50 repetitions for each of 72 different oriented grating stimuli (Graf et al., 2011). For each neuron, we fit three different models by maximum likelihood using all 50 × 72 = 3600 spike count responses. The negative binomial model (red line) and flexible overdispersion model with exponential nonlinearity (yellow) both had 73 parameters (an input level for each of the 72 orientations, and the noise variance ${\sigma }_n^2$), while the flexible overdispersion model with soft-rectification power nonlinearity (yellow) had 74 parameters (including power parameter p). For all four neurons shown, the flexible overdisperion model with soft-rectification power (soft-rect-p) nonlinearity achieved the best model fit as measured by the Akaike information criterion (AIC). The different distributions of the data in each figure show significant diversity in neural spiking, even within V1. When the mean-variance data behavior is decidedly not quadratic (neurons 2, 3, and 4), the soft-rect-p model can adapt to the wide range of statistics. The soft-rec-p model can even capture subtle effects, such as Fano factors decreasing at higher firing rates (neurns 3 and 4). Interestingly, when the data behavior does look quadratic (neuron 1), the soft-rect-p automatically recovers the quadratic behavior modeled by the NB and Exp models. While in this case the soft-rect-p model still had the best AIC score, the difference from the NB AIC value for this example is only 3, indicating that both models approximately recover the same behavior.

Figure 5:

Fits of the hierarchical overdispersion model with soft-rectified power nonlinearity. (Left) Selected variance-mean curves obtained from fits to individual neurons in V1 (each trace represents the mean-variance relationship for a single neuron). Curves are colored in order of increasing exponent power p (lighter lines have higher p). (Center) Histogram of the distribution of inferred soft-rectification power parameters p for neurons in V1 demonstrates the required flexibility in fitting overdispersion behavior. (Right) The distribution in inferred latent noise standard deviations σ_n shows the range in the amount of overdispersion noise in the population of V1 neurons.

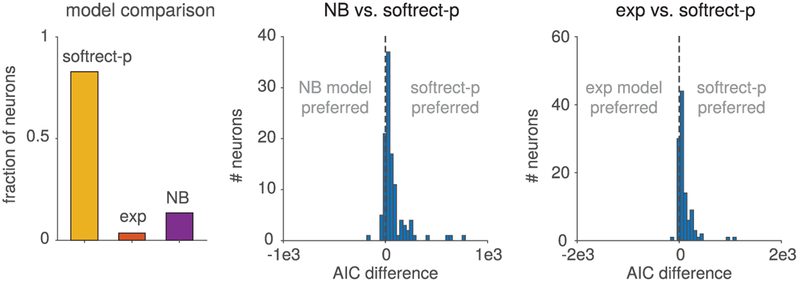
We quantified the performance of different models by comparing the Akaike information criterion (AIC) across all three fits (power soft rectification, exponential, and negative binomial). The calculated AIC values, displayed as histograms in Figure 6, demonstrate that the softrect-p model provided the best fit for the majority of neurons, achieving the highest AIC values for 83.4% of the 112 neurons analyzed. This result indicates that despite the AIC penalization for requiring an additional parameter, the softrect-p fit best modeled approximately 83% of the tuned V1 neurons in the Graf data set. Interestingly, we also note that the exponential nonlinearity model, a model commonly used as an inverse link function in machine learning and neuroscience (Nelder & Baker, 1972), was a worse model for 65.8% of the neurons according to AIC, even having performed worse than the NB model (as shown in Figure 6). This result may seem contrary to the fact that the model with exponential nonlinearity belongs to the same class of multiplicative-noise models as the negative binomial and thus also exhibits a quadratic mean-variance curve. Figure 4 demonstrates this behavior, showing that data fits to both quadratic models can still differ significantly in their curvature. The implication here is that while the full mean-variance curve may provide basic overdispersion properties, it is insufficient to describe a neural spiking model. Specifically, model fitting with a full probabilistic model implies assumptions on higher-order moments that will affect the mean-variance curve fit.

Figure 6:

Model comparison between negative binomial (NB) and flexible overdispersion model with exponential and soft-rectification power nonlinearity using AIC. The soft-rectification power (with fitted power p) performed best for 82% of the neurons, while the NB model performed best for 13.5% (left panel). Pairwise comparisons (middle and right panels) show the distribution of AIC differences across all neurons for pairs of models, in agreement with the overall comparison results.

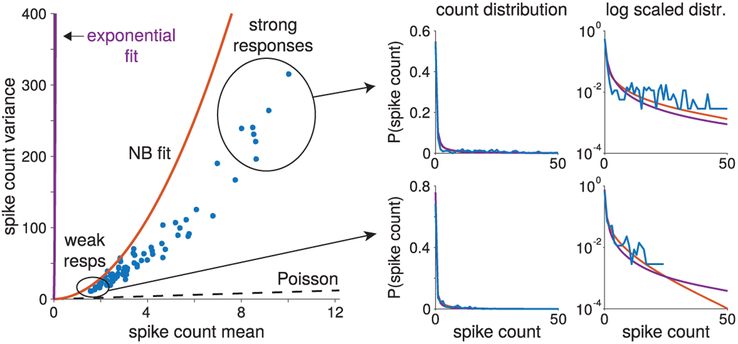
To emphasize the potential insufficiency of the mean-variance curve as a model summary, Figure 7 shows an example case where the exponential nonlinearity yielded a very different mean-variance curve than the negative binomial model, despite the fact that both are multiplicative noise models defined by a stochastic gain variable with a mean of 1. Specifically, for this neuron, both the exponential and NB models seem to have significantly overestimated the variance as a function of the mean. The exponential fit overestimation was so extreme that the curve for the exponential fit is barely visible in the mean-variance plot. After ruling out potential numerical or approximation error with the Laplace approximation technique, we observed that while the mean-variance curves did not match the data, the full count distributions did seem to match the data. The upper-right and upper-left plots show that overall, both models fit the data distributions for both high and low mean spike counts. Plotting the spike count distributions on a log scale, however, shows that despite matching the data well at low firing rates, both models have higher tails than what would be expected. These heavy tails contributed directly to the overfitting of the spike count variance. In fact, the exponential nonlinearity’s spike count distribution has a much heavier tail than even the NB model, correlating with how the exponential nonlinearity model nonlinearity modeled the variance to a higher degree. To understand why the erroneous fits were obtained, we observe that up to a certain value of spike counts, the tails of the data distribution actually look heavy-tailed. In fact the log distributions shown in the lower-left and lower-right panels of Figure 7 do follow the data. Thus, heavy tails stemmed from matching the data in the maximum likelihood (ML) estimation. Unlike the data, however, our models are unbounded, indicating that heavy tails could have an impact on the model variance calculations in ways that would not affect the data fits. This analysis demonstrates that attempting to fit the higher-order moment of the model (as ML-type methods do) may be detrimental to accurately fitting the mean-variance curve.

Figure 7:

Heavy tails can cause significant model mismatch when fitting overdispersed models. An example neuron where model fits (left) produced significant overestimation of the variance. The extreme case here produced an NB fit (red curve) with higher variance and an exponential fit (purple curve) that barely reaches the data points (blue dots indicate mean and variance over the 50 trials per stimulus) in the mean-variance plot. Both fits, however, seem to match the basic statistics of the data when viewed as a distribution. Specifically, when restricted to the stimuli trials eliciting either low or high levels of activity (right plots; bottom plots for low activity and top pots for high activity), we see that the fits did match the spike count distributions (linear y-axis scale on the left and logarithmic scale on the right for clarity) over the support where data were available. The tails of the model distributions, however, differed significantly in both cases, indicating that the model fits are imputing the distribution of spike counts in unobserved counts. Thus, the inherent bias of the models manifested as the observed model mismatch.

6. Application: Adaptive Closed-Loop Experiments

While improved models of neural spiking processes are important from a basic scientific understanding standpoint, these models also have applications as replacing the Poisson model as a front-end in data analysis and efficient recording methods. To illustrate one of the potential uses of the flexible overdispersion model, we developed an application to adaptive stimulus selection for closed-loop neurophysiology experiments. Such methods, known as active learning in machine learning and adaptive optimal experimental design in statistics, seek to select stimuli based on the stimuli and responses observed so far during an experiment in order to characterize the neuron as quickly and efficiently as possible (Lindley, 1956; Bernardo, 1979; MacKay, 1992; Chaloner & Verdinelli, 1995; Cohn, Ghahramani, & Jordan, 1996; Paninski, 2005). Adaptive stimulus selection is particularly useful in settings where data are limited or expensive to collect and can substantially reduce the number of trials needed for fitting an accurate model of neural responses (Paninski, Pillow, & Lewi, 2007; Benda, Gollisch, Machens, & Herz, 2007; Lewi, Butera, & Paninski, 2009; DiMattina & Zhang, 2011, 2013; Bölinger & Gollisch, 2012; Park & Pillow, 2012; Park, Weller, Horwitz, & Pillow, 2014; Pillow & Park, 2016).

Here we introduce a method for adaptive stimulus selection for estimating a neuron’s multidimensional tuning curve, or firing rate map, under the flexible overdispersion model. Our method involves computing the posterior distribution over the tuning curve given the previously observed responses in an experiment and selects the stimulus for which the value of the tuning curve has maximal posterior variance. We illustrate the performance gain using this adaptive learning method for estimating color tuning curves of V1 neurons recorded in awake, fixating monkeys (Park et al., 2014). For simplicity, we use the exponential nonlinearity f(z) = exp(z), which has the advantage of having analytical expressions for the mean and variance of the spike count given an input level z and noise variance ${\sigma }_n^2$.

6.1. GP Tuning Curve Model with Flexible Overdispersion.

Building on prior work (Rad & Paninski, 2010; Park et al., 2014; Pillow & Park, 2016), we model tuning curves by placing a GP prior over the input function g(x). Here g(x) can be considered a log of the tuning curve plus a constant, since the tuning curve (expected spike count given a stimulus) for the exponential nonlinearity is $\lambda (\mathbf{x})=\text{exp}(g(\mathbf{x})+\frac{1}{2}{\sigma }_n^2)$ (see Table 1).

The GP specifies a multivariate normal distribution over the input function values {g(x₁), …, g(x_n)} at any finite collection of stimulus values {x₁, … x_n}, namely:

$$\left[\begin{array}{c}\hfill g({\mathbf{x}}_1)\hfill \\ \hfill ⋮\hfill \\ \hfill g({\mathbf{x}}_n)\hfill \end{array}\right]~\mathcal{N}\left(\left[\begin{array}{c}\hfill m({\mathbf{x}}_1)\hfill \\ \hfill ⋮\hfill \\ \hfill m({\mathbf{x}}_n)\hfill \end{array}\right],\left[\begin{array}{ccc}\hfill k({\mathbf{x}}_1,{\mathbf{x}}_1)\hfill & \hfill \cdots \hfill & \hfill k({\mathbf{x}}_1,{\mathbf{x}}_n)\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill k({\mathbf{x}}_n,{\mathbf{x}}_1)\hfill & \hfill \cdots \hfill & \hfill k({\mathbf{x}}_n{\mathbf{x}}_n)\hfill \end{array}\right]\right),$$ (6.1)

where m(x) is the mean function, specifying the a priori mean of the function values, and k(x, x′) is the covariance function, specifying the prior covariance for any pair of function values g(x), g(x′). Here we use a zero mean function, m(x) = 0 and a gaussian or radial basis function (RBF) covariance function,

$$k(\mathbf{x},{\mathbf{x}}^{\prime })=\rho \text{exp}\left(\frac{-{\Vert \mathbf{x}-{\mathbf{x}}^{\prime }\Vert }^2}{2{\delta }^2}\right),$$ (6.2)

which is controlled by two hyperparameters: the marginal prior variance ρ and length scale δ. Increasing ρ increases the expected prior range of tuning curve values (i.e., increasing the spread between minimal to maximal log firing rates), while increasing δ increases its degree of smoothness. Functions g(·) sampled from a GP with this covariance function are continuous and infinitely differentiable.

We combine the GP prior with the likelihood from the flexible overdisperion model (see equation 3.3) to obtain a complete model for Bayesian adaptive stimulus selection. The complete tuning curve model can therefore be summarized:

$$\text{GP prior}:g~\mathcal{GP}(0,k),$$ (6.3)

$$\text{Latent noise}:n~\mathcal{N}(0,{{\sigma }_n}^2),$$ (6.4)

$$\text{Conditionally Poisson spiking}:r\mid \mathbf{x},n~\text{Poiss}(\text{exp}(g(\mathbf{x})+n)).$$ (6.5)

The necessary steps in our stimulus selection algorithm include include updating the posterior over g(·) after each trial, updating hyperparameters using the Laplace approximation-based marginal likelihood, and selecting the stimulus for which the tuning curve has maximal posterior variance.

6.2. Inference and Laplace Approximation.

The tuning curve inference problem here is similar to that of fitting the flexible overdispersion model (see section 4), except that we have added a prior over the values of g(x) that encourages smoothness and shrinks them toward zero. After each trial, we maximize marginal likelihood under the Laplace approximation to update the hyperparameters (ρ, δ) governing the GP prior’s scale and smoothness, as well as the noise variance ${\sigma }_n^2$.

Let ${\mathcal{D}}_t=\{({\mathbf{x}}_1,r_1),\dots ,({\mathbf{x}}_t,r_t)\}$ denote the data set after t trials, which is simply a paired list of stimuli and spike counts collected so far in the experiment. For the purposes of our derivation, let z = [g(x₁), …, g(x_t)] denote the stimulus input values for the observed stimulus set X = [x₁, …, x_t], and let n = [n₁, …, n_t] and r = [r₁, …, r_t] be the unobserved gaussian input noise and observed spike counts on each trial, respectively.

The first step in the inference procedure is to maximize the log of the joint posterior over z and n, also known as the total-data posterior, after each trial:

$$P(\mathbf{z},\mathbf{n}\mid {\mathcal{D}}_t,\varphi )\propto \left(\prod _{i=1}^{(t)}\text{Poiss}(r_i\mid \text{exp}(z_i+n_i))\right)P(\mathbf{z}\mid \rho ,\delta )P(\mathbf{n}\mid {\sigma }_n^2),$$ (6.6)

where $P(\mathbf{z}\mid \rho ,\delta )=\mathcal{N}(0,K)$ is the GP-induced gaussian prior over the function values (see equation 6.1) with covariance matrix K_ij = k(x_i, x_j), and $P(\mathbf{n}\mid {\sigma }_n^2)=\mathcal{N}(0,{\sigma }_n^{2}I)$ is the distribution of the (unobserved) overdispersion noise for each trial. The full set of hyperparameters is denoted $\varphi =\{{\sigma }_n^2,\rho ,\delta \}$.

This optimization is simplified by considering a change of variables to take advantage of the fact that the Poisson likelihood relies only on the sums of z_i + n_i for each trial. Therefore, let us define

$$\mathbf{s}=\mathbf{z}+\mathbf{n}$$ (6.7)

so that s represents the total input to f(·) on each trial and the latent noise is now n = s − z.

The total-data log posterior can now be written in terms of s and z:

$$\begin{gathered} \log P(\mathbf{s},\mathbf{z}\mid {\mathcal{D}}_t)=\log P({\mathcal{D}}_t\mid \mathbf{s})+\log P(\mathbf{s}\mid \mathbf{z})+\log P(\mathbf{z})+\mathit{const} \\ ={\mathbf{r}}^{⊺}\log (f(\mathbf{s}))-1^{⊺}f(\mathbf{s})-\frac{1}{2{{\sigma }_n}^2}{(\mathbf{s}-\mathbf{z})}^{⊺}(\mathbf{s}-\mathbf{z}) \\ -\frac{1}{2}{\mathbf{z}}^{⊺}{K}^{-1}\mathbf{z}+\mathit{const}, \end{gathered}$$ (6.8)

where 1 is a length-t vector of ones and const denotes constants that are independent of s and z. Note that the total-data log posterior is quadratic in z, meaning that the conditional maximum in z given s can be obtained analytically:

$${\mathbf{z}}_{\mathit{map}}\mid \mathbf{s}={\left(\frac{1}{{\sigma }^2}K+I\right)}^{-1}\frac{1}{{\sigma }^2}K\mathbf{s}.$$ (6.9)

We can substitute this expression for z in equation 6.8 to obtain the profile log-likelihood:

$$\begin{gathered} \log P(\mathbf{s}\mid {\mathcal{D}}_t)={\mathbf{r}}^{⊺}\log (f(\mathbf{s}))-1^{⊺}f(\mathbf{s}) \\ -\frac{1}{2}{\mathbf{S}}^{⊺}{(K+{{\sigma }_n}^{2}I)}^{-1}\mathbf{s}+\mathit{const}, \end{gathered}$$ (6.10)

which we can optimize efficiently to obtain the MAP estimate:

$${\mathbf{s}}_{\mathit{map}}=\text{arg}\underset{\mathbf{s}}{\max }\log P(\mathbf{s}\mid {\mathcal{D}}_t).$$ (6.11)

Note the vector s grows by one element after every trial, but this optimization can be made efficient by initializing the first t − 1 elements of the vector to its value from the previous trial. The joint optimum of the total data log posterior can be obtained by plugging s_map into equation 6.9 to obtain z_map, and setting n_map = s_map − z_map.

The Laplace approximation of the total data posterior can then be computted as

$$P_{lapl}(\mathbf{z},\mathbf{n}\mid {\mathcal{D}}_t,\varphi )=\mathcal{N}\left(\left[\begin{array}{c}\hfill {\mathbf{z}}_{\mathit{map}}\hfill \\ \hfill {\mathbf{n}}_{\mathit{map}}\hfill \end{array}\right],{\left[\begin{array}{cc}\hfill L+K^{-1}\hfill & \hfill L\hfill \\ \hfill L\hfill & \hfill L+\frac{1}{{{\sigma }_n}^2}I\hfill \end{array}\right]}^{-1}\right),$$ (6.12)

where the blocks of the inverse covariance come from the negative Hessians of the total data log posterior:

$$-{\nabla }_{\mathbf{z}}{\nabla }_{\mathbf{z}}\log P(\mathbf{z},\mathbf{n}\mid {\mathcal{D}}_t)=L+K^{-1},$$ (6.13)

$$-{\nabla }_{\mathbf{z}}{\nabla }_{\mathbf{n}}\log P(\mathbf{z},\mathbf{n}\mid {\mathcal{D}}_t)=L,$$ (6.14)

$$-{\nabla }_{\mathbf{n}}{\nabla }_{\mathbf{n}}\log P(\mathbf{z},\mathbf{n}\mid {\mathcal{D}}_t)=L+\frac{1}{{{\sigma }_n}^2}I,$$ (6.15)

where $L=-{\nabla }_{\mathbf{z}}{\nabla }_{\mathbf{z}}\log P({\mathcal{D}}_t\mid \mathbf{z},\mathbf{n})=\text{diag}[\text{exp}(\mathbf{z}+\mathbf{n})]$ is a diagonal matrix with second derivatives from the Poisson term, all evaluated at z = z_map and n = n_map.

From the joint gaussian posterior, equation 6.12, we can compute the marginal posterior over z, the tuning curve inputs at the stimuli in our training set:

$$P(\mathbf{z}\mid {\mathcal{D}}_t)\approx \mathcal{N}({\mathbf{z}}_{\mathit{map}},\Lambda ),\Lambda ={(K^{-1}+{(L^{-1}+{{\sigma }_n}^{2}I)}^{-1})}^{-1}.$$ (6.16)

For stimuli not in our training set, denoted x* (e.g., candidate stimuli for the next trial), we can compute the marginal posterior distribution over the input value z* = g(x*) using the gaussian identities that arise in GP regression (Rasmussen & Williams, 2006):

$$P(z^{\ast }\mid {\mathbf{x}}^{\ast },\mathcal{D})\approx \mathcal{N}({\mu }_{{\mathbf{x}}^{\ast }},{\sigma }_{{\mathbf{x}}^{\ast }}^2),$$ (6.17)

where

$${\mu }_{{\mathbf{x}}^{\ast }}={\mathbf{k}}^{\ast ⊺}{K}^{-1}{\mathbf{z}}_{\mathit{map}},$$ (6.18)

$${\sigma }_{{\mathbf{x}}^{\ast }}^2=k({\mathbf{x}}^{\ast },{\mathbf{x}}^{\ast })-{\mathbf{k}}^{\ast ⊺}{(L^{-1}+K+{{\sigma }_n}^{2}I)}^{-1}{\mathbf{k}}^{\ast },$$ (6.19)

where ${\mathbf{k}}_i^{\ast }=k({\mathbf{x}}_i,{\mathbf{x}}^{\ast })$ is the GP covariance function evaluated at the ith presented stimulus x_i and test stimulus x*.

6.3. Hyperparameter Optimization.

To optimize hyperparameters $\varphi =\{{\sigma }_n^2,\rho ,\delta \}$ governing the GP prior and the over-dispersion noise, we use the Laplace approximation to compute the marginal likelihood,

$$P({\mathcal{D}}_t\mid \varphi )\approx \frac{P({\mathcal{D}}_t\mid \mathbf{z},\mathbf{n})P(\mathbf{n}\mid {{\sigma }_n}^2)P(\mathbf{z}\mid \rho ,\delta )}{P_{lapl}(\mathbf{z},\mathbf{n}\mid {\mathcal{D}}_t,\varphi )},$$ (6.20)

evaluated at z = z_map and n = n_map, where the denominator is the gaussian approximation to the posterior, equation 6.12. This gives

$$\begin{gathered} \log P({\mathcal{D}}_t\mid \varphi )\approx {\mathbf{r}}^{⊺}\log f({\mathbf{s}}_{map})-f({\mathbf{s}}_{\mathit{map}})-\frac{1}{2}{{\mathbf{z}}_{\mathit{map}}}^{⊺}{K}^{-1}{\mathbf{z}}_{\mathit{map}} \\ -\frac{1}{2{{\sigma }_n}^2}{{\mathbf{n}}_{\mathit{map}}}^{⊺}{\mathbf{n}}_{\mathit{map}}-\frac{1}{2}\log \mid K\mid -\frac{1}{2}\log \mid {{\sigma }_n}^{2}I\mid \\ +\frac{1}{2}\log \mid J\mid , \end{gathered}$$ (6.21)

where smap = zmap + nmap, and J is the covariance matrix of the Laplace approximation in equation 6.12, with determinant given by $\mid J^{-1}\mid =\mid L(K^{-1}+\frac{1}{{{\sigma }_n}^2}I)+\frac{1}{{{\sigma }_n}^2}{K}^{-1}\mid$.

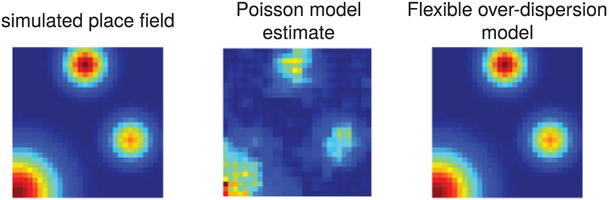
Figure 8 shows the consequences of overdispersed spike responses on the estimation of tuning curves and their hyperparameters. We generated a 2D firing rate map as a mixture of gaussian bumps (left), and simulated spike counts from the flexible overdispersion model (with exponential nonlinearity) at a random collection of 2D locations. We then performed inference using either the Poisson model (center) or the flexible overdispersion model (right). We found that the Poisson estimate suffered from systematic underestimation of the GP length scale, resulting in an estimate that is significantly rougher than the true map. In essence, the Poisson model attributes super-Poisson variability of the responses as reflecting structure in the firing rate map itself rather than noise, thus necessitating a shorter length scale δ.

Figure 8:

Proof-of-concept experiments on simulated data show that accounting for super-Poisson firing statistics can increase accuracy in recovering unknown firing maps. The true simulated firing map (left) drove a model with overdispersed spiking. We used the simulated spike counts to infer the underlying firing rate map using a Poisson response model (center) and the flexible overdispersion model (right). The center plot demonstrates how the Poisson assumption can impair estimates of tuning curve smoothness; accounting for overdispersed spike count statistics improves the estimate substantially by allowing for more accurate estimation of the GP length-scale hyperparameter δ that governs smoothness.

6.4. Adaptive Stimulus Selection Method.

To adaptively select stimuli during an experiment, we search for the stimulus for which the posterior variance of the tuning curve is maximal. This approach, commonly known as uncertainty sampling, is motivated by the idea that we would like to minimize posterior uncertainty about the tuning curve at all points within the stimulus range.

To recap, the tuning curve given the input function g(·) is the expected spike count given a stimulus:

$$\lambda (\mathbf{x})=\mathbb{E}[r\mid \mathbf{x},g(\mathbf{x})]=\int f(g(\mathbf{x})+n)P(n\mid {{\sigma }_n}^2)dn=\text{exp}\left(g(\mathbf{x})+\frac{1}{2}{{\sigma }_n}^2\right).$$ (6.22)

However, during inference from data, we have uncertainty about g(·), which is characterized by the (approximate) gaussian posterior derived in the previous section (see equation 6.17). To compute the posterior mean and variance over the tuning curve λ(x*) at any candidate stimulus x*, we have to transform the posterior distribution over g(x*) through the nonlinearity f.

Letting z* = g(x*) as before, the mean and variance of the tuning curve given by

$$\mathbb{E}[\lambda ({\mathbf{x}}^{\ast })\mid {\mathcal{D}}_t]=\int e^{z^{\ast }+\frac{1}{2}{{\sigma }_n}^2}P(z^{\ast }\mid {\mathcal{D}}_t)d{z}^{\ast }=\text{exp}\left({\mu }_{{\mathbf{x}}^{\ast }}+\frac{1}{2}{{\sigma }_n}^2+\frac{1}{2}{\sigma }_{{\mathbf{x}}^{\ast }}^2\right)$$ (6.23)

$$\begin{gathered} \text{var}[\lambda ({\mathbf{x}}^{\ast })\mid {\mathcal{D}}_t]=\int \text{exp}(2z^{\ast }+{{\sigma }_n}^2)P(z^{\ast }\mid {\mathcal{D}}_t)d{z}^{\ast }-{(\mathbb{E}[\lambda ({\mathbf{x}}^{\ast })\mid {\mathcal{D}}_t])}^2 \\ =(\text{exp}({\sigma }_{{\mathbf{x}}^{\ast }}^2)-1){[\lambda ({\mathbf{x}}^{\ast }\mid {\mathcal{D}}_t)]}^2, \end{gathered}$$ (6.24)

with stimulus-specific mean and variance μ_x* and ${\sigma }_{{\mathbf{x}}^{\ast }}^2$ given in equations 6.18 and 6.19. In practice, our method involves computing posterior variance (see equation 6.24) for a grid of candidate stimuli {x*} and selecting the one for which the posterior variance is largest:

$${\mathbf{x}}_{t+1}=\arg \underset{{\mathbf{x}}^{\ast }}{\max }\text{var}[\lambda ({\mathbf{x}}^{\ast })\mid {\mathcal{D}}_t].$$ (6.25)

6.5. Results: Adaptive Stimulus Selection for Color Tuning Curves.

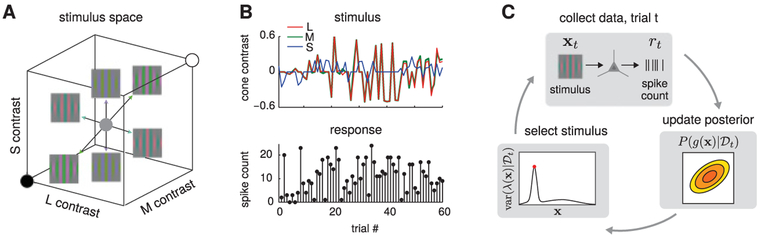
We applied our method to the problem of estimating color tuning functions for V1 neurons recorded in awake, fixating monkeys under two paradigms. In the first paradigm, Gabor patches (gaussian windowed sinusoidal gratings) were drifted across the receptive field. The orientation, spatial frequency, and direction of drift in each Gabor patch were tailored to each neuron. In the second paradigm, gaussian-smoothed rectangular bars drifted across the receptive field. The length and width of the bar, as well as its direction of drift, were tailored to each cell. Figure 9 shows a schematic illustration of the stimulus space, the raw experimental data, and the adaptive stimulus stimulus selection protocol.

Figure 9:

Schematic of stimulus space, data, and adapative stimulus selection method. (A) The stimulus on each trial was a drifting Gabor patch, aligned with the cell’s preferred orientation, whose color varied from trial-to-trial. The axes of this space are the inputs to long (L), medium (M), and short (S) wavelength-sensitive cones. The center of this space represents a neutral gray stimulus with no spectral modulation. (B) Example data for one cell. The stimulus on each trial was uniquely defined by three numbers (cone contrasts for L, M, and S in the upper-diagonal half-cube) and produced a spike count responsemeasured over 667 ms. (C) Schematic of the adaptive stimulus selection procedure. On each trial, we presented stimulus xt and recorded spike response r_t. Next, we updated the posterior over the tuning curve g using the full data set collected so far, ${\mathcal{D}}_t$. Finally, we computed the posterior variance of the tuning curve, $\text{var}(\lambda ({\mathbf{x}}^{\ast })\mid {\mathcal{D}}_t)$, for a grid of points x* spanning the stimulus space, and selected the point with maximal variance as the stimulus for the next trial.

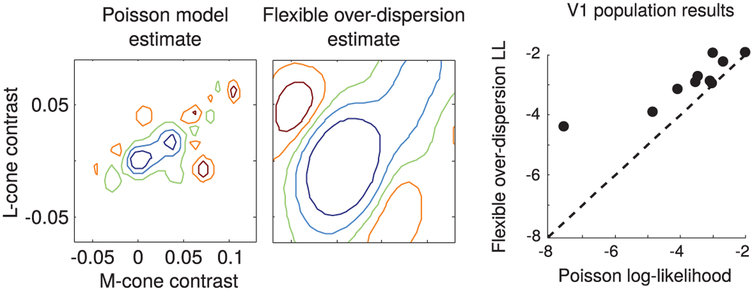
In interleaved trials, individual V1 neurons were tested with stimuli that were chosen either adaptively (using our method; see Figure 9C) or nonadaptively. In nonadaptive trials, stimulus selection was independent of responses. In adaptive trials, stimulus selection was based on the posterior variance of the firing rate map in the overdispersed GP-Poisson model. Results showed that the adaptive method yielded faster convergence and more accurate firing map estimates than the nonadaptive method. As shown in Figure 10, the estimates of the Poisson model are much coarser than would be expected. As a result, the flexible over-dispersion model achieved on average a four-times-higher likelihood on test data compared to the Poisson model.

Figure 10:

Comparison of tuning curve estimates under the GP-Poisson model and GP-flexible-over-dispersion model. (Left) A 2D slice through the 3D color tuning curve for a V1 cell corresponding to the L-M plane (with S = 0) under Poisson (left) and flexible overdispersion model (right). The flexible overdispersion achieved a 25-times-higher likelihood for the test data set of 76 trials (763 total trials, 90%-10% split for cross-validation), corresponding to 4.3% higher per trial likelihood, and exhibited a smoother estimate (larger length scale δ, as observed in Figure 7). (Right) The test log likelihood from 10 V1 cells, averaged over 10-fold cross validation. Each dot represents the log likelihood of the data collected from each cell. On average, the flexible overdispersion model achieved a four-times-higher test likelihood than the Poisson model, indicating its greater suitability for application to closed-loop experiments.

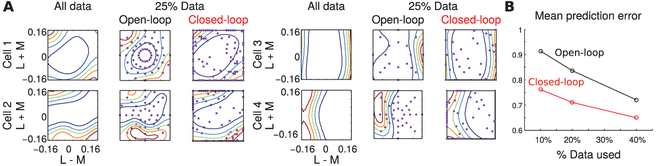
In the closed-loop design, we selected the stimulus that had the highest posterior variance of firing rate map in each trial. In the open-loop design, we sampled the stimuli uniformly. In Figure 11, we show the estimated tuning functions from the drifting bar paradigm using all data collected from adaptive and non-adaptive designs, as well as estimates using a quarter of the data collected from each design. The estimates obtained using the closed-loop design look more similar to the estimates obtained using all the data. Finally, we computed the average prediction error using data collected from each design. The closed-loop method achieved substantially lower prediction error and faster convergence than the open-loop method.

Figure 11:

Closed-loop versus open-loop designs of neurophysiology experiments. (a) Contour plot of the estimated firing rate maps of four different V1 cells. Purple dots indicate stimuli selected by each experimental paradigm.(b) Average prediction error as a function of the amount of data. The closed-loop method achieved 16% higher prediction accuracy compared to the open-loop method.

7. Discussion

We have presented a flexible model for super-Poisson spike count responses and demonstrated both its properties when fit to V1 spiking data and its practical use by applying the new model to closed-loop neurophysiology experiments. Our model, which introduces extra-Poisson variability via a gaussian noise term added to the stimulus response level and passed through a nonlinearity, provides flexibility in accounting for neural overdispersion and permits efficient model fitting. We find that this model better fits individual mean-variance relationships for neurons in V1. Furthermore, we find that when used as a likelihood in lieu of the Poisson likelihood, our model can significantly improve closed-loop estimation of color tuning curves in V1.

7.1. Relationship to Previous Work.

A wide variety of other approaches to overdispersed spike count distributions have been proposed in the recent literature. These include mixtures of Poisson distributions (Wiener & Richmond, 2003; Shidara, Mizuhiki, & Richmond, 2005) and the Twiddle distribution, which is characterized by a polynomial mean-variance relationship $\text{var}[r]=\alpha {(\mathbb{E}[r])}^{\rho }$ for some α and ρ (Moshitch & Nelken, 2014; Koyama, 2015; Gershon et al., 1998). Although these models offer substantial improvements over models that specify a single Fano factor, they are still restricted in the forms of overdispersion they can capture, and in some cases they are more difficult to connect to mechanistic interpretations (i.e., how such counts might be generated). In contrast to these approaches, recent work on neural partitioning and negative binomial spike counts (Onken, Grünewälder, Munk, & Obermayer, 2009; Goris et al., 2014; Pillow & Scott, 2012a) instead seeks more descriptive, interpretable models of overdispersion via hierarchical (or doubly stochastic) modeling.

Other methods to quantify neural overdispersion rely on describing more general count distributions, such as the Bernoulli or Conway-Maxwell-Poisson (COM-Poisson) distributions (Zhu, Sellers, Morris, & Shmueli, 2017; Sellers, Borle, & Shmueli, 2012), rather than layering on top of the Poisson distribution (Gao et al., 2015; Stevenson, 2016). These models may be limited by requiring many additional parameters (Gao et al., 2015) or may require that the mean-variance curves be monotonically increasing (Stevenson, 2016), reducing the model’s ability to explain neurons that exhibit higher variance at lower means. While completely replacing the Poisson distribution is satisfying in that the mean-variance relationship is no longer restricted at any stage by Poisson behavior, we feel that layering additional variability inside the Poisson rate is more intuitive (Goris et al., 2014). Specifically, we find that such hierarchical models can isolate variables responsible for overdispersion and allow mechanistic theories to attempt to explain these factors.

Our model can be considered as a significant generalization of the mixture-of-Poisson models (Wiener & Richmond, 2003; Shidara et al., 2005), as our model is essentially an infinite mixture of Poissons, as well as a generalization of prior work using latent hierarchical dispersion variables (Goris et al., 2014). In terms of the power law models of (Moshitch & Nelken, 2014; Koyama, 2015), our model also includes as a subset any power law where the exponent is between one and two (i.e., $\text{var}[r]=a{(\mathbb{E}[r])}^{\rho }$ for 1 ≤ ρ ≤ 2). Although our model is incapable of achieving ρ > 2 or ρ < 1, the achievable range of ρ includes experimentally observed values in the literature, for example, ρ ≈ 1.3 (Shadlen & Newsome, 1998) or 1.1 ≤ ρ ≤ 1.5 for cat auditory cortex (Moshitch & Nelken, 2014). Interestingly, however, our analysis demonstrates that power-law-type characterizations might still be insufficient for assessing neural overdispersion. In particular, our model exploration indicates that a full discussion of the firing statistics should also include the full count distributions (see Figure 7). Our results demonstrated that our model more accurately captures the variation in V1 neural responses, as compared to both traditional and more recent Poisson-based models.

7.2. Interpretation and Future Directions.

The origins of neural response variability are still a subject of debate (Renart & Machens, 2014; Masquelier, 2013), and we admit that our model does not attempt to explain how overdispersion arises. Our model only implies that the unknown nuisance variable is well modeled by an addition of stimulus-dependent drive and gaussian noise, followed by a nonlinearity and Poisson spike generation. In terms of the nonlinearity used, we found that the single-parameter power soft-rectification function was flexible enough to account for a large range of neural behavior, despite its reliance on a single parameter. The inference cost for the flexible overdispersion model therefore remains modest and is, moreover, justified by the substantial gain in model expressibility (e.g., as shown by the AIC results in Figure 6). Other nonlinearities are certainly possible in this framework, and the general properties we describe in section 3 guarantee that aside from perhaps requiring numerical integration, the model will be well behaved (i.e., the variance-mean curve will remain a proper function). For example, we found that the exponential nonlinearity allowed for more computationally efficient calculations for the closed-loop inference procedure.

While we focus here on explaining super-Poisson behavior of neural firing, we note that our model does not attempt to account for the underdispersion sometimes observed in certain neural circuits, such as retina or auditory cortex, that exhibit higher degrees of response regularity (DeWeese & Zador, 2002; Kara, Reinagel, & Reid, 2000; Gur et al., 1997; Maimon & Assad, 2009). Comparable flexible models for underdispersed spike counts therefore pose an important open problem for future work. In terms of neural populations, our model focuses only on explaining the spiking process for a single neuron. The increasing number of simultaneously recorded neurons thus poses the future challenge of explaining correlations in overdispersion between neurons (e.g., Goris et al., 2014). Such population overdispersion models would carry through the benefits of more accurate spike count models that we observe here for single-neuron closed-loop experiments to cases where entire populations are analyzed simultaneously. Finally, we note that we have modeled spike counts using a single time bin size, corresponding roughly to the window during which each stimulus was presented. We have therefore not addressed how spike count variability varies with time binning, which may be important for understanding population coding of information on different timescales. In preliminary work, we have found that fits to spike counts in smaller time bins yield different parameters for the model in Goris et al. (2014) and flexible overdispersion model than those we have shown here (Charles & Pillow, 2017). Therefore, an important future direction for future research will be to extend current overdispersion models to provide a single, consistent account for spike count variability in arbitrary time bin sizes.

Appendix A: Modulated Poisson and the NB model

Here we review the connection between the modulated Poisson model introduced by Goris et al. (2014) and the negative binomial model. The modulated Poisson model was introduced generally as having a Poisson rate λ(x) modulated by a stochastic gain G with a distribution satisfying $\mathbb{E}[G]=1$ and $\text{var}(G)={\sigma }_G^2$. The general mean-variance relationship of the marginal spike counts under this model was shown to always satisfy a quadratic relationship (i.e., $\text{var}[r\mid \mathbf{x}]=\lambda (\mathbf{x})+{\sigma }_G^2\lambda {(\mathbf{x})}^2$). However, fitting the model parameters to data required additional assumptions about the distribution of G. In particular, Goris et al. used a gamma distribution, which makes the integral over G analytically tractable, producing a negative binomial distribution over spike counts.

To see this connection formally, we can write the model, substituting z = λ(x) for the stimulus-dependent firing rate:

$$G~\text{Gamma}\left(\frac{1}{{\sigma }_G^2},{\sigma }_G^2\right),$$ (A.1)

$$r\mid G,z~\text{Poiss}(Gz),$$ (A.2)

where $1∕{\sigma }_G^2$ and ${\sigma }_G^2$ correspond to the shape and scale parameters for the gamma distribution, which ensures $\mathbb{E}[G]=1$ and $\text{var}[G]={\sigma }_G^2$. The spike count r then has a negative binomial distribution:

$$r\mid z~\text{NB}\left(\frac{1}{{\sigma }_G^2}\frac{{\sigma }_G^{2}z}{{\sigma }_G^{2}z+1}\right).$$ (A.3)

The derivation of the negative binomial PMF from a Poisson distribution with a gamma prior can be obtained via the following straightforward integration:

$$\begin{gathered} P(r\mid \beta ,p)={\int }_0^{\infty }{P}_{\text{Poisson}}(r\mid z,G)\cdot P_{\text{Gamma}}(G\mid \beta ,\theta )\mathrm{d}\lambda \\ ={\int }_0^{\infty }\left(\frac{{(Gz)}^r}{r!}{e}^{-Gz}\right)\cdot \left(G^{\beta -1}\frac{e^{-G{\theta }^{-1}}}{{\theta }^{\beta }\mathrm{\Gamma }(\beta )}\right)\mathrm{d}G \end{gathered}$$ (A.4)

$$=\frac{z^r}{{\theta }^{\beta }r!\mathrm{\Gamma }(\beta )}{\int }_0^{\infty }{G}^{\beta +r-1}{e}^{-G({\theta }^{-1}+z)}\mathrm{d}G$$ (A.5)

$$=\frac{z^r}{r!{\theta }^{\beta }\mathrm{\Gamma }(\beta )}{\left(\frac{1}{{\theta }^{-1}+z}\right)}^{\beta +r}\mathrm{\Gamma }(\beta +r)$$ (A.6)

$$=\frac{\mathrm{\Gamma }(\beta +r){(\theta z)}^r}{r!\mathrm{\Gamma }(\beta )(1+\theta z)\beta +r}$$ (A.7)

$$=\frac{\mathrm{\Gamma }(\beta +r)}{r!\mathrm{\Gamma }(\beta )}{\left(\frac{\theta z}{1+\theta z}\right)}^r{\left(1-\frac{\theta z}{1+\theta z}\right)}^{\beta },$$ (A.8)

which for $\beta ={\sigma }_G^{-2}$ and $\theta ={\sigma }_G^2$ results in the above NB distribution.

Appendix B: Parameter Optimization Using Laplace Approximation

The general method we present for estimating the parameters of the nonlinearity that modulates neural spiking is outlined in algorithm 1. For a particular nonlinearity (i.e., the soft rectification raised to a power in equation 3.7, these steps can be written more explicitly. Here we fit data using both the exponential nonlinearity, for which the fitting algorithm is provided in algorithm 3, and the power-soft-rectification nonlinearity, corresponding to the model fitting in algorithm 2). Note that the estimation of ${\sigma }_0^2$ and the gradient descent steps for θ and z can be accomplished analytically; however, the estimation of n₀ would typically need to be calculated numerically.