Translating surveillance data into incidence estimates

Abstract

Monitoring a population for a disease requires the hosts to be sampled and tested for the pathogen. This results in sampling series from which we may estimate the disease incidence, i.e. the proportion of hosts infected. Existing estimation methods assume that disease incidence does not change between monitoring rounds, resulting in an underestimation of the disease incidence. In this paper, we develop an incidence estimation model accounting for epidemic growth with monitoring rounds that sample varying incidence. We also show how to accommodate the asymptomatic period that is the characteristic of most diseases. For practical use, we produce an approximation of the model, which is subsequently shown to be accurate for relevant epidemic and sampling parameters. Both the approximation and the full model are applied to stochastic spatial simulations of epidemics. The results prove their consistency for a very wide range of situations. The estimation model is made available as an online application.

This article is part of the theme issue ‘Modelling infectious disease outbreaks in humans, animals and plants: epidemic forecasting and control’. This theme issue is linked with the earlier issue ‘Modelling infectious disease outbreaks in humans, animals and plants: approaches and important themes’.

1. Introduction

Monitoring programmes are used to keep track of the invasion and spread of human, animal and plant pathogens. They are often structured in discrete rounds of inspection, during which subsamples of the host population are assessed for disease status [1]. Given a sequence of monitoring rounds, a key question in interpreting these data is the estimation of the incidence¹ of the disease in the host population. There are two special cases of this general question that have received some attention.

Firstly, monitoring is often motivated by the need for early responses to enable eradication or containment. For example, early detection of the disease permits reduced culling of animal and plant hosts [2–4], as well as limited deployments of emergency quarantines or travel restrictions for human hosts (applied e.g. for SARS [5]). Secondly, monitoring is frequently motivated by the desire to prove disease absence from a host population [6], which is important for the transport and trade of hosts. The main question then concerns the sufficient sample size [7]. An example of this is the practical ‘rule of three’ [8,9]. It gives the upper bound of the 95% confidence interval (CI) of the incidence when all of the N sampled hosts are assessed as healthy: Q₉₅ = 3/(N + 1). Estimating disease incidence (denoted q hereafter), or proving its absence, is of most interest during the early stages of epidemics, i.e. when incidences are low and containment measures are still promising.

Simple practices like the ‘rule of three’ make the assumption that the samples are independent binomial draws with probability q and size N. However, as a pathogen spreads across the surveyed population, our samples will carry dependencies on the underlying epidemic process. For example, by pooling all the samples together, we neglect the fact that early monitoring rounds have most likely sampled a lower incidence q than the current one, resulting in an underestimation of the incidence. An alternative and unbiased solution is to estimate q only from the last round to date. But obviously, such a poor use of data would only be tolerable in cases where the monitoring interval and epidemic growth rate are both very large, so that the previous monitoring rounds can be deemed uninformative. The temporal dependence of samples has been addressed by [10] in the design of appropriate monitoring programmes, as well as by Parnell et al. [11] and Bourhis et al. [12] for the estimation of the disease incidence after the disease’s first discovery or before its discovery (disease absence), respectively.

We propose here a generalized solution to the incidence estimation problem. Making use of all monitoring data, it applies to the previously addressed first discovery and disease absence cases but extends to any monitoring outcome. Building on the simple logistic equation, our estimation model accounts for the progression of the disease during the monitoring period. Following the idea of the rule of three, and similar to Parnell et al. [13] and Alonso Chavez et al. [14], we also produce an approximation of this model. Its derivation only requires simple algebraic operations which makes it more suitable for practitioners than the full estimation model. Both the estimation model and its approximation are then confronted with epidemic simulations: first with non-spatial and deterministic simulations, and secondly with spatially explicit and stochastic simulations of epidemics running on contrasted distributions of hosts. The results support the accuracy and practical usefulness of the estimation model, which has subsequently been made available as an online software application (https://yo-b.shinyapps.io/incidence-estimation/).

2. Material and methods

Monitoring a population for a disease results in sampling series as shown in table 1. We define K as the number of monitoring rounds iterated in time. N_k is the sampling size of monitoring round k, i.e. the number of hosts whose pathological status is assessed at time t_k. M_k is the number of infected hosts detected during round k. Finally, Δ_k is the time interval between monitoring rounds k and k + 1.

Table 1.

Variables and structure of a sampling series.

monitoring round	1	2	k	K − 1	K
no. of samples	N1	N2	Nk	NK−1	NK
no. of positives	M1	M2	Mk	MK−1	MK
time interval	Δ1	Δ2	Δk	ΔK−1	—

(a). One monitoring round

Considering q the disease incidence in the population, the probability of M positive observations out of a sample of size N is given by the binomial probability distribution

$$P(M|q;N)=\left(\begin{array}{c}N\\ M\end{array}\right){(1-q)}^{N-M}{q}^M.$$ 2.1

A more general form, accounting for the occurrences of false positives and negatives in the detection process, is

$$\begin{array}{rl}P(M|q;N)=& \left(\begin{array}{c}N\\ M\end{array}\right){[(1-q)(1-{\theta }_{\mathrm{fp}})+q{\theta }_{\mathrm{fn}}]}^{N-M}\\ & {[(1-q){\theta }_{\mathrm{fp}}+q(1-{\theta }_{\mathrm{fn}})]}^M,\end{array}$$ 2.2

where θ_fn and θ_fp are, respectively, the rates of false negatives and false positives [15]. For simplicity, the following developments do not explicitly incorporate those rates, which are nonetheless part of the estimation model provided in the application.

In a practical context, q is the variable that we want to estimate from samples characterized by their size N and their outcome M. To this end, we use Bayes’ rule:

$$P(q|M;N)=\frac{P(q)P(M|q;N)}{{\int }_0^{1}P(q)P(M|q;N)\hspace{0.17em}\text{d}q},$$ 2.3

where P(q|M; N) is the probability distribution of q given M and N. Assuming no information on the incidence before sampling, we set a uniform prior P(q), resulting in P(q|M; N) ∝ P(M|q; N) [16].

(b). K monitoring rounds

To account properly for the dynamic incidence between monitoring rounds, we inform the binomial probability distribution with an epidemiological component Z_k (as in [17], whose maximum-likelihood approach is equivalent to our Bayesian formulation with flat priors). Z_k gives the relation between q_K, the incidence to estimate and q_k, the incidence at sampling time t_k, as q_k = Z_kq_K. Hence,

$$P(\mathit{M}|q_K;\mathit{N})=\prod _{k=1}^K\left(\begin{array}{c}{N}_k\\ M_k\end{array}\right){(1-Z_k{q}_K)}^{N_k-M_k}{(Z_k{q}_K)}^{M_k},$$ 2.4

where M and N on the left-hand side represent the whole sampling series, i.e. M₁, M₂, … , M_K and N₁, N₂, … , N_K.

We assume that the disease incidence, q, evolves logistically [18,19] between times t_k and t_K:

$$q_K=\frac{q_k{e}^{r(t_K-t_k)}}{1+q_k(e^{r(t_K-t_k)}-1)},$$ 2.5

where r is the epidemic growth rate, while q_k and q_K, respectively, stand for q(t_k) and q(t_K). For simplicity, we hereafter express time relative to t_K = 0, the time of both the last sampling round and the estimation. Hence, we define Z_k as:

$$Z_k=\frac{q(t_k)}{q(t_K)}=\frac{q_K{e}^{r{t}_k}}{1+q_K(e^{r{t}_k}-1)}/q_K=\frac{e^{r{t}_k}}{1+q_K(e^{r{t}_k}-1)},$$ 2.6

where t_k < 0 as t_K = 0.

Similarly to the case of one monitoring round, we use Bayes’ rule to get the unnormalized posterior distribution P(q_K|M; N). Practically, it is given by equation (2.4), which is computed for a discretized array of q ∈ [0, 1], and from which quantiles Q_X can be derived (a method called grid approximation, see e.g. [20]).

(c). A useful approximation

The upper bound of the CI is a useful measure of the highest, still likely, incidence we can expect in the population given the outcome of a monitoring programme. We propose in this section an approximation of this quantity not requiring the derivation of the full probability distribution of P(q_K|M; N). Various methods exist for approximating the CI of a binomial parameter [21]. After preliminary testing of those methods against the binomial-shaped probability density given by equation (2.4), we choose the Agresti–Coull interval for its accuracy for low incidences [22]. Therefore, the approximated upper limit of the X% CI is defined as

$${\tilde{Q}}_X=\hspace{0.17em}\text{min}(1,\widetilde{\hspace{0.17em}p}+z\sqrt{\text{max}(0,\frac{\widetilde{\hspace{0.17em}p}}{N+z^2}(1-\widetilde{\hspace{0.17em}p}))}),$$ 2.7

where

$$\widetilde{\hspace{0.17em}p}=\frac{1}{N+z^2}(M+\frac{z^2}{2}),$$ 2.8

and where z is the corresponding 1 − α/2 quantile of the standard normal distribution (with α the probability of type I error). For the one-sided 95% CI, we derive ${\tilde{Q}}_{95}$ by setting z = 1.645.

The approximated ${\tilde{Q}}_X$ also needs to account for the epidemic growth. As previously with Z_k, we now define ${\tilde{Z}}_k$ to quantify the disease evolution between rounds. In this case, we are unable to use the logistic model because its non-linearity makes the derivation of ${\tilde{Q}}_X$ intractable. This, however, was no concern for the full model and the grid approximation method used to derive P(q_K|M; N). Consequently, approximating the logistic growth model by its exponential variant, ${\tilde{Z}}_k$ is given by

$${\tilde{Z}}_k=e^{r{t}_k}=\hspace{0.17em}\text{exp}(-r\sum _{i=k}^K{\mathrm{\Delta }}_i).$$ 2.9

In practice, the exponential assumption is realistic as, during early infection, the epidemic growth is exponential, even according to the logistic model [19]. Finally, we aggregate the samples together with respect to the epidemic growth via ${\tilde{Z}}_k$:

$$M=\sum _{k=1}^K{M}_k\text{and}N=\sum _{k=1}^K{N}_k{\tilde{Z}}_k.$$ 2.10

These aggregated values of M and N are then substituted in equations (2.8) and (2.7) to derive ${\tilde{Q}}_X$. Scaling only N_k with Z_k has two effects: (1) the historic sampling rounds k contribute less than the recent ones to the reduction of the uncertainty (reduced sample size N); and (2) the sampling rounds k that include detection events (M_k > 0) see their contribution to ${\tilde{Q}}_X$ increased (larger M/N), hence accounting for the putative spread of the disease from those M_k infected hosts between times t_k and t_K. The min and max operators in equation (2.7) are added to deal with the possibility of having N < M for some values of ${\tilde{Z}}_k$.

As mentioned in the introduction, this estimation model and its approximation cover the two specific contexts of first discovery and disease absence addressed, respectively, by Parnell et al. [13] and Bourhis et al. [12] (see electronic supplementary material for details). Their strength is, however, that they extend to any sampling series, no matter its outcome M_k and regularity in sampling size or frequency.

(d). Asymptomatic period

For most diseases, infected hosts develop symptoms after an asymptomatic (or incubation) period [23]. Often, asymptomatic hosts contribute to the epidemic dynamics by spreading the disease while still undetectable (cryptic) when sampled. The logistic equation handles this period, noted σ, as in Alonso Chavez et al. [14]:

$$q_T(t_K)=\frac{q(t_k)e^{r(t_K-t_k+\sigma )}}{1+q(t_k)(e^{r(t_K-t_k+\sigma )}-1)}.$$ 2.11

This relates the total incidence q_T at the last sampling round t_K (i.e. the quantity to estimate) to the detectable incidences at the different sampling times q(t_k) (i.e. the sampled quantities). Hence, Z_k becomes:

$$Z_k=\frac{q(t_k)}{q_T(t_K)}=\frac{e^{r(t_k-\sigma )}}{1+q_T(t_K)(e^{r(t_k-\sigma )}-1)}.$$ 2.12

For the exponential approximation, equation (2.9) simply becomes

$${\tilde{Z}}_k=e^{r(t_k-\sigma )}.$$ 2.13

(e). Testing the model

The consistency of the full model and the accuracy of its approximation are first tested against simulations of stochastic sampling on non-spatial logistic epidemics. We consider a uniform distribution of incidences q_T that we want to estimate individually. For each one of them, an epidemic is simulated until incidence q_T is reached and a monitoring programme is designed with N_k and Δ_k drawn from Poisson distributions of mean $\overline{N}$ and $\overline{\mathit{\Delta }}$, respectively. From the logistic equation (equation (2.5)), the detectable incidence q is derived for every sampling date t_k. Then binomial draws with probability p = q(t_k) and size n = N_k simulate the sampling process of the hosts, resulting in M_k. For every q_T, an exact upper bound of its CI, Q_X, is derived with the full model, while an approximated one, ${\tilde{Q}}_X$, is derived with the approximation. To test our model, we check that the upper limits of the $X\text{\%}$ CI are above q_T in X% of cases. This test is done for contrasted values of the sampling ($\overline{N}$ and $\overline{\mathit{\Delta }}$) and epidemic parameters (r and σ).

The full model and its approximation are also tested against spatially explicit and stochastic epidemic simulations (as in [24]). In this case, the epidemics are no longer modelled with the logistic equation but through a transmission rate and a dispersal kernel of the pathogens. To this end, the hosts are distributed in a two-dimensional space and aggregated randomly in field-like structures mimicking the distribution of the trees in an orchard. Details of this landscape model are given as electronic supplementary material. Transmission is governed by an exponential power kernel [25]. The probability of a susceptible individual becoming infected in a unit of time is then given by

$$p(s\in S)=\beta \frac{b\mathcal{A}}{2\pi {\theta }^2\mathit{\Gamma }(2/b)}\sum _{i\in I}\hspace{0.17em}\text{exp}(-\frac{|{\mathit{x}}_i-{\mathit{x}}_s{|}^b}{{\theta }^{\hspace{0.17em}b}}),$$ 2.14

where s is a susceptible host among the set of all susceptible hosts S. Similarly, i and I represent the infected hosts. $\mathcal{A}$ is the area occupied by one host and Γ is the gamma function. β is the probability of infection, θ is the dispersal scale and b is a shape parameter (producing fat-tailed kernels for b < 1). The coordinates x mark the locations of the hosts. Following Klein et al. [26], the mean dispersal distance for this two-dimensional kernel is given by:

$$\delta =\frac{\theta \mathit{\Gamma }(3/b)}{\mathit{\Gamma }(2/b)}.$$ 2.15

These epidemics are simulated with the τ-leap version of the Gillespie stochastic simulation algorithm (see e.g. [27]). The estimation model and its approximation are evaluated in the same way as the non-spatial case.

3. Results

(a). Model behaviours

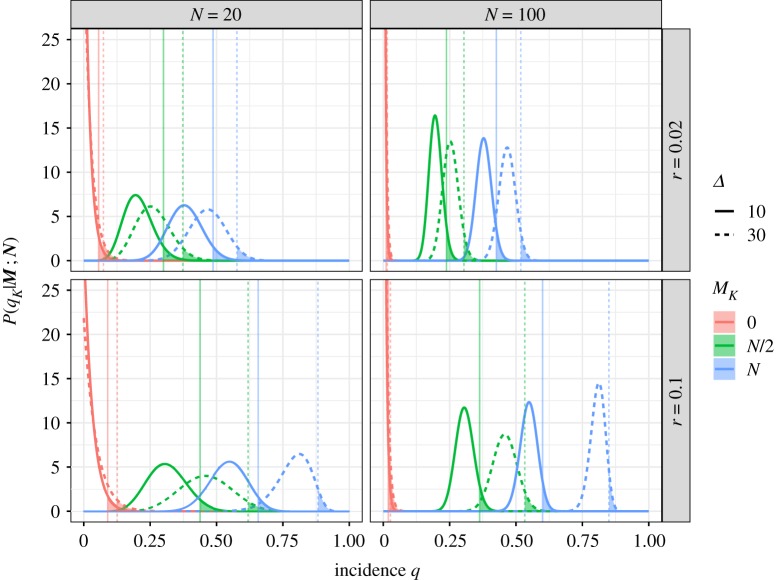
Figure 1 illustrates the effects of the epidemic and sampling parameters on the resulting probability distributions of the incidence and upper quantiles Q₉₅. Increasing M_k, the number of detected infected hosts in the sample, unsurprisingly increases the estimated incidence. Increasing the sample size N_k reduces the uncertainty in the estimates. Increasing the sampling interval Δ decreases the impact of the historic samples on the estimation. This reflects the fact that samples taken further back in time are less informative of current disease incidence. As for the epidemic parameters, the growth rate r and the asymptomatic period σ (not shown in figure 1 for dimensional reasons) have very similar effects to Δ. Increasing them increases the estimated incidence by decreasing the impact of the historic samples (which are the ones sampling lower incidences q). Increasing any of the parameters Δ, r or σ also reduces the effective sample size (i.e. $\sum _{k=1}^K{N}_k{Z}_k$), which increases the uncertainty on the estimates (i.e. producing probability distributions with larger variance).

Figure 1.

Probability distributions of the incidence q given by equations (2.4) and (2.3). The vertical lines mark Q₉₅, the upper limit of the 95% CI. The distributions result from a sampling series composed of K = 3 monitoring rounds, of which the first two are fully negative (i.e. M₁ = M₂ = 0) and the last varies from M₃ = 0 (i.e. all sampled hosts are negative) to M₃ = N (i.e. all sampled hosts are positive). These probability distributions are represented for varying values of epidemic growth rate r, sampling size N and sampling interval Δ. (Online version in colour.)

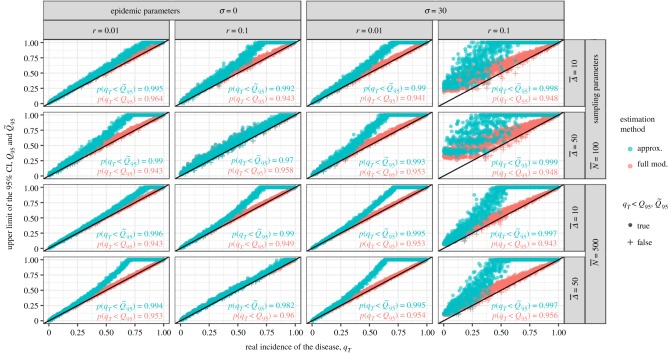
(b). Test against logistic epidemics

Figure 2 shows the distribution of the exact and approximated upper bounds of the 95% CI, Q₉₅ and ${\tilde{Q}}_{95}$, for uniform distributions of q_T and different values of the epidemic and sampling parameters. The full model, which similarly to the simulations builds on the logistic equation, behaves exactly as expected: it ensures that 95% of the Q₉₅ are above their respective q_T, for every set of parameters tested. On the other hand, the approximation displays another behaviour which is explained by its underlying exponential growth model. For the low incidences which are relevant to practice (i.e. say q_T < 0.25), the approximation is accurate (the distributions of Q₉₅ and ${\tilde{Q}}_{95}$ do overlap). For higher incidences, i.e. when the logistic growth decelerates unlike the exponential growth, the approximation overestimates the incidence (increasingly with r, σ and Δ).

Figure 2.

Estimation of Q₉₅ and ${\tilde{Q}}_{95}$ from sampling series of non-spatial epidemics, i.e. simulated with the logistic equation (equation (2.5)). These estimations are made for contrasted values of sampling and epidemic parameters (and for K = 5 monitoring rounds). Using here the 95% CI, we expect 95% of the estimated Q₉₅ and ${\tilde{Q}}_{95}$ to be above the actual incidence in the field at the end of monitoring q_T, i.e. above the oblique black line. The inserted text summarizes these scores for the full model (in red) and its approximation (in blue). (Online version in colour.)

Another model behaviour of particular interest occurs when r and σ are large (see the rightmost column of figure 2). We observe that the estimated Q₉₅ and ${\tilde{Q}}_{95}$ do not align well with the diagonal for small incidences q_T. For those cases of very hazardous pathogens with high epidemic growth rates and long asymptomatic periods, the sampling size N is too small to allow discrimination between the non-detection cases (i.e. the ones for which all the M_k = 0), and a larger sampling effort is needed for the estimation to be informative.

Although increasing r and σ accelerates the divergence between the logistic and the exponential curves, the approximation appears accurate for early infections even considering very high values of epidemic parameters such as $r=0.1\hspace{0.17em}{\text{day}}^{-1}$ or $\sigma =100\hspace{0.17em}\text{days}$.

(c). Test against spatial epidemics

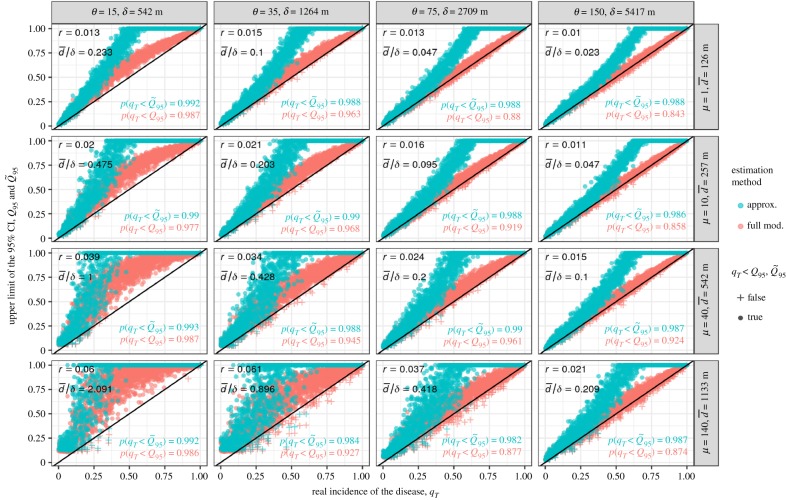
When locating the hosts in space, the epidemic becomes driven by two new elements: the dispersal range of the pathogen and the intensity of host clustering [28]. Both determine how easily the pathogen spreads across the landscape or remains restricted to a local group of hosts. Random distributions of hosts and long dispersal ranges result in smooth progressions of the pathogen across the landscape, following a logistic-like curve. However, as the dispersal range decreases and host aggregation increases, the simulated epidemics will tend to include interruptions between periods of seemingly logistic growth within host clusters. Questions then arise regarding the performance of our estimation model on such epidemics.

The estimation model and its approximation are tested for varying host aggregations and dispersal ranges. Host aggregation is summarized by μ, the number of hosts in a field (sensu host cluster). For a given landscape-scale population of hosts, more hosts per field means fewer but more populated fields (see the electronic supplementary material for an illustration). The dispersal scale θ is translated in terms of mean dispersal distance δ (see equation (2.15)), while μ is translated in terms of $\hspace{0.17em}\overline{d}$, a landscape metric measuring the mean minimal distance between the fields within a landscape (see Euclidean nearest distance in [29]).

Similar to figure 2, figure 3 shows the performance of the model and its approximation for gradients of dispersal scales θ (columns) and host aggregations μ (rows). For each parameter set θ and μ (i.e. each panel in figure 3), 50 epidemics are first simulated for 50 different landscapes in order to identify the value of r that produces the best fitting logistic curve (with least squares). This r then informs the incidence estimation model and its approximation for the subsequent testing set of 2000 epidemics and landscapes. Most of figure 3 agrees with expectations: the estimated Q₉₅ align neatly above the diagonal, showing in practice the accuracy of the estimation model. The approximation appears to be a good simplification of the full model for early detection. However, the estimation model also produces overestimations of the incidence, specifically in the bottom row and left column (i.e. where the dots do not align above the diagonal). These are cases of epidemics for which the distance between host clusters (quantified by $\hspace{0.17em}\overline{d}$) is too large for the pathogen dispersal range (quantified by δ), hence producing unsteady progressions of the pathogens across the landscapes. This illustrates that our model is of limited interest in such cases where $\hspace{0.17em}\overline{d}/\delta \le 0.5$.

Figure 3.

Estimation of Q₉₅ and ${\tilde{Q}}_{95}$ from sampling series realized on spatially explicit epidemics, i.e. simulated with the dispersal kernel (equation (2.14)). These estimations are made for varying dispersal ranges θ and host aggregations μ, while maintaining constant values of the non-spatial parameters (N = 100, Δ = 30, σ = 30, K = 5, as well as β = 75 and b = 0.45 for the remaining kernel parameters). For better understanding, θ and μ are shown with their distance translation in metres, δ and $\hspace{0.17em}\overline{d}$. The identified logistic growth rate r is given for each experiment. The resulting distributions of Q₉₅ and ${\tilde{Q}}_{95}$ are qualitatively similar for other realistic values of the fixed parameters. (Online version in colour.)

We note also that p(q_T < Q₉₅) can be below the 95% expectation. This results from the fact that the stochasticity of the simulations scatters the realized epidemic curves symmetrically around the fitted logistic one (whose identified parameter r is subsequently used by the estimation model). This is no concern in practice where the epidemic parameters are taken conservatively from previous observations of similar outbreaks (e.g. highest observed values of r or σ). Here we choose central estimates (through least squares) for illustrative purposes. Nonetheless, parameter uncertainty can be accounted for in the online application assuming that r and σ can be described with normal distributions. On how to deal with epidemic parameter uncertainty, see Neri et al. [30] and Hyatt-Twynam et al. [24].

4. Discussion

The model developed in this paper is suitable for many monitoring designs, including those with irregular sampling sizes and time intervals between rounds. The model weights the monitoring outcomes according to an estimate of the population incidence at their respective sampling time, before aggregating them into a single binomial-shaped probability distribution of the incidence. The quantiles of this distribution have practical interests for policy makers. The model is directly applicable for situations in which surveillance does not depend on the self-reporting of symptomatic hosts, which makes it appropriate for most animal and plant species. Our model is also appropriate for certain monitoring schemes aimed at pathogens of humans, for example, visitations of rural villages to find Ebola infections where access to healthcare is limited [31,32].

Calculating the probability density of the incidence from the sampling series is computationally inexpensive, but still requires technical proficiency. Therefore, we have produced an online application interfacing the full model as exhaustively as possible, as well as an approximation of the model that can be derived with simple algebraic operations (https://yo-b.shinyapps.io/incidence-estimation/). Our intention is to equip the widest audience of practitioners with this incidence estimation capability. The approximation is as flexible as the original model, and we have shown that its inaccuracies are restricted to high levels of incidences that are less relevant when dealing with emerging epidemics. However, in case such high incidence estimation is needed, we have seen that the approximation is conservative, i.e. biased towards an overestimation of disease progress (which is not always acceptable, since it might lead to overzealous control, see e.g. [33]).

The model relies on the simple and deterministic logistic equation. That it is consistent with more complex systems is not obvious. The tests presented here against spatial and stochastic simulations of epidemics show that our non-spatial model is robust to the significant deviations from the logistic equation, products of both spatiality and stochasticity. The model gives accurate estimates of the disease incidence for most simulated epidemics considered here. However, for highly aggregated host distributions and short distance dispersing pathogens, the deviation from the logistic equation can be too great. In those contexts, the disease progression across the landscape is not steady but punctuated by rare events: the pathogen jumps between distant host clusters. Then, the very distinctive trajectories this epidemic can take do not simplify well into a single logistic curve. In such cases, reduced pathogen dispersal and increased host aggregation result in habitat fragmentation for the pathogen. The estimation should then be attempted on individual clusters, or a multiscale approach considered (as in [34,35]).

From plants to animals, the major shift regarding epidemics lies in individual movement. In many cases, this can be overlooked as it does not necessarily imply movement of the sampling units (e.g. herds/farms in [36]). When sampling individuals, however, our model is applicable to well-mixed populations, i.e. where the pathogen spread is steady and not too impacted by spatio-temporal structure in the host population. We saw the limits of this assumption in figure 3, where highly clustered distributions of hosts cause significant deviations from model predictions. Such deviations may, for example, be increased if clustering correlates with heterogeneous susceptibility of hosts (e.g. age-related aggregation like schools), or attenuated by mutable clusters (e.g. commuting).

Recent technological innovations are changing epidemiological surveillance for more timely and exhaustive censuses. For example, the monitoring of human epidemics is already augmented by the supervision of social networks [37] and internet search queries [38,39]. Tree monitoring could also be assisted by satellite high-resolution imagery [40,41]. Those innovations will still need robust and epidemiologically informed estimation methods and, even if monitoring is conducted continuously, there is no reason to see them incompatible with an adaptation of our model. However, in any foreseeable future, most contagions will still be monitored through discrete and censored inspections and hence remain within the immediate scope of the estimation model presented here.

Data accessibility

The estimation model is available at https://gitlab.com/Yo-B/estimationApp.

Competing interests

We declare we have no competing interests.

Funding

The work at Rothamsted forms part of the Smart Crop Protection (SCP) strategic programme (BBS/OS/CP/000001) funded through the Biotechnology and Biological Sciences Research Council (BBSRC) Industrial Strategy Challenge Fund and the BBSRC Newton Fund project 'Real time deployment of pathogen resistance genes in rice', grant no. BB/N01362X/1. The authors are also thankful to the US Department of Agriculture (USDA) for funding support.