Perfect counterfactuals for epidemic simulations

Abstract

Simulation studies are often used to predict the expected impact of control measures in infectious disease outbreaks. Typically, two independent sets of simulations are conducted, one with the intervention, and one without, and epidemic sizes (or some related metric) are compared to estimate the effect of the intervention. Since it is possible that controlled epidemics are larger than uncontrolled ones if there is substantial stochastic variation between epidemics, uncertainty intervals from this approach can include a negative effect even for an effective intervention. To more precisely estimate the number of cases an intervention will prevent within a single epidemic, here we develop a ‘single-world’ approach to matching simulations of controlled epidemics to their exact uncontrolled counterfactual. Our method borrows concepts from percolation approaches, prunes out possible epidemic histories and creates potential epidemic graphs (i.e. a mathematical representation of all consistent epidemics) that can be ‘realized’ to create perfectly matched controlled and uncontrolled epidemics. We present an implementation of this method for a common class of compartmental models (e.g. SIR models), and its application in a simple SIR model. Results illustrate how, at the cost of some computation time, this method substantially narrows confidence intervals and avoids nonsensical inferences.

This article is part of the theme issue ‘Modelling infectious disease outbreaks in humans, animals and plants: epidemic forecasting and control’. This theme issue is linked with the earlier issue ‘Modelling infectious disease outbreaks in humans, animals and plants: approaches and important themes’.

1. Introduction

Dynamic models are frequently used to assess the likely impact of disease control strategies. These exercises range from modelling the impact of a new intervention or strategy on an established pathogen [1–4], to modelling the containment and control of emergent epidemics [5–7]. While deterministic models are frequently used [2,4,8–10], stochastic simulations are increasingly common as they can account for both uncertainty in the underlying parameters and the random nature of the disease process [6,7,10–13]. In both stochastic and deterministic models, the impact of intervention is typically determined via comparison of simulations with and without the intervention.

In the deterministic setting, this comparison is straightforward, as with a given set of parameters and starting conditions the epidemic will always behave exactly the same; hence, any comparison between an intervention scenario and its non-intervention ‘counterfactual’ can only be attributed to the intervention itself. When stochastic models are used, things become more complicated. Typically, two sets of simulations are conducted, one with the intervention and one without. The distribution of outcomes from the two sets is compared to estimate the intervention effect. Because these are independent sets of simulations, there may be some simulations in the non-intervention scenario where the disease dies out quickly due to random chance, and fewer cases occur than in the majority of intervention simulations. Likewise, there may be cases in the intervention scenario where large numbers are infected through ‘bad luck’ for the virtual populations involved. If these stochastic effects are large, they may lead to uncertainty intervals in effect estimates that include the intervention having no effect, or even a negative impact, even if the intervention is modelled in such a way that it can only have a beneficial effect. For example, the results of a study of measles vaccination strategies by Lessler et al. appear to leave open the possibility that more cases of measles could occur in a country if supplementary vaccination activities were conducted than if those campaigns had not been conducted [3]. Likewise, results in Rivers et al. are consistent with low coverage of pharmaceuticals causing additional cases of Ebola when compared with no coverage, even though the model assumes they have a beneficial effect [14]. Burke et al. examine multiple increasing levels of intervention, but leave open the possibility that each performs worse than the level below it [15]. These effects will be exacerbated if the systems being modelled include complex and interrelated stochastic processes or if they are simultaneously sampling over parameter uncertainty.

Comparison of two independent simulations (reflecting scenarios with and without the intervention) has a very specific interpretation: it represents the difference between what we expect to be observed in an uncontrolled epidemic compared with a completely independent epidemic where the intervention occurred (conditional on the initial state). However, what we often want to know is what would have happened had the intervention occurred in the exact same epidemic. This is analogous to the problem of counterfactual inference in randomized trials and observational studies, where we take one set of individuals (or populations) as a stand-in for what would have happened in the counterfactual situation where they had (or had not) experienced some exposure. A number of techniques of trial design and statistical analysis have been developed to help real-world studies better approximate the true counterfactual situation ([16–18] are just a few examples of the large literature on the subject).

However, in computational simulations, it is possible to take a more exact approach. For example, Cook et al. proposed an approach to separate random elements of an epidemic from the intervention by simulating each separately [19]. However, they found this approach computationally infeasible and instead developed a less general, computationally tractable approach based on an alternative parameterization by Sellke [19,20].

Here, we present a computationally tractable method for simulation of direct counterfactuals to stochastic simulations using principles borrowed from the percolation approach to epidemic simulation [21]. We illustrate this ‘single-world’ approach using simulations of interventions against an influenza-like illness. Although we have chosen a human pathogen as our main example, robustly characterizing the effect of intervention is a general challenge also relevant to animal (e.g. [22]) and plant (e.g. [23]) pathogens. We also outline how the general approach can be adapted to a wide variety of disease systems and simulation methodologies.

2. Methods

(a). Overall approach

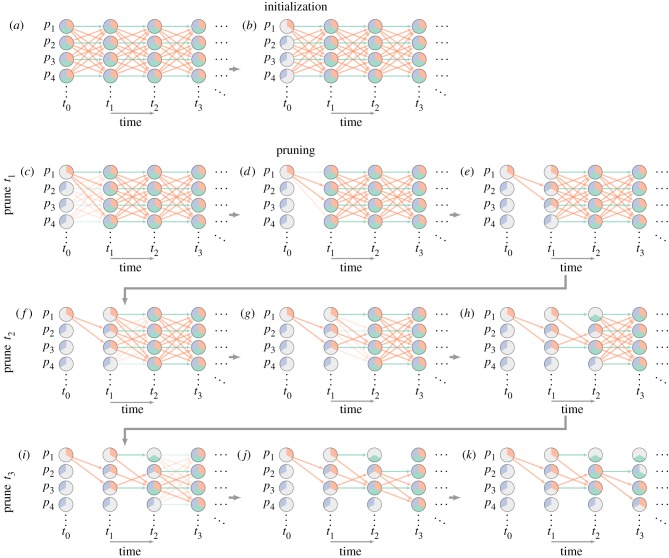
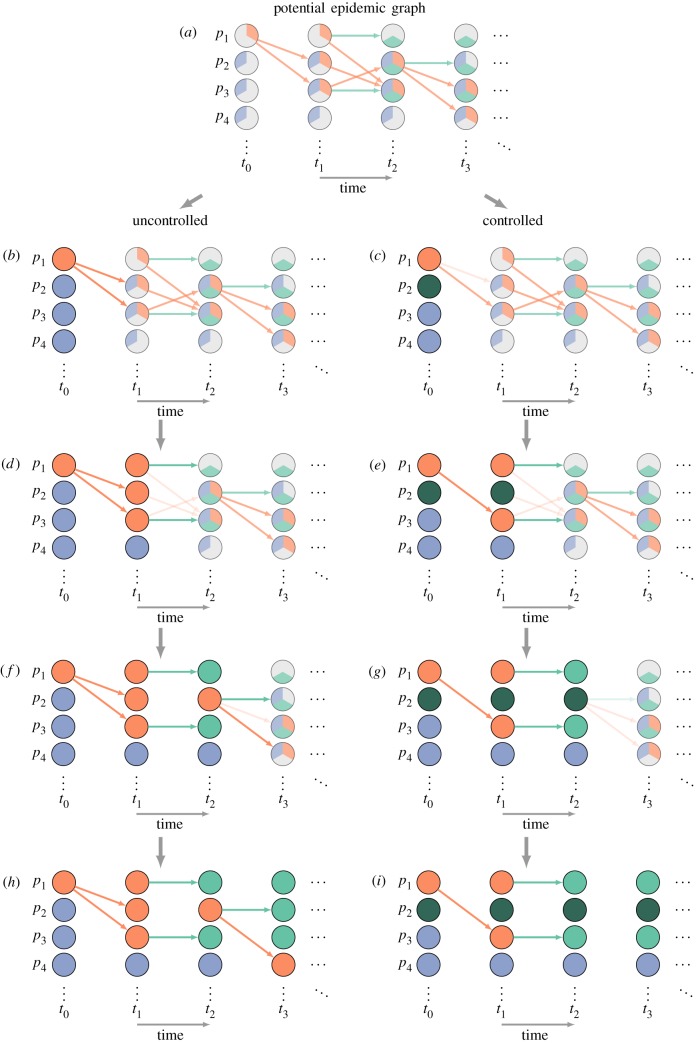
Our goal is to simulate an uncontrolled epidemic and then simulate one or more controlled epidemics that are entirely consistent with the uncontrolled epidemic. That is, all events (e.g. transmissions, recoveries, etc.) that occur in the uncontrolled epidemic also occur in its controlled counterpart unless precluded (directly or indirectly) by the intervention; and no stochastic events that did not occur but were possible in the uncontrolled epidemic happen in its controlled counterpart unless explicitly caused by an intervention. To accomplish this, we describe the epidemic in terms of potential events (figure 1), and then prune them according to a model, based on stochastic simulation, to create a ‘potential epidemic graph’ (PEG; figure 2). We then use this graph to ‘realize’ consistent epidemics in controlled and uncontrolled scenarios (figure 3).

Figure 1.

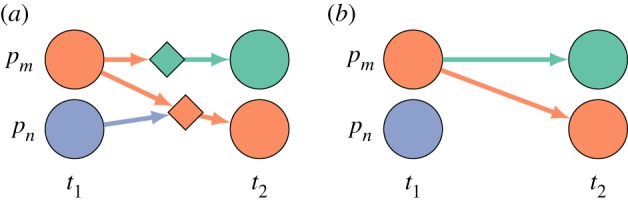
Anatomy of an event. Each event has preconditions based on the state of one or more individuals p in the population at time t_i, a probability of occurrence, and an outcome that sets the state of an individual at time t_i+1. (a) In its full representation, an event is represented as a node on the graph (diamonds) with incoming edges representing the preconditions individuals (circle nodes) must meet for that event to occur. In this case, both events require individual p_m to be infectious (orange) and the bottom event additionally requires individual p_n to be susceptible (purple). The outgoing edge captures the outcome of the event, in this case removed (green) and infectious (orange). (b) We use a reduced representation where the event nodes are implicit. Edges are coloured by their outcome, and infectious edges (orange) carry an implicit precondition that the target is susceptible. Here, the reduced representation in panel (b) is equivalent to the full graph in panel (a).

Figure 2.

‘Single-world’ simulation process. To simulate an initial epidemic and intervention, we start with a (implicit) complete graph. We represent potential states using coloured wedges; an individual can be susceptible (purple pie slice), infectious (orange) or removed (green). We start by using our initial conditions to eliminate all but one potential state for each individual in the population at time t₀ (b); here individual p₁ starts infectious, and other individuals start susceptible. We next prune all events with at least one precondition that we know is not satisfied by the initial state (c). We then prune those events selected not to occur in this particular simulation according to our underlying infection model (d). We set the possible states of each individual at t₁ based on the remaining events in the graph, so each individual’s set of potential states encompasses both the outcomes of any remaining events and (for events potentially prevented by the intervention) the outcomes of their absence (e). We now repeat steps (c–e) for events connecting t₁ to t₂ (f–h), t₂ to t₃ (i–k) and so on. Note that when we prune the events with unattainable preconditions (i), we still keep the events for p₁ and p₂ infecting p₃, even though p₃ was potentially infectious at t₁, because susceptible is still a potential state for p₃ at t₂ in an intervention scenario (i.e. removing the transmission event at t₁ could lead to a scenario where p₃ is susceptible at t₂). This final potential epidemic graph (PEG) can then be used to obtain simulated epidemics with and without interventions (figure 3).

Figure 3.

‘Single-world’ simulation process (continued). In order to measure the impact of the intervention on the epidemic, we use the PEG (figure 2) to construct two epidemics: one uncontrolled (left), one with intervention (right). We start by setting the actual state (denoted by colouring the whole circle) of each individual at time t₀ to their initial condition, and then changing their state according to the intervention, in this case setting p₂ as vaccinated (dark green). We then prune events between t₀ and t₁: removing inconsistent events and allowing the intervention to stochastically remove events (b,c). We then use those events to determine the actual state of each individual at t₁, allow the intervention to alter that state, then prune inconsistent events again (d,e). We repeat the process for times t₂ (f,g), t₃ (h,i) and so on. This final graph can be used to extract our outcome of interest. Any graphs made from the same PEG represent the results of different interventions in a ‘single world’.

Specifically, our approach begins with an implicit complete graph that includes a representation of all possible events (example in figure 2). In the complete graph, there are two types of nodes: one representing individuals at times, and one representing events (figure 1). A node representing an individual at a particular time is considered to potentially belong to any of a set of potential states (e.g. susceptible, infectious, removed). Directed edges represent dependence. An edge from an individual node to an event node means that the individual node has to be in a particular state (or set of states) as a precondition for that event. An edge from an event node to an individual node means that an outcome of that event is a change in the state of the target node (e.g. ‘immune’ is the outcome of a recovery event). The underlying epidemic model assigns each event a probability of occurring if its preconditions are met. In the case where all events represent either a transition in an individual’s state, dependent only on their prior state (e.g. recovery events), or infections resulting from contact between individuals, a simplified representation is possible (figure 1). In this simplification, events are represented by edges and infection events have the implicit precondition of the target being susceptible at the previous time point. For clarity in text and figures, we will focus on this simplified representation for the rest of this manuscript, but it should be noted that the full representation allows a greater diversity of models.

As illustrated in figure 2, to create the potential epidemic graph (PEG), we first assign individuals an initial state at time 0 (equivalent to removing all but one of their potential states). We then prune from the complete graph all of the events whose preconditions are inconsistent with the remaining potential states of each individual at time 0. Next, we stochastically prune the remaining events based on their probability. We then remove all states at time 1 that are inconsistent with both the states at time 0 and the remaining events. This process is then repeated iteratively until a predefined time limit is reached.

Once the PEG is created, an uncontrolled epidemic can be realized by iterating through times, assuming all events whose preconditions are met occur and setting each event’s target node to the outcome of that event (figure 3). To simulate an intervention, the same process is performed, but events are removed or node states are changed probabilistically based on the intervention process.

Below, we describe how this process can be performed for disease systems specified by certain compartmental models.

(b). Compartmental models to potential epidemic graphs

One way to specify an epidemic model is by using a system of probabilistic state (i.e. compartment) transitions, such as a stochastic susceptible–infected–resistant (SIR) model [24,25]. These models most commonly include two types of transitions: contact transitions triggered by infectious contacts and independent transitions resulting from the natural history of infection (e.g. recovery) or demographic changes (e.g. death; figure 4).

Figure 4.

Two types of transitions commonly present in compartmental models: (a) independent transitions occur with probability α_i,j independent of the state of the model and (b) contact transitions occur between two specific individuals with probability β_i,j,k.

Here, we consider the set of models with K states whose behaviour can be described using only independent and contact transitions (this includes most SIR-type models) and demonstrate how to construct the complete graph from these types of events. We assume that the probability of independent transitions between states i and j is α_i,j, and that the probability of contact transitions between i and j, depending on the number of people in state k, is β_i,j,k. In most models, α_i,j will be 0 for most combinations of i and j, and, likewise, β_i,j,k will be 0 for the vast majority of combinations of i, j and k.

To construct the (implicit) complete graph, we create a node for each individual at each time point and assign their set of potential states to include all K states. We then add events between nodes for all pairs of adjacent time points. For each type of independent transition, we create an event between every individual and itself in the next time step. Similarly, for each contact transition, we create an event between each individual and every other individual in the next time step. To set the initial conditions, for each compartment i, we set X_i individual nodes to have i as their only possible state at time 0. However, in some cases we may want to allow additional states if considering an intervention that can assign those states (see Interventions below for details). This complete graph can then be used to construct the PEG using the algorithm described above.

(c). Interventions

Interventions can remove events (e.g. eliminate infection events) or change the states of individuals (e.g. make a host immune by vaccination). As outlined above, interventions are applied as we iterate over times when realizing the PEG, but for this process to work, the PEG must also subsume the courses of the epidemic that are possible under the intervention (i.e. edges pruned as impossible never occur in the epidemic).

Therefore, in order to eliminate potential states when pruning, we need to make some assumptions about potential control strategies. Otherwise, the control strategy could change any node to any state at any time. Hence, the algorithm is significantly faster if we restrict the set of states that control measures can cause an individual to enter, W, and the types of events control measures can remove, Z. These assumptions aid pruning by guaranteeing that no individual can enter a state not in W unless caused by an event, and that outcomes caused by events in Z will always occur if their preconditions are met. The latter allows us to prune states that must be exited from the set of possible states (e.g. if recovery is in Z and individual i has a potential recovery at time t_i, then i cannot be infectious at time t_i+1 unless an infection event occurs, or infectious in W).

(d). Simple example

As an example, we demonstrate our proposed method using a simple susceptible (S), infectious (I), removed (R) compartmental model in a closed population, with a force of infection βI and a recovery rate of γ. We set the parameters of the model for a disease similar to influenza (β_S,I,I = β = 0.78(1/N), α_I,R = γ = 0.44(1/days)) [26]. We consider the impact of three different control strategies, selected to capture common ways in which interventions work: antivirals, which reduce the period of infectiousness; hand washing, which reduces the probability of transmission; and vaccination, which removes individuals from the susceptible pool.

We ran 10 000 simulations using both classical techniques and the single-world approach for each intervention on a population of 4000 for 100 days with five initial infected, and calculated the estimated number of cases averted. To model antivirals, we assumed that 10% of individuals are given antivirals upon infection, increasing their recovery rate by 20%. To model hand washing, we assumed that 5% of transmission events are prevented. To model vaccination, we assumed that 10% of individuals are vaccinated at the start of the epidemic and that 33% of those are successfully immunized, and the epidemic in a vaccinated state is started. While we demonstrate our method here using a simple SIR model, our method is applicable to a much wider class of models, as detailed above.

We have posted a software package, cfepi, on GitHub https://github.com/HopkinsIDD/cfepi, that implements our method. It follows the procedures outlined above, assuming that interventions never put any individual in a non-terminal state and that interventions do not prune independent events. We also provide a pseudocode implementation of a more general example using the W and Z construction from Interventions above (§2c) (electronic supplementary material, SA). Estimates for computational time and space were made using this package.

3. Results

The time complexity of the single-world approach is O(TN²) for both the construction of the PEG and the realization, where T is the number of time steps and N is the number of nodes (i.e. it is limited by the number of possible combinations of individual pairs at each time point). In practice, realization is far faster owing to the extensive pruning during construction of the PEG. Storing the PEG can also take significant space, depending on the model and amount of pruning being done. In comparison, a standard implementation of a stochastic SIR model based on binomial draws is O(T). In our implementation, the example SIR disease system in a population of 400 000 requires less than 1 min to create one PEG, less than 20 s for each realization, and approximately 2 GB of storage (significant speed-ups may be possible using GPU-based parallelization). This is compared with less than 1 s to run an iteration in a standard stochastic SIR model. However, there is some reduction in the number of simulations needed to achieve a specific precision in the effect estimate owing to the reduced variance in the intervention effects in the single-world approach (e.g. a reduction of about 2.5 times in our example).

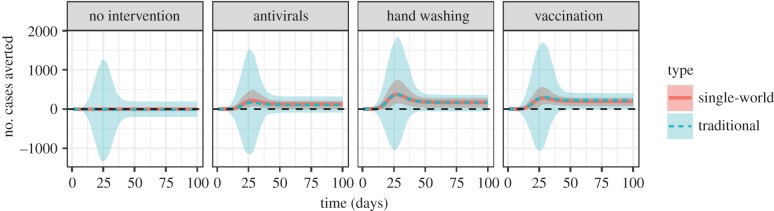
Though it comes at a computational cost, the benefit for estimating intervention effects using the single-world approach is evident in our simulations. For all of our illustrative interventions, we see virtually the same point estimate of impact in the single-world approach and standard approaches (exactly the same at higher number of simulations), but the single-world approach gives confidence intervals that both are narrower and do not include negative effects. In a population of 4000 (average uncontrolled epidemic size 2851), the single-world approach estimated antivirals to prevent an average of 92 (90% CI: 1–188) cases, versus 109 (90% CI: −94 to 293) in the standard approach. The single-world approach estimated hand washing to prevent an average of 154 (90% CI: 29–282) cases, versus 157 (90% CI: −37 to 379). The single-world approach estimated vaccination to prevent an average of 187 (90% CI: 86–293) cases, versus 190 (90% CI: −3 to 394). Differences between single-world and independent approaches are even more pronounced if we compare intervention effects at different points during the epidemics (figure 5). We examined the effects of our different model/simulation parameters on the outcome. We tested other parameters (electronic supplementary material, SB) and found that the single-world approach always outperforms the independent approach; moreover, this performance often resulted in qualitatively different interpretations (significant effect versus no significant effect).

Figure 5.

Time series showing cumulative number of cases averted at each time caused by the intervention calculated using our method (single-world) and a standard method. Shaded regions denote 90% confidence intervals. Note that there is more variation in the middle of the epidemic, so it may seem as though the number of cases averted is large during those times. (Online version in colour.)

4. Discussion

In this paper, we present a method that allows simulation studies to more exactly estimate the precise impact of an intervention by comparing epidemic simulations with their exact ‘counterfactual’. We demonstrate the ability of our method to factor away cross-epidemic variation, which can lead to counterintuitive results, such as uncertainty intervals that suggest that an intervention programmed to have only beneficial effects instead has some small chance of having a negative effect. We further show our method is tractable when applied to many familiar models and control strategies and have implemented software to aid in its use in common cases.

This ‘single-world’ approach of matching controlled epidemic simulations with their exact uncontrolled counterfactual answers a subtly different question compared with comparisons between independently simulated sets of epidemics with and without control. The single-world method estimates how many cases we expect to be prevented by using a control measure, while the independent simulation approach estimates the expected difference in size between two different epidemics, one with and one without the control measure. To put it in more concrete terms, an example of the first type of question is, ‘How many cases of influenza will we prevent next year if we increase vaccination rates by 15%?’, while an example of the latter is, ‘How many fewer influenza cases do we expect next year compared with last if vaccination increases by 15%?’. Both are important public health questions, but authors are not always clear which they are answering, with a tendency to write as if they are answering the former, while performing simulations that answer the latter. This may seem unimportant, as in their expectation they have the same answer (ignoring season-to-season inter-dependence in influenza epidemics for the sake of argument); but, as illustrated by our simple examples, their overall distributions can differ substantially, and in ways that might lead one to discard an intervention that has an important effect. While in our simple SIR model the intervention effect had to be small for the predicted effects to cross zero, in more complex systems this can happen even for interventions with a large impact (as in [3]).

We are not the first group to examine the refined counterfactual question. A few other groups have measured the effect of a single intervention to a single model [27,28], but their approaches do not easily generalize beyond the presented examples. Our method explicitly models time structure and includes all state transitions rather than just infection events, thus extending beyond Kenah & Miller [27]. Our method permits counterfactual events that did not occur in the factual case, thus extending beyond Haydon et al. [28]. Ackley et al. explore the relationship between causal diagrams and compartmental models [29], and one could think of our complete graph as constructing a causal diagram from a compartmental model. However, Ackley et al. seem primarily interested in the other direction: converting causal diagrams to compartmental models. Cook et al. take a different approach to the same problem we present here, replacing ‘events’ with ‘resistance to accumulated infection’ as their random component [19]. As stated in their paper, however, this approach does not exactly preserve the impact of interventions (though it is a good approximation under some assumptions) and cannot be used to model certain interventions. Our method preserves the impact of interventions and supports a wider class of control measures (e.g. ring vaccination, electronic supplementary material, SC).

Here, we focus on a common class of discrete-time stochastic state-based models to illustrate our method, but the diversity of models used in practice is far greater. While the general idea presented here could be applied to any epidemic model, it is the efficient pruning of possible states and events that makes this approach tractable. We expect our approach to extend trivially to certain classes of models (e.g. network models, simple agent-based models), with effort to others (e.g. discretizing continuous time approaches), and not at all for certain classes of complex models (e.g. agent-based models where disease state changes behaviour). Even within the class of discrete-time compartmental models, models with a larger number of compartments (e.g. certain metapopulation models) may prevent practical use without significant speed-ups. Going forward, there are clear opportunities to improve the applicability and practical utility of this work by optimizing computation and refining pruning assumptions. Also, the current software package is somewhat limiting in the types of control strategies that can be implemented, and we plan to add methods for users to specify their own classes of interventions and appropriate pruning assumptions. Moreover, our approach handles event removal better than event addition, so interventions that are phrased in terms of adding events (e.g. ending an existing vaccination campaign) may work better if the intervention and uncontrolled cases are swapped (e.g. continuing the vaccination campaign). The method can also be trivially extended to situations where we are sampling over parameter uncertainty as well as epidemic stochasticity. Perhaps most excitingly, conceptual parallels between our approach and data augmentation approaches (e.g. [30]) suggest ways in which we might more precisely explore how interventions might have worked in real-world epidemics.

Precisely characterizing the potential impacts of interventions is often an important component of scenario modelling analyses for public health, in both pathogen-emergent and -elimination scenarios. Modelling approaches are also increasingly central to economic analyses to identify the best control strategies for animal [31] and plant pathogens [32]. We hope that the methods we develop here lay the groundwork for broadening the set of approaches available to achieve this goal, allowing more precisely targeted inference in a variety of complex scenarios.

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests.

Funding

This work was funded by the National Institutes of Health (grant no. R01 AI102939).