Transmission routes of rare seasonal diseases: the case of norovirus infections

Abstract

Norovirus (NoV) is the most commonly recognized cause of acute gastroenteritis, with over a million cases globally per year. While usually self-limiting, NoV poses a substantial economic burden because it is highly contagious and there are multiple transmission routes. Infection occurs through inhalation of vomitus; faecal-oral spread; and food, water and environmental contamination. While the incidence of the disease is predictably seasonal, much less is known about the relative contribution of the various exposure pathways in causing disease. Additionally, asymptomatic excretion and viral shedding make forecasting disease burden difficult. We develop a novel stochastic dynamic network model to investigate the contributions of different transmission pathways in multiple coupled social networks representing schools, hospitals, care-homes and family households in a community setting. We analyse how the networks impact on transmission. We used ward-level demographic data from Northumberland, UK to create a simulation cohort. We compared the results with extant data on NoV cases from the IID2 study. Connectivity across the simulated cohort was high. Cases of NoV showed marked seasonality, peaking in early winter and declining through the summer. For the first time, we show that fomites and food appear to be the most important exposure routes in determining the population burden of disease.

This article is part of the theme issue ‘Modelling infectious disease outbreaks in humans, animals and plants: epidemic forecasting and control’. This theme issue is linked with the earlier issue ‘Modelling infectious disease outbreaks in humans, animals and plants: approaches and important themes’.

1. Introduction

Norovirus (NoV) (formally known as Norwalk virus, Norwalk-like virus or small round-structured virus) is a comparatively recently identified calcivirus originally discovered following an outbreak of acute gastroenteritis in Norwalk, Ohio [1]. Norovirus is the most common cause of acute gastroenteritis worldwide [2]. The disease is usually self-limiting in the immunocompetent but poses particular issues for semi-closed social settings where there are population mixing and potential for close contact between infectious individuals [3], contaminated environments and susceptible individuals. The virus may contaminate food [4] or water [5] causing infection through the faecal-oral route. Symptomatic individuals generate millions of viral particles which are aerosolized in vomitus and faeces thus contaminating the environment [6]; the dose required for infection has been estimated to be less than 18 particles [7]; the virus may persist on surfaces in the environment for up to 50 days after deposition [8] and individuals may shed virus for several weeks after recovery [9]. Furthermore, up to 16% of the population may be asymptomatic excretors [10]. These features pose particular problems for human environments where social mixing takes place. Outbreaks often lead to closures of healthcare, care-home and educational establishments, posing further burdens for health and social care. The annual costs of norovirus infection in the UK are estimated to be £80 M [11].

While the pattern of disease is strongly seasonal in temperate countries [12], predicting the burden and incidence of disease in any particular place is difficult for several reasons. Firstly, the incidence of the disease is comparatively rare (47 community cases per 1000 person-years) [13]. Secondly, as the disease is self-limiting, it is under-recorded [14] as many cases do not seek medical care and it has been estimated that only around 1 in 300 cases are recorded in official statistics [13]. The problem of predicting disease is also further complicated by hyper-mutation leading to rapid strain evolution [15].

Forecasting norovirus disease is difficult unless due attention is paid to the different modes of transmission. While faecal-oral, droplet-oral and vomitus-oral and transmission via fomites are known pathways for infection, it is not clear which of these mechanisms is responsible for spread and persistence in the wider community [16]. Outbreaks are recorded in UK public health systems, but these are usually associated with institutional settings like schools, hospitals and care-homes for the elderly [17] where case ascertainment is straightforward. While outbreaks in these institutions can be expensive and have high local impact, these systems usually have comparatively small populations at risk. It is essential to quantify the relative importance of transmission pathways and sources of infection at the wider community level so that risks of outbreaks at the institutional level can be minimized at a higher level [18]. Conventional deterministic SEIR (susceptible/exposed/infected/resistant) models are not ideal to investigate disease spread in these scenarios as transmission events are unlikely to be described adequately using these models. Here we develop and validate a microsimulation model of norovirus infections which investigates transmission pathways in a community in the context of both the social networks within it and also the underlying host–pathogen interaction represented by the immune response, recovery, asymptomatic shedding and environmental contamination. Networks associated with being in a family, attending education, attending hospital and care-homes are linked dynamically through time in relation to the working week and community demographics. The model identifies the relative significance of different mechanisms of exposure and transmission in the social setting of a digital representation of the population of a voting ward in NE England. We link exposure, transmission in relation to dose response and changes in immunity in individuals in the population following exposure. Model results are compared to observations of community-level norovirus infections from a prospective, population-based cohort study (IID2, January 2009–September 2011) [13] and also with norovirus incidence from public health records for NE England.

2. Material and methods

The model consisted of a combined microsimulation and individual-based model for predicting the temporal dynamics of norovirus spread among individuals in a spatially defined community on the basis of different contact mechanisms.

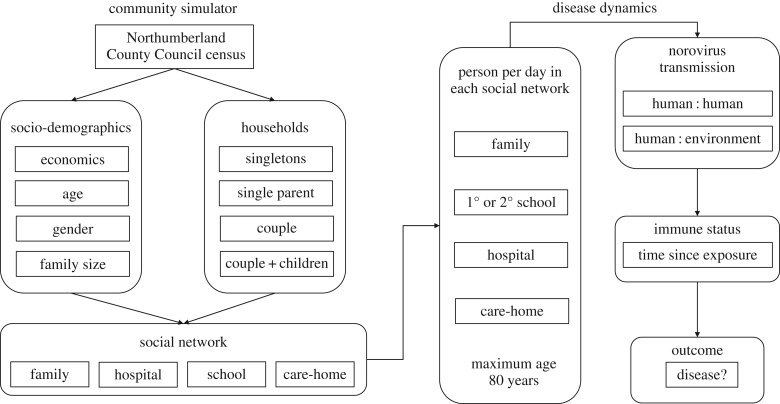
The model has two components (figure 1):

• 1. Community simulator to create a modelled cohort.

• 2. Disease dynamics simulator within-cohort disease spread.

Figure 1.

Schematic overview of modelling process.

(a). Community simulator

The community simulator was a microsimulation model that was used to define a population and the network of interactions between individuals in terms of four types of social network: family, schools, hospitals and care-homes. An individual belonged to one or more networks depending on their age (primary/secondary school, care-home) or health (hospital). Disease spread occurred through daily contacts between individuals as they came into contact through the relevant social network. The simulator created a population with the defined socio-economic structure at the level of the census ward. Since census wards typically have populations of 4000–6000, a model cohort of 5000 people was implemented. Data describing population age, gender, socio-economic status, household composition and family size were used as parameters to define a simulated cohort. A cohort was created to reflect a representative ward, with individual age, gender, family, school, hospital and care-home residency allocated stochastically. Input data for the model were obtained from Northumberland County Council which characterize the socio-demographics of the population in each ward in Northumberland [19]. The simulator assumed that individuals lived in households/families that exist as single-person households, single parents with children, couples and couples with children. The proportion of the modelled population in each category was determined on the basis of the known age distribution among known household structure in the ward. Children above the age of 5 were assumed to attend a primary school; those greater than 11 a secondary school and all children attended school until age 18, for 5 days a week. Individuals in a ward were assumed to have access to one or more hospitals and care-homes. Both the number of schools and hospitals were defined as model inputs, and we assumed that there were four primary schools and one secondary school. Hospital attendance was a stochastic variable determined on the basis of admission rates to hospitals. Patients were assumed to remain in the hospital for 7 days. Care-home residency was modelled on the basis of the known proportion of the over 65 population known to occupy care-homes. The network structure of the model cohort was then analysed in terms of the connectivity of individuals within the population as determined by the social networks in which they participated (specifically schools and families). The population aged over time in the disease dynamics model, with individuals dying after 80 years; babies were born during the simulation to replace deaths. Data were analysed using the igraph and network packages [20].

(b). Disease dynamics

Disease dynamics was modelled at the individual level. Disease transmission was assumed to occur when susceptible individuals consumed contaminated food and/or came into contact with infected individuals or environments in which infected individuals had been ill, in four social settings. These were in the home (within-family exposure); primary school (within-school exposure); secondary school (within-school exposure); hospitals (within-hospital exposure) and care-homes (within-care-home exposure). The disease model operated on a daily time step by simulating weeks with 5-day school attendance and 2-day weekends for each individual in each network as appropriate (figure 1). Each social setting was effectively a sub-section of the total population of the cohort which changed with the day. Individuals attending any of the settings came into contact with other individuals in that setting (family, primary schools, secondary schools, hospitals and care-homes) who may or may not have been infectious/carriers of norovirus (figure 1). In the case of human:human transmission, the probability of a susceptible individual becoming infected on any day was then modelled as a Poisson process similar to that of the Kermack–McKendrick SEIR model, where individual infection is calculated as the product of a transmission coefficient (representing the number of individuals that become infected by contact with one infected individual) and the number of infected individuals currently in that group in that setting at that time point. Individuals may also come into contact with residual viral particles left in the environment of the premises following illness having occurred there. The viability of these viral particles following deposition from an infected individual was assumed to decline following a Weibull distribution [21,22]. In both cases, the dose of viral particles that a susceptible individual received on contact with an infectious individual or contaminated environment was modelled stochastically. Individuals were also exposed to infection through consumption of contaminated oysters. While this may technically be considered an environmental source of contamination, in practice, the contamination was spatially external to the community. Presence of an infectious individual in a social setting was assumed to take precedence over a contaminated environment in causing disease. The probability that an individual became ill after exposure was then determined on the basis of the received dose of viral particles [23] and the estimated immune status of the individual. Immune status was modelled as an exponential decline in immunity from the time of last exposure. The proportional decline in immunity in each time step was estimated from the value of the exponent needed to reduce the estimated immunity from complete (1) to a low level (less than 10⁻²⁰) by the maximum duration of immunity. The duration of the infectious state and the rate of decline of immune status were variable as model inputs.

The model was constructed in the R programming language using custom scripts [24].

(c). Sensitivity analysis to quantify impacts of transmission mechanism, food and environmental exposure and immunity on disease spread

We varied four groups of epidemiological parameters. Firstly, the risk of transmission under the different social settings of family, primary/secondary school, care-home and hospital. Secondly, the risk from environmental contamination and the level of contamination arising from the presence of sick individuals in each social setting. Thirdly, the extent to which members of the cohort consumed contaminated oysters, ignoring age, and finally, the duration of the infectious period in which individuals could spread disease and the duration of immunity following becoming colonized/infected.

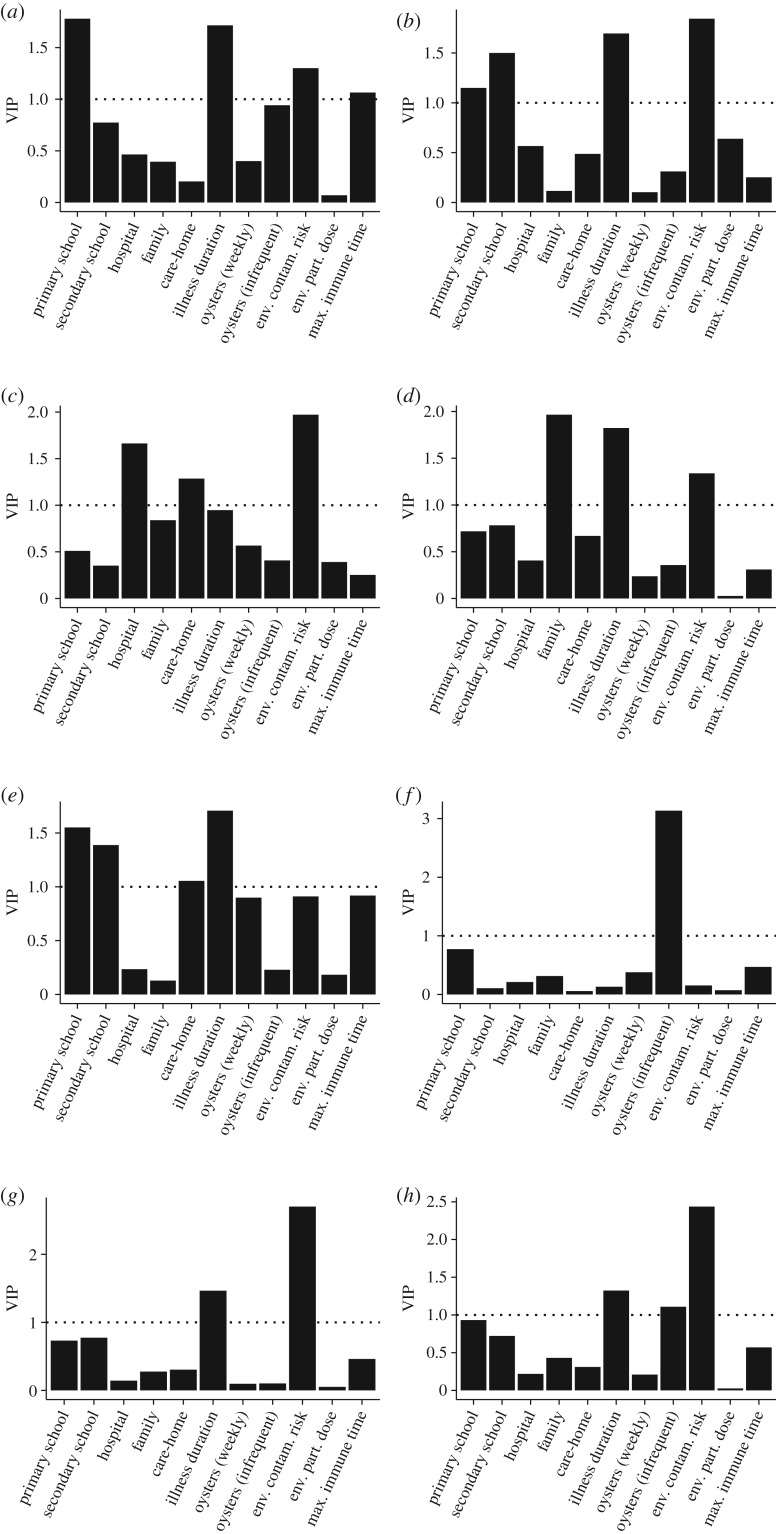
We used Latin Hypercube Sampling (LHS) [25] to create ranges for these parameters and ran the model for 3 years for 40 runs with different input parameters. (See table 1 for details of the range of inputs used in the model.) Where we had no data, we used plausible ranges. LHS provides a robust method for sensitivity analysis where, as in our study, there was considerable uncertainty as to the true parameter values (see §3.1 of Shirley et al. [28]). The total number of norovirus cases arising from each transmission pathway each day was collated from the outputs. Since the predicted number of cases was highly periodic, we detrended the case data in relation to time using harmonic regression. We then used the intercept from the harmonic regressions as an indicator of baseline disease burden after adjusting for seasonality under each LHS scenario. We used each intercept as the dependent variable and the epidemiological parameters as independent variables in partial least-squares regression to calculate the relative contribution of the covariate to the baseline disease burden. We calculated Variable Influence on Projection (VIP) factors to compare the relative contributions of the epidemiological parameters to the total burden of disease and burden arising under each transmission setting (family school, etc.). VIP values greater than 1.0 have an above-average weight in explaining the dependent variable [29], while accounting for any collinearity between predictions.

Table 1.

Parameter ranges used in LHS sensitivity analysis.

parameter	primary schoola (probability)	secondary schoola (probability	hospitala (probability)	familya (probability)	care-homea (probability)	infectious durationb (days)	probability of eating oystersc	frequency of eating oystersc	environmental contamination riska	environmental viral particle dosea	maximum immune timed (days)
minimum–maximum	0.0001–0.005	0.0001–0.005	0.0001–0.005	0.0001–0.005	0.0001–0.005	2–14	0.0001–0.005	0.0001–0.0060	0.0001–0.0050	10–1800	10–720

^aReliable data not available; plausible ranges used.

^bAtmar et al. [10].

^cFood Standards Agency [26].

^dParrino et al. [27].

(d). Comparison of microsimulation model predictions with observed data

The model output daily counts of cases of norovirus disease by mode of contact, specifically: oysters, contact in family, schools, hospitals and care-homes and via environmental contamination in each setting. We summarized outputs in a number of ways to produce data that could be compared with the observed patterns of disease. Observed data consisted of monthly occurrence of norovirus outbreak cases collated from the cohort study in the IID2 study [13] and from public health records of outbreaks in the UK over the period 2000–2010. Neither of these datasets provide a perfect cohort against which to compare model outputs. The model was run for the period May 2010 to June 2011 for comparison with data derived from the sampling period of the IID2 study and for 3 years to compare with the disease burden in NE England. Individuals were assigned age, gender and socio-economic class based on the socio-economic structure in NE England. We used the outputs for the runs of the sensitivity analysis to predict cases for the whole community and compared these with the observed monthly number of cases recorded in the IID2 study and regional data using correlation.

3. Results

(a). Disease network characteristics derived from community simulator

The social community model produced an initial population of 4969 individuals in 2638 families (households). The connectivity between members of the population was very high. When considering membership of schools and families alone, the mean distance on a weekday between any two members of the population was 3.3 links indicating high connectivity in this community. While 1245 individuals (particularly single member households) were effectively isolated, 1300 individuals had only one link (suggesting childless couples) and 6 individuals had 481 connections to other members of the population. The mean number of connections (the degree) for individuals in the community was 55.7, but the degree distribution was highly bimodal, with one peak at the average size of a primary school (100) and another at the size of the single local secondary school (477). The four schools (3 primary, 1 secondary) are ‘hubs’ of dense connections, with every child at a school linked to every other child at that school.

(b). Sensitivity analysis

We first assessed the extent to which the total burden of disease in the cohort was dependent on the disease parameters before investigating the extent to which burden arising from contact in the family, school, hospital, care-home and environmental settings was related to these parameters (figure 2h). Environmental contamination risk, infrequent consumption of oysters and duration of illness had VIP greater than 1, indicating a significant contribution to baseline burdens of disease for the community as a whole. At the level of individual transmission setting (figure 2a–g), the transmission coefficient for that setting was a major predictor of baseline disease for that setting (figure 2a–e, VIP values greater than 1). In all these settings, illness duration was also a particularly important factor. In care-homes, there appeared to be particular risks from hospital and families, as well as within the care-home itself (figure 2e). The major food risk was via infrequent consumption of oysters (figure 2f).

Figure 2.

Variance inflation projections for different settings (a–e) or transmission pathways (f,g). (a) Primary school; (b) secondary school; (c) hospital; (d) family; (e) care-home; (f) food; (g) environment; (h) total.

(c). Comparison of microsimulation model predictions with observed data

The predicted number of cases followed a cyclic pattern, with cases lowest in summer but rising to a peak in winter. Of the 40 sets of output from the LHS sensitivity analysis, one set provided a close match between model predictions and observed number of cases for both datasets, with a correlation of 0.872 between predicted cases of disease and the observed number of IID2 cases. For these model scenarios, transmission coefficients within primary school, secondary school, hospital, family and care-home networks were low (0.00140, 0.00465, 0.0036, 0.0011, 0.00329). The duration of illness (including asymptotic shedding) was 11 days, environmental contamination risk was also low at 0.002, environmental particle dose was 1320 virions and the period of immunity was 253 days. Food and environmental contamination were the most important exposure pathways (figure 2f,g). Predictions using the best-fit parameters for IID2 data for a new dataset based on estimated number of cases for the NE of England are shown as means ± s.d. for 10 replicates in figure 3.

Figure 3.

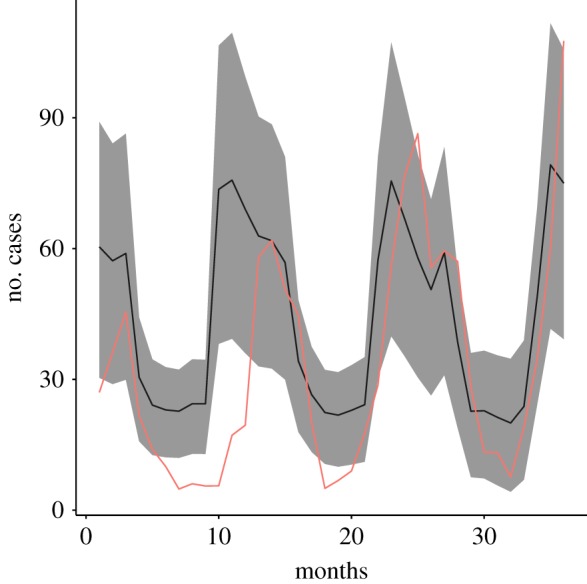
Observed (red line) and predicted (±s.e.) cases of norovirus in northeast England.

We classified predicted number of cases each month into seven age classes: less than 6; 6–10; 11–15; 16–20; 21–40; 41–60; and greater than 60. The distribution of cases among different age-groups was skewed. We used the total number of cases and individuals to calculate the expected number of cases in age class and the risk for each group. The ratio of predicted cases to expected cases was 1.06 for the under 6 age class; 1.75 for 6–10-year-olds; 4.58 for 10–15-year-olds; 2.68 for 15–20-year-olds; 0.52 for 20–40-year-olds; 0.49 for 40–60-year-olds and 0.56 for greater than 60-year-olds; i.e. the burden of disease was predominant among children. Three epidemics were identified in the output of the model; a new epidemic was assumed to have begun if a number of days had passed between cases that exceeded the generation time of the disease (11 days, estimated from the best LHS run). The first epidemic started on the first day of the model (1 January) and lasted 465 days, ending in April of the following year. The R0 of this epidemic was estimated to be 0.98 (95% CI = 0.97–0.99) by the exponential growth (EG) method and 1.07 (95% CI = 0.93–1.22) by the maximum-likelihood (ML) method. The second epidemic began in September of the second year, lasted 269 days and ended in June of the third year. The estimates for R0 were 1.01 (EG: 95% CI = 0.92–1.11) and 1.17 (ML: 95% CI = 0.93–1.45). The third epidemic began in September of the third year, lasted 89 days and ended in December of the third year. The estimates for R0 were 1.25 (EG: 95% CI = 0.59–2.56) and 2.83 (ML: 95% CI = 1.77–4.23). All calculations of R0 were performed using the ‘R0’ package [30].

4. Discussion

There have been many attempts to model the epidemiology of norovirus in the past. Much of this research has focused on outbreak modelling, as outbreaks are most economically significant because they may lead to shut-down of institutions until the disease is past or controlled [31]. They provide more clearly defined bouts of disease and form an easy basis with which to validate models. The results of outbreak modelling studies differ widely in their estimations of disease dynamics when measured in terms of R₀: Gaythorpe et al. [32] quotes model R₀ ranges of between just over 1 and 7. Variation in R₀ is known to have impacts on the utility of such models in outbreak settings of nosocomial disease [33]. This diversity probably reflects two features of the disease. First, populations are relatively small, so exposure and transmission become highly stochastic rather than deterministic processes, leading to a wide variation in disease progression. Second, outbreak settings are unlikely to be environmentally or socially homogeneous, with the role of fomites and social interaction varying between settings. Research on disease epidemiology in the community in contrast is logistically difficult because of the diversity of exposure and transmission pathways, and environments in which transmission occurs. We have attempted to model at the community level, including outbreaks in institutional settings, but capturing the whole population as a network of linked individuals as well as the institutional settings. Our results suggest that network linkages impacted on disease spread.

Theoretical models have demonstrated that epidemiological spread is highly dependent on network topology, as represented by linkages between members of the community at risk (e.g. [34,35]). Much research has assumed that such a network remains static, or changes over timescales longer than that of the transmission and infectious period of the disease. Spread in static networks is most rapid when the path length (i.e. shortest route through the network) is comparatively small as it was in our network. At a mechanistic level, the spread is higher because of ‘hubs’ in the network, where some individuals have connections with many individuals and when contacts are more assortative, that is, where contacts are similar demographically. In our community networks, assortative features were a precondition because children were modelled as attending a restricted number of schools as well as families and hospital, while adults were modelled as belonging to families, hospitals and (eventually) care-homes. The number of connections to other nodes in the network for children would therefore have inevitably been higher than that of the adults. Furthermore, older people were more likely to be single without children and effectively isolated. Moosong et al. [36] demonstrated that children were the most socially connected individuals in communities and concluded that this might explain the high prevalence of droplet-borne diseases (e.g. SARS) among children in epidemics generally.

Our models also simulated changes in the overall community network with time. This was both in the short term through changes in participation in networks in the week and also through movement of individuals between networks as individuals aged, which resulted in them changing schools, going into hospital or entering care-homes. Empirical studies of contacts between individuals in settings such as schools [37,38], as well as more large-scale studies of social clustering across countries [39], have also shown that contact networks may be highly dynamic. When networks are dynamic, the spread of disease through them also changes. Adaptive behaviour derived from knowledge of the existence of the disease could change network structure and impact on transmission, and effectively stop epidemic spread [40]. Read et al. [41] concluded that spread was dependent on the type of contact (close and casual) and the mode of transmission of the pathogen. They found that behavioural contacts in their network, which were more fine-scale than those used in our study, led to a network that was effectively a random-mixing model. Our results demonstrate that the burden of disease arising in the broad institutional settings of school, family and hospital is dependent on transmission coefficients specific to each setting but that duration of infectiousness and risk of environmental contamination were important drivers of predicted cases. At the community level, however, the burden of illness was dependent on environmental contamination risk, duration of illness, oyster consumption and transmission in secondary schools. Part of the difference reflects the serial dependency in norovirus with environmental contamination in any setting necessarily following a vomitus/faecal episode in that setting.

At a larger scale, norovirus tends to be periodically pandemic (there were pandemics of norovirus in 1996, 2002, 2004, 2006, 2009 and 2012 [42]) attributed to the pathogen undergoing hyper-mutation [43], leading to rapid evolution of new strains, as pandemic strains eventually lead to herd immunity. Norovirus variants may circulate in the population at low levels before acquiring other necessary mutations to facilitate their emergence as a pandemic virus [44]. Brockman & Helbing [45], in a study of global network patterns of passenger transport, demonstrated that the arrival time for the epidemic disease at a place was independent of disease parameters and more concerned with the effective distance across the contact network. It is possible that the periodic pandemic nature of norovirus disease reflects an interaction between the evolution of new strains and the nature of spread in disease via the contact networks in which it finds itself. Pandemic disease would then reflect populations linked through the presence of a small number of even more highly connected hubs than those in smaller population and institutional units with which we associate outbreaks.

There are obvious limitations to the modelling. Firstly, even though we created a simulation cohort that represented the demography of a real population, our conceptual model of social interactions and connectivity in the population was simplified. We did not include adult workplace settings nor other individual-level interactions in intergenerational links or extended families. In addition, our assessment of contact was rather crude and not based on actual measurable human behaviours, compared to empirical work on contact transmission. We also did not include all forms of food that are known to be contaminated: outbreaks in Canada, Belgium and France have been associated with the consumption of salad vegetables and berry fruit [46]. However, the impacts of these simplifications are comparatively easy to assess. Workplace settings will mainly involve individual workers at establishments out with the community. In this context, their impact on network connectivity is probably minimal, except insofar as outside contacts with workplaces may act as foci for introgression of infection external to the ‘residential’ community. Introgression of disease into the community from these sources is likely to be highly stochastic, as it would be at the sparse but highly linked hubs occurring at scales leading to pandemic behaviour. The absence of intergenerational links and extended families means that the connectivity in the social networks was highly conservative and as such the model will have underestimated network connectivity. We did not model variation in immune response to different norovirus strains, treating all as homologous in their impacts on the development of disease and subsequent immunity. We did not model age-specific immunity, which is likely to be lower in care-homes and among the elderly [47], nor the effects of natural immunity that arise from the lack of histo-blood group antigens necessary for virus binding. We also ignored age-related dietary preferences, for example, oysters are less likely to be consumed by children. Finally, the data used to validate the modelling were necessarily crude. Neither the regional-level nor IID2 data were at the same spatial scale and we only had data on recorded disease not the pathways that produced them. In effect, our simplifications and assumptions about the social system and disease epidemiology and the mismatch between observed cases are likely to have led to a conservative and more hierarchically structured estimate of the social networks and their impacts on likely disease dynamics in this community setting.

Our research integrates different and coupled dynamic social networks with the immunology, demography and sources of contamination at a scale larger than the outbreak setting. The models suggest that environmental contamination and food were major drivers of the number of norovirus cases in this social system. Oyster contamination, which was highly seasonal, acted as a source of repeated introgression into the community. Our results suggest that norovirus disease is multiply scaled in time and space, and attention to different transmission routes and networks of exposure pathways is important if norovirus is to be managed other than retrospectively at the outbreak scale.

Data accessibility

Analysis scripts and example data are available at https://doi.org/10.17605/OSF.IO/T64MG.

Authors' contributions

S.P.R., P.R.H. and S.J.O. developed the overall project aims and objectives and collated the relevant datasets. S.P.R. authored the original R scripts; R.A.S. ran model simulations and analysed outputs. M.D.F.S. contributed to the R code and analysis. All authors contributed to the final manuscript.

Competing interests

We have no competing interests.

Funding

There is no funding to report for this project.