Applying optimal control theory to complex epidemiological models to inform real-world disease management

Abstract

Mathematical models provide a rational basis to inform how, where and when to control disease. Assuming an accurate spatially explicit simulation model can be fitted to spread data, it is straightforward to use it to test the performance of a range of management strategies. However, the typical complexity of simulation models and the vast set of possible controls mean that only a small subset of all possible strategies can ever be tested. An alternative approach—optimal control theory—allows the best control to be identified unambiguously. However, the complexity of the underpinning mathematics means that disease models used to identify this optimum must be very simple. We highlight two frameworks for bridging the gap between detailed epidemic simulations and optimal control theory: open-loop and model predictive control. Both these frameworks approximate a simulation model with a simpler model more amenable to mathematical analysis. Using an illustrative example model, we show the benefits of using feedback control, in which the approximation and control are updated as the epidemic progresses. Our work illustrates a new methodology to allow the insights of optimal control theory to inform practical disease management strategies, with the potential for application to diseases of humans, animals and plants.

This article is part of the theme issue ‘Modelling infectious disease outbreaks in humans, animals and plants: epidemic forecasting and control’. This theme issue is linked with the earlier issue ‘Modelling infectious disease outbreaks in humans, animals and plants: approaches and important themes’.

1. Introduction

Mathematical modelling plays an increasingly important role in informing policy and management decisions concerning invading diseases [1,2]. However, model-based identification of effective and cost-efficient controls can be difficult, particularly when models include highly detailed representations of disease transmission processes. There is a variety of mathematical tools for designing optimal strategies, but no standard for putting the results from mathematically motivated simplifications into practice. An open question is how to incorporate enough realism into a model to allow accurate predictions of the impact of control measures, while ensuring that the truly optimal strategy can still be identified [3]. In this paper, we identify the difficulties—as well as potential solutions—in achieving a practically useful optimal strategy, highlighting the potential roles of open-loop and model predictive control by way of a simple example.

(a). Realistic simulation models

The optimization of disease management involves determining the most appropriate control method(s), e.g. vaccination, quarantine or roguing, and the best deployment strategy for that method or combination of methods to minimize impacts of the disease. This minimization can be difficult when resources are limited and there are economic costs associated with both control measures and disease. Methods that simulate the expected course of an epidemic and explicitly model effects of interventions can rapidly quantify the potential impact of a given strategy [4]. These simulation models accurately capture the dynamics of the real system and so have become important tools for assessing policy decisions relating to real-time management responses as well as to increased preparedness for future threats. Examples include vaccination policies for human papillomavirus in the UK [5,6], livestock culling policies [7,8] and vaccination optimization [9,10] for foot-and-mouth disease, and optimal host removal strategies for tree diseases of citrus [11–14] and sudden oak death [15].

Various complexities of disease dynamics, for example spatial heterogeneities and inherent individual differences in susceptibility and pathogen transmission (risk structure), have been shown to be important determinants of patterns and rates of epidemic spread [16–18]. To ensure accurate epidemic predictions, these factors must be included in simulation models designed to aid decision making. However, inclusion of these heterogeneities typically results in highly complex models with many possible control measures, making optimization computationally infeasible when interventions can be combined, and particularly when control measures can also vary over time, in space or according to disease risk [19]. For most simulation models, the only viable option is then to use the model to evaluate a small subset of plausible strategies that remain fixed during the epidemic, potentially scanning over a single parameter such as a culling radius. We shall refer to this approach as ‘Strategy Testing’. Using this approach makes it difficult to have high confidence in the best-performing strategy, since with no framework for choosing it, the set of strategies under test is likely to be biased. Further to this, as the set to test cannot span the entire space of control options, it is unlikely that the true optimum will be found.

(b). Optimal control of epidemiological models

Many mathematical techniques exist for characterizing the true optimal control for a disease, such as equilibrium or final size analysis, depending on the system being analysed [16]. We here focus on optimizing time-varying control of dynamical systems, for which optimal control theory (OCT) is widely used [20]. By analysing a set of equations describing the disease dynamics, OCT can mathematically characterize the optimal deployment strategy for a given control method and provide insight into the underlying dynamics, without the repeated simulation required to optimize simulation models. However, because of the underlying mathematical complexity, little progress can be made with OCT unless the underpinning models for disease spread are highly simplified. Early work in OCT focused on optimal levels of vaccination and treatment [21], with extensions to consider further interventions including quarantine, screening and health-promotion campaigns appearing later [22]. Disease models can also be coupled with economic effects [23–25], and within OCT this has been used to balance multiple costs, such as surveillance and control [26], or prophylactic versus reactive treatment [27].

The optimal strategies identified by OCT can be very complex, often specifying controls that switch strategies at specific times during the course of an epidemic. The added complexity of these switching controls can significantly improve disease management when tested on a spatially explicit model, but can lead to poor performance if the exact time of the switch is not known [28], for example, when parameter uncertainty gives a wide range of possible switch times. This demonstrates that uncertainties and additional complexities often prohibit OCT from being directly applicable to the real world. It is also unclear how insight from OCT alone could be translated into practical advice. To move towards robust strategies that could be used practically, more recent work has focused on including additional features and heterogeneities in the models used in OCT, in particular spatial dynamics. Space is usually only included to a limited extent, for example, by using metapopulation models (e.g. [29,30]), or partial differential equations (e.g. [31]) to optimize spatial strategies, so whether the heterogeneities added are sufficient to identify robust and practical control strategies remains an open question.

(c). Moving towards practical control

Despite finding the mathematically optimal control strategy, major simplifications to the system as modelled are required to allow progress to be made using OCT. It is therefore often unclear how these strategies would perform if adopted by policy-makers. On the other hand, models with sufficient realism to inform policy directly are often impossible to optimize fully. Therefore, a framework is needed to combine the optimization capabilities of OCT with the accurate predictions of simulation type models as required in policy making. The question is then how should we make practical use of OCT?

In §2, we describe two methods from control systems engineering for applying OCT results, and compare these versus Strategy Testing using a simple illustrative model in §3. We seek to answer how, under current computational constraints, results from OCT can be applied while maintaining the realism required for practical application.

2. Applying optimal control to realistic systems

Outside of epidemiology, OCT has had wider use on approximate models of complex systems. A recent study reviews the use of OCT for agent-based models (ABMs) [32], a type of model that simulates the individual behaviour of autonomous agents. An et al. [32] suggest the use of a model that approximates the dynamics of the ABM, designed to be simple enough to allow mathematical analysis of the optimal control. A suitable approximate model is chosen and fitted either to real data, or to synthetic data from the ABM. The OCT results from the approximating model are then mapped onto the ABM to be tested: a process referred to as ‘lifting’, which could equally well apply to the detailed epidemic simulation models considered in this paper. We now describe two possible frameworks from control systems engineering for making use of this control lifting approach.

(a). Open-loop control

The first method is the simplest application of control lifting, and the framework implicitly suggested by An et al. [32]. Control is optimized on the approximate model once using the initial conditions of the simulation model. The resulting optimal control strategy is lifted to the simulator and applied for the full simulation run time (figure 1). Repeated simulation of the OCT strategy on the simulation model allows assessment against other possible control strategies. The optimization gives a single, time-dependent strategy for all simulation realizations, and so does not incorporate any feedback. It is therefore referred to as ‘open-loop’ control, as it is fully specified by the simulation initial conditions and the trajectory predicted by the approximate model. Use in epidemiology is uncommon, although Clarke et al. [33] use OCT in an approximate model to find optimal levels of chlamydia screening and contact tracing which are then mapped onto a network simulation.

Figure 1.

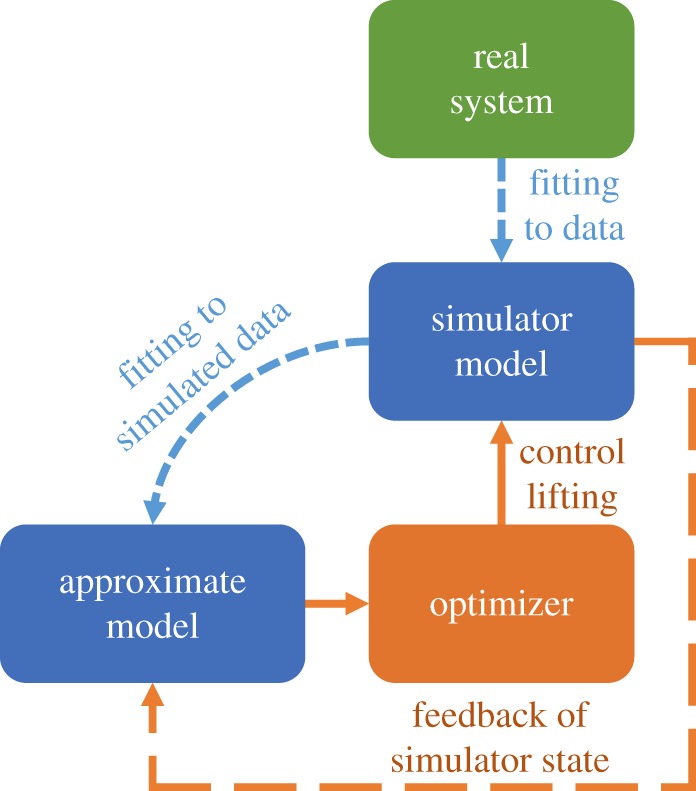
Open-loop and model predictive control (MPC). The model hierarchy is shown, with optimized controls from the approximate model directly lifted to the simulation model. The real system is in green, the models and fitting processes are in blue, and the control framework is in orange. Without the orange dashed feedback loop, this is open-loop control. MPC resets the state of the approximate model at regular update steps, before re-optimizing and lifting controls to the simulation model until the next update time.

(b). Model predictive control

Open-loop control requires the approximate model to remain accurate over the time scale of the entire epidemic. However, for tractability the approximate model must necessarily omit many heterogeneities present in the simulation model, such as spatial effects and risk structure. When strategies resulting from OCT are then applied to the simulation model or to the real system, the disease progress is likely to deviate systematically from the trajectory predicted by the approximate model. Model predictive control (MPC) is an optimization technique incorporating system feedback that can take such perturbations into account [34,35]. At regular update times, the values of the state variables in the approximate model are reset to match those in the simulation at that time. The control is then re-optimized and the new control strategy is applied to the simulation until the next update time. The approximate and simulation models are therefore run concurrently, with multiple optimizations per realization, to ensure that the approximate model and control strategy closely match each individual simulation realization (figure 1). These multiple optimizations are computationally costly but tractable, unlike performing optimization on the full simulation model.

MPC has had some use within the epidemiological literature, the majority being for control of drug applications for single individuals rather than control of epidemics at the population level. Examples include finding management strategies for HIV that are robust to measurement noise and modelling errors [36,37], and control of insulin delivery in patients with diabetes [38]. These studies highlight the benefits of MPC for robust control, i.e. control that remains effective despite system perturbations. However, only one study concentrates on epidemic management [39], and that does not explicitly test the feedback control on simulations.

3. Optimizing strategies on an illustrative network model

(a). Methods

To demonstrate open-loop and MPC for epidemic management, we use a stochastic SIR network model including host demography and risk structure. The model is deliberately kept simple to show how the underpinning idea is broadly applicable across human, animal and plant diseases. While the model and its parameters are arbitrary and do not represent a specific disease, we use it to represent a scenario in which a simulation model has already been fitted to a real disease system; the network model is therefore used here as a proxy for a potentially very detailed simulation model.

(i). Simulation model

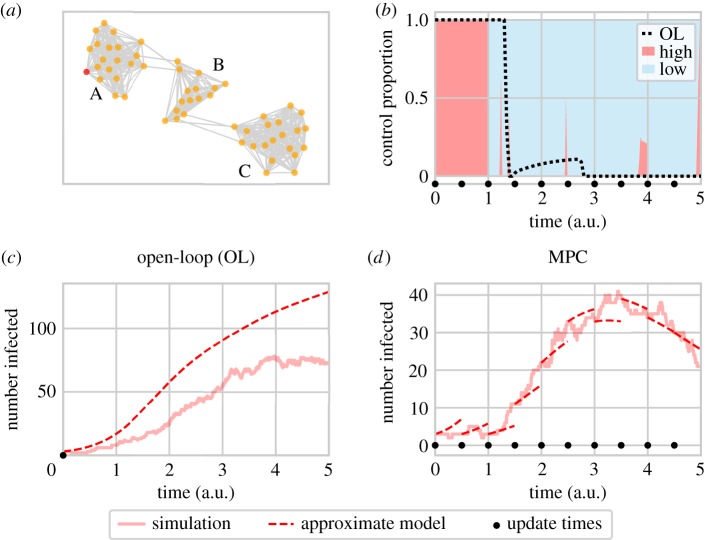
In our model, infection spreads stochastically across a network of nodes that are clustered into three distinct regions (figure 2a). Each node contains a host population stratified into high- and low-risk groups. The infection can spread between individuals within nodes and between connected nodes. The net rate of infection of risk group r in node i is given by

$$S_i^{\mathrm{r}}\sum _{\hspace{0.17em}j}{\sigma }_{ij}\hspace{0.17em}\hspace{0.17em}({\rho }^{\mathrm{r}\mathrm{H}}{I}_{\hspace{0.17em}j}^{\mathrm{H}}+{\rho }^{\mathrm{r}\mathrm{L}}{I}_{\hspace{0.17em}j}^{\mathrm{L}}),$$ 3.1

where S and I are numbers of susceptible and infected hosts, respectively, subscripts identify the node, and superscripts specify high (H) or low (L) risk group. The sum is over all connected nodes including the focal node itself, with the relative transmission strength into node i from node j given by σ_ij, and risk structure given by the 2 × 2 matrix ρ. Full details of the model are given in electronic supplementary material, S1. Although not limited to these applications, the model in equation (3.1) could represent crop or livestock diseases spreading through farms, or sexually transmitted infections spreading through towns, cities or countries.

Figure 2.

(a) The network used for the illustrative simulation model, including region labels. The epidemic is seeded in the red node in region A, and can spread between connected nodes (grey lines). In (b), the control allocation is shown for a single space-based MPC run, with the corresponding open-loop allocation indicated by the black dotted line. (c) The total number of infected individuals under a single run of space-based open-loop control. Control is based on the prediction of the approximate model starting from the initial conditions. (d) The number of infected individuals in the simulation and space-based approximate model corresponding to the MPC control carried out in (b). Here the prediction is reset to match the simulation at every update step (0.5 time units) and the control is re-optimized. By repeatedly correcting for differences between short-term model predictions and realized numbers of infected individuals—rather than relying on a potentially increasingly inaccurate prediction made at the initial time—MPC gives better predictions of the simulation state as well as improved control when compared with open-loop (note different y-axis scales). a.u., arbitrary units.

Mass vaccination is the only intervention we consider, with the potential to target based on both risk group and region but randomized across host infection status (i.e. the vaccine is given to all hosts but is only effective on susceptibles). Logistical and economic constraints are included through a maximum total vaccination rate (η_max) that can be divided between risk groups and regions. Within each group susceptibles are vaccinated at rate: fη_maxS/N, where f is the proportion of control allocated to that group, and N is the total group population.

Optimal allocation of the vaccination resources minimizes an epidemic cost J representing the disease burden of the epidemic across all infected hosts over the simulation time (T): $J=$ ${\int }_{t=0}^{T}I(t)\hspace{0.17em}\text{d}t$. In common with the particular control we consider and the risk and spatial structures, this simple choice of objective function was made merely to illustrate our methods, but the framework generalizes immediately to more complex settings.

(ii). Approximate models

Exhaustive optimization of control using the simulation model, across space, risk group and time, is clearly very computationally expensive. To assess the best level of approximation, we consider two different deterministic approximate models of the simulator. The first model is purely risk structured, factoring out all spatial information and leaving one high-risk and one low-risk population group. This model is deterministic and based on the assumption that all nodes are spatially well mixed with each other. The second approximate model is more complex, in as much as it is also deterministic and risk structured, but additionally includes a first approximation to the host spatial structure by including the regional host information. Spatial dynamics are included between but not within the three regions to maintain enough simplicity to obtain optimal control results, thereby assuming that nodes are spatially well mixed within each region. This could represent, for example, optimizing control at the country level, but not at the regional level. We refer to this model as the spatial approximate model. A single set of parameters is fitted for each model to data from an ensemble of simulation model runs. We then test which of the two approximate models is the more useful for control optimization. Full details of the approximate models, fitting and optimization procedures are given in electronic supplementary material, S1 and S2.

(iii). Control scenarios

We test six different control scenarios, which compare Strategy Testing of controls based purely on the simulation model (scenarios 1 and 2) with open-loop and MPC applied using both of our approximate models (scenarios 3–6):

• (1) ‘High’: exclusively vaccinate high-risk individuals.

• (2) ‘Split’: partition control resources between high- and low-risk groups based on an optimization performed in advance.

• (3) ‘Risk OL’: open-loop control using the risk-based approximate model.

• (4) ‘Risk MPC’: MPC using the risk-based approximate model.

• (5) ‘Space OL’: open-loop control using the spatial approximate model.

• (6) ‘Space MPC’: MPC using the spatial approximate model.

The optimal constant allocation for the ‘Split’ strategy was found by running many simulation model realizations for each of a range of partition values, as in [11], and selecting the value that gave the lowest average epidemic cost (electronic supplementary material, figure S8). The six strategies are assessed by repeatedly running the simulation model under each control scenario.

(b). Results

The OCT results for optimizing the vaccination strategy in the risk-based approximate model lead to initial vaccination of high-risk individuals only, before switching priorities and treating the more populous low-risk group almost exclusively. The OCT results from the spatial approximate model show this same switch (figure 2b), but a number of spatial switches are also seen, allowing control to track the epidemic as it progresses through the three regions (electronic supplementary material, figure S9). The spatial strategies are therefore much more complex than the risk-based controls.

Applying the control scenarios to the simulation model and comparing epidemic costs shows that incorporating greater realism, through a more complex approximate model as well as by using MPC, allows improved disease management (figure 3 and electronic supplementary material, figure S10). Of the constant and purely simulation-based ‘user-defined’ strategies, splitting control between risk groups is slightly more effective than just vaccinating the high-risk group. The optimal allocation to the high-risk group used in the ‘Split’ strategy is 63% of vaccination resources, with the rest used to vaccinate low-risk individuals, although this does occur in a broad minimum of epidemic cost (electronic supplementary material, figure S8). Applying the optimizations from the risk-based approximate model to the simulation model gives an improvement over either of the ‘user-defined’ strategies, although there is little difference in epidemic cost between the open-loop and MPC frameworks (see below). Adding space into the approximate model improves control further, leading to the smallest epidemic costs when the spatial MPC framework is used.

Figure 3.

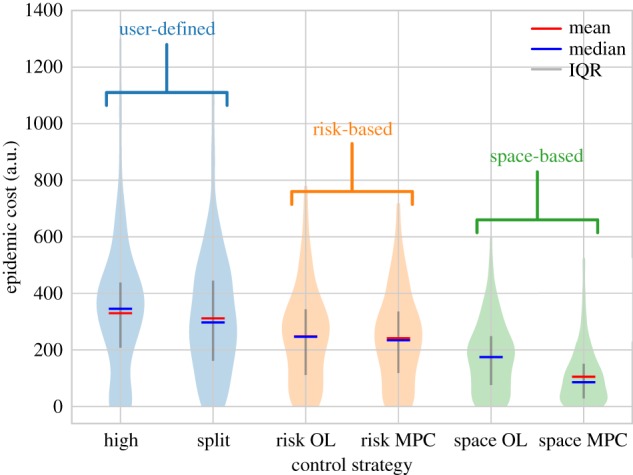
Results of different control optimization schemes on the illustrative simulation model. Spatial MPC performs best, showing an improvement over both open-loop (OL) and user-defined strategies. a.u., arbitrary units.

The illustrative model demonstrates the management improvements that can be achieved by combining OCT with both open-loop and MPC. The key results of the OCT analyses are the control switching times. Using the switching controls from either approximate model with open-loop control gives lower epidemic costs than the naively chosen ‘user-defined’ strategies. The feedback present in the MPC controllers allows further reductions to the epidemic cost. By re-evaluating the timing of the switches during the epidemic, and potentially including additional switches, the control can respond more closely to the exact trajectory of the current simulation realization (figure 2b–d). This gives control that is more robust to uncertainty and systematic errors in the approximate model, and hence performs better on the complex simulation model.

In the risk-based strategies, there is little difference between open-loop and MPC. This is because the precise timing of the switch from high- to low-risk group vaccination does not significantly affect the epidemic cost (electronic supplementary material, figure S11). The timings of disease introduction into regions B and C are highly variable between simulation runs (electronic supplementary material, figure S2). The potential for additional switches in the spatial approximate model gives more flexibility for the MPC controller to respond to this variability, and so spatial MPC shows a significant improvement over open-loop, which cannot adapt to perturbations. The performance of the control is closely linked to the accuracy of the approximate model. In our example, spatial dynamics are clearly important because of the timing of spread between regions, and so the more informed controls of the spatial model outperform the risk-based strategies.

4. Discussion

Our results show that the choice of approximate model affects the performance of both open-loop and MPC strategies. Here we have found a suitable approximate model in an ad hoc manner, but a key challenge for the future is to develop a more formal method for choosing the most appropriate approximate model. A more accurate model may give better predictions, and hence control that is closer to the true optimum, but simpler models are often sufficient [40] and accuracy must be balanced with added complexity and optimization constraints. One difficulty in doing this is that it is not always clear where the boundary of mathematical or computational feasibility is, and so how complex the model can be made in practice. It is also difficult to determine mathematically, in a systematic way, which aspects of the dynamics are important to capture accurately. This key issue must be considered though, since the implications relate directly to applications in the real world.

Practical disease control requires surveys of the real system to assess the state of the epidemic. Both open-loop and MPC optimize control using predictions of the future dynamics, making them both feed-forward controllers. The approximate model underlying these frameworks allows more informed decisions between surveys, resulting in control that is closer to the true optimum. Accurate predictions can avoid continuous or very frequent surveys which may be expensive or logistically challenging. As discussed previously, the repeated updates in the feedback loop of MPC improve these predictions and hence the performance of the control. However, each update will require surveillance of the real system, so the frequency of updates must be chosen so as to balance improved knowledge of the system with any surveillance constraints.

In this paper, we have focused on a top-down approach, finding robust, practically applicable strategies by making use of OCT to optimize simulation models. Equally, many studies use OCT without simulation models, rarely considering practical application of the resulting optimal controls. With this bottom-up approach, a system for testing the results on realistic systems is vital to ensure that these results are robust to additional realism. Using an MPC framework as considered here could be one way in which OCT researchers could demonstrate the potential impact of their work to a wider audience.

Exhaustive testing of alternative simulation model parameterizations is beyond the scope of this study, but we generally find that spatial MPC also performs best across other reasonable parameter sets (electronic supplementary material, S3). We have assumed throughout that an accurate simulation model of the real system in question can be built, and that a single set of parameters can be fitted for the chosen deterministic approximate model. In reality, there may be considerable uncertainty in parameters for the simulator, so fitting a single deterministic model may be challenging. A question for future study would be how to handle these uncertainties, perhaps also incorporating improved knowledge of parameters as the simulation proceeds [41].

The strategies found by OCT are highly dependent on the exact form of the objective function, which we have here chosen to be very simple. Extending the objective to include costs associated with control as well as with each switch in strategy would allow a more detailed assessment of the practicality of implementing these complex strategies. More research is needed into how to quantify the balancing of very different costs though, for example, treatment costs and disease burden [29]. In human disease, cost-effectiveness analyses are usually based on quality-adjusted life years [42]. A similar concept could perhaps be used for plant and animal diseases, including calculations of yield losses [43] as well as effects on welfare, biodiversity and tourism, for example [44]. The methods we have described, however, are not dependent on the form of the control or objective function. For an appropriate approximate model, the feedback in MPC ensures accurate predictions and so should always improve performance over open-loop. The frameworks we describe can be used to provide an additional, unbiased control scenario to the Strategy Testing process that is already in common use.

In this paper, we have shown that coupling feedback control with simulation models and OCT can help to design effective and robust intervention strategies for managing pathogens of human, animal and plant populations. While these techniques may be able to transfer optimal control results to more realistic simulations and so to practical application, the strategies found do raise the issue of communicability of results. With complex feedback strategies between two models, one complex in structure and the other mathematically complex, the overall result is no longer simple to explain. Future research must therefore focus on improving the accuracy of simulation models, and analysing their reliability, so that simulations can be used to establish conclusively the benefit of these complex OCT-based strategies.

Data accessibility

All code and animations are available at https://github.com/ehbussell/Bussell2018Model.

Authors' contributions

E.H.B., C.E.D. and N.J.C. designed the study; E.H.B. conducted the analysis and wrote the initial draft of the manuscript. All authors contributed to data interpretation, manuscript editing and discussion.

Competing interests

We have no competing interests.

Funding

E.H.B. acknowledges the Biotechnology and Biological Sciences Research Council of the United Kingdom (BBSRC) for support via a University of Cambridge DTP PhD studentship.