New methodologies for the estimation of population vulnerability to diseases: a case study of Lassa fever and Ebola in Nigeria and Sierra Leone

Abstract

Public health practitioners require measures to evaluate how vulnerable populations are to diseases, especially for zoonoses (i.e. diseases transmitted from animals to humans) given their pandemic potential. These measures would be valuable to support strategic and operational decision making and allocation of resources. Although vulnerability is well defined for natural hazards, for public health threats the concept remains undetermined. Here, we develop new methodologies to: (i) quantify the impact of zoonotic diseases and the capacity of countries to cope with these diseases, and (ii) combine these two measures (impact and capacity) into one overall vulnerability indicator. The adaptive capacity is calculated from estimations of disease mortality, although the method can be adapted for diseases with no or low mortality but high morbidity. As an example, we focused on the vulnerability of Nigeria and Sierra Leone to Lassa Fever and Ebola. We develop a simple analytical form that can be used to estimate vulnerability scores for different spatial units of interest, e.g. countries or regions. We show how some populations can be highly vulnerable despite low impact threats. We finally outline future research to more comprehensively inform vulnerability with the incorporation of relevant factors depicting local heterogeneities (e.g. bio-physical and socio-economic factors).

This article is part of the theme issue ‘Modelling infectious disease outbreaks in humans, animals and plants: epidemic forecasting and control’. This theme issue is linked with the earlier issue ‘Modelling infectious disease outbreaks in humans, animals and plants: approaches and important themes’.

1. Introduction

There is a general consensus that the accelerating changes to Earth’s natural systems pose significant threats to global human health [1,2]. Identifying populations vulnerable to these threats and assessing relevant mitigating strategies are two important priorities for the scientific community, public health practitioners, international organizations such as the World Health Organization (WHO) and relevant national government agencies [3]. Although the term is sometimes used in a loose way, vulnerability is a well-established concept in the field of climate change and disaster risk reduction/management [4–6].

By contrast, integration of vulnerability in the control of infectious diseases is still relatively new, although the literature on the subject is growing, especially owing to the impact of climate change on vector-borne and food-/water-borne infections [7–12]. Here, we focus on vulnerability to infectious diseases only. Specifically, by disease vulnerability we refer to the ability of a community (e.g. a country) to limit the spread of infectious diseases [3]. The definition comprises two important concepts: disease impact and adaptive capacity, i.e. the ability of the community to cope with the disease. Below we will introduce an ‘operational definition’ (i.e. a definition in terms of the procedure to measure the variable of interest) for these concepts, but we can anticipate that vulnerability to infectious diseases is expected to be affected by changes in economic development (e.g. change in healthcare infrastructures [3,13]), shift in socio-cultural practices (e.g. changes in the funeral practices in West Africa following the Ebola epidemics [14,15]), variation in the demographic structure of a population (e.g. increase in the proportion of older people [15]), trade and travel patterns (e.g. incursion of Aedes albopictus in south Europe owing to trade in international tyres and lucky bamboo (Dracaena braunii) [16,17] followed by outbreaks of Chikungunya fever in north-eastern Italy in 2007 [18,19], and autochthonous cases of dengue fever in 2010 in France [20] and Croatia [21], and in Madeira in 2012 [22,23]), and immunization-related phenomena (e.g. increasing anti-vaccine movements [24]), etc.

This is not surprising, considering the impact of socio-economic, environmental and ecological factors on infectious diseases [25].

Ebola and Lassa fever are two illuminating examples of the intricate interactions between disease vulnerability and these broad drivers. Ebola and Lassa fever are zoonotic, viral haemorrhagic fevers endemic in Central and West Africa [26–28].

There are four pathogenic strains of Ebola virus (Zaire, Sudan, Tai Forest and Bundibugyo) causing Ebola virus disease (EVD) with a high case fatality rate in diagnosed patients [29]. Fruit bats have been suggested to be the reservoir of Ebola virus [30]; however, other candidates might play an important role either as a reservoir or amplifying host [28,31]. Socio-economics factors, e.g. bush meat hunting, enhance opportunities for bat-to-human interactions, and therefore spillovers. Behaviour, e.g. family interactions [32], funeral practices [14] and healthcare responses [33], further impact the epidemiology of the disease.

Lassa fever is caused by Lassa fever virus (LASV), an enveloped RNA virus of the Arenaviridae. According to one estimation [34], there are 300 000 cases of the disease each year in West Africa, and some 3000 deaths, although the calculation is highly uncertain. Since the identification of LASV, human-to-human transmission has been documented in several nosocomial outbreaks ([35] and references therein) leading to the initial perception that the virus was both highly contagious and virulent [36]. Soon after, however, its zoonotic origin was recognized and Mastomys natalensis, one of the most common African rodents, was identified as the reservoir of the virus [37]. As the risk of nosocomial transmission was shown to be dramatically reduced by using the simple barrier nursing method ([35] and references therein), the general consensus has shifted towards the idea that the disease is primarily transmitted by the Mastomys natalensis, with human-to-human transmission limited to nosocomial transmission. In the past few years, this narrative started to be challenged, with more evidence of other host reservoirs [38] and further indication that human-to-human transmission might play an important role [35]. This appears to be in contrast with recent studies in Nigeria [39,40], according to which extensive human-to-human transmission does not occur, although occasional, possible cases of human-to-human transmission have been detected. It is important to emphasize that according to [35], most cases have zoonotic origins, interspersed with cases (about 20%, although the estimate is uncertain) ascribable to human-to-human transmission arising from a few super-spreaders [35] (and therefore ladder-like genetic structure of the phylogenetic tree is not expected [39]). Another important aspect to be considered in future studies is the role of asymptomatic cases (in about 80% of cases, symptoms are mild and are undiagnosed [41]); samples from asymptomatic cases are, in general, not included in the viral sequencing and this might affect the conclusions of phylogenetic analysis. The impact of Lassa fever and Ebola as well as communities’ adaptive capacity, and therefore their vulnerability to the diseases, are expected to be affected by a wide range of environmental, biological, ecological, socio-economic and political drivers. Examples of such drivers for impact are demographic pressure, human mobility, the practice of burning fields after harvesting (driving M. natalensis towards villages), interaction with wildlife via bush-meat hunting, seasonal crowding of miners in dwellings etc. Examples of such drivers for adaptive capacity are income, infrastructure such as hospitals and network of family support. Current approaches to the assessment of population vulnerability to infectious diseases suffer from limitations: they tend to be qualitative in nature, they are usually structured in an ad hoc fashion based on a particular threat and their transparency is often challenged when formulated as complex integrated assessment models [42].

Here, we propose to address some of these limitations. We focus on the formulation of a mechanistic model to measure vulnerability; the model is structured such that the complex range of factors depicting local heterogeneities can be incorporated into the model. The model can also be dynamically updated as new information becomes available.

2. Material and methods

(a). Formal definitions

Vulnerability (V) is formally defined as the ratio of impact, I, and adaptive capacity, AC (see [6,43] and references therein), i.e.

$$V=\frac{I}{AC}.$$ 2.1

In our context, we use the expected number of infected cases at time t as the operational definition of impact (representing the burden of zoonotic diseases on a given population) and we use the expected number of recovered cases out of all infected as the operational definition of adaptive capacity (representing the ability of such populations to cope with the impact of such disease). We distinguish two situations: ‘severe cases’ and ‘general cases’. For the former, we do not take into account individuals who naturally recover from the disease as they do not require costly resources such as hospitalization; we also make the underlying assumption that health-seeking behaviour, resulting in hospitalization for which we have data, occurs only in severe cases. Asymptomatic cases, assumed to be undetected, are not taken into account in the definition of vulnerability for severe cases. Individuals who naturally recovered are taken into account in the definition of vulnerability for general cases as the infection status will result in loss of working days, personal cost for medicines etc. Here and throughout the paper, we use the suffix ~^sev and ~^gen to represent these situations.

(b). Epidemiological scenarios

We consider the following epidemiological scenarios. The rationale for this choice was the epidemiological relevance of these scenarios and the natural mathematical progression, by extending the simplest model for pure spillover events to more complex ones (table 1 and electronic supplementary material).

• —Spillover events with no human-to-human transmission and no variation in the number of susceptibles. This scenario exemplifies a situation such as rare infections of pathogens with no or limited human-to-human transmission, e.g. rabies virus infection, in a large pool of susceptibles for which changes in their number are negligible.
• —Spillover events with no human-to-human transmission and depletion of susceptibles. The second scenario is when the pool of susceptibles is limited, and infections from spillover events result in either the death of the hosts or in their immunity. As susceptibles are continuously depleted, the rate of infections is reducing with time and the epidemics are self-correcting [44]. This scenario exemplifies a situation such as a long chain of spillover events in small, isolated communities (e.g. Brucellosis in a community of pastoral herders).
• —Spillover events with human-to-human transmission and depletion of susceptibles. The third scenario is similar to the situation above with additional contribution of human-to-human transmission. If the contribution of human-to-human transmission is small, resulting in a basic reproductive number less than one, the epidemiological scenario is referred to as a stuttering chain. As a human infection triggers other infections, the rate of infections owing to human–human transmission increases with time. In the absence of depletion of susceptibles, the epidemic is self-exciting; otherwise, the two mechanisms, self-exciting and self-correction, coexist [44]. This scenario exemplifies a situation such as Ebola for which human-to-human transmission plays a dominant role, MERS Coronavirus [45], or Lassa fever owing to human-to-human transmissions arising from super-spreading events [35].
• —Multiple (two) diseases. In general, diseases do not occur in isolation and the simultaneous occurrence of multiple epidemics is expected to have a large impact on communities' vulnerability. For instance, when the Kenema government hospital Lassa fever Team mobilized in Sierra Leone to establish Ebola virus surveillance and diagnostic capabilities during the 2013–2016 Ebola outbreak [46], the additional strain on healthcare facilities and resources meant that they were then unable to respond to Lassa. Interactions among infections may also affect the burden of diseases. For example, several studies have indicated an association between HIV infection and other sexually transmitted diseases [47].
• —Extension to larger regions (e.g. country level). The model is formulated at the smallest spatial resolution, which is dictated by ecological and epidemiological factors. For example, for Lassa fever the smallest spatial unit is a region of size comparable to the dispersal range of Mastomys natalensis and where the assumption of uniform mixing (everyone is in contact with each other) is valid. In some instances, it may be more relevant, however, to know the vulnerability of a larger geographical region, region or administrative unit such as a province or a country. The underlying model (based on a Poisson processes) can be readily extended to measure vulnerability at a larger scale (as the sum of two independent Poisson distributed random variables is still a Poisson random variable).

Table 1.

Functional forms of vulnerabilities for a range of epidemiological scenarios. The suffixes ~^sev and ~^gen represent the situations for ‘severe cases’ and ‘general cases’; suffixes ~${\hspace{0.17em}}^{{\mathrm{dis}}_A}$ and ~${\hspace{0.17em}}^{{\mathrm{dis}}_B}$ refer to diseases A and B; (x, y) identify the coordinates of the particular spatial unit; γ is the probability of recovering naturally, γ_H is the probability of recovering following some kind of intervention, x is the proportion of detected cases; ${\lambda }_{\hspace{0.17em}j}^{\mathrm{suffix}}$ is the rate at which infections occur, ${\varphi }_{\hspace{0.17em}j}^{\mathrm{suffix}}$ is the rate at which individuals recover at time t_j during the interval t_j ∈ [(j − 1)τ, jτ], where τ is the chosen time step.

epidemiological scenarios	vulnerability
pure spillover events (no human to human transmission)	$V^{\mathrm{gen}}=\frac{1}{(1-x)\gamma +x{\gamma }_H}$
	$V^{\mathrm{sev}}=\frac{1}{{\gamma }_H}$
pure spillover events (no human to human transmission) during a time T with change in the number of susceptibles	$V^{\mathrm{gen}}=\frac{1}{(1-x)\gamma +x{\gamma }_H}$
	$V^{\mathrm{sev}}=\frac{1}{{\gamma }_H}$
spillover events and human to human transmission during a time T	$V^{\mathrm{gen}}=\frac{1}{(1-x)\gamma +x{\gamma }_H}$
	$V^{\mathrm{sev}}=\frac{1}{{\gamma }_H}$
multiple (two) diseases	$V^{\mathrm{gen}}=\frac{\sum {\lambda }_{\hspace{0.17em}j}^{{\mathrm{dis}}_A}+\sum {\lambda }_{\hspace{0.17em}j}^{{\mathrm{dis}}_B}}{[(1-x^{{\mathrm{dis}}_A}){\gamma }^{{\mathrm{dis}}_A}+x^{{\mathrm{dis}}_A}{\gamma }_H^{{\mathrm{dis}}_A}]\sum {\lambda }_{\hspace{0.17em}j}^{{\mathrm{dis}}_A}+[(1-x^{{\mathrm{dis}}_B}){\gamma }^{{\mathrm{dis}}_B}+x^{{\mathrm{dis}}_B}{\gamma }_H^{{\mathrm{dis}}_B}]\sum {\lambda }_{\hspace{0.17em}j}^{{\mathrm{dis}}_B}}$
	$V^{\mathrm{sev}}=\frac{x^{{\mathrm{dis}}_A}\sum {\lambda }_{\hspace{0.17em}j}^{{\mathrm{dis}}_A}+x^{{\mathrm{dis}}_B}\sum {\lambda }_{\hspace{0.17em}j}^{{\mathrm{dis}}_B}}{[x^{{\mathrm{dis}}_A}{\gamma }_H^{{\mathrm{dis}}_A}]\sum {\lambda }_{\hspace{0.17em}j}^{{\mathrm{dis}}_A}+[x^{{\mathrm{dis}}_B}{\gamma }_H^{{\mathrm{dis}}_B}]\sum {\lambda }_{\hspace{0.17em}j}^{{\mathrm{dis}}_B}}$
extension to larger regions (e.g. country level)	$V^{\mathrm{gen}}=\frac{\mathit{\Lambda }}{{\mathit{\Phi }}^{\mathrm{gen}}}$
	$V^{\mathrm{sev}}=\frac{\mathit{\Lambda }}{{\mathit{\Phi }}^{\mathrm{sev}}}$
	$\mathit{\Lambda }=\sum {\lambda }_{\hspace{0.17em}j}(x,y)$ ; ${\mathit{\Phi }}^{\mathrm{gen}}=\sum {\varphi }_{\hspace{0.17em}j}^{\mathrm{gen}}(x,y)$; ${\mathit{\Phi }}^{\mathrm{sev}}=\sum {\varphi }_{\hspace{0.17em}j}^{\mathrm{sev}}(x,y)$. ${\mathit{\Phi }}^{\mathrm{gen}}=\sum {\varphi }_{\hspace{0.17em}j}^{\mathrm{gen}}(x,y)$

(c). Modelling approach

Based on this definition (2.1) and building on a mathematical model for spillover events (as Poisson processes) and stuttering chain (as Hawkes processes) [44], we derived analytical expressions for vulnerability for the epidemiological scenarios as described above. Below we show the mathematical derivation for the simple case of vulnerability to diseases with no human-to-human transmission. Mathematical derivations of the more complex situations follow similar steps and are presented in the electronic supplementary material. Following [44], spillover events can be treated as a Poisson process, and complex drivers are incorporated in the functional form of the rate, λ, of the Poisson process. More precisely, in the simplest scenario the human population is uniformly subjected to random and independent (direct or mediated) contacts with the animal reservoir. Only a fraction of these contacts, equal to the infection prevalence of the reservoir, are a potential source of infection. We also distinguish the detected infections from the undetected ones. Accordingly, we assume:

$$\begin{array}{rl}\lambda & =x{N}_{\mathrm{H}}{\eta }_{\mathrm{R}}(N_{\mathrm{R}}){\mathrm{Pr}}_{\mathrm{R}}(N_{\mathrm{R}}){\chi }_{\mathrm{R}}+(1-x)N_{\mathrm{H}}{\eta }_{\mathrm{R}}(N_{\mathrm{R}}){\mathrm{Pr}}_{\mathrm{R}}(N_{\mathrm{R}}){\chi }_{\mathrm{R}}\\ & =N_{\mathrm{H}}{\eta }_{\mathrm{R}}(N_{\mathrm{R}}){\mathrm{Pr}}_{\mathrm{R}}(N_{\mathrm{R}}){\chi }_{\mathrm{R}},\end{array}$$ 2.2

where x is the proportion of detected cases; N_H is the human population size of the geographical unit of interest, e.g. total number of people in a village; η_R(N_R) is a measure of exposure; Pr_R(N_R) is the prevalence of the infected reservoir; both exposure and prevalence are expected to depend on the reservoir population size N_R; χ_R is a parameter combining two complex mechanisms: the ability of the reservoir to excrete a suitable dosage of the agent/pathogen/hazard and the human response to it. We refer to this parameter as infection-response efficiency. We assume that all detected cases result in some intervention. Similarly, we assume that the probability of a person recovering, i.e. the adaptive capacity AC, is given by a Poisson process with rate ϕ^sev or ϕ^gen depending on whether we are considering the situation for severe cases or general cases. Namely:

Adaptive capacity for severe cases. In this case, the rate ϕ^sev(t) of the Poisson process is given by

$${\varphi }^{\mathrm{sev}}=x\lambda {\gamma }_{\mathrm{H}},$$ 2.3

where γ_H is the probability that an infected person seeking intervention (and therefore drawn from the expected number of detected, spillover cases xλ) recovers following some kind of intervention, e.g. treatment, hospitalization, other forms of healthcare aid. Accordingly, the quantity xλγ_H represents the expected number of recovered cases (as a proportion of detected, spillover cases xλ) per time unit.

Adaptive capacity for general cases. In this case, the rate ϕ^gen(t) of the Poisson process is given by

$${\varphi }^{\mathrm{gen}}=(1-x)\lambda \gamma +x\lambda {\gamma }_{\mathrm{H}},$$ 2.4

where γ is the probability that a person naturally recovers without intervention. For the severe cases scenario, the impact I is represented by the fraction of detected infected cases xλ and the vulnerability is

$$V^{\mathrm{sev}}=\frac{I}{AC}=\frac{x\lambda }{{\varphi }^{\mathrm{sev}}}=\frac{1}{{\gamma }_{\mathrm{H}}}.$$ 2.5

In the general cases scenario, the impact I is represented by the total number of infected cases λ and the vulnerability is

$$V^{\mathrm{gen}}=\frac{I}{AC}=\frac{\lambda }{\varphi }=\frac{1}{(1-x)\gamma +x{\gamma }_{\mathrm{H}}}.$$ 2.6

Thus, the method requires estimates of (i) the probability of recovering following intervention, γ_H; (ii) the probability of recovering naturally γ; and (iii) the probability of detection, x. For a disease with high mortality, the probability of recovering owing to intervention can be inferred as

$${\gamma }_{\mathrm{H}}=\frac{D-F}{D},$$ 2.7

where D is the cumulative number of cases detected during a certain time T and F is the cumulative number of fatal cases out of those detected during the time T. Here, we consider any non-fatal cases as recovered, hence D − F represents the number of recovered cases at time T and γ_H is the proportion of recovered cases, out of all detected cases, at time T. The method could be adapted to diseases with low or no mortality but high morbidity, for instance by estimating the probability of recovering owing to intervention as γ_H = S_treat/D, where S_treat is the cumulative number of cases during a time T resulting in a successful medical treatment. Confidence intervals around vulnerability measures were calculated based on a Poisson log-linear model for the ratio of two independent Poisson rates [48]. The probability of natural recovery could be obtained from survival/mortality data if information on the undetected, including asymptomatic, cases is available (see [41]). The probability of detection, x, can be inferred from the literature, surveillance data or other modelling exercises.

Alternatively, the relevant parameters, for example, the probability of recovering following intervention γ_H, could be further modelled using other proxies such as number of hospital beds, income, etc.

(d). Case studies and data

We studied the vulnerability of Sierra Leone to Ebola, and the vulnerability of Sierra Leone and Nigeria to Lassa fever. We used data (number of laboratory-confirmed cases and number of deaths) from the 2013–2016 Ebola epidemics in Sierra Leone, the Lassa fever epidemic in Sierra Leone during 2008–2012 and from the 2017–2018 Lassa fever epidemic in Nigeria. Data were extracted from publicly available repositories [49–51] and from Kenema Government hospital in Sierra Leone (available from [35]).

3. Results

(a). Some simple expressions for vulnerability

Table 1 shows the analytical expressions of vulnerability for the general and severe situations for some key epidemiological scenarios. Accordingly, we showed that vulnerability can be simply estimated as the inverse of the probability of recovering. For the severe situation, this simply reduces to one parameter, γ_H, representing the probability of recovering following intervention. For the general situation, the probability of recovering is a linear (additive) combination of the fraction of detected cases × the probability of recovering following intervention and the fraction of undetected cases × the probability of natural recovery, γ. The functional form of vulnerability is not dependent on the number of diseased cases; this is strictly valid when the system under consideration (e.g. a country) is able to cope with any magnitude of disease burden and the probability of recovering is not affected by the number of diseased cases. When the number of diseased cases overcomes a certain threshold, there will no longer be beds in hospital and/or medical personnel available. In this case, the functional form of vulnerability would still scale as the inverse of the probability of recovering, but this would be a function of the number of diseased cases, i.e. γ_H → γ_H(λ), rather than a simple constant.

In the co-presence of multiple diseases, the analytical expression for vulnerability becomes a function incorporating (i) the sum of the two disease cases, (ii) the probabilities of recovering and (iii) the fraction of detection for the different diseases. In this situation, the functional form of vulnerability depends on the number of cases of the two specific diseases, with relevant parameters (e.g. proportion of detection and probability of recovering for the two diseases) being weighted by factors representing the relative burden of disease A and disease B (electronic supplementary material). This reflects the fact that the diseases can have a differential effect on impact and adaptive capacity (for instance, when a country can cope better with one disease rather than the other). As above, in a more general situation, the probability of recovering should be substituted with the adequate function of the number of cases for both diseases.

Extension of the model at larger spatial resolution also leads to a transparent expression for vulnerability, which is simply the ratio of the overall impact (i.e. the sum of the impacts for each spatial unit) and overall adaptive capacity (i.e. the sum of the adaptive capacity for each spatial unit).

Finally, it is important to emphasize that the terms in the rate λ (e.g. the reservoir population size N_R and the prevalence of the infected reservoir Pr_R(N_R)) can be seasonal (leading to an in-homogeneous Poisson process) and stochastic (leading to Cox processes, and if the rate λ is a gamma-distributed variable, the Cox process is described by a negative binomial distribution [44]). Similar consideration can be applied to the adaptive capacity and in turn to the vulnerability, i.e. estimations of vulnerability are expected to be seasonal and stochastic.

(b). Vulnerability to Lassa fever and Ebola in Nigeria and Sierra Leone

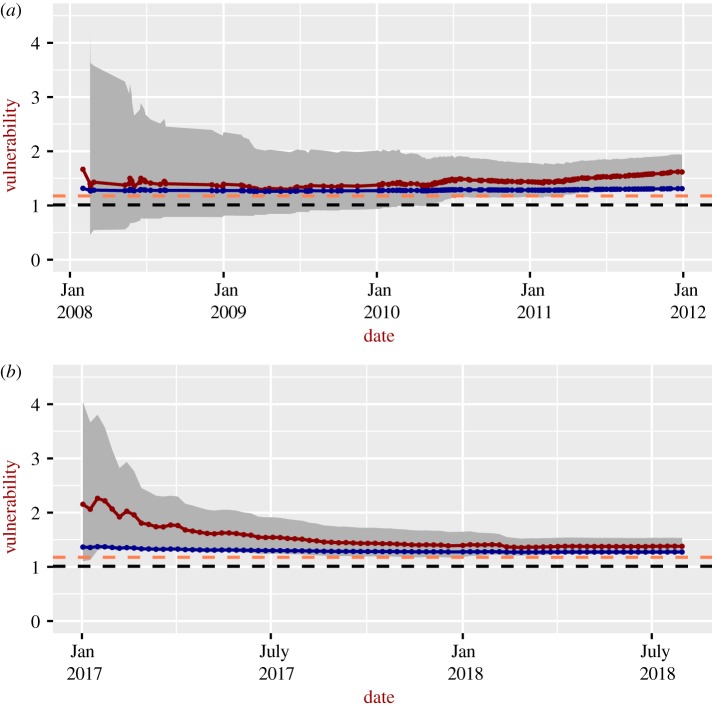
Figure 1 shows the vulnerability to Lassa Fever during the 2017–2018 epidemic in Nigeria (figure 1b), and for 2008–2012 in Sierra Leone (figure 1a). Estimations for both the general and severe situations are presented. For Nigeria, vulnerability decreases with time, reaching the asymptotic values between 1.25 and 1.50 (severe situation) and between 1.25 and 1.30 (general situation). Note that according to our definition, a vulnerability equal to 1 means that all infected cases recover. In Sierra Leone, vulnerabilities increase with time after 2010 and tend to be slightly higher than the corresponding values for Nigeria. The vulnerabilities for the general situation tend to be lower than those for the severe situation. The vulnerability to Lassa fever in Nigeria shows a marked decrease during the time of the epidemics compared with the vulnerability for Sierra Leone (1). The decreasing trend in Nigeria is largely driven by the fact that the number of fatal cases decreases with time, although the number of detected cases also increases. The reasons are not entirely clear, but we suspect that this is owing to the fact that Lassa fever in Sierra Leone might not prompt any exceptional response (being hyperendemic in that area), while in Nigeria the outbreak triggered a stronger response, especially following the 2013–2016 Ebola outbreak. The uncertainty decreases with time, reflecting the increasing number of detected cases and of fatal cases out of the detected ones, which reduces the uncertainty in the estimation.

Figure 1.

Time-dependent vulnerability to Lassa fever for Sierra Leone (a) and Nigeria (b) during recorded epidemics. Continuous dark red lines: severe situations; grey areas: 95% confidence intervals for the severe situations; continuous blue lines: general situation; orange dashed-lines: overall, crude estimates of vulnerability for severe situation based on an observed case-fatality rate of 15% among patients hospitalized with severe cases of Lassa fever [41], i.e. V = 100/(100 − 15); black dashed-lines: overall, crude estimate of vulnerability for general situation based on an overall case-fatality rate of 1% [41], i.e. V = 100/99. Data from the first month were removed to avoid potential death cases associated with infections occurred the month before and not detected.

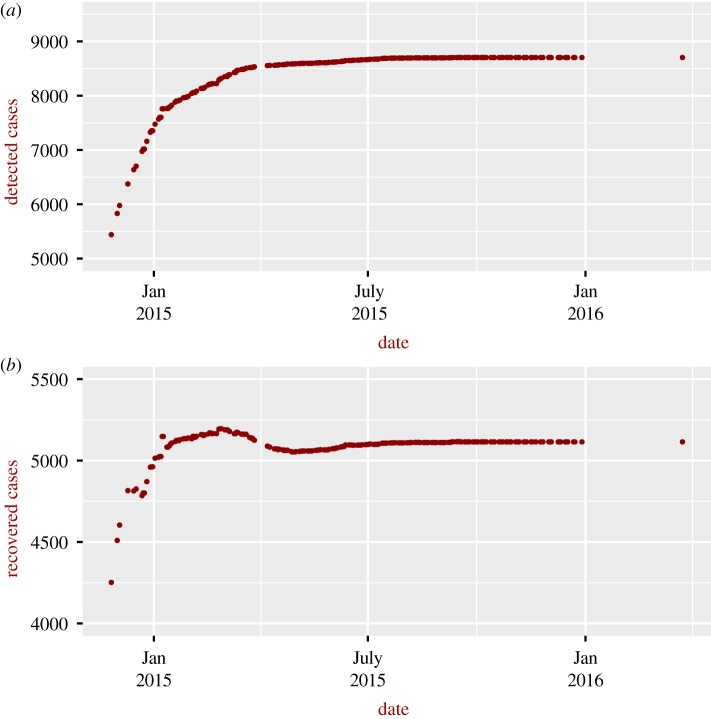
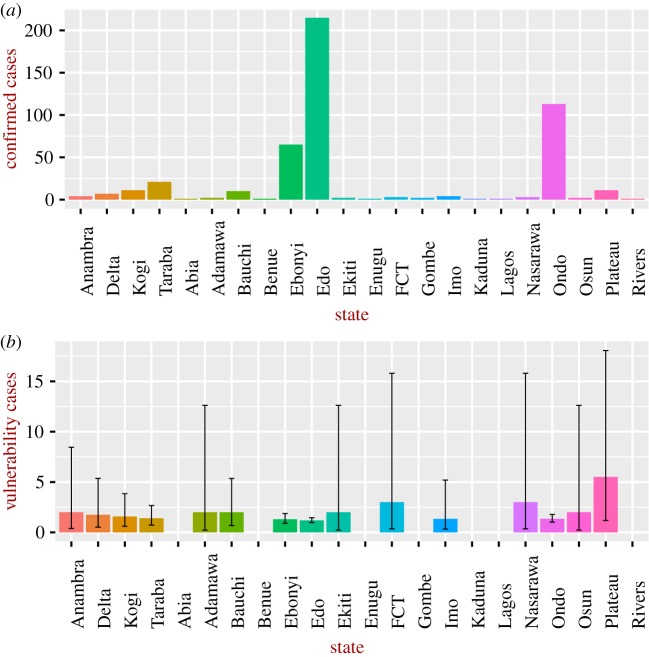
For Ebola in Sierra Leone (figure 2), we consider only the severe situation, as no information on detection and the probability of natural recovery was available to the authors (vulnerability for the general case can be readily estimated as soon as these data become available). Vulnerability increased sharply during the 2015–2016 epidemic, reaching a higher value than that estimated for Lassa fever. To understand these patterns, it is instructive to look at the number of detected and recovered cases; as can be seen in figure 3, the number of recovered cases was, in general, higher in January–March 2015 compared to the value after July 2015, explaining the larger vulnerability after July 2015. The reasons for the larger number of recovered cases in January–March 2015 are not clear. Figure 4 shows the vulnerability of the different Nigerian administrative states to the Lassa epidemic in 2017–2018; the figure also shows the burden of disease. The most vulnerable states are not necessarily those with higher impact, for instance the state of Plateau is the most vulnerable despite the relatively low burden of disease.

Figure 2.

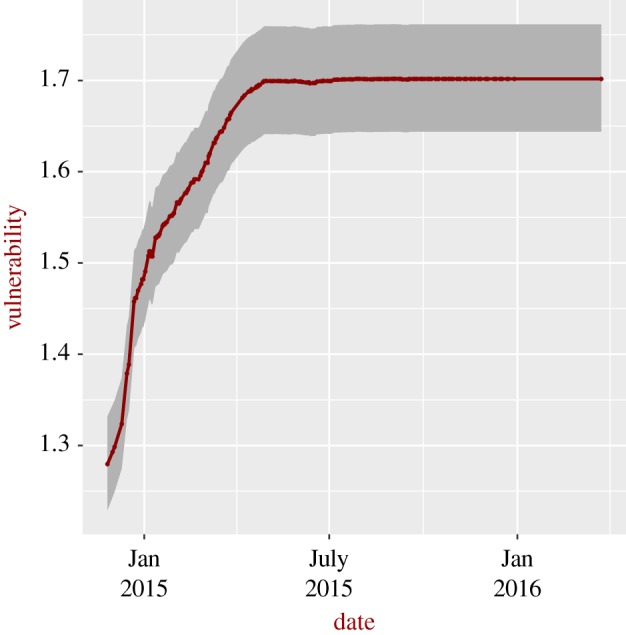
Time-dependent vulnerability to Ebola for Sierra Leone during recorded epidemics. Continuous dark red line: severe situations; grey area: 95% confidence interval for the severe situations. Data from the first month were removed to avoid potential death cases associated with infections that occurred the month before and were not detected.

Figure 3.

Cumulative number of (a) detected and (b) recovered Ebola cases in Sierra Leone. Data from the first month were removed to avoid potential death cases associated with infections that occurred the month before and were not detected.

Figure 4.

(a) Number of confirmed cases and (b) vulnerability for Lassa fever for different states in Nigeria based on cases up to 22 April 2018. For some states (Abia, Benue, Enugu, Gombe, Kaduna, Lagos) the vulnerability was undefined (as adaptive capacity was zero) and therefore not included in the analysis. The vertical lines represent the 95% confidence intervals. FCT, Federal Capital Territory. (Online version in colour.)

4. Discussion

Vulnerability is a complex concept and estimating its value is a highly dimensional problem largely affected by a diverse range of cultural/anthropological, environmental, political and socio-economic drivers [52,53]. Examples of these factors are perception of the disease, urbanization, deforestation, infrastructures and service disruption, new technologies, climate, weather, land use, resources to implement necessary programmes, etc. This poses enormous challenges to measure and predict vulnerability and to its understanding.

To overcome this problem, we propose to focus on established definitions of impact, adaptive capacity and therefore vulnerability. Accordingly, the impact was measured as the number of infected cases and adaptive capacity as the number of recovered out of the diseased cases. An important advantage of this approach is the simplicity of the functional forms of vulnerability, especially when only one disease is considered. Another important benefit is that the expressions for vulnerabilities, for both general and severe situations, are identical for several different scenarios, e.g. pure spillover and spillover with human-to-human transmission. It is important to recognize, however, that the formulation of the model, and thus the specific functional form of vulnerability, depends on the epidemiological scenario and specific problem that we want to address. Guidance from other approaches such as expert opinion [6,10] and participatory research [54,55] would be highly beneficial in identifying the scenario of interest and critically scrutinizing the analytical expression for vulnerability.

The analytical expressions for vulnerabilities for the relevant scenarios are the key result from this work. We applied our analytical framework on Lassa fever and Ebola. Because direct evidence on key parameters was not available, we inferred them from data. As an illustrative example, the probability of recovering following intervention γ_H was crudely estimated from the cumulative number of detected and fatality cases. We would recommend, however, more detailed analyses [56] to estimate the probabilities of recovering.

Our approach can produce a time-dependent estimation of vulnerability as the epidemics progress (as shown in figures 1 and 2). An important difference between vulnerability to Lassa fever and Ebola is the observed temporal trend of the estimations. In contrast with that to Lassa fever, vulnerability to Ebola increases sharply as the epidemics progress, followed by a plateau. It is also important to note that the accuracy of estimates of vulnerability is expected to increase towards the end of the epidemics, as the estimation of the probability of recovering following intervention is more robust owing to the larger samples.

(a). Future development

Future development will extend our simple models to incorporate relevant factors describing local heterogeneities to identify potential associations with the estimated vulnerability. For instance, the probability of recovery from diseases owing to intervention could be linked with indicators such as proximity to healthcare facilities, number of hospital beds and others. In turn, these factors could be associated with more general socio-economic factors such as literacy rate, poverty rate, government expenditure on health and so on. Identifying the relevant indicators and factors potentially affecting vulnerability is not a trivial task, especially as these factors are often correlated ([57] and references therein). Nevertheless, the formal incorporation of these local heterogeneities in our analytical framework would allow prioritization of vulnerability predictors and support targeted investments. Institutions like the WHO require impartial measures to assess the vulnerabilities of countries to diseases to support strategic decision making and allocate resources. As we showed, there are potential situations with high vulnerability but low impact (e.g. compare the Nigerian states of Edo and Plateau). Instead, we envisage the need for an exhaustive framework that takes into account both impact and vulnerability (despite vulnerability being a function of impact). Here, we used Lassa fever and Ebola as examples, but the generality of the approach clearly allows application to other pathogens of humans, animals and plants. In order to produce robust estimates of vulnerability, the method requires complete datasets of disease cases and mortality, ideally at high spatio-temporal resolution, which is a prevailing problem for many neglected diseases and a challenge for emerging ones. To identify the drivers of vulnerability, the method also requires linkage, at high spatio-temporal resolution, between estimates of vulnerability at certain times and locations, with potential predictors (e.g. environmental variables) that are not commonly available [57,58]. Sensitivity and resilience are two additional important concepts related to vulnerability, which also suffer from ambiguous definitions. Vulnerability can be formally and rigorously linked to sensitivity by studying the dependence of vulnerability on relevant parameters (climate, hospital facilities, poverty, literacy rate etc.) and exploring how variations in these parameters differentially impact vulnerability. Low vulnerability can be achieved by the system’s ability to adapt to new threats; however, this does not imply that the system remains unchanged. An additional important tool is a measure of the ability of the system to return to the same conditions before a perturbation, such as an epidemic (resilience) [5], and how quickly the recovery process happens. Stability analysis is an example of a theoretical approach that can be used to assess resilience, as recently done in [59] where we identified the environmental conditions leading either to stable oscillation in the mosquito population and prevalence of Rift Valley Fever, i.e. the eco-system is resilient to control measures (note that in this context the term ‘resilience’ has a negative meaning from a public health perspective), or to the extinction of the mosquitoes/infection. Understanding and assessing health threats in the Anthropocene epoch requires an integration of theoretical tools; vulnerability and resilience are promising examples of such tools.

Data accessibility

Data are available from publicly available repositories [49–51] and from Kenema Government hospital in Sierra Leone (available from [35]).

Authors' contributions

G.L.I. and V.d.R.V. designed the study; G.L.I. formulated the model; G.L.I. and O.K. performed the analysis; G.L.I., V.d.R.V., O.K. and J.L.N.W. wrote the paper.

Competing interests

The authors declare no competing interests.

Funding

Funding for this work was provided by FRSF Pump Prime Grant: New methodologies towards the assessment of countries’ vulnerabilities to diseases, Project AC0587.