Abstract
The cationic Ru–H complex was found to be an effective catalyst for the dehydrative C–H coupling of phenols with ketones to form the trisubstituted olefin products. The coupling of phenol with linear ketones led to highly stereoselective formation of the (Z)-olefin products. The dehydrative coupling of phenol with enones and diones efficiently formed the benzopyrene and related oxacyclic derivatives. The reaction of 3,5-dimethoxyphenol with cyclohexanone-2,2,6,6-d4 showed a significant H/D exchange to both vinyl and α-CH2 positions on the olefin product (72–75% D). A significant carbon isotope effect was observed on the ortho-arene carbon of the olefin product. The free energies of intermediate species for the entire catalytic cycle were successfully computed by using the DFT method. The DFT study revealed that the E/Z stereoselectivity is a result of the energy difference in the insertion step of ortho-metalated phenol to an enol form of the ketone substrate (ΔΔE = 9.6 kcal/mol). The coupling method provides a direct catalytic C–H olefination method for ketones to form trisubstituted olefins without employing any reactive reagents or forming any wasteful byproducts.
Graphical Abstract
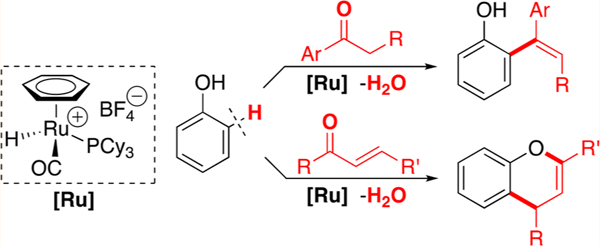
INTRODUCTION
Carbonyl olefination methods have long been considered as one of the most versatile C–C coupling protocols for the synthesis of complex organic molecules.1 Traditionally, phosphorus ylide and related main group reagents have been widely used for the Wittig type of coupling reactions, but early transition metal reagents were also employed for McMurry2 and Tebbe-Petasis3 olefination reactions. Peterson olefination and related nucleophilic addition–elimination methods for aldehydes and ketones have also been successfully developed to form substituted olefins.1b,4 From the viewpoint of sustainable synthesis, these classical carbonyl olefination methods pose inherent drawbacks in that the usage of a stoichiometric amount of ylide or transition metal reagents results in the formation of a copious amount of toxic and wasteful byproducts. To overcome shortcomings associated with classical olefination methods, a concerted research effort in recent decades has been devoted to the development of strategies for catalytic carbonyl olefination. In a seminal work, Pd-catalyzed Negishi couplings of carbonyl derivatives with organozinc reagents have been extensively used for the synthesis of highly functionalized olefins and related molecules.5 More recently, the Schindler group devised a remarkably effective intramolecular carbonyl-to-olefin metathesis reaction by using FeCl3 as a catalyst.6 Milstein and co-workers utilized pincer-ligated Ru catalysts to promote a selective carbonyl olefination via the coupling of alcohols with alkylsulfonates.7 Zhou and co-workers cleverly designed a Nicatalyzed olefination method from the coupling of arylketones with organoboron reagents.8 Li recently reported a Rucatalyzed carbonyl olefination method via hydrazine promoted reductive coupling of carbonyl compounds.9 Despite such remarkable advances in designing catalytic olefination methods, these coupling methods still require reactive boron and sulfur reagents, which lead to the formation of salt byproducts. Additionally, they exhibit tendencies of undergoing undesired side reactions such as dehydrogenation and aldol-type condensation reactions. Catalytic C–H coupling methods have emerged as a step-efficient and direct olefination protocol for arenes,10 although their synthetic utility has yet to be fully exploited in carbonyl olefination reactions.
One of the pertinent issues in carbonyl olefination methods has been concerned with controlling the stereochemistry of olefin products. In particular, designing (Z)-selective olefination methods has been considered the most challenging, since classical olefination methods generally favor the formation of (E)-olefins. In this regard, Peterson4 and Horner–Wadsworth–Emmons11 olefination methods have been extensively used for the synthesis of (Z)-olefin products, but the major issues on employing stoichiometric reagents and the formation of toxic byproducts have not been resolved for these methods. In terms of catalytic olefination methods, both Grubbs and Schrock-type metal-carbene catalysts have been successfully designed and utilized for a ring-closing metathesis reaction in forming biologically active (Z)-selective macrocyclic olefin products.12 Pd-catalyzed Negishi-type coupling methods have also been successfully employed for the synthesis of (Z)-selective trisubstituted olefins.5a
We previously discovered that the cationic ruthenium hydride complex [(C6H6)(PCy3)(CO)RuH]+BF4− (1) is a highly effective catalyst precursor for a number of dehydrative C–H coupling reactions of alkenes and arenes with alcohols.13 Since these coupling reactions are driven by the formation of water, we reasoned that the analogous dehydrative C–H coupling reactions with carbonyl compounds might be feasible in achieving carbonyl olefination reactions. Herein, we report the scope and mechanistic study of ruthenium-catalyzed dehydrative coupling reaction of phenols with ketones, which leads to a highly (Z)-selective synthesis of trisubstituted olefin products. We combined experimental and computational analyses to establish a detailed mechanism as well as to elucidate the origin of stereoselectivity for the olefination reaction. The catalytic method features a direct catalytic C–H olefination method of ketones with phenols without employing any reactive reagents or forming any wasteful byproducts, while tolerating a number of common organic functional groups.
RESULTS AND DISCUSSION
Reaction Scope.
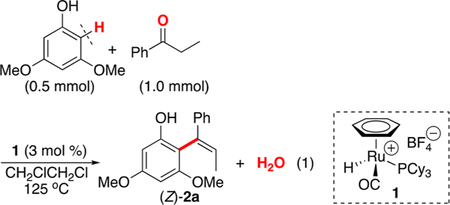
In an effort to extend the scope of dehydrative C–H coupling method of arenes,13 we initially probed the feasibility of the coupling reaction of phenols with simple ketones by using the Ru–H catalyst. Thus, the treatment of 3,5-dimethoxyphenol (0.5 mmol) with propiophenone (1.0 mmol) in the presence of 1 (3 mol %) in 1,2-dichloroethane (2 mL) led to the formation of the alkenylated product (Z)-2a (eq 1). Among the screened catalysts, the Ru–H complex 1 exhibited distinctively high activity in forming the coupling product, as analyzed by both GC and NMR spectroscopic methods (Table S1, Supporting Information (SI)). Moreover, a highly stereoselective formation of (Z)-2a was observed, and its structure was unambiguously established by NMR spectroscopy (vide infra).
The substrate scope of the olefination reaction was explored using the catalyst 1, as summarized in Table 1. An electron-rich 3,5-dimethoxyphenol was found to be a suitable substrate for the coupling with aryl-substituted linear ketones to form ortho-alkenylated phenol products 2a–2n (entries 1–14). For these aryl-substituted ketones, highly (Z)-selective olefin products 2a–2i were formed in the crude mixture, as analyzed by GC-MS (entries 1–9). In contrast, the coupling with aliphatic linear ketones resulted in a mixture of (E)/(Z)-olefins, with the (Z)-isomer being the major products for 2k–2n (entries 11–14). The analogous treatment of 3,5-dimethoxyphenol with cyclic ketones led to the clean formation of 2q–2s (entries 17–19), while the coupling with 2-indanone yielded the indenyl-substituted product 2t (entry 20). The coupling of 1-naphthol with linear and cyclic ketones led to the formation of the coupling products 2o and 2v, respectively (entries 15 and 22). The coupling reaction of phenols with an electron-withdrawing group was quite sluggish leading to low olefin product yields.
Table 1.
Dehydrative C–H Olefination of Phenols with Ketonesa
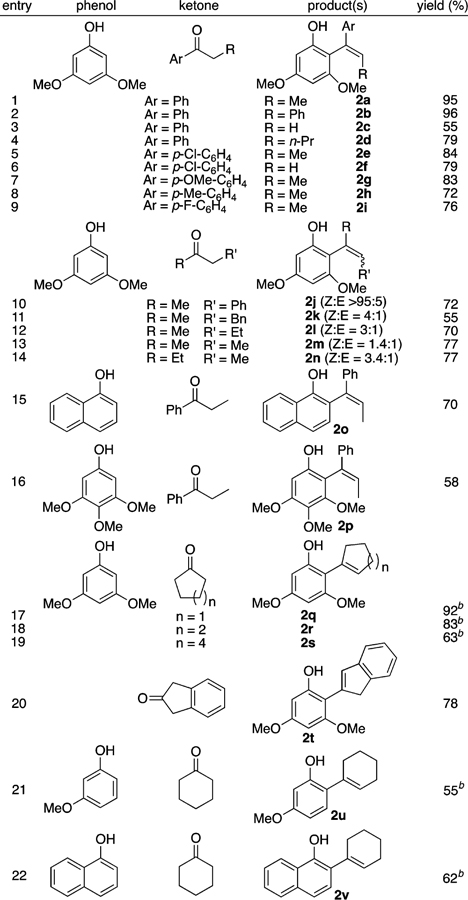 |
Reaction conditions: phenol (0.5 mmol), ketone (1.0 mmol), 1,2-dichloroethane (2 mL), 1 (3 mol %), 125 °C, 16 h.
1.5 mmol of ketone was used.
To further demonstrate its synthetic utility, we next surveyed the substrate scope of the catalytic carbonyl olefination method by employing a number of biologically active ketone substrates (Table 2). Thus, the coupling of 3,5-dimethoxyphenol with 4-hydroxycoumarin yielded the coupling product 2w, while the reaction with (+)-nootkatone led to the alkenylated product 2x in a single step. Treatment with an anti-inflammatory agent nabumetone also readily afforded a 5:1 Z/E mixture of alkenylated product 2y. Treatment with (+)-4-cholesten-3-one and adrenosterone predictively yielded the corresponding diene products 2z and 2aa, respectively.
Table 2.
Dehydrative Coupling of 3,5-Dimethoxyphenol with Functionalized Ketonesa
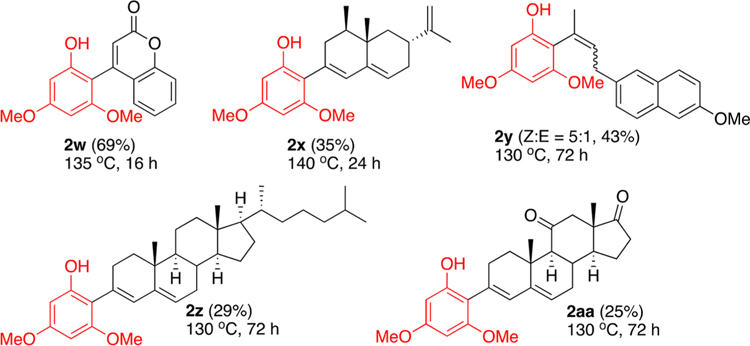 |
Reaction conditions: phenol (0.5 mmol), ketone (1.0 mmol), 1,2-dichloroethane (2 mL), 1 (3 mol %).
The (Z)-stereochemistry of these olefin products was established by NMR spectroscopic methods. One of the most diagnostic features of the (Z)-olefin products is that allylic CH2 protons of (Z)-2 exhibited an ABX type of second-order pattern in the 1H NMR spectrum due to a diastereotopic environment resulted from restricted rotation of the phenol group. In contrast, allylic CH2 protons of (E)-2 showed a simple first-order pattern. The stereochemistry of (Z)-2a was also definitively established by X-ray crystallography (Figure S3, SI). From both synthetic and environmental points of view, the salient features of the catalytic method are that it facilitates a direct C–H coupling of readily available phenol and ketone substrates in a highly regio- and stereoselective fashion and that it forms synthetically valuable trisubstituted olefin products 2 without using any reactive reagents or forming wasteful byproducts.
Computational Study.
Inspired by related ruthenium-catalyzed dehydrative C–H coupling reactions, we initially compiled a plausible mechanistic pathway for the olefination reaction, which involves an initial ortho-C–H metalation of phenol, migratory insertion of the ketone substrate, and the subsequent dehydration and elimination steps (Scheme 1).13a However, despite our best efforts, we have not been able to detect or trap any catalytically relevant intermediate species, which made it difficult to establish a detailed mechanism of the coupling reaction experimentally. Thus, to attain deeper insights into the reaction mechanism and to elucidate the origin of (E)/(Z) selectivity, we turned to the DFT calculations. We have successfully computed the entire catalytic cycle for the coupling reaction of 3,5-dimethoxyphenol with 1,2-diphenylethanone substrates, and the free energy profile diagram has been constructed, as shown in Figure 1. The catalytic cycle begins with the Ru–H complex 1 forming a loosely bound transient adduct 4 with the phenol substrate, which can readily extrude the originally η6-bound benzene ligand and proceed with the ortho-C–H metalation mediated by the phenolic OH directing group. The ortho-metalation step is associated with a barrier of 23.7 kcal/mol to generate the key intermediate complex 5, which is only 5.1 kcal/mol uphill energetically, driven by the release of hydrogen gas (Figure S5, SI). As supporting experimental evidence for the benzene ligand dissociation, we previously observed a facile arene exchange reaction and the formation of free benzene from the coupling reactions mediated by the Ru–H catalyst 1.14
Scheme 1.
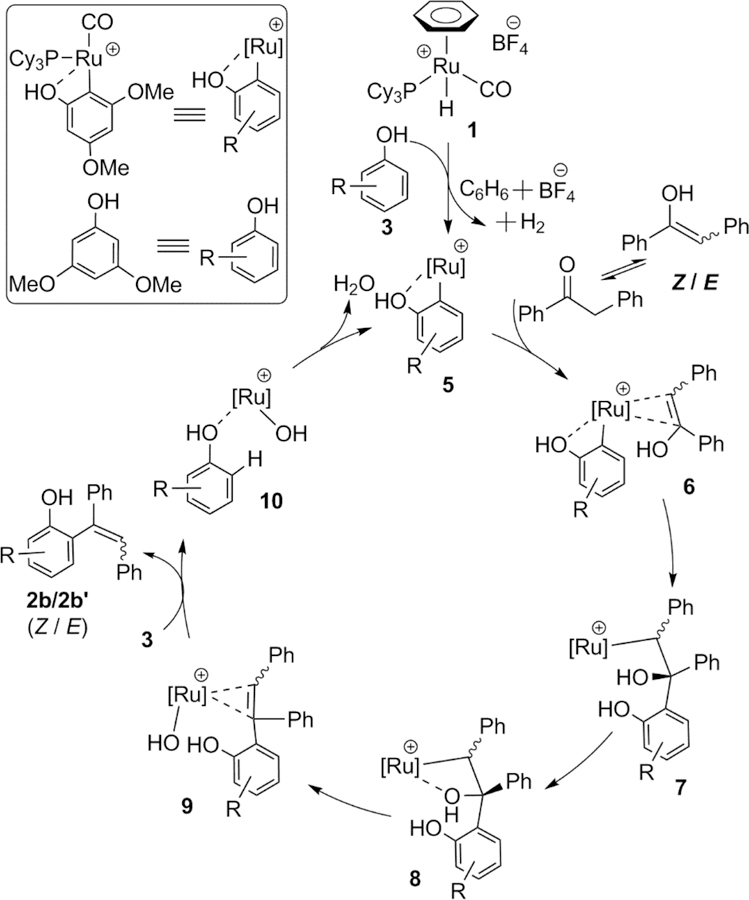
Proposed Catalytic Cycle for the Coupling of 3,5-Dimethoxyphenol with 1,2-Diphenylethanone
Figure 1.
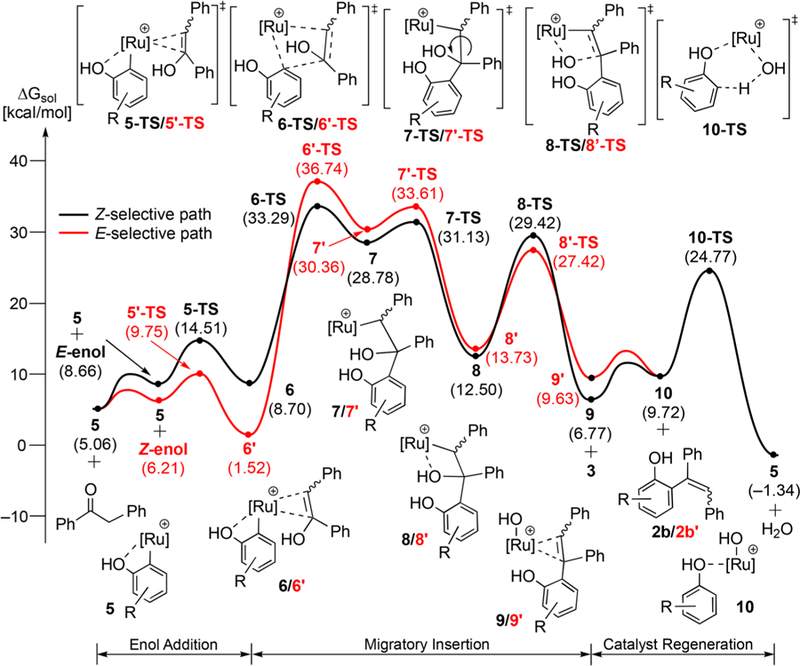
Free energy profile for the formation of (E)-2b′ (red) and (Z)-2b (black) with water as the byproduct.
The intermediate 5 initiates the catalytic cycle by binding (E)- and (Z)-enol form of the ketone substrate to form the adducts 6 and 6′, respectively. Interestingly, the adduct 6′ made by coordinating the (Z)-enol substrate is lower in energy by ~7 kcal/mol than the analogue formed from (E)-enol substrate 6. Subsequent migratory insertion affords intermediate 7′ and 7 traversing via the transition state 6′-TS and 6-TS, where the relative energy between two stereoisomers is inverted during the migratory insertion step. At the transition state, the 6-TS formed from the (E)-enol substrate is nearly 3.5 kcal/mol lower in energy than 6′-TS, which contains the (Z)-enol substrate. This energy difference is notably diminished to ~1.5 kcal/mol, but the relative ordering is maintained in the transient, high-energy intermediate 7 and 7′. Rotation around the C–C bond leads to the much more stable intermediates 8 and 8′, where the alkoxide group is appropriately positioned to act as a Lewis base and coordinated to the metal. The two diastereoisomers are predicted to be nearly isoenergetic at this intermediate state. To push the reaction forward, the hydroxyl group originating from the enol substrate must be eliminated via a dehydration step, as mentioned above. We explored several possible ways of accomplishing this task and found that the heterolytic cleavage of the C–OH bond accompanied by hydroxyl transfer to the Ru-center and reconstitution of the olefinic double bond of the substrate is energetically the most favorable pathway to give complex 9 and 9′. Release of the product 2b or 2b′ and addition of a new equivalent of phenol gives the ruthenahydroxyl-complex 10, which can restart the catalytic cycle by activating the phenolic ortho-C–H bond and extruding an equivalent of water to generate intermediate 5.
To understand the stereoselectivity described above, we performed a detailed fragment energy analysis on the migratory insertion step for both stereoisomers. In this analysis, we first fragment the intermediates 6/6′ and the transition states 6-TS/6′-TS into chemically meaningful fragments, namely, the olefin substrate marked in blue and the ruthenium fragment carrying the ligands “RuL” as shown in red in Figure 2. Then, the energies of these fragments are calculated independently, which allows for evaluating how much energy is required to distort each of the fragments to the geometry found in the transition state.15 Figure 2 summarizes the fragment and interaction energies, which can be computed by subtracting the sum of fragment energies from the total molecular energy. Interestingly, the majority of the energy difference between the two transition states is caused by the RuL fragment distortions. The RuL fragments in 6 must invest 17.2 kcal/mol to reach the structure found in 6-TS, whereas 24.7 kcal/mol must be invested to distort the structure of RuL in 6′ to what is found in 6′-TS. This difference of 7.5 kcal/mol is by far the largest contributor to the electronic transition state energy difference of 9.6 kcal/mol. The olefin fragments require 25.3 and 26.1 kcal/mol energy, which is mostly invested into lengthening the C–C double bond in preparation of the migratory insertion. These distorted fragments interact with each other allowing recovery of 15.2 and 13.9 kcal/mol to afford the final transition state energies of 27.3 and 37.0 kcal/mol, as illustrated in Figure 2. It is curious that the interaction energy in 6-TS is 1.3 kcal/mol greater although the fragment distortions are more severe in 6′-TS. The degree of fragment distortion is generally related to the transition state being late, which means that both the bond breaking and bond forming processes should have progressed further. That is typically reflected in greater fragment distortion, but also in greater interaction energies.
Figure 2.
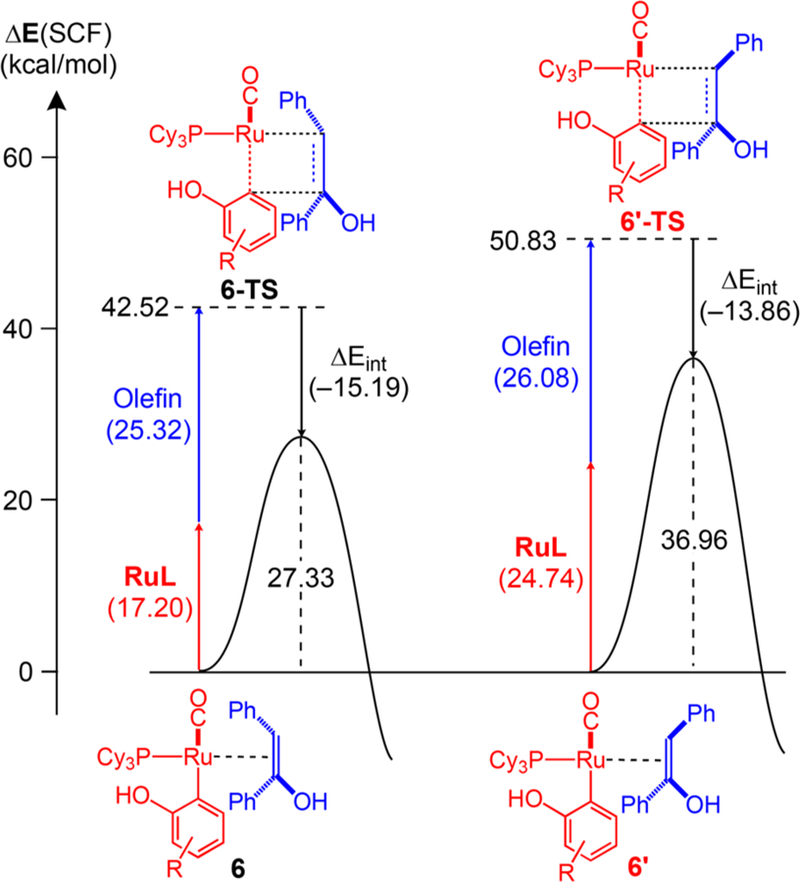
Fragment energy analysis of the migratory insertion step for the formation of (Z)-2b vs (E)-2b.
Figure 3 illustrates the structural difference between 6-TS and 6′-TS, which offers an explanation for the aforementioned energy components. In order to promote the insertion, the double bond between C2 and C3 must be broken, in conjunction with the formation of a new single bond between C1 and C2. The most relaxed geometry for this transition state features a square-planar metallacyclobutane-like structure. The 6-TS adopts a fairly planar structure with the dihedral angle ∠Ru–C1–C2–C3 being ~5°, as shown in Figure 3a. In contrast, 6′-TS has an unfavorable steric interaction between the phenyl group of the enol and the carbonyl group of the Ru-catalyst, which leads to a significant departure from planarity with the ∠Ru–C1–C2–C3 dihedral angle of ~26°, as illustrated in Figure 3b. The four bond lengths in the four-membered metallacycle directly report on how far the transition state has progressed away from the reactant state. The Ru–C1 bonds are 2.11 and 2.23 Å in 6-TS and 6′-TS, respectively, which is consistent with 6′-TS being more distorted than 6-TS, as discussed above. The C1–C2 bond is much longer at 2.17 Å in 6-TS compared to 1.94 Å in 6′-TS, again consistent with 6-TS being an “earlier” transition state. The sterically induced deviation from planarity also explains why the interaction energy computed in the fragment energy analysis is notably diminished in 6′-TS. As the π-orbitals from the olefin substrates and the in-plane d-orbitals on Ru cannot be optimally arranged due to the steric demand of the enol in 6′-TS, the interaction remains weak despite the larger structural distortion of each fragment, which is also a consequence of the steric clash between the carbonyl and the aromatic substituent on the enol.
Figure 3.
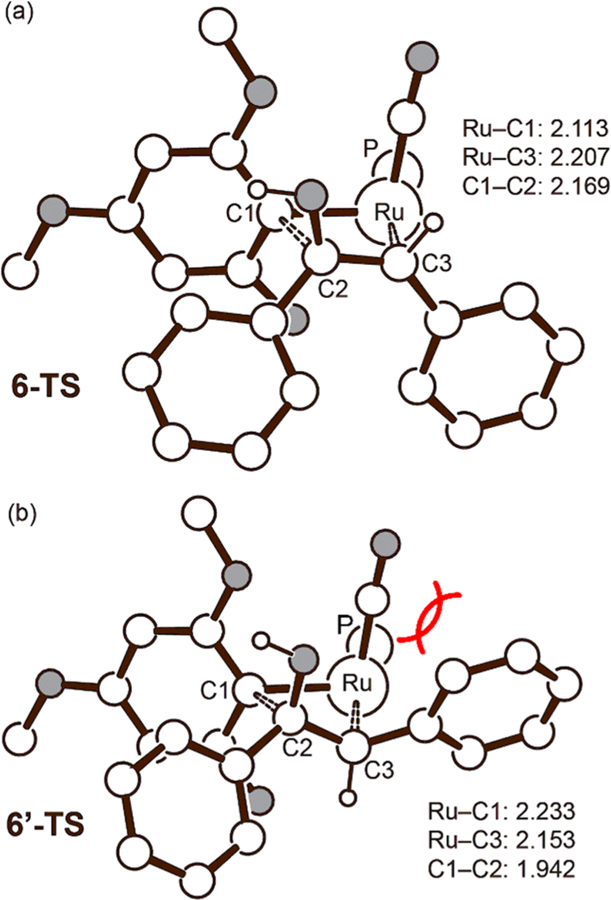
Optimized structures of the transition state (a) 6-TS and 6′-TS. Oxygen atoms are shown in gray color. Nonessential atoms, such as the cyclohexyl groups on the phosphine ligand and nonessential hydrogen atoms, are not shown. Bond lengths are given in Å.
Experimental Support for the Mechanism.
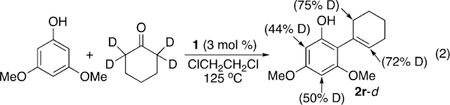
Several kinetic experiments were performed to assess the validity of the DFT computed mechanism. First, the H/D exchange pattern was examined from the reaction of 3,5-dimethoxyphenol with cyclohexanone-2,2,6,6-d4 (93% D) (eq 2). The isolated product 2r-d showed a significant amount of H/D exchange to both vinyl and α-CH2 positions (72–75% D) as well as to the arene positions (Figure S1, SI). This H/D exchange pattern indicates a facile keto–enol tautomerization of the substrate under the reaction conditions. The extensive H/D exchange on the arene positions can readily be explained via the chelate assisted ortho-arene C–H metalation process; such a process has been well-known to occur rapidly and reversibly in metal-mediated coupling reactions via arene C–H activation.16 To confirm the facile nature of the arene C–H activation step, the reaction rate was measured separately from the reaction of 3,5-dimethoxyphenol with cyclohexanone and cyclohexanone-2,2,6,6-d4. A negligibly small deuterium isotope effect of kH/kD = 1.1 ± 0.1 was obtained from the first-order rate plot (Figure S2, SI), again supporting the notion of a rapid and reversible arene C–H activation step for the coupling reaction.
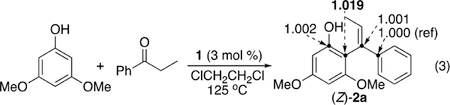
As discussed above, our DFT calculations indicate that the migratory insertion of ketone substrate is the most likely rate-determining step. To confirm this computational result, we measured the carbon isotope effect from the coupling reaction of 3,5-dimethoxyphenol with propiophenone by employing Singleton’s high-precision NMR technique (eq 3).17 The most significant carbon isotope effect was observed on the ortho-arene carbon of the product (Z)-2a when the 13C ratio of the product from a high conversion was compared with the sample obtained from a low conversion (13C(avg 96% conversion)/13C(avg 19% conversion) at Cortho = 1.019; average of two runs) (Table S2, SI). No significant carbon isotope effect was observed on the carbonyl carbon, and this can be rationalized via an early asynchronous transition state of the multi-insertion steps as depicted in Figure 1.18 Overall, the results are in good agreement with the calculated reaction energy profile as shown in Figure 1, further reinforcing that the C–C bond forming migratory insertion of the ketone substrate is the turnover-limiting step of the coupling reaction.
Synthetic Applications.
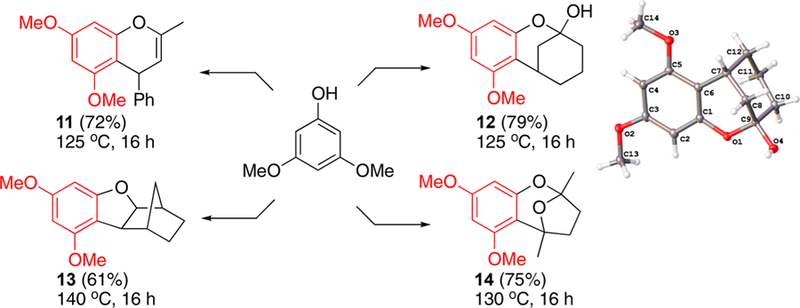
These experimental and computational studies provided a new mechanistically driven rationale for designing stereoselective carbonyl olefination methods to construct biologically relevant structural motifs. In an effort to further extend its synthetic utility, we have begun to explore the dehydrative coupling method with enones and related carbonyl compounds (Scheme 2). For example, the coupling of 3,5-dimethoxyphenol with a linear enone 4-phenyl-3-buten-3-one led to the direct formation of chromene core structure 11. In contrast, the coupling with a cyclic enone 2-cyclohexenone selectively yielded a bicyclic hemiketal product 12 with >95% diastereoselectivity. The molecular structure of 12 was definitively established by X-ray crystallography (Figure S4, SI). The couplings with 2-norbornanone and 2,5-hexanedione smoothly formed the bicyclic products 13 and 14, respectively. These exploratory examples clearly demonstrate the synthetic power of dehydrative C–H coupling strategy in constructing oxygen heterocycle core structures without using any reactive reagents or forming toxic byproducts. We are currently pursuing to establish the scope of the coupling reactions between electron-rich arene substrates with these carbonyl compounds, and the results will be published in a separate article.
Scheme 2.
Dehydrative Coupling of 3,5-Dimethoxyphenol with Ketones
CONCLUSIONS
In summary, we have successfully developed a highly chemo- and stereoselective dehydrative C–H olefination method of phenols with ketones to form trisubstituted olefins. The well-defined cationic ruthenium hydride catalyst was found to exhibit uniquely high activity and selectivity for promoting (Z)-olefin products. The experimental and computational studies provide a detailed mechanistic picture for the catalytic cycle, which consists of the ortho-metalation of phenol, migratory insertion of the carbonyl substrate, and dehydration steps in forming the olefin products. The DFT computational analysis revealed that the stereoselective formation of (Z)-olefins results from an unfavorable steric interaction between the substrate substituents and the axial carbonyl ligand of the Ru-catalyst during the migratory insertion step. The analogous C–H coupling reactions of enones and diones directly led to the formation of synthetically useful benzo-fused oxacyclic derivatives. Studies toward expanding the arene substrate scope as well as for exploiting mechanistic insights to increase synthetic applicability for this catalytic method are underway in our laboratories.
EXPERIMENTAL SECTION
General Information.
All operations were carried out in a nitrogen-filled glovebox or by using standard high vacuum and Schlenk techniques unless otherwise noted. Solvents were freshly distilled over appropriate drying reagents. Benzene, toluene, and hexanes were distilled from purple solutions of sodium and benzophenone, and dichloromethane was dried over calcium hydride prior to use. All organic substrates were received from commercial sources and were used without further purification. Column chromatography was performed on Dynamic Absorbents silica gel 60A (32–63 μm particle size), and thin layer chromatography was performed on Agela TLC plates precoated with silica gel MF254. The NMR spectra were recorded on a Varian 300 or 400 MHz FT-NMR spectrometer, and the data are reported in parts per million (ppm) relative to TMS. Mass spectra were recorded from an Agilent 6850 GC-MS spectrometer with an HP-5 (5% phenylmethylpolysiloxane) column (30 m, 0.32 mm, 0.25 μm). High-resolution mass spectra (HRMS) were obtained at the Mass Spectrometry/ICP Lab, Department of Chemistry and Biochemistry, University of Wisconsin Milwaukee, Milwaukee, WI. Elemental analyses were performed at the Midwest Microlab, Indianapolis, IN.
General Procedure for the Coupling Reaction of Phenol with Ketone.
In a glovebox, a phenol (0.5 mmol), a ketone (1.0–1.5 mmol), and complex 1 (9 mg, 3 mol %) were dissolved in 1,2-dichloroethane (2 mL) in a 25 mL Schlenk tube equipped with a Teflon stopcock and a magnetic stirring bar. The tube was brought out of the glovebox and was stirred in an oil bath preset at 125–140 °C for 16–72 h. The reaction tube was taken out of the oil bath and was cooled to room temperature. After the tube was open to air, the solution was filtered through a short silica gel column by eluting with CH2Cl2 (10 mL), and the filtrate was analyzed by GC-MS. Analytically pure product was isolated by column chromatography on silica gel (230–460 mesh, hexanes/EtOAc). The product was completely characterized by NMR and GC-MS spectroscopic methods.
Computational Details.
All calculations were carried out using DFT19 as implemented in the Jaguar 9.1 suite20 of ab initio quantum chemistry programs. Geometry optimizations were performed with the B3LYP21 functional including Grimme’s D3 dispersion correction22 and the 6–31G** basis set. Ruthenium was represented using the Los Alamos LACVP basis23 that includes effective core potentials. The energies of the optimized structures were reevaluated by additional single-point calculations on each optimized geometry using Dunning’s correlation consistent triple-ζ basis set cc-pVTZ(-f)24 that includes a double set of polarization functions. For ruthenium, we used a modified version of LACVP, designated as LACV3P, in which the exponents were decontracted to match the effective core potential with triple-ζ quality. Solvation energies were evaluated by a self-consistent reaction field (SCRF)25 approach based on accurate numerical solutions of the Poisson–Boltzmann equation. In the results reported, solvation calculations were carried out with the 6–31G**/LACVP basis at the optimized gas phase geometry employing the dielectric constant of ε = 10.36 for 1,2-dichloroethane. As is the case for all continuum models, the solvation energies are subject to empirical parametrization of the atomic radii that are used to generate the solute surface. We employed26 the standard set of optimized radii in Jaguar for H (1.150 Å), C (1.900 Å), N (1.600 Å), P (2.074 Å), and Ru (1.481 Å). Analytical vibrational frequencies within the harmonic approximation were computed with the 6–31G**/LACVP basis to confirm proper convergence to well-defined minima or saddle points on the potential energy surface.
The energy components have been computed with the following protocol. The free energy in solution phase G(Sol) has been calculated as follows:
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
G(gas) is the free energy in gas phase; G(solv) is the free energy of solvation as computed using the continuum solvation model; H(gas) is the enthalpy in gas phase; T is the temperature (298.15 K); S(gas) is the entropy in gas phase; E(SCF) is the self-consistent field energy, i.e. “raw” electronic energy as computed from the SCF procedure; and ZPE is the zero-point energy. Note that by entropy here we refer specifically to the vibrational/rotational/translational entropy of the solute(s); the entropy of the solvent is incorporated implicitly in the continuum solvation model.
To locate transition states, the potential energy surface was first explored approximately using the linear synchronous transit (LST)27 method, followed by a quadratic synchronous transit (QST)28 search using the LST geometry as an initial guess.
Supplementary Material
ACKNOWLEDGMENTS
Financial support from the National Science of Foundation (CHE-1358439, CHE-1664652) and the National Institute of Health General Medical Science (R15 GM109273) is gratefully acknowledged. This research was supported in part the Institute for Basic Science (IBS-R010-D1) in Korea.
Footnotes
ASSOCIATED CONTENT
Supporting Information
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.8b05875.
Experimental procedures, characterization data for organic products, and Cartesian coordinates of all computed structures and energy components (PDF) Crystallographic data for (Z)-2a (CIF)
Crystallographic data for 12 (CIF)
The authors declare no competing financial interest.
REFERENCES
- (1) (a).Maryanoff BE; Reitz AB Chem. Rev 1989, 89, 863–927. [Google Scholar]; (b) Flynn AB; Ogilvie WW Chem. Rev 2007, 107, 4698–4745. [DOI] [PubMed] [Google Scholar]
- (2) (a).Fürstner BA; Bogdanović B Angew. Chem., Int. Ed. Engl 1996, 35, 2442–2469. [Google Scholar]; (b) Ephritikhine M Chem. Commun 1998, 2549–2554. [Google Scholar]; (c) Takeda T; Tsubouchi A Org. React 2013, 82, 1–470. [Google Scholar]
- (3) (a).Herrmann WA Adv. Organomet. Chem 1982, 20, 159–263. [Google Scholar]; (b) Beadham I; Micklefield J Curr. Org. Synth 2005, 2, 231–259. [Google Scholar]; (c) Hartley RC; Li J; Main CA; McKiernan GJ Tetrahedron 2007, 63, 4825–4864. [Google Scholar]
- (4) (a).Chan T-H Acc. Chem. Res 1977, 10, 442–448. [Google Scholar]; (b) van Staden LF; Gravestock D; Ager DJ Chem. Soc. Rev 2002, 31, 195–200. [DOI] [PubMed] [Google Scholar]
- (5) (a).Negishi E; Huang Z; Wang G; Mohan S; Wang C; Hattori H Acc. Chem. Res 2008, 41, 1474–1485. [DOI] [PubMed] [Google Scholar]; (b) Hatakeyama T; Nakagawa N; Nakamura M Org. Lett 2009, 11, 4496–4499. [DOI] [PubMed] [Google Scholar]; (c) Hu F; Xia Y; Ye F; Liu Z; Ma C; Zhang Y; Wang J Angew. Chem., Int. Ed 2014, 53, 1364–1367. [DOI] [PubMed] [Google Scholar]
- (6) (a).Ludwig JR; Zimmerman PM; Gianino JB; Schindler CS Nature 2016, 533, 374–379. [DOI] [PubMed] [Google Scholar]; (b) Ludwig JR; Phan S; McAtee CC; Zimmerman PM; Devery JJ III; Schindler CS J. Am. Chem. Soc 2017, 139, 10832–10842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Srimani D; Leitus G; Ben-David Y; Milstein D Angew. Chem., Int. Ed 2014, 53, 11092–11095. [DOI] [PubMed] [Google Scholar]
- (8).Lei C; Yip YJ; Zhou JS J. Am. Chem. Soc 2017, 139, 6086–6089. [DOI] [PubMed] [Google Scholar]
- (9).Wei W; Dai X-J; Wang H; Li C; Yang X; Li C-J Chem. Sci 2017, 8, 8193–8197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Recent reviews on C–H olefination:; (a) Wencel-Delord J; Dröge T; Liu F; Glorius F Chem. Soc. Rev 2011, 40, 4740–4761. [DOI] [PubMed] [Google Scholar]; (b) Arockiam PB; Bruneau C; Dixneuf PH Chem. Rev 2012, 112, 5879–5918. [DOI] [PubMed] [Google Scholar]; (c) Kozhushkov SI; Ackermann L Chem. Sci 2013, 4, 886–896. [Google Scholar]; (d) Yeung CS; Dong VM Chem. Rev 2011, 111, 1215–1292. [DOI] [PubMed] [Google Scholar]
- (11) (a).Stec WJ Acc. Chem. Res 1983, 16, 411–417. [Google Scholar]; (b) Patois C; Savignac P; About-Jaudet E; Collignon N Org. Synth 1996, 73, 152–155. [Google Scholar]
- (12) (a).Hansen EC; Lee D Org. Lett 2004, 6, 2035–2038. [DOI] [PubMed] [Google Scholar]; (b) Ibrahem I; Yu M; Schrock RR; Hoveyda AH J. Am. Chem. Soc 2009, 131, 3844–3845. [DOI] [PMC free article] [PubMed] [Google Scholar]; (c) Rosebrugh LE; Herbert MB; Marx VM; Keitz BK; Grubbs RH J. Am. Chem. Soc 2013, 135, 1276–1279. [DOI] [PMC free article] [PubMed] [Google Scholar]; (d) Mann TJ; Speed AWH; Schrock RR; Hoveyda AH Angew. Chem., Int. Ed 2013, 52, 8395–8400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13) (a).Lee D-H; Kwon K-H; Yi CS J. Am. Chem. Soc 2012, 134, 7325–7328. [DOI] [PubMed] [Google Scholar]; (b) Kim J; Lee D-H; Kalutharage N; Yi CS ACS Catal 2014, 4, 3881–3885. [Google Scholar]; (c) Lee H; Yi CS Organometallics 2016, 35, 1973–1977. [DOI] [PMC free article] [PubMed] [Google Scholar]; (d) Kim J; Pannilawithana N; Yi CS ACS Catal 2016, 6, 8395–8398. [Google Scholar]
- (14) (a).Lee DW; Yi CS Organometallics 2010, 29, 3413–3417. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Kim J; Yi CS ACS Catal 2016, 6, 3336–3339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15) (a).Xie S; Lopez SA; Ramström O; Yan M; Houk KN J. Am. Chem. Soc 2015, 137, 2958–2966. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Ess DH; Houk KN J. Am. Chem. Soc 2008, 130, 10187–10198. [DOI] [PubMed] [Google Scholar]; (c) Ess DH; Houk KN J. Am. Chem. Soc 2007, 129, 10646–10647. [DOI] [PubMed] [Google Scholar]
- (16) (a).Kakiuchi F; Murai S Acc. Chem. Res 2002, 35, 826–834. [DOI] [PubMed] [Google Scholar]; (b) Kakiuchi F; Kochi T; Mizushima E; Murai SJ Am. Chem. Soc 2010, 132, 17741–17750. [DOI] [PubMed] [Google Scholar]
- (17) (a).Singleton DA; Thomas AA J. Am. Chem. Soc 1995, 117, 9357–9358. [Google Scholar]; (b) Frantz DE; Singleton DA; Snyder JP J. Am. Chem. Soc 1997, 119, 3383–3384. [Google Scholar]; (c) Nowlan DT III; Gregg TM; Davies HML; Singleton DA J. Am. Chem. Soc 2003, 125, 15902–15911. [DOI] [PubMed] [Google Scholar]
- (18).Nowlan DT III; Singleton DA J. Am. Chem. Soc 2005, 127, 6190–6191. [DOI] [PubMed] [Google Scholar]
- (19).Parr RG; Yang W Density Functional Theory of Atoms and Molecules; Oxford University Press: New York, 1989. [Google Scholar]
- (20).Bochevarov AD; Harder E; Hughes TF; Greenwood JR; Braden DA; Philipp DM; Rinaldo D; Halls MD; Zhang J; Friesner RA Int. J. Quantum Chem 2013, 113, 2110–2142. [Google Scholar]
- (21) (a).Slater JC Quantum Theory of Molecules and Solids, Vol. 4: The Self-Consistent Field for Molecules and Solids; McGraw-Hill: New York, 1974. [Google Scholar]; (b) Vosko SH; Wilk L; Nusair M Can. J. Phys 1980, 58, 1200–1211. [Google Scholar]; (c) Becke AD Phys. Rev. A: At., Mol., Opt. Phys 1988, 38, 3098–3100. [DOI] [PubMed] [Google Scholar]; (d) Lee C; Yang W; Parr RG Phys. Rev. B: Condens. Matter Mater. Phys 1988, 37, 785–789. [DOI] [PubMed] [Google Scholar]; (e) Becke AD J. Chem. Phys 1993, 98, 5648–5652. [Google Scholar]
- (22).Grimme S; Antony J; Ehrlich S; Krieg HJ Chem. Phys 2010, 132, 154104. [DOI] [PubMed] [Google Scholar]
- (23) (a).Hay PJ; Wadt WR J. Chem. Phys 1985, 82, 270–283. [Google Scholar]; (b) Wadt WR; Hay PJ J. Chem. Phys 1985, 82, 284–298. [Google Scholar]; (c) Hay PJ; Wadt WR J. Chem. Phys 1985, 82, 299–310. [Google Scholar]
- (24).Dunning TH Jr. J. Chem. Phys 1989, 90, 1007–1023. [Google Scholar]
- (25) (a).Marten B; Kim K; Cortis C; Friesner RA; Murphy RB; Ringnalda MN; Sitkoff D; Honig BJ Phys. Chem 1996, 100, 11775–11788. [Google Scholar]; (b) Edinger SR; Cortis C; Shenkin PS; Friesner RA J. Phys. Chem. B 1997, 101, 1190–1197. [Google Scholar]; (c) Friedrichs M; Zhou R; Edinger SR; Friesner RA J. Phys. Chem. B 1999, 103, 3057–3061. [Google Scholar]
- (26).Rashin AA; Honig B J. Phys. Chem 1985, 89, 5588–5593. [Google Scholar]
- (27).Halgren TA; Lipscomb WN Chem. Phys. Lett 1977, 49, 225–232. [Google Scholar]
- (28).Peng CY; Schlegel HB Isr. J. Chem 1993, 33, 449–454. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


