A Measurement‐Model Fusion Approach for Improved Wet Deposition Maps and Trends

Abstract

Air quality models provide spatial fields of wet deposition (WD) and dry deposition that explicitly account for the transport and transformation of emissions from thousands of sources. However, many sources of uncertainty in the air quality model including errors in emissions and meteorological inputs (particularly precipitation) and incomplete descriptions of the chemical and physical processes governing deposition can lead to bias and error in the simulation of WD. We present an approach to bias correct Community Multiscale Air Quality model output over the contiguous United States using observation‐based gridded precipitation data generated by the Parameter‐elevation Regressions on Independent Slopes Model and WD observations at the National Atmospheric Deposition Program National Trends Network sites. A cross‐validation analysis shows that the adjusted annual accumulated WD for NO₃ ⁻, NH₄ ⁺, and SO₄ ²⁻ from 2002 to 2012 has less bias and higher correlation with observed values than the base model output without adjustment. Temporal trends in observed WD are captured well by the adjusted model simulations across the entire contiguous United States. Consistent with previous trend analyses, WD NO₃ ⁻ and SO₄ ²⁻ are shown to decrease during this period in the eastern half of the United States, particularly in the Northeast, while remaining nearly constant in the West. Trends in WD of NH₄ ⁺ are more spatially and temporally heterogeneous, with some positive trends in the Great Plains and Central Valley of CA and slightly negative trends in the south.

Key Points

• Modeled estimates of the wet deposition across the United States are improved by fusion with gridded precipitation data and observed wet deposition

• The fused wet deposition estimates evaluate well against observed values and maintain the spatial heterogeneity in the original model output

• Temporal trends in observed wet deposition of nitrate, ammonium, and sulfate from 2002 to 2012 are well captured by the adjusted model output

1. Introduction

The ultimate fate of atmospheric sulfur (SO_x = SO₂ + SO₄ ²⁻) and reactive nitrogen compounds (NO_y = NO + NO₂ + other oxidized forms of N excluding N₂O and NH_x = NH₃ + NH₄ ⁺) is removal by wet scavenging and dry deposition, which in turn lead to a variety of environmental effects including changes in net primary production (LeBauer & Treseder, 2008), acidification (Driscoll et al., 2003), eutrophication (Bergström & Jansson, 2006; Bouwman et al., 2002), and other nutrient‐loading effects (Bowman et al., 2008). Long‐term wet deposition (WD) and dry deposition (DD) data are needed to assess the changes and trends in total deposition (TD = WD + DD), as well as their effect on ecosystems. In the United States, the National Atmospheric Deposition Program/National Trends Network (NADP/NTN; https://nadp.slh.wisc.edu/ntn) provides the nation's primary WD data. These observed WD values are often used to estimate past and current loads of acidic (S + N) and nutrient (N) deposition on sensitive ecosystems for critical loads exceedance studies in the United States (Nanus et al., 2003; Sickles & Shadwick, 2007, 2015). Using NADP/NTN data from 1985 to 2012, Du et al. (2014) found a positive trend in ammonium WD at the national scale and a significant negative trend in nitrate WD, especially in the Northeast. Sickles and Shadwick (2015) found a significant decrease of wet and DD of both S and N in the east from 1990 to 2009, using deposition data from 34 paired dry and wet monitoring sites.

More accurate, highly spatially resolved fields of deposition are needed for regional and national scale assessment of nitrogen and sulfur budgets and comparison of deposition loads of N + S with critical loads (i.e., the level of a pollutant below which no harmful ecological effect occurs) for different ecosystems and ecological endpoints. Previous studies have used different spatial interpolation methods, such as inverse distance weighting or kriging, to estimate the spatial distribution of N deposition (Grimm & Lynch, 1991, 2004; Jia et al., 2014; Li et al., 2016; Qu et al., 2017; Schwede & Lear, 2014) and temporal trends. Because deposition monitoring data are relatively sparse (on the order of 230–250 NADP/NTN sites across the United States, depending on the year) interpolation methods can miss important emission sources and geographic features that impact deposition unless additional covariate information is incorporated (e.g., regression kriging). Air quality model simulations offer an alternative to observation‐only interpolation methods and have the advantage of incorporating detailed emissions information on hundreds of sources while also explicitly accounting for geographic features in the parameterization of physical and chemical processes.

Air quality model simulations have been extensively used to determine the distribution (Dennis et al., 2013; Dentener et al., 2006; Gu et al., 2015; Mathur & Dennis, 2003; Zhang et al., 2012) and temporal trends (Lamarque et al., 2013; Zhang et al., 2018) of nitrogen and sulfur WD and to assess critical load exceedances (Ellis et al., 2013; Sun et al., 2017; Williams et al., 2017), as they can provide more spatially complete coverage of TD. However, model simulations also have bias for estimating WD, especially at coarse resolution (Appel et al., 2011; Lamarque et al., 2013; Simon et al., 2012; Zhao et al., 2017). Zhang et al. (2018) showed that the long‐term model simulation from coupled Weather Research and Forecasting (WRF)‐Community Multiscale Air Quality Model (CMAQ) at 36 km underestimated WD of both nitrogen and sulfur in the United States from 1990 to 2010, as well as their negative trends by more than 20%. The biased model simulation of WD could lead to false negative or false positive deposition exceedances in critical loads analyses (Williams et al., 2017).

Measurement‐model fusion methods have been widely used to improve air quality model output for ambient concentrations (e.g., Berrocal et al., 2010a, 2010b; Berrocal et al., 2012; Robichaud et al., 2016; Robichaud & Ménard, 2014), with more limited application to WD data (e.g., Makar et al., 2018; Sahu et al., 2010). In 2017 the World Meteorology Organization hosted a 3‐day workshop on measurement‐model fusion for global total atmospheric deposition. The resulting published report summarizes existing products and plans for developing improved maps of wet, dry, and total atmospheric deposition to “enable research into biogeochemical cycles and assessments of ecosystems and human health effects” (World Meteorological Organization (WMO), 2017).

One of the modeling products included in the WMO report was the annual TD maps for the contiguous United States (CONUS) developed by the NADP Total Deposition Science Committee (TDEP; Schwede & Lear, 2014). TDEP maps for DD are based on a measurement‐model fusion method using CMAQ output and observations from the Clean Air Status and Trends Network, while spatial maps of annual WD are based on NADP/NTN measurements and Parameter‐elevation Regressions on Independent Slopes Model (PRISM) precipitation data. In this study, we evaluate a measurement‐model fusion method to combine CMAQ‐simulated WD of major nitrogen (NO₃ ⁻ and NH₄ ⁺) and sulfur (SO₄ ²⁻) species with the NADP/NTN measurements and PRISM precipitation data used by TDEP. Bias‐adjusted CMAQ WD fields are created for 2002–2012 and evaluated against NADP/NTN measurements through a cross‐validation analysis. The bias‐adjusted spatial fields reduce bias and improve correlation with observed values, without smoothing out the spatial heterogeneity of the original model output. We assess the long‐term trends in WD of these species in the United States during the same period and find that estimated trends in bias‐adjusted model WD evaluate well against observed trends. Although TD of both nitrate and sulfate can be dominated by DD in the United States (Zhang et al., 2018), improvements to DD maps are beyond the scope of the current work due to the lack of measured DD data currently available.

2. Methodology

2.1. Model Inputs and Outputs

The model simulations used in this analysis were conducted using CMAQ (Byun & Schere, 2006) version 5.0.2 (Appel et al., 2013; doi:10.5281/zenodo.1079898), which includes bidirectional NH₃ air‐surface exchange (Bash et al., 2013; Pleim et al., 2013) and the Carbon Bond version 2005 (CB05) chemical mechanism (Yarwood et al., 2005) updated with toluene reactions (CB05‐TU; Whitten et al., 2010). The simulations were performed over the CONUS from 1 January 2002 to 31 December 2012 at 12‐km × 12‐km horizontal resolution with 35 vertical layers from the surface to the top of the free troposphere and a nominal height of 19 m for layer one. Meteorological inputs were developed using the WRF model version 3.4 using the Kain‐Fritsch trigger for convective precipitation (Ma & Tan, 2009), the Pleim‐Xiu land‐surface model (Gilliam & Pleim, 2010), and four‐dimensional data assimilation (Gilliam et al., 2012). From 2002 to 2005, the 2001 National Land Cover Database((NLCD) land cover data were used as an input to the WRF simulations; remaining years were based on 2006 NLCD land cover data. The land use classification methods and changes in the land use over time were documented and evaluated in Homer et al. (2015). Output from WRF was processed to create inputs for CMAQ using the Meteorology‐Chemistry Interface Processor (Otte & Pleim, 2010) version 4.1.3. Emission inputs were based on 2002, 2005, 2008, and 2011 National Emission Inventory data (NEI; https://www.epa.gov/air‐emissions‐inventories, accessed April 26, 2018) using the Sparse Matrix Operator Kernel Emissions (Houyoux et al., 2000) processing system version 3.1 and included year‐specific continuous emission monitoring system data for large combustion and industrial processes (mainly electric generating units). Year‐specific mobile emissions were derived from U.S. Environmental Protection Agency (EPA) Motor Vehicle Emission Simulator (www.epa.gov/otaq/models/moves, accessed 26 April 2018) version 2010b, and the Biogenic Emissions Inventory System version 3.14 was used for inline biogenic emissions (Carlton & Baker, 2011). NEI data on annual total ammonia emissions from confined animal feeding operations were based on national estimates from the Carnegie Mellon University model (Davidson et al., 2004) and state submitted information. These annual totals were temporally allocated using the Sparse Matrix Operator Kernel Emissions programme with the temporalization from Zhu et al. (2015). Ammonia emissions from fertilizer were estimated using CMAQ with bidirectional exchange; in this parameterization, the net flux is broken into emissions and deposition components, the former making use of a compensation point concentration with zero ambient ammonia, the latter from assuming zero stomatal and soil compensation point concentrations (Bash et al., 2013). Emission inputs also included inline NO produced from lightning using year‐specific flash rate data from the National Lightning Detection Network (Allen et al., 2012). For simulation years 2005 to 2012 chemical boundary conditions for CMAQ were based on year‐specific simulations of GEOS‐Chem version 8–03‐02 (http://wiki.seas.harvard.edu/geos‐chem/index.php/Main_Page, accessed 26 April 2018) using version 8‐02‐01 chemistry, GEOS‐5 meteorology and ICOADS shipping emissions (Henderson et al., 2014). The CB05 aerosol chemical mechanism used in CMAQ has more aerosol species than that in GEOS‐Chem, and so speciation remapping between these two models was done following Henderson et al. (2014). GEOS‐Chem simulations were not available for 2002–2004; chemical boundary conditions for these years were based on the monthly median values from the 2005 simulation. We expect the influence of these boundary conditions to be relatively small, especially compared to other uncertainties in the modeling system such as uncertainties in the emissions inventories in the early 2000s. Additional information on model inputs is provided in the supporting information.

2.2. Observational Data Sets

Model predicted WD for nitrate (NO₃ ⁻), ammonium (NH₄ ⁺), and sulfate (SO₄ ²⁻) were compared to observed WD values from NADP/NTN (National Atmospheric Deposition Program) (NRSP‐3) (2019). Modeled and observed values were paired in space by matching the observations to the model values from the grid cell that contains the monitor. See Appel et al. (2011), section 2.4, for a description of how the chemical species in the CMAQ model were configured to match the measured WD values. There were 282 NADP/NTN sites that had data for at least 1 year of the study period. The number of sites with available data in each year ranged from 231 to 252. In addition, NADP/NTN provides four completeness criteria (CC) to ensure the reported values represent a valid annual accumulated measurement. About 20% of the sites in the network in any given year are dropped through application of these CC. As a result, only 68 sites met all four criteria for the full 11‐year time series, complicating spatial analysis of temporal trends. Here we have relaxed the CC and included any site that had 10 or 11 years of data that met the revised criteria, resulting in a final sample size of 183 sites. Figure 1 shows the location of the 183 sites used in the analysis and highlights which of these sites met the full NADP/NTN criteria. A full description of the CC used in this analysis is included in the supporting information.

Figure 1.

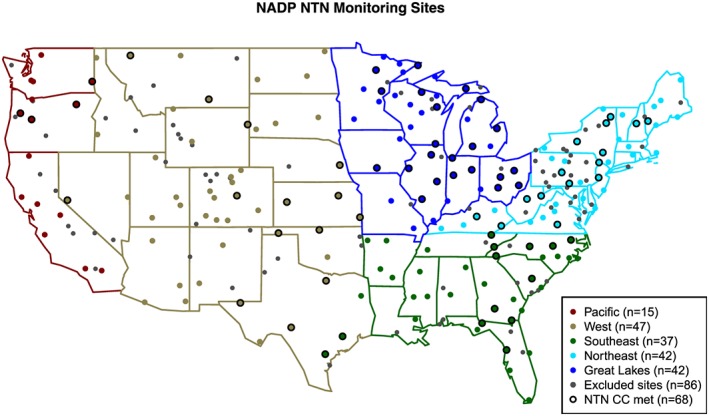
Location of 183 NADP/NTN monitors used in the analysis. Color‐coded regions are used in Figure 4 and Figures S3, S4, and S7 provided in the supporting information. The black‐boarded colored circles (NTN CC met) indicate sites that met the full NADP/NTN completeness criteria for the entire 11‐year time series. NADP = National Atmospheric Deposition Program; NTN = National Trends Network; CC = completeness criteria.

The observation‐based gridded precipitation fields generated by the PRISM (Daly et al., 2008; PRISM Climate Group, Oregon State University, http://prism.oregonstate.edu, created 10 September 2015) were used to evaluate model‐predicted accumulated precipitation from the WRF meteorological model. Annual accumulated PRISM precipitation data at 4‐km resolution were regridded to the CMAQ 12‐km resolution grid for the entire time series, which were then used to scale the CMAQ WD fields, as described in section 2.3. The precipitation estimates from PRISM have been used to improve maps of WD provided by NADP/NTN and TDEP in complex terrain regions in the United States, as PRISM incorporates point observation, elevation, and climatic factors when estimating precipitation (Latysh & Wetherbee, 2012; Schwede & Lear, 2014). The gridded PRISM precipitation estimates are also more commensurable with the WRF grid cell volume precipitation values compared to the precipitation measurements at NADP/NTN sites which represent rainfall totals at a single point location.

2.3. Description of the Measurement‐Model Fusion Approach to Combine CMAQ Output and Observations

The relationship between WD and precipitation is affected by the frequency, duration, and intensity of the rainfall as well as the ambient concentration. While this relationship is typically nonlinear on hourly and daily time scales, on an annual accumulation basis the relationship can become more linear. For example, Figure 2 shows the modeled and observed relationship between annual accumulated precipitation and WD of sulfate at the 42 sites in the Great Lakes subregion. At locations where the modeled and observed relationships are similar, the model/observed errors in annual accumulated WD can also be highly correlated with model/observed errors in precipitation as shown in Figure 3.

Figure 2.

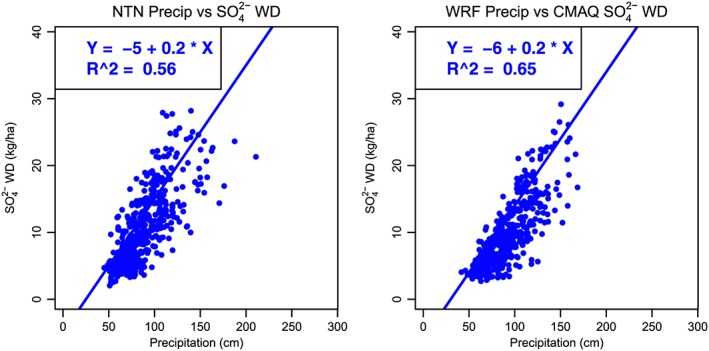
Strength of linear relationship between annual accumulated precipitation and sulfate wet deposition at NTN sites in the Great Lakes subregion based on observed data (left) and modeled data (right). NTN = National Trends Network.

Figure 3.

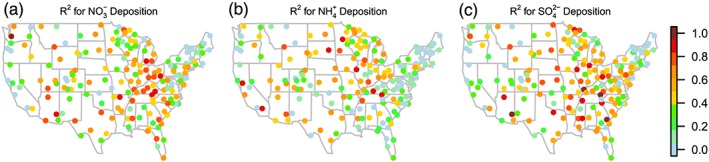
Coefficient of determination (i.e., Pearson correlation squared or R ²) between the natural log of model/observed annual wet deposition, (a) for NO₃ ⁻, (b) for NH₄ ⁺, and (c) for SO₄ ²⁻, for 2002–2012. A seasonal version of this plot is included in the supporting information (Figure S1).

The variability in the log of the ratio of model/observed annual accumulated precipitation explains at least 40% of the variability in the log of the ratio of annual accumulated modeled/observed WD at 94, 78, and 104 of the observation stations for nitrate, ammonium, and sulfate, respectively (i.e., 52%, 43%, and 57% of the stations). For about a quarter of the locations in the eastern half of the United States, these R ² values are on the order of 60–90%, particularly in the Great Lakes subregion (Figures 3a and 3c). While high correlations do not hold for all stations, we have made use of the calculated linear relationships to recalculate the modeled WD using PRISM rainfall volume. Specifically, the modeled WD for grid cell s and year t (WD_mod(s,t)) was converted to precipitation concentration by dividing the modeled precipitation (Precip_mod(s,t)) and then converted back to deposition by multiplying by the gridded PRISM precipitation (Precip_obs(s,t)) for that location and year

$${\mathrm{WD}}_{\text{precip}-\mathrm{adj}}\left(s,t\right)=\frac{{\mathrm{WD}}_{\mathrm{mod}}\left(s,t\right)}{{\text{Precip}}_{\mathrm{mod}}\left(s,t\right)}\times {\text{Precip}}_{\mathrm{obs}}\left(s,t\right)$$ (2.1)

where WD_{precip − adj}(s, t) is the precipitation adjusted WD at grid cell s and year t.

While this precipitation adjustment (precip‐adj) increased the correlation between observed and modeled WD, model bias remained due to (1) cases where the WD does not scale with changes in precipitation in a one‐to‐one linear fashion and (2) bias in emission inputs (including missing emissions sources) and/or errors in other model processes effecting deposition. A second bias‐adjustment (bias‐adjust) was applied to the precip‐adj WD (WD_precip‐adj(s,t)), based on interpolating the ratio of the precip‐adj WD and the NADP/NTN WD observations using a kriging model. A cross‐validation analysis was used to select the interpolation approach used in the bias adjustment. Cross‐validation results are provided in section 3.2 with supporting figures in the supporting information. The cross‐validation analysis showed that the model bias at a single NADP/NTN site can be influenced by very local emission sources and precipitation events and is not necessarily representative of the bias at surrounding grid cells. Specifically, the cross‐validation analysis showed that kriging the bias extended the influence of sites with very high bias to other locations, degrading the effectiveness of the bias‐adjustment. To account for this, a moving window averaging approach was applied prior to kriging to reduce the influence of these very site‐specific biases. At each site, the median of the ratio, WD_precip‐adj/WD_obs, of all sites within a 300‐km radius was calculated, dampening any large bias values to create a more regional estimate of bias. The new median biases were then interpolated using universal kriging with a linear trend in the spatial coordinates and an exponential covariance structure (Cressie, 1993). Note that since the bias metric was a ratio, the averaging and kriging steps were done on a log scale and then back transformed. Both the moving average calculation and the universal kriging were done using the gstat library in the R statistical software package (Pebesma, 2004) The cross‐validation analysis was used to determine the size of the moving window (300 km) and the choice of the type of kriging model.

The result of the spatial interpolation steps above is a set of estimated spatial bias fields for each year, $\widehat{b}\left(s,t\right)$. The final adjusted WD for a given grid cell and year t was calculated based on multiplying the WD_precip‐adj(s,t) and the inverse of the estimated bias at that location:

$${\mathrm{WD}}_{\mathrm{adj}}\left(s,t\right)=\frac{1}{\widehat{b}\left(s,t\right)}\times {\mathrm{WD}}_{\text{precip}-\mathrm{adj}}\left(s,t\right)$$ (2.2)

An example of the spatial bias field and the map of the final adjustment factor for WD of nitrate in 2012 is provided in the supporting information (Figure S5).

A second cross‐validation analysis was performed to compare this precip‐adjusted and bias‐adjusted approach (Method 1) with three other measurement‐model fusion methods. First, the individual precipitation and bias adjustments were tested separately. Method 2 includes the precipitation adjustment (precip‐adj) of CMAQ WD using PRISM based on equation (2.1) with no additional bias adjustment. Method 3 uses the bias‐adj CMAQ model outputs using NADP/NTN WD data with no initial PRISM adjustment. A fourth method (Method 4) that does not use CMAQ output was also compared. In this case, WD measurements from NADP/NTN were divided by the regridded 12‐km resolution PRISM precipitation for the grid cell containing the monitor to create a precipitation‐weighted wet concentration value. The precipitation‐weighted wet concentrations for each ion were kriged using the same kriging approach as Method 1 (i.e., universal kriging with a linear trend and exponential covariance) to produce a spatial field (units = mg/L) and then multiplied by the full PRISM precipitation grid (units converted to millimeter per year) to estimate WD at every grid cell (units = kg/ha) (Latysh & Wetherbee, 2012; Nanus et al., 2003). Results of the cross‐validation analysis comparing the different methods are provided in section 3.2.

Note that Method 4 differs from the TDEP approach for combining PRISM and WD observations. TDEP uses inverse distance weighting to interpolate precipitation‐weighted concentrations from NADP/NTN and AIRMoN and adjusts the PRISM data based on the precipitation amounts measured at NADP/NTN monitoring network sites (http://nadp.slh.wisc.edu/committees/tdep/tdepmaps/; accessed 26 April 2018). It was not possible to incorporate this method into the cross‐validation study applied in this paper; however, differences between the TDEP maps and the methods applied here are discussed in section 3.3.

2.4. Description of Trend Analysis

The temporal trends in modeled and observed WD were estimated using the Theil‐Sen slope estimator (Sen, 1968; Theil, 1950). Theil‐Sen slopes were calculated using the mblm library in the R statistical software package. The Theil‐Sen estimator is a nonparametric method for estimating the slope through a set of points, in this case the annual accumulated deposition for each year at a given grid cell or NADP/NTN location. This data set has a very small sample size (n = 10 or 11) and can exhibit large interannual variability in some locations driven by year‐to‐year changes in precipitation. The Theil‐Sen estimator was used because it is insensitive to outliers and offers a more robust approach compared to simple linear regression. The Kendall rank test was used to test if the linear trend in the observed time series was statistically significant.

3. Results

3.1. Evaluation of Model Estimated WD

Figure 4 provides the normalized mean bias (NMB) of annual precipitation (top left), WD of sulfate (top right), nitrate (bottom left), and ammonium (bottom right) based on WRF precipitation and CMAQ WD estimates compared to NADP/NTN observations from 2002 to 2012. The time series of NMB was calculated for each of the five subregions to compare how the bias differs across space. Observed precipitation totals in the intermountain West are very low yet are consistently overestimated by the model by 20–40%. Precipitation is also overestimated every year in Pacific Coast states, with the greatest overestimation in 2008 (NMB = 35%). There is less model bias throughout the eastern half of the United States, particularly for the latter half of the time series when the NMB is within ±10%. For most years, the NMB for both NO₃ ⁻ and SO₄ ²⁻ WD is less than 10% in the Northeast, Great Lakes and Southeast, with a slight tendency toward more underestimation of SO₄ ²⁻ WD. In the Pacific Coast states NO₃ ⁻ and SO₄ ²⁻ WD are overestimated with SO₄ ²⁻ WD NMB values exceeding 100% in seven of the 10 years. The year with the largest NMB for the Pacific region for all three WD species is 2008, corresponding to the peak in the precipitation bias. The modeled ammonium WD is comparable to observations in the Northeast and Southeast regions (NMB within ±15%) but is underestimated in the Great Lakes and Pacific regions. The underprediction of ammonium WD in the central United States may be the result of missing emissions from large concentrated animal feeding operations (Warner et al., 2017; Zhang et al., 2018). The overestimation in Pacific Coast states is seen in previous studies (Appel et al., 2011; Zhang et al., 2018) and could be caused by complex terrain effects. Besides the errors in modeled precipitation, other errors could also lead to the bias in modeled WD: errors in atmospheric concentrations due to misspecification of precursor emission levels, imperfect representation of the chemical and physical processes related to the nitrogen and sulfur cycles, the underestimation of deposition velocity of ammonia gas, and errors in the bidirectional fluxes (Bash et al., 2013; Pleim et al., 2013).

Figure 4.

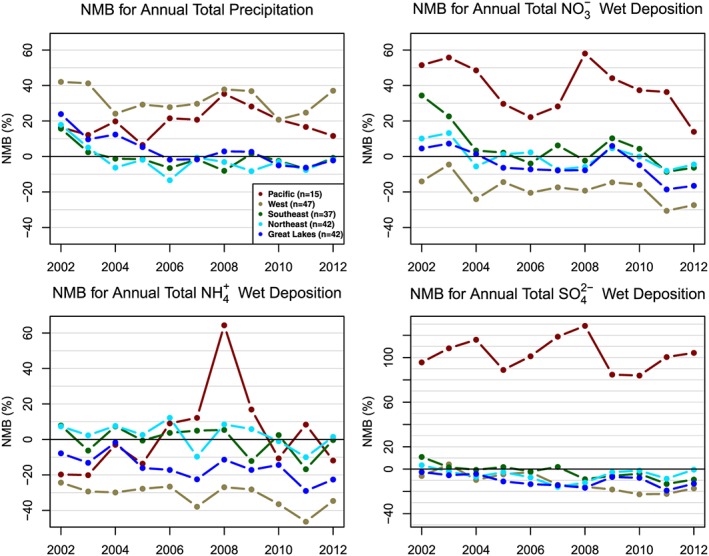
Time series of normalized mean bias (NMB; %) of annual Weather Research and Forecasting precipitation and annual Community Multiscale Air Quality Model wet deposition for 2002 to 2012 based on model sums compared to National Atmospheric Deposition Program/National Trends Network observations. NMB values were calculated for each of the five subregions shown in Figure 1. NMB = normalized mean bias.

Table 1 provides performance statistics for the simulated annual and seasonal totals for WRF precipitation and CMAQ WD of nitrate, ammonium, and sulfate for the entire time series. The model consistently overestimates precipitation except during fall, with NMB for the annual total of 5.3%. R ² between modeled and observed seasonal precipitation is lowest in summer (0.47) and highest in winter (0.65). Correlation for the annual accumulated precipitation is higher, with an R ² value of 0.67. The model overestimates nitrate WD in winter (8.6%) and fall (12.4%) and underestimates it in spring (−8.2%) and summer (−6.7%) with NMB of the annual accumulation values of −11.0%. R ² for seasonal nitrate WD between the model and measurements is highest in spring (0.73) and lowest in summer (0.54), with a higher annual R ² of 0.76. The model generally underestimates ammonium WD for all seasons except for summer (NMB = 12.6%), with annual NMB of −11.0%. R ² for seasonal accumulated ammonium WD is below 0.5 except for spring (0.55), with an annual R ²of 0.60. For sulfate WD, the model only overestimates in summer (2.0%), with annual NMB of −4.5%. The R ² is comparable for all seasons (from 0.69 to 0.71), with slightly lower values in winter (0.57). In general, the model had better performance in simulating the WD of nitrate and sulfate than that of ammonium. As an additional reference, Table S1 in the supporting information provides the NMB for the precipitation and WD of nitrate, ammonium, and sulfate, based on years 2002–2006 compared to the analogous statistics from the evaluation of CMAQv4.7 WD estimates published in Appel et al. (2011).

Table 1.

Performance Metrics for Annual and Seasonal Accumulated WRF Precipitation Predictions and CMAQv5.0.2 Wet Deposition Predictions for Sulfate, Nitrate, and Ammonium Including Observation Mean (MEAN OBS), Model Mean (MEAN MOD), Mean Bias (MB), Normalized Mean Bias (NMB), Root‐Mean‐Square Error (RMSE), Mean Error (ME), Normalized Mean Error (NME), and Pearson Correlation Squared (R²)

Seasons	Variables	N	MEAN OBS	MEAN MOD	MB	NMB (%)	RMSE	ME	NME (%)	R 2
	Precipitation	1,964	94.41	99.4	4.99	5.3	26.81	19.82	21.9	0.67
	NO3 −	1,964	7.53	7.43	−0.09	−1.2	2.19	1.60	21.2	0.76
Annual	NH4 +	1,964	2.46	2.19	−0.27	−11.0	0.94	0.68	27.6	0.60
	SO4 2−	1,964	8.87	8.47	−0.40	−4.5	2.76	1.92	21.7	0.81
	Precipitation	1,631	20.94	22.37	1.43	6.8	9.69	7.02	33.5	0.65
	NO3 −	1,631	1.45	1.58	0.13	8.6	0.77	0.55	37.8	0.58
Winter	NH4 +	1,631	0.32	0.24	−0.07	−23.4	0.20	.012	37.9	0.46
	SO4 2−	1,631	1.51	1.23	−0.28	−18.6	0.85	0.57	37.4	0.57
	Precipitation	1,801	24.35	29.06	2.71	11.1	9.61	6.99	28.7	0.61
	NO3 −	1,801	2.20	2.02	−0.18	−8.2	0.77	0.57	26.0	0.73
Spring	NH4 +	1,801	0.85	0.63	−0.22	−26.2	0.46	0.31	36.9	0.55
	SO4 2−	1,801	2.63	2.53	−0.10	−3.7	1.09	0.74	28.3	0.71
	Precipitation	1,802	27.24	29.15	1.91	7.0	13.35	9.34	34.3	0.47
	NO3 −	1,802	2.59	2.42	−0.17	−6.7	1.04	0.77	29.7	0.54
Summer	NH4 +	1,802	0.87	0.98	0.11	12.6	0.49	0.36	41.3	0.41
	SO4 2−	1,802	3.14	3.20	0.06	2.0	1.51	0.99	31.5	0.69
	precipitation	1,853	23.77	22.11	−1.65	−7.0	8.87	6.38	26.9	0.64
	NO3 −	1,853	1.44	1.62	0.18	12.4	0.71	0.48	33.5	0.65
Fall	NH4 +	1,853	0.46	0.39	−0.07	−14.9	0.25	0.17	36.5	0.50
	SO4 2−	1,853	1.83	1.73	−0.10	−5.4	0.79	0.54	29.6	0.69

Note. The definition of the evaluation metrics can be found in the supporting information. Statistics are based on the modeled and observed data from 183 NADP/NTN sites. Note that not all 183 sites have a valid observation for every season of every year (i.e., N < 183 sites×11 years). Modeled and observed values were paired in space by matching the observations to the model values from the grid cell that contains the monitor. The units are centimeter for precipitation, and kilogram/hectare for wet deposition. WRF = Weather Research and Forecasting; cmaq = Community Multiscale Air Quality Model.

3.2. Cross‐Validation Comparison of Five Methods for Creating WD Maps

Two leave‐one‐out, cross‐validation analyses were conducted to evaluate different methods for combining NADP/NTN, PRISM, and model data to create WD maps. The cross validation was conducted as follows. For each year and each monitoring location, the annual WD from that site and any site within 48 km (four grid cells) was withheld from the estimation of the bias adjustment field for that year. This approach was used to evaluate how well the methods perform in areas without a NADP/NTN measurement. The cross‐validation prediction for the location and year of the withheld observation was then compared to the original NADP/NTN measurement.

3.2.1. Smoothing Radius

The first cross‐validation comparison was used to select the radius of the moving window averaging used to smooth the bias in the precipitation‐adjusted model values. The first row of Figure S2 shows the NMB, NME, and R ² values for WD of nitrate, ammonium, and sulfate for a radius of 100–700 km compared to not performing the smoothing step prior to creating bias maps via kriging. Results for a radius of 300–600 km are very similar. A radius of 300 km was selected because, on aggregate, this distance produced the best cross‐validation statistics for WD of sulfate and nitrate. For ammonium, the moving window smoothing increases the bias but decreases the error and improves the R ². The second row of Figure S2 shows a similar comparison across seven spatial interpolation methods available in the gstat library. Inverse distance weight (IDW) was compared to ordinary kriging (constant mean) and universal kriging (linear trend in site coordinates). Five different spatial covariance models were also compared: spherical and Matérn with smoothness parameter 0.5, 1.0, 1.5, and 2.0. The bias and error are reduced for all three species by using a kriging approach as opposed to the IDW. The statistics for the different kriging approaches are very similar, with some worsening of performance with the increased smoothness parameters. Universal kriging was selected with a Matérn covariance model with smoothness parameter 0.5, which is equivalent to what is referred to as an exponential covariance model.

3.2.2. Comparison of Five Methods for Creating WD Maps

A second cross validation was used to compare the raw CMAQ output and four methods for combining different sources of model and observed data. Table 2 provides evaluation summary statistics based on 1,964 observations, which include the 10 or 11 years of data from the 183 sites used in the study. Using only a precip‐adj (Method 2) or only a multiplicative deposition bias‐adjustment (Method 3) to adjust the modeled WD decreases the negative bias and increases the correlation with observations, compared to the unadjusted model values. Method 1, which combines both adjustments, provides additional improvement over using only one adjustment (i.e., even lower bias and higher R ² compared to Methods 2 and 3; see Table 2). The precip‐adj and bias‐adj results show very good agreement with observations, with NMB within 3% and R ² values between 0.77 and 0.90 (Figure S4). This is a clear improvement over the raw model output, especially for the Pacific, West, and Great Lakes regions (Figures S3 and S4) where the model performance for WD is usually poor due to terrain effects (Appel et al., 2011; Zhang et al., 2018). This result illustrates the value in incorporating data for both precipitation and WD in the bias‐adjusting of the model‐simulated WD. By taking advantage of the improved WD estimations from Method 1 in this study, Williams et al. (2017) found reduced bias in informing critical load exceedance calculations in the Pacific Northwest.

Table 2.

Cross‐Validation Statistics for the WD From CMAQv5.0.2 Output Only and Four Measurement‐Model Fusion Methods (Precip‐ Adj and Bias‐Adj (Method 1), Only Precipitation‐Adjustment (Precip‐Adj, Method 2), Only Bias‐Adjustment (Bias‐Adj, Method 3), and NTN × PRISM (Method 4)

Species	Fusion method	Mean Obs (kg/ha)	Mean mod (kg/ha)	MB (kg/ha)	NMB (%)	RMSE (kg/ha)	ME (kg/ha)	NME (%)	R 2
NO3 −	CMAQ outputs	7.53	7.43	−0.09	−1.2	2.19	1.60	21.2	0.76
	Method 1 (precip‐adj and bias‐adj)	7.53	7.53	0.00	0.0	1.53	1.10	14.6	0.86
	Method 2 (precip‐adj)	7.53	7.47	−0.05	−0.7	1.95	1.48	19.6	0.81
	Method 3 (bias‐adj)	7.53	7.63	0.10	1.4	1.92	1.36	18.1	0.79
	Method 4 (NTN × PRISM)	7.53	7.54	0.00	0.1	1.48	1.09	14.5	0.86
NH4 +	CMAQ outputs	2.46	2.19	−0.27	−11.0	0.94	0.68	27.6	0.60
	Method 1 (precip‐and bias‐adj)	2.46	2.39	−0.07	−2.9	0.69	0.48	19.6	0.76
	Method 2 (precip‐adj)	2.46	2.21	−0.25	−10.2	0.87	0.65	26.3	0.66
	Method 3 (bias‐adj)	2.46	2.41	−0.05	−1.8	0.79	0.57	23.0	0.70
	Method 4 (NTN × PRISM)	2.46	2.37	−0.09	−3.6	0.82	0.58	23.5	0.67
SO4 2−	CMAQ outputs	8.87	8.47	−0.40	−4.5	2.76	1.92	21.7	0.81
	Method 1 (precip‐and bias‐adj)	8.87	8.84	−0.03	−0.3	1.98	1.35	15.3	0.90
	Method 2 (precip‐adj)	8.88	8.56	−0.31	−3.4	2.37	1.66	18.7	0.86
	Method 3 (bias‐adj)	8.87	8.97	0.10	1.1	2.57	1.72	19.4	0.84
	Method 4 (NTN × PRISM)	8.87	8.86	−0.01	−0.1	2.08	1.39	15.7	0.89

Note. Summary statistics are based on N = 1,964 observations and include observation mean (MEAN OBS), model mean (MEAN MOD), mean bias (MB), normalized mean bias (NMB), root mean square error (RMSE), mean error (ME), normalized mean error (NME), and Pearson correlation squared (R ²). Evaluation metrics with the best performance values are shown in bold. WD = wet deposition; NTN = National Trends Network; PRISM = Parameter‐elevation Regressions on Independent Slopes Model.

Using NADP/NTN wet concentration and PRISM data alone (NTN × PRISM) in Method 4 provides estimates for WD of sulfate and nitrate that have similar correlation and bias compared to the approach of precip‐adj and bias‐adj, which utilizes CMAQ output. For ammonium, Method 1 offers a higher correlation (R ² of 0.77 compared to 0.67) as well as slightly lower bias (NMB of −2.9% compared to 3.6%) compared to Method 4, which relies on observations only. Additional differences in the methods that are not reflected in the cross‐validation are evident in the final spatial maps of WD shown in the next section.

3.3. Spatial Maps of WD

Figure 5 shows maps of annual accumulated WD of nitrate in 2012 based on four different approaches. TDEP in the top left and the NTN × PRISM approach (Method 4) in the bottom left are observation‐based approaches. The base model CMAQ and precip‐adjusted and bias‐adjusted CMAQ maps (Method 2) are shown in the top right and bottom right, respectively. Maps of the bias adjustment applied to the base model output to produce the final map of WD of nitrate are shown in supporting information Figure S5. Maps of precip‐adjusted and bias‐adjusted CMAQ WD of sulfate and ammonium for 2012 are provided in Figure S6.

Figure 5.

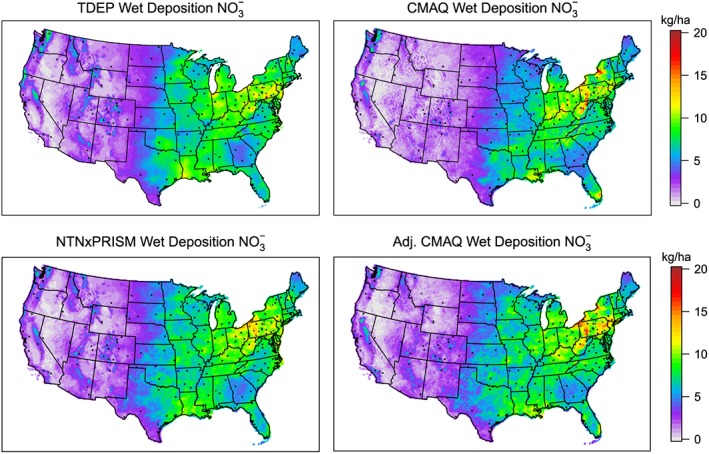
Annual wet deposition of nitrate (kg/ha) in 2012 based on TDEP (top left), CMAQ (top right), NTN × PRISM (Method 4; bottom left) and precip‐adjusted and bias‐adjusted CMAQ (Method 2; bottom right). National Atmospheric Deposition Program/National Trends Network monitor locations with annual data for 2012 are shown on all the maps. Sites that were dropped from the trend analysis in section 3.4 because they did not have a sufficiently long time series of measurements are shown in gray. TDEP = NADP Total Deposition; CMAQ = Community Multiscale Air Quality Model; NTN = National Trends Network; PRISM = Parameter‐elevation Regressions on Independent Slopes Model.

The TDEP map in Figure 5 is more spatially smooth than the other approaches, with some “bullseye” spatial gradients common with IDW interpolation. The NTN × PRISM map has less of this bullseye effect but is missing some of the hot spots in the Northeast that are captured by the model. The base model output underestimates the WD throughout much of the domain west of the Mississippi River. The spatial gradients in the precip‐ adjusted and bias‐adjusted map in this region are more consistent with the observation‐only based maps without smoothing out the spatial heterogeneity of the original model output. These differences are not necessarily reflected in the evaluation in section 3.2 because the cross validation is limited by the spatial coverage of the observation network. The model‐based approaches reflect spatial heterogeneity in local emissions sources that cannot be captured by the measurement network.

3.4. Evaluation of Model Predicted Trends

A trend analysis was used to assess the CMAQv5.0.2 system's ability to predict changes in WD during 2002 to 2012 with and without the precipitation and bias adjustments. During this 11‐year period, emission reduction programs such as the EPA's Acid Rain Program, Nitrogen Oxides State Implementation Plan Call, and Clear Air Interstate Rule led to a substantial decrease in emissions of nitrogen oxides and sulfur dioxide (e.g., Gilliland et al., 2008; Hand et al., 2014). The impact of such emission reductions on WD can be seen in Figure 6 which shows the Theil‐Sen slope estimator for the annual WD of nitrate, ammonium, and sulfate. The trends shown in Figure 6 are based on raw CMAQ output (left column) and adjusted CMAQ values (right column, Method 1). Trends based on the NADP/NTN measurements are overlaid on these spatial fields and show that there has been a steady decrease in WD of nitrate and sulfate from 2002 to 2012 in the eastern half of the United States, particularly in the Northeast where the average decrease across the entire 11 years is 30% for nitrate and 50% for sulfate. Figure S7 provides scatterplots of the observed versus modeled and adjusted modeled trends at the 68 NADP/NTN locations that met the full CC. Use of the raw CMAQ output led to an overestimation of this observed negative trend in the Great Lakes and Northeast regions and parts of states on the Pacific Coast. The trends in WD of nitrate based on the adjusted model output are more consistent with the spatial patterns in the observed data, with the root‐mean‐square error (RMSE) of the estimated trends decreasing from 0.35 to 0.24 kg/ha/year in the Northeast and from 0.22 to 0.18 in the Great Lakes (Figure S7). Trends in WD of nitrate and sulfate are also improved in the Southeast with the RMSE for nitrate decreasing from 0.29 to 0.10 kg/ha/year and the RMSE for sulfate decreasing from 0.29 to 0.17 kg/ha/year. This improvement illustrates the value of adjusting the model output to account for errors in modeled precipitation and model bias due to emissions or other processes impacting WD. Note that the 68 NADP/NTN locations that met the full CC are plotted in Figure 5 as circles. The sites that were added with the relaxed CC (plotted as squares) help fill in spatial information, while not changing the overall conclusions drawn from the model predicted trends.

Figure 6.

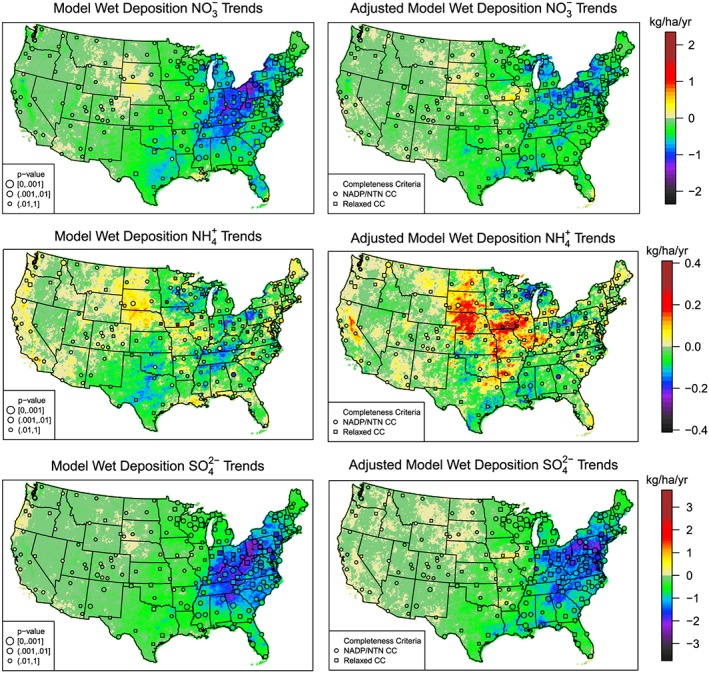
Theil‐Sen trends (i.e., slopes) for the 2002–2012 time series of annual wet deposition at each NADP/NTN location and each model grid cell based on raw Community Multiscale Air Quality Model output (left column) and precip‐and bias‐adjusted Community Multiscale Air Quality Model output (right column) for wet deposition of nitrate (top row), ammonium (middle row) and sulfate (bottom row). Note the change in scale for ammonium. Trends at the NADP/NTN locations that met the full NADP/NTN completeness criteria are shown as colored circles with the remaining sites used in the analysis shown as colored squares. The size of the circle/square is based on the p‐value of a nonparametric Kendall rank test. A larger symbol indicates a statistically significant linear trend in the time series. NADP/NTN = National Atmospheric Deposition Program/National Trends Network; CC = completeness criteria.

Trends in WD of ammonium from the adjusted model outputs are more spatially and temporally heterogeneous, with essentially no trend throughout much of the CONUS except for some slightly positive trends in parts of the Great Plains and Central Valley of California. (Note the change in scale in Figure 6 for ammonium compared to the maps for nitrate and sulfate.) Spatial features in ammonium are better captured by the adjusted model time series compared to the raw model output, with the RMSE of the trends decreasing in the West, Southeast, and Great Lakes and remaining constant in the other regions (Figure S7).

4. Summary and Conclusions

Using observational data from NADP/NTN, we evaluated an 11‐year time series of CMAQv5.0.2 simulations to assess the model's performance in estimating annual WD. The model underestimates the annual WD of NO₃ ⁻, NH₄ ⁺, and SO₄ ²⁻, with NMB of −1.2%, −11.0%, and −4.5%, respectively. To further improve the model's performance in simulating annual WD, we developed an approach to bias correct CMAQ model outputs using observation‐based gridded PRISM precipitation and the WD measurements at the NADP/NTN sites. Cross‐validation analysis shows that the new bias‐adjusted model outputs have much lower bias and higher R ² compared to the unadjusted model values. The NMB values for the annual WD of NO₃ ⁻, NH₄ ⁺, and SO₄ ²⁻ from the adjusted model outputs are 0.0%, −2.9%, and 0.3%, respectively. Spatial maps of the adjusted WD reflect spatial heterogeneity in local emissions and precipitation compared to the observation‐based approaches considered here that tended to be more spatially smooth. The improved measurement‐model fused WD estimates can be used to develop more precise cause‐effect relationships between atmospheric deposition and sensitive aquatic and terrestrial ecosystems, particularly at high elevations that are impacted by orographic effects on precipitation.

The temporal trends in annual WD of NO₃ ⁻, NH₄ ⁺, and SO₄ ²⁻ are also captured by the model. Statistically significant negative trends are found for WD of NO₃ ⁻ and SO₄ ²⁻, especially in the eastern United States using the precipitation‐ adjusted and bias‐adjusted model outputs, while this trend is underestimated using the raw model outputs. The trends based on the precipitation‐ adjusted and bias‐adjusted model outputs show much greater consistency with the spatial patterns in the observed data, illustrating the merits of our new methods. The use of air quality modeling for estimating trends offers the ability to perform accountability studies where simulations are used to quantify the impact of the control measures on ambient concentrations and WD. Air quality modeling also allows for assessment of alternative emission strategies, changes in land use and meteorology. Future simulations are typically run using base‐year meteorology, allowing for the same precipitation adjustment to be applied. The appropriateness of applying the second bias adjustment to future or alternative simulations will depend on the scenario being modeled.

Accurate quantification of WD and DD is essential for assessing critical loads exceedances and effects on ecosystems. Improvements to WD have been demonstrated in the current work. Measurement‐model fusion can be used to correct biases in model output while maintaining the spatial detail that the model provides. As described in the GAW report (WMO, 2017), measurement‐model fusion approaches for deposition have already been adopted by multiple groups. TDEP is widely used in the United States and uses a measurement‐model fusion approach for the calculation of DD. Inclusion of measurement‐model fusion for WD has been identified by the NADP TDEP committee as a next step for U.S. TD maps. The analysis presented here can inform the selection of the fusion method for WD. Note that the incommensurability between volume‐average model output values and point measurements can impact evaluation results and interpretation. This issue is present in model evaluation and data fusion methods for all modeled pollutants and has been discussed in the literature most frequently for ambient concentration of ozone and PM_2.5 (e.g., Gelfand et al. (2001); Fuentes and Raftery (2005); Swall and Foley (2009)). Addressing the issue of incommensurability in WD estimates is complicated by the fact that the subgrid variability in precipitation can be quite different from the subgrid variability in concentrations, and these differences will vary across the country. For example, a WD measurement in the Rocky Mountains might be different from a 12‐km × 12‐km average due to orographic effects while a measurement site in the Ohio River Valley may not be representative because it is upwind of a large source that does influence the 12‐km × 12‐km volume average. The NADP/NTN network is not dense enough to evaluate how much subgrid variability in WD can be expected within a 12‐km × 12‐km grid cell and how this subgrid variability changes across the country. Based on our current and prior analyses, we believe that the issue of incommensurability does not preclude the use of the NADP/NTN measurements to provide information on broad regional biases in the model due to errors in emissions, meteorology, chemistry, and boundary conditions. Future work will include a comparison of alternative fusion methods such as the optimal interpolation methods developed by Robichaud et al. for the GEM‐MACH air quality model (WMO, 2017). Improvements to deposition modeling within the CMAQ system can also reduce the need for bias correction of model outputs. Finally, the analysis methods developed here focused on the estimation of annual total WD. An assessment of data fusion methods for seasonal totals is needed to evaluate the effectiveness of these adjustment methods across different seasons.

Supporting information

Supporting Information S1

Zhang, Y. , Foley, K. M. , Schwede, D. B. , Bash, J. O. , Pinto, J. P. , & Dennis, R. L. (2019). A measurement‐model fusion approach for improved wet deposition maps and trends. Journal of Geophysical Research: Atmospheres, 124, 4237–4251. 10.1029/2018JD029051