Detection of Fossil and Biogenic Methane at Regional Scales Using Atmospheric Radiocarbon

Abstract

Regional emissions of methane and their attribution to a variety of sources presently have large uncertainties. Measurements of radiocarbon (¹⁴C) in methane (CH₄) may provide a method for identifying regional CH₄ emissions from fossil versus biogenic sources because adding ¹⁴C‐free fossil carbon reduces the ¹⁴C/C ratio (Δ¹⁴CH₄) in atmospheric CH₄ much more than biogenic carbon does. We describe an approach for estimating fossil and biogenic CH₄ at regional scales using atmospheric Δ¹⁴CH₄ observations. As a case study to demonstrate expected Δ¹⁴CH₄ and Δ¹⁴CH₄‐CH₄ relationships, we simulate and compare Δ¹⁴CH₄ at a network of sites in California using two gridded CH₄ emissions estimates (Emissions Database for Global Atmospheric Research, EDGAR, and Gridded Environmental Protection Agency, GEPA) and the CarbonTracker‐Lagrange model for 2014, and for 2030 under business‐as‐usual and mitigation scenarios. The fossil fraction of CH₄ (F) is closely linked with the simulated Δ¹⁴CH₄‐CH₄ slope and differences of 2–21% in median F are found for EDGAR versus GEPA in 2014, and 7–10% for business‐as‐usual and mitigation scenarios in 2030. Differences of 10% in F for >200 ppb of added CH₄ produce differences of >10‰ in Δ¹⁴CH₄, which are likely detectable from regular observations. Nuclear power plant ¹⁴CH₄ emissions generally have small simulated median influences on Δ¹⁴CH₄ (0–7‰), but under certain atmospheric conditions they can be much stronger (>30‰) suggesting they must be considered in applications of Δ¹⁴CH₄ in California. This study suggests that atmospheric Δ¹⁴CH₄ measurements could provide powerful constraints on regional CH₄ emissions, complementary to other monitoring techniques.

Key Points

• Approach for using ¹⁴C to detect fossil and biogenic CH₄ at regional scales is described and ¹⁴CH₄ is simulated in California

• Strong potential for estimating the fossil fraction of regional CH₄ emissions and evaluating bottom‐up estimates with ¹⁴CH₄ observations

• Simulated influences of nuclear power plant emissions on ¹⁴CH₄ in California are small on average but highly variable

1. Introduction

Current estimates of methane (CH₄) emissions on global and regional scales have large uncertainties and large discrepancies, particularly for the attribution of CH₄ emissions to specific sectors (Bergamaschi et al., 2018; Jeong et al., 2016; Kirschke et al., 2013; Miller, Wofsy, et al., 2013). Observations of radiocarbon (¹⁴C) in atmospheric methane currently provide the main observational constraint on the fossil fraction of global total CH₄ emissions (Etiope et al., 2008; Kirschke et al., 2013; Lassey, Lowe, & Smith, 2007). Radiocarbon is absent from fossil fuels because of the radioactive decay that occurs over the long time required for fossil fuels to be formed. In contrast, biogenic carbon incorporates the ¹⁴C/C ratio (Δ¹⁴C; Stuiver & Polach, 1977) from atmospheric CO₂, and CH₄ produced from biogenic sources reflects the Δ¹⁴C in atmospheric CO₂ as well as the residence time of the biogenic carbon before it is released as CH₄.

The Δ¹⁴C in atmospheric CH₄ (Δ¹⁴CH₄) is influenced by the amount of CH₄ emitted from fossil and biogenic sources, the Δ¹⁴C of biogenic sources, and the emissions of ¹⁴CH₄ from nuclear power plants. Over the industrial period, Δ¹⁴CH₄ has increased due to anthropogenic emissions of ¹⁴C from nuclear weapons testing and nuclear power plants.

Studies of Δ¹⁴CH₄ have primarily focused on the global long‐term trend in Δ¹⁴CH₄ (Lassey, Lowe, et al., 2007; Lowe et al., 1988; Quay et al., 1991; Wahlen et al., 1989), with few studies reporting measurements in polluted areas. Townsend‐Small et al. (2012) measured Δ¹⁴CH₄ in six samples collected over 2 days at Mount Wilson in the Los Angeles area of California, USA, in 2009, concluding qualitatively that there was evidence for fossil methane emissions in Los Angeles because samples enhanced in CH₄ were generally lower in Δ¹⁴CH₄. The only other continental observations of atmospheric Δ¹⁴CH₄ have been at European continental sites, which are strongly influenced by emissions of ¹⁴CH₄ from nuclear power plants (Eisma et al., 1995; Levin et al., 1992).

Even though very few regional‐scale observations have been made to date, atmospheric Δ¹⁴CH₄ could provide powerful constraints on the fossil fraction of regional CH₄ emissions. In this paper, we will examine regional CH₄ emissions in California. In California, reductions in total greenhouse gas emissions of 40% below 1990 levels are planned for 2030, with separate mitigation targets for CH₄ emissions from different sectors including landfills, livestock, and oil and gas (California Air Resources Board [CARB], 2017b, 2017c). However, there are large discrepancies across sector‐specific CH₄ emission estimates in California, with fossil fractions spanning 11% to 31% for state totals (Jeong et al., 2013).

Some prior studies have used measurements of stable isotopes of CH₄, ethane, or other trace gases to assess CH₄ emissions from different sectors in California. Using stable isotope measurements at Mount Wilson, made over the same 2 days as the Δ¹⁴CH₄ observations in 2009, Townsend‐Small et al. (2012) found that δ¹³C and δD data were consistent with a dominant fossil source of CH₄, which has heavier stable isotopic signatures than biogenic CH₄. Measurements of ethane, which is coemitted from fossil sources including natural gas distribution, made with aircraft campaigns in Los Angeles over 2 months in 2010 were used to estimate that biogenic and fossil emissions in Los Angeles were roughly equal (Peischl et al., 2013), whereas another study from the same campaign suggested fossil emissions were larger (Wennberg et al., 2012). Jeong et al. (2017) found that CH₄ emissions in the San Francisco Bay were primarily biogenic, derived from landfills, by applying an inversion technique with measurements of three volatile organic compounds where ethane data provided the main constraint on source partitioning. There can be large uncertainties in these estimates due to variable or poorly known isotopic or trace gas source signatures and due to short sampling periods of some field campaigns. Discrepancies can also arise from differences in the specific geographical areas of influence on the different measurements. More development of atmospheric observations to evaluate sector‐level emissions is needed to refine understanding of CH₄ emissions and attribute the causes of emissions changes over time.

The aim of this paper is to develop the application of Δ¹⁴CH₄ measurements to assess regional‐scale CH₄ emissions. We present a framework to use regional‐scale Δ¹⁴CH₄ and CH₄ measurements to estimate fossil‐derived and biogenic CH₄, and we discuss the associated uncertainties. As a case study, we simulate gradients in Δ¹⁴CH₄ and in CH₄ concentration in California for the full year 2014, given current estimates of biogenic and fossil CH₄ emissions. Then, we simulate the expected changes in Δ¹⁴CH₄ and CH₄ gradients under the mitigation targets from the CARB and under a business‐as‐usual (BAU) scenario (CARB, 2017c). We then assess the impact of ¹⁴CH₄ emissions from nuclear power plants on Δ¹⁴CH₄ in California in 2014. These simulations explore how observed Δ¹⁴CH₄ could be expected to vary over California, a region of mixed CH₄ sources, if Δ¹⁴CH₄ measurements were deployed in a regional atmospheric observation network. Finally, we discuss and provide recommendations for implementation of regional‐scale Δ¹⁴CH₄ observation and analysis systems.

2. Approach for Estimating Biogenic and Fossil CH₄ From Δ¹⁴CH₄

In this section, we describe how biogenic and fossil‐derived CH₄ could be estimated from atmospheric Δ¹⁴CH₄ measurements at regional scales. The approach follows more extensive prior work on the use of radiocarbon to estimate fossil‐derived CO₂ using atmospheric Δ¹⁴CO₂ measurements at regional scales (Graven et al., 2018; Levin et al., 2003; Turnbull et al., 2009), but we emphasize some important differences between Δ¹⁴CO₂ and Δ¹⁴CH₄. These differences include the larger disequilibrium between biogenic and atmospheric CH₄, which is also generally of opposite sign compared to CO₂, the potential for larger measurement uncertainty in Δ¹⁴CH₄ than in Δ¹⁴CO₂, and the potential for stronger influence of nuclear power plant emissions in certain regions.

Calculation of biogenic CH₄ (C_b) and fossil CH₄ (C_f) is based on mass balances for CH₄ and for ¹⁴CH₄:

$${\mathrm{C}}_{\mathrm{m}}={\mathrm{C}}_{\mathrm{bg}}+{\mathrm{C}}_{\mathrm{b}}+{\mathrm{C}}_{\mathrm{f}}-{\mathrm{C}}_{\mathrm{s}}$$ (1)

$${∆}_{\mathrm{m}}{\mathrm{C}}_{\mathrm{m}}={∆}_{\mathrm{bg}}{\mathrm{C}}_{\mathrm{bg}}+{∆}_{\mathrm{b}}{\mathrm{C}}_{\mathrm{b}}+{∆}_{\mathrm{f}}{\mathrm{C}}_{\mathrm{f}}-{∆}_{\mathrm{m}}{\mathrm{C}}_{\mathrm{s}}+{\mathrm{A}}_{\mathrm{n}}$$ (2)

Here C_m indicates the CH₄ concentration measured at an observation site, C_bg indicates the background or reference CH₄ concentration upwind of the region of interest, C_f indicates the CH₄ concentration caused by fossil‐derived CH₄ emissions over the region of interest, and C_b indicates the CH₄ concentration caused by biogenic CH₄ emissions over the region of interest. C_s indicates the decrease in CH₄ concentration caused by CH₄ sinks over the region of interest. In equation (2), an approximate mass balance for ¹⁴CH₄ is constructed by multiplying the terms in equation (1) by their Δ¹⁴C values indicated by Δ. For C_s, the Δ¹⁴C measured at the observation site is used, assuming that the CH₄ being removed by sinks in the region has approximately the same Δ¹⁴C as the Δ¹⁴CH₄ measured. While isotopic fractionation occurs during CH₄ sink reactions, the Δ¹⁴C notation includes a correction for mass‐dependent fractionation and is therefore unaffected by fractionation from CH₄ sinks. An additional term in equation (2), A_n, relates to the ¹⁴CH₄ present due to nuclear power plant emissions in the region of interest. This term does not appear in equation (1) because the emissions are too small to affect the CH₄ concentration. For consistency with the other terms, A_n includes a factor of 1,000‰/R_s, where R_s is the ratio ¹⁴C/C in the Modern radiocarbon standard.

Rearranging these equations to solve for C_f and C_b results in

$${\mathrm{C}}_{\mathrm{f}}=\left({\mathrm{C}}_{\mathrm{m}}+{\mathrm{C}}_{\mathrm{s}}\right)\frac{\left({∆}_{\mathrm{m}}-{∆}_{\mathrm{b}}\right)}{\left({∆}_{\mathrm{f}}-{∆}_{\mathrm{b}}\right)}-{\mathrm{C}}_{\mathrm{bg}}\frac{\left({∆}_{\mathrm{bg}}-{∆}_{\mathrm{b}}\right)}{\left({∆}_{\mathrm{f}}-{∆}_{\mathrm{b}}\right)}-\frac{{\mathrm{A}}_{\mathrm{n}}}{\left({∆}_{\mathrm{f}}-{∆}_{\mathrm{b}}\right)}$$ (3)

$${\mathrm{C}}_{\mathrm{b}}={\mathrm{C}}_{\mathrm{m}}+{\mathrm{C}}_{\mathrm{s}}-{\mathrm{C}}_{\mathrm{bg}}-{\mathrm{C}}_{\mathrm{f}}$$ (4)

C_f can be calculated from equation (3) given measurements or estimates of the variables on the right hand side. Δ_f is defined as −1,000‰ since fossil carbon has no ¹⁴C. Then, C_b can be calculated using C_f from equation (3). The fossil fraction (F) of added CH₄ (C_f + C_b) relates to C_f and C_b by

$$F=\frac{{\mathrm{C}}_{\mathrm{f}}}{{\mathrm{C}}_{\mathrm{f}}+{\mathrm{C}}_{\mathrm{b}}}=1-\frac{{\mathrm{C}}_{\mathrm{b}}}{{\mathrm{C}}_{\mathrm{f}}+{\mathrm{C}}_{\mathrm{b}}}.$$ (5)

The formulation of C_f in equation (3) differs from the calculation of fossil fuel‐derived CO₂. For CO₂, the biogenic source term (CO₂ from respiration and/or biomass burning) appears in the equation for fossil fuel‐derived CO₂ in a correction term that can be ignored, approximated, or estimated using models (Graven et al., 2018; Turnbull et al., 2009). In contrast, the biogenic source term for CH₄, C_b, is one of the unknowns we want to solve for. Therefore, we manipulate the equations in a different way in order to eliminate C_b from equation (3).

In regional studies of CH₄, CH₄ sinks are typically ignored (C_s assigned to be zero) because the timescales of atmospheric mixing and transport over regional scales (days to weeks) are much shorter than the chemical lifetime of CH₄ (a decade) (Manning et al., 2011). The term A_n is expected to vary strongly by region, depending on the number of nuclear power plants nearby. Previous studies have shown large influences in Europe, which has a high density of pressurized water reactors that emit ¹⁴CH₄ (Eisma et al., 1995; Levin et al., 1992). The influence of these reactors on Δ¹⁴CH₄ is larger than for Δ¹⁴CO₂ because most of the ¹⁴C is emitted as ¹⁴CH₄ and because the concentration of CH₄ in the atmosphere is 200 times lower than for CO₂. Uncertainties in regional nuclear power plant influences on Δ¹⁴CH₄ include uncertainties in ¹⁴CH₄ emissions and in the simulated transport of ¹⁴CH₄ to the measurement site, both of which strongly depend on the region of interest. We explore the magnitude of A_n for California in section 4.3.

The current level of Δ¹⁴CH₄ in background air is likely close to 350‰, based on the most recently reported observations (Townsend‐Small et al., 2012). However, we note that there are no published measurements of atmospheric Δ¹⁴CH₄ after 2009. For a regional observation network, it is likely that Δ_bg would be specified by an observation site in the network that is upwind of the region of interest. Uncertainty in Δ_bg would be influenced by the uncertainty in Δ¹⁴CH₄ measurements as well as variability in Δ_bg. Uncertainty in measured Δ¹⁴CH₄, contributing to uncertainty in Δ_m and Δ_bg, was ±5‰ to ±11‰ in the most recently reported observations from Townsend‐Small et al. (2012). This is substantially higher than the uncertainty in measurements of Δ¹⁴CO₂ (±2‰ to ±3‰, Miller, Lehman, et al., 2013), indicating that additional sample processing or smaller sample size for CH₄ compared to CO₂ contribute substantial uncertainty to Δ¹⁴CH₄ measurements. Since there are very few measurements of Δ¹⁴CH₄ it is difficult to assess variability in Δ_bg. Observations made between 1986 and 2000 show standard deviations of ±7‰ in annual, hemispherically binned data (Lassey, Etheridge, et al., 2007), but variability on regional scales may be larger, particularly for places that may receive air from continental rather than marine upwind areas. In order to quantify Δ_bg and its uncertainty, regional observation networks should include one or more regional background sites.

The Δ¹⁴C of biogenic CH₄ emissions, Δ_b, for recently assimilated organic material that is the substrate for CH₄ from livestock, rice paddies, and landfills will be similar to atmospheric Δ¹⁴CO₂, approximately 20‰ in 2014 (Graven et al., 2017). For CH₄ produced from older organic material Δ_b may be higher or lower, depending on the age of the organic material (Chanton et al., 1995; Garnett et al., 2013; Nakagawa et al., 2002). Materials aged on the order of decades would have higher Δ_b due to nuclear weapons testing and the subsequent decline in Δ¹⁴CO₂, whereas materials aged over centuries or millennia would have lower Δ_b due to radioactive decay. In California, natural biogenic CH₄ emissions from wetlands and biomass burning are estimated to be much smaller than biogenic CH₄ emissions from human activities; however, in other regions, these natural emissions may be substantial.

Determination of C_f, C_b, and F using equations (3)–(5) also depends on C_bg, which had a global average value of 1,823 ppb in 2014 (www.esrl.noaa.gov/gmd/ccgg/trends_ch4/). While uncertainty in individual CH₄ measurements (uncertainty in C_m) is typically ±1 ppb (Andrews et al., 2014; Verhulst et al., 2017), uncertainty in C_bg can be substantially larger, depending on the region and season of interest. In Jeong et al. (2013), uncertainty in C_bg was estimated to be 17–25 ppb for observation sites in central California, and analysis by Verhulst et al. (2017) indicated similar magnitudes in C_bg uncertainty for southern California sites.

Comparing these estimates of uncertainty shows that the main contributors of uncertainty in C_f, C_b, and F calculated with Δ¹⁴CH₄ and CH₄ measurements are uncertainties in Δ_m, Δ_bg, and C_bg. Depending on the region's proximity to nuclear power plants, uncertainty in A_n could also contribute a large uncertainty. Considering a scenario with C_m approximately 200 ppb above C_bg, using current estimates above and neglecting C_s and A_n, estimated uncertainties in C_f and C_b would be roughly 20–30 ppb, with approximately 10–15% uncertainty in F. Uncertainties in C_f, C_b, and F would likely improve with strong efforts to reduce measurement uncertainty in Δ¹⁴CH₄ and to characterize background CH₄ concentration.

As an alternative to direct estimation of F, C_b, and C_f, observed relationships between Δ¹⁴CH₄ and CH₄ could be compared to model simulations to detect biases in the fossil fraction of CH₄ emissions estimates. Both fossil CH₄ (Δ_f = −1,000‰) and biogenic CH₄ (Δ_b = 20‰, for Δ¹⁴CO₂ in 2014) are lower in Δ¹⁴C than atmospheric CH₄ (Δ_bg = 350‰, estimated from available data). Therefore, both fossil and biogenic emissions will act to decrease Δ¹⁴C of atmospheric CH₄, but fossil emissions have a larger influence per ppb of added CH₄ because fossil CH₄ has a larger disequilibrium with atmospheric Δ¹⁴CH₄.

The influence of different individual processes on atmospheric CH₄ concentration and Δ¹⁴CH₄ is summarized in the diagram in Figure 1, constructed using equations (1) and (2). Here we use the radiocarbon signatures and background CH₄ concentration described above. As shown in Figure 1, if only a pure biogenic source of CH₄ were added to atmospheric CH₄, then CH₄ concentration would increase and Δ¹⁴CH₄ would decrease following the green line. If only a pure fossil source of CH₄ were added to atmospheric CH₄, then CH₄ concentration would increase and Δ¹⁴CH₄ would decrease following the black line. For a mixture of fossil and biogenic sources, the changes would fall between the green and black lines, and the dashed lines show examples of mixtures in 25% increments. If atmospheric CH₄ were affected only by CH₄ sinks, the CH₄ concentration would decrease while Δ¹⁴CH₄ would not change. If atmospheric CH₄ were affected only by nuclear power plant emissions, which produce a very small amount of ¹⁴CH₄ that is negligible compared to atmospheric CH₄ concentrations, Δ¹⁴CH₄ would increase while CH₄ concentration would not change.

Figure 1.

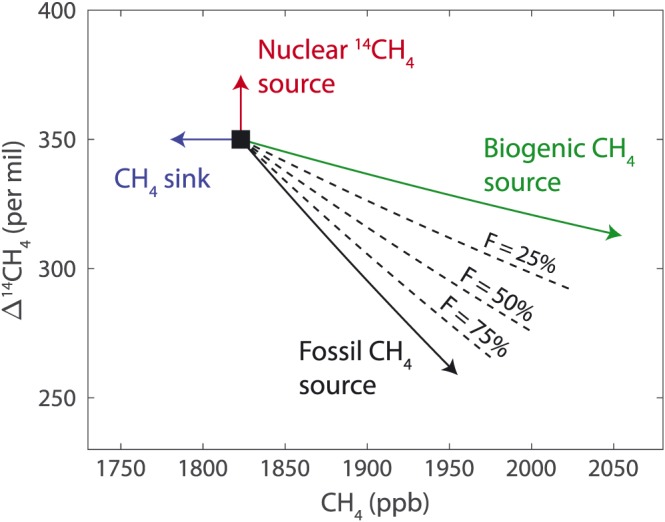
Diagram showing the expected change in CH₄ concentration and change in Δ¹⁴CH₄ from background values for different processes in 2014. Estimated global mean background composition in 2014 is shown with the black square. The dashed lines show the changes expected from mixed biogenic and fossil CH₄ sources, with F denoting the fossil fraction of emissions.

When nuclear ¹⁴CH₄ emissions and CH₄ sinks can be neglected or otherwise accounted for, the decrease in Δ¹⁴CH₄ expected per 10 ppb of added biogenic CH₄ is approximately 1.8‰, whereas the decrease in Δ¹⁴CH₄ per 10 ppb of added fossil CH₄ is approximately 7.1‰ (green and black lines in Figure 1) for CH₄ additions of up to 200 ppb. Comparing a pure biogenic CH₄ source (F = 0%) with a mixed source of 25% fossil CH₄ and 75% biogenic CH₄ (F = 25%), the decrease in Δ¹⁴CH₄ is approximately 3.1‰ per 10 ppb of added CH₄, about 70% more than for a pure biogenic CH₄ source. Similarly, going from a fossil fraction of 25% to 50%, the impact on Δ¹⁴CH₄ is about 1.3‰ per 10 ppb larger (4.4‰ per ppb; Figure 1). However, the sensitivity of Δ¹⁴CH₄ to a 10 ppb addition of CH₄ diminishes for large additions of CH₄. For large CH₄ additions more than a few hundred parts per billion, the overall sensitivities will be smaller than those quoted here.

Based on these sensitivities, we can consider how a bias in F simulated using an emission estimate with an atmospheric model could be detected using observations of CH₄ and Δ¹⁴CH₄. A bias of 10% in F for a 200‐ppb addition of CH₄ will result in a 10‰ difference in the observed decrease in Δ¹⁴CH₄ below Δ_bg, a difference that might be discernible with current measurement precision in Δ¹⁴CH₄. A larger CH₄ addition will have a slightly lower sensitivity but a larger absolute magnitude; for example, a 10% difference in F for a 500‐ppb addition of CH₄ will cause a 22‰ difference in the simulated decrease in Δ¹⁴CH₄. Regular observations could enable detection of differences in simulated and observed CH₄‐Δ¹⁴CH₄ relationships and therefore differences in F, with a larger number of measurements providing improved detectability.

Interpretation of observed CH₄‐Δ¹⁴CH₄ relationships will be sensitive to the uncertainties presented above, primarily the measurement uncertainty in Δ¹⁴CH₄, and comparisons with simulations will also be sensitive to uncertainty in modeled atmospheric transport. In this paper, we will present simulations of CH₄ and Δ¹⁴CH₄ in California in a similar way as Figure 1, demonstrating differences in the simulated CH₄ and Δ¹⁴CH₄ relationships arising from differences in the CH₄ emissions used.

3. Model Simulations in California

As a demonstration of expected regional Δ¹⁴CH₄ gradients and CH₄‐Δ¹⁴CH₄ relationships, we conduct simulations for the year 2014 in western North America, focused on the state of California. California has a relatively dense network of observation sites, run by several laboratories, where atmospheric gases are measured. Some of these sites have been used previously for field campaign measurements of Δ¹⁴CO₂ (Graven et al., 2018), and they could feasibly be used in the future for Δ¹⁴CH₄ measurements.

We run three types of forward simulations. The first uses current estimates of CH₄ emissions to simulate CH₄ and Δ¹⁴CH₄ for the year 2014 using two different CH₄ emissions estimates. These simulations demonstrate the expected regional Δ¹⁴CH₄ gradients and CH₄‐Δ¹⁴CH₄ relationships in contemporary atmospheric measurements. They demonstrate how Δ¹⁴CH₄ gradients and CH₄‐Δ¹⁴CH₄ relationships change when the relative amount of fossil and biogenic emissions differs between different CH₄ emissions estimates, providing an indication of how Δ¹⁴CH₄ measurements could help to evaluate CH₄ emissions estimates. The second type of simulation scales current emissions according to expected changes for the year 2030, following either targeted emissions mitigation policies or “business‐as‐usual” changes in emissions. These simulations show how changes in emissions will be reflected in atmospheric CH₄ and Δ¹⁴CH₄ and provide an indication of how atmospheric CH₄ and Δ¹⁴CH₄ measurements might detect these changes. The final type of simulation includes nuclear power plant ¹⁴CH₄ emissions in the contemporary simulations to assess the magnitude of Δ¹⁴CH₄ enhancement by nuclear power plant emissions, which counteracts the influences of local fossil and biogenic CH₄ emissions.

In practice, the measurements of atmospheric CH₄ and Δ¹⁴CH₄ that we simulate here could be deployed in a regional inversion system to separately estimate regional fossil and biogenic emissions. We do not explicitly quantify the performance of such an inversion system using radiocarbon data, as in the simulation experiments using Δ¹⁴CO₂ in, for example, Basu et al. (2016) and Fischer et al. (2017). Instead, our aim is to elucidate how CH₄ and Δ¹⁴CH₄ are likely to vary in California's region of mixed anthropogenic sources. This provides a first step in understanding how atmospheric Δ¹⁴CH₄ measurements could contribute to studies of regional CH₄ sources and in planning for optimal deployment of Δ¹⁴CH₄ measurements at regional scales.

3.1. Atmospheric Transport Modeling With CarbonTracker‐Lagrange

We conduct simulations using the atmospheric modeling system CarbonTracker‐Lagrange (https://www.esrl.noaa.gov/gmd/ccgg/carbontracker‐lagrange/). CarbonTracker‐Lagrange couples an atmospheric model (Weather Research and Forecasting model) with a Lagrangian model (Stochastic Time‐Inverted Lagrangian Transport model) to compute station sensitivity footprints. A footprint is a spatial grid of scaling factors that show how much a unit of emission in each grid cell would increase the concentration of an atmospheric species at a particular location and time. Footprints from CarbonTracker‐Lagrange are available with hourly resolution on a low‐resolution 1.0° × 1.0° grid for the 10 days preceding the observation time and on a high‐resolution 0.1° × 0.1° grid for 24 hr preceding the observation time. Here we consider time‐invariant CH₄ emissions, so we integrate the high‐resolution footprint for the first 24 hr and the low‐resolution footprint for the second day onward to calculate a total, 10‐day footprint for each observation.

The observation sites we consider are listed in Table 1 and shown in Figure 2i. We use local afternoon observation times of 15:00 that are included in CarbonTracker‐Lagrange. In a previous study of fossil fuel‐derived CO₂ at nearly the same sites in California, simulations using these CarbonTracker‐Lagrange footprints were compared with two other modeling systems (Brophy et al., 2018). Similar mean values and ranges of variability were found across simulations using the three different modeling systems, indicating that our simulations of CH₄ and Δ¹⁴CH₄ would likely be comparable if a different model were used.

Table 1.

Observation Site Locations Used in the Simulations

Site	Code	Lat (°N)	Lon (°W)	Sampling height (m.a.g.l.)
Sutter Buttes	STB	39.206	121.821	10
Walnut Grove	WGC	38.265	121.491	30
Sandia‐Livermore	LVR	37.674	121.708	27
Arvin	ARV	35.239	118.789	10
Victorville	VTR	34.609	117.287	100
Mount Wilson	MWO	34.223	118.063	10
Caltech	CIT	34.137	118.126	10
San Bernardino	SBC	34.085	117.313	58
Scripps Inst. Ocean.	SIO	32.867	117.257	10

Note. Sampling height is in meters above ground level.

Figure 2.

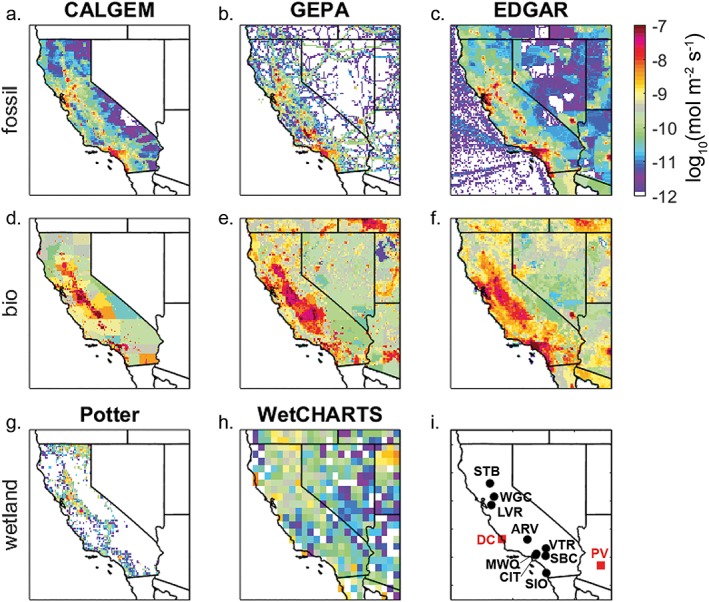
. Estimates of CH₄ emissions from fossil sources (a–c), anthropogenic biogenic sources (d–f), and natural wetlands (g–h). In the top two rows, the estimates are from CALGEM (Jeong et al., 2012) in a and d, GEPA (Maasakkers et al., 2016) in b and e, and EDGAR (2011) in c and f. Wetland emissions from Potter et al. (2006) are shown in g and WetCHARTS (Bloom et al., 2017) in h. The locations of the observation sites and the two nuclear power plants Diablo Canyon (DC) and Palo Verde (PV) are shown in i. The color bar in the upper right applies to all panels a–h.

3.2. Estimates of Current CH₄ Emissions in California

Emissions of CH₄ in California from anthropogenic sources were taken from two products providing spatially resolved estimates: EDGAR v4.2FT (Emissions Database for Global Atmospheric Research [EDGAR], 2011) and GEPA (Gridded Environmental Protection Agency; Maasakkers et al., 2016). The spatially resolved estimates have different geographical domains and use different methodologies. The GEPA product contains emissions for the continental United States at 0.1° × 0.1° resolution. Total emissions for the United States in GEPA are consistent with estimates of 2012 emissions made by the EPA and are distributed spatially according to various data sets (Maasakkers et al., 2016). EDGAR is a global product with 0.1° × 0.1° resolution. In Table 2 and Figure 2, we compare these two products with statewide totals from the CARB Greenhouse Gas Emissions Inventory (CARB, 2017a) and another spatially resolved estimate: California Greenhouse Gas Emissions Measurement (CALGEM) v2.2 (Jeong et al., 2012). The CALGEM product contains emissions for California only, with 0.1° × 0.1° resolution. The total emissions in each category in CALGEM are distributed spatially according to various data sets and scaled to match the corresponding category totals for 2010 from a prior version of the CARB Greenhouse Gas Emissions Inventory (Jeong et al., 2012).

Table 2.

Estimates of California Total Emissions in Gigagrams of CH₄ Per Year from CARB (2017a), CALGEM v2.2 (Jeong et al., 2012), GEPA (Maasakkers et al., 2016), and EDGAR v4.2FT (EDGAR, 2011)

	CARB	CALGEM	GEPA	EDGAR
Year	2013	2010	2012	2008
Total	1615	1282	1898	1849
Biogenic	1318	1138	1552	1272
Fossil	298	144	346	577
Fossil fraction	18%	11%	18%	31%

Note. Emissions are separated by type: biogenic (e.g., livestock, landfill, wastewater, rice farming, and biomass burning) or fossil (e.g., natural gas, petroleum, and combustion). The year corresponding to each estimate is given in the first row, and the fossil fraction is given in the last row. Specific sectors included for GEPA and EDGAR are listed in Table S1.

Each of the four emissions estimates contains different categories, largely following the emission categories set out by the Intergovernmental Panel on Climate Change. Annual emissions from individual categories were grouped into biogenic or fossil sources (Figure 2 and Tables 2 and S1). These four emissions estimates include only anthropogenic emissions. Natural wetland emissions are estimated to be much smaller: 62 Gg CH₄ per year from the WetCHARTs extended model ensemble average (Bloom et al., 2017) and 35 Gg CH₄ per year by Potter et al. (2006; Figure 2). We exclude natural wetland emissions in our simulations as well as other natural sources such as biomass burning, geological seeps, reservoirs, and wild animals. By excluding natural emissions, we will slightly underestimate increases in CH₄ and decreases in Δ¹⁴CH₄, relative to background levels.

California state total emissions vary by approximately 20% across the four estimates, from 1,282 Gg CH₄ per year in California Greenhouse Gas Emissions Measurement (CALGEM) to 1,898 Gg CH₄ per year in GEPA (Table 2). The CARB estimate for 2013 from the 2017 inventory is in the middle of the range, 1,615 Gg CH₄ per year. Total emissions in GEPA and EDGAR are similar (1,898 and 1,849 Gg per year), but the partitioning into fossil and biogenic categories is quite different. EDGAR shows the highest fossil fraction, 31%, while CARB and GEPA have similar fossil fractions of 18%. The fossil fraction in CALGEM is even lower, 11%.

The spatially resolved estimates show that the Central Valley, the San Francisco Bay, and the South Coast (Greater Los Angeles) areas of the state have the highest emissions (Figure 2). The U.S.‐specific GEPA and CA‐specific CALGEM estimates show finer detail related to gas distribution networks and point sources for landfill and wastewater sites, whereas EDGAR emissions are more evenly distributed over the state. EDGAR shows much higher emissions in the South Coast than the other two estimates.

3.3. Simulations Using Current Methane Emissions From GEPA and EDGAR

We use the CarbonTracker‐Lagrange footprints together with the emissions from GEPA (Maasakkers et al., 2016) and EDGAR v4.2FT (EDGAR, 2011; Figure 2) to simulate the excess CH₄ concentration from fossil and biogenic sources in California and surrounding areas. Simulations are made at each observation site in Table 1 for each afternoon in 2014. We calculate the change in Δ¹⁴CH₄ based on the simulated concentrations of fossil and biogenic CH₄ and the assumed background composition and source signatures following section 2 and using equations (1) and (2). Emissions are assumed to be constant in time and CH₄ sinks and natural wetland emissions are not included. In these simulations, we do not include nuclear power plant emissions of ¹⁴CH₄.

3.4. Simulations Using Projected Changes in Emissions for 2030

We use the Short‐Lived Climate Pollutant Reduction Strategy report (CARB, 2017c) produced by the CARB to predict the CH₄ emissions in 2030 in California. In the report, several quantitative methane emission reduction targets to be reached by 2030 are presented. Relative to 2013 levels, a reduction of 40% in dairy and livestock emissions and in wastewater and other industrial emissions is planned. A slightly larger reduction of 45% is planned for oil and gas emissions and a smaller reduction of 28% in landfill emissions. In addition to these policy targets, expected changes in CH₄ emissions from existing policies in a BAU case are outlined in the report.

Combining the policy targets and the BAU case with the sectoral EDGAR emissions estimates, we create spatially resolved emissions estimates for 2030. We scale the EDGAR sectoral emissions by the expected fractional changes in sectoral emissions in each scenario. Implementation of policy targets is expected to reduce state total CH₄ emissions by 35% and reduce the fossil fraction of state total emissions from 31% to 29%, compared to the EDGAR emissions in 2008 (Target scenario, Table 3). Following a BAU scenario would instead increase emissions slightly and increase the fossil fraction of state total emissions from 31% to 35%.

Table 3.

Scaling Factors for Emissions in Different Categories Used in Simulations for the Business‐as‐Usual Scenario and the Target Mitigation Scenario

Scenario	Year	Livestock	Wastewater and other industrial	Landfill	Oil and gas	Other	F (%)	Total emissions (Gg CH4 per year)
Base/EDGAR	2008	1	1	1	1	1	31	1,849
BAU	2030	0.97	1.10	0.89	1.14	1	35	1,858
Target	2030	0.60	0.60	0.72	0.55	1	29	1,200

Note. Base refers to current estimates taken to be representative of 2014, where we use the EDGAR estimate for 2008. F is the statewide fossil fraction in each scenario. BAU refers to projected changes under existing regulations (CARB, 2017c). Target refers to projected changes as a result of new regulations (CARB, 2017c).

In order to simulate Δ¹⁴CH₄ in California in 2030, we need to account for changes in background composition and in biogenic Δ¹⁴CH₄ (Table 4). Based on the BAU scenario used by the Intergovernmental Panel on Climate Change in 2013, Representative Concentration Pathway 8.5 (van Vuuren et al., 2011), CH₄ concentration will be 2,132 ppb in 2030. Atmospheric Δ¹⁴CO₂ has been simulated to decrease to approximately −41‰ in 2030 in this scenario (Graven, 2015), which we use to specify Δ_b. No projections for Δ_bg (Δ¹⁴CH₄ in background air) have been made for 2030, so we assume a fixed value of 350‰.

Table 4.

Estimated Values for C_bg, Δ_bg, and Δ_b Used in the Simulations

Variable	2014	2030
Cbg	1,823 ppb	2,132 ppb
Δbg	350‰	350‰
Δb	20‰	−41‰

Note. Values for 2014 are as given in section 2. Values for C_bg and Δ_b in 2030 are based on a business‐as‐usual scenario, Representative Concentration Pathway 8.5 (Graven, 2015; van Vuuren et al., 2011).

Following the same method as for the simulations for 2014, we use the CarbonTracker‐Lagrange footprints for 2014 together with the scaled emissions from EDGAR to simulate the excess CH₄ concentration from fossil and biogenic sources in California and surrounding areas in 2030. We use these to calculate the fossil fraction and change in Δ¹⁴CH₄ at each site following section 2. Again, emissions are assumed to be constant in time, and we do not include natural wetland emissions, CH₄ sinks or nuclear power plant emissions of ¹⁴CH₄.

3.5. Simulations Including Nuclear Power Plant ¹⁴CH₄ Emissions

Nuclear power plants of the pressurized water reactor type produce gaseous emissions of ¹⁴C that are primarily in the form of ¹⁴CH₄ (Kunz, 1985; Zazzeri et al., 2018). In California, there is one nuclear site with two pressurized water reactors operating, Diablo Canyon, located in the central coast region (35.211°N, 120.856°W). There is another nuclear site in southwestern Arizona with three pressurized water reactors operating, Palo Verde (33.389°N, 112.865°W). We took ¹⁴CH₄ emission data reported to the Nuclear Regulatory Commission for 2014–2015 (https://www.nrc.gov/reactors/operating/ops‐experience/tritium/plant‐info.html). We converted emissions reported in Curies to units of mole per year as described in the SI. For Diablo Canyon, reported ¹⁴CH₄ emissions average 0.25 mol/year over 2014 and 2015, and for Palo Verde, reported emissions are 0.52 mol/year over 2014 and 2015. These emission data are estimates based on recommendations by the Electric Power Research Institute (2010), not actual measurements of emissions.

We simulated nuclear influences on Δ¹⁴CH₄ for 2014 at the observation sites in Table 1 using the CarbonTracker‐Lagrange footprints in the same way as described above, using equation (2). We combine these with the CH₄ simulations for 2014 made with the EDGAR emissions estimate. Simulations of nuclear influences on Δ¹⁴CH₄ were made assuming time‐invariant emissions, even though prior studies have shown that nuclear power plant emissions can be highly intermittent (Kunz, 1985; Vogel et al., 2013). Here the simulations with the CarbonTracker‐Lagrange footprints apply the emissions uniformly over the grid cell containing the site, which has an area of approximately 100 km². Simulating the emissions from a smaller point source may result in narrower but more intense plumes of influence that may be more realistic; however, it was not possible to simulate point source emissions with this model.

We run simulations of nuclear influences on Δ¹⁴CH₄ for 2014 only. Current operating contracts on the Diablo Canyon nuclear site expire in 2024–2025 and the operator announced decommissioning plans in 2016, indicating that the site may be shut down by 2030. Palo Verde is the largest nuclear power plant in the United States and is likely to continue operating through 2030.

4. Results

4.1. Simulations for 2014 in California With EDGAR and GEPA Emissions Estimates

Simulations of CH₄ at the sites in California show differences in the CH₄ concentration and fossil fraction caused by differences in the spatial distributions of fossil and biogenic CH₄ emissions in the EDGAR and GEPA emissions estimates (Figure 3). Excess CH₄ concentration above the background level is higher at all sites in Southern California and at LVR in simulations using EDGAR, whereas excess CH₄ concentration is higher at STB, WGC, and ARV using GEPA (Figure 3a). Median values differ by a factor of 2 at several sites. The differences in excess CH₄ concentration largely reflect the allocation of more emissions in densely populated regions in EDGAR compared to GEPA (Figure 2; Maasakkers et al., 2016), which are generally associated with higher fossil fractions (Table 2 and Figure 3b).

Figure 3.

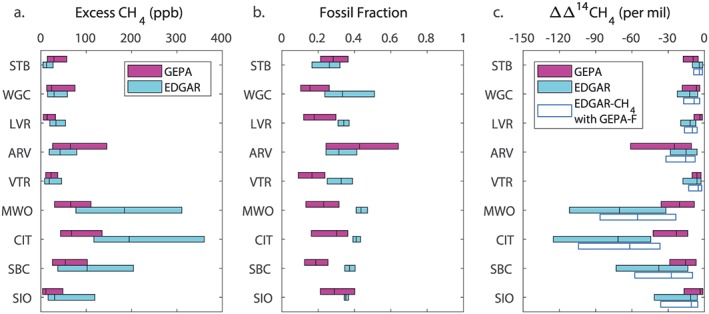
Distributions of excess CH₄ concentration (left), fossil fraction (middle), and change in Δ¹⁴CH₄ (right) in simulations using the GEPA and EDGAR emissions maps. Bars show the median and interquartile range (middle 50% of the data, between the 25th and 75th quantiles) for each variable at each observation site simulated in the afternoon for 2014 using CarbonTracker‐Lagrange. In the right panel, the change in Δ¹⁴CH₄ is also shown for a simulation in which the excess CH₄ concentration is determined using EDGAR but the fossil fraction is determined using GEPA.

The simulated fossil fractions of excess CH₄ concentration are shown in Figure 3b. These reflect the average fossil fractions of CH₄ emissions of the areas of influence on each site, weighted by the magnitude of emissions and their dilution before reaching the observation site. Only two sites show higher median fossil fractions of excess CH₄ concentration in GEPA: STB and ARV. Higher excess CH₄ concentration and fossil fraction at ARV appears to be associated with intense oil and gas activities in the southern Central Valley that are captured in GEPA but not in EDGAR. Fossil fractions of excess CH₄ generally show more variation in simulations using GEPA than in EDGAR (Figure 2b). This indicates the fossil fraction of emissions is more spatially variable in GEPA, particularly in Southern California. The fossil fraction is somewhat higher at Los Angeles area sites (MWO, CIT, and SBC) than at the site further south in San Diego (SIO) with EDGAR, but the fossil fraction is somewhat lower at Los Angeles area sites than in San Diego with GEPA (Figure 3b), indicating differing distributions of emissions, for example, from natural gas, landfills, and dairies within Southern California in EDGAR and GEPA.

The Δ¹⁴CH₄ calculated following section 2 similarly shows large differences in simulations using EDGAR or GEPA emissions (Figure 3c). We use the notation ΔΔ¹⁴CH₄ to indicate the difference between the Δ¹⁴CH₄ at the site and the background Δ¹⁴CH₄ in the simulations (analogous to Δ_m‐Δ_bg). The simulated ΔΔ¹⁴CH₄ is more negative at all sites in Southern California and at LVR in simulations using EDGAR compared to GEPA. At these sites, the fractional differences in ΔΔ¹⁴CH₄ are even larger than for excess CH₄ concentration because the higher excess CH₄ concentrations and higher fossil fractions both contribute to more negative ΔΔ¹⁴CH₄, compared to GEPA. At STB and ARV, the opposite is true, as both excess CH₄ concentration and fossil fraction are higher in GEPA as compared to EDGAR. At WGC, median ΔΔ¹⁴CH₄ is more negative for EDGAR than GEPA, but the interquartile ranges largely overlap.

In addition to the simulations of ΔΔ¹⁴CH₄ based on EDGAR and GEPA emissions, we conduct another calculation to help illustrate how much the difference in fossil fraction and difference in excess CH₄ concentration each contribute to the difference in simulated ΔΔ¹⁴CH₄. We use the simulated excess CH₄ concentration from EDGAR with the simulated fossil fraction from GEPA to calculate ΔΔ¹⁴CH₄ (Figure 3c). This calculation indicates that differences in excess CH₄ concentration are the primary cause (>70%) of the differences in ΔΔ¹⁴CH₄ at most sites. At WGC and SBC, differences in the fossil fraction did account for a large fraction of the difference between the median values of ΔΔ¹⁴CH₄ between the GEPA and EDGAR simulations (66% and 47%, respectively). However, this comparison of median values does not fully quantify the separate effects of excess CH₄ and fossil fraction as the medians are not necessarily additive: at STB and VTR, the median of ΔΔ¹⁴CH₄ was not in between the medians of the GEPA and EDGAR simulations, indicating that correlations between excess CH₄ and fossil fraction also contribute to resulting median ΔΔ¹⁴CH₄.

To illustrate the relationships between ΔΔ¹⁴CH₄ and excess CH₄ concentration in the EDGAR and GEPA simulations, in Figure 4, we show two‐dimensional histograms for three of the sites in California. Other sites are shown in Figure S1. The figures show the distribution of excess CH₄ and ΔΔ¹⁴CH₄ in the range of 0 to 125 ppb and 0‰ to −50‰. For reference, the relationships for constant fossil fractions of 0.25 and 0.75 are also shown (see section 2 and Figure 1). At all three sites, simulations with EDGAR have a higher fossil fraction and a stronger (steeper) slope between ΔΔ¹⁴CH₄ and excess CH₄. There is a relatively tight relationship (high correlation) between simulated ΔΔ¹⁴CH₄ and excess CH₄ in the simulations at SBC and SIO using EDGAR, reflecting the low variance in simulated fossil fraction (Figure 3b). For the other simulations, there is more scatter, reflecting a variety of fossil fractions in excess CH₄. In the simulation for WGC using GEPA, the fossil fraction appears to decrease when excess CH₄ concentration is high, showing that certain atmospheric conditions result in strong biogenic CH₄ influences at WGC.

Figure 4.

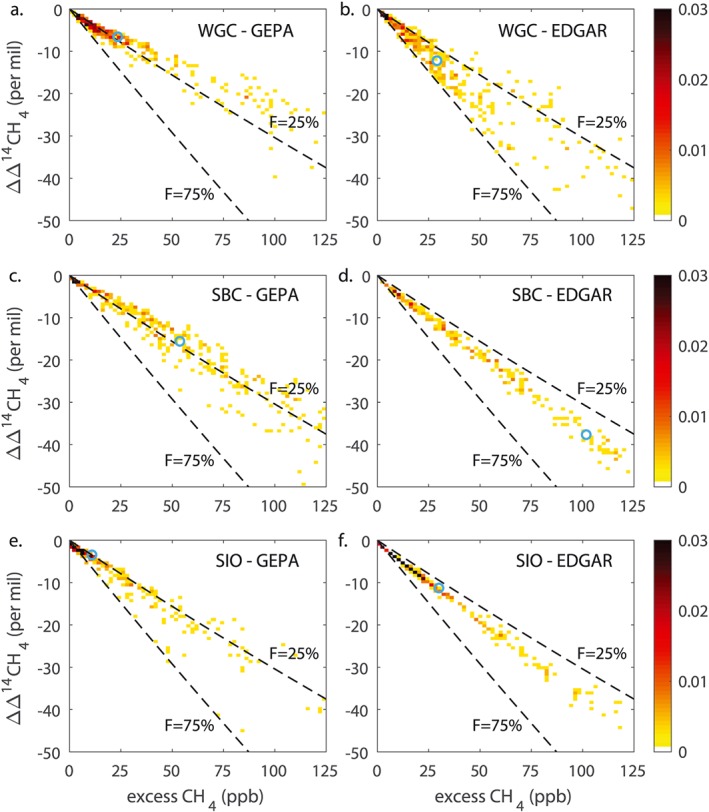
Distributions of the simulated change in Δ¹⁴CH₄ versus excess CH₄ concentration, shown as two‐dimensional histograms at three selected sites. Other sites are shown in Figure S1. The top row shows WGC, middle row SBC, and bottom row SIO. Simulations shown in the left column use GEPA emissions, and the right column use EDGAR emissions. Colors show the fraction of the data contained in each bin. Blue circles show the median of the simulated change in Δ¹⁴CH₄ and the median of the excess CH₄ concentration in each case. Dashed lines show the relationship expected from constant fossil fractions of 25% and 75%, for reference.

These simulations demonstrate the magnitude and patterns of ΔΔ¹⁴CH₄ that could be measured in the near future in California, as well as the expected differences from different emissions estimates, which can be used to evaluate the utility of ΔΔ¹⁴CH₄ observations. Median values of ΔΔ¹⁴CH₄ of −4‰ to −25‰ in GEPA and −4‰ to −62‰ in EDGAR suggest that current measurement precision could detect ΔΔ¹⁴CH₄ signals for high pollution events with excess CH₄ concentration in the upper quartiles at all sites, but also for pollution events in the lower quartiles at ARV, MWO, CIT, and SBC. As pollution events are stronger in winter (Jeong et al., 2016), it is likely that deployment of ΔΔ¹⁴CH₄ observations in winter would provide more precise determination of fossil fractions than in other seasons.

In practice, observations of ΔΔ¹⁴CH₄ and excess CH₄ concentration at an observation site could be plotted in a similar way as Figure 4 to analyze the fossil fraction of excess CH₄ and its variability and to compare with the simulations using EDGAR and GEPA. Observations of ΔΔ¹⁴CH₄ could also be used to calculate C_b and C_f following section 2, which could then be used in an inversion for regional biogenic and fossil CH₄ emissions in California, for example, using EDGAR or GEPA as a prior emissions estimate.

4.2. Simulations for 2030 BAU and Target Emission Scenarios

Using a similar analysis as in the previous section, we now compare simulated excess CH₄ concentrations, fossil fractions, and ΔΔ¹⁴CH₄ in 2030 for Target and BAU scenarios in California (Figure 5). Taking the EDGAR emissions estimate as the baseline emissions in 2013–2014, we find that median excess CH₄ concentrations increase by no more than a few percent in the BAU scenario, but median excess CH₄ concentrations decrease by 36–39% in the Target scenario. For the BAU scenario, there is some compensation between small overall decreases in biogenic emissions and small increases in fossil emissions. Median fossil fraction of excess CH₄ is 3–5% higher for BAU but 3–5% lower for Target, compared to the excess CH₄ simulated with EDGAR.

Figure 5.

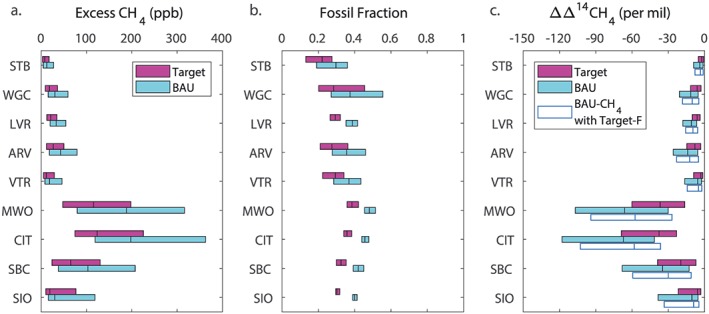
Distributions of excess CH₄ concentration (left), fossil fraction (middle), and change in Δ¹⁴CH₄ (right) in simulations using the Target and BAU scenarios with EDGAR emissions. Bars show the median and interquartile range of each variable at each observation site, similar to Figure 3. In the right panel, the change in Δ¹⁴CH₄ is also shown for a simulation in which the excess CH₄ concentration is determined using the BAU scenario but the fossil fraction is determined using the Target scenario.

Median ΔΔ¹⁴CH₄ is slightly less negative (7–9%) in the BAU scenario but 47–50% less negative in the Target scenario, compared to EDGAR (Figures 5c and 3c). This implies that, in the case where the Target scenario is followed, an observation network for ΔΔ¹⁴CH₄ should demonstrate that the magnitude of ΔΔ¹⁴CH₄ grows smaller. Moreover, changes in the magnitude of ΔΔ¹⁴CH₄ are even more than expected from emissions reductions alone (47–50% decrease in ΔΔ¹⁴CH₄ compared with a 35% decrease in total emissions, Table 3). In an additional calculation where we use the simulated excess CH₄ concentration from BAU with the simulated fossil fraction from Target to calculate ΔΔ¹⁴CH₄, similar to Figure 3c, it can be seen that the differences in ΔΔ¹⁴CH₄ between Target and BAU are mostly attributable to differences in the excess CH₄ concentration rather than differences in the fossil fraction. However, this does suggest that in the case that total emissions changes follow the BAU scenario, but the fossil fraction follows the Target scenario (decreasing rather than increasing fossil fraction, Table 3), then the magnitude of ΔΔ¹⁴CH₄ is expected to be smaller.

The relationships between ΔΔ¹⁴CH₄ and excess CH₄ concentration in the BAU and Target simulations are shown in Figure 6 at WGC, SBC, and SIO. Note that the reference lines have flatter slopes than in Figure 4 because of the differences in C_bg and Δ_b in 2030. As expected from the higher fossil fraction in the BAU scenario compared to the Target scenario (Figure 5b), there are steeper slopes between ΔΔ¹⁴CH₄ and excess CH₄ in simulations of the BAU scenario compared to the Target scenario. These simulations suggest that changes in total emissions could be observed by regional CH₄ measurements and that changes in fossil fractions of emissions could be evaluated with the addition of ΔΔ¹⁴CH₄ measurements.

Figure 6.

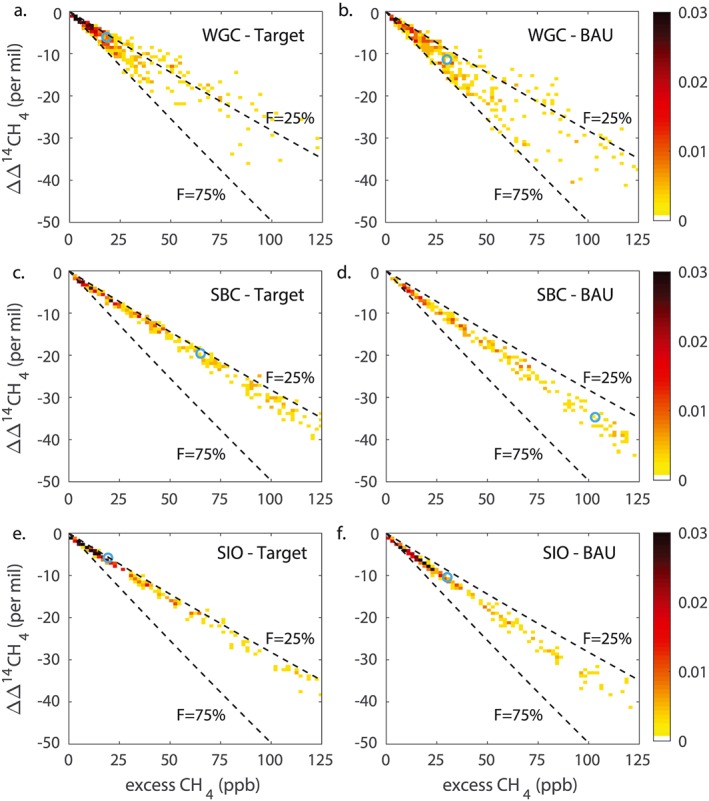
Distributions of the simulated change in Δ¹⁴CH₄ versus excess CH₄ concentration, shown as two‐dimensional histograms at three selected sites, as in Figure 4. Here the simulations shown in the left column are for the Target scenario, and the right column for the BAU scenario. Other sites are shown in Figure S2.

Here again, in practice ΔΔ¹⁴CH₄ and excess CH₄ observations could be used to calculate C_f and C_b, which could be implemented in an atmospheric inversion to estimate fossil and biogenic CH₄ emissions in 2030. Figures similar to Figure 6 could help to illuminate whether the observed fossil fractions are similar to those expected with policy implementation. Differences in the ΔΔ¹⁴CH₄ and excess CH₄ relationships could indicate that certain policies have not been met or that other policies have been more successful than expected.

4.3. Nuclear Power Plant Influences on Δ¹⁴CH₄ in California

Nuclear power plant influences on Δ¹⁴CH₄ vary strongly across the nine sites. At the three sites north of Diablo Canyon median values of ΔΔ¹⁴CH₄ from nuclear ¹⁴CH₄ emissions are 0‰ and the extent of the interquartile range is less than 1‰ (Figure 7a). However, there are a few instances of high nuclear influences of more than 25‰ at these sites. Nuclear influences shift the median in total ΔΔ¹⁴CH₄ toward slightly less negative values at these sites (+1‰ to +3‰). For the sites in Central and Southern California, median values of ΔΔ¹⁴CH₄ from nuclear ¹⁴CH₄ emissions range from 2‰ (ARV) to 7‰ (CIT) (Figure 7a). Nuclear influences shift the median total ΔΔ¹⁴CH₄ by +4‰ (ARV) to +19‰ (CIT). For SIO, the interquartile range shifts into positive values.

Figure 7.

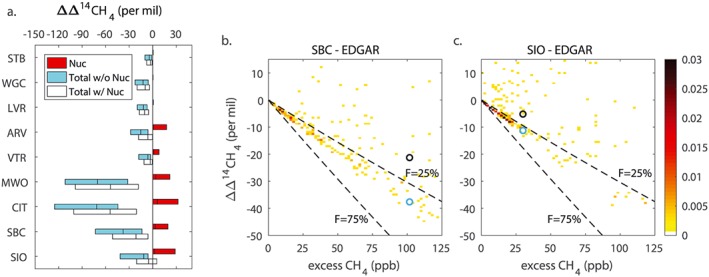
Simulated median and interquartile range of the difference in Δ¹⁴CH₄ from the background level for simulations using EDGAR emissions (left). Blue bars show the simulated ΔΔ¹⁴CH₄ when nuclear ¹⁴CH₄ emissions are neglected, as shown in Figure 3c. White bars show the simulated ΔΔ¹⁴CH₄ when nuclear ¹⁴CH₄ emissions are included, and red bars show the simulated nuclear influences on ΔΔ¹⁴CH₄. The right two panels show the simulated ΔΔ¹⁴CH₄ versus the simulated excess CH₄ concentration when nuclear ¹⁴CH₄ emissions are included for two sites: SBC and SIO. Black circles show the median values and blue circles show the median values when nuclear ¹⁴CH₄ emissions are neglected, as shown in Figures 4d and 4f. Other sites are shown in Figure S3.

The high correlation seen previously between ΔΔ¹⁴CH₄ and excess CH₄ at SBC and SIO (Figures 4d and 4f) is replaced with more scatter as a result of nuclear emissions (Figures 7b and 7c). There are now data lying above the reference line for a fossil fraction of 0.25, whereas before there were none. There are even some data lying above a zero fossil fraction or lying above 0 in ΔΔ¹⁴CH₄, indicating an increase in Δ¹⁴CH₄ with an increase in CH₄. In practice, these outliers could be easily flagged as having a strong nuclear influence. Perhaps more important would be correcting for smaller nuclear influences that could bias the interpretation on ΔΔ¹⁴CH₄, where the simulations we show here would be one approach for making such a correction. We note that in many cases, the most densely populated bins in the ΔΔ¹⁴CH₄ and excess CH₄ histograms are largely unchanged when nuclear influences are included.

Most of the nuclear influence in California is from ¹⁴CH₄ emissions from the Diablo Canyon nuclear site. The impact of emissions from Palo Verde was minor at all sites except for Victorville where it was comparable to emissions from Diablo Canyon.

5. Discussion

We have introduced a framework for interpreting Δ¹⁴CH₄ observations in regional atmospheric measurement networks, showing that Δ¹⁴CH₄ observations could likely provide useful information on fossil and biogenic CH₄ emissions on regional scales. Differences in the fossil fraction of added CH₄ are associated with differences in the slope between Δ¹⁴CH₄ and CH₄ concentration. Deployment of Δ¹⁴CH₄ observations in California could help to distinguish whether the current fossil fraction of CH₄ emissions in California is more consistent with EDGAR or GEPA. Continued observation of Δ¹⁴CH₄ through 2030 could help to validate the reductions in fossil fraction of CH₄ emissions that are expected through current mitigation policies. Detectability of C_f, C_b, and F, and their changes over time, would benefit from improvements in measurement uncertainty in Δ¹⁴CH₄.

Simulated fossil fractions of excess CH₄ concentration differ at each site according to the spatial distribution of biogenic and fossil fuel emissions and according to atmospheric transport. General patterns in the spatial variation of fossil fraction of emissions are reflected in the fossil fraction of excess CH₄ concentration (Figure S4), suggesting that CH₄ and Δ¹⁴CH₄ data alone could indicate errors in the regional fossil fractions of assumed emissions, particularly when compared to atmospheric simulations such as those we present here. More quantitative estimation of fossil and biogenic emissions would require an inversion system making use of CH₄ and Δ¹⁴CH₄. Such an inversion system could be constructed using CH₄ and Δ¹⁴CH₄ explicitly or using estimates of C_f and C_b based on CH₄ and Δ¹⁴CH₄ measurements, similar to prior studies on CO₂ and Δ¹⁴CO₂ (Basu et al., 2016; Fischer et al., 2017; Graven et al., 2018), resulting in observation‐based estimates of fossil and biogenic CH₄ emissions for well‐defined regions.

As an example of a more qualitative comparison between observations and simulations, we can apply the framework from section 2 to the Δ¹⁴CH₄ observations made at Mount Wilson in August 2009 by Townsend‐Small et al. (2012). Townsend‐Small et al. (2012) made six measurements over 2 days, observing a range of 1,760–2,060 ppb in CH₄ and 262–344‰ in Δ¹⁴CH₄. They concluded that the Δ¹⁴CH₄ data supported the presence of some fossil CH₄ emissions in the Los Angeles Basin; however, they did not conduct a quantitative analysis of the Δ¹⁴CH₄ data because they did not find a clear relationship between Δ¹⁴CH₄ and CH₄ concentration. One of their samples with low CH₄ concentration also showed low Δ¹⁴CH₄. Excluding this sample, comparisons of the other five samples show that Δ¹⁴CH₄ decreased by approximately 2‰ per 10 ppb increase in CH₄. Comparison with the slopes calculated in section 2 above suggests that the fossil fraction of excess CH₄ was actually rather low in these samples, probably less than 25%. Our simulations for Mount Wilson show an interquartile range in fossil fraction of excess CH₄ that is 13% to 32% for GEPA emissions but 41% to 47% for EDGAR (Figure 3b). This suggests the data from Townsend‐Small et al. (2012) may be more consistent with the fossil fraction in GEPA.

In the simulations for California, we analyzed potential Δ¹⁴CH₄ observations made at nine sites every afternoon for an entire year, but it is unlikely that observations could be made with this frequency. Based on our results and consideration of the likely uncertainties in the method, Δ¹⁴CH₄ measurements would be most useful for the sites and times of year with large additions of CH₄ and/or with large discrepancies in different estimates of the fossil fraction of emissions (Figure 3, Peischl et al., 2013; Wennberg et al., 2012). In California, these sites include the Los Angeles‐South Coast region (MWO, CIT, and SBC) and the Southern Central Valley (ARV). Wintertime measurements would likely enable more precise determination of fossil fractions than in other seasons because pollution events are stronger in winter (Jeong et al., 2016). In addition to these relatively polluted sites, measurement sites that can characterize background air composition in Southern‐Central California are also needed (e.g., SIO and VTR).

Our simulations including nuclear power plant ¹⁴CH₄ emissions suggest that nuclear influences on Δ¹⁴CH₄ in California can sometimes be large, particularly in Southern California (Figure 7). These results suggest that nuclear emissions can be important not only in regions with high densities of nuclear power plants such as in Europe (Eisma et al., 1995; Levin et al., 1992) but also in other regions with one or two pressurized water reactor sites. To better quantify the nuclear power plant emissions and their effect on Δ¹⁴CH₄ in California, measurements of the ¹⁴C emissions from each nuclear site are needed. Currently, U.S. nuclear power plants are required to estimate their ¹⁴C emissions according to standard guidelines but not to measure their ¹⁴C emissions, unlike some other countries. Implementation of the measurement and reporting of ¹⁴C emissions at Diablo Canyon and Palo Verde nuclear power plants, particularly with monthly or higher temporal resolution, would improve the application of Δ¹⁴CH₄ measurements in California. As the main influence on Δ¹⁴CH₄ was from Diablo Canyon, the potential shutdown of Diablo Canyon in 2025 would greatly improve the application of Δ¹⁴CH₄ measurements in California.

The approach for investigating CH₄ emissions using Δ¹⁴CH₄ that we outline here could be implemented with other techniques that use stable isotope or trace gas observations (Jeong et al., 2017; Peischl et al., 2013; Townsend‐Small et al., 2012; Wennberg et al., 2012). Observations of Δ¹⁴CH₄ could help to quantify regional‐scale trace gas emission ratios or stable isotopic signatures in fossil CH₄ sources and how these change over time. Observations of Δ¹⁴CH₄ could also be combined with satellite remote sensing measurements and spatially resolved inverse CH₄ emissions estimates based on satellite CH₄ data (Jacob et al., 2016) to provide constraints on regional fossil fractions in CH₄ emissions. Implementation of regional‐scale Δ¹⁴CH₄ observations together with new or existing stable isotope, trace gas, and satellite observation networks in relatively well‐instrumented regions like California would provide a testbed for applying multiple constraints and identifying best practices in deploying and interpreting different measurements.

6. Conclusions

Observations of radiocarbon in atmospheric CH₄ presently provide a main constraint on the global fossil fraction of CH₄ emissions, but they have not been developed to examine CH₄ sources at regional scales. We present a general framework for interpreting regional‐scale atmospheric Δ¹⁴CH₄ observations and suggest that the uncertainty in estimating regional fossil‐derived and biogenic CH₄ is likely dominated by the measurement uncertainty in Δ¹⁴CH₄ and the uncertainty in background CH₄ concentration. Simulations of CH₄ and Δ¹⁴CH₄ in California using EDGAR versus GEPA emissions estimates show substantial differences related to the generally higher fossil fraction in EDGAR. Projections of potential changes in CH₄ emissions for 2030 suggest that mitigation will tend to reduce the fossil fraction, resulting in flatter atmospheric Δ¹⁴CH₄‐CH₄ slopes, compared to a BAU scenario. Simulations suggest influences on Δ¹⁴CH₄ in California from ¹⁴CH₄ emissions from the Diablo Canyon and Palo Verde nuclear power plants are small on average but should be considered in interpretation of Δ¹⁴CH₄ observations.

Supporting information

Supporting information S1

Data Set S1

Graven, H. , Hocking, T. , & Zazzeri, G. (2019). Detection of fossil and biogenic methane at regional scales using atmospheric radiocarbon. Earth's Future, 7, 283–299. 10.1029/2018EF001064