A probabilistic model of nuclear import of proteins

Abstract

Motivation: Nucleo-cytoplasmic trafficking of proteins is a core regulatory process that sustains the integrity of the nuclear space of eukaryotic cells via an interplay between numerous factors. Despite progress on experimentally characterizing a number of nuclear localization signals, their presence alone remains an unreliable indicator of actual translocation.

Results: This article introduces a probabilistic model that explicitly recognizes a variety of nuclear localization signals, and integrates relevant amino acid sequence and interaction data for any candidate nuclear protein. In particular, we develop and incorporate scoring functions based on distinct classes of classical nuclear localization signals. Our empirical results show that the model accurately predicts whether a protein is imported into the nucleus, surpassing the classification accuracy of similar predictors when evaluated on the mouse and yeast proteomes (area under the receiver operator characteristic curve of 0.84 and 0.80, respectively). The model also predicts the sequence position of a nuclear localization signal and whether it interacts with importin-α.

Availability: http://pprowler.itee.uq.edu.au/NucImport

Contact: m.boden@uq.edu.au

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Nucleo-cytoplasmic trafficking of proteins is a core regulatory process that involves traversing large membrane structures termed nuclear pore complexes (NPCs) (Aitchison and Wozniak, 2007; Alber et al., 2007). The translocation of cargo macromolecules through the pore is facilitated by a number of nuclear transport factors, termed karyopherins. To shed light on the mechanisms that are employed by individual nuclear proteins, this article proposes a probabilistic model of nuclear import that leverages recent experimental results to accurately and transparently recognize biologically relevant features.

The main determinant of nuclear localization of proteins is the nuclear localization signal (NLS). The best-characterized NLS is the classical nuclear localization sequence (cNLS), which is recognized by the carrier protein importin-α (karyopherin-α). Importin-α acts as an adaptor protein, binding in turn to importin-β (karyopherin-β1), which docks the trimeric complex to the nuclear pore complex for further transport into the nucleus (Marfori et al., 2010). The cNLS contains one (mono-partite) or two (bi-partite) clusters of basic amino acids (Hodel et al., 2001; Kosugi et al., 2009a). Structural studies have shown that peptides bind along a groove in importin-α, with charged amino acids at ‘minor’ and ‘major’ binding sites along this groove (Conti et al., 1998; Fontes et al., 2003). A recent study subdivided cNLSs further into six groups (Kosugi et al., 2009a).

In addition to the classical nuclear import pathway, several alternative import pathways have been characterized. Features of the targeting signal have been identified in the case of the proline–tyrosine (PY)-NLS pathway, which employs the carrier karyopherin-β2 (Lee et al., 2006). At present, the definition of an NLS common to different cargoes used by a single carrier has only been possible for the classical and karyopherin-β2-mediated pathways. Many nuclear proteins do not contain any known NLS (Christophe et al., 2000).

Many predictors identify homologs of a query protein and assign their subcellular location to it without explicitly considering if a localization signal is present. As a consequence, such predictors fail to provide both mechanistic explanations of predicted translocation and reliable output in the absence of well-characterized homologs (Ba et al., 2009; Brameier et al., 2007; Marfori et al., 2010; Nakai and Horton, 1999). Predicting which proteins are imported on the basis of targeting signals without resorting to homology is a major challenge. Simple sequence matching using known NLS patterns renders many false positives and negatives (Brameier et al., 2007; Cokol et al., 2000). To explain why import sometimes goes awry in biological terms, we require models that transparently capture and appropriately weigh in relevant aspects of nuclear import (e.g. interaction with karyopherins and cNLS recognition).

A number of predictors are available to identify novel nuclear proteins from known localization features, against which new models should be benchmarked. For reasons explained below, we use NLStradamus (Ba et al., 2009) and cNLS Mapper (Kosugi et al., 2009a) as representatives for the current state of the art on technical and biological grounds, respectively.

PredictNLS (Cokol et al., 2000) explicitly matches a protein sequence against entries in the NLSdb database (Nair et al., 2003). NucPred also uses sequence matching (Brameier et al., 2007) complemented by ‘genetic programming’ to recognize new putative NLSs. According to its authors, NucPred is more accurate than PredictNLS, LOCtree (Nair and Rost, 2005) and BaCelLo (Pierleoni et al., 2006). Ba et al. (2009) evaluated the performance of localization signal predictors, finding that they do not perform well on truly novel examples which suggests that current methods are unable to identify the features relevant to import. They developed NLStradamus (Ba et al., 2009) in response to this observation. NLStradamus is a hidden Markov model that predicts localization signal sites more accurately than those benchmarked against in their study. Its high accuracy is potentially due to the flexibility in signal recognition afforded by the probabilistic model. It is trained on alignments of yeast NLSs but extends well to other species (Ba et al., 2009).

Kosugi et al. (2009a) generated and experimentally screened random peptide libraries to identify importin-α binding sequences. Using yeast, plant (rice) and mammalian (human) importin-α proteins, six different groups of mono- and bi-partite cNLSs were identified by cluster analyses of the sequences of the bound (and imported) peptides. The authors developed a computational method, cNLS Mapper, that incorporates a sequence scoring matrix based directly on the statistics gathered from the collected peptides (Kosugi et al., 2009b). cNLS Mapper is more accurate than PSORT II (Nakai and Horton, 1999) and PredictNLS (Cokol et al., 2000) on several yeast positive-only datasets (Kosugi et al., 2009b).

cNLS Mapper identified 406 mono-partite, and 306 bi-partite cNLSs in the yeast proteome. The yeast–GFP fusion localization database by Huh et al. (2003) identifies 447 of these as nuclear. Yeast–GFP records nuclear import status confirmed by microscopy for yeast strains tagged with green fluorescent protein (GFP). Kosugi et al. experimentally demonstrated that 29 out of 30 false ‘mono-partite’ positives indeed exhibited NLS activity, attesting to the high specificity of their predictor.

NLSs appear to operate similarly across species. Indeed, only one group in Kosugi and colleagues' study was deemed specific to a single species (rice). It is, thus, of general interest to gauge the ability of nuclear import models to deal with not only yeast but also a mammalian system. We note that NucProt (Fink et al., 2008) offers a complementary resource for developing and evaluating models of nuclear import. NucProt maps the mouse nuclear proteome, identified primarily from experimental assays, enriched using computational methods.

To enhance a model's ability to recognize species-specific targeting signals in sequence data, we develop probabilistic scoring functions from experimentally determined sequence patterns matched to actual sequences from the proteome under consideration. As a result, these functions accurately reflect the proteome-specific distributions. We use data from the studies by Kosugi et al. (2009a), Huh et al. (2003) and Fink et al. (2008) to develop and evaluate our model.

Protein interaction data offer a complementary view of how cargoes interface with the import machinery. Thus, to improve further on their recognition, we extract data indicating interaction with importin-α/β and the GTP-binding protein Ran–all of which are essential for the translocation of proteins through the NPC. Finally, to increase the sensitivity to non-classical import signals, we incorporate matching of all patterns stored in NLSdb. We also use a support vector machine (SVM) to detect more subtle sequence similarities.

We develop a model that recognizes NLSs, links interactions to localization signals and incorporates sequence similarity. We demonstrate that the model predicts the protein import into the nucleus more accurately than both NLStradamus and cNLS Mapper. It identifies interactions with core NPC members, and correctly identifies cNLSs for novel proteins in both mouse and yeast. Our probabilistic model is transparent and provides biologically meaningful explanations for predictions.

2 MATERIAL AND METHODS

To integrate the information gleaned from the datasets and to enforce constraints from known relationships between features (discussed below), we use a custom-designed Bayesian network.

2.1 Bayesian network

Bayesian networks are directed acyclic graphs in which nodes are (random) variables and directed edges represent (causal) dependencies between the variables (parent to child). The full joint probability distribution for all random variables X₁ = x₁, X₂ = x₂,…, X_n = x_n can be calculated by taking the product of related elements of the conditional probability tables (CPTs) in the probabilistic network; P(x₁, x₂,….., x_n) = ∏^N_i=1(P(x_i|pa(X_i)) where pa(X_i) is the set of parents of X_i.

In our Bayesian network model, variables are either ‘Boolean’ (true/false) or ‘continuous’ (real valued). Nodes with Boolean parents are essentially conditional probability tables, in which each entry consists of a binomial distribution (Boolean nodes) or a Gaussian density (continuous nodes).

The parameters in the conditional probability tables are learned from the data using expectation–maximization (EM) (Do and Batzoglou, 2008). Prior probabilities (root nodes) are determined from the relative counts of observations in training data. The conditional probabilities (nodes with parents) are similarly determined from the relative counts of outcomes, but are subject to observed conditions of parent nodes. In some cases, values of variables are not observed in datasets. For so-called latent variables, the expected values—computed from those variables that are observed—are used to maximize the likelihood of the data.

To understand the contribution of different features to accuracy, we design several smaller Bayesian networks, and then two Bayesian networks that combine the full range of features in ways reflecting domain knowledge. Each can take a protein as input—represented by sequence and/or interactions—and can output the probability of nuclear import (see Section 2.3). We fix the network structure. Some of the models utilize the output of position weight matrices (PWMs) and support vector machines (SVMs). The SVM and PWMs are trained separately (on non-overlapping data) and prior to invoking EM as explained below.

2.2 Model features

Below we discuss features that can be used to assign values to variables in the model to support accurate inference of nuclear import.

2.2.1 Classical nuclear localization signals: f(c, x

The detection of NLSs is crucial to accurate modeling of nuclear import. Kosugi and colleagues recently identified six groups of cNLSs corresponding to distinct importin-α binding properties. Classes 1 and 2 interface with the major binding site of importin-α while classes 3 and 4 bind to the minor binding site. Class 6 is the bi-partite nuclear localization signal. Class 5 is a plant-specific cNLS variant (Kosugi et al., 2009a) and is not included in our mouse or yeast specific models. We also omit Class 3 because there are very few matches in the yeast and mouse datasets, preventing reliable analysis. Below we discuss how we use cNLS Classes 1, 2, 4 and 6 as features in our models.

From their peptide data, Kosugi et al. constructed ‘optimal consensus patterns’ in the form of regular expressions for each of the six cNLS classes. They also remarked that flanking residues exerted some influence on NLS activity, but that this was species specific. cNLS Mapper is directly based on the statistics of their random peptide library, captured by matrices with scores for each amino acid at each position in an NLS. This scoring method demonstrates an ability to deal with the degeneracy of real sites, not afforded by direct matching of regular expressions. Rather than using the matrices of Kosugi et al., to account for any species bias, we infer parameters for probabilistic PWMs directly from proteomes.

First, we use the four regular expressions to identify all candidate NLSs in the known nuclear proteins of mouse and yeast, respectively. Secondly, for each cNLS class and species, we form an alignment by centering each match to create an PWM. We define a probability matrix P_C for a cNLS class C ∈ {1, 2, 4, 6} as in Equation (1).

(1)

P_C(a, i) is the probability of amino acid a, at position i of the cNLS-specific alignment, n_C,a,i is the count of a at the i-th position (in class C-matching nuclear protein sequences), s(a) is a pseudocount function (here a unit increment), N_C is the total number of matches to the regular expression for NLS class C and A is the set of the 20 amino acids.

The class-specific PWM, W_C, is the ‘log-odds’ of the position-specific probability and a zero-order background probability of the amino acid a at position i in the matching sequence [see Equation (2)].

(2)

P_C(a) is the background probability (prior) of amino acid a in all C-matching sequences.

We define a scoring function f(c, x) for a cNLS class c where x is any amino acid sequence. Each of the resulting PWMs can generate a cNLS-specific score for each position i in a query sequence x [see Equation (3)].

(3)

The overall class c score for the sequence, is f(c, x) = max_if(c, x, i). We additionally define the location of a candidate cNLS of class c as l(c, x) = arg max_if(c, x, i).

To find an appropriate PWM width (common to all classes), we also considered amino acids at the flanks of matching sequences. A total matrix width of 20 positions (for each cNLS class) gave the maximum accuracy in preliminary tests on a subset of the full protein dataset. We show the resulting PWMs in Supplementary Figure S1.

In summary, the features described above require the specification of a sequence x, and assign a real value that indicates the presence of cNLS c ∈ {1, 2, 4, 6} in x.

2.2.2 Alternative localization signals: NLSdb(x)

The classical import pathway involving the interaction with importin-α is utilized by a large number of proteins. Alternative pathways, possibly involving direct interaction with other karyopherins, are not normally detected via cNLS.

NLSdb contains 114 experimentally determined nuclear localization signals. These signals are described by regular expressions. It also contains 194 carefully qualified permutations of the original 114, required not to overlap with a negative reference set (Nair et al., 2003).

As a feature complementary to cNLSs, we define NLSdb(x) where x is the amino acid sequence of a protein. The function assigns true or false by simply matching the sequence to all regular expressions in NLSdb.

2.2.3 Protein interaction: ppi_α(x), ppi_β(x) and ppi_Ran(x)

Compared with detailed binding sites in cargo (NLSs), protein interaction datasets offer a different experimental resource to determine the probability of nuclear translocation. In particular, interactions with karyopherins are relevant and below we discuss their incorporation as features.

We collect all interaction partners of importin-α, importin-β and Ran in the BioGRID protein–protein interaction datasets (Stark et al., 2006). We note that coverage is very limited. For our mouse data, there are only 9 interactions with importin-α, 32 interactions with importin-β and 184 interactions with Ran. For yeast, the respective numbers are 215, 375 and 132. To compensate for this lack of data for mouse, we also included indirect interactions with importin-α and importin-β, i.e. interactions via a single ‘proxy’ partner.

In order to incorporate protein interaction dataset, we define three features ppi_α(x), ppi_β(x) and ppi_Ran(x), assigning true or false depending on whether the query protein is known to interact with importin-α, importin-β and Ran, respectively.

2.2.4 Sequence similarity based on shared k-mers: SVM(x)

There may be yet unknown sequence signals and domains that are involved in nuclear import. Hawkins et al. (2007) demonstrated that detecting sequence segments that were shared with already known nuclear proteins can be used to establish import status. SVMs have been used successfully in the past for predicting nuclear import (Hawkins et al., 2007; Nair and Rost, 2005) and are known to be very sensitive to sequence similarity and domain sharing.

We use an SVM to classify known nuclear and non-nuclear protein sequences. We define a feature SVM(x) to assign a score to a sequence x, indicating whether it is similar to known nuclear proteins, or not.

A kernel function K maps a pair of data items (in our case protein sequences) to a feature space in which their inner product is evaluated. In all our tests, we use the Spectrum kernel (Hawkins et al., 2007; Leslie et al., 2002) which simply counts the occurrences of shared sequence segments known as k-mers. Since known NLSs are naturally represented as short sequence patterns, we expect this kernel to be suited to capturing such signals but not limited to them. We consistently use k = 3, i.e. segments are three amino acids long. As a result of training, the SVM finds a hyperplane in this 3mer feature space (defined in terms of the so-called support vectors) that optimally separates items of the two classes.

2.3 Model designs

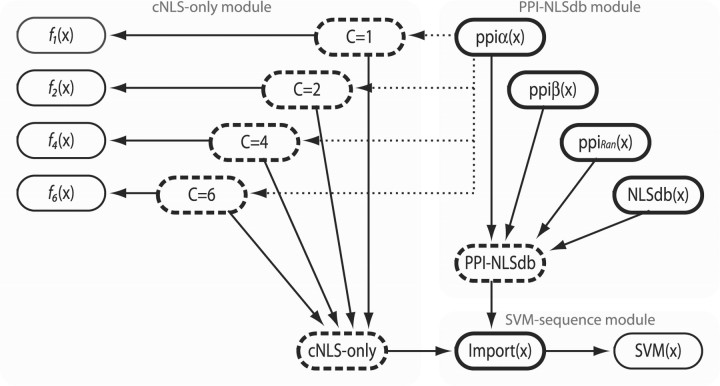
We develop three basic Bayesian network models, a ‘cNLS-only model’, a ‘PPI-NLSdb model’ and a ‘SVM-sequence model’. Each model involves a distinct set of input features: cNLSs, protein interactions and k-mer sequence similarity, respectively. We then construct two versions of a full-blown model by combining the three basic models, thereby integrating the different features (see Fig. 1 for an illustration of the combined Bayesian network, composed of the basic models). Each model has a Boolean node ‘Import’ that represents the probability of nuclear import. Each model is trained to maximize the likelihood of reproducing the training data using EM, and can be used to predict import status from input features.

Fig. 1.

Version 1 of a combined model for nuclear import of proteins, with nodes shown as rounded rectangles, with solid arrows illustrating causal dependencies (parent to child). Version 2 subsumes version 1 and adds parent to child dependencies as shown by dotted arrows. Modules of nodes are shaded to indicate the structure of the three basic models. Latent nodes have a dashed outline. Other nodes are labelled with the features that assign values to them, Boolean nodes have a thicker outline than continuous nodes.

2.3.1 cNLS-only model

We are interested in evaluating the presence and impact of classical nuclear localization signals in isolation and design a cNLS-only model to this end. This model incorporates a feature set and operation very similar to that of cNLS Mapper, enabling us to analyse their differences.

For a query protein x, we have four cNLS class-specific scores, f_C(x): C ∈ {1, 2, 4, 6}. In our model, we represent them as four continuous random variables, each with a latent Boolean parent variable (see Fig. 1). Each of these unobserved variables represents the (independent) probability of a functional cNLS binding site using two Gaussian densities N, each specified by a mean μ and a variance σ² [see Equation (4)].

(4)

Of course with C unknown, the truth value of ‘x is C’ is not known. Instead, each ‘class’ node (C = 1, C = 2, C = 4 and C = 6) is a parent of the ‘Import’ node whose value is available during training. The latent nodes can thus be inferred, and their parameters can be learned using EM. After training these cNLS, class nodes will indicate the presence (the score is in the ‘true’ density) or absence (‘false’ density) of each cNLS in the query sequence.

To avoid overfitting, we divide training data between training the parameters of the cNLS PWMs and the parameters of the Bayesian network.

2.3.2 The PPI-NLSdb model

The PPI-NLSdb model incorporates information of interactions with essential import factors and the presence of uncategorized NLSs. Specifically, this model has four Boolean variables assigned values according to ppi_α, ppi_β, ppi_Ran and NLSdb for a candidate cargo x. These variables are all parents to Import (see Fig. 1).

There may be dependencies between different interactions and some of the patterns in NLSdb, and the structure of the PPI-NLSdb model enables the capture of some of these. Note that ppi_α and f_C : C ∈ {1, 2, 4, 6} are dependent, but f_C is not represented in PPI-NLSdb model.

2.3.3 The SVM-sequence model

The final basic model incorporates sequence similarity between a query protein and each of the known nuclear and non-nuclear proteins in the training set via a SVM. The model only contains a continuous variable that takes the value of SVM(x) and Import as its parent (see Fig. 1). We fit two Gaussian densities over the continuous SVM score similar to each of the PWM scores above. In this case, the component labels are known during training (Import is known to be true or false).

With this simple transformation of the SVM's output to a probability, the SVM sequence model essentially doubles as a benchmark for how well the import classification problem is handled by the machine learning method alone. [As an aside we did explore a SVM with a logistic output function (Platt et al., 2000) with near identical import classification accuracy.] The advantage of designing the network such that the SVM is a continuous node becomes apparent in the combined model where the SVM is one out of many variables that inform the final decision.

Similar to the cNLS-only model, training data are divided so that the SVM is trained on separate data from that used for training the Bayesian network.

2.3.4 A combined model

It is intuitive to combine the basic models to construct a more powerful model (see Fig. 1). We propose two versions of a combined model. Version 1 combines the basic models as three modules in the simplest possible way without recognizing any dependencies that may exist between feature sets. Two new latent nodes are added to alleviate generalization issues brought by an increase of model parameters. (The number of parameters increase exponentially with the number of parents. For example, Import with 2 Boolean parent nodes implies 2² parameters, Import with 4 + 4 Boolean parents implies 2⁸ parameters.) Version 2 explicitly connects the node for ppi_α to the latent cNLS class nodes, thereby recognizing dependencies between importin-α interactions and cNLSs.

2.4 Model inference

From the joint probability, it is trivial to determine conditional probabilities involving a subset of the variables (including latent) using marginalization. We describe and use three inference scenarios of biological interest, of many afforded by our probabilistic modelling framework.

2.4.1 Predicting nuclear import

To predict import status of a query protein, we infer P(Import = true|e) where e is the possibly incomplete ‘evidence’ for a query protein, i.e. a set of instantiated variables representing features. In particular, we consider the probability of nuclear import of a protein given its sequence and interactions with the import machinery. From the sequence, we can determine cNLS scores, NLSdb matches and the SVM score, all of which are typically used as evidence when the variable is represented by the model.

It is sometimes useful to view the inferred probability of nuclear import as either true or false, in particular for validation purposes. We thus need to set a probability threshold θ that needs to be exceeded for a ‘positive’ prediction.

2.4.2 Predicting location of cNLS

In the combined models, we are able to infer cNLS class and location from evidence of sequence, and interaction. Specifically, we determine P(C = c|e): C ∈ {1, 2, 4, 6 }, and find the class with the greatest probability. With c known, we use l(c, x) to find the most likely location of the cNLS.

2.4.3 Predicting importin-α interaction

The combined models integrate several features that complement one another. We are particularly interested in investigating whether we can predict the interaction with the adapter importin-α from sequence-based scores, i.e. P(ppi_α|e) where e includes evidence of sequence, import and interaction with non-importin-α partners. Again, to validate prediction it is useful to threshold the inferred probability.

2.5 Evaluation metrics, datasets and methodology

All three inference scenarios produce a probability as output, e.g. the posterior probability of import or the posterior probability of importin-α interaction. To measure the accuracy of predictions, we rely on two standard metrics for classifiers: the area under the receiver operator characteristic curve (AUC) (Fawcett, 2004) and the Matthews' Correlation Coefficient (MCC; specific to a threshold θ) (Baldi et al., 2000).

The performance coefficient (PC) (Tompa et al., 2005) is used to quantify the accuracy of NLS location and width predictions. It measures the accuracy by considering the overlap of residue-level predictions and actual sites. Definitions of each metric are provided in the Supplementary Material.

NucProt (Fink et al., 2008) is used for training and testing mouse-specific models. The yeast–GFP fusion dataset (Huh et al., 2003) is used for training and testing yeast-specific models. An independent test dataset is extracted from UniProt (Hawkins et al., 2007). We use BioGRID (Stark et al., 2006) to identify relevant protein–protein interaction data. Finally, NLS test data are extracted from UniProt. We describe the construction of all datasets in detail in the Supplementary Material.

We use 6-fold cross-validation for all models: the dataset is split into six subsets, with one kept aside for testing and the remaining five are used for training the Bayesian network, the SVM and the set of PWMs. The process is repeated so that all permutations of subsets are used for training resulting in six Bayesian networks, six SVMs and six sets of PWMs. As indicated previously, we further ensure that the SVM and PWMs are not trained on the same data as that used for the Bayesian network. All reported tests are generated with model components that have not been trained on the same data. We report the average test accuracies and their SD. To evaluate the impact of homology on the prediction performance, we constructed a ‘redundancy reduced’ version where proteins with sequences sharing more than 30% identity were removed.

When possible we compare accuracies of our models to those of cNLS Mapper and NLStradamus. We are unable to control testing procedures when using these models but expect there to be minimal impact of overlap between their training data and our test data. In the case of cNLS Mapper, we are indebted to the authors for running their predictor on our data. The output that were provided does not include scores lower than 6, precluding us from distinguishing between weak predictions when determining AUC and maximum MCC. (According to cNLS Mapper documentation, a score of 8–10 means that the protein is exclusively localized to the nucleus, a score of 7–8 means partial localization to the nucleus, a score of 3–5 means cytoplasmic and nuclear co-localization and a score of 1–2 represents cytoplasmic localization.)

In the case of NLStradamus, we were able to run predictions locally and produce a graded score for each NLS location. We use this score to indicate the support of nuclear import.

3 RESULTS

3.1 Accuracy of predicting nuclear import

Table 1 lists the accuracies of the different models used in this study and that of cNLS Mapper and NLStradamus on the full mouse and yeast datasets. Many NLSs are shared between yeast and mammalian species. It needs to be emphasized, however, that cNLS Mapper and NLStradamus were developed on the basis of yeast data and their use on mouse proteins incorrectly assumes that cNLS recognition mechanisms are identical between the two species.

Table 1.

Accuracy of predicting nuclear imported proteins with different models as measured using AUC and maximum MCC

Model	Mouse		Yeast
	AUC	MCC	AUC	MCC
Combined model v 1	0.84 ± 0.02	0.57 ± 0.02	0.80 ± 0.01	0.44 ± 0.01
Combined model v 2	0.82 ± 0.02	0.52 ± 0.02	0.79 ± 0.01	0.42 ± 0.02
cNLS Mapper	0.66	0.29	0.61	0.24
NLStradamus	0.68	0.29	0.60	0.19
cNLS-only model	0.71 ± 0.01	0.31 ± 0.01	0.70 ± 0.01	0.24 ± 0.01
PPI-NLSdb model	0.62 ± 0.01	0.16 ± 0.01	0.60 ± 0.01	0.16 ± 0.01
SVM-sequence model	0.78 ± 0.01	0.51 ± 0.01	0.76 ± 0.01	0.37 ± 0.01

When available, SDs are provided.

For the mouse dataset, the basic cNLS-only model achieves slightly higher accuracy as that of cNLS Mapper and NLStradamus. All other Bayesian network models except PPI-NLSdb model exceed the accuracy of cNLS Mapper and NLStradamus. The SVM sequence model gets an AUC of 0.78 illustrating how well an SVM-based classifier is expected to do. As we envisaged, the models that combine all features have significantly higher accuracy than any of the other models on the mouse dataset with an AUC of 0.84 and 0.82 and a maximum MCC of 0.57 and 0.52, for version 1 and version 2, respectively.

For the yeast dataset, the cNLS-only model roughly achieves the same classification accuracy as that of cNLS Mapper (MCC is 0.24). However, the cNLS-only model is more accurate than NLStradamus. All other Bayesian network models except the PPI-NLSdb model exceed the classification accuracy of cNLS Mapper and NLStradamus. For yeast, the AUC is 0.80 and 0.79, for the combined models (version 1 and version 2, respectively), 0.61 for cNLS Mapper and 0.60 for NLStradamus. The combined models again achieve superior AUC and MCC (see Table 1).

Nucleo (Hawkins et al., 2007) uses the Spectrum kernel for its SVM model, not unlike the SVM used in the SVM sequence model. Nucleo was shown to outperform all other publicly available protein import predictors on a carefully composed, mixed-species, independent dataset (Hawkins et al., 2007). We attempt to benchmark our model against Nucleo and by extension of all other predictors in that study using the same independent test set. (The datasets used for testing above overlap substantially with Nucleo's training data.) We split the test data from the Nucleo study into yeast and mouse, to evaluate our species-specific models as well as cNLS Mapper and NLStradamus. To determine the accuracy of our combined model, we ensured there was no overlap with our training dataset. (We had to remove these proteins from our original sets, and re-train the models.) The results are shown in Table 2. For the mouse subset, our combined model outperforms all other predictors (MCC of 0.56) while for the yeast subset our model performed equally well as Nucleo (MCC of 0.32).

Table 2.

Accuracy of predicting nuclear import for independent datasets (Hawkins et al., 2007)

Model	Accuracy (MCC)
	Mouse	Yeast	All species
Combined model	0.56	0.32	0.39
Nucleo	0.24	0.32	0.38
cNLS Mapper	0.41	0.26	0.27
NLStradamus	0.37	0.13	0.25

For completeness, we re-trained our model collectively on our yeast and mouse datasets (again excluding proteins that are present in the independent test set). On the complete mixed-species test, our combined model (v 1) achieved an MCC of 0.39, which is slightly higher than Nucleo (MCC of 0.38). We note that Nucleo has the highest sensitivity (76%) and that cNLS Mapper has the highest specificity (87%) at their optimal MCC (data not shown).

To investigate the role of homology in the model's generalization, as opposed to features relevant to translocation, we re-trained and re-tested the model on a set with less than 30% sequence similarity. We note that the accuracy of the combined model (v 1) drops slightly but still outperforms that of cNLS Mapper and NLStradamus when tested on the same homology-free data (see Table 3).

Table 3.

Accuracy of predicting nuclear import for proteins with less than 30% sequence similarity

Model	Accuracy (MCC)
	Mouse	Yeast
Combined model	0.50	0.41
cNLS Mapper	0.28	0.26
NLStradamus	0.29	0.19

3.2 Accuracy of predicting location of a cNLS

The results also show that predicting nuclear import is moderately accurate in the cNLS-only model. However, only a subset of all nuclear proteins are expected to utilize cNLSs, so perfect accuracy is not reasonable. To demonstrate the accuracy of the cNLS feature set and to evaluate the confidence we can put in this particular module of the combined models, we probe how well the model predicts the location of the cNLS.

We tested the combined model (version 1) on proteins with at least one known nuclear localization signal to investigate if (i) predicted locations are accurate; if (ii) correct import predictions are due to the detection of NLS; and if (iii) generic sequence similarity contributes positively specifically to the recognition of cNLSs, and not only to determining nuclear import. We use a nuclear localization signal dataset extracted from UniProt. These data assign only location but not type, for NLSs in protein sequence data.

First for reference, for each query protein, we inferred the probability of nuclear import (see Section 2.4.1). We then identified the most probable location of an NLS (see Section 2.4.2).

We considered prediction of NLS location ‘correct’ if there is any overlap between predicted cNLS location and the known NLS location. We similarly used cNLS Mapper and NLStradamus to predict NLS locations. We observed that for mouse and yeast proteins, our model is more sensitive than cNLS Mapper and NLStradamus. For the mouse dataset, our combined model correctly predicts 51% of all NLS sites compared with 33 and 42% for cNLS Mapper and NLStradamus, respectively. For the yeast dataset, our model correctly predicts 68% of known nuclear localization signals, compared with 53% for cNLS Mapper and 23% for NLStradamus. It needs to be emphasized that UniProt annotations do not distinguish NLS type, are not limited to classical NLSs and many are not marked as experimentally verified.

We note that our models identify a 20-residue window as the site of a cNLS. Both cNLS Mapper and NLStradamus often predict shorter segments and could thus exhibit better specificity. However, in terms of the performance coefficient, which captures prediction specificity and sensitivity, the combined model still performs better than the other two predictors. The results are shown in Table 4.

Table 4.

Performance coefficient comparing the accuracy of predicting NLSs

Model	Mouse		Yeast
	PC	Correct (%)	PC	Correct (%)
Combined model	0.23	162 (51)	0.24	74 (68)
cNLS Mapper	0.13	103 (33)	0.09	58 (53)
NLStradamus	0.13	135 (42)	0.11	25 (23)

If more than one cNLS signal is predicted for a single query, only the most probable NLS is considered. Where more than one equiprobable NLS, the one which gives maximum overlap with known NLS(s) is selected. This increases the overall PC for cNLS Mapper and NLStradamus but has no effect on the PC of our combined model. The number of correct predictions is also shown.

To investigate if cNLS detection is essential for predicting nuclear import, we observe the difference in import probability when either removing a known NLS or an equally wide random subsequence. If detection is non-essential, the two situations should render a positive or negative difference with equal probability. Again we refer to the UniProt NLS data, and count positive versus negative prediction differences, for removal of actual NLSs versus random subsequences. Fisher's exact test clearly supports that if a functional cNLS is removed from a protein sequence, the overall nuclear import probability decreases (P < 10⁻¹³).

We note that in some exceptional cases, there is an increase in nuclear import probability upon removing the cNLS, which suggests the existence of alternative pathway signals. For instance, the proteins Zfp161 and Nufip1 possess PY-NLS motifs (Lee et al., 2006), a karyopherin-β2-dependent targeting signal, not recognized by our model. For Frg1, a spurious bipartite signal is uncovered (KK FQSFQDHKLKISKEDSKILKKAK) after removing the known NLS.

We can confirm that the sequence similarity detected by the SVM contributes to recognizing NLSs as defined by UniProt. By repeating the experiments above with a combined model where the SVM is taken out, we note that the performance coefficient falls from 0.23 to 0.17 for mouse and from 0.24 to 0.19 for yeast. This suggests that the SVM increases the ability of the model to discern true cNLSs, by either finding (complementary) NLS features or other nucleus-associated domains.

Having established that the combined model recognizes four different cNLS classes, we turn to the prediction of novel targeting signals. For the biologist, knowing the location of an NLS enables manipulation and the diagnosis of aberrant localization. Additionally, knowing the site in a multitude of proteins allows statistical analyses of properties, e.g. local structure. Therefore, we predict the cNLS class and cNLS location of both mouse and yeast nuclear proteomes. We show predicted cNLS locations for proteins with high probability (greater than optimal threshold for maximum MCC) of nuclear import in the Supplementary Material.

3.3 Predicting novel importin-α interactions

In the absence of specific information about interactions with the import machinery, predicting the importins with which a candidate nuclear protein interacts provides useful hints of its localization behaviour. Our combined model (version 2) recognizes the biologically meaningful dependency between importin-α and the four cNLS classes and is thus ideally suited to this problem.

We follow the scenario outlined in Section 2.4.3 to infer the value of the variable representing the feature ppi_α given all the other features, including import status. We predict the probability of importin-α interaction for all proteins in the yeast and mouse proteomes. To validate predictions, we leave the variable (ppi_α) unspecified in all cases even when it is known.

Using the yeast protein interaction dataset as a ‘gold standard’ for importin-α interactions, we determine the AUC of predicting importin-α interaction to be 0.67. Using the much less reliable mouse interaction set to validate all predictions for the mouse proteome, the AUC (for importin-α interactions) dropped only slightly to 0.64. However, we believe that the limited data (of importin-α interaction) for validation renders the AUC inconclusive.

To further explore the model's ability to model importin-α interaction, we manually inspected the top 20 predicted importin-α partners in yeast. Out of these 20 interactors, 19 are not in our gold standard set. Instead, we searched for evidence of interaction in the literature. We also looked broadly in existing interaction sets for protein complexes involving both proteins (the cargo and importin-α), and in paired interaction data linking both proteins via an intermediate protein. (An indirect interaction with importin-α may indicate that a group of proteins combine to interact with importin-α.)

Indeed, two of our predicted proteins (HMO1, PXR1) have evidence of direct physical importin-α interaction (Ito et al., 2001). Four high scoring proteins (YTM1, RTG3, BUR2, RPN2) are found to be part of the protein complexes involving importin-α (Gavin et al., 2002, 2006; Ho et al., 2002). Additionally, YTM1 and BUR2 may indirectly interact with importin-α (Jensen et al., 2009). Finally, nine high scoring proteins (SGD1, RGT1, UGA3, BUD23, IFH1, YRM1, POL3, SLD3, PRP21) are found to have evidence of indirect interaction with importin-α (Jensen et al., 2009). In summary, we managed to anecdotally establish association between importin-α and 16 of the top 20 proteins predicted by our model. The predicted and validated interaction network, annotated with evidence, is provided in the Supplementary Material.

4 CONCLUSION

We present a model that incorporates three different types of features to predict nuclear localization and responsible localization signals and interactions. The model predicts whether a protein is imported into the nucleus with an accuracy surpassing that of comparable predictors on the mouse and yeast proteomes. The MCC is 0.57 and 0.44 for mouse and yeast, respectively, and the AUC is 0.84 and 0.80.

To understand the importance of explicitly recognizing NLSs for nuclear import prediction, we compare our approach with localization predictors that do not incorporate such features directly. Nucleo has previously been shown to outperform six different predictors in terms of classifying import status of proteins (Hawkins et al., 2007) and falls predominately into this category. By re-using the independent dataset developed for evaluating Nucleo, we are able to show that our Bayesian network model outperforms the other predictors (MCC is 0.39 on the species-combined data), with Nucleo as a clear second. The explicit recognition of NLS is thus not critical for predicting import accurately—at least when limited to the dominant but far-from-exclusive classical NLSs. By testing our model on a dataset with low sequence redundancy, we show that the generalization performance of our model is not the simple result of matching homology.

A key benefit of our model (in relation to most models including Nucleo) is that it transparently indicates the influence of relevant variables. Thereby, it allows biologists to dissect predictions to find which features are responsible for importing each individual protein. We illustrate this principle by also using the model to predict the most probable cNLS for the mouse and yeast nuclear proteomes.

We establish on a smaller dataset that the model accurately recognizes NLSs and interactions with the import machinery. We verify that the predicted NLSs match 68 and 51% of known independent yeast and mouse NLSs, respectively. Additionally, by hiding functional NLSs from the model and observing a significant decrease in support, we confirm that the model is sensitive to this biologically essential feature. Our Bayesian network-based model can thus enable biologists to identify the nuclear localization signals responsible for binding with karyopherins.

By integrating protein–protein interaction data, biologists are able to tap into an emerging data source. It is clear from our tests that interaction data contributes to prediction accuracy. In the absence of reliable interaction data, the model is flexible enough to operate with these variables unspecified, and to predict several novel importin-α interactors. We validate our top predictions using the literature and argue that the model assists in identifying novel importin-α interactions. Anecdotal evidence offers additional support for 16 of our top 20 importin-α interaction predictions. Considering the sparsity of training and test interaction data, we find the accuracy of predicting importin-α interactions encouraging (AUC is 0.64 and 0.67 for mouse and yeast, respectively).

The current model is easy to extend with recently discovered localization signals, for example the PY-NLS. Cross-referenced with the appropriate data, we believe that predicted NLSs can be used to further characterize proteome-specific NLSs, both structurally and functionally.

Conflict of Interest: none declared.