Incentivizing Better Quality of Care: The Role of Medicaid and Competition in the Nursing Home Industry

Abstract

This paper develops a model of the nursing home industry to investigate the quality effects of policies that either raise regulated reimbursement rates or increase local competition. Using data from Pennsylvania, I estimate the parameters of the model. The findings indicate that nursing homes increase the quality of care, measured by the number of skilled nurses per resident, by 8.7% following a universal 10% increase in Medicaid reimbursement rates. In contrast, I find that pro-competitive policies lead to only small increases in skilled nurse staffing ratios, suggesting that Medicaid increases are more cost effective in raising the quality of care.

1. Introduction

Shortcomings in the quality of care in U.S. nursing homes have been an ongoing public concern for decades. Many studies indicate that nurse-to-resident staffing ratios remain very low (Harrington et al., 2016), which may harm a sizable portion of a particularly vulnerable elderly population. As the U.S. population ages and spending on nursing homes increases, it is important to understand why nursing homes lack incentives to improve the quality of care so that appropriate policy instruments can be designed.

In this paper, I develop a structural model of the nursing home industry to simulate the effects of policies that either raise regulated Medicaid reimbursement rates or increase local competition via directed entry on the quality of care. Using data from Pennsylvania, I find that low Medicaid reimbursement rates are an important contributor to shortfalls in the quality of care. Moderate increases in Medicaid reimbursement rates lead to significant increases in the quality of care. On the other hand, I find that an increase in competition has a relatively small positive effect on the quality of care.

These exercises are motivated by two common institutional features of healthcare markets that can result in low quality of care. First, prices for nursing home care are largely regulated. Nationwide, Medicaid and Medicare regulate the reimbursement rates for 62% and 14% of nursing home residents, respectively. Only 24% of residents pay the private rate set by the nursing home. If reimbursement rates are very low, as is commonly claimed for Medicaid, nursing homes have little incentive to compete for Medicaid beneficiaries through better quality of care. Second, competition in the nursing home industry is muted not only because of vertical and horizontal (geographic) product differentiation, but also because state Certificate of Need (CON) laws restrict entry and investment decisions. Spence (1975) shows that quality can be inefficient if there is market power although the direction of the inefficiency is ambiguous within the Spence framework. White (1972) specifically considers the case when prices are regulated, arguing that market power then leads to lower quality, providing an alternative explanation for observed quality shortfalls in this industry. Whether increases in reimbursement or competition increase social welfare is theoretically ambiguous (Gaynor, 2006) and ultimately an empirical question.

I investigate these questions using data on Pennsylvania’s nursing home industry. One important advantage of this empirical context, besides data availability, is that I can isolate a source of plausibly exogenous variation in Medicaid reimbursement rates. In Pennsylvania, the regulated Medicaid reimbursement rate of each nursing home is based on previously reported costs of all nursing homes in a peer group determined by facility size and region. Each peer group region combines several counties that are commonly assumed to represent locally segmented nursing home markets. My identification strategy isolates the reported cost variation of those nursing homes in the peer group that operate in different counties. Specifically, I assume that, conditional on a rich set of observables, cost shocks to nursing homes located in distant counties affect staffing and pricing decisions of a local nursing home through the reimbursement rule only.

Applying the methodology to the data, I find that an increase in the Medicaid reimbursement rate leads to an economically and statistically significant increase in the number of licensed practical and registered nurses (henceforth skilled nurses) per resident. I find no evidence for changes in other quality inputs. The preliminary evidence suggests a key mechanism through which nursing homes can influence the quality of care: staffing of skilled nurses. The skilled nurse to resident ratio is commonly considered to be a direct quality of care measure. Furthermore, many studies have shown a positive relationship between skilled nurses and quality of care outcomes including improvements in clinical outcomes and reductions in nursing home complaints and deficiencies, see e.g. Kaiser Family Foundation (KFF, 2015).

Building on the preliminary evidence and empirical methods developed in Berry, Levinsohn, and Pakes (1995) and Fan (2013), I next develop and estimate a static industry model in which nursing homes compete in the private rate and the skilled nurse staffing ratio as the key input towards better quality of care. The model captures the role of regulated Medicaid and Medicare reimbursement rates, differences in market structure, and allows for non-pecuniary objectives among not-for-profit and public nursing homes, which may mitigate the quality concerns. To estimate the model, I combine Census and nursing home survey data with administrative resident assessment data from the Long Term Care Minimum Data Set (MDS) and Medicaid and Medicare claims data. I construct additional cost moments from Medicaid cost reports to identify differences in objectives between for-profits, not-for-profits, and publicly operated nursing homes.

My findings indicate that current skilled nurse staffing ratios are inefficiently low. Nursing home residents value an additional skilled nurse at $133,000 per year on average, which exceeds the annual cost of employment of $83,000, considering wages and fringe benefits. My estimates also imply that current staffing ratios fall short of the social optimum by 34% on average. While these calculations abstract away from income effects, I find qualitatively similar results in extensive robustness exercises which build on staffing recommendations and estimated returns on nursing from the literature, or estimated income effects based on observed asset spend-down or bequest decisions. I find no evidence for inefficiently low staffing ratios in the small fraction of nursing homes that do not accept Medicaid residents, suggesting that low Medicaid rates are a potentially important contributor to quality shortfalls in this industry.

I revisit this conjecture in the first counterfactual exercise. Here, I simulate the effects of a universal 10% increase in Medicaid reimbursement rates. I find that nursing homes increase the number of skilled nurses per resident by 8.7% and decrease their private rates by 4.5% on average. The decrease in private rates indicates “cost-shifting” between Medicaid beneficiaries and private payers, which has been studied in the hospital industry (Frakt, 2011) but not for nursing homes. Combining the effects on consumer surplus, provider profits, and public spending, I find a welfare gain of $31 million per year, about 9.3% of the increase in Medicaid spending. The welfare gains are muted by an unintended market expansion effect. As the quality of care increases, elderly people substitute from community to nursing home care raising Medicaid spending considerably. The baseline logit model may overstate the market expansion effect as it allows for more elastic substitution between different forms of care, when compared to a nested logit model (nesting all nursing home goods). In the robustness section, I bound the market expansion effect from below by considering an alternative demand model that does not allow for substitution between different forms of care. This model predicts very similar changes in staffing and pricing but larger increases in social welfare ($68 million).

I compare these findings to the effects of an increase in local competition via directed entry of a new public nursing home. I find very small changes in incumbent skilled nurse staffing ratios. My results point to a reduction in social welfare as the consumer gains are smaller than the reduction in industry profits, when adding the fixed costs of the new entrants. I also find that new entrants are unable to recover their fixed costs. Considering the annual losses of the new entrants as required additional public spending, I find a return in skilled nurses per resident per $100 million in public spending of only 0.4%. In contrast, I find a return of 2.6% in the former policy counterfactual, which suggests that raising Medicaid reimbursement rates is more cost effective in improving the quality of care.

In order to focus the analysis on the interplay of Medicaid rates, competition, and the quality of care, the baseline model abstracts away from capacity constraints. I relax this assumption in the robustness section by estimating alternative demand models that allow for rationing. I also revisit the staffing responses to Medicaid rate changes when excluding nursing homes close to capacity. While each approach relies on strong assumptions, they all indicate that the key findings of the main analysis are robust to potential rationing, perhaps because Pennsylvania does not restrict entry and capacity investments through a CON law.¹

The main contribution of this paper is to provide new evidence on the dependence of the quality of nursing home care on Medicaid reimbursement rates and local market power. Previous studies investigated the link between Medicaid reimbursement rates and nurse staffing ratios both theoretically (Scanlon, 1980; Ma, 1994; Rogerson, 1994) and empirically (Gertler, 1989; Grabowski, 2001; Harrington et al., 2008; Feng et al., 2008).² Other studies have investigated the link between measures of concentration and staffing (Lin, 2015) and pricing decisions (Nyman, 1988).

My analysis contributes to this literature in two important ways. First, I explore a novel source of plausibly exogenous variation in the Medicaid reimbursement rate and thereby address the endogeneity concerns of previous related studies. Second, this paper is the first to develop and estimate an explicit model of demand and supply of the nursing home industry using a novel combination of survey and administrative data sources. The model allows me to analyze the welfare consequences of quality shortfalls and to quantify the demand and supply mechanisms through which alternative policies can mitigate these concerns.³

My demand analysis is related to Ching, Hayashi, and Wang (2015), who develop a novel methodology to quantify how binding capacity constraints, induced by a CON law in Wisconsin, restrict access to care for Medicaid beneficiaries. My paper is primarily concerned with the quality of nursing home care. To this end, I simplify their demand model by abstracting away from rationing in the baseline analysis. Instead, I extend their analysis by adding an endogenous quality of care component. I take advantage of rich administrative resident data, which allow me to include Medicare beneficiaries, and model residents with multiple payer sources. I use more precise information on distances to nursing homes, which is a key source of horizontal product differentiation. These institutional details are important in understanding the link between quality, pricing, Medicaid reimbursement rates, and local competition.

My supply side analysis is related to Lin (2015), who develops a rich dynamic model of nursing home entry and exit. Lin’s paper studies important dynamic considerations in the interdependence between quality choices and market structure, which my paper abstracts away from. My analysis focuses on explaining the large cross-sectional differences in the quality of care. To this end, I adopt a simpler static modeling approach and replace the author’s reduced form profit function with an explicit model of demand and supply. Shifting the focus towards separating demand and supply is integral for welfare analysis and for understanding the mechanisms through which Medicaid reimbursements affect staffing and pricing incentives.

A second contribution is the identification of non-pecuniary objectives among non-profit and public nursing homes, which have been argued to be important in this industry (Chou, 2002). Combining the model with marginal cost data allows me to decompose observed quality differences by profit status into differences in local demand, cost structures, and non-pecuniary objectives. This extends previous empirical studies on the hospital industry which have not been able to separate differences in objectives from differences in costs (Gaynor and Vogt, 2003). My findings indicate that non-pecuniary objectives of non-profits can explain quality differences between for-profit and not-for-profit nursing homes.

Finally, my counterfactual entry analysis relates to an older theoretical literature on the social inefficiencies of free entry (Spence, 1976; Dixit and Stiglitz, 1977; Mankiw and Whinston, 1986). In the presence of fixed costs, free entry can be excessive when entrants steal business from incumbents. Conversely, entry can be insufficient when entrants cannot appropriate all of the consumer surplus. This study provides new empirical evidence on these inefficiencies in a policy relevant context, given that CON laws restrict entry of new nursing homes in several states.

The rest of this study proceeds as follows. Section 2 describes institutional details of the industry with an emphasis on the quality of care. In Section 3, I describe the data and present preliminary evidence from Pennsylvania. I discuss the empirical industry model in Section 4, and present estimation and counterfactual results in Sections 5 and 6, respectively. Finally, I consider robustness checks in Section 7, and Section 8 concludes.

2. Institutional Background

2.1. Quality of Care

Quality shortfalls in nursing home care have been an ongoing concern for decades as evidenced by very low nurse staffing ratios, poor clinical outcomes, and a high number of process or outcome based deficiencies (Deparment of Health and Human Services, 1999; Harrington et al., 2016). In an effort to improve the quality of care, various policy attempts have been made including minimum staffing regulations, nursing homes inspections, resident health reporting, reimbursement reform, and public reporting of quality outcomes, with only partial success (Werner and Konetzka, 2010). With Medicaid being the primary payer for most nursing home residents, reimbursement rates continue to be a priority policy area for state governments to address low nurse staffing ratios and nursing home deficiencies.

In this paper, I focus on licensed practical and registered nurse (skilled nurse) staffing ratios as the key mechanism through which nursing homes influence the quality of care. I make this modeling choice for three main reasons. First, skilled nurses play an important role in monitoring and coordinating the delivery of care and many studies have found a positive relationship between skilled nurse staffing and better outcomes of care. These include fewer deficiencies (Lin, 2014), better clinical outcomes such as improved physical functioning, less antibiotic use, fewer pressure ulcers, catheterized residents, urinary tract infections, less weight loss, and less dehydration (see KFF (2015) for an overview), as well as lower mortality rates (Friedrich and Hackmann, 2017). Second, skilled nurse staffing ratios are published on publicly available quality report cards (screen shots are provided in Figures A.1 and A.2) giving nursing homes an economic incentive to improve staffing in order to attract more residents. Finally, I provide direct evidence that nursing homes primarily adjust the number of skilled nurses per resident in response to changes in the regulated Medicaid reimbursement rates.⁴

2.2. Market Structure, Regulation, and the Quality of Care

Nursing home expenditures totaled $170 billion in 2016, about 5% of total health care spending, up from 3% in 1965. Over the next decade, nursing home expenditures are expected to grow roughly proportionately to total health care spending at an annual rate of 5.3%.⁵ This poses a substantial burden for state budgets given that Medicaid is the primary payer for most nursing home stays. In Pennsylvania (and nationwide), about 62% of residents are covered by Medicaid at any given point in time, who meet the state-specific income and asset criteria. Medicaid pays the nursing home a regulated capitation payment per Medicaid-resident day, the Medicaid reimbursement rate, which is intended to cover the provider’s expenses for health care services as well as room and board. Most states, including Pennsylvania, calculate nursing home specific reimbursement rates based on a prospective, risk-adjusted, cost-based reimbursement methodology, which I discuss in greater detail in Section 3.1.

The average Medicaid reimbursement rate per resident and day equals about $189 in Pennsylvania, exceeding the national average by $25 or about one standard deviation in state averages (see Table A.1 for a comparison of Medicaid rates and other institutional details). The Medicaid rates generally fall short of the private rate, set by the nursing home, which are charged to about 27% of residents in Pennsylvania who pay out-of-pocket (compared to 24% nationwide). In Pennsylvania, private rates exceed the Medicaid reimbursement rate by 17% on average and nursing homes are not allowed to charge Medicaid or Medicare beneficiaries on top of the regulated rate. The residual 11% of residents are generally covered by Medicare and only a very small fraction of residents has private long term-care insurance. Medicare pays the nursing home a more generous reimbursement rate per resident and day, but only covers up to 100 days of post-acute care following a qualifying hospital stay.

Medicare’s day limit and the asset eligibility criteria for Medicaid also imply that a large fraction of residents transitions between multiple payer sources during a nursing home stay. In Pennsylvania, 52% of residents are covered by Medicare at the time of admission but more than 90% of these residents are covered by Medicaid or pay out-of-pocket at the end of their stay (see Table A.2 for details). Also, 34% of residents are initially paying out-of-pocket but almost 60% of these residents are covered by Medicaid at their time of discharge.

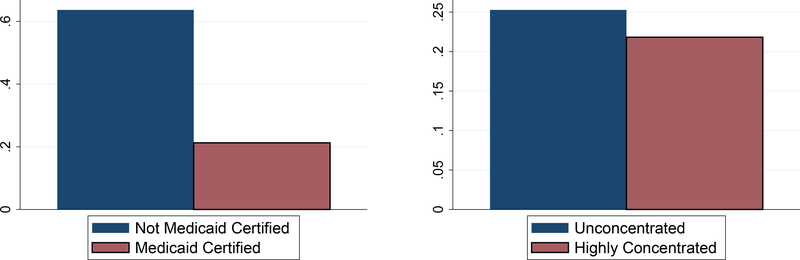
Since the daily revenues differ across payer types, nursing homes have an economic incentive to differentiate the quality of care. However, federal regulations require that nursing homes offer the same quality of care to all payer types within a facility. Existing studies have shown that nursing homes comply with the regulation (Angelleli, Grabowski, and Gruber, 2008). Therefore, I model quality of care as a public good across different payer types. Nevertheless, one would expect quality differences between nursing homes based on the composition of payer types served. In the left graph of Figure 1, I compare the number of skilled nurses per resident between Medicaid certified nursing homes (93%) and nursing homes that do not accept Medicaid beneficiaries (7%) using national data from LTC focus from 2010. The large staffing difference provides the first evidence that Medicaid reimbursement plays a potentially important role for the quality of care. I revisit this hypothesis in the next section using detailed data on Medicaid reimbursement rates in Pennsylvania.

Figure 1:

Skilled Nurses per Resident by Medicaid Certification and Concentration

Notes. The vertical axis measures the number of skilled nurses per resident. Following the merger guidelines from the Federal Trade Commission, the right graph divides counties into highly concentrated (HHI >2,500) and non-concentrated (HHI <1,500) markets. The national data come from LTC Focus in 2010.

A competing explanation for quality shortfalls in this industry is a lack of local competition. The average Herfindahl index (HHI), using the county as the market definition, equals 1,200 in Pennsylvania compared to 2,000 nationwide. The difference in concentration (about one standard deviation in state averages) may be partially attributed to CON laws which restrict entry and capacity investments in two thirds of the states but not in Pennsylvania. The HHI measures suggest that the nursing home industry is less concentrated than the hospital industry. However, the county market definition may understate the market concentration if nursing homes compete in more narrowly defined geographic markets. In the right graph of Figure 1, I compare average staffing ratios between highly concentrated markets (29%) and non-concentrated markets (57%). The observed difference suggests that an increase in competition might lead to better quality of care.

Motivated by the evidence from Figure 1, I now turn to a rigorous analysis of the dependence of staffing and pricing decisions on Medicaid reimbursement rates and market structure using detailed data from Pennsylvania.

3. Data and Preliminary Evidence from Pennsylvania

I collect administrative resident level micro data from the Minimum Data Set (MDS), which provides at least quarterly information on a variety of health measures for all nursing home residents in Medicaid or Medicare certified nursing homes, about 98% of all nursing homes. The MDS has become increasingly more popular among researchers who study the health profiles of nursing home residents. However, this is the first study, to the best of my knowledge, which uses the MDS to estimate the demand for nursing home care.

Nursing home residents typically struggle with multiple physical and cognitive disabilities. I focus on a subset of health measures, evaluated at the time of the senior’s admission to the nursing home, to model potential differences in the senior’s preferences for nursing home characteristics. For instance, I measure whether the resident was diagnosed with Alzheimer’s disease and allow for a particular preference for nursing homes with an Alzheimer’s unit. I also reduce a large number of health measures and disabilities to a one-dimensional individual case-mix index (CMI). The CMI is used in reimbursement methodologies and summarizes the expected resource utilization relative to the average resident. I use the admission date and the discharge date to calculate the length of the nursing home stay, which is the unit of observation in the empirical analysis.⁶ The MDS also provides the zip code of the resident’s former address, which allows me to incorporate the role of distance in the demand model.

One disadvantage of the MDS is that the provided payer type information is not particularly accurate. Therefore, I merge the MDS with Medicaid and Medicare claims data, which allow me to specify which days during any stay were covered by Medicaid or Medicare. I assume that the residual days are paid out-of-pocket because only a very small fraction of residents has access to private long-term care insurance.⁷

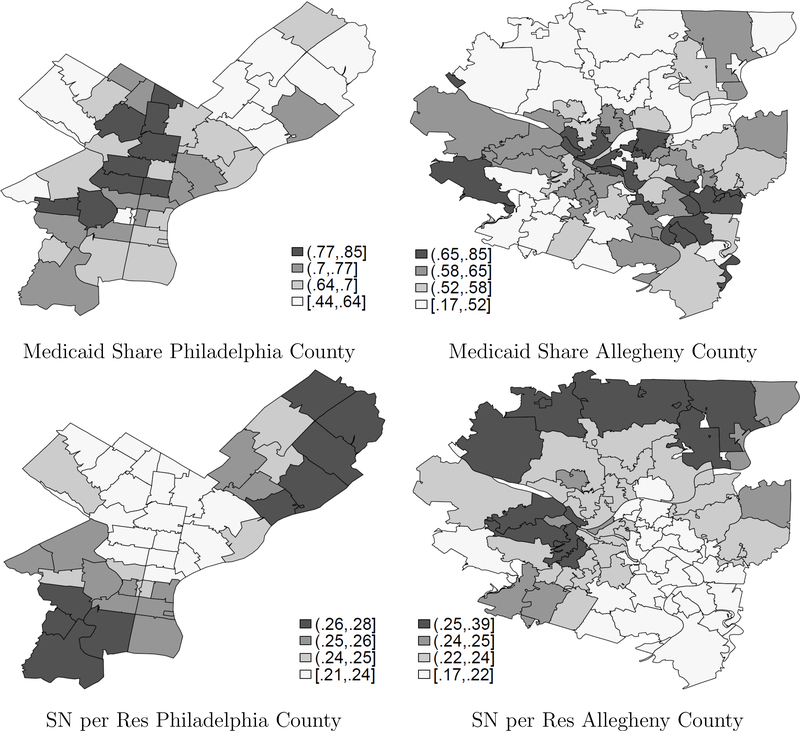
I focus on seniors who were admitted to a nursing home in Pennsylvania in the years 2000–2002, which reduces the sample population to about 287,000 nursing home stays, about 96,000 admissions per year. The top graphs of Figure 2 describe spatial variation in the fraction of Medicaid beneficiaries by zip code of former residence in two urban counties, Philadelphia County and Allegheny County (which includes the city of Pittsburgh). The graphs indicate that there is considerable heterogeneity in the payer mix across zip codes within the same county. This provides rich spatial variation in nursing home’s staffing and pricing incentives since the distance between the senior’s former residence and the nursing home is critical for the nursing home choice. The first row of Table 1 indicates that the median senior chooses a nursing home within 7km of the senior’s former residence. There is also considerable heterogeneity in the length of stay among nursing home residents, see the second row of Table 1. While some residents stay for several years, about 50% are discharged within 1 month.

Figure 2:

Local Medicaid Share and Skilled Nurses per Resident

Notes. The top graphs summarize the spatial variation in the share of Medicaid beneficiaries by the zip code of their former residence. The lower graphs display distance-weighted averages in the number of skilled nurses per resident. I construct the average over all nursing homes within 10km of the zip code centroids.

Table 1:

Summary Statistics 2000–2002

	N	Mean	10th	50th	90th
Distance traveled (in 100km)	287,364	0.11	0.02	0.07	0.23
Length of Stay (in days)	287,364	222	8	34	868
Share Medicaid	2,079	0.59	0.14	0.66	0.85
Licensed Practical Nurses per Resident	2,079	0.14	0.07	0.13	0.21
Registered Nurses per Resident	2,079	0.13	0.06	0.11	0.21
Daily Private Rate	2,079	223	175	212	261
Daily Medicaid Rate	1,834	183	158	181	210
Marginal Costs per Resident Day	1,824	159	123	155	194
Fixed Costs per Year (in million dollars)	1,781	1.25	0.48	1.11	2.05

Notes. The top two rows describe the data from the MDS and are based on newly admitted residents between 2000 and 2002. Travel distance is weighted by length of stay. The remaining rows describe the data from the annual nursing home survey and the annual cost reports for the years 2000–2002.

I combine the MDS with data from annual nursing home surveys, which were provided by the Bureau of Health Statistics and Research of the Pennsylvania Department of Health.⁸ The survey provides information on various nursing home characteristics for all licensed nursing homes in Pennsylvania, including the Medicaid reimbursement rate, the private rates charged to seniors who pay out-of-pocket, and the number of full-time and part-time employees by profession. I aggregate the employment information to full-time equivalent employees by dividing the part-time employees by 2 and adding them to the number of full-time employees.

I use survey data from 1996–2002 for the preliminary analysis on the effect of Medicaid reimbursement rates on staffing and pricing decisions and focus on the years 2000–2002 in the structural estimation. Similar to Feng et al. (2008), I exclude nursing homes that primarily target residents requiring expensive rehabilitative care (provided by specialized therapists) as opposed to support with their chronic disabilities, and thereby compete in a different market.⁹ I also exclude nursing homes that focus on out-of-state residents (more than 85% of residents). This reduces the sample population by about 10% to 5,000 nursing home-year observations including 2,079 observations for the years 2000–2002, summarized in the middle rows of Table 1. There is considerable variation in the share of Medicaid residents between nursing homes as indicated by the third row, which is (positively) spatially correlated with the variation in Medicaid beneficiaries across their former residences. About 8% of nursing homes are not Medicaid certified and cannot serve any Medicaid beneficiary. There is also substantial variation in the number of licensed practical and registered nurses per resident across nursing homes. The 90th percentile exceeds the 10th percentile by a factor of three. The lower graphs in Figure 2 summarize the distance-weighted spatial distribution of skilled nurses per resident across zip codes for the two urban example counties. The graphs visualize the negative spatial correlation between skilled nurse staffing ratio and the local share of Medicaid beneficiaries in the two urban counties.¹⁰ This provides additional evidence that Medicaid reimbursements are a potentially important determinant of the quality of care.

I merge the survey data with detailed cost information for Medicaid certified nursing homes. Every year, certified nursing homes submit reimbursement relevant cost reports to Pennsylvania’s Department of Human Services (DHS). Following the detailed Medicaid reimbursement guidelines, the DHS isolates allowable costs, which are considered as necessary costs to provide nursing home care and are used directly in the Medicaid reimbursement methodology.¹¹ I treat these allowable costs as economic costs, which is consistent with the Medicaid reimbursement goal to cover economic costs. I follow the interpretation of the DHS and treat health related costs (mostly salaries and fringe benefits of health care professionals) and other health related costs (mostly spending on room and board) as variable costs.¹² In the empirical model, I assume constant marginal costs, whereby average variable costs and marginal costs per resident and day are equal. Hence, I can recover marginal costs by dividing the total annual variable costs by the number of resident days in the given year, which equal $155 per resident and day, on average.¹³ The annual fixed costs equal $1.1 million on average, which comprise administrative and capital costs, see the last row of Table 1.

Finally, I calculate the county level share of elderly people with long term care needs in nursing home care using complementary population data from the Census 2000 5% sample. I restrict the Census populations to seniors aged 65 and older, who indicate a physical or mental health condition. These conditions define plausible prerequisites for considering any long term care support and institutional nursing home care in particular. Scaling the sample to the full population, I find that 32% of the 225,000 seniors with physical or mental conditions live in a nursing home. The standard deviation of county level shares equals 9.4%.

3.1. Medicaid Reimbursement, Staffing, and Pricing

In this section, I provide first direct evidence on the effects of regulated Medicaid provider reimbursement rates on staffing and pricing decisions. To this end, I consider the following empirical specification for Medicaid certified nursing homes:

$$log(Y_{jt})={\gamma }_{1}log(R_{jt}^{mcaid})+\alpha X_{jt}+{\varphi }_{ct}+{ϵ}_{jt}.$$ (1)

Here, log(Y_jt) denotes the respective outcome measure in nursing home j and year t, such as the log number of skilled nurses per resident or the log daily private rate for a semi-private room. $log(R_{jt}^{mcaid})$ refers to the log Medicaid reimbursement rate per resident and day, ϕ_ct captures county-year fixed effects, and X_jt contains additional nursing home specific control variables. The key parameter of interest is γ₁ which denotes the effect of an increase in the log Medicaid reimbursement rate on staffing and pricing decisions.

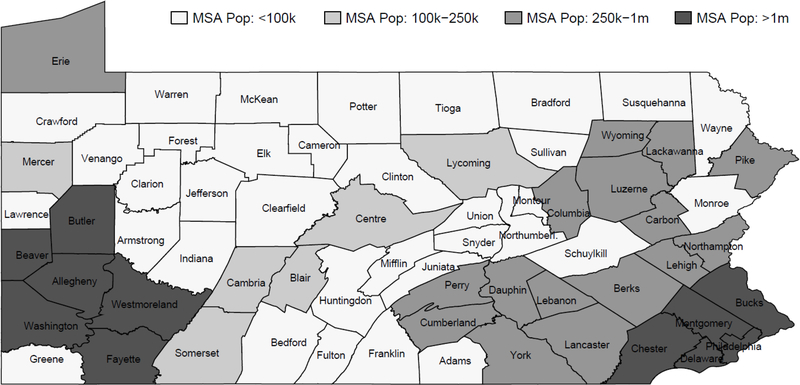
Before discussing the identification of γ₁, it is important to describe Pennsylvania’s reimbursement methodology. The Medicaid reimbursement rate is based on reported costs (from 3–5 years ago) of all nursing homes in a peer group determined by size and region. The DHS distinguishes between small (<120 beds), medium-sized (120–269 beds), and large nursing homes (>269 beds) in each of the four reimbursement regions indicated in Figure 3, defining 12 peer groups.¹⁴ The regions are determined based on the population size of the Metropolitan Statistical areas (MSAs) and combine several counties that are commonly assumed to define separate nursing home markets (Zwanziger, Mukamel, and Indridason, 2002).

Figure 3:

Reimbursement Peer Group Regions in Pennsylvania

Specifically, the Medicaid reimbursement rate for nursing home j depends on j’s lagged average costs from 3–5 years ago, AC_jt–3,₄,₅ = {AC_jt–3, AC_jt–4, AC_jt–5}, as indicated by the first argument in the reimbursement formula g(·), see Appendix A.4 for details:

$$R_{jt}^{mcaid}=g\left(A{C}_{jt-3,4,5},median(A{C}_{c,t-3,4,5}^{p(j)},A{C}_{-c,t-3,4,5}^{p(j)})\right).$$ (2)

Furthermore, $R_{jt}^{mcaid}$ also depends on the median of lagged average costs of all nursing homes in j′s peer group, p(j), as indicated by the second argument. This includes average costs of nursing homes located in j′s county c, abbreviated by $A{C}_{c,t-3,4,5}^{p(j)}$ and, importantly, average costs of nursing homes located in other counties –c, captured by $A{C}_{-c,t-3,4,5}^{p(j)}$. For example, the Medicaid reimbursement rate for a nursing home located in Allegheny County (Southwest corner in Figure 3) depends in part on lagged costs of nursing homes located in Bucks County (Southeast corner), if they are of similar size.

Finally, I decompose average costs into observable cost shocks Z_jt ⊂ X_jt, which is a subset of X_jt, staffing decisions $Y_{jt}^s$ scaled by input prices w^s, and unobservable cost shocks η_jt:

$$A{C}_{jt}={\varphi }^z{Z}_{jt}+\sum _s{w}^s{Y}_{jt}^s+{\eta }_{jt}.$$ (3)

Identification

An empirical challenge to the estimation of γ₁ is the potential correlation between $log(R_{jt}^{mcaid})$ and ϵ_jt, which would add bias to the ordinary least squares estimator. This is of particular concern because j′s lagged average costs affect $log(R_{jt}^{mcaid})$ directly, see the first argument in equation (2). The correlation between $log(R_{jt}^{mcaid})$ and ϵ_jt can be positive or negative. For example, unobserved positive demand shocks, may increase staffing and consequently average costs and future reimbursement rates, suggesting a positive correlation. Alternatively, unobserved supply shocks, such as higher input prices, may lower staffing but increase costs, suggesting a negative correlation. Furthermore, the staffing decisions of j′s local competitors may affect $log(R_{jt}^{mcaid})$ through the median argument in equation (2) if they belong to the same peer group. Rival staffing decisions may also affect j′s staffing decisions directly suggesting a positive or negative correlation depending on whether staffing decisions are strategic complements or substitutes. This effect is, however, attenuated by costs of distant non-competitors that enter the median argument as well.

To mitigate these concerns, I assume that nursing homes compete in locally segmented markets both for new residents and inputs (e.g. nurses). In my primary specification, I assume that counties define segmented markets suggesting that lagged costs from nursing homes located in different counties, $A{C}_{-c,t-3,4,5}^{p(j)}$, do not affect the optimal staffing and pricing decision directly and are therefore excluded from equation (1). However, these costs affect the Medicaid reimbursement rate, see equation (2), and can therefore serve as instrumental variables. For example, the for-profit penetration affects the equilibrium distribution of staffing ratios and private rates and thereby affects the cost distribution of providers in the given county. The exclusion restriction states that the county-specific for-profit penetration does not affect staffing and pricing decisions in other counties, conditional on the for-profit penetration in these distant counties, other than through the reimbursement formula.

More formally, $A{C}_{-c,t-3,4,5}^{p(j)}$ must be independent of ϵ_jt, conditional on X_jt and ϕ_ct. As shown in Appendix B.1, this holds true if the following two assumptions are satisfied:

• (SP) ϵ_jt is independent of lagged shocks to providers located in other counties from 3 or more years ago, conditional on X_jt and ϕ_ct:

  $${ϵ}_{jt}⫫{\left\{{ϵ}_{-ct-k},{\eta }_{-ct-k},X_{-ct-k},{\varphi }_{-ct-k}\right\}}_{k\in 3,4,..}|X_{jt},{\varphi }_{ct}$$
• (SE) ϵ_jt is independent of lagged shocks to peer group members located in the focal county c from six or more years ago, conditional on X_jt and ϕ_ct, if γ1 ≠ 0:

  $${ϵ}_{jt}⫫{\left\{{ϵ}_{ct-k},{\eta }_{ct-k},X_{ct-k},{\varphi }_{ct-k}\right\}}_{k\in 6,7,\mathrm{..}}|X_{jt},{\varphi }_{ct}$$

Assumption (SP) may be violated if shocks to staffing decisions, governed by equation (1), are spatially as well as serially correlated. Assumption (SE) may be violated if local staffing shocks are serially correlated, adding bias if they affect the instrumental variable, average costs in other counties, $A{C}_{-c,t-3,4,5}^{p(j)}$, as well. Intuitively, this bias operates through a “feedback loop” in future years. For example, ϵ_jt–6 affects Y_jt–6 and consequently AC_jt–6, through equations (1) and (3), respectively. This in turn affects $R_{-c,t-3,4,5}^{mcaid}$ through equation (2) and in turn $Y_{-ct-3,4,5}^{p(j)}$ and $A{C}_{-c,t-3,4,5}^{p(j)}$ through (1) and (3). Hence, ϵ_jt–6 may “feed” back into $R_{jt}^{mcaid}$ through $A{C}_{-c,t-3,4,5}^{p(j)}$ adding bias if ϵ_jt–6 is correlated with ϵ_jt.

In this context, I find that serial correlation alone can only add a small upward bias to the two stage least squares (2SLS) estimator discussed below. Using a bounding exercise detailed in Appendix B.2, I find an upward bias of at most 5%. This is largely because of the long time lag of 6 or more years in assumption (SE) and because I control for serial correlation at the county level through county-year fixed effects. Furthermore, the “feedback loop” operates through the median argument in equation (2), which is attenuated by cost shocks from several other counties. Regarding assumption (SP), I find very little spatial correlation in marginal costs and staffing decisions between counties, see Figure B.1, in parts because the median senior chooses a nursing home within only 7km of her former residence. I return to a more thorough discussion of assumptions (SE) and (SP) at the end of this section.

To use the large number of instrumental variables most effectively, I employ a simulated instrument approach (Currie and Gruber, 1996). This method increases statistical power by exploiting knowledge of the functional relationship between instruments and the endogenous regressor. To apply this method, I use the exact reimbursement formula but simulate an analogue Medicaid reimbursement rate that only varies in exogenous cost components, costs from peer group affiliated nursing homes located in different counties:

$$R_{jt}^{mcaid,sim}=\frac{1}{N^{sim}}\sum _{i=1}^{N^{sim}}g\left(x_i,median(x_i,A{C}_{-c,t-3,4,5}^{p(j)})\right)$$

Here, x_i is a random average cost draw from the distribution of all nursing homes in the state and N^sim is the number of simulation draws. Following Currie and Gruber (1996), this instrument can be thought of as a “convenient parametrization” of the generosity of a nursing home’s Medicaid reimbursement rate, purged of variation due to the nursing home’s own costs as well as it’s rival’s costs, see Appendix A.4 for details.¹⁵

Table 2 presents the 2SLS regression results. The first column shows the first stage parameter estimate, which indicates that a 1% increase in the simulated reimbursement rate raises the endogenous Medicaid reimbursement rate by 1.15%. The point estimate is statistically significant at the 1% level with an F statistic of 42. The remaining columns present the second stage effects. The estimate in the second column indicates an economically and statistically significant effect for skilled nurses. Nursing homes increase the number of skilled nurses per resident by 1.17% in response to a 1% increase in the Medicaid reimbursement rate. To put this effect into perspective, I assume that a full-time skilled nurse works 2,080 hours per year, which corresponds to 52, 40-hour weeks. The number of skilled nurses per resident equals 0.24 on average, which corresponds to 2,080 *0.24/365=1.37 hours per resident and day. This suggests that a 10% increase in Medicaid rates raises the time a skilled nurse spends per resident and day by about 10 minutes on average.

Table 2:

Medicaid Reimbursement Rates, Staffing, and Pricing

	(1)	(2)	(3)	(4)	(5)
	1st Stage	log(SNres)	log(NAres)	log(Thres)	log(P)
Log Simulated Rate	1.15 (0.18)
Log Medicaid Rate		1.17 (0.29)	0.07 (0.49)	0.66 (2.25)	0.03 (0.20)
Observations	4022	4022	3872	3307	4022
R2	0.189	0.090	0.039	0.122	0.101

Notes.log(SN^res), log(NA^res), and log(Th^res) abbreviate the log number of skilled nurses, nurse aides, and therapists per resident, respectively. log(P) is the log daily private rate. All specifications control for county-year fixed effects, ownership type, having an Alzheimer’s unit, average distance to closest competitors, local demographics, and a fourth order polynomial in beds interacted with year fixed effects. Standard errors are displayed in parentheses and are clustered at the county level.

I find no evidence for systematic changes in other inputs including the number of nurse aides or therapists, see columns 3 and 4, as well as pharmacists, physicians, psychologists, social workers, and dietetic technicians, see Table B.2. I also explore the effects on additional inputs captured by overall changes in costs and find that about three quarters of the overall change in costs can be explained by changes in the skilled nurse staffing ratios, see Table B.3. While the large standard errors on other staffing measures make it difficult to rule out other endogenous characteristics, the cost estimates suggest that skilled nurses are the most important measure. For tractability reasons and following the reasons outlined in Section 2.1, the structural analysis focuses on a single quality of care measure: the number of skilled nurses per resident. Finally, column 5 displays the effect on private rates, which equals 0.03 and is statistically insignificant.

I repeat the analysis with a leave-one-out instrumental variable approach. Instead of using the exact reimbursement formula, I compute the average over reported costs from providers located in different counties. The findings are qualitatively similar. The first stage coefficient decreases to 0.61 (se=0.16) and the second stage coefficient for skilled nurses decreases to ${\widehat{\gamma }}_1^{2SLS}=0.83$ (se=0.36). Again, I find no evidence for systematic changes in the number nurse aides per resident, therapists per resident, or the private rate, see Table B.4.

Robustness

Whether potential violations of assumptions (SP) and (SE) add significant bias to ${\widehat{\gamma }}_1^{2SLS}$ depends on the specific context. In Appendix B, I show in an extensive list of robustness checks that the potential bias from serial and spatial correlation is probably small in this context. With respect to serial correlation, I revisit the point estimates exploring identifying variation in observable distant cost shocks, Z_–ct–3,₄,₅, only. These include the number of licensed beds, the ownership type, the distance to a nursing home’s closest competitors, and local demographics. This refinement allows me to drop assumption (SE) as I do not have to account for the “feedback loop” relationship between endogenous staffing and average costs in equation (3). I can also relax assumption (SP) as follows: ϵ_jt ⫫ {Z_–ct–k}_k∈3,4,..| X_jt, ϕ_ct, with Z_–ct–k ⊂ X_–ct–k. Here, I find a point estimate for skilled nurses of ${\widehat{\gamma }}_1^{2SLS}=1.41$, see column 2 of Table B.5. I also consider robustness to concurrent trends at the peer group-county level, which may violate assumption (SE). To this end, I add data from 1993–1995 to the analysis and take advantage of a change in the reimbursement methodology in 1996. The reimbursement rates from 1996 onward are not correlated with staffing ratios prior to 1996, which provides evidence against biases arising from concurrent trends, see Figure B.2. With respect to spatial correlation, I consider robustness to a more conservative geographic market definition: the MSA. Exploring cost variation of nursing homes located in different MSAs, I find ${\widehat{\gamma }}_1^{2SLS}=1.01$ for skilled nurses, see column 3 of Table B.5.

4. Empirical Model of Demand and Supply

Motivated by the preliminary evidence, I now turn to the empirical industry model, which allows me to analyze the positive and normative implications of counterfactual experiments.

Demand:

I employ a static model of demand for a cohort of seniors considering nursing home care in year t.¹⁶ I assume that senior i with payer type τ decides between an outside good and the nursing home j which maximizes her average daily indirect conditional utility:¹⁷

$$\begin{gathered} u_{it\tau j}={\beta }_1^d{D}_{ij}+{\beta }_2^d{D}_{ij}^2+{\beta }_i^{sn}log(S{N}_{jt}^{res})+\sum _x{\beta }_i^x{X}_{jt}+{\beta }_{\tau }^p{P}_{jt}+{\xi }_{jt}^{\tau }+{\nu }_{ijt} \\ \text{with}{\beta }_i^k={\beta }^k+\sum _r{z}_{ir}{\beta }_r^k. \end{gathered}$$ (4)

Here, D_ij measures the distance between the senior’s former residence and the nursing home. $log(S{N}_{jt}^{res})$ denotes the log number of skilled nurses per resident and X_jt captures characteristics that remain exogenous in the empirical analysis. These include, for example, the presence of an Alzheimer’s unit. P_jt captures the daily private rate charged to elderly people who pay out-of-pocket. ${\xi }_{jt}^{\tau }$ denotes facility and payer type specific preference shocks which are observed by person i but remain unobserved to the econometrician and ν_ijt refers to an i.i.d. extreme value taste shock. The ${\beta }_i^k$ parameters represent the taste of senior i for nursing home characteristic k, which may vary in the senior’s health profile (evaluated at admission) and payer type, captured by vector z_i.

I distinguish between three payer types: residents who pay the entire stay out-of-pocket, elderly people who are covered by Medicaid or Medicare for the entire stay, and elderly people who are partially covered but also pay some days of their stay out-of-pocket. I refer to these payer types as private, public, and hybrid payers, respectively. I allow the price coefficients in equation (4) to differ between payer types. Intuitively, one would expect that hybrid payers respond less elastically to prices than private payers. Finally, I assume that public payers do not respond to private rates and set their price parameter to zero. This is equivalent to setting their price to zero. I also allow for differences in unobserved preference shocks, ${\xi }_{jt}^{\tau }$, which may capture differences in room amenities.

These differences in preferences between payer types are summarized in the nursing home mean utilities, δ_τjt, which vary at the product-payer-type-year level:

$${\delta }_{\tau jt}=\{\begin{array}{ll}{\beta }^{sn}log(S{N}_{jt}^{res})+{\sum }_x{\beta }^x{X}_{jt}+{\beta }_{priv}^p{P}_{jt}+{\xi }_{jt}^{priv}\hfill & ifprivatepayer\hfill \\ {\beta }^{sn}log(S{N}_{jt}^{res})+{\sum }_x{\beta }^x{X}_{jt}+{\beta }_{hyb}^p{P}_{jt}+{\xi }_{jt}^{hyb}\hfill & ifhybridpayer\hfill \\ {\beta }^{sn}log(S{N}_{jt}^{res})+{\sum }_x{\beta }^x{X}_{jt}+{\xi }_{jt}^{pub}\hfill & ifpublicpayer.\hfill \end{array}$$ (5)

Instead of choosing nursing home care, seniors can also remain in their community and demand other formal and informal forms of long term care. I capture the demand for community-based care by an outside good. Senior i′s utility from choosing this option is:

$$u_{it,out}={\phi }_{c(i)}+{\nu }_{it,out},$$

where φ_c captures differences in the quality of the outside good between counties of residence. Senior i′s probability of choosing nursing home j is then given by:

$$s_{ijt}=\frac{exp({\beta }_1^d{D}_{ij}+{\beta }_2^d{D}_{ij}^2+{\sum }_{k,r}{z}_{ir}{\beta }_r^k{\tilde{X}}_{jt}+{\delta }_{\tau jt})}{exp({\phi }_c)+{\sum }_{l\in C{S}_i}exp({\beta }_1^d{D}_{il}+{\beta }_2^d{D}_{il}^2+{\sum }_{k,r}{z}_{ir}{\beta }_r^k{\tilde{X}}_{lt}+{\delta }_{\tau lt})},$$ (6)

where ${\tilde{X}}_{jt}=\left[X_{jt},log(S{N}_{jt}^{res})\right]$ to abbreviate notation. CS_i denotes senior i′s choice set of nursing homes. This includes all nursing homes in a 50 km radius around the senior’s former address. I impose this choice set restriction for computational reasons as it reduces the data memory requirements considerably. However, only 2% of the seniors choose a nursing home that is farther away, see Figure C.1.

Supply:

I consider a static oligopoly model. Nursing homes compete in private rates and the number of skilled nurses per resident for a cohort of seniors who begin their nursing home stay in year t. To deal with stays that overlap multiple years, I assume that nursing homes commit to the cohort-specific staffing ratio and private rate throughout the entire stay.

I assume that nursing homes operate under constant marginal costs per resident and day, MC_jt, which depend on the skilled nurse staffing ratio, their unobserved input price W_jt, and an unobserved cost shifter ζ_jt The total cost of serving residents from cohort t is then:

$$C_{jt}=M{C}_{jt}\sum _i{s}_{ijt}LO{S}_i+F{C}_{jt}=({\zeta }_{jt}+W_{jt}S{N}_{jt}^{res})\sum _i{s}_{ijt}LO{S}_i+F{C}_{jt}.$$

Here, LOS_i denotes resident i′s potential length of (nursing home) stay in days should she choose any nursing home care. FC_jt denotes fixed costs.¹⁸ Combining demand and costs, I can express nursing home profits over cohort t as:

$$\begin{gathered} {\mathrm{\Pi }}_{jt}=\sum _i{s}_{ijt}(P_{jt}Day{s}_i^{priv}+R_{jt}^{mcaid}Day{s}_i^{mcaid}+R_t^{mcare}Day{s}_i^{mcare})-C_{jt} \\ =\sum _i{s}_{ijt}LO{S}_i({\overline{R}}_{ijt}-M{C}_{jt})-F{C}_{jt}. \end{gathered}$$

Here $Day{s}_i^{priv}$ refer to days paid out-of-pocket and $Day{s}_i^{mcaid}$ and $Day{s}_i^{mcare}$ denote days reimbursed by Medicaid and Medicare respectively, which are known to the nursing home at the beginning of each stay. $R_{jt}^{mcaid}$ and $R_t^{mcare}$ denote the Medicaid and Medicare reimbursement rates per resident day and ${\overline{R}}_{ijt}$ captures the average daily revenue rate over the nursing home stay of the elderly i. Hence, the model captures the effect of local variation in demographics and socioeconomic status on staffing and pricing decisions through the combination of detailed payer source information and individual choice probabilities in the profit function.

Nursing Home Objectives:

Not all nursing homes are necessarily profit maximizers. 46% of nursing homes are for-profits, 48% are private and not-for-profit, and 6% are public. While there is no agreement in the literature on a general model for non-profits, most models assume an objective function that depends on profits and an additional argument such as quantity or quality (Gaynor and Town, 2011). Following Lakdawalla and Philipson (1998), I assume that not-for-profit as well as public nursing homes maximize a utility function which is additive in profits and output quantity, capturing the motive to provide access to care:

$$U_{jt}={\alpha }_j{\mathrm{\Pi }}_{jt}+(1-{\alpha }_j)\sum _i{s}_{ijt}LO{S}_i.$$ (7)

Specifically, I allow α ≠ 1 for non-profits and public nursing homes. Nursing homes choose private rates and staffing ratios simultaneously. Rewriting the first order conditions yields:

$$M{C}_{jt}=\frac{{\sum }_i{s}_{ijt}Day{s}_i^{priv}+{\sum }_i\frac{\partial s_{ijt}}{\partial P_{jt}}{\overline{R}}_{ijt}LO{S}_i}{{\sum }_i\frac{\partial s_{ijt}}{\partial P_{jt}}LO{S}_i}+\frac{1-{\alpha }_j}{{\alpha }_j}$$ (8)

$$W_{jt}=\frac{{\sum }_i\frac{\partial s_{ijt}}{\partial S{N}_{jt}^{res}}({\overline{R}}_{ijt}-M{C}_{jt}+\frac{1-{\alpha }_j}{{\alpha }_j})LO{S}_i}{{\sum }_i{s}_{ijt}LO{S}_i}.$$ (9)

The non-pecuniary objectives enter equation (8) as a marginal cost shifter. Intuitively, non-profits behave as for-profits with a perceived marginal cost advantage of $\frac{1-{\alpha }_j}{{\alpha }_j}$, see Lakdawalla and Philipson (1998).

4.1. Estimation and Identification

My estimation strategy proceeds in two steps, similar to Goolsbee and Petrin (2004).

Step 1: To recover the nursing home mean utilities, δ_τjt, as well as preference heterogeneity over nursing home characteristics, $({\beta }_r^k,{\beta }_1^d,{\beta }_2^d)$, I first focus on seniors in nursing home care, e.g., seniors who chose an “inside” good. Using the MDS, I construct the share of seniors in a given nursing home as a fraction of seniors in any nursing home. Building on the logit structure, I derive the analogues choice probabilities predicted by the model and estimate $({\delta }_{\tau jt},{\beta }_r^k,{\beta }_1^d,{\beta }_2^d)$ via Maximum likelihood (ML).^19,20 Turning to the outside good, I combine these parameter estimates with the observed county level shares of seniors in community care to recover the outside good parameters, φ_c, see Appendix C.2 for details.²¹

Step 2: In the second step, I use a generalized method of moments (GMM) estimator to recover the remaining mean preferences for nursing home characteristics, see equation (5), as well as the cost and nursing home objective parameters. In the model, nursing home managers observe the unobservable taste shocks, ${\xi }_{jt}^{\tau }$, before they choose the skilled nurse staffing ratios and the private rates. Therefore, these choices are likely correlated with the unobservables.

To address this endogeneity concern, I employ an instrumental variables approach. Motivated by the preliminary evidence from Table 2, I use the simulated Medicaid reimbursement rate as an instrument for the skilled nurse staffing ratios. I assume that the identifying cost variation (stemming from nursing homes located in different counties) is orthogonal to unobserved preference shocks in the given nursing home county. Unfortunately, the simulated Medicaid rate has no significant effect on private rates, see Table 2. Therefore, I consider two additional sets of instrumental variables to address the price endogeneity concerns.²² First, I use region specific housing and wage price indices interacted with the payer type. Higher input prices raise marginal costs and lead nursing homes to charge higher private rates in equilibrium (the first stage). A common assumption in the industrial organization literature is that these marginal cost shifters do not affect preferences directly, which allows me to exclude them from equation (5). Second, I use observable and exogenous product characteristics of local competitors (ownership type and number of beds), which do not enter the indirect conditional utility function directly. However, they affect the rival’s costs, staffing, and pricing decisions and thereby have an indirect effect on staffing and pricing decisions of local competitors through competitive spillover effects. The instrumental variables form the “demand” moment conditions E[ξ · IV] = 0 and the following sample analogue:

$$G^{Demand}(\theta )=\frac{1}{N}\sum _{\tau ,t,j}{\xi }_{jt}^{\tau }I{V}_{jt}^{\tau }.$$

Here, θ summarizes the structural parameters and N = 3 · 3 · J, where J is the number of nursing homes multiplied by 3 payer types and 3 sample years. $I{V}_{jt}^{\tau }$ is the demeaned vector of instruments.²³ To recover the objective parameters for non-profits and publicly operated nursing homes, I construct additional “cost” moments. Similar to Byrne (2015), I match the cost predictions from the first order conditions, see equations (8) and (9), with cost data from Medicaid cost reports by ownership type, own. Let J^own be the set of for-profits (FP), not-for-profits (NFP), or public nursing homes (Pub). The moment conditions are E[mc_j – MC_j(θ)|j ∈ J^own] = 0 and E [w_j – W_j(θ)|j ∈ J^own] = 0, where lower and upper case variables refer to data and model predictions, respectively. The sample analogues are:

$$\begin{gathered} G_{1,own}^{Cost}(\theta )=\frac{1}{N}\sum _{\tau ,t,j\in J^{own}}\left(m{c}_{jt}-M{C}_{jt}(\theta )\right),own\in \{FP,NFP,Pub\} \\ {G}_{2,own}^{Cost}(\theta )=\frac{1}{N}\sum _{\tau ,j\in J^{own}}\left(w_{j,02}-W_{j,02}(\theta )\right),own\in \{FP,NFP,Pub\}. \end{gathered}$$

Here, w and mc denote the observed compensation package for a skilled nurse and marginal costs per resident and day, respectively, see Section 3 for the derivation of marginal costs.²⁴ Due to data limitations, I only use data on compensation packages from 2002, which is also the base year for the following counterfactual analysis. Finally, I also match variances in marginal costs and compensation packages. The moment conditions are Var(mc) = Var(MC(θ)) and Var(w) = Var(W(θ)), motivating the following sample analogues:

$$\begin{gathered} G_3^{Cost}(\theta )=\frac{1}{N}\sum _{\tau ,t,j}{\left[m{c}_{jt}-\frac{1}{N}\sum _{\tau ,t,j}m{c}_{jt}\right]}^2-\frac{1}{N}\sum _{\tau ,t,j}{\left[M{C}_{jt}(\theta )-\frac{1}{N}\sum _{\tau ,t,j}M{C}_{jt}(\theta )\right]}^2 \\ {G}_4^{Cost}(\theta )=\frac{1}{N}\sum _{\tau ,j}{\left[{\omega }_{j,02}-\frac{1}{N}\sum _{\tau ,j}{\omega }_{j,02}\right]}^2-\frac{1}{N}\sum _{\tau ,j}{\left[W_{j,02}(\theta )-\frac{1}{N}\sum _{\tau ,j}{W}_{j,02}(\theta )\right]}^2. \end{gathered}$$

Finally, I stack G^Demand(θ), $G_{1,type}^{Cost}(\theta )$, $G_{2,type}^{Cost}(\theta )$, $G_3^{Cost}(\theta )$, and $G_4^{Cost}(\theta )$ and use the two-step GMM estimator (Hansen, 1982) of θ from the stacked moments. ²⁵

5. Results

Table 3 presents relevant demand and firm objective function parameter estimates in column 1. I find that residents value higher skilled nurse staffing ratios $({\widehat{\beta }}^{sn}>0)$ in particular sicker residents with a higher CMI $({\widehat{\beta }}_{cmi}^{sn}>0)$. Residents dislike paying higher private rates if they pay at least partly out-of-pocket $({\widehat{\beta }}_{hyb}^p<0,{\widehat{\beta }}_{priv}^p<0)$.²⁶ Not surprisingly, private payers have a higher disutility for private rates than hybrid payers since they pay the private rate on all days, as opposed to only on some days of the stay.²⁷ Consistent with the suggestive evidence from Table 1, I find that residents value proximity to the former residence.²⁸ ${\widehat{\beta }}_1^{th}$, ${\widehat{\beta }}_2^{th}$ and ${\widehat{\beta }}_{alz}^{alz}$ provide further evidence for taste heterogeneity based on observable resident characteristics. For example, residents with a stay of fewer than 100 days have a higher valuation for the number of rehabilitative care therapists per resident if they are assigned a larger number of rehabilitative care minutes $({\widehat{\beta }}_2^{th}>0)$. Also, residents with a diagnosed Alzheimer’s disease value nursing homes that have an Alzheimer’s unit.

Table 3:

Preference and Nursing Home Objective Parameters

		(1)	(2)	(3)	(4)	(5)
βsn:	log(SN/Resident)	0.888 (0.009)	1.526 (0.748)	1.923 (0.808)	1.786 (0.821)	1.878 (0.844)
${\beta }_{hyb}^p$:	Price*Hybrid	−0.007 (0.000)	−0.012 (0.002)	−0.006 (0.002)	−0.012 (0.002)	−0.012 (0.002)
${\beta }_{priv}^p$:	Price*Private	−0.011(0.001)	−0.018 (0.004)	−0.019 (0.004)	−0.019 (0.004)	−0.018 (0.004)
${\beta }_{cmi}^{sn}$:	log(SN/Resident)*CMI	0.226 (0.003)	0.226 (0.003)	0.221 (0.003)	0.231 (0.003)	0.230 (0.003)
${\beta }_1^d$:	Distance in 100km	−25.79 (0.014)	−25.79 (0.014)	−25.86 (0.014)	−25.80 (0.014)	−25.79 (0.014)
${\beta }_2^d$:	Distance2	22.45 (0.037)	22.45 (0.037)	22.47 (0.037)	22.44 (0.037)	22.42 (0.037)
${\beta }_1^{th}$:	Therapist/Res*Min	−0.124 (0.001)	−0.124 (0.001)	−0.133 (0.001)	−0.122 (0.001)	−0.122 (0.001)
${\beta }_2^{th}$:	Therapist/Res*Min*Short-Stay	0.314 (0.007)	0.314 (0.007)	0.306 (0.008)	0.312 (0.007)	0.312 (0.007)
${\beta }_{alz}^{alz}$:	Alzheimer*Alzheimer Unit	0.414 (0.002)	0.414 (0.002)	0.419 (0.002)	0.413 (0.002)	0.413 (0.002)
ϑ:	Occupancy< $\overline{oc}$				0.757 (0.002)	0.628 (0.002)
ϑhyb:	Occupancy< $\overline{oc}$ *Hybrid				−0.027 (0.003)	−0.088 (0.002)
ϑpriv:	Occupancy< $\overline{oc}$ *Private				−0.044 (0.005)	−0.058 (0.002)
$\frac{1-{\alpha }_{NFP}}{{\alpha }_{NFP}}$	Non-Profit Objective Parameter	23.05 (0.944)
$\frac{1-{\alpha }_{Pub}}{\alpha p_{ub}}$	Public Objective Parameter	36.14 (1.659)
	Avg Benefit per SN/year	$133,336 ($15,605)	$139,607 ($72,999)	$166,511 ($76,278)	$154,711 ($76,513)	$171,685 ($84,130)
	Avg Wage+Fringe Benefits/SN	$83,171	$83,171	$83,171	$83,171	$83,171
	Benefit-Cost	$50,165 ($15,605)	$56,436 ($72,999)	$83,340 ($76,278)	$71,540 ($76,513)	$88,514 ($84,130)
	Cost Moments	Y	N	N	N	N
	Rationing	N	N	100%	97%	95%

Notes. The table displays the estimated preference and nursing home objective parameters. Column 1 shows the baseline parameter estimates that are identified off from demand and cost moments. Estimates in column 2 are derived from demand moments only. Column 3 presents estimates from a first-come-first-serve rationing model. Columns 4 and 5 allow for asymetric rationing by payer type when occupancy falls short of 97% and 95%, respectively. Average benefits as well as average wage and fringe benefits per SN are measured in 2002. Th/res, SN/res, and Min abbreviate therapists per resident, skilled nurses per resident, and rehabilitative care minutes respectively. Standard errors are displayed in parentheses.

Turning to the firm objective parameters, $\frac{1-{\widehat{\alpha }}_{NFP}}{{\alpha }_{NFP}}>0$ indicates that non-profits depart from profit maximization. The positive parameter estimate implies that non-profits maximize a weighted average of profits and total resident days. Publicly operated nursing homes depart even further from profit maximization as evidenced by a larger parameter estimate $(\frac{1-{\widehat{\alpha }}_{Pub}}{{\alpha }_{Pub}}>\frac{1-{\widehat{\alpha }}_{NFP}}{{\alpha }_{NFP}}>0)$. The coefficients indicate that not-for-profits and public nursing homes act, all else equal, as if they had a marginal cost advantage of $23 and $36, respectively.

In column 2, I present analogous results that only exploit the more traditional demand moments in the second step of the empirical strategy. This specification also provides a natural benchmark for further robustness exercises that do not exploit the cost moments either. The point estimates in the second panel remain unchanged since I have not changed the first step in the estimation algorithm. Therefore, I focus the discussion on the mean parameter estimates listed in the first three rows. The point estimates increase slightly in absolute magnitude, both for private rates and the skilled nurse staffing, but the ratio of the parameters remains almost identical, which is important for the normative implications as discussed below. However, the standard errors increase substantially (in particular for ${\widehat{\beta }}^{sn}$). In that sense, adding the additional cost moments primarily increases the precision of the point estimates. Another disadvantage of an exclusive analysis of demand moments is that they do not separately identify the firm objective parameters from marginal costs.

Turning to the cost estimates, the predicted marginal costs and annual compensations for skilled nurses coincide closely with their observed counterparts. This also holds true if I exclude the cost moments from the GMM estimation procedure, see Figures C.2 and C.3.²⁹

Normative Implications:

Next, I turn to a comparison of the marginal benefit and the marginal cost of an additional skilled nurse. As shown in Appendix C.4, the marginal benefit per resident is given by the marginal utility of a skilled nurse divided by the marginal utility of income. The latter is inherently difficult to quantify for Medicaid and Medicare residents, who do not pay for their nursing home stays.³⁰ To address this concern, I assume that all seniors have the same marginal utility of income given by the estimated price parameter of private payers,${\beta }_{priv}^P$. I revisit this assumption in the robustness check section 7. It is important to note, however, that this assumption does not affect the positive results in the counterfactual analysis. To this end, I also compare the quality returns per public dollar spent of different policy interventions in Section 6.

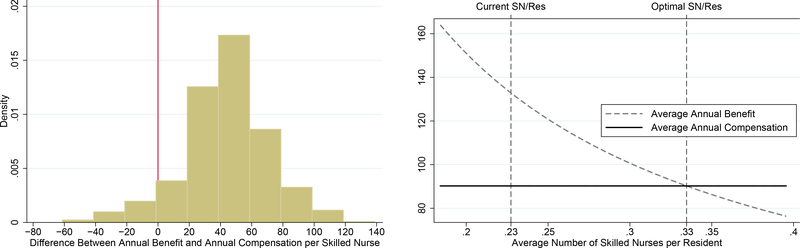
Aggregating the resident benefits at the nursing home level in 2002 and taking a weighted average by the number of beds, I find a marginal benefit of $133,000 per year, see the lower end of Table 3. The marginal costs of employing an additional skilled nurse equal only $83,000 per year when considering wages and fringe benefits. The difference of $50,000 is statistically significant at the 1% level, suggesting that skilled nurse staffing ratios are, on average, inefficiently low.³¹ To assess potential heterogeneity across nursing homes, I display the distribution of differences between the marginal benefit and the annual compensation in the left graph of Figure 4. The histogram indicates that staffing standards are inefficiently low in about 96% of the nursing homes as shown by a positive wedge. However, a few nursing homes have negative wedges. Interestingly, 91% of these nursing homes do not accept Medicaid residents. This indicates that low Medicaid reimbursement rates may play a relevant role in explaining inefficiently low staffing levels in Medicaid certified nursing homes.

Figure 4:

Normative Implications in 2002 (in $1,000)

Next, I study the optimal skilled nurse staffing ratios in a simple social planner problem. Here, the social planner allocates residents to nursing homes and chooses the skilled nurse staffing ratio in order to maximize the sum of consumer surplus and provider profits. To simplify the analysis, I assume that annual earnings for skilled nurses are constant within a county. In the optimum, the marginal cost of an additional skilled nurse (the compensation package) equals the marginal benefit in each nursing home. Finally, I take an average of these optimality conditions over nursing homes in each county.

In the right graph of Figure 4, I test the condition in Allegheny County, which lies within the Pittsburgh MSA. The horizontal line indicates the marginal cost of employing an additional skilled nurse, assuming perfectly elastic labor supply, which equals $90,000 in Allegheny County.³² The downward sloping curve indicates the marginal benefit of an additional skilled nurse. The benefit curve decreases in the staffing ratio because of diminishing marginal utilities. The optimality condition suggests a nurse staffing ratio of 0.33 (1.9 hours per resident and day), as indicated by the right vertical line. This estimate exceeds the observed average staffing ratio of 0.23 in 2002 (1.3 hours per resident and day), indicated by the left vertical line, by 43%. Both observed and optimal staffing ratios are substantially higher than the regulated minimum staffing ratio of 0.07. On average over all counties, the optimal staffing ratio equals 0.38, which exceeds the observed staffing ratio by 51% (see Table C.1 for details)

6. Counterfactuals

Medicaid Rate Increase:

First, I study the effects of a universal 10% increase in the Medicaid reimbursement rates.³³ The bottom rows of Table 4 display the average change in the skilled nurse staffing ratio and the private rate between the old and the new equilibrium. On average, the staffing ratio increases by 8.7%, which translates into an extra 7.2 skilled nurse minutes per resident and day.³⁴ This estimate falls into the 95% confidence interval from the preliminary analysis, which suggests a staffing increase of 11.7%, see Table 2.

Table 4:

Counterfactual: Universal 10% Increase in Medicaid Rates

	Baseline		No Market Expansion
	Absolute	%Δ Spending	Absolute	%Δ Spending
Δ CS	212.0	64.1%	202.6	89.0%
Δ Profits	149.4	45.2%	103.7	45.5%
Δ Spending	330.7	100.0%	227.7	100.0%
Δ Welfare	30.7	9.3%	78.6	34.5%
Avg Δ SN/Res		8.7%		8.7%
Avg Δ P		−4.5%		−4.5%

Notes. Absolute values are measured in million dollars. The right panel presents welfare estimates holding nursing home demand (market shares) fixed.

The sign of the effect on private rates is theoretically ambiguous. The increase in skilled nurses raises marginal costs, which encourages nursing homes to raise their private rates. However, an increase in Medicaid rates also raises the profitability of hybrid payers who are partially covered by Medicaid, partially pay out-of-pocket, and who respond to changes in private rates. Hence, nursing homes have an incentive to lower their private rates in order to attract additional hybrid payers. My results indicate that the second effect dominates. On average, I find a 4.5% reduction in the private rate, which indicates “cost-shifting” between Medicaid beneficiaries and private payers (Frakt, 2011).³⁵ While common theories rationalize cost-shifting with revenue or income targets of health care providers, my context provides a novel mechanism: multiple payer sources among hybrid payers.

Turning to the welfare implications, Medicaid spending increases by $331 million, see the third row, for two reasons. First, holding nursing home demand fixed, the rate increase raises Medicaid spending by 10% or $228 million as evidenced in the third column. Second, higher staffing ratios and lower private rates lead to a market expansion, increasing the overall demand for nursing home care by 6.7%. This raises Medicaid spending by $103 million because of an additional 790,000 Medicaid days for seniors, who previously lived in the community.³⁶

Nursing homes take advantage of the increase in Medicaid spending: profits increase by $149 million, about 45% of the increase in Medicaid spending. That means that nursing homes pass about 55% on to residents through lower private rates and higher nurse staffing ratios. To evaluate the effects on consumer surplus, I again extrapolate the price coefficient of private payers to the entire nursing home population, which implies:

$$\mathrm{\Delta }C{S}_t=\frac{1}{{\beta }_{priv}^P}\left[\sum _{i}log(\sum _{j}exp({\delta }_{i\tau jt}^1))LO{S}_i-\sum _{i}log(\sum _{j}exp({\delta }_{i\tau jt}^0))LO{S}_i\right]$$

Here, ${\delta }_{i\tau jt}^1$ and ${\delta }_{i\tau jt}^0$ denote the indirect conditional daily utility, net of the extreme value shock, evaluated at new and old product characteristics, respectively. Holding market shares fixed, lower private rates and higher nurse staffing ratios raise consumer surplus annually by about $203 million, see the first entry in the third column. Substitution between community and nursing home care options raises the consumer surplus gains to $212 million.

Combining the overall increase in consumer surplus, provider profits, but also Medicaid spending, I find an annual welfare gain of $31 million, about 9.3% of the increase in Medicaid spending. Ignoring the market expansion effect, the welfare gain increases to $79 million or 34.5% of the increase in Medicaid spending. This is largely because the marginal seniors between substituting from community based care to nursing home care add only 4.4% to the gains in consumer surplus despite their significant impact on Medicaid spending.

The welfare estimates ignore the deadweight loss of higher taxes, which are required to fund the additional Medicaid spending. Common estimates of the deadweight loss of taxation cluster around 30% of tax revenues (Poterba, 1996), which exceeds the baseline return on Medicaid spending. The baseline logit model overstates the substitutability of different forms of care, when compared to a more flexible nested logit model, providing a potential lower bound on the welfare return of increased Medicaid spending. However, the return on Medicaid spending increases to only 34.5% when holding market shares fixed, suggesting that the deadweight loss of taxation is at best fully offset by welfare gains in this industry. I return to the substitution between different forms of care in Section 7.

I also revisit the entire analysis for a greater increase in Medicaid rates of 30%. The findings are generally very similar. However, I find smaller welfare gains, relative to Medicaid spending, because of diminishing marginal utilities in the quality of care and a disproportionate increase in the overall demand for nursing home care. This suggests that increases in Medicaid rates can lead to larger welfare gains in other U.S. states, given that the average Medicaid reimbursement rate in Pennsylvania exceeds the national average by 17%. Finally, the estimated Medicaid elasticities also indicate that differences in Medicaid rates can fully explain the observed 11% difference in skilled nurse staffing ratios between Pennsylvania and the national average, see Table A.1 for details.

Directed Entry:

Next, I simulate the effects of a new public nursing home in four rural counties in an effort to understand the gains from competition in a market with only a hand full of providers. Furthermore, the rural elderly continue to be of particular policy interest to the extent that the lack of healthcare professionals impedes access to health care services. In each county, I add a publicly operated nursing home located at the size-weighted average of longitude and latitude coordinates of the respective incumbents. To calculate the product characteristics and the cost structure of new entrants, I regress these variables on a polynomial in licensed beds, county population, and ownership types and assign the predicted values assuming that new entrants operate with 100 licensed beds. I use the structural model to calculate the private rate and staffing ratio distribution in the new equilibrium, holding the staffing ratios and the private rates of the new entrants fixed. On average, incumbents adjust their staffing ratios and private rates by less than 1% in each county as indicated by the top panel of Table 5. Incumbents in Monroe and Jefferson County respond slightly more elastically to entry in parts because the new entrant steals 6% of county demand as opposed to only 3% in Northumberland and Lycoming County.³⁷

Table 5:

Directed Entry and Counterfactual Comparison

	Northumberland	Lycoming	Monroe	Jefferson	PA
Var. Profit Entrant	0.2	0.3	0.5	0.2	1.1
Fixed Costs	1.1	1.1	1.1	1.1	4.4
Δ Profit	−1.1	−1.0	−1.0	−1.1	−4.2
Δ CS	0.6	0.8	1.5	0.6	3.6
Δ Spending	0.4	0.5	0.9	0.3	2.0
Δ Welfare	−0.9	−0.7	−0.4	−0.8	−2.6
Avg ΔSNres	0.06%	0.08%	0.88%	0.75%	0.01%
Avg Δ P	0.02%	0.07%	−0.73%	−0.35%	0.00%
Medicaid Expansion with Outside Good			Entry with Outside Good
ΔSNres	Δ Spending	ΔSNres/100m	ΔSNres	Δ Spending	ΔSNres/100m
8.70%	331 million	2.63%	0.01%	3.3 million	0.35%
8.70%	181 million	4.81%	0.01%	4.2 million	0.28%

Notes. The top panel compares the effects of directed entry between rural counties and illustrates the aggregate effects at the state level in the last column. Average staffing and pricing effects are weighted by market shares. The lower panel compares the return on public spending between directed entry in rural counties and a 10% increase in Medicaid rates. Absolute values are measured in million dollars. SN^res indicates skilled nurses per resident.

I next turn the results into welfare estimates. The variable annual profits of new entrants vary between $0.2 million and $0.5 million, see the first row of Table 5. Assuming that new entrants incur annual fixed costs of $1.1 million, the median fixed costs displayed in Table 1, I conclude that the new entrants accumulate annual losses of $3.3 million. This finding is consistent with recent industry trends that indicate net exit of nursing homes in Pennsylvania as well as nationwide. Industry losses are even larger not only because incumbents raise staffing ratios on net, but also because the variable profits of new entrants stem from “business stealing”, see the third row. This compares with potential gains in consumer surplus of $3.6 million per year, see the fourth row of column 5. Holding market shares fixed, changes in incumbent nursing home characteristics raise consumer surplus by only $0.3 million, which is the key object of interest in this exercise. Hence, most of the increase in consumer surplus captures gains from variety, which combines the gains from a convenient location and an additional extreme value draw. I interpret this estimate as an upper bound on the consumer welfare gains to the extent that the lack of random coefficients loads unobserved taste heterogeneity onto the extreme value taste shock (Petrin, 2002). Yet, the consumer welfare gains fall short of the additional annual fixed costs of operating the new nursing homes ignoring additional sunk costs of entry. Finally, adding the increase in Medicaid spending (following a 3.6% demand expansion for nursing home care in the four counties) I find an annual welfare loss of $2.6 million.

Quality Returns on Spending:

Finally, I compare the quality returns on public spending between raising Medicaid reimbursement and directed entry. This exercise does not require an assumption on the marginal utility of income. The results are summarized in the lower panel of Table 5. Dividing the increase in skilled nurse staffing by the increase in Medicaid spending suggests a skilled nurse return of 2.6% per $100 million in additional public spending. Repeating this calculation in the entry counterfactual suggests a return of only 0.35% per $100 million in public spending when considering new entrants’ annual losses of $3.3 million as required additional public spending. I also analyze the effects of directed entry in four urban counties and find qualitatively similar results. For example, I find a quality return of 0.33% in urban counties, see Table D.1. This comparison indicates that moderate increases in Medicaid rates are about 7.5 times as effective in raising the quality of care than encouraging local competition via directed entry in rural (urban) counties.

In the second row, I revisit this comparison considering the effects on incumbent profits. Here, I adjust public spending by the change in incumbent profits, which are relevant if the state has to compensate incumbents for their incurred losses in the case of directed entry. Conversely, I assume that the increase in profits following an increase in Medicaid rates can be levied via additional taxes. This comparison indicates that a 10% increase in Medicaid rates is about 17 times as effective in raising the quality of care than encouraging local competition via directed entry in rural counties.

Non-Pecuniary Objectives, Staffing, and Pricing:

I also revisit the role of non-pecuniary quantity motives, which may give non-profits an incentive to raise the quality of care and to lower private rates in order to increase demand. To investigate this hypothesis, I remove the non-pecuniary objectives of not-for-profit and public nursing homes (1 – α_j = 0) and simulate the new equilibrium. I find that not-for-profits and public nursing homes would lower the skilled nurse staffing ratio by 10% and 23%, respectively, if they were maximizing profits. Furthermore, the non-pecuniary objectives can fully explain the observed difference in staffing ratios between for-profits and not-for-profits in Pennsylvania. I also find that not-for-profits and public nursing homes would increase their private rates by 16% and 29%, respectively. Nationwide, about 70% of nursing homes are for-profit compared to only 50% in Pennsylvania providing an alternative explanation for quality differences between states. However, the difference in staffing ratios between for-profits and not-for-profits scaled by differences in for-profit penetration among states can only explain a 2% difference (out of an 11% difference) in staffing ratios between Pennsylvania and the national average.

7. Robustness

Rationing.

The baseline analysis abstracts away from capacity constraints, which may introduce bias to the demand and supply elasticities. To assess the role of capacity constraints in this context, I start by quantifying the fraction of seniors who may not access their preferred nursing home due to rationing. Unfortunately, I do not observe rejected seniors directly. Instead, I test for a reduction in observed successful admissions at high occupancy rates which would be indicative of rationing behavior. To mitigate the effect of confounding changes in the arrival rate of seniors, I control for nursing home-year fixed effects and test for a correlation between week-to-week variation in the occupancy rate and the weekly number of newly admitted seniors.³⁸ While I find no evidence for systematic reductions in occupancy rates between 75 and 90% occupancy, I estimate that weekly admissions fall by 12% at occupancy rates exceeding 95% (see Figure D.1 and Table D.2). This reduction is less pronounced among more profitable private payers (−4%). To quantify the potential demand for care absent of rationing, I scale the realized admissions at occupancies exceeding 95% by 12%. About 29% of all admitted seniors enter the nursing home at an occupancy of more than 95% (see Table D.3). Hence, nursing home demand could increase by 29%*12%=3.5% suggesting that only 3.5% of seniors cannot access their preferred nursing home because of rationing.

Next, I revisit the demand estimates using two alternative models that allow for rationing. First, I consider a universal capacity limit of 100% occupancy for all payer types and assume that residents are admitted on a first-come-first-serve basis. Consequently, I leave only those nursing homes in the senior’s choice set that have at least one open bed on the day the resident was admitted to any nursing home. Using the revised choice set, I estimate the preference parameters excluding the cost moments in the second step.³⁹ The parameter estimates are presented in the third column of Table 3. ${\widehat{\beta }}^{sn}$ and ${\widehat{\beta }}_{priv}^p$ differ by less than 26% from the baseline parameters in column 2 and remain within the respective confidence interval. Importantly, these estimates indicate even larger welfare gains from an increase in Medicaid rates as evidenced by the larger marginal benefit estimate.

Second, and motivated by heterogeneous reductions in weekly admissions across payer types, I consider alternative asymmetric rationing models. Here, I add an indicator variable to the indirect conditional utility function from equation (4), interacted with payer type, that turns on if the average occupancy of the nursing home in the respective week, oc_ij, falls short of 97% and 95%, respectively:

$$u_{i\tau jt}^{AR}=u_{i\tau jt}+\vartheta 1\left\{o{c}_{ij}<\overline{oc}\right\}+{\vartheta }_{hyb}1\left\{o{c}_{ij}<\overline{oc}\right\}1\{\tau =hyb\}+{\vartheta }_{priv}1\{o{c}_{ij}<\overline{oc}\}1\{\tau =priv\}.$$

The results are summarized in columns 4 and 5 of Table 3. The first interaction effect, ϑ, is positive indicating that seniors are more likely to choose a nursing home with an occupancy of less than 97% or 95%. This suggests that capacity constraints restrict access to nursing home care for all payer types, possibly through a first-come-first-serve admission process. The interaction terms, ϑ_hyb and, ϑ_priv are negative (although small in relative magnitude) indicating that rationing is less pronounced for hybrid and private payers. Importantly, ${\widehat{\beta }}^{sn}$ and ${\widehat{\beta }}_{priv}^p$ differ by less than 23% from the baseline parameters and suggest again a higher marginal benefit of a skilled nurse.

Despite the larger marginal benefit estimates, the consumer gains from Medicaid increases could be smaller if the overall increase in demand amplifies rationing and leads to a crowd-out of inframarginal seniors with high utility from nursing home care. To investigate this possibility, I combine the baseline preference coefficients with a random rationing model as in Ching, Hayashi, and Wang (2015), to predict demand under counterfactual private rates and staffing ratios (see Appendix D.2.2 for more details). Rationing reduces the gain in consumer surplus to $181 million but also lowers profits and public spending since some of the rationed seniors choose the outside good instead. While the new estimates imply a smaller welfare gain of $14.5 million, they imply a higher return on public spending.

Finally, I also revisit the effect of rationing on the supply side behavior. To this end, I exclude nursing homes with an average occupancy of more than 97% (95%) and re-estimate the preliminary regression models that investigate the link between Medicaid reimbursement rates, staffing and pricing decisions. The key estimates from the first two columns are differ from the baseline estimates by less than 6% (see Table D.4 for details). This provides further evidence that the main findings of this paper are robust to potential capacity constraints.

Overall, the presented evidence indicates that the key demand and supply elasticities are robust to potential rationing in this context. Nevertheless, the reductions in admissions at high occupancy rates suggest that binding capacity constraints may affect the behavior of nursing homes with very high average occupancy rates.

Normative Findings.

The consumer welfare estimates rely on the estimated marginal utility of income for private payers. This may understate the marginal utility of income for poorer Medicaid beneficiaries and therefore overstate the marginal benefit of an additional skilled nurse and the optimal staffing ratio. To corroborate my normative findings, I first compare the derived optimal staffing ratio with staffing recommendations from the literature (Harrington et al., 2000). In 1998, a group of national experts discussed adequacy in staffing levels in U.S. nursing homes and recommended that the skilled nurse hours per resident day should at least equal 1.85 hours.⁴⁰ The implied staffing ratio of 0.32, see the second row of Table 6 exceeds the average staffing ratio in 2000 of 0.24 by 35%.

Table 6:

Normative Estimates Using Alternative Approaches/ Benchmarks

	Benefit of SN in $1,000	Optimal SN per Res
Baseline Estimates	133.3	0.38
Harrington et al. (2000)		≥0.32
Health Returns Approach	157.3
Life-Cycle Approach	96.6
Assets Among Private Payers	133.8

Notes. Harrington et al. (2000) recommend a minimum staffing ratio of 0.32.

Second, I revisit the marginal benefit estimate by multiplying the marginal health benefits, estimated in Friedrich and Hackmann (2017), with the statistical value of life. In this paper, we find that a federally funded parental leave program in Denmark reduced the number of skilled nurses in nursing homes by 670 nurses and increased nursing home mortality by 1,700 elderly per year, about 2.5 life years per nurse. Considering a quality-of-life-adjusted statistical value of a life year for an 85 year old of $62,000, see Cutler et al. (1997), this suggests a marginal benefit of $157,313 per year, see the third row of Table 6.

Third, I revisit the marginal utility of consumption though the lenses of the calibrated life-cycle model from Lockwood (2014). In this model, individuals trade-off between consumption and bequest motives. Combining the first order condition over consumption and bequest decisions with bequest data from the Health and Retirement Study, I am able to quantify the marginal utility of consumption (income), see Appendix D.3.1 for details. I find that the marginal utility of consumption for Medicaid payers exceeds the marginal utility of private payers by 27.5%. This would lower the marginal benefit per nurse by 27.5% to $96,600 if all residents were Medicaid beneficiaries, see the fourth row.

Fourth, I test for wealth effects directly by taking advantage of observed asset spend-down patterns in the data. Based on Medicare and Medicaid claims data, I can identify the number of days paid out-of-pocket before the senior becomes eligible for Medicaid. I multiply the number of days with the daily private rate to quantify the amount of tangible assets that are not protected under Medicaid. Next, I assign predicted asset levels to private payers, based on a rich set of demographics, and test for different price elasticities in asset levels. The analysis provides evidence against wealth effects and suggests an annual marginal benefit of $133,800 which exceeds the baseline estimate by 0.4% (see Appendix D.3.2 for details).⁴¹

Outside good.

The baseline model might overstate substitution between different modes of long term care and thereby reduce the welfare gains from a universal increase in Medicaid rates. To investigate this possibility, I have estimated an alternative demand model that does not allow for an outside good.⁴² I find very similar average increases in staffing (+8.8%) and reductions in private rates (−4.9%) following a universal 10% increase in Medicaid reimbursement rates. The welfare gain increases to $68 million (30% of public spending) largely because Medicaid spending increases by only $226 million without the market expansion effect. Turning to the entry counterfactual, I find very small changes in staffing and pricing and an overall welfare loss of $2.1 million per year. Consistent with the baseline results, I find that raising Medicaid rates is about 7.1 times as effective in increasing the quality of care than encouraging local competition via directed entry.

8. Conclusion

This paper investigates the dependence of the quality of care in nursing homes on Medicaid reimbursement rates and local competition. Combining detailed industry data from Pennsylvania with a model of demand and supply, I find that low Medicaid reimbursement rates are a key contributor to quality shortfalls in this industry. Specifically, I find that nursing homes increase the number of skilled nurses, who play an integral role in monitoring and coordinating the delivery of care, by 8.7% following a universal 10% increase in Medicaid reimbursement rates. On the other hand, I find that an increase in competition has relatively small positive effects on the quality of care.

At the same time, raising the quality of care via increases in the Medicaid reimbursement rates poses a burden on tight state budgets. This is in parts because nursing homes keep 45% of the Medicaid increases as profits and only pass 55% on to residents via higher nurse staffing ratios and lower private rates. A second reason is that increases in the quality of care may lead to a market expansion effect, which may raise Medicaid spending considerably. Therefore, connecting Medicaid payments with the quality of care more directly and containing a potential market expansion effect may provide a more cost-effective approach in addressing quality shortfalls in this industry.