Abstract
The treatment of metastatic brain tumors with stereotactic radiosurgery requires that the clinician first locate the tumors and measure their volumes. Thoroughly searching a patient scan for brain tumors and delineating the lesions can be a long and difficult task when done manually and is also prone to human error. In this paper, we present an automated method for detecting changes in brain tumor lesions over longitudinal scans to aide the clinician’s task of determining tumor volumes. Our approach jointly registers the current image with a previous scan while estimating changes in intensity correspondences due to tumor growth or regression. We combine the label map with correspondence changes with tumor segmentations from a previous scan to estimate the metastases in the new image. Alignment and tumor tracking results show promise on 28 registrations using real patient data.
1. Introduction
Brain metastases are the most common type of tumor in the brain, with an incidence of over 10 times the rate of primary tumors and an estimated 200,000 cases per year in the United States [1]. Treatment may include resection of tumors, but this can only be performed in limited cases. Currently, the primary mode of treatment is whole brain radiation therapy, especially for those with poor prognosis, leading to 2 – 7 months increase in survival [1]. However, whole brain radiation includes side effects such as radiation necrosis and neurocognitive decline. Another method of treatment is stereotactic radiosurgery (SRS), which is often used for patients with favorable prognostic factors. SRS administers a high dose of focused radiation using multiple beams to the tumor site, which is an attractive treatment option since it spares most of the healthy brain tissue. There is evidence that the addition of SRS to whole brain radiation results in better control of tumors as well as increased survival of up to one year [2].
To perform SRS, the physician must first locate the tumors and determine tumor volumes in order to create the treatment plan. As part of planning, the patient will be scanned using T1-gadolinium contrast-enhanced MRI, which makes active tumors appear brighter than normal tissue in the image, while necrotic tumors will generally appear darker. The current clinical workflow for tumor estimation involves visually searching a brain image slice by slice for evidence of tumors, then comparing again slice by slice to a scan at the previous time point to determine tumor correspondence (new or old tumor) and changes in tumor volume and activity. This manual task is time consuming and tedious, especially since metastases in one patient can involve tens of very small tumors. Even for patient cases with a few known larger tumors, the clinician must search the whole brain to determine if any new metastases have appeared.
Prior work in automating tumor tracking and estimation generally involves two main approaches. One is to first register the images with tumors, and then examine the image differences directly or analyze the deformation field to see how the tumors change [3]. The other approach is to run an automated or a semiautomated segmentation method on the current image, with [4,5] or without [6,7] knowledge of the lesion identified at a previous time point. Other related methods include the use of biomechanical models to simulate tumor growth before registering a patient brain to a normal atlas [8], but we are interested in intrapatient registration.
The goal of this work is to create an automated method for detection of tumor changes in contrast-enhanced MRI to assist the clinician in analysis and planning of brain metastases treatment. Note that if the images from consecutive scans are perfectly aligned, then we could more easily determine where tumor changes have occurred. On the other hand, if we knew exactly which parts of the image do not have matching correspondences due to lesion growth/regression, we could more easily register the images by only trying to align voxels with known matching correspondences. Thus, since the registration estimate can benefit from the segmentation of the tumors and vice versa, we frame the problem as a simultaneous estimation of the registration parameters and the labeling of the changes between two images.
The algorithm that we formulate is general and can be applied to other missing or changed correspondence problems as we make no assumptions about tumor growth/regression. We describe a specific implementation for the alignment of our longitudinal scans with brain metastases. Using the label map of correspondence changes, we can estimate tumors in the newer image, given a segmentation of the tumors at a previous time point. We test our method for both registration and tumor estimation accuracy with real patient data.
2. Methods
2.1. Registration Algorithm
The registration framework is based on the method introduced in [9] for registering preoperative and postresection brain images. We adapt the general frame work to our method as follows. Posing the problem in a maximum a posteriori estimation framework, the goal is to find
| (1) |
where is the optimal registration parameters, S is the source image, and T is the target image, scanned at a previous time to the image S. The registration parameters R map a voxel x with intensity S (x) in the source image to a position T (R(x)) in the target image.
We aid the registration process by incorporating a label map L, where L (x) denotes the intensity correspondence relation between S and T. Here we will use four labels to describe the possible intensity relations: no intensity changes in the brain, i.e. there are matching features; an increase in intensity in the brain, which will likely denote active tumor; a decrease in intensity in the brain, which may correspond to tumor necrosis or edema; and near 0 intensity and thus no intensity change in the background. We include L in the estimation by marginalizing the probability in (1) over all possible label maps,
| (2) |
Using the expectation-maximization (EM) algorithm, we can iteratively solve for R and L. At iteration k + 1, in the E-step, we update the label map using the current registration parameters Rk. Then, in the M-step, we update the registration parameters Rk+1 with our current estimate of the label map. In the following, to simplify computation, we assume voxels to be independent.
The E-step evaluates the probability that a voxel will be assigned a label, given all other variables,
| (3) |
Here, we have made the common assumption that the voxels in the image are independent, and also assume that the source intensities are independent of the registration parameters given the labels. Also, we will model the term p (R (x) | L (x) = l) so that it changes very little or likely not at all with the change in labeling of just one voxel, so we consider it a constant; the nominator and denominator terms thus disappear.
The M-step then updates the registration parameters,
| (4) |
where is our current estimate for the label map using the weights from the previous E-step. Note that we have applied a conditional maximization approach [10], so that the prior p (R (x) | Lk+1) only depends on the current most likely label map, greatly simplifying computation. Once the EM algorithm converges, we estimate the final label map .
2.2. Model Instantiation
We now need to define each probability model to compute (3) and (4). The first probability in (4) is the weight of a label assignment as calculated from the previous E-step. Thus, we have four probability distributions to define.
Data Terms
The probability p (T(R (x)) | S, R, L(x) = l) describes the image similarity between the source and target images, given the registration parameters and the label map. For each label, we can define a different probability distribution describing how we expect the voxels to match. Background voxels should have no signal, and thus we assume that background intensity should be the same in the source and target images. Since we are dealing with monomodal image registration, we assume intensities are correlated if the same features in the brain appear in both images (corresponding to “valid corr” labels below). Recall that high correlation implies that the image intensities in S and T have a linear relationship. However, for lesion areas, the intensities will likely not be correlated. For example, an active tumor may become necrotic, causing a large change from bright to dark in contrast-enhanced MRI. Thus, we use the following model to measure image similarity:
| (5) |
where is the normal distribution with mean μ and variance σ2 and C is the uniform distribution parameter.
Considering the coefficients a0 and a1 as part of the parameters that we’d like to estimate along with the registration parameters R in the MAP framework, we can iteratively solve for them by maximizing the objective function in (4) not only over R, but also over a0 and a1. Using a conditional maximization approach [11], we update the parameters for the image similarity model while keeping all other parameters, i.e. the registration parameters, constant.
The coefficients a0 and a1 are iteratively estimated from the source and transformed target image intensities S (x) and T (R (x)), with the weights calculated from the current iteration according to (3). First, define vS as the weighted mean of the intensities in S,
| (6) |
where the intensities of S are weighted by p (L (x) = valid corr | S, T, Rk). Similarly, vT is the weighted mean of the intensities in the transformed target image. Then, the weighted covariance φS,T of the source and transformed target images is given by
| (7) |
and the weighted correlation coefficient ρ is calculated as
| (8) |
Note that the weighted correlation coefficient rather than the traditional correlation coefficient essentially becomes the metric for similarity, as it measures the alignment of the images based on the current estimate of the voxels in S that have matching correspondences. Finally, with these definitions we can update the coefficients .
In addition, we update the standard deviations of the normal distributions and the parameter for the uniform distribution at each iteration, conditioned on the current registration and label map estimate. We update by again weighting the variance calculation by the probabilities of the voxels being labeled as having valid correspondences. We then set so that the algorithm will not try to match the background at the expense of aligning brain features. We set the uniform distribution parameter C such that intensities further than 2σv from S (x) are considered more likely to belong to the missing correspondence classes.
The second data term p (S (x) | L (x) =l) is the source image intensity prior and describes the likelihood of a voxel’s intensity given the voxel is labeled l. We use the same approach as described in [9], where we use Gaussian models for enhanced (relating to active tumor) and darkened (relating to edema or necrosis) voxel intensities and find the maximum likelihood estimate of the parameters using manually segmented training data,. We assume a uniform distribution for voxels with valid correspondences. Unlike in [9], here we take into consideration that different images have different scales of intensity values. Thus, we normalize the image intensities in each image by its mean of intensities before performing the parameter estimation and use this same normalization when evaluating the intensity prior in the registration algorithm.
Prior Terms
The registration prior p (R (x) | L) depends on a label map L. We use a free-form deformation B-spline model for the transformation model [12]. We then model the motion of a voxel x as following a normal distribution with mean equal to the starting position of the voxel under the uniform control point mesh with spacing δ. We set the variance of the normal distribution to be inversely proportional to the distance away from the closest abnormal intensities in L, leveling off at some distance d for the minimum allowed variance. Thus, points closer to lesions will be allowed to deform more since the variance will be greater, while points farther away will be more restricted since we expect more rigid motion.
We use the prior on the label map p (L (x) = l) to enforce smoothness in the segmentation. We model the label map as a Markov random field and use a mean-field like approximation to make the calculation tractable [13]. Applying a Potts smoothing model, the prior probability of a label at a voxel is
| (9) |
where is the partition function which normalizes the values such that p (L (x) = l | β) is a proper probability distribution, δ is the Kronecker delta function, and n is a voxel in the neighborhood N (x) of x. Similar to the way we update the coefficients for the similarity term, we iteratively update the weighting parameter β conditioned on the current registration parameters,
| (10) |
where p (β) is the prior on the weighting parameter β. For this prior, we assign a normal distribution on β with small mean and variance such that the label map estimation does not depend too strongly on the prior.
2.3. Estimation of Tumor Changes
Once the registration is complete, the final label map gives an estimate of where the intensities have changed. Given a segmentation tT of the tumors from the earlier image T, we can calculate positions of the tumors in the later image S. First we deform the target segmentation into the space of the S using the optimal registration parameters . We then fuse the estimated label map for the intensity changes with the target segmentation to create our tumor segmentation tS of the source image. For all voxels labeled as having valid correspondences, we carry over the labels from tT to tS. Voxels labeled as having no correspondence due to an increase in intensity are likely part of new tumor or growth from an old tumor, and thus are labeled as tumor. On the other hand, a voxel labeled as having no correspondence due to a decrease in intensity could signify an active tumor necrosed or appearance of edema. In this work we focus on the locating and measuring of only active tumors.
2.4. Algorithm Implementation Details
The M-step maximization in (4) and the weighting parameter estimation in (10) are performed using simple gradient ascent. For the training set for estimating the parameters for the source image intensity prior, we used a different set of brain tumor treatment images than those used in the experiments here. For the transformation prior, we set the maximum distance to d = 2δ, after which we keep the variance constant. So that the weighting parameter is not too large, we set the prior on the weighting parameter to have a mean of 0.3 and variance of 0.36 (these values were based on previous experiments, which also found that the method is not sensitive to the prior in values around this range). Note that all other parameters (such as the similarity metric model parameters and coefficients) are iteratively estimated as our algorithm runs. The model parameters that are estimated by the EM algorithm are initialized as the values calculated from the source and target images after affine alignment. Finally, we perform initial segmentation of tumors manually.
3. Experiments
3.1. Data and Setup
We had available a total of 14 images from 3 metastatic brain tumor patients: 5 scans from patient 1, 6 from patient 2, and 3 from patient 3. Patients were scanned at approximately 6 week intervals. For each patient, we registered all possible pairs, setting the source S to be the later image, resulting in a total of 28 registrations. The scans were T1-weighted MRI taken post-gadolinium contrast so that voxels containing active tumors should show enhancement.
Prior to registration, each image was first skull-stripped and resampled to have 1 mm isotropic voxel resolution. Each non-rigid registration was initialized by first running an affine registration method using Bioimage Suite software [14]. We mostly compare the registration and tumor estimation results of our method with the affine registration and manual delineations since this is the current clinical workflow. In addition, we compare our registrations to results from an out-of-the-box, “standard” intensity-based non-rigid registration method (SNRR) in Bioimage Suite [14,15,12]. We chose this intensity-based registration method since it also uses B-spline FFDs for the transformation, and we set the control point spacing to be the same as those used in our algorithm.
3.2. Results
We first qualitatively compare sample results. Then, we computed various measures to quantify the accuracy and differences in the registration and labeling results between methods.
Sample Qualitative Results
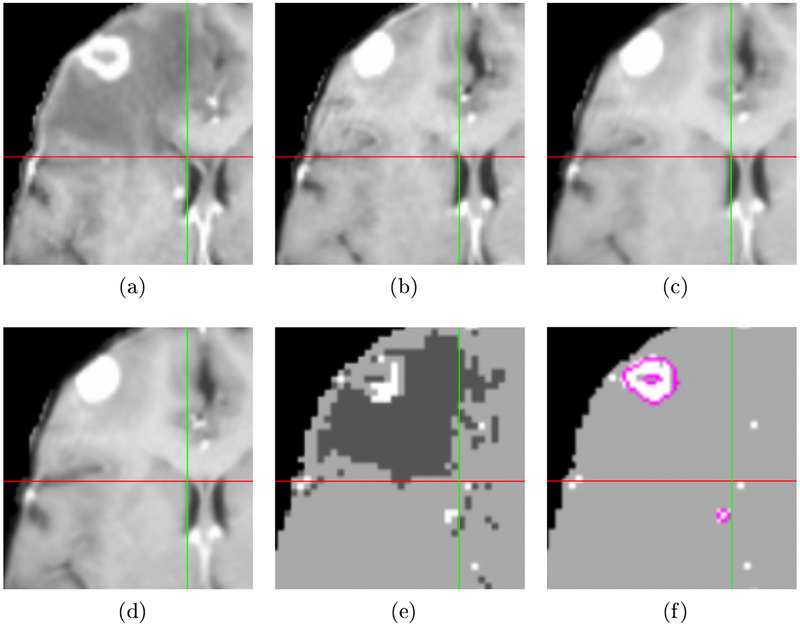
An example of a registration and labeling result for one patient is shown in Fig. 1. The crosshairs in each image mark the same location in the aligned space. Note that the edges of the right ventricle, highlighted by the crosshairs, are better aligned using our method shown in Fig. 1(d) compared to affine registration in Fig. 1(b) and the SNRR method in Fig. 1(c). The corresponding label map estimating the intensity correspondence changes is shown in Fig. 1(e). and the final estimate for tumors in the source image in Fig 1(a) is displayed in Fig 1(f).
Fig. 1:
Example of registration and label map estimation results. Crosshairs mark the same position in the aligned space. (a) Source image. (b) Target image aligned using affine registration. (c) SNRR result. (d) Result using proposed method. Note the right ventricle is better aligned compared to the results in (b) and (c). (e) Label map showing increased (brighter) and decreased (darker) intensity in source compared to target. (f) Active tumor estimate for source image with hand-segmented tumors outlined in pink. The tumor estimate identifies the large tumor and the small metastases by the right ventricle (just left of vertical green line).
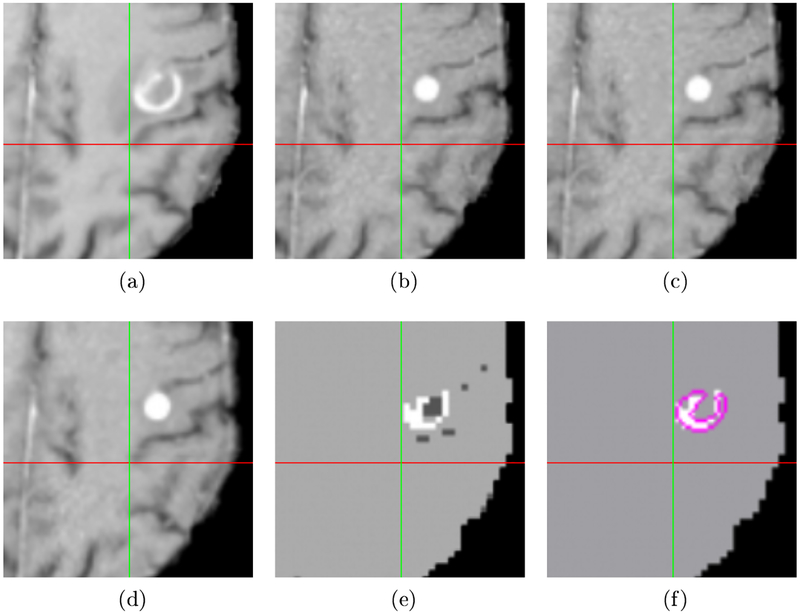
Another example of a registration and labeling result from a different patient is shown in Fig. 2. The subfigures represent the same ordering of data and results as in Fig. 1. In the first example, SNRR does move the target toward better alignment, though not as accurately as in our method. However, in this patient case note that SNRR, displayed in Fig. 2(c), cannot move the image at all due to the disparity in tumor signal: in the source image in Fig. 2(a), the tumor becomes necrotic in the center with a ring of enhancement, while in the target image in Fig. 2(b), the whole tumor appears brighter. Our method in Fig. 2(d) does a much better job of aligning the sulci marked by the crosshairs. The label map result showing the changes in intensity in Fig. 2(e) correctly identifies the enhancing outer ring of the metastases and darkening of the inner portion due to necrosis.
Fig. 2:
A second example of registration and label map results, with crosshairs showing the same location in the aligned space. (a) Affine registration result. (c) SNRR result. Note SNRR is unable to move toward better alignment due to tumor signal. (d) Result using proposed method, showing proper alignment of the sulcus. (e) Label map showing increased and decreased intensity in source compared to target. (f) Active tumor estimate for source image with hand-segmented tumor delineated in pink.
Quantitative Results
We first evaluated the registration results by comparing center of tumor mass locations in the source images and registered target images. For corresponding tumors that appear in both images, we expect that their centers of mass should be aligned after registration. Note that we assume this specifically for our tumor type, since brain metastases usually have a spherical shape, suggesting they grow outward from the initial site of tumor foci arrest [16]. Since we have the manual segmentations of all the tumors, this method allows a quick and automatic way of locating many corresponding landmarks.
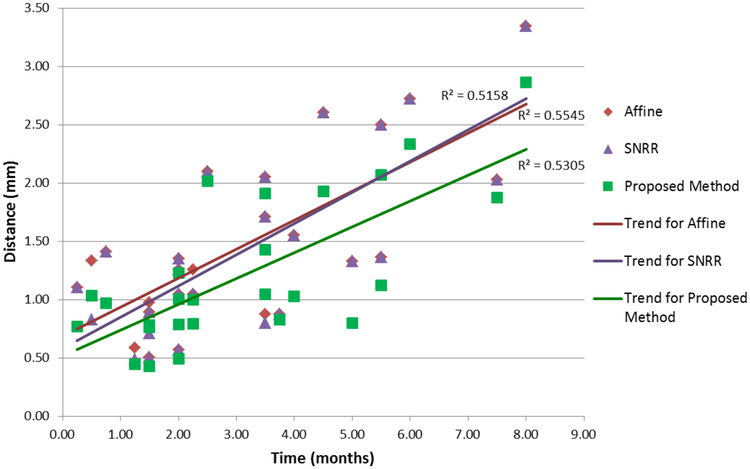
We calculated the center of mass for each tumor in the target segmentation tT deformed to the space of S using and computed the distance between the center of mass of the same tumors that appeared in both S and T. Errors categorized by the time between scans are shown in Fig. 3, with 2 registrations having greater than a 10 month interval between scans omitted to highlight the general trend. Note that according to paired one-tailed t-tests, the overall distance between the centers of mass of corresponding tumors was significantly reduced by our algorithm compared to affine registration (p < 4e − 8), which is generally the most complex level of registration performed in the clinic when evaluating tumor changes. In addition, we saw that our method was significantly more accurate compared to SNRR (p < 6e − 6). While SNRR did overall show significant improvement over affine registration (p < 0.01), the level of significance is not as high compared to the reduced error achieved by our registration algorithm.
Fig. 3:
Distance between centers of mass of tumors after registration as a function of time. According to a one-tailed paired t-test, registration via our proposed method statistically significantly reduced errors compared to affine registration (p < 4e − 8) and SNRR (p < 6e − 6).
The general upward trend for all registration methods as time between scans increased is expected since larger changes are likely to have occurred, and thus, the alignment problem becomes harder. Also, note that at lower time intervals between scans, SNRR tends to do better than affine, but at higher time intervals, the reverse is true. This supports the idea that with larger changes between images (due to longer time between scans), SNRR has difficulty with proper alignment as it attempts to match the large regions with missing correspondences. On the other hand, our method always stays below both affine and SNRR trends. Thus, the overall smaller and slower increase in errors over time using our approach suggest it is more robust to large differences compared to the other methods.
For the labeling results, we calculated the rate of active tumor detection, the true positive rate (TPR) for estimated and true tumor overlap, and the dice coefficient for the overlap of true detected tumors. A tumor was detected if there was any overlap between the estimated and true tumor volumes. Since larger tumors should be easier to detect, to see the effects of tumor size on detection and segmentation, we categorized results based on size, dividing the data at approximately the quarter percentile marks. Table 1 summarizes our results for tumor identification and quantification. The median tumor detection rate per image registration pair was 97%. Thus, our method shows high sensitivity for detecting tumors, which is very important since treatment by targeted radiation will only be administered to prescribed locations.
Table 1:
Tumor detection and volume estimation.
| Tumor Volume Range | Number of Tumors | Detection Rate (%) | Median TPR (%) | Median Dice |
|---|---|---|---|---|
| < =0.05 cm3 | 119 | 80 | 62 | 0.49 |
| >0.05 – 0.1 cm3 | 68 | 94 | 68 | 0.47 |
| >0.1 – 0.25cm3 | 77 | 100 | 65 | 0.54 |
| > 0.25 cm3 | 88 | 100 | 72 | 0.63 |
| All | 352 | 92 | 69 | 0.51 |
Note that volume segmentation rates are similar to those seen in the literature, such as reviewed in [6], which showed accuracy scores ranging from ~ 27% – 90%. In addition, in brain metastases there are many very small tumors; over half of our tumor examples are less than 100 voxels in volume in images that contain about 3 – 4 million voxels. This makes higher overlap values much more difficult to achieve compared to results in other experiments which often have very large examples (such as aggressive glioblastoma multiformes) with high signal changes. Also, inter-rater variability will play a role in our accuracy measurements, as observers’ readings have previously been reported to vary by as much as ~ 30% [17].
4. Conclusions
We have presented a method for the joint registration and labeling of changed correspondences in the registered images with application to brain metastases detection and volume estimation. Our framework provides a general way for dealing with missing correspondences and physical changes in longitudinal data.
The many registrations over time showed that our method can robustly register the images even with many months between scans. Finally, the sensitivity of our method for tumor detection is high, helping to achieve our goal of providing guidance to the clinician in finding metastases.
In future work, we may incorporate labels for white and grey matter into the labeling scheme. In addition, the availability of multimodal data provides rich information that is important for better analysis of brain tumors. We aim to incorporate multiple channels of MRI data into our joint registration and labeling algorithm to further improve tumor volume estimation.
Not surprisingly, we saw that it was much harder to detect very small metastases, which may be contained in as few as 12 voxels in our examples. As mentioned above, metastases tend to have a spherical shape. Thus, we may look to include this prior shape information into our method to aid in the detection of new very small metastases. Another problem we see is with false positive identification of tumors. Again, including some measure of sphericity should help to reduce the number of false positives that are due to bright CSF signal that is not properly suppressed in the contrast-enhanced image. In addition, we could first register the images to some template to perform better brain stripping. A template image would also be useful for better identifying metastases, as they tend to form at grey-white matter junctions; we could incorporate this prior knowledge into the label map prior.
Acknowledgments
This work was supported by NIH 5R01EB000473–10 and 3R01EB000473–08S1.
References
- 1.Maher EA, Mietz J, Arteaga CL, DePinho RA, Mohla S: Brain metastasis: Opportunities in basic and translational research. Cancer Research 69 (2009) 6015–6020 [DOI] [PubMed] [Google Scholar]
- 2.Mehta MP, Tsao MN, Whelan TJ, Morri DE, Hayman JA, Flickinger JC, Mills M, Rogers CL, Souhami L: The american society for therapeutic radiology and oncology (astro) evidence-based review of the role of radiosurgery for brain metastases. International Journal of Radiation Oncology Biology Physics 63 (2005) 37–46 [DOI] [PubMed] [Google Scholar]
- 3.Rey D, Subsol G, Delingette H, Ayache N: Automatic detection and segmentation of evolving processes in 3d medical images: Application to multiple sclerosis. Medical Image Analysis 6 (2002) 163–179 [DOI] [PubMed] [Google Scholar]
- 4.Rouchdy Y, Bloch I: A chance-constrained programming level set method for longitudinal segmentation of lung tumors in ct. In: Conf Proc IEEE Eng Med Biol Soc (2011) 3407–3410 [DOI] [PubMed] [Google Scholar]
- 5.Xu J, Greenspan H, Napel S, Rubin DL: Automated temporal tracking and segmentation of lymphoma on serial ct examinations. Medical Physics 38(11) (November 2011) 5879–5886 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Corso JJ, Sharon E, Dube S, El-Saden S, Sinha U, Yuille A: Efficient multilevel brain tumor segmentation with integrated bayesian model classification. IEEE Trans Med Imaging 27 (2008) 629–640 [DOI] [PubMed] [Google Scholar]
- 7.Prastawa M, Bullitt E, Ho S, Gerig G: A brain tumor segmentation framework based on outlier detection. Medical Image Analysis 8 (2004) 275–283 [DOI] [PubMed] [Google Scholar]
- 8.Zacharaki EI, Hogea CS, Shen D, Biros G, Davatzikos C: Non-diffeomorphic registration of brain tumor images by simulating tissue loss and tumor growth. Neuroimage 46(3) (2009) 762–774 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chitphakdithai N, Duncan JS: Non-rigid registration with missing correspondences in preoperative and postresection brain images. In: MICCAI 2010. Volume 6361 of LNCS. (2010) 367–374 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Celeux G, Govaert G: A classification em algorithm for clustering and two stochastic versions. Comput Statist Data Anal 14 (1992) 315–332 [Google Scholar]
- 11.Meng XL, Rubin DB: Maximum likelihood estimation via the ecm algorithm: A general framework. Biometrika 80(2) (1993) 267–278 [Google Scholar]
- 12.Rueckert D, Sonoda LI, Hayes C, Hill DL, Leach MO, Hawkes DJ: Non-rigid registration using free-form deformations: application to breast mr images. IEEE Trans Med Imaging 18 (1999) 712–721 [DOI] [PubMed] [Google Scholar]
- 13.Celeux G, Forbes F, Peyrard N: Em procedures using mean field-like approximations for markov model-based image segmentation. Pattern Recognition 36 (2003) 131–144 [Google Scholar]
- 14.Papademetris X, Jackowski M, Rajeevan N, Okuda H, Constable R, Staib L: Bioimage Suite: An integrated medical image analysis suite. Section of Bioimaging Sciences, Dept, of Diagnostic Radiology, Yale School of Medicine, http://www.bioimagesuite.org [Google Scholar]
- 15.Jackowski AP, Papademetris X, Klaiman C, Win L, Pober B, Schultz RT: A non-linear intensity-based brain morphometric analysis of williams syndrome. Human Brain Mapping (2004) [Google Scholar]
- 16.Meadows GG, ed.: Integration/Interaction of Oncologic Growth Volume 15 of Cancer Growth and Progression. Springer; (2005) [Google Scholar]
- 17.Weltens C, Menten J, Feron M, Bellon E, Demaerel P, Maes F, den Bogaert WV, van der Schueren E: Interobserver variations in gross tumor volume delineation of brain tumors on computed tomography and impact of magnetic resonance imaging. Radiotherapy and Oncology 60 (2001) 49–59 [DOI] [PubMed] [Google Scholar]