Abstract
With the availability of large-scale biobanks, genome-wide scale phenome-wide association studies are being instrumental in discovering novel genetic variants associated with clinical phenotypes. As increasing number of such association results from different biobanks become available, methods to meta-analyse those association results is of great interest. Because the binary phenotypes in biobank-based studies are mostly unbalanced in their case-control ratios, very few methods can provide well-calibrated tests for associations. For example, traditional Z score-based meta-analysis often results in conservative or anti-conservative type I error rates in such unbalanced scenarios. We propose two meta-analysis strategies that can efficiently combine association results from biobank-based studies with such unbalanced phenotypes, using the saddlepoint approximation-based score test method (SPA). Our first method involves sharing the overall genotype counts from each study, and the second method involves sharing an approximation of the distribution of the score test statistic from each study using cubic Hermite splines. We compare our proposed methods with a traditional Z score-based meta-analysis strategy using numerical simulations and real data applications, and demonstrate the superior performance of our proposed methods in terms of type I error control.
Keywords: Biobank, Meta-analysis, GWAS, Saddlepoint Approximation, Case-Control studies
Introduction
Genome-wide scale phenome-wide association analysis (Hebbring, 2014) is gaining increasing attention in the human genetics community in the recent years. The availability of detailed phenotypic information from the electronic health record (EHR) systems in large biobanks as well as the recent advancements in genotyping and imputation technologies (Das et al., 2016) are allowing researchers to phenotype thousands of traits and genotype tens of millions of variants in large cohort studies. Several biobank studies, including UK-Biobank (Bycroft et al., 2017), Michigan Genomics Initiative and Nord-Trøndelag Health Study (Krokstad et al., 2013) currently attempt to test for associations in all genotype-phenotype pairs, which results in billions of tests. These large-scale analyses have great potential to find novel genotype-phenotype associations, which will help uncover underlying molecular mechanism of clinical phenotypes.
In a typical phenome-wide association study (PheWAS) in biobanks, most of the phenotypes are binary with unbalanced (1:5) or often extremely unbalanced (1:500) case-control ratios, which results in performing 1000s of unbalanced case-control GWASs. For example, ~1400 case-control studies in the UK Biobank interim release data have more than 100 controls per case (see histogram in Figure S1, supplementary materials A). Under such case-control imbalance, the standard asymptotic tests such as the Wald test, score test and likelihood ratio test can severely inflate the type I errors resulting in several spurious associations, especially for the low frequency (0.01<MAF<0.05) and rare (MAF<0.01) variants (Dey, Schmidt, Abecasis, & Lee, 2017; Ma, Blackwell, Boehnke, Scott, & investigators, 2013). To obtain well-calibrated p values in such situations, Ma et al. (2013) proposed to use the Firth’s penalized likelihood ratio test (Firth, 1993). Since the Firth’s test is computationally too expensive to be used for billions of association tests, Dey et al. (2017) developed a fast saddlepoint approximation-based score test, fastSPA, which is computationally much faster than the Firth’s test.
As more and more association results from different biobanks become available, meta-analysing (Evangelou & Ioannidis, 2013) the results from the unbalanced GWASs is the logical next step to improve the power to detect novel genotype-phenotype associations. Z-score based approach, (Cooper, Hedges, & Valentine, 2009) which converts p-values to normal Z-scores for combining multiple study p-values, has been a standard meta-analysis method in GWASs (Evangelou & Ioannidis, 2013). However, even though p-values from fastSPA and Firth’s test are well calibrated in a single study, combining them through Z-score method can fail to control for type I errors. Ma et al. (2013) has shown that combining Firth’s test-based p values through Z-score method can produce conservative or anti-conservative behaviours especially when the case-control ratio is unbalanced and the variant minor allele count (MAC) is small. This may be because the study-specific p-values have discrete distribution due to case-control imbalance and small MAC. As shown in our simulation studies, the same problem also occurs in the meta-analysis using fastSPA-based p values. To facilitate the meta-analysis of the biobank-based GWASs, we need a robust method to control for type I errors regardless case-control ratios and MAC.
In this paper, we first evaluate the performance of the Z-score based meta-analysis procedure using the fastSPA test-based p values under extensive simulation settings and real datasets, and propose two alternative meta-analysis strategies to obtain well-calibrated meta-analysis p values. The first method involves sharing the overall number of homozygous minor and heterozygous genotypes for each genetic variant, in addition to the case-control sample size and p value shared in the Z-score-based meta-analysis strategy. The second method involves sharing the observed within-study score statistics and the cumulant generating functions (CGF) of those score statistics using a spline-based approach, which will be used to carry out saddlepoint approximation to obtain the meta-analysis p value. The additional information facilitates approximating the distributions of the study-specific score statistics, which can be discrete, asymmetric and different from the traditionally used normal distribution. Through extensive simulation studies and an analysis of the UK Biobank data, we show that the proposed methods can control the type I error rates and retain similar power as a joint analysis as well as being scalable to large scale PheWASs.
Methods
Model for single study association test and saddle point approximation (SPA)
We consider J case-control studies, where the jth study has sample size nj. Within each individual study, we follow the regression model and testing procedure described in Dey et al. (2017). For the ith subject in the jth study, let denote the case-control status, denote the k × 1 vector of non-genetic covariates (including the intercept) and denote the number of minor alleles of the variant to be tested. Let β(j) be the k × 1 vector of coefficients for the non-genetic covariates and γ(j) be the genotype log odds ratio. We use the following logistic regression model to perform association test in the jth study.
| (2.1) |
Let be the maximum likelihood estimator of under the null hypothesis . Further, let be the nj × k matrix of covariates, be the genotype vector, W(j) be a diagonal matrix with ith diagonal element , and be the covariate-adjusted genotype vector. Then, the score statistic for testing will be . To apply the saddlepoint approximation-based score test (SPA test), we first need to calculate the cumulant generating function (CGF) of the score statistic and its first and second derivatives given by,
Using the saddlepoint approximation method (Barndorff-Nielsen, 1990; Daniels, 1954), the distribution function of S(j) at the observed score statistic s can be approximated by,
where , , is the solution to the equation , and Φ is the standard normal distribution function. The fastSPA (Dey et al., 2017) test implements a faster version of this saddlepoint approximation method, which can be applied to obtain the p value p(j). One of the steps implemented in the fastSPA test is to apply the saddlepoint approximation method only if the score statistic lies outside a certain standard deviation threshold from the mean. If the score statistic lies inside the standard deviation threshold, then the fastSPA test uses the normal approximation to calculate the p values because the normal approximation behaves well near the mean. In this paper, we will consider the p values using two such standard deviation threshold, 2 and 0.1, and will denote the tests by fastSPA – 2 and fastSPA – 0.1, respectively.
P value-based meta-analysis and Normal distribution-based Z-score method
We first introduce a framework for p value-based meta-analysis. In this framework, the study-specific p values (p(j) s) are inverted to obtain the signed scores R(j) s using some distributions F(j) s, for j = 1,…, J, where the signs are determined by the directions of associations. We call F(j) s reference distributions. Then, the meta-analysis score is given by where each R(j) ~ F(j) under the null hypothesis of no association. Traditional Z-score-based meta-analysis is a special case of this framework, where the reference distributions are normal distributions with means zero and variances given by the effective sample sizes of the individual studies. The effective sample size (Han & Eskin, 2011) is calculated as , where nj1 and nj0 are the number of cases and controls in the jth study, respectively. This meta-analysis method first inverts the p-values using a standard normal distribution to obtain the signed Z-scores Z(j) = ±Φ−1 (p(j) / 2), where the signs depend on the directions of associations. Then, the scores R(j) s are calculated as , for j = 1,…, J, and the meta-analysis score is given by under the null hypothesis. We can test the null hypothesis of no association between the phenotype and the variant by testing , which follows N(0,1) under the null hypothesis.
This meta-analysis strategy can control for type I error rates when each study-specific p-value follows the uniform distribution. When the case-control is unbalanced and variants are rare, however, each study-specific test statistic S(j) can have a discrete and often very skewed null distribution, which can result in the set of possible study-specific p values to be discrete, and the two-sided probabilities that constitute those p values, to be asymmetric. In such situations, although saddlepoint approximation (SPA) can be applied to control type I error rates within each individual study, inverting such SPA-based p values to normally distributed Z-scores might not be appropriate, and can introduce systematic bias.
We notice that the best possible reference distribution F(j) would be the null distribution of the score statistic S(j) under model (2.1) (let it be ). In that case, R(j) s will be the same as S(j) s. Within each individual study, can be approximated based on the CGF of the score statistic, using the SPA method. However, it is difficult to share the CGFs as summary level statistics. In our first method, we suggest sharing the overall genotype counts from the individual studies to construct our reference distributions. For the second approach, we propose a simpler technique to approximate using summary level statistics and suggest sharing S(j) s instead of the p values so that we can directly use R(j) = S(j). This is equivalent to a p value-based meta-analysis using the approximations of as the reference distributions F(j) s, because R(j) s will closely approximate S(j) s when F(j) s closely approximate . Although our approaches require more information than just the p-values, case-control sample sizes and directions of associations, the additional information is also summary level information and hence does not need individual level data.
Genotype-count-based method
Here we propose a practical approach to approximate the CGFs using the genotype counts (number of 0, 1, 2 genotypes) at different markers. For rare variants where homozygous minor genotypes are usually not present in the data, or for variants that follow Hardy-Weinberg equilibrium, sharing only the minor allele counts (MAC) will be sufficient, as the genotype counts can be easily calculated based on the MACs.
Suppose, for the jth study, the genotype counts for the variant to be tested are mj0, mj1 and mj2 (mj0 + mj1 + mj2 = nj) corresponding to the genotypes 0,1 and 2 respectively. Then, we can construct the genotype vector G(j)* of length nj where the first mj2 elements are 2s, next mj1 elements are 1s, and the rest are 0s. We propose using the null distribution (let it be F(j)*) of the score statistic in the following genotype-only model (2.2) as our reference distribution,
| (2.2) |
where is the ith elements of G(j)*, α(j)* is the intercept and γ(j)* is the genotype log odds ratio. Intuitively, when the non-genetic covariates are relatively balanced across cases and controls, the discreteness and asymmetry in the null distribution of the score statistic mainly depend on the imbalance or the rarity of the phenotype and the genotype. Therefore, the null distribution of the score statistic under the genotype-only model can be a reasonable alternative to the traditionally used normal distribution, as a reference distribution. To apply this method, we first need to calculate the CGF of the score statistic and its first and second derivatives in the genotype-only model (2.2) given by,
where is the mean-centered genotypes, and , is the maximum likelihood estimator of under the null hypothesis . Based on this CGF, we can approximate the distribution F(j)* and calculate the score R(j) by inverting F(j)* at the signed fastSPA p-value, ±p(j), which is calculated from the model (1.1) with all covariates. Since the signed p values have one-to-one relationships with the score values, the inversion of ±p(j) to obtain the score R(j) can be performed using root-finding algorithms such as Newton-Raphson (Press, 1992), Brent (Brent, 1973), bisection (Press, 1992) etc. In our implementation, we applied Brent’s method for this purpose. The meta-analysis score will then have the CGF , and we can apply the SPA test on Rmeta to obtain the meta-analysis p-value.
CGF sharing-based method
The aforementioned genotype count sharing-based method assumes relatively balanced covariates, which have little effect on the discreteness and asymmetry of the null distribution of the score statistics. A more general and mathematically appropriate approach would be to share and utilize the whole CGFs of the within-study score statistics for constructing the reference distribution. Since sharing a complicated function like a CGF using only summary statistics is very difficult, we propose to share the function only at some node-points, and reconstruct the function at the meta-analysis stage using spline approximations. Detailed methodology for this approach is provided in Appendix A, supplementary materials A.
Software implementation
We implemented all our proposed methods and the Z-score-based method in our R package SPAtest (available on CRAN). The software can be used to perform fastSPA or Score test and prepare summary level information relevant to the different meta-analysis methods, as well as to perform the final meta-analysis. The software can also perform a hybridized meta-analysis based on the availability of different kinds of summary level information. For example, suppose one study provides only the p value and direction of association, a second study additionally provides the genotype counts or minor allele count (if it is a rare variant), and a third study provides the score statistic and spline-based information. Then, a hybrid meta-analysis approach will be to use a normal reference distribution for the p value from the first study, and a reference distribution based on the genotype-only model for the p value from the second study to calculate the converted scores and their corresponding CGFs. The CGF of the score statistic in the third study can be reconstructed based on spline approximation. Then, the final meta-analysis score will be the sum of those individual scores, and the corresponding CGF will be the sum of those individual CGFs. The meta-analysis p value can then be obtained using the saddlepoint approximation method.
Numerical Simulations
We evaluated the type I error rates and empirical powers of the Z-score based and proposed methods through extensive simulation studies. We considered three different simulation study settings. For the first setting, we meta-analysed seven studies coming from the same population where the genotypes and the non-genetic covariates are simulated independently. For the second setting, we considered a meta-analysis of seven studies where the genotypes and the non-genetic covariates were simulated based on the MAF and principal component (PC) scores in different ethnic groups in the UK Biobank data. In the third setting, we assessed the performance of the methods when a smaller but balanced case-control study is meta-analysed along with a small number of larger but unbalanced biobank-based studies.
Simulation Study 1:
Our first simulation study was designed to represent a meta-analysis of multiple studies from the same population. We considered seven studies with sample sizes nj = 2000 for all j = 1,…, 7. We further considered three case-control ratios: balanced with the case-control ratio of 1:1 within each study, moderately unbalanced with the case-control ratio of 1:9 within each study, and extremely unbalanced with the case-control ratio of 1:49 within each study. For each choice of case-control ratio, the phenotypes in the jth study were simulated using the following logistic model,
| (3.1) |
where and were the non-genetic covariates, and the genotypes were generated from a Binomial(2, p) distribution where p(same across the seven studies) was the minor allele frequency (MAF). The intercepts (α(j)s) were selected such that the prevalence within each study would become 0.01. The parameters γ(j)s represent the within-study log-odds ratios. For the type I error comparisons, all γ(j)s were set to be 0. A wide range of γ(j) values were used for the power calculations (see Results).
To compare the type I error rates of different methods under different MAFs, we considered five different MAFs, p = 0.001, 0.005, 0.01, 0.05, 0.1, and simulated 5 × 108 variants for each of the MAFs and the three case-control ratios. We recorded the number of rejections at α = 5 × 10−5 and 5 × 10−8 genome-wide significance levels. We further performed a power comparison with 5000 simulated variants for each of the three case-control ratios and two choices of the MAF, p = 0.01, and 0.05, at different values of γ(j). As the genome-wide significance threshold for power calculations, we used both a nominal α = 5 × 10−8, and a type I error adjusted empirical α where the corresponding method has type I error 5 × 10−8. The empirical α level was calculated based on 5 × 108 simulated datasets from the simulation setting described above (seven studies, each with 2000 samples) where the MAFs were sampled from the MAF spectrum (Figure S2, supplementary materials A) of the white British ancestry group (~117K samples) in the UK Biobank interim release data.
Simulation study 2:
Our second simulation study was designed to represent a trans-ethnic meta-analysis, where contrary to the first simulation study setting, we not only allow the MAFs to be different across the studies, but also simulate the genotypes in a way such that they are correlated with the covariates to adjust for. We considered seven studies with sample sizes nj = 2000 for all j = 1,…, 6, and n7 = 1500. To simulate the genotypes and the non-genetic covariates from a realistic meta-analysis of GWAS, we used genotype data from the UK Biobank interim release data (UK Biobank, 2015). The first five studies included first four principal component (PC) scores as covariates and genotypes simulated from the MAF spectrum of the white ancestry group in the UK Biobank samples. To maintain the correlated nature of the genotypes and the PC scores, genotypes were simulated using PC scores. We further added a binary covariate generated from a Bernoulli(0.5) distribution independent of the PC scores and the genotypes. Covariates and genotypes were simulated in a similar way for study six and seven based on the south Asian and black ancestry groups, respectively. The model to simulate the phenotypes was similar to the one used in the first simulation study, except for different non-genetic covariates. Detailed explanation of the simulation procedure is provided in Appendix B, supplementary materials A.
In Transethnic studies, variants have different MAFs across different ancestry groups. To calculate the type I error rates for diverse scenarios of MAFs, we first considered three MAF bins for the alleles of the simulated variants: rare variants with MAF < 0.01, low frequency variants with 0.01 < MAF < 0.05 and common variants with MAF > 0.05. We then categorized the simulated variants in four categories based on their allele frequencies (AF): a) all rare, when the variant has the same minor rare allele in all seven studies, b) all low frequency, when the variant has the same low frequency allele in all seven studies, c) all common, when the variant has the same common allele in all seven studies, and d) different AF, when the variant falls in different MAF bins in at least two different studies. The different AF category also includes variants which have different alleles as the minor alleles in different studies. For each variant category and case-control ratio, we simulated 5 × 108 datasets under the null hypothesis and recorded the number of rejections at the genome-wide significance levels α = 5 × 10−5 and α = 5 × 10−8.
Simulation Study 3:
We investigated the performance of different meta-analysis strategies when a balanced case-control study, which is smaller in sample size, is meta-analysed along with two larger biobank-based unbalanced studies. This simulation study represents the real-world meta-analyses where the researchers collect balanced case-control data on rare traits/diseases, and attempt to meta-analyse them with association results from a small number of larger cohort-based studies. To simulate the genotypes, non-genetic covariates and the phenotypes, we used the same simulation and logistic regression models as in our first simulation study setting. The sample size for the balanced case-control study was 2000 with 1000 cases and 1000 controls, and the unbalanced studies had sample size 10000 each. We considered two case-control ratios for these unbalanced studies: moderately unbalanced with case : control = 1 : 9 within each study, and extremely unbalanced with case : control = 1 : 49 within each study. For each of the case-control ratio, we compared the type I error rates of different methods under five different MAFs, p = 0.001, 0.005, 0.01, 0.05, 0.1 based on 5 × 108 simulated variants each.
For the first two simulation settings and the unbalanced studies in the third simulation setting, the within-study p values were calculated using the traditional score test (Score), fastSPA test with 2 standard deviations threshold (fastSPA – 2), and fastSPA test with 0.1 standard deviations threshold (fastSPA – 0.1). Since score test is relatively well-calibrated for balanced case-control studies (Dey et al., 2017), only Score p values were calculated for the balanced study in the third simulation setting. We then considered the following meta-analysis methods to compare their type I error rates and empirical powers: Z-score-based meta-analysis (Z-score), genotype count sharing-based meta-analysis (GC), and CGF sharing-based meta-analysis (CGF-Spline). Score p values were meta-analysed using the Z-score method, fastSPA – 2 and fastSPA – 0.1 p values were meta-analysed using the Z-score and GC methods, and the within-study observed score statistics were meta-analysed using the CGF-Spline method. For the balanced case-control study in the third simulation setting, the Z-scores obtained from the Score p values were used in the GC method, and the corresponding normal distribution-based CGFs were used in the CGF-Spline method. We also compared the type I error rates and the empirical powers of a joint analysis (Joint) using the fastSPA – 2 test on the pooled data as the gold standard. We further provided a computation time comparison of our proposed methods in Appendix C, supplementary materials A.
UK Biobank data analysis
We demonstrated the performance of our proposed methods by analysing two phenotypes based on the UK Biobank interim release data (UK Biobank, 2015). The UK Biobank (Bycroft et al., 2017) contains detailed phenotypic information based on electronic health records for ~500K individuals in the United Kingdom. In the interim release (May 2015), information on ~150K individuals were released to the public. Details about the data and pre-processing are provided in Appendix D, supplementary materials A. A histogram of the case-control ratios (Figure S1, supplementary materials A) of different binary phenotypes shows that the ratios are heavily skewed towards zero, which means the binary phenotypes are mostly unbalanced.
To compare our proposed methods with the Z-score-based meta-analysis method, we analysed two phenotypes, Ulcerative Colitis (PheWAS code: 555.2, case : control ≈ 1:100), and Psoriasis (PheWAS code: 696.4, case : control ≈ 1:165) based on 117,494 unrelated samples from the white British ancestry group of the interim release data. The samples were then divided into 22 groups based on the assessment centre where they first consented to be included in the biobank. We selected 19 centres (Table S1, supplementary materials A) with at least 5 cases for each of the two phenotypes, and treated these centres as our individual studies to perform association analyses of the phenotypes on the autosomal variants within each of them. For the within-study association analyses, we applied fastSPA – 2, fastSPA – 0.1 and Score tests, adjusting for age, sex, genotyping array, and first four principal components. Individuals which had phenotype or at least one covariate information missing, were removed from the analysis of that corresponding phenotype. We only applied the within-study tests for variants with within-study MAC at least three. Because the genotype count-based meta-analysis requires the overall genotype counts, we applied our within-study tests on the best called genotypes instead of dosages in the imputed data. We then meta-analysed the results using the Z-score-based meta-analysis (Z-score), genotype count sharing-based meta-analysis (GC), and CGF sharing-based meta-analysis (CGF-Spline). The meta-analysis methods were only applied for variants that were tested in at least two different studies, and the overall MACs were at least ten. For each phenotype, ~29 million variants were meta-analysed. We further performed a joint analysis (Joint) with the pooled samples using the fastSPA – 2 test, adjusting for the assessment center. Due to the computational burden of performing a pooled joint analysis, we only performed it for the variants with GC – fastSPA – 2 p values smaller than 5 × 10−3. Otherwise, we recorded the p values from GC – fastSPA – 2 method as the joint analysis p values.
Results
In this section, we evaluate the performance of the proposed methods against the Z-score-based meta-analysis based on the numerical simulations and the UK Biobank data application described above.
Numerical Simulations
Type I error comparison:
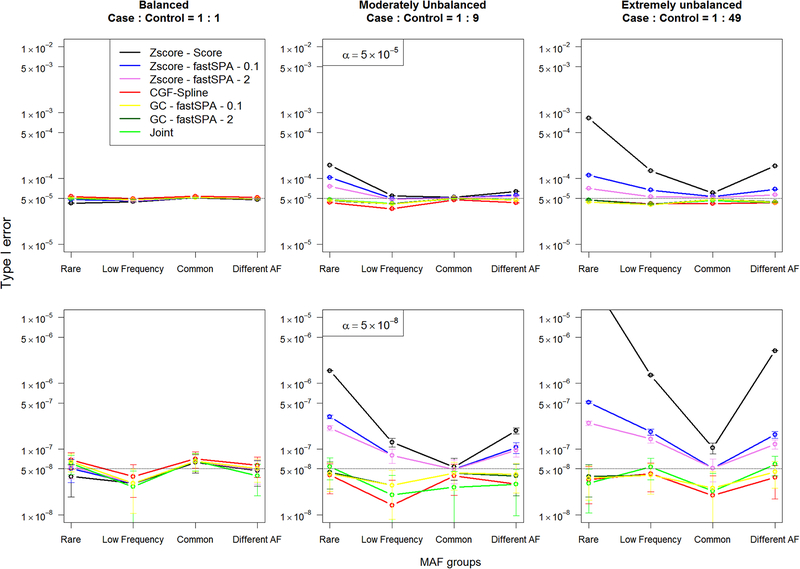
The type I error comparison based on simulation study 1 (Figure 1) clearly shows that the proposed CGF-Spline and GC methods provided well-controlled type I error rates across all the MAFs and all the case-control ratios. Expectedly, the joint analysis also controlled the type I error rates. On the other hand, the Z-score method resulted in inflated type I error rates in moderately unbalanced and extremely unbalanced settings, especially for the rarer minor allele frequencies. Interestingly, the Z-score method with fastSPA-0.1 performed worse than that with fastSPA-2, although fastSPA-0.1 used the saddlepoint approximation to more variants. This further verifies our assertion that using normal distributions to invert the study-specific p values which are possibly discrete, asymmetric and originally calculated using the saddlepoint approximation, can result in failure to control type I error in the meta-analysis process. In contrast, the GC method shows similar performance using fastSPA – 0.1 and fastSPA – 2 p values, which shows its robustness in meta-analysing p values regardless of whether they were originally calculated using the normal approximation or the saddlepoint approximation. For MAF = 0.001 under the extremely unbalanced setting, there is conservative behaviour shown by the Z-score method when using fastSPA – 0.1 or fastSPA – 2 p values at α = 5 × 10−5 level. All methods provided well-controlled type I error rates for the balanced case-control ratio. We further simulated 5 × 108 datasets under the settings of simulation study 1 with a much more extreme case-control ratio (1:99), and even under such extreme case-control imbalance, our proposed methods showed well-controlled type I errors, whereas the Z-score method overall resulted in type I error inflation (Figure S3, supplementary materials A). Similar observation follows for simulation study 2. The type I error comparison (Figure 2) suggests that our proposed methods showed no sign of type I error inflation across different MAFs and case-control ratios, whereas the Z-score method resulted in inflated type I error rates for the moderately unbalanced and extremely unbalanced settings, especially for the all rare, all low frequency and different MAF categories. Z-score method using Score p values had the maximum inflation across all categories.
Figure 1:
Type I error comparison between the Z-score based meta-analysis and our proposed CGF-Spline and Genotype Count (GC) methods where the phenotypes, non-genetic covariates and the genotypes are simulated as described in simulation study 1. Joint represents the joint analysis with the pooled data. The top and the bottom panels show empirical type I error rates at genome-wide significance levels α = 5 × 10−5 and α = 5 × 10−8, respectively. From left to right, the plots consider the within-study case-control ratios 1:1, 1:9 and 1:49, respectively. In each plot, the X-axis represents MAFs with expected MACs per study in parenthesis, and the Y-axis (in logarithmic scale) represents the empirical type I error rates. 95% confidence intervals at different MAFs are also presented.
Figure 2:
Type I error comparison between the Z-score based meta-analysis and our proposed CGF-Spline and Genotype Count (GC) methods where the phenotypes, non-genetic covariates and the genotypes are simulated as described in simulation study 2. Joint represents the joint analysis with the pooled data. The top and the bottom panels show empirical type I error rates at genome-wide significance levels α = 5 × 10−5 and α = 5 × 10−8, respectively. From left to right, the plots consider the within-study case-control ratios 1:1, 1:9 and 1:49, respectively. In each plot, the X-axis represents different MAF groups: Rare (variant is rare in all studies), Low frequency (variant is low frequency in all studies), Common (variant is common in all studies) and Different AF (variant is in different allele frequency group in at least two different studies). The Y-axis (in logarithmic scale) represents the empirical type I error rates. 95% confidence intervals at different MAFs are also presented.
In simulation study 3, we also have similar results (Figure 3) for our proposed methods. However, the Z-score method using the fastSPA – 0.1 or fastSPA – 2 p values showed no sign of significant type I error inflation in the extremely unbalanced case-control setting, and only slight inflation in the moderately unbalanced setting. This suggests that the Z-score-based method can be adequate for controlling the type I error rates when only a small number of biobank-based studies are included in the meta-analysis. However, as seen from the other two simulation studies, the Z-score method may fail to control type I error rates when large number of unbalanced studies are involved.
Figure 3:
Type I error comparison between the Z-score based meta-analysis and our proposed CGF-Spline and Genotype Count (GC) methods where the phenotypes, non-genetic covariates and the genotypes are simulated as described in simulation study 3. Joint represents the joint analysis with the pooled data. The top and the bottom panels show empirical type I error rates at genome-wide significance levels α = 5 × 10−5 and α = 5 × 10−8, respectively. The left and right panels consider the within-study case-control ratios 1:9 and 1:49, respectively for the unbalanced studies. In each plot, the X-axis represents MAFs with expected MACs in parenthesis, and the Y-axis (in logarithmic scale) represents the empirical type I error rates. 95% confidence intervals at different MAFs are also presented. The empirical type I error rates were almost identical between ZScore – fastSPA – 2 and ZScore – fastSPA – 0.1, and between GC – fastSPA – 2 and GC – fastSPA – 0.1, and hence the lines are sometimes overlapped in this plot.
Power comparison:
Next, we compare the empirical powers of different meta-analysis strategies along-with the joint analysis as the gold standard under the first simulation setting. Because the Z-score-based meta-analysis method provided inflated type I error rates as seen in the type I error comparisons, we used empirical α levels calculated from type I error simulations for each method where the empirical type I error rate becomes 5 × 108. The power curves (Figure 4) show that the Z-score method has slightly lower power (lowest when using score test p values) in the moderately and extremely unbalanced case-control ratios. Our proposed methods provide very similar power to the joint analysis, and all methods provide similar power in the balanced case-control setting. When nominal α = 5 × 10−8 level was used (Figure S4, supplementary materials A), the Z-score method expectedly showed higher powers in the unbalanced settings since it is not calibrated for its type I errors.
Figure 4:
Power curves for the Z-score, CGF-Spline and Genotype Count (GC) methods. Top panel considers MAF = 0.01 and bottom panel considers MAF = 0.05. From left to right, the plots consider case-control ratios 1:1, 1:9 and 1:49, respectively. In each plot the X-axis represents genotype odds ratios and the Y-axis represents the empirical power. Empirical power was estimated from 5000 simulated datasets at their type I error adjusted empirical α levels where their empirical type I errors are equal to 5 × 10−8.
UK Biobank data analysis
We meta-analysed the results from 19 individual studies (assessment centers) for the phenotypes Ulcerative Colitis and Psoriasis, using the Z-score-based meta-analysis (Z-score), genotype count sharing-based meta-analysis (GC), and CGF sharing-based meta-analysis (CGF-Spline). The quantile-quantile (QQ) plots presented in Figure 5 and Figure 6 show that the meta-analysis p values from our proposed methods closely follow the uniform distribution, whereas those from the Z-score method are either much smaller (Z-score method using Score or fastSPA – 0.1 p values) or larger (Z-score method using fastSPA – 2 p values) than expected for rare variants (MAF < 0.01). This suggests conservative behaviour of the Z-score method when using the fastSPA – 2 p values, and extremely anti-conservative behaviour when using fastSPA – 0.1 or Score p values. On the other hands, both the GC and CGF-Spline methods improve the accuracy of the meta-analysis p values and provide well-calibrated QQ plots. Further, the QQ plots from our proposed methods show similar behaviour to the QQ plots from the Joint analysis (Figure S5, supplementary materials A). We also presented the genomic control inflation factors (λ) of different meta-analysis strategies in Table S2, supplementary materials A. For Ulcerative Colitis, all our proposed methods showed no inflation or deflation in the genomic controls at p value quantiles q = 0.01 and 0.001, whereas the Z-score method showed severely inflated inflation factors when using the Score (eg. λ = 1.34 at q = 0.01) and fastSPA – 0.1 (eg. λ = 3.16 at q = 0.01) p values and deflated inflation factors when using the fastSPA – 2 (eg. λ = 0.82 at q = 0.01) p values at those p value quantiles. This result further supports the observations made from the QQ plots. When considering the inflation factors at the median p value quantile (q = 0.5), the CGF-Spline (λ = 0.74) and GC method using fastSPA – 2 p values (λ = 0.84) showed deflated inflation factors, and GC method using fastSPA – 0.1 p values (λ = 1.40) showed inflated inflation factor. This is expected, since the SPA test p values near the median are not calculated using the saddlepoint approximation as discussed in Dey et al. (2017). In that paper, they also found inflated genomic control factors for fastSPA – 0.1 and deflated genomic control factors for fastSPA – 2 p values at the median level for extremely unbalanced case-control ratios. The inflation factors showed similar patterns for Psoriasis. However, at p value quantile q = 0.001, the GC method using fastSPA – 2 p values, and the CGF-Spline method showed slightly larger than expected inflation factors (λ = 1.10 for both methods). This might be due to the presence of the Major Histocompatibility Complex (MHC) in the 6p21 region which contains a large number of polymorphic variants and it is a known associated region for Psoriasis (Stuart et al., 2015). After excluding the MHC region from the inflation factor calculation, the inflation factors became very close to unity.
Figure 5:
QQ plots for Ulcerative Colitis based on the UK Biobank interim release data. QQ plots using the Z-score method are provided in the left panel, and the QQ plots using our proposed methods are provided on the right panel. The plots are color-coded based on different MAF categories.
Figure 6:
QQ plots for Psoriasis based on the UK Biobank interim release data. QQ plots using the Z-score method are provided in the left panel, and the QQ plots using our proposed methods are provided on the right panel. The plots are color-coded based on different MAF categories.
The top genome-wide significant SNPs in different regions, identified by the CGF-Spline method, are listed in Table S3, supplementary materials A. The top significant SNPs were identical for the genotype count method. The p values for the top significant SNPs were similar for all the methods, except Z-score-based meta-analysis using Score and fastSPA – 0.1 p values. Zscore method using Score p values resulted in much smaller meta-analysed p values for all of those SNPs, and Z-score method using fastSPA – 0.1 p values resulted in surprisingly large p values for testing Psoriasis on the two SNPs on chromosome 22 (rs549956609 and rs560106765). All other meta-analysis procedures and the joint analysis on these two SNPs resulted in p values which were close to the genome-wide significance level (GC – fastSPA – 2, CGF-Spline, and Joint analysis p values smaller than, and GC – fastSPA – 0.1 and Zscore – fastSPA – 2 p values larger than α = 5 × 10−8 level.)
Applicability on imputed dosages:
To assess the performance of our methods with genotype dosage data, we further performed our within-study tests to calculate the p values, scores and spline-based summary statistics using the dosage data, and then meta-analysed the results using our proposed methods. For the GC method, we calculated the within-study p values based on the dosages, but constructed the genotype-only model using genotype counts calculated using three methods: counting the best-called genotypes (BCG), rounding off the dosages to the nearest integers and counting them (Rounded Dosages), and genotype counts obtained from the MACs assuming Hardy-Weinberg equilibrium (HWE). We also compared the results with a joint analysis performed in the same way described for the genotype data analysis. The resulting QQ plots (Figure S6, S7 and S8, supplementary materials A) showed no sign of inflation or deflation for the GC methods, and showed very similar behaviour to the QQ plots from the CGF-Spline method and the Joint analysis (Figure S9, supplementary materials A). which suggests that the methods are robust for the analysis of dosage data.
We further generated the QQ plots for four different ranges (< 0.3, 0.3 – 0.6, 0.6 – 0.9, and ≥ 0.9) of imputation quality Impute-INFO scores (Howie, Donnelly, & Marchini, 2009) (supplementary materials B). Overall, our proposed methods provided close to uniform QQ plots. For variants with smaller INFO scores (INFO < 0.6), the GC method using fastSPA – 0.1 p values showed small amount of inflation when the best-called genotypes (BCG) or rounded dosage values (Rounded Dosage) were used. However, GC method using only MAC information provided the most calibrated (close to the uniform distribution) QQ plots. This is expected, because lower imputation quality is more often observed for rare variants, for which MAC information is enough to calculate the genotype counts, as we do not usually observe homozygous minor genotypes.
Discussion
In this paper, we evaluated the performance of the traditional Z-score-based meta-analysis strategy to combine association results from multiple unbalanced genome-wide association studies, and proposed two alternative strategies that can provide well-calibrated meta-analysis p values, even when the case-control ratios are extremely unbalanced and the minor allele counts are small. Through extensive numerical studies and an application on the UK Biobank data, we showed that the Z-score-based method can result in conservative or anti-conservative behaviour in the meta-analysis p values, whereas our proposed methods provided well-controlled type I error rates. The proposed methods also showed similar empirical powers as a joint analysis on the pooled data.
When the effect sizes are not available, such as in the case of the saddlepoint approximation-based test, it is widely popular to use the Z-score-based meta-analysis approach and combine the individual p values into a meta-analysis p value. In our third simulation setting, we showed that the Z-score-based approach can still be appropriate when only a small number of biobank-based studies with unbalance phenotypes are included in the meta-analysis. However, we will suggest the researchers to be cautious when using the Z-score-based approach, as including more such unbalanced studies can result in a loss of calibration in the meta-analysis p values. When effect size estimates are available, for example when using the Firth’s bias-corrected likelihood ratio test (Firth, 1993), the inverse variance-weighted method is another popular meta-analysis approach used by the researchers. However, Ma et al. (2013) showed that the inverse variance-weighted meta-analysis method using the Firth’s bias-corrected effect size estimates also results in type I error inflation when meta-analysing several unbalanced studies.
In this paper, we assumed that the individual studies do not have genetically related samples. In presence of related samples, the SAIGE test (Zhou et al., 2017) can properly account for the sample relatedness and provide accurate p values in single studies with unbalanced case-control ratios. As the SAIGE p values are calculated using the saddlepoint approximation method based on the score statistic and its CGF, the spline-based meta-analysis method can still be applicable for combining multiple studies that are analysed using SAIGE. However, the genotype count-based method may not be appropriate in such scenarios as the genotype-only model does not contain any information about the sample relatedness. The applicability of our methods in studies containing genetically related samples, is left for future research.
Comparing the two proposed methods, the spline-based method (CGF-Spline) does not require any assumption on the effect of the non-genetic covariates since it reconstructs spline approximations of the null distributions of the score statistics and uses them to calculate the meta-analysis p values. Thus, it is more suitable to be applied regardless of the covariate effects. On the other hand, the genotype count-based method (GC) assumes relatively balanced non-genetic covariates with low covariate effects. However, the numerical simulations with very strong covariate effects (Figure S10, supplementary materials A) also showed no sign of type I error inflation or deflation for this method. Another difference between the proposed methods is in their applicability on imputed dosage data. As the GC method requires the overall genotype counts to construct the genotype-only model, it is more suitable to be applied when the within-study analyses are performed on the best-called genotypes instead of dosages. The CGF-spline method is robust in this aspect as it can utilize the CGFs of the test statistics regardless of whether they were calculated from genotype or dosage data. However, in our UK Biobank data analysis example, both our proposed methods showed no sign of inflation or deflation of type I errors, even when the within-study tests were performed on dosage data. Therefore, for practical application purposes, the genotype count-based method can be used to obtain accurate meta-analysis p values. One advantage of the genotype count-based method is that it is software-independent, and requires information which are more readily available compared to the spline-based method.
Supplementary Material
Acknowledgements
This research has been conducted using the UK Biobank Resource under application number 24460. We would like to thank the investigators of UK Biobank for providing us with access to the genotype and phenotype data. SL and RD were supported by NIH R01 HG008773.
Grant Support: NIH R01 HG008773
Footnotes
Supplementary Materials
Additional technical details on the CGF sharing-based method (Appendix A), simulation settings (Appendix B), computation time comparisons (Appendix C), UK Biobank data description (Appendix D), tables S1 – S3 and figures S1 – S15, can be found in the on-line Supplementary Materials A. QQ plots of the p values using imputed data for different range of INFO scores can be found in the on-line Supplementary Materials B.
References
- Barndorff-Nielsen OE (1990). Approximate Interval Probabilities. Journal of the Royal Statistical Society. Series B (Methodological), 52(3), 485–496. [Google Scholar]
- Brent RP (1973). Algorithms for Minimization without Derivatives. Englewood Cliffs, NJ: Prentice-Hall. [Google Scholar]
- Bycroft C, Freeman C, Petkova D, Band G, Elliott LT, Sharp K, … Marchini J (2017). Genome-wide genetic data on ~500,000 UK Biobank participants. bioRxiv 166298 doi: 10.1101/166298. [DOI] [Google Scholar]
- Cooper HM, Hedges LV, & Valentine JC (2009). The handbook of research synthesis and meta-analysis (2nd ed.). New York: Russell Sage Foundation. [Google Scholar]
- Daniels HE (1954). Saddlepoint Approximations in Statistics. Annals of Mathematical Statistics, 25(4), 631–650. doi: 10.1214/aoms/1177728652 [DOI] [Google Scholar]
- Das S, Forer L, Schonherr S, Sidore C, Locke AE, Kwong A, … Fuchsberger C (2016). Next-generation genotype imputation service and methods. Nature genetics, 48(10), 1284–1287. doi: 10.1038/ng.3656 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dey R, Schmidt EM, Abecasis GR, & Lee S (2017). A Fast and Accurate Algorithm to Test for Binary Phenotypes and Its Application to PheWAS. Am J Hum Genet, 101(1), 37–49. doi: 10.1016/j.ajhg.2017.05.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evangelou E, & Ioannidis JP (2013). Meta-analysis methods for genome-wide association studies and beyond. Nat Rev Genet, 14(6), 379–389. doi: 10.1038/nrg3472 [DOI] [PubMed] [Google Scholar]
- Firth D (1993). Bias reduction of maximum likelihood estimates. Biometrika, 80(1), 27–38. doi: 10.1093/biomet/80.1.27 [DOI] [Google Scholar]
- Han B, & Eskin E (2011). Random-effects model aimed at discovering associations in meta-analysis of genome-wide association studies. Am J Hum Genet, 88(5), 586–598. doi: 10.1016/j.ajhg.2011.04.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hebbring SJ (2014). The challenges, advantages and future of phenome-wide association studies. Immunology, 141(2), 157–165. doi: 10.1111/imm.12195 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howie BN, Donnelly P, & Marchini J (2009). A Flexible and Accurate Genotype Imputation Method for the Next Generation of Genome-Wide Association Studies. PLOS Genetics, 5(6), e1000529. doi: 10.1371/journal.pgen.1000529 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krokstad S, Langhammer A, Hveem K, Holmen TL, Midthjell K, Stene TR, … Holmen J (2013). Cohort Profile: the HUNT Study, Norway. Int J Epidemiol, 42(4), 968–977. doi: 10.1093/ije/dys095 [DOI] [PubMed] [Google Scholar]
- Ma C, Blackwell T, Boehnke M, Scott LJ, & investigators GD (2013). Recommended joint and meta-analysis strategies for case-control association testing of single low-count variants. Genet Epidemiol, 37(6), 539–550. doi: 10.1002/gepi.21742 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Press WH F. BP; Teukolsky SA; and Vetterling WT (1992). Numerical Recipes in FORTRAN: The Art of Scientific Computing (2 ed.). Cambridge, England: Cambridge University Press. [Google Scholar]
- Stuart PE, Nair RP, Tsoi LC, Tejasvi T, Das S, Kang HM, … Elder JT (2015). Genome-wide Association Analysis of Psoriatic Arthritis and Cutaneous Psoriasis Reveals Differences in Their Genetic Architecture. Am J Hum Genet, 97(6), 816–836. doi: 10.1016/j.ajhg.2015.10.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- UK Biobank. (2015). Genotyping and quality control of UK Biobank, a large-scale, extensively phenotyped prospective resource. Available from: http://biobank.ctsu.ox.ac.uk/crystal/docs/genotyping_qc.pdf.
- Zhou W, Nielsen JB, Fritsche LG, Dey R, Elvestad MB, Wolford BN, … Lee S (2017). Efficiently controlling for case-control imbalance and sample relatedness in large-scale genetic association studies. bioRxiv. doi: 10.1101/212357 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.