Cortical dynamics during psychedelic and anesthetized states induced by ketamine

Abstract

Ketamine is a unique drug that has psychedelic and anesthetic properties in a dose-dependent manner. Recent studies have shown that ketamine anesthesia appears to maintain the spatiotemporal complexity of cortical activation evoked by transcranial magnetic stimulation, while a psychedelic dose of ketamine is associated with increased spontaneous magnetoencephalographic signal diversity. However, a systematic investigation of the dose-dependent effects of ketamine on cortical complexity using the same modality is required. Furthermore, it is unknown whether the complexity level stabilizes or fluctuates over time for the duration of ketamine exposure. Here we investigated the spatiotemporal complexity of spontaneous high-density scalp electroencephalography (EEG) signals in healthy volunteers during alterations of consciousness induced by both subanesthetic and anesthetic doses of ketamine. Given the fast transient spectral dynamics, especially during the gamma-burst pattern after loss of consciousness, we employed a method based on Hidden Markov modeling to classify the EEG signals into a discrete set of brain states that correlated with different behavioral states. We characterized the spatiotemporal complexity specific for each brain state as measured through the Lempel-Ziv complexity algorithm. After controlling for signal diversity due to spectral changes, we found that the subanesthetic dose of ketamine is associated with an elevated complexity level relative to baseline, while the brain activity following an anesthetic dose of ketamine is characterized by alternating low and high complexity levels until stabilizing at a high level comparable to that during baseline. Thus, spatiotemporal complexity associated with ketamine-induced state transitions has features of general anesthesia, normal consciousness, and altered states of consciousness. These results improve our understanding of the complex pharmacological, neurophysiological, and phenomenological properties of ketamine.

1. Introduction

Ketamine is a unique drug that, depending on its dose, has anesthetic, analgesic, anti-depressant, and psychedelic properties (Berman et al., 2000; Corssen and Domino, 1966; Domino et al., 1965; Krystal et al., 1994). Ketamine differs from canonical anesthetics in that it (1) does not appear to work primarily through gamma-aminobutyric acid (GABA) receptors, (2) suppresses sleep-promoting regions of the hypothalamus, (3) activates arousal-promoting regions of the brainstem and diencephalon, and (4) increases gamma activity in the cortex (Mashour, 2014). Like its GABAergic counterparts, ketamine anesthesia disrupts frontal-parietal connectivity in the human (Blain-Moraes et al., 2014; Bonhomme et al., 2016; Lee et al., 2013; Vlisides et al., 2017) and nonhuman primate brain (Schroeder et al., 2016), but appears to maintain spatiotemporal complexity, as measured through the perturbational complexity index (PCI) (Sarasso et al., 2015). The PCI measures the Lempel-Ziv complexity (LZC) in a compressed spatiotemporal pattern of cortical activation evoked by transcranial magnetic stimulation (TMS), which has been demonstrated to be a reliable discriminator of the level of consciousness (Casali et al., 2013). It has been reported that the PCI is decreased during propofol, midazolam and xenon anesthesia (Casali et al., 2013) but maintains the baseline level (as observed during wakefulness) during ketamine anesthesia (Sarasso et al., 2015). This is not entirely unexpected given the activation of subcortical arousal-promoting nuclei in association with ketamine anesthesia (Lu et al., 2008).

As a psychoactive drug, ketamine differs from canonical psychedelics in that it does not appear to work primarily through 5-hydroxytrypta-mine receptors and induces a sense of disembodiment more prominently than classical serotonergic drugs such as psilocybin (Studerus et al., 2010). However, subanesthetic doses of ketamine do evoke typical features of psychedelic phenomenology and increase neural signal complexity in a manner similar to psilocybin and lysergic acid diethylamide. Specifically, Schartner et al. reported increased single-channel temporal LZC and spatiotemporal LZC in spontaneous magneto-encephalographic (MEG) signals for psychedelic doses of ketamine (Schartner et al., 2017).

Despite this body of work, important questions remain unanswered. First, prior studies provide only a disjointed picture by investigating the effect of anesthetic dose in TMS-evoked cortical activation (Sarasso et al., 2015) or subanesthetic dose in spontaneous MEG signals (Schartner et al., 2017). For a more complete understanding of ketamine’s psycho-active effects, a systematic investigation of the dose-dependent effects of ketamine on cortical complexity using the same modality is required. Second, prior studies typically assessed the cortical complexity on average over the duration spanning several minutes, but temporal variation has not yet been examined. In particular, a number of electroencephalographic (EEG) studies have reported that slow delta oscillations that alternate with gamma oscillations (so-called “gamma-burst pattern”) occur during ketamine anesthesia (Akeju et al., 2016; Schwartz et al., 1974). Since slow wave activity has been associated with depressed consciousness induced by GABAergic anesthetics such as propofol (Ni Mhuircheartaigh et al., 2013; Warnaby et al., 2017), it is unknown whether ketamine alters cortical dynamics in a way that is more similar to canonical anesthetics, canonical psychedelics, both or neither.

Here we investigate the spatiotemporal complexity of spontaneous high-density scalp electroencephalographic (EEG) signals during baseline consciousness, subanesthetic ketamine dosing (infusion of 0.5 mg kg⁻¹), anesthetic dosing of ketamine (bolus of 1.5 mg kg⁻¹), and recovery. We assessed the complexity during different states of ketamine-induced alterations of consciousness, with reference to baseline and recovery states and with special attention to complexity during the gamma-burst pattern after anesthetic dosing. Based on the unique pharmacology, neurophysiology, and phenomenology, we tested the hypothesis that what is typically referred to as “dissociative anesthesia” induced by ketamine (Corssen and Domino, 1966; Domino, 2010) has elements of general anesthesia, normal consciousness, and altered states of consciousness, in connection with the reduced, maintained, and elevated complexity level as measured through LZC.

2. Materials and methods

This study was approved by the Institutional Review Board (HUM00061087) of the University of Michigan Medical School, where all studies were conducted, and written informed consent was obtained from all participants after careful discussion. Fifteen healthy volunteers (7 males, 8 females, ages 20–35 years) were recruited using flyers posted throughout the medical school and main hospital. We published a distinct EEG analysis for 10 of these participants that examined dose-dependent effects of ketamine on oscillatory and connectivity patterns (Vlisides et al., 2017) as well as a study of altered states of consciousness during subanesthetic exposure of ketamine in all 15 participants (Vlisides et al., 2018). The current study is unique because, unlike past investigations, it focuses on the dose-dependent effects of ketamine on complexity of spatiotemporal patterns.

2.1. Study population

Inclusion criteria were: American Society of Anesthesiologists Class 1 physical status, 20–40 years of age, body mass index <30, and no predictors of a difficult airway. Exclusion criteria were: cardiovascular disease, cardiac abnormalities, hypertension, obstructive sleep apnea, asthma, respiratory illness, gastroesophageal reflux, history of drug use (or positive drug screen prior to ketamine exposure), family history of problems with anesthesia, neurologic disorders, psychiatric disorders or current pregnancy.

2.2. Experimental protocol

Details of the protocol can be found in prior publication (Vlisides et al., 2017). Ketamine administration was conducted as follows. The first period (baseline consciousness) was 5 min of rest with eyes closed. The second period was 40 min with eyes closed during a continuous infusion of subanesthetic (0.5 mg kg⁻¹ total) ketamine, followed by a brief physical examination, intravenous ondansetron (8 mg) administration for nausea prophylaxis, and assessment for altered states of consciousness. We chose this subanesthetic dosing regimen for ketamine because of its common and safe use in psychiatry. The third period was initiated with a 1.5 mg kg⁻¹ bolus dose of ketamine to induce general anesthesia, as assessed by loss of responsiveness to an audio command to squeeze left or right hands (in random order). The fourth period was defined by a return of consciousness, as evidenced by return of responsiveness to command.

2.3. EEG analysis

2.3.1. Acquisition and processing

Data were acquired with 128-channel EGI Hydrocel Nets (Eugene, OR, USA) digitized continuously at 500 Hz with a vertex reference; channel impedances were kept below 50 kΩ as recommended by the manufacturer. The raw EEG signals were exported into MATLAB (version 2017a; MathWorks, Inc., Natick, MA), and down-sampled to 250 Hz. Electrodes on the lowest parts of the face and head were removed, leaving 90 channels on the scalp for the analysis. Bad channels were detected and interpolated by using the spherical spline interpolation method in EEGLAB toolbox (Delorme and Makeig, 2004), and then the EEG signals were re-referenced to the average reference. Data segments with obvious noise or non-physiological artifacts were identified and removed by visual inspection of the waveform and spectrogram of the EEG signals. Prior to the analysis, the EEG signal was detrended using a local linear regression method with a 2-s window at a 1-s step size in Chronux analysis software (http://chronux.org/) (Mitra and Bokil, 2007), lowpass filtered at 50 Hz via butterworth filter of order 5.

For each participant, the preprocessed signals during the first 2-min of eyes-closed baseline, the last 5-min of subanesthetic ketamine, anesthetic ketamine, and the first 2-min of post-recovery, eyes-closed period were concatenated for the analysis, as illustrated in Fig. 1 A. For the anesthetic period, the EEG data from loss of consciousness (LOC) to recovery of consciousness (ROC) (defined by loss or recovery of responsiveness, with acknowledgment that disconnected subjective experience could occur during ketamine anesthesia) was included in the analysis, with the duration of 10.1 ± 3.4 (mean ± SD) min across the participants. Only last 5-min was analyzed the for the subanesthesia period because, based on a pilot study with the same subanesthetic dosing regimen, we assume the ketamine infusion reached pharmacological steady-state conditions by that epoch and the data length is comparable to that analyzed for the anesthetic period. Finally, the 2-min period during baseline and recovery was analyzed because it was the shortest data length among the participants.

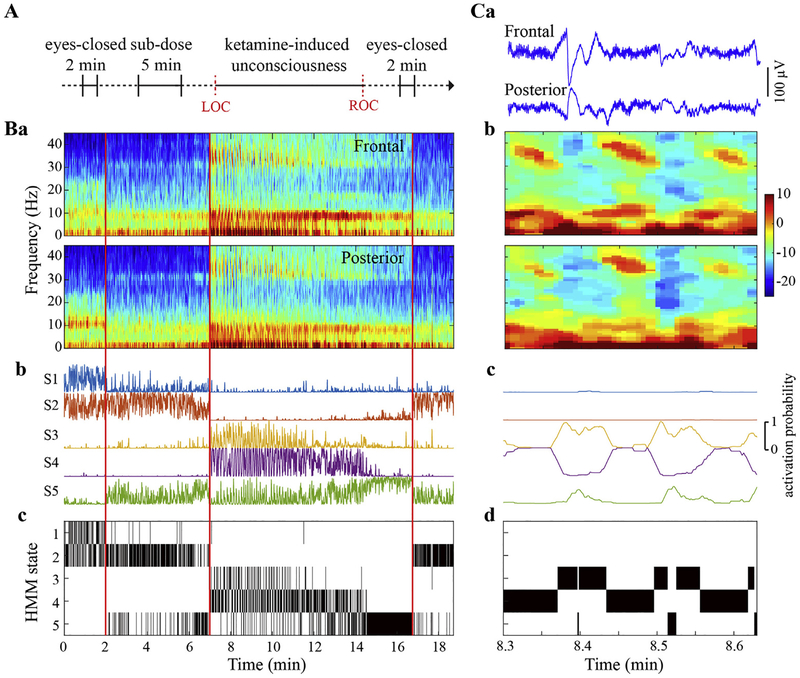
Fig. 1.

Experimental design and the inference of Hidden Markov Model (HMM) states. (A) Experimental design and timeline. The electroencephalographic (EEG) data was recorded throughout the entire experiment and the four periods during eyes-closed baseline, subanesthetic, anesthetic, and recovery, as indicated in bold horizontal lines, were concatenated for the analysis. LOC, loss of consciousness. ROC, recovery of consciousness. (B) Representative spectrograms from frontal (average of F1, F2, and Fz) and posterior (average of PO3, PO4, POz) channels (a) were estimated via multitaper method in 1-s window with 0.5-s overlap, time-bandwidth product = 2, number of tapers = 3. Five HMM states were inferred from Hidden Markov modeling based on the frontal-posterior spectral dynamics, with the probability time course (smoothed via a 1-s sliding window) indicating the probability of each HMM state being active (b) and the HMM states time courses showing the most probable state at each time point (c). The black vertical lines differentiate the baseline, subanesthetic, anesthetic and recovery periods respectively. (C) Representative EEG signals (a), spectrograms (b), and HMM state time courses (c and d) during gamma-burst pattern after LOC. The gamma-burst pattern is characterized by alternating delta and theta-gamma activities, as evident in EEG signals and spectrograms, which were classified into distinct HMM states (c and d).

Brain activity exhibits fast transient spectral changes across the studied periods, especially during the gamma-burst patterns that appears after LOC (see the illustrative example in Fig. 1 Ba and Ca-b). The presence of such alternating activities that have short and irregular duration time precludes a conventional analysis with fixed-length windows, since the analysis windows may be composed of intermingled delta- and gamma-dominant episodes. To investigate the complexity for these episodes separately, we adopted a method based on Hidden Markov model (HMM) (Vidaurre et al., 2016) to adaptively classify the EEG signals into a discrete set of states (i.e. transient brain activities with distinct spectral properties), with each correlated with different behavioral state induced by different doses of ketamine. We extracted the EEG analysis epochs that correspond to each HMM state in each participant and then characterized the HMM state-specific complexity property using spatiotemporal LZC measures, with a control procedure employed to test if the LZC changes arise from more than just the changes in the power spectrum of the signal. The schematic diagram of the analysis pipeline is illustrated in Fig. S1, with each processing step described as following.

2.3.2. Hidden Markov modeling

The HMM (Juang and Rabiner, 1985) assumes that the time series can be described as a sequence of a finite number of states, where each state has its own model of the observed data and the probability of being in a given state at each time point depends on its state assignment at the previous time point. The observation model corresponds to a multivariate autoregressive (MAR) model (Penny and Roberts, 2002), which can capture the spectral dynamics of the data and characterize its behavior by linear historical interactions between multiple brain regions (Vidaurre et al., 2016). More explicitly, if y_t represents the N_ch -channel EEG signal and s_t ∈ {1, …, K} represents the hidden state at time point t, the MAR model is (Vidaurre et al., 2016)

$$y_t|s_t=k~\mathcal{N}\left(\sum _{l\in A}{y}_{t-l}{W}_l^{(k)},{\Sigma }^{(k)}\right)$$ (1)

where A is the set of lags considered by the MAR model, $W_l^{(k)}$ is the N_ch × N_ch matrix representing the autoregressive coefficients for lag l, and Σ^(k) is the N_ch × N_ch noise covariance matrix codifying the variance and covariances between channels when state k is active (Vidaurre et al., 2016, 2017). The noise is assumed to be Gaussian with zero mean and the covariance matrix is assumed to be a full matrix and state-dependent. The variational Bayes inference algorithm (Bishop, 2006) was used to estimate the model parameters, which acts on a group of parameters and iterates through the different groups of parameters until convergence is attained by minimizing the so-called free energy as the cost function. Comprehensive details about the HMM inference algorithm can be found in (Vidaurre et al., 2016).

In this study, the bivariate EEG time series was derived from frontal (average of F1, F2, and Fz) and posterior channels (average of PO3, PO4, POz), and downsampled to 125 Hz for the principle of parsimony, which was then concatenated across all the participants to infer the HMM model at the group level using the HMM-MAR toolbox (Vidaurre et al., 2016). We chose the frontal and posterior channels because of their relevance to ketamine anesthesia based on our recent studies (Lee et al., 2013; Vli-sides et al., 2017). We assume each HMM state to be associated with a different behavioral state (baseline, subanesthesia, the delta- and gamma-dominant periods at post-LOC, and pre-ROC), so the number of HMM states was set to be 5. For MAR parametrization, we followed Vidaurre et al. (2016) and used the configuration of exponential spacing, i.e. A = {P₀ + P_, P₀ + Q, P₀ + Q², …, P} where the number of lags |A| = 12 the offset P₀ = 1 to avoid over the maximal lag P = 125 that corresponds to one=cycle of the lowest frequency of interest (1=Hz), and the elapse $Q={\left(P-P_0\right)}^{{(\left|A\right|-1)}^{-1}}$.

To validate the HMM model described above, we compared the models with different number of HMM states and variants of MAR coefficients matrix ($W_l^{(k)}$in Eq. (1)). Moreover, the HMM inference is sensitive to initialization (Vidaurre et al., 2016, 2018a), and the strategy that we employed in this study consists of running the HMM inference procedure 10 times with random initialization and using the one with the lowest free energy as a starting point for the inference in the final solution. We evaluated the robustness of this initialization strategy by assessing the consistency of the HMM inference results across multiple realizations.

2.3.3. Assessing the relationship between HMM states and behavioral states

The Hidden Markov modeling yields the probability of each HMM state being active at each time point, from which the HMM state with the highest probability was determined as the state that best represents the data on a ‘winner-take-all’ basis. To assess how well the resultant HMM states relates to the behavioral states, the following five equal-length segments were selected: 2-min baseline, last 2-min during sub-anesthesia, 2-min immediately after LOC, 2-min just before ROC, and 2-min during recovery. For each segment, we quantified the fractional occupancy, which is defined as the fraction of time spent in each HMM state at both group-level and participant-level, and which reveals the dominant HMM state(s) for each behavioral state under consideration. Additionally, to evaluate if any two behavioral states are associated with the same set of HMM states, cosine similarity was used to measure the similarity between the distributions of fractional occupancy, by using the pdist function with the option of ‘cosine’ distance metric in Matlab Statistics and Machine Learning Toolbox.

2.3.4. Epoch selection

The HMM time series provides a highly time-resolved representation of the brain dynamics in different states. However, instead of characterizing the temporal dynamics of the HMM states, this study was intended to investigate the complexity properties of the EEG signals associated with these states. To achieve this, EEG epochs that have a certain duration, for which we assume stationarity, are required to calculate the complexity metric and its variant that controls for spectral changes through surrogate data (involving the application of Fourier transform) (see HMM state-specific complexity analysis). Specifically, we smoothed the HMM state time series via a 1-s moving average filter and extracted 1-s epochs from the 90-channel EEG signals that correspond to each HMM state in each participant. This selection allows for an acceptable spectral resolution for the spectrum analysis and also provides a tradeoff between the number of achieved epochs and the mean activation probability of the HMM state at the achieved epochs (which indicates how well the HMM state can represent the brain activity among all the states) (See Fig. S2 in Appendix).

Due to the data-driven inference of HMM states and inter-individual variability, we expect the number of achieved epochs to be unequal across HMM states and participants. To alleviate the effect of unbalanced sample sizes on the estimation of EEG measures, we set the maximal number of epochs to be 30 and calculated the EEG measures based on a random subset of at most 30 epochs drawn for each HMM state, which were then averaged as the estimation of the HMM state-specific properties for each participant. This selection allows for at least 60% of participants to have 30 epochs for each HMM state; the detailed information on the sample size is listed in Table S1. We corroborated the epoch selection strategy by performing supplementary analysis with (1) a random subset that consists of only participants in which 30 1-s epochs could be extracted, (2) a random subset of at most 60 0.5-s epochs, and (3) a random subset of at most 12 2-s epochs extracted for each HMM state and participant.

2.3.5. HMM state-specific spectral power analysis

Although the spectral properties can be obtained directly from the MAR parameters derived from the HMM inference procedure or through the weighted non-parametric approach that uses the inferred HMM state time series (Vidaurre et al., 2016), we chose to calculate the spectral power based on the extracted EEG epochs as described above. The analysis on the same dataset allows for a further examination of the associations between spectral power and spatiotemporal complexity metrics (see HMM state-specific complexity analysis). Specifically, the extracted EEG epoch was analyzed using the multitaper method in Chronux analysis software (Mitra and Bokil, 2007) for each channel, with time-bandwidth product = 2, number of tapers =3. The relative power was calculated from the absolute power normalized by the total power. For statistical comparisons, the mean spectrum was obtained by taking the average across all the available epochs for each HMM state, and the EEG power values were calculated for delta (0.5–4 Hz), theta (4–8 Hz), alpha (8–13 Hz), beta (13–25 Hz), and gamma (25–45 Hz) bands. The topographic maps of group-level spectral power for each HMM state and frequency band were constructed using the topoplot function in EEGLAB toolbox (Delorme and Makeig, 2004).

2.3.6. HMM state-specific complexity analysis

The HMM state-specific complexity properties were characterized by LZC. LZC is a method of symbolic sequence analysis that counts the number of times a new word is encountered in a sequence (Lempel and Ziv, 1976), which has been shown to be a valuable tool to investigate the spatiotemporal complexity of brain activity (Abásolo et al., 2015; Casali et al., 2013; Hudetz et al., 2016; Sarasso et al., 2015; Schartner et al., 2015, 2017).

For a multichannel EEG epoch, the instantaneous amplitude was estimated by applying the Hilbert transform (Schartner et al., 2015, 2017), which was binarized using its mean value as the threshold for each channel (supplementary analysis was performed to test the effect of threshold selection). The data epoch was then converted into a binary matrix, in which rows represent channels and columns represent time points. The complexity of the spatiotemporal matrix was assessed by spatiotemporal LZC (Casali et al., 2013). It searches the binary matrix, time point by time point, and counts the number of different spatial patterns across different time points. If the matrix is random, the spatiotemporal LZC tends to be high; on the other hand, it will be low if all the channels behave identically. Since the LZC value for a sequence of fixed length is maximal if it is entirely random (Schartner et al., 2015, 2017), we normalized the raw spatiotemporal LZC by the mean of those from N = 50 surrogate data generated by randomly shuffling the original spatial order for each time point; thus, the resultant spatiotemporal LZC values range from 0 to 1.

Since each HMM state has distinct spectral profiles, we further tested whether the state-dependent difference in the LZC is entirely due to spectral changes. We generated surrogate data through phase randomization that preserves the spectral profiles of the signal for each channel (Schartner et al., 2015, 2017), and normalized the spatiotemporal LZC by the mean of those from N = 50 surrogate time series (supplementary analysis was performed to test an alternative method in the generation of surrogate data). If the complexity change is entirely due to spectral changes, the difference in the LZC values across the HMM states will be completely preserved in the LZC values from the surrogate data, thus the normalized LZC, spatiotemporal LZC_N, will be close to 1 and equal across the HMM states. If there is complexity change not due to spectral changes, the alterations of LZC values from the surrogate data will be distinct from those of spatiotemporal LZC, and spatiotemporal LZC_N will reflect the signal diversity beyond the spectral changes. For statistical comparisons, the spatiotemporal LZC and LZC_N values were averaged across all the available epochs as the final estimate for each HMM state and participant.

An alternative metric to spatiotemporal LZC is temporospatial LZC, which searches the spatiotemporal matrix, channel by channel, and counts the number of different temporal patterns across channels. The temporospatial LZC tends to be high if the binary matrix is random and will be low if temporal variations do not occur in every channel. The temporospatial LZC and spatiotemporal LZC are theoretically distinct but nonetheless highly correlated measures (Casali et al., 2013). We performed supplementary analysis with temporospatial LZC and its normalized metric (temporospatial LZC_N) that controls for spectral changes and assessed their correlations with spatiotemporal LZC metrics. Moreover, to further evaluate the associations between spectral power and cortical complexity, we used multivariate linear regression to test whether and to what extent the spectral power (across brain regions [frontal and posterior] and frequency bands [delta, theta, alpha, beta and gamma]) predicted the state-dependent differences as revealed by LZC measures.

2.4. Statistical analysis

Statistical analyses were conducted using IBM SPSS Statistics version 24.0 for Windows (IBM Corp. Armonk, NY). Statistical comparisons were performed using linear mixed models (LMM) (West et al., 2014), to test the difference across the HMM states for the EEG power and LZC measures. LMM analysis offers more flexibility in dealing with missing values and accounting for individual differences by including a random intercept associated with each participant. For the models of EEG power values, the fixed effects included the HMM state, region (frontal and posterior), and the interaction between them; repeated effects included the HMM state and region. For the LZC measures, the HMM state was modeled as the fixed effects and repeated effects. We used restricted maximum likelihood estimation, compound symmetry as covariance structure of repeated effects, and variance components as covariance structure of random effects. For the EEG power values, the post-hoc pairwise comparisons were performed between each HMM state relative to the baseline-associated state S1, and between frontal and posterior regions if the regional fixed effects were statistically significant (p < 0.001); only the significant levels were reported (Bonferroni corrected p < 0.05). For the LZC measures, the post-hoc pairwise comparisons were performed between each pair of HMM states. A p-value < 0.05 using Bonferroni correction was considered statistically significant if not specifically stated. In addition, the mean and 95% confidence interval (CI) values of the estimated difference along with the exact uncorrected p-values were reported in Table S2.

3. Results

3.1. Inference of HMM states

Brain activity exhibited distinct spectral profiles during the sub-anesthetic infusion and ketamine anesthesia. There was a reduction of alpha power and a mild increase of gamma power during subanesthesia (Fig. 1 Ba). After LOC, the gamma-burst pattern was visibly evident with alternating delta, theta, and gamma activities (Fig. 1 Ca and Cb), which evolved into a distinct pattern with more stable theta and gamma power before ROC (Fig. 1 Ba). The spectral profile at recovery seemed to be comparable to that during subanesthesia (Fig. 1 Ba). These phenomena were observed, although quantitatively different, in both frontal and posterior regions (Fig. 1 Ba and Cb).

The EEG signals for the frontal and posterior regions were used to train the HMM model, which was driven by both the auto- and cross-spectral dynamics of the bivariate time series. Five HMM states were inferred and the probability of each state being active at each time point was estimated (Fig. 1 Bb and Cc), from which the HMM state that best represents the data was obtained (Fig. 1 Bc and Cd). It is notable that the HMM states seemed to track the evolution of spectral profiles with ketamine anesthesia. The HMM state 1 (S1) was dominant at baseline, which turned to S2 during subanesthesia. The two HMM states, S3 and S4 concentrated at delta and gamma activity respectively, co-existed and alternated at the early stage of the anesthetic period, which shifted to S5 before the ROC. The dominant pattern returned to S2, but not S1, in the recovery period (as might be expected in the shift from anesthetic to subanesthetic effect-site drug concentrations). To test the robustness of the inferred results, we ran the HMM algorithm multiple times. The high correlation (>0.97) of the HMM state time series across different realizations suggests consistency of the inference results due to different initializations (Fig. S3D).

3.2. Association of inferred HMM states with different behavioral states

To evaluate how well the HMM states track the evolution of behavioral states associated with ketamine, Fig. 2 shows the fractional occupancy of HMM states for each considered behavioral state at both group-level (A) and individual participant-level (B). HMM state S1 was most often seen during the baseline eyes-closed period (60.37%), while S2 was the dominant state at subanesthesia (46.52%), which was followed by S5 (28.52%). The HMM states mostly seen in post-LOC were S3 (31.16%) and S4 (41.31%), while the one that dominates the pre-ROC period was S5 (58.89%). Similar to subanesthesia, S2 (39.19%) and S5 (33.40%) were dominant states at recovery. There was a fair amount of participant-to-participant variability, which was most prominent for the sub-anesthesia and recovery periods (Fig. 2 B). Instead of HMM state S2, the subanesthesia period was occupied mostly by HMM state S5 or S1 in N = 6 participants, and the recovery period was more distributed across the HMM states. Brain activity at recovery did not return to baseline, while the distribution of fractional occupancy appeared to be comparable to that observed in subanesthesia, with the cosine similarity of 0.90 ± 0.25 significantly higher than those with the other periods (0.60 ± 0.29, 0.21 ± 0.17, 0.47 ± 0.32 for baseline, post-LOC and pre-ROC, respectively) (Bonferroni corrected p < 0.005, Wilcoxon rank sum test).

Fig. 2.

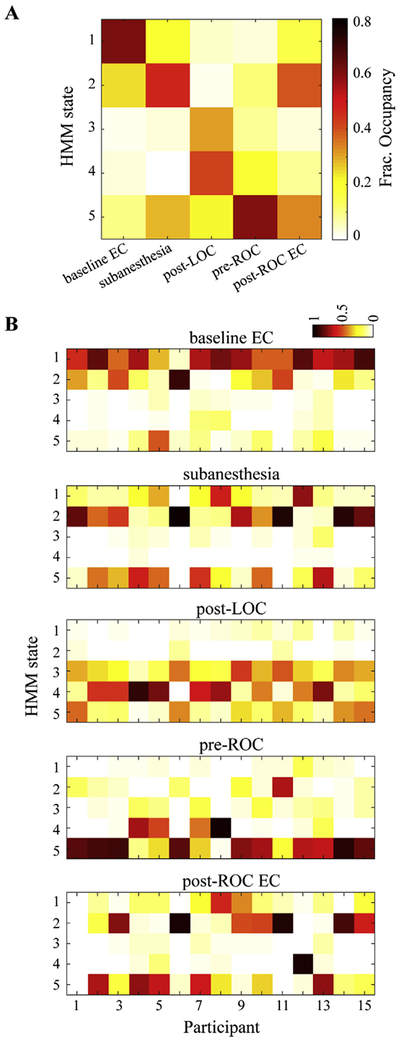
The inferred HMM states are associated with different behavioral states. (A) Fractional occupancy, i.e., the fraction of time spent in each HMM state for each behavioral state across all participants. For each participant, five segments of 2-min were selected to represent the different behavioral states: eyes-closed baseline, subanesthesia, post-LOC, pre-ROC, and recovery. (B) fractional occupancy of HMM states for each behavioral state at the single participant level. The recovery period was not recorded for participant 01, as indicated by all zero occupancy across all HMM states for this participant in the bottom-most panel. EC, eyes-closed.

Additionally, Fig. S3 (A–C) presents the associations between the behavioral states and the HMM states inferred from different variants of HMM model, suggesting that the employed model correlates best with the behavioral states of interest in this study.

3.3. HMM state-specific spectral power analysis

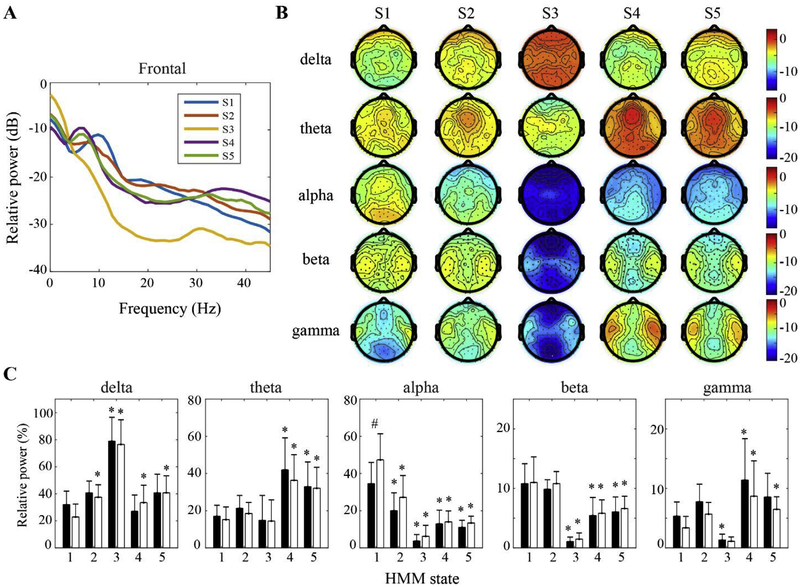
The HMM state-specific spectral properties were characterized by the power analysis of the EEG epochs extracted from the 90-channel EEG signals for each HMM state, as shown in Fig. 3. The HMM state S1, the dominant pattern of the baseline period, was characterized by a predominance of alpha power in posterior channels (frontal vs. posterior: p < 0.001). A decrease in alpha (p < 0.001 for both frontal and posterior regions) and a mild increase in theta and gamma were observed for the subanesthesia-associated state S2 (Fig. 3A–C). For the two alternating HMM states correlated with post-LOC, S3 was characterized by prominent delta power throughout the scalp (p < 0.001 for both regions) and the lowest power at alpha and gamma bands (p < 0.05 for both regions), while S4 was dominant with significantly higher theta and gamma power (p < 0.05 for both regions). Although the pre-ROC-associated state S5 demonstrated a slightly lower theta and gamma power (Fig. 3A and B), there was no statistically significant difference between S4 and S5 (Fig. 3 C).

Fig. 3.

HMM state-specific spectral power analysis. (A) Group-level power spectrum of frontal EEG, averaged across F1, F2, Fz channels. (B) Scalp topography of the power values at delta (0.5–4 Hz), theta (4–8 Hz), alpha (8–13 Hz), beta (13–25 Hz), and gamma (25–45 Hz) bands across the HMM states. (C) The mean and SD (frontal: black bars; posterior: white bars) of the power values at each frequency band across the HMM states. * indicates significant changes relative to S1, while # indicates significant difference between frontal and posterior regions, using linear mixed model analysis (Bonferroni corrected p < 0.05).

3.4. HMM state-specific complexity analysis

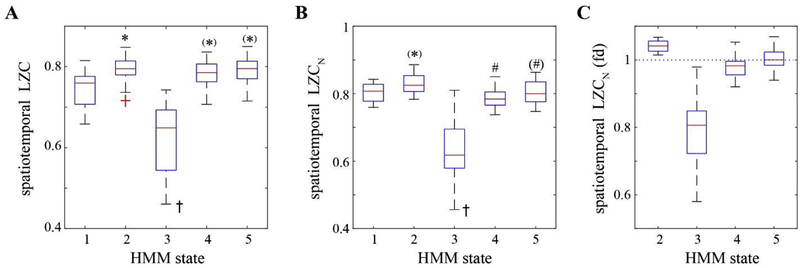
To characterize the HMM state-specific complexity properties, Fig. 4 presents the changes of spatiotemporal LZC and its normalized measure that excludes the possibility that any observed changes could be attributed solely to changes in spectral profile. We found increased complexity for the subanesthesia-associated state S2 as compared to S1 (spatiotemporal LZC: p < 0.05, 0.056 [0.021–0.090] for mean and 95% CI), spatiotemporal LZC_N: uncorrected p = 0.038, 0.035 [0.002–0.067]), while the HMM state S3 demonstrated the lowest complexity values across all the states (p < 0.001). For the other two HMM states that correlated with ketamine-induced unconsciousness, the LZC measures behaved differently. The spatiotemporal LZC values at S4 and S5 were –0.065], higher than those at S1 (S4: uncorrected p = 0.047, 0.033 [0.000 S5: uncorrected p = 0.007, 0.044 [0.013–0.076]) while comparable to that at S2, but its normalized measure LZC_N demonstrated lower complexity than S2 (S4: p < 0.05, −0.053 [−0.086 to −0.020], S5: uncorrected p = 0.039, −0.034 [−0.067 to 0.002]), which was comparable to that at S1. There was no statistically significant difference between S4 and S5 for any LZC measure (Table S2). Similar state-dependent changes of spatiotemporal LZC_N were observed despite different strategies in the selection of EEG epochs, the threshold for binarization, and the method of generating surrogate data (Fig. S4).

Fig. 4.

HMM state-specific complexity analysis. The complexity changes across the HMM states as assessed by spatiotemporal LZC (A) and its normalized measure, spatiotemporal LZC_N (B, and C in the form of fold changes from the baseline-associated state S1). On each box, the central line and edges indicate the median and the interquartile range (IQR) of the values across the participants, the whiskers extend to the most extreme values, and the outliers are marked as red crosses. * indicates significant increase relative to S1, # indicates significant increase relative to S2, while y indicates significant decrease as compared to all the other states, using linear mixed model analysis (Bonferroni corrected p < 0.05, while (*) or (#) indicating uncorrected p < 0.05).

As with spatiotemporal complexity, the temporospatial LZC measures achieved the minimal values at state S3 (p < 0.001). However, there was no statistically significant increases detected at S2 relative to S1 (Fig. S5 A–C, and Table S2). The temporospatial LZC values at S4 and S5 were higher than those at S1 (S4: p < 0.001, 0.081 [0.043–0.119], S5: p < 0.05, 0.060 [0.023–0.097]) but the differences were attenuated in temporospatial LZC_N after controlling for the spectral changes, suggesting that temporospatial LZC may mainly reflect the signal diversity due to power spectrum. Across all states except S3, the temporospatial LZC and spatiotemporal LZC were strongly correlated (Spearman’s correlation r = 0.73, p < 0.001), while there was no relationship between their normalized measures (r = 0.13, p = 0.34) (Fig. S5 D–E). Additionally, the spectral power across brain regions and frequency bands (Fig. 3 C) jointly accounted for 85% and 61% of total variance in the temporospatial LZC and spatiotemporal LZC, which were reduced to 31% and 42% for the temporospatial LZC_N and spatiotemporal LZC_N, respectively (Fig. S6). Collectively, these results suggest it is likely that the HMM state-dependent difference in spatiotemporal LZC was considerably influenced by spectral changes, but this association was largely mitigated for spatiotemporal LZC_N, where at least 58% of the total variance cannot be explained by the effect of EEG spectral characteristics.

4. Discussion

In this study of human volunteers, we investigated the spatiotemporal complexity in spontaneous high-density scalp EEG recordings during both subanesthetic and anesthetic dosing of ketamine, but without the confound of other psychoactive medications. Given the fast transient spectral changes of brain activity, we employed a method based on Hidden Markov modeling to classify the EEG signals into a discrete set of brain states that correlated with different behavioral states. We found that these inferred states demonstrated distinct features of spatiotemporal complexity as assessed by LZC. After controlling for the spectral changes, the complexity increased at the HMM state associated with subanesthesia and recovery (S2) relative to baseline (S1), while it alternated between low (S3) and high (S4) levels during gamma-burst pattern after loss of consciousness until stabilizing at the high level (S5) before recovery of consciousness. The complexity levels at S4 and S5 were comparable to that during baseline (S1). These findings demonstrate the unique complexity dynamics during the alteration of consciousness induced by different doses of ketamine.

We observed the dose-dependent effect of ketamine on spectral characteristics, which is in line with previous EEG/MEG findings that ketamine suppresses alpha oscillations at subanesthetic doses (de la Salle et al., 2016; Lee et al., 2013; Muthukumaraswamy et al., 2015; Schartner et al., 2017; Vlisides et al., 2017), and increases delta, theta, and gamma power during general anesthesia (Blain-Moraes et al., 2014; Lee et al., 2013; Purdon et al., 2015; Vlisides et al., 2017). Specifically, a gamma-burst EEG pattern has been associated with ketamine-induced unconsciousness following a bolus dose of ketamine, which evolves into a stable gamma pattern likely due to decreasing plasma levels of ketamine (Akeju et al., 2016). Motivated by the time-varying spectral changes (Fig. 1 Ba), we adopted a data-driven method to infer the HMM states inherent in the EEG signals based on their spectral and cross-spectral dynamics in frontal and posterior channels. This method enabled us to investigate the spatiotemporal complexity separately for each HMM state and associated behavioral state (Fig. 2 A). As compared to conventional analysis directly performed on these behavioral states (Fig. S7), we not only assessed the spatiotemporal complexity associated with the gamma-burst pattern, but also revealed a considerably richer picture of the cortical dynamics during the alterations of consciousness induced by different doses of ketamine. For example, the transient gamma-dominant pattern and the stable gamma pattern, which usually occur at the early and later stages of the ketamine-induced unconsciousness period respectively, are associated with distinct EEG characteristics, while the post-recovery and subanesthesia infusion periods share similar cortical dynamics, irrespective of the number of HMM states inferred (Fig. 2A and S3A).

The spatiotemporal complexity was assessed by the LZC that measures the diversity of spatial patterns over time, which is different from temporospatial LZC that measures the temporal variability across space (in this case, EEG channels). Consistent with (Casali et al., 2013), the spatiotemporal LZC and temporospatial LZC were found to be highly correlated, but this is not the case for spatiotemporal LZC_N and temporospatial LZC_N after controlling for spectral changes (Fig. S5D–E). As opposed to the spatiotemporal measures, the temporospatial LZC could be mainly driven by EEG spectral characteristics, because the temporospatial LZC exhibited the highest complexity in conjunction with the highest theta and gamma power at S4 (Fig. 3), with differences among the states (except S3) reduced after correction (Figs. S5A–B). In this study, we focused on spatiotemporal LZC_N, which mitigates the effect of EEG spectrum, as corroborated by linear regression analysis suggesting that spectral power data cannot entirely account for the complexity changes as revealed by spatiotemporal LZC_N (Fig. S6B). The dose-dependent effect of ketamine on spatiotemporal complexity (Fig. 4 C) is in line with previous neurophysiological studies that found increased signal diversity in spontaneous MEG at a psychoactive dose of ketamine (Schartner et al., 2017), while the PCI index in the TMS-evoked EEG at general anesthesia level was comparable to those obtained during wakefulness (Sarasso et al., 2015). The most interesting finding in the current study is the complexity dynamics following a bolus dose of ketamine, i.e., the complexity alternated between low (S3) and high (S4) levels during gamma-burst pattern after loss of consciousness, which stabilized at a high level (S5) before recovery of consciousness. Furthermore, we found that the fractional occupancy of HMM states after recovery of consciousness was similar to that at subanesthesia (Fig. 2), which suggests that brain activity (in terms of frontal-posterior spectral dynamics) does not return to baseline with return of conscious responsiveness, but transitions to a state similar to subanesthesia.

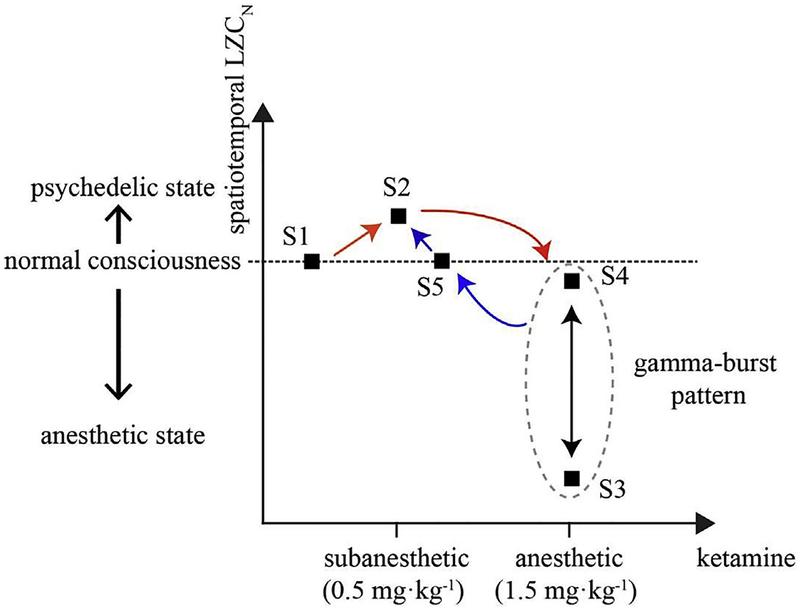
The findings in this study suggest that the spatiotemporal complexity associated with ketamine-induced state transitions has features of general anesthesia (delta activity, lowest complexity), normal consciousness (gamma-dominant periods during post-LOC ‘gamma-burst’ pattern and pre-ROC, baseline complexity), and altered states of consciousness (during subanesthesia and recovery, highest complexity). If we accept the argument of Schartner et al. (2017) that LZC might represent a measure of neural signal complexity along one axis that represents both anesthesia (low LZC) and psychedelic experience (high LZC), then what we currently call “ketamine anesthesia” is actually a fragmented state characterized by a rapidly alternating pattern of conscious states (high complexity) and anesthetic states (low complexity) (Fig. 5). This is consistent with the known disruption of connected consciousness (i.e., consciousness of environmental events) with the unique preservation of vivid disconnected consciousness (e.g., dream states or hallucinations) during ketamine anesthesia (Grace, 2003). It also suggests that temporal continuity of requisite complexity levels is likely required for the sustained state of consciousness experienced in the waking state.

Fig. 5.

Schematic summary of the complexity dynamics during ketamine-induced alterations of consciousness. The black squares indicate the inferred HMM states, which correlated with different behavioral states under consideration. For each HMM state, the spatiotemporal complexity (averaged value of spatiotemporal LZC_N across all the participants) were plotted relative to S1. The arrows in red represent the alterations from baseline (S1) to subanesthesia (S2) and then LOC following a bolus dose of ketamine (alternating between S3 and S4), whereas the progression into late anesthesia (S5) and then recovery of consciousness (S2) is indicated in blue arrows. The brain dynamics after recovery of consciousness didn’t return to baseline (S1), but shared the same dominant state (S2) with subanesthesia. This suggests that the spatiotemporal complexity associated with ketamine-induced state transitions has features of general anesthesia (S3), normal consciousness (S4, S5), and altered states of consciousness (S2).

There were methodologic limitations that should be considered. First, we assessed the cortical complexity of spontaneous EEG in terms of signal diversity or variability of the spatiotemporal patterns (Schartner et al., 2015, 2017), but not in the same way that the PCI index assesses the joint presence of functional integration and differentiation (Casali et al., 2013) as proposed in the integrated information theory of consciousness (Tononi et al., 2016). Second, despite controlling for the overall spectral changes through surrogate data, the spatiotemporal LZC_N is not independent of the temporal diversity, which may be sensitive to the temporal variations in higher-order properties. Third, we inferred the HMM model to match the studied behavioral states, in order to connect the complexity dynamics with the alterations of consciousness induced by different doses of ketamine. It is likely that a finer-grained inference with more HMM states may reveal other dynamic states beyond these behavioral changes. Fourth, the HMM states were identified based on the spectral dynamics in frontal and posterior regions (also see the results with four regions in Fig. S8), which was determined by our prior findings (Lee et al., 2013; Vlisides et al., 2017) and for optimizing efficiency of the HMM inference procedure. The number of model parameters quadratically increases with the number of channels, which may lead to over-fitting problems and also increased computational costs. The incorporation of a dimensionality reduction strategy such as time-delay embedded HMM model might be a useful direction for future studies of whole brain dynamics (Vidaurre et al., 2018b).

In summary, we demonstrated that the subanesthetic dose of ketamine is associated with an elevated complexity level relative to baseline consciousness, while brain activity following a bolus dose of ketamine is characterized by alternating levels of low and high complexity until stabilizing at a level comparable to that observed during baseline consciousness. These results improve our understanding of the complex pharmacological, neurophysiological, and phenomenological properties of ketamine, which can serve as a unique tool to probe different states of consciousness.