Suitability of gridded climate datasets for use in environmental epidemiology

Abstract

Epidemiologic analyses of the health effects of meteorological exposures typically rely on observations from the nearest weather station to assess exposure for geographically diverse populations. Gridded climate datasets (GCD) provide spatially resolved weather data that may offer improved exposure estimates, but have not been systematically validated for use in epidemiologic evaluations. As a validation, we linearly regressed daily weather estimates from two GCDs, PRISM and Daymet, to observations from a sample of weather stations across the conterminous United States and compared spatially resolved, population-weighted county average temperatures and heat indices from PRISM to single-pixel PRISM values at the weather stations to identify differences. We found that both Daymet and PRISM accurately estimate ambient temperature and mean heat index at sampled weather stations, but PRISM outperforms Daymet for assessments of humidity and maximum daily heat index. Moreover, spatially-resolved exposure estimates differ from point-based assessments, but with substantial intercounty heterogeneity. We conclude that GCDs offer a potentially useful approach to exposure assessment of meteorological variables that may, in some locations, reduce exposure measurement error, as well as permit assessment of populations distributed far from weather stations.

1. INTRODUCTION

There is considerable interest in quantifying the health effects of meteorological conditions, such as temperature extremes, heat index, and humidity. For example, numerous studies have assessed relationships between ambient temperature and mortality [1–5] or morbidity [6–9]. Others have considered the health effects of heat index (a measure of apparent temperature that incorporates both temperature and relative humidity [10]) and mortality [11, 12], or the association between absolute humidity and influenza [13, 14].

Meteorological exposure assessments typically use point-based weather observatories located primarily at airports, such as “first-order” stations (i.e., those directly maintained by the National Weather Service), as the de facto “gold standard” measurement for meteorological exposures. Although these primary data sources undergo quality control [15], their usage for exposure estimates applied to populations across entire metropolitan areas introduces the possibility of exposure measurement error [16]. This concern is particularly germane to areas where airports are located far from the population-dense parts of a city. For example, the weather observation at an exurban airport may be unable to capture the “urban heat-island effect,” in which urban centers are substantially warmer than surrounding areas [17]. Moreover, there are large parts of the country with few first-order weather observatories, which may partly explain why epidemiologic assessments of weather-related exposures are typically focused on populations in larger metropolitan areas.

Lee et al. recognized these limitations of using station-based data for exposure assessment [16], and both they and others [18] have used spatially resolved temperature data derived from satellite imagery in their analyses as alternative exposure metrics that provide continuous data across space. Although these studies have demonstrated the potential utility of spatially resolved temperature estimates for exposure assessment, the remotely sensed datasets they used lack spatially resolved information on humidity, are limited to more recent years by the availability of satellite data, and do not appear to be readily available to others in their derived forms.

Publicly available gridded climate datasets (GCDs; sometimes referred to as “spatial climate data” or “gridded meteorological data”) address these shortcomings by estimating high-resolution, spatially resolved weather data for a number of variables across entire regions, providing an opportunity for more spatially explicit analyses of temperature, humidity, and other meteorological conditions that can cover larger populations. Although such datasets have been used in many geoscientific applications [19–21], to date, they have not been used in epidemiologic analyses. This may be due partly to the lack of validation for specific health-relevant variables that can be derived from GCD data. In particular, although the dataset authors typically describe validation assessments for the variables directly reported [22–24], there appears to be no systematic validation of user-derived values of daily absolute humidity, relative humidity, and heat index, all of which are relevant to epidemiologic studies.

Accordingly, the primary aim of this paper is to determine whether, and to what extent, GCDs accurately estimate not only ambient temperature, but also relative humidity, absolute humidity, and heat index compared to in situ weather observations. To do this, we compared daily data from two publicly available GCDs, the Parameter-elevation Relationships on Independent Slopes Model (PRISM) and Daymet version 3.0, to coincident observations from two networks of weather observatories in the conterminous United States (CONUS): the commonly used, longstanding network of first-order weather stations in the Integrated Surface Database Lite (ISD-Lite), and the newer, more highly quality-controlled US Climate Reference Network (USCRN). The secondary aim is to evaluate whether using these spatially resolved estimates provides substantively different estimates of population exposures to ambient temperature or heat index versus traditional single-point observations, and whether such differences could affect epidemiologic assessments. We achieved this by comparing population-weighted county mean values from PRISM to singular PRISM grid cells at the locations of first-order weather stations. Finally, in two populous US counties, we applied a preliminary proof-of-concept analysis to see whether estimates of the impact of temperature on health could potentially differ when using spatially resolved temperature estimates as the exposure (versus the more commonly used weather station observations). Resolving the aforementioned questions is an important first step in encouraging more spatially explicit meteorological assessments, as well as potentially reducing exposure measurement error in future epidemiologic analyses.

2. MATERIALS AND METHODS

2.1. Datasets

We obtained observed data from two networks of weather stations (ISD-Lite and USCRN) for comparison to two GCDs (PRISM and Daymet) covering the conterminous US, as described below (Table 1). All of these datasets are publicly available as described in the accompanying references.

Table 1:

Overview of the Meteorological Datasets Used in the Analysis

	First-Order Stations (ISD-Lite)	USCRN Stations	PRISM	Daymet
Spatial Coverage	274 stations in the US, located primarily at airports	137 stations in the US, located at sites minimally affected by anthropogenic land uses	Conterminous United States (CONUS) at horizontal spatial resolution of 4 km or 800 m	North America at horizontal spatial resolution of 1 km
Temporal Coverage	Hourly or sub-hourly observations over the past several decades	Sub-hourly observations since as early as 2000	Daily from 1981 to six months prior to present	Daily since 1980; updated annually
Day Definition	00:00 – 23:59 UTC	00:00 – 23:59 UTC	12:01 UTC on day i-1 - 12:00 UTC on day i	00:00 – 23:59 UTC
Meteorological Variables Reported	Temperature Dew-point T Precipitation Atm. Pressure Wind Cloud cover	Temperature Relative humidity Precipitation Solar radiation IR surface T	Tmin, Tmax, Tmean TDmean VPDmin, VPDmax Precipitation	Tmin, Tmax VPmean Precipitation Solar radiation Snow-water eq. Day length
User-Derived Variables	Heat index Relative humidity Absolute humidity	Heat index Absolute humidity	HImin, Hmax, HImean RHmin, RHmax, RHmean AHmean	Tmean HImax, HImean RHmin, RHmean AHmean

Table 1: Abbreviations: minimum, maximum, and mean temperature (T_min, T_max, and T_mean); mean vapor pressure (VP_mean); minimum and maximum vapor-pressure deficits (VPD_min and VPD_max); minimum, maximum, and mean relative humidity (RH_min, RH_max, and RH_mean); mean absolute humidity (AH_mean); and minimum, maximum, and mean heat index (HI_min, HI_max, and HI_mean).

2.1.1. PRISM

The PRISM dataset [23–25] is a GCD that provides daily estimates of minimum, maximum, and mean temperature (T_min, T_max, and T_mean); mean dew-point temperature (TD_mean); minimum and maximum vapor-pressure deficit (VPD_min and VPD_max); and precipitation for CONUS between 1 January 1981 and approximately six months prior to present. Continuous surfaces were developed by spatially interpolating meteorological observations from several US weather station networks using a regression model that applies spatial weighting to account for climatically important landscape features, as described elsewhere [23, 24]. Daily data are publicly available at no cost at a horizontal spatial resolution of four kilometers. As described in Section 2.3 and in the Supplementary Material, the variables provided by PRISM allow for user- derived calculations of minimum, maximum, and mean relative humidity (RH_min, RH_max, and RH_mean); minimum, maximum, and mean heat index (HI_min, HI_max, and HI_mean); and mean absolute humidity (AH_mean). PRISM defines a “day” as the 24 hours prior to noon UTC; for example, the PRISM “day” for 2 January refers to noon UTC on 1 January through noon UTC on 2 January.

2.1.2. Daymet

The Daymet version 3 dataset [22, 26] is another GCD that provides daily estimates for T_min and T_max, mean vapor pressure (VP_mean), precipitation, snow-water equivalent, incident shortwave radiation, and daylight duration for all of North America since 1 January 1980 (updated annually) at a horizontal spatial resolution of one kilometer. The dataset was developed by interpolating daily meteorological observations in the Global Historical Climatology Network Daily (GHCN-Daily) dataset [15] with a truncated Gaussian filter and digital elevation model, as described elsewhere [22]. Compared to PRISM, Daymet uses a different network of weather observations and accounts for fewer topographic features. In addition, Daymet assumes that the dew-point temperature (T_dew) does not vary throughout the day and is equal to the ambient minimum temperature [22]. Consequently, only VP_mean is provided by Daymet and hence only RH_mean, AH_mean, and HI_mean can be derived directly (see Section 2.3). However, HI_max and RH_min can be estimated by using the assumption that T_dew at T_max is equal to T_min, as described in more detail in Section S1 of the Supplementary Material. Daymet defines a “day” as the 24 hours preceding midnight UTC.

2.1.3. ISD-Lite (First-Order Stations)

The Integrated Surface Database Lite (ISD-Lite) is a global database of hourly weather observations from numerous sources [27]. ISD-Lite provides hourly observations of ambient temperature, dew-point temperature, precipitation, wind, cloud cover, and atmospheric pressure, measured within ten minutes prior to the hour reported. Of interest here are the first-order weather stations in CONUS, which were determined using station identifiers from the Historical Observing Metadata Repository [28]. Observations from this network are used as the primary comparison for the GCD validations in this study, since first-order weather stations are the de facto “official” observations of US weather.

2.1.4. USCRN

The US Climate Reference Network (USCRN) is a more recent weather observation network developed to establish long-term, standardized, and highly quality-controlled meteorological observations for the purpose of assessing climatic trends [29]. Measurements of temperature and precipitation began in the first observatories as early as 2000, but it was not until 2012 that all stations were collecting the full range of measurements, including soil moisture, wind, and relative humidity [30]. The stations are strategically located across 137 sites (114 in CONUS, 21 in Alaska, and two in Hawaii) that are unlikely to be affected by land-use change over the next several decades, in order to minimize influence from anthropogenic sources [29]. Every station has three separate sensors, which allows for real-time detection of instrumentation failure and highly robust measurements. We included this network of observations as an additional analysis in order to: (1) assess the performance of PRISM and Daymet in areas that are less populated and less developed in order to provide insights into the utility of GCDs for exposure assessment in rural areas; and (2) leverage the triple quality- controlled measurement methodology to serve as an additional validity check on observations.

2.2. Data Preparation

2.2.1. Selecting Observations

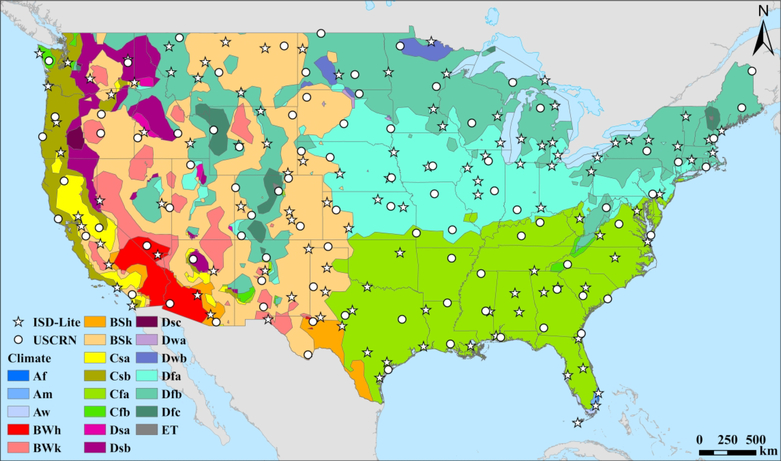
We subset data from the three principle sources (PRISM, Daymet, and first-order stations in ISD-Lite) to CONUS for the period from 1 January 1981 to 31 December 2016, which constitutes the longest period of full-year records and geographic extents shared by all three datasets at the time of analysis. First-order weather stations in CONUS that had at least 18 hours of observations per day for at least 90% of days during the study period were eligible for inclusion in the analysis; newer stations that began taking measurements later than 1981 or older stations that were decommissioned before 2016 were excluded. From the total 170 stations meeting these criteria, we further subset to get a climatically representative sample based on the Köppen-Geiger climate classification distribution of CONUS ([31]; data provided by [32, 33]), using a stratified random sampling procedure with the doBy package in R [34]. We did this to account for potential climate-specific performance differences in the PRISM and Daymet algorithms. We included only station-days with complete data (24 observations for T and T_dew) from this sample; we dropped approximately 3.5% of observations from the final sample due to incomplete data. The final, climatically representative sample size was 116 first-order weather stations (Figure 1), yielding 1,471,135 station-days of observations for validation. The full list of first-order weather stations used in the analysis can be found in Table S1 in the Supplementary Material.

Figure 1:

Map of climates and locations of weather observatories in climatically representative sample. First-order weather stations in the ISD-Lite database (represented as stars) are located primarily at airports, while stations in the US Climate Reference Network (represented as circles), are located primarily in land-conservation areas. The stations in both networks are representative of the climate zones in CONUS, based on the Köppen-Geiger classification system [31], indicated by various colors (shapefile of data provided by ORNL DAAC [32, 33]). The nomenclature for the climate zones begins with the first letter for the broad climate type (“equatorial,” “arid,” “warm temperate,” “snow,” and “polar” for A, B, C, D, and E, respectively), then denotes the intra-annual precipitation and temperature characteristics (if applicable) within those zones in the second and third letters, respectively [31]. Background mapping provided by ArcWorld and ArcWorld Supplement from Esri®.

We selected observations from the USCRN stations following a similar process to ISD-Lite, deviating only in temporal extent: we used observations between 1 January 2012 to 31 December 2016, in order to reflect the complete record of relative humidity measurements in the USCRN data [30] and to coincide with the latest date of full-year data availability for the GCDs. Since USCRN provides sub-hourly measures, we used the mean hourly values for this analysis. We excluded station-days missing any hourly observations. The final, climatically representative sample was of 89 stations in the USCRN, constituting 155,654 station-days of observations for validation (Figure 1). The full list of USCRN stations used in the analysis can be found in Table S2 in the Supplementary Material.

2.2.2. Aligning Observations by “Day”

We collapsed the hourly observations into two separate “days” of daily values for comparisons with PRISM and Daymet, which define “days” based on different hours. We ascribed the noon and midnight UTC observations to the 24 hours preceding them, rather than having them mark the beginning of the next day for PRISM and Daymet, respectively, since hourly observations at first-order stations are taken during the ten minutes leading up to the hour reported. Therefore, the PRISM value for day i was compared to hourly observations from 13:00 UTC on day i-1 to 12:00 UTC on day i. The Daymet “day” was calculated using observations reported at hours from 01:00 UTC on day i to 00:00 UTC on day i+1.

2.2.3. Calculating Population-Weighted County Average Values

As a preliminary assessment of the capacity for GCDs to reduce exposure measurement error, single-pixel PRISM values at each of the first-order weather stations in the sample were compared to spatially resolved, population-weighted mean values for the concomitant county. The purpose of aggregating the spatial data in this way is to reflect the need for a single exposure metric to represent the population unit of analysis (here, a singular county-level mean estimate). We calculated the spatially resolved county mean by first extracting the PRISM pixels at the population centroids for each census tract (based on the 2000 Census [35]) within a county for T_max and HI_max. We then calculated a weighted average of these variables based on the proportion of the county population residing in that tract. For missing data on T_max or HI_max, the weighting was based on the proportion of the county population with non-missing data; additionally, county-days with less than 80% of census tracts reporting non-missing weather estimates were excluded (56 out of 1,525,284 county-days [0.004%] were dropped due to missing HI_max values; we assumed a negligible effect of missing data on the weighting procedure).

2.3. Calculating Health-Relevant Variables

Health-relevant meteorological variables of interest to this validation study are ambient temperature (T), absolute humidity (AH), relative humidity (RH), and heat index (HI). See Davis et al. for an overview of humidity-dependent metrics in epidemiologic contexts [36]. While all the datasets in our analysis report T, the remaining variables had to be derived (with the exception of RH, which is reported directly by USCRN). We calculated daily minimum, maximum, and mean values for each of these variables using hourly values for respective PRISM and Daymet “days,” as described previously. For heat index, we used the weathermetrics R package [10], which follows the calculations used by the National Weather Service. A summary table with equations used to calculate derived variables for each dataset is found in Table S3 of the Supplementary Material, and additional background information on the derivations of these meteorological variables can be found in Sections S1 and S2.

2.4. Statistical Analyses

In a first analysis, we linearly regressed daily minimum, maximum, and mean meteorological observations from the ISD-Lite and USCRN observations against the coincident, single-pixel PRISM and Daymet grid cell estimates. The goal of this analysis is to assess the direct, linear concordance between PRISM or Daymet estimates and meteorological observations at the same point in space. For each comparison, we calculated goodness of fit (r²), slope and intercept of the lines of best fit, and mean absolute errors (MAE). GCDs with higher r² values, lower MAEs, and lines of best fit with slopes (m) closer to one and y-intercepts closer to zero were considered better estimates of the observed data. Given the interest in exposure assessment in the context of heat-related health effects, we fit additional models to a subset of days in which the maximum observed temperature was greater than or equal to 70°F (21.1°C; hereafter “warm days”). We performed regression analyses separately for the USCRN and ISD-Lite observation networks.

In a second set of analyses, we compared PRISM estimates of county-level population-weighted meteorological variables to PRISM estimates from the singular pixel value at the location of the relevant first-order weather station. The goal of this analysis is to assess the difference between population-weighted and point estimates of county-level exposures to meteorological variables. If there is a material, statistically significant difference between meteorological variables reported at the location of the weather station versus meteorology experienced by the population across the county, then this may be indicative of potential exposure measurement error when using data from the weather station as the exposure metric. We hypothesized that counties with more spatially heterogeneous weather would benefit more greatly from the use of spatially resolved meteorological data. Specifically, we conducted two-tailed Welch’s t-tests for differences of means between the population-weighted county mean PRISM value and the singular PRISM pixel value at the location of the coincident first-order weather station. Comparison groups in t-tests had nearly identical sample sizes and generally had differences in variance of less than 5%, with the exception of a few individual stations. Although the distributions were often skewed, the very large sample sizes in our analyses allowed for robustness in t-test estimates [37]. We used a p-value of 0.05 as the threshold for statistical significance.

Finally, to illustrate how the use of temperature observations from first-order weather stations versus spatially explicit temperature metrics could potentially result in different estimates of the impact of temperature on health, we modeled the association between daily T_mean and mortality in two counties: Los Angeles County, California (including the city of Los Angeles) and Marion County, Indiana (including the city of Indianapolis). We hypothesized that using spatially resolved estimates would result in differences in exposure-response functions (ERFs) compared to the weather station data in some places more than others, driven primarily by the spatial heterogeneity of county-level temperatures. We selected Los Angeles and Marion Counties to demonstrate this dichotomy, since the former shows strikingly large differences in temperatures across the county compared to the weather station, while the latter is more spatially homogeneous. To calculate the ERFs, we used distributed lag non-linear models [38] with an overdispersed Poisson distribution to estimate the 21-day cumulative association between daily T_mean and daily counts of all-ages mortality (excluding external causes) obtained from the National Center for Health Statistics using: (1) daily values of T_mean taken at first-order weather stations within each county; and (2) daily county-level population-weighted estimates of T_mean constructed from PRISM, with one spatially explicit mean value per county per day. We controlled each model for seasonal and long-term trends (natural cubic spline with eight degrees of freedom per year), day of week, and federal holidays, and used the same modeling choices with respect to the exposure-response form and lag-response form as in [39].

We used R software [40] for all of the statistical analyses and ArcGIS® software by Esri for geophysical visualization and mapping.

3. RESULTS

3.1. GCD Validation

Univariate regression between GCD and first-order ISD-Lite data showed very strong agreement (all r² > 0.97 and 0.97 < m ≤ 1.00) between the modeled and observed values of T_max, T_min, and T_mean for all days for both PRISM and Daymet (Table 2). When restricted to warm days (observed T_max ≥ 70˚F), both PRISM and Daymet provide estimates that strongly agree with observed conditions for all metrics of ambient temperature (all r² > 0.94 and 0.96 ≤ m < 1.00), with the exception of T_max for Daymet, which had an r² of 0.90. Mean absolute errors were smaller for PRISM than Daymet: MAEs for ambient temperatures in PRISM were all < 1.6˚F, while for Daymet, they went as high as 2.71˚F (T_min on all days).

Table 2:

Univariate Linear Regression of First-Order Weather Station Observations on GCD Estimates

Variable	Days	PRISM				Daymet
		r2	Slope	Y-Int	MAE	r2	Slope	Y-Int	MAE
Tmax	All	0.99	0.98	1.52	1.20	0.98	0.98	1.62	2.20
	Warm	0.96	0.97	2.46	1.03	0.90	0.98	1.90	1.93
Tmim	All	0.99	0.98	0.29	1.58	0.98	0.98	−1.38	2.71
	Warm	0.96	0.96	1.42	1.56	0.94	0.97	−0.26	2.68
Tmean	All	0.99	1.00	−0.05	1.49	0.99	0.98	0.65	1.66
	Warm	0.95	0.98	0.81	1.41	0.95	0.98	1.22	1.57
RHmax	All	0.94	1.02	−2.64	2.59	-	-	-	-
	Warm	0.96	1.02	−2.62	2.47	-	-	-	-
RHmin	All	0.96	0.99	2.11	2.88	0.52	0.50	23.97	10.68
	Warm	0.97	0.98	1.83	2.36	0.64	0.54	22.99	9.92
RHmean	All	0.91	0.95	−0.49	4.96	0.47	0.73	7.02	14.12
	Warm	0.95	0.93	0.30	4.68	0.58	0.79	1.88	13.34
AHmean	All	>0.99	0.97	−0.04	0.32	0.87	0.95	−0.12	1.36
	Warm	>0.99	0.97	−0.02	0.44	0.79	0.98	−0.55	1.87
HImax	All	-	-	-	-	-	-	-	-
	Warm	0.93	0.96	3.57	1.56	0.85	1.13	−9.81	3.20
HImin	All	-	-	-	-	-	-	-	-
	Warm	0.96	0.96	1.48	1.65	-	-	-	-
HImean	All	-	-	-	-	-	-	-	-
	Warm	0.96	1.01	−1.24	1.50	0.94	1.02	0.78	2.74

Table 2: Results of univariate linear regression of observed meteorological conditions at first-order weather stations in the ISD-Lite sample on modeled data from PRISM and Daymet. “Warm” refers to days with observed maximum temperature ≥ 70°F. “MAE” is the mean absolute error and measures the average difference between modeled and observed data; units are the same as for the variable measured. Higher r², lower MAE, slopes closer to one, and y-intercepts closer to zero indicate greater agreement between modeled and observed meteorological conditions.

For relative humidity, PRISM estimates were substantially closer to observed values than those estimated by Daymet. For all days, RH_min, RH_max, and RH_mean estimates from PRISM all had values of r² > 0.91, slopes of 0.95 < m ≤ 1.02, and MAE < 5 percentage points; for warm days, modeled values showed even stronger agreement with observations (r² > 0.95, 0.92 < m ≤ 1.02). PRISM estimates had stronger agreement with minimum and maximum RH values than for RH_mean, both for all days and for warm days (MAEs for RH_mean are approximately two percentage points greater than for RH_min or RH_max). In contrast, Daymet did not provide reliable estimates of observed relative humidity, as calculated using Daymet’s assumption of T_dew equaling T_min throughout the day: all r² values were less than 0.64 and slopes were between 0.49 and 0.79 for RH_min and RH_mean.

For absolute humidity, PRISM estimates were extremely highly correlated with observations for AH_mean, both for all days (r² > 0.99, m = 0.97, and MAE = 0.32 g/m³) and warm days (r² > 0.99, m = 0.97, and MAE = 0.44 g/m³). Daymet estimates showed less agreement for both subsets of days (both r² < 0.87 and MAE > 1.35 g/m³).

Finally, heat index measures showed strong agreement in the PRISM data for HI_max (r² = 0.93, m = 0.96, and MAE = 1.56˚F), HI_min (r² = 0.96, m = 0.96, MAE=1.65°F), and HI_mean (r² = 0.96, m = 1.01, and MAE = 1.50°F). Daymet similarly offered robust estimates of mean heat index, albeit with greater MAE (r² = 0.95, m = 1.02, and MAE = 2.74°F), but it showed bias in its estimates of maximum heat index (r² = 0.85, m = 1.13, and MAE = 3.20°F).

Comparison of PRISM and Daymet to the USCRN data showed similar performances as compared to the ISD-Lite data (Table 3): PRISM provided robust estimates of ambient temperature (T_max, T_min, and T_mean for all days and for warm days), AH_mean, and heat index (HI_max, HI_min, and HI_mean for warm days). PRISM estimates of RH showed somewhat less agreement with observed values in the USCRN data versus the ISD-Lite data. For example, for warm days, the slope of the best-fit line for RH_mean was 0.89 (compared to 0.93 for ISD-Lite) and, for all days, the r² for RH_mean was 0.89 (compared to 0.92 for ISD-Lite). Daymet showed similar performances when assessed using the USCRN data as it did with the first-order stations.

Table 3:

Univariate Linear Regression of USCRN Station Observations on GCD Estimates

Variable	Days	PRISM				Daymet
		r2	Slope	Y-Int	MAE	r2	Slope	Y-Int	MAE
Tmax	All	0.99	0.99	2.12	1.87	0.97	0.99	1.70	2.56
	Warm	0.96	0.98	3.10	1.72	0.88	0.98	2.13	2.21
Tmim	All	0.98	0.98	0.87	2.05	0.97	0.98	−0.90	2.74
	Warm	0.93	0.94	3.56	1.98	0.91	0.94	2.33	2.54
Tmean	All	0.99	1.00	0.50	1.75	0.98	0.99	0.93	1.94
	Warm	0.94	0.98	1.76	1.68	0.94	0.98	2.13	1.76
RHmax	All	0.85	0.94	6.31	4.98	-	-	-	-
	Warm	0.89	0.96	5.39	5.03	-	-	-	-
RHmin	All	0.91	0.94	3.23	4.43	0.51	0.42	26.72	12.25
	Warm	0.94	0.93	3.06	3.52	0.63	0.44	26.33	11.65
RHmean	All	0.89	0.93	1.27	5.83	0.48	0.65	11.71	14.76
	Warm	0.93	0.89	2.15	5.56	0.65	0.74	4.90	13.50
AHmean	All	0.99	0.97	0.08	0.35	0.87	0.93	0.21	1.24
	Warm	0.98	0.96	0.26	0.49	0.82	0.93	0.31	1.64
HImax	All	-	-	-	-	-	-	-	-
	Warm	0.93	1.02	−0.24	2.06	0.84	1.18	−12.76	3.60
HImin	All	-	-	-	-	-	-	-	-
	Warm	0.94	0.95	2.91	2.03	-	-	-	-
HImean	All	-	-	-	-	-	-	-	-
	Warm	0.95	1.03	−1.62	1.69	0.94	1.03	1.64	3.61

Table 3: Results of univariate linear regression of observed meteorological conditions at USCRN weather stations on modeled data from PRISM and Daymet. “Warm” refers to days on which the observed maximum temperature was at least 70°F. “MAE” is the mean absolute error and measures the average difference between modeled and observed data; units are the same as for the variable measured. Higher r², lower MAE, slopes closer to one, and y-intercepts closer to zero indicate greater agreement between modeled and observed meteorological conditions.

3.2. Spatially Resolved County Estimates

To assess the potential for spatially resolved weather data to improve estimates of county-level meteorological exposures over singular point-based observations, we compared the population-weighted mean PRISM estimate over the entire county to the single-pixel PRISM value at the location of the weather station. Differences between these values would indicate that the weather experienced by the population, on average, across the entire county is distinct from the weather experienced at the weather station and, thus, that station-based estimates may introduce exposure measurement error. In the aggregate, across the full sample of locations from 1981–2016, there was no statistically significant difference between the mean values of T_max taken at the location of the weather station and the spatially resolved county average, for either all temperatures (mean difference of −0.0085°F; 95% confidence interval [CI]: −0.055°F, 0.038°F) or for warm days (mean difference of −0.0058°F; 95% CI: −0.032°F, 0.020°F). There was a statistically significant, albeit substantively negligible, difference in HI_max for warm days (mean difference of −0.058°F; 95% CI: −0.089°F, −0.028°F).

However, this nationwide sampling masks large heterogeneity between individual counties; the difference between county-average and weather station temperatures is much larger in some locations than others. Considering each of the 116 counties in the analysis individually, 32 (27.6%) showed statistically significant differences in T_max for all days, 63 (54.3%) were statistically significantly different for T_max on warm days, and 55 (47.4%) were statistically significantly different for HI_max on warm days. Moreover, 10 (8.6%) had an absolute difference of means of T_max ≥ 1°F for all days, 15 (12.9%) had an absolute difference of means of T_max ≥ 1°F for warm days, and 15 (12.9%) had an absolute difference of means of HI_max > 1°F for warm days. Four stations in particular showed especially large differences for T_max on warm days: Los Angeles County, California (an average of 6.0°F cooler [95% CI: 5.8°F, 6.2°F] at the station versus the county-wide average); Clatsop County, Oregon (2.1°F cooler [95% CI: 1.8°F, 2.5°F]); Navajo County, Arizona (4.5˚F warmer [95% CI: 4.2°F, 4.7°F]); and White Pine County, Nevada (3.1°F warmer [95% CI: 2.9°F, 3.4°F]).

The average results above mask variability of temperature differentials on particular days. A strong majority of counties (71.6%) had at least 5% of warm days over the study period in which the T_max at the location of the weather station differed by at least 1°F from the county average; even more stations met this criterion for HI_max (81.9%). Similarly, 28 stations (24.1%) had at least 5% of warm days with differences between station and county T_max > 2°F, and eight stations (6.9%) had at least 5% of warm days with differences of T_max > 3°F. These proportions are even greater when considering HI_max on warm days (81.9%, 31.9%, and 10.3%, for HI_max differences greater than at least 1°F, 2°F, and 3°F, respectively).

3.3. Exposure-Response Functions

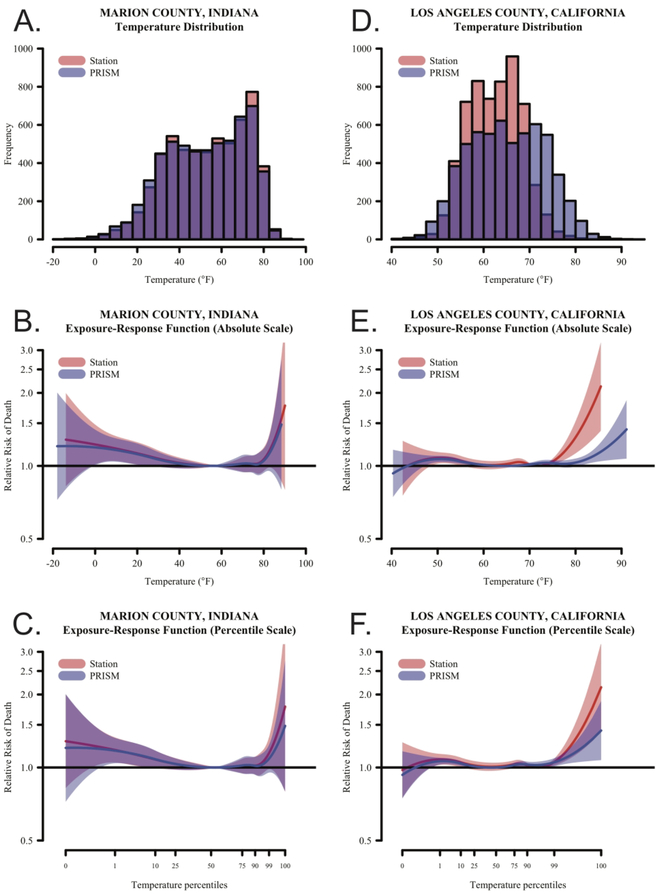
We selected two case-study counties as preliminary, illustrative examples of whether differences between observations at a given weather station and population-weighted county average values could potentially affect the estimated association between mean daily temperature and rates of mortality (Figure 2). In Marion County, Indiana, the distribution of daily population-weighted county average T_mean estimated from PRISM was similar to the distribution of daily observations from the local weather station. Moreover, the shape and magnitude of the association between mean daily temperature and relative rate of death were similar for both weather station observations and the spatially explicit estimates constructed from PRISM. By contrast, in Los Angeles County, California, the distribution of daily T_mean estimated from PRISM spanned a larger range of values than for weather station observed T_mean. The heterogeneity of temperatures on a single day across Los Angeles County is shown in Figure 3. Moreover, in Los Angeles County, the estimated association between daily mean temperature and rates of mortality differed substantially when using county average daily T_mean versus observed station data. The observed differences in the exposure-response functions were reduced, but not eliminated, when considering temperature percentiles rather than absolute values.

Figure 2:

Comparison of epidemiologic analyses of the association between mean daily temperature and mortality rates using either observations from the nearest first-order weather station or population-weighted county means from PRISM. The distribution of daily mean temperature (A. and D.), 21-day cumulative exposure-response function between daily mean temperature and mortality on an absolute scale (B. and E.), and 21-day cumulative exposure-response function between daily mean temperature and mortality on a percentile-based scale (C. and F.) for Marion County, Indiana (left panels) and Los Angeles County, California (right panels), 1988–2003. Results based on observed station data are shown in red, results based on PRISM estimates are shown in blue, and the overlap between the two is shown in purple.

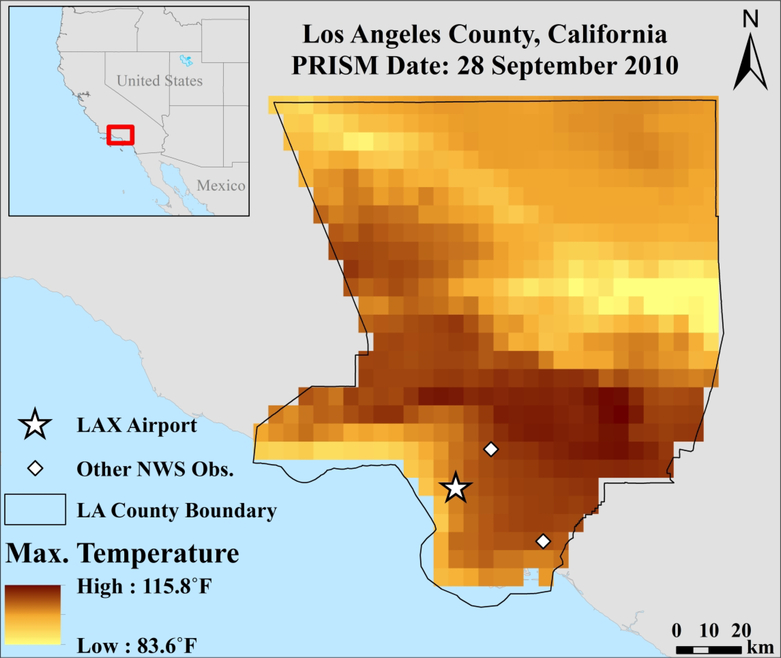
Figure 3:

Spatial heterogeneity of ambient temperatures across Los Angeles County, California on an extreme-heat day. This geographic schematic shows the range and distribution of ambient maximum temperatures on the PRISM date of 28 September 2010 across Los Angeles County, California. The star symbol indicates the location of Los Angeles International Airport (LAX), which was included in the climatically representative sample in this paper; the diamond symbols indicate other first-order NWS stations. None of these stations are located in the hottest part of LA County on this day, and they cannot capture the large temperature differential experienced across the area (ranging from approximately 83.6˚F to 115.8˚F on this day). Note that adjacent islands, including those that are part of LA County, are not displayed. Background mapping provided by ArcWorld and ArcWorld Supplement from Esri®.

4. DISCUSSION

This validation of PRISM and Daymet, two GCDs publicly available at no cost, suggests that PRISM provides reliable estimates of health-relevant meteorological exposures when compared to station observations. Specifically, we found that PRISM provides robust estimates of ambient temperature (T_min, T_max, and T_mean), mean absolute humidity (AH_mean), relative humidity (RH_min, RH_max, and RH_mean), and heat index (HI_min, HI_max, and HI_mean) when compared to co-located first-order weather stations. Results were similar when PRISM estimates were compared to observations in the USCRN stations, suggesting that PRISM estimates are reliable, even in areas that are less populated and away from urban and suburban development.

Although Daymet offers similarly robust estimates of ambient temperature for all days, its values for T_max on warm days are less satisfactory. Moreover, nearly all of the moisture- dependent values for Daymet are unsatisfactory (low r² values and/or slopes substantially different from one), with the exception of AH_mean for all days and HI_mean for warm days. The lower performance for humidity variables is likely due to the assumption in Daymet that T_dew is equal to T_min throughout the day [22], an assumption that may be untenable in the arid and semiarid southwestern US [41]. Our analysis suggests that this assumption is problematic for the calculation of RH more broadly across CONUS and that, consequently, RH derivations from Daymet are not consistently reliable. Despite this limitation, Daymet’s daily HI_mean, which relies on RH, performed well against observations, despite the relatively weak representation of RH_mean. This may reflect a canceling of errors between T_mean and RH_mean that has the net effect of a more accurate HI_mean estimate than would be expected. Fischer and Knutti [42] observed a potentially similar phenomenon in their analysis of general circulation models, in which the derived simplified wet-bulb globe temperature (a composite variable of temperature and humidity) showed less uncertainty than would be expected from each variable individually.

Future epidemiologic assessments of meteorological exposures could potentially benefit from using spatially explicit weather data, particularly in places with few weather observations or in cities where the weather reported at the observatory is not representative of the weather experienced by the population. Our analysis comparing point-based weather estimates to population-weighted county mean values throughout CONUS suggests that the substantive difference between station observations and spatially resolved estimates varies considerably. For example, in Los Angeles County, California, temperatures reported at Los Angeles International Airport (LAX) are generally much cooler than downtown Los Angeles. As an example, according to PRISM, during a period of extreme heat on 28 September 2010, maximum temperatures across Los Angeles County ranged from approximately 84°F to 116°F (Figure 3). Observations at a single weather station cannot represent this spatial differentiation and hence could lead to substantial exposure measurement error. Data from GCDs, such as PRISM, offer more nuanced exposure information that could improve future epidemiologic analyses. In particular, we posit that applying population-weighted, spatially resolved meteorological data may more accurately represent the outdoor weather conditions to which populations are actually exposed versus point-based station data. We further suggest that the use of spatially resolved exposure information may lead to different conclusions about the magnitude of the association between temperature and health outcomes in some locations within the US. For example, we found that the association between very high temperatures and mortality in Los Angeles County was larger when using T_mean observed at a weather station than when using a population-weighted average constructed for the county from the PRISM data. Similarly, Lee et al. found different relative risks of mortality for extreme temperatures in the southeastern US when using weather-station observations compared to a derived temperature surface using satellite data [16]. However, in Marion County, IN, the association between mean temperature and daily mortality rate was similar regardless of the choice of exposure dataset. This concurs with the findings of Guo et al., which showed that a spatiotemporal model of temperature-mortality relationships performed similarly to a model using non-spatially resolved temperature metrics in Brisbane, Queensland, Australia [43]. Additional work is needed to expand on these illustrative findings.

An important caveat to the potential benefits of spatially resolved weather data, however, is that the performance of the model cannot be directly assessed in places without station-based observations [44]. The developers of PRISM addressed this limitation by using “leave-one-out” cross-validation, which provides an assessment of model performance at locations without observations [23, 24]. This validation method demonstrated strong performance, with monthly MAE values ranging from 0.36°C to 0.77°C for T_max and from 0.57°C to 1.35°C for T_min, depending on the month and region [23]. Although these and other errors in PRISM estimates are not necessarily spatially homogeneous or randomly distributed [23], we posit that the exposure measurement error from PRISM estimates is likely to be less than the error presented by using observations from a singular weather station observatory to represent the average exposure of an entire geographically heterogeneous county. Therefore, the use of spatial weather data seems to offer an opportunity for improved assessments of population-average exposures versus observations from a sparse network of meteorological monitors.

The determination of which GCD to use for epidemiologic analyses, however, is dependent not only on the meteorological variables of interest, but also on the spatial scale required. Daymet may be preferable to the free daily PRISM product for studies needing higher spatial resolution and only the daily T or HI_mean. However, PRISM may be preferable in studies requiring optimal estimates of RH or AH, even if at a lower spatial resolution of 4 km. Finally, for HI_max, PRISM provides reliable estimates, but Daymet does not. It should be noted that an 800-meter product is also available from PRISM, but it is not freely available to the public and hence was not evaluated here. Nonetheless, given that many population-scale health data are available only at aggregated spatial extents (e.g., counties or zip codes), the four-kilometer PRISM data may be appropriate for many epidemiologic assessments interested in meteorological exposures.

Additional considerations should be noted for epidemiologists seeking to use GCD information for spatially explicit exposure assessments. Perhaps most important is recognizing how the GCDs define a “day.” As described in the Methods, a PRISM “day” ends at noon UTC, meaning that the high temperature reported for anywhere in CONUS probably occurred on the previous local day. For analyses that average several days of weather data, this distinction is largely inconsequential; however, when data for a specific day are important, analysts should be careful to correctly ascribe the PRISM daily values to the local time periods of interest.

More research is needed to determine the extent to which spatially explicit meteorological data can reduce exposure measurement error in epidemiologic studies, and to what extent usage of GCD data substantively changes previously described exposure-response functions relating meteorological variables to health outcomes overall and throughout various locations in the US. While our preliminary analysis here suggests that using spatial data instead of discrete weather station observations can make more of a difference in some places than others, additional research is needed to determine the impact of using GCD versus point estimates of temperature or other meteorological variables on health effects analyses across the US.

In addition, GCDs offer the possibility to expand the spatial extent of populations included in epidemiologic analyses to include individuals in places farther from first-order weather stations. We found consistency between the GCDs and observations made at USCRN stations, which have been intentionally located in places less affected by anthropogenic influences. This suggests that both PRISM and Daymet may perform approximately as well in less populated and rural areas as they do at the first-order stations, which creates the potential for expanding epidemiologic assessments of weather-related exposures to under-studied populations.

5. CONCLUSIONS

Gridded climate datasets offer the possibility of more spatially explicit meteorological assessments by providing continuous weather data across space that is not possible with a finite number of point-based, first-order weather stations. Two freely and publicly available GCDs, PRISM and Daymet, provide reliable daily estimates of ambient temperature and mean heat index, but PRISM outperforms Daymet for relative humidity and absolute humidity and, additionally, is capable of providing robust estimates of minimum and maximum heat index. Although more research is needed, there is evidence that using these spatially resolved meteorological data as exposures could potentially reduce exposure measurement error in epidemiologic studies of temperature-related morbidity and mortality, depending on the location of interest. Epidemiologists seeking to use GCDs as their exposure measurements must balance tradeoffs between accuracy of various meteorological variables versus available spatial resolution.