Population genomics perspectives on convergent adaptation

Abstract

Convergent adaptation is the independent evolution of similar traits conferring a fitness advantage in two or more lineages. Cases of convergent adaptation inform our ideas about the ecological and molecular basis of adaptation. In judging the degree to which putative cases of convergent adaptation provide an independent replication of the process of adaptation, it is necessary to establish the degree to which the evolutionary change is unexpected under null models and to show that selection has repeatedly, independently driven these changes. Here, we discuss the issues that arise from these questions particularly for closely related populations, where gene flow and standing variation add additional layers of complexity. We outline a conceptual framework to guide intuition as to the extent to which evolutionary change represents the independent gain of information owing to selection and show that this is a measure of how surprised we should be by convergence. Additionally, we summarize the ways population and quantitative genetics and genomics may help us address questions related to convergent adaptation, as well as open new questions and avenues of research.

This article is part of the theme issue ‘Convergent evolution in the genomics era: new insights and directions’.

1. Introduction

Convergence is the independent evolution of similar features in two or more lineages [1]. Examples of convergence have played a fundamental role in our understanding of adaptive evolution (see [1], for review). Classically, convergent evolution has been used as one line of evidence for the adaptive value of a trait. When convergence is the result of natural selection producing the same solution in response to repeatedly encountered biotic and abiotic pressures, we treat these as natural replicates of a similar process to understand the ecological and phenotypic bases of convergence [2] and the molecular basis of evolution [3–6].

The broad definition of convergence permits us to think of convergence occurring at multiple levels. At the broadest scale, convergence in function may occur in species facing similar ecological challenges, consistent with view that there are sometimes many phenotypic ways to achieve a similar function [7]. For example, carnivorous plants have evolved similar strategies to adapt to their low-nitrogen environments but have done so via many distinct morphological and physiological mechanisms across five orders of flowering plants [8]. Convergence may also occur on the level of a specific phenotype. Carnivorous pitcher plants have striking convergence for trap morphology [9]. When convergent phenotypes arise in highly diverged species, it has often been presumed that these changes are owing to divergent genetic mechanisms (see [5], for review). However, perhaps surprisingly, there is increasing evidence that some phenotypes often converge because of selection on similar molecular mechanisms, with selection occurring at the same gene or even the same mutational change [3,5,10]. Again within carnivorous plants, Fukushima [11] found convergent amino acid substitutions in the evolution of digestive enzymes across four species. Despite these distinctions, all levels can be encapsulated in the term convergence. Additionally, following Arendt & Reznick [12], the single term can be used to describe both parallelism and convergence, regardless of the phylogenetic scale, ancestral state, or whether the underlying genetic mechanisms are the same or different. In this opinion piece, we discuss how adaptive convergence at the level of phenotypes, genes and allele frequency change can be studied with population genomic data. In establishing a case of convergent adaptation, two main conditions must be satisfied. First, the character must be adaptive. That is, it enhances the fitness of the organisms that bear it, relative to the ancestral state [13], with many definitions additionally requiring adaptations to be the product of natural selection for their current role [14,15]. Second, the adaptive changes in the different populations must be independent from each other. Below, we expand upon these conditions and show how they might be quantified through measures of the independent work done by natural selection in different populations. Throughout this article, we focus on how population-level genomic data both forces us to grapple with the issues that arise in identifying convergent adaptation among closely related taxa and provides novel ways to approach these and related questions.

(a). Identifying adaptations

Many different lines of evidence from developmental biology to field studies must often be brought together to demonstrate that a character is an adaptation. Often, one of the first steps in assessing whether some set of convergent characters are adaptations is to establish that the changes observed are unexpected by chance (i.e. under simple null evolution models). To address this problem for convergence at macro-evolutionary scales, phylogenetic null models and methods have been developed both for discrete and continuous traits [16–21], as well as for testing the association of a character with some specific ecological or environmental variable [2,22]. Convergence changes that are not because of the vagaries of divergence or genetic drift are good candidates for adaptations. However, even if the convergence is unexpected, this does not necessarily mean that it is adaptive. For example, it could be owing to developmental constraint or releases from constraint in similar ecological environments. Therefore, it is important to provide evidence that the changes are associated with increased fitness in the relevant environments. One way of doing this is to provide evidence that directional selection repeatedly drove the convergent change. The field of population genetics has a long history of discerning phenotypic and allele frequency shifts owing to selection from those due to neutral processes. In this article, we review some of the ways these approaches can be used and extended to studying cases of convergence.

(b). Establishing independence

Showing that changes observed were truly independent is necessary to gain insight about adaptation from studies of convergence; otherwise, they may just represent a single replicate of the adaptive process. Establishing that changes were truly independent is difficult. Even with a well-resolved phylogeny, with no gene flow and nodes with sufficient temporal separation such that there is no incomplete lineage sorting (ILS), secondary loss must be distinguished between convergent evolution to show that a trait is not shared from a common ancestor [23]. Establishing independence for more closely related taxa can be even more challenging. Closely related populations may be more likely to share independently derived states that were absent or rare in their ancestor. This may occur not only through independent mutations recurrently becoming a substitution in different parts of the phylogeny, but from shared variation present in their ancestor and introgression. These latter modes are expected to be more prevalent between closely related taxa because of their higher likelihood of interbreeding and retention of ancestral polymorphism.

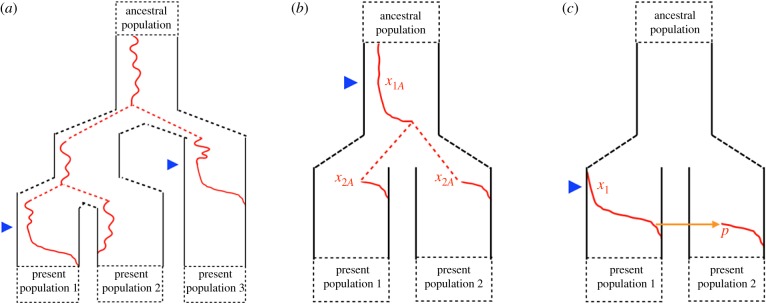
The sharing of traits or alleles incongruent with the population or species tree owing to ancestral variation (i.e. ILS shown in figure 1a) has been termed hemiplasy (to contrast it with homoplasy [23, 24]). This term has also been more generally applied to alleles shared by gene flow and with some authors seeing it as an alternative explanation to convergence [25–27]. While these approaches to assess discordance between gene trees and species trees that lead to spurious inference of convergence are important, we argue that the sharing of an allele owing to ILS or introgression does not invalidate the case for convergent adaptation. Rather, these questions are focused on identifying the level of independence. When convergence at the level of the same molecular substitution between distant species is observed, we can usually assume that this was owing to multiple, independent mutations (i.e. convergent mutations). However, the key question is whether selection has independently increased the allele to fixation multiple times (i.e. there has been convergent substitutions). Taxa sharing the same substitution owing to ILS or gene flow means there has not been independence at the level of the mutational change; however, the allele frequency change at the locus can still be independent, that is convergent, across populations. For example, following populations 1 and 3 in figure 1a, even if an allele was shared owing to ILS, selection may have repeatedly driven up the allele in each population separately.

Figure 1.

Allele frequency trajectories (red) at a single locus for two or more populations. (a) The allele was standing in the ancestor of three populations where it was fixed in populations 1 and 3 but lost in population 2. This case of incomplete lineage sorting (ILS) may falsely resemble independent mutations in populations 1 and 3, but may still be convergent adaptation if selection for the allele occurred twice independently (e.g. onsets of selection marked by blue triangles). (b) The beneficial allele was standing in the ancestral population of our present-day populations. Selection started when the ancestral allele frequency was x_1A and increased in frequency such that it was at x_2A when the populations split. Then, it continued to increase in both daughter populations to fixation. (c) The beneficial allele arose in a single present-day population and spread via introgression into the other population. The allele was at frequency x₁ at the onset of selection and migrated into the recipient population at frequency p where it also increased in frequency to fixation.

In highlighting levels of independence, it is not our intention to add more vocabulary to a perhaps already complex area. Instead, we aim to make clear the questions we seek to address when studying convergence at various levels. We, in particular, are interested in dissecting these levels of independence in cases of convergence at the same gene [28], to gain insights about adaptation into how a particular variant or haplotype offers a selective benefit. For example, seeing different mutations is informative about the mutational target for adaptation. Yet, the repeated use of standing variation, especially if those alleles are very rare, still informs us about the mutational target size. An example of both instances exist in marine populations of threespine stickleback that have repeatedly, independently have adapted to freshwater environments via changes at the EDA and PITX1 genes. The fact that many independent mutations at PITX1 underlie adaptation [29,30] suggests that this state is relatively accessible to the population by mutation or that other possible mutations may be too constrained by pleiotropy. Conversely, the EDA haplotype, which had been standing and reused many times by adaptation in freshwater sticklebacks [31], is suggestive that populations cannot access a similar, relatively low pleiotropy state more rapidly by mutation. The frequency of these different modes of convergence speaks to the extent to which populations are mutation-limited and to the role of standing variation and gene flow in adaptation [32]. Thus, regardless of the precise terminology we use, it is important to keep clear statements about the level of independence and the role selection has played in these changes. In this article, we introduce a conceptual framework to quantify the degree to which allele frequency shifts have been independent. We then review current approaches in population and quantitative genetics and genomics and how those can be extended to include more explicit tests for independence.

2. Quantifying the independence of convergent adaptation, the accumulation of information, or when to be surprised

One conceptual way forward in quantifying convergent adaptation may be to assess the degree to which selection has independently driven phenotypic and allele frequency change. Quantifying the work done by selection among taxa can help to guide intuition as to when to be impressed by convergence. One reason why adaptive convergence among lineages that are phylogenetically distant is surprising is that these are clear examples of selection independently, repeatedly reaching similar states that would be unlikely under chance or drift alone. One measure of this is the extent to which selective deaths (or births) underlying an adaptation in two or more populations are independent. For example, if light coloured pelts are an adaptation to artic environments, we have high confidence in calling the light coloured pelts of arctic foxes and hares convergent adaptations because the individuals who died owing to predation pressure, that drove the adaptation via allele frequency change, were clearly different sets of individuals (being foxes and hares, respectively).

More formally, we can calculate the number of selective deaths needed to generate a given allele frequency change. In a population of size N, the selective deaths imposed under a deterministic, directional selection model where the fittest homozygote has selection coefficient s, move an additive allele from frequency x₁ to x₂ in t₁ to t₂ generations is N L where L is

$$\begin{array}{rl}L& ={\int }_{t_1}^{t_2}s(1-x_t)\hspace{0.17em}\mathrm{d}t=2{\int }_{x_1}^{x_2}\frac{1}{x}\hspace{0.17em}\mathrm{d}x\\ & =2\log \left(\frac{x_2}{x_1}\right),\end{array}$$ 2.1

as originally derived by Haldane [33] in his discussion of the substitution load. (We return to the issues with Haldane’s load argument below.) We will focus on fixed alleles such that

$$L=2\log \left(\frac{1}{x_1}\right)=-2\log (x_1).$$ 2.2

This measure of the work done in fixing an allele owing to selection does not depend on the strength of selection because it takes a longer time to fix a more weakly selected allele than a strongly selected allele so the same total number of selective deaths are incurred. Additionally, most of the work done by selection to increase fitness occurs when the allele is very rare in the population. When the allele becomes common in the population, the majority of individuals carry the allele so fewer individual deaths are owing to differences in the genotype at this locus. Under this measure of work done by selection, we should be much more impressed by selection that repeatedly moves an allele from 10⁻⁴ to 50% than 50% to 100%, despite being comparable frequency changes and taking roughly the same time under an additive model.

We can extend this idea to obtain a metric of the proportion of the work done by selection that is shared between populations that both have experienced allele frequency change at the same locus. Here, we apply this to two cases shown in figures 1b,c. We first study the case that a selected allele has increased in frequency in the ancestral population from x_1A to x_2A, and following a population split increased from x_2A to fixation in both of the daughter populations (figure 1b). Here, the work done by selection in the ancestral population (L_A, i.e. that shared between our populations), the work independently done in the two daughter populations (L_D), and their ratio can be written as

$$L_{\mathrm{A}}=2\log \left(\frac{x_{2A}}{x_{1A}}\right),$$ 2.3

$$L_{D1}=2\log \left(\frac{1}{x_{2A}}\right)=-2\hspace{0.17em}\log (x_{2A})$$ 2.4

$$\text{and}\frac{L_{\mathrm{A}}}{L_{\mathrm{A}}+L_{D1}+L_{D2}}=\frac{\log (x_{2A}/x_{1A})}{\log (x_{2A}/x_{1A})+2\log (1/x_{2A})}.$$ 2.5

Thus, if the allele selectively increased from a low to intermediate frequency in the ancestral population before the split (x_1A ≪ x_2A), much of the work done by selection is shared between the daughter populations. In the absence of other information, it is parsimonious to assume that 100% of the selective deaths are shared between the two sister populations and that the allele fixed in the ancestral population (x_2A = 1). This agrees with our intuition and ideas of phylogenetic parsimony that, in the absence of other evidence, all of the change occurred only once in the ancestral population. That is, we should not infer the repeated work of selection where it is unnecessary. This measure also emphasizes that we should be much more impressed by repeated adaptation from very rare standing variation than common variation. Similarly, in the ILS example shown in figure 1a, in the absence of other information it is parsimonious to assume that the allele fixed in populations 1 and 3 was relatively common in the ancestral population; so, its repeated fixation by drift was not unlikely. Only in the case where we have other information, for example that neutral ILS is very rare given the timespan involved, do we have some evidence that convergence is unusual.

As a final scenario, we consider the case when a selective allele increases in frequency in one population (i) owing to selection before being introduced into a second population (ii) by gene flow and fixing in the second population (figure 1c). For simplification, we assume a single pulse of admixture that introduces the allele into the second population at frequency p. The work done by selection in populations 1 and 2 are L₁ = −2log (x₁) and L₂ = −2log (p), respectively, for a total load of L_T = −2 (log (x₁) + log (p)). Therefore, the proportion of selective deaths that are shared is

$$\frac{\log (x_1)}{(\log (x_1)+\log (p))}.$$ 2.6

Because most of the selective deaths involved in fixing an allele occurs when the allele is rare, they are shared between populations unless the frequency that the allele is introduced into population 2 is small (i.e. p close to x₁). For example, if the allele fixed from an initial frequency of 1 in 1000 in population 1 and admixture into population 2 initially pushed the allele to 10% frequency, a large portion, 75%, of the work done by selection is shared.

We can also relate this measure to the amount of information gained independently in different populations. As noted by Kimura [34], the load involved in fixing a single substitution (equation (2.2)) is twice the log of the probability of a neutral allele fixing from x₁ and so is a measure of the information accumulated by selection as compared to a neutral model (in an information theoretic sense, [35,36]). We explain this connection in appendix Aa and how it follows from the fact that equation (2.2) can be seen as the average log-likelihood ratio of the probability of an allele fixing under the selective model compared to the neutral model. This information gain under a model of selection compared to neutrality is a measure of the unlikeliness of the state of the system encoded by selection as compared to a neutral model. Extending this argument in appendix Aa, we show that the decomposition of the shared and independent work done by selection through selective deaths, e.g. equations (2.3)–(2.6), corresponds to the shared and independent gain of information owing to selection. Specifically, we can express the additional work done by selection in a second population in terms of how improbable the allele frequency change was in a second population under a model of genetic drift, given the change already achieved in the first or ancestral population. We also show how this measure of convergence, as the independent work performed by selection, can also be expressed as the statistical ‘surprise’, under a neutral model, as observing what has been achieved in a second population conditional on what happened in a first or ancestral population. While we have considered just two populations here, we can extend this framework to larger numbers of populations. However, the main insight, that we want to see repeated large allele frequency changes from initially rare alleles, is clear from just the two population cases.

This framework may be useful in aiding our intuition about the degrees to which selective events have been independent and so can be considered to be convergent. At the macro-evolutionary scale, with no gene flow or ILS, convergent substitutions in different taxa can be thought of as completely independent allele frequency changes. Thus, seeing a specific, selection-driven substitution twice offers double the information gain by selection. It seems natural to then think of simply summing up the information gained over multiple substitutions across loci. However, one issue with this approach is that we cannot simply sum the work done by selection (i.e. selective deaths) across multiple loci, unless the loci contribute multiplicatively to fitness. The same information content can be accumulated for far fewer deaths under negative fitness epistasis (e.g. most efficiently owing to truncation selection). This argument forms the basis of the rejection of Haldane’s substitution load argument, and Kimura’s gain of information extension, as a limit on the rate of evolution [37–39]. Combining information over loci additively, that is assuming multiplicative epistasis, seems a fine first approximation, but this limitation should be borne in mind. However, pushing beyond that limitation the information gained through selection is a more general concept of a statistical measure of the work done by selection in pushing evolution towards highly improbable states. A number of authors have explored the idea of statistical information as a measure of work done by selection and more broadly the role of selection in decreasing the entropy of states including in the presence of different forms of epistasis [40–44]. These ideas extend naturally to quantitative traits [40,41,45] as well as substitution models from molecular evolution [41]. The null models that we judge our gain of information owing to selection against can also include mutation and mutational biases. Therefore, convergent adaptation, at the genetic or phenotypic level, can potentially be conceptualized in this way as the independent gain of information owing to selection.

3. Using population genetics to identify convergent adaptation

Population and quantitative genetics and genomics can provide evidence for convergent adaptation both by helping to establish the degree to which evolutionary changes among populations are independent and by providing evidence that, historically, individuals with a given allele had enhanced fitness relative to the ancestral state. In this section, we review how single locus and quantitative trait tests, and haplotypic or linked variation data, can be used to test the conditions of convergence.

(a). Single locus and quantitative trait tests

In evolutionary studies of characters across species, comparative methods [2,46] make use of the phylogeny to judge whether the sharing of a character among taxa is expected under some null model (e.g. independent evolution down a phylogeny) and whether characters are correlated with some ecological variable beyond null expectations (see [22], for a recent review). For example, in phylogenetic mixed models, the phenotypes of a set of species is regressed on some environmental variable as a fixed effect and divergence along the phylogeny is incorporated as a random effect, with the covariance structure of the random effect being specified by the matrix of shared branch lengths [47,48]. Comparative methods provide a series of tools for evaluating convergence for discrete and continuous characters and use convergence to gain independent information to test evolutionary hypotheses.

There is an equivalent body of work in population genetics which involves shorter evolutionary time scales. In answering these questions on short time scales, one equivalent to the phylogeny is the relatedness or kinship matrix [49,50]. There are different ways of defining this matrix, but broadly the elements of this matrix specify the amount of sharing of alleles between two individuals or populations, above that expected in a reference population (often some hypothetical ancestral population or the total sample), owing to shared coancestry and genetic drift [51]. This is conceptually similar to how a species phylogeny specifies the shared branch lengths for pairs of species back to their common ancestors and hence the degree of shared ancestry relative to the most recent common ancestor of all the samples. However, using the relatedness matrix is a somewhat different statement from the importance of species phylogeny in judging trait similarity because introgression and ILS increase the chance that alleles and traits can be discordant with a species phylogeny [25–27]. This issue is well accommodated for by using the relatedness matrix which naturally accounts for allele sharing that is discordant with the species tree. An additional benefit is that models based on the relatedness matrix can be used in situations where population relationships are not well described by a simple branching phylogeny, for example, isolation by distance, which is frequently encountered when dealing with populations separated by short timespans.

Tests of selection involving an empirical relatedness matrix have become more common with the increase in data from large numbers of closely related populations. For example, the association between allele frequencies at a locus and an ecological variable can be assessed by using the relatedness matrix to model the null expectations of populations that vary and covary in their deviations owing to genetic drift [52–54]. A similar body of work tests for non-neutral population differentiation while accounting for population structure by using the relatedness matrix or the eigen-vectors (principal components) of this matrix [55–58]. By incorporating the relatedness matrix as a null model into population-genetic tests, shared population history and gene flow is naturally accommodated for in assessing environmental correlations or non-neutral allele frequency divergence. While these tests use the independent evidence of allele frequencies across populations to test for deviations away from a null model, they do not generally test explicitly for adaptive convergence. This is because they are not usually used to take the extra step of determining whether similar patterns of non-neutral allele change in distinct subsets of the species range are, in fact, independent or can be explained by selection-driven allele frequency change in one region followed by gene flow and drift spreading the change to other regions. However, researchers do already informally test for convergence of allele frequency change across species ranges, for instance in studying parallel selective clines on multiple continents or at smaller geographical scales. (See, for example, the work on Drosophila genomic clines of [59–61].) One possibility to formalize a test of convergence is to condition on the observed allele frequency change in one subset of the species range, using the relatedness matrix, while testing for non-neutral allele frequency change elsewhere. Additionally, frameworks that use admixture graphs, parameterized versions of the relatedness matrix [62], to determine whether multiple instances of selection on distinct branches are being developed to examine allele frequency change across populations [63]. Therefore, we are now in position to move towards formally testing for non-neutral convergence in allele frequency changes among populations.

In studying phenotypes, we can also address similar questions across closely related populations. Quantitative geneticists have long asked whether common-garden phenotypes are too variable across populations compared to the allele frequency differentiation (often using Q_ST – F_ST comparisons; see [64,65] for reviews). These tests were originally restricted to relatively simple models of population structure. Recently, there has been a move to using kinship matrices to test for non-neutral divergence in phenotypes or polygenic scores across populations, allowing shared neutral trait divergence owing to shared population history and gene flow to be more fully accounted for [66–70]. These tests are predicated on the idea that the additive genetic phenotypic variation among populations is the sum of allele frequency changes at many loci. Therefore, its neutral properties are well captured by the relatedness matrix in a conceptually similar way to how Brownian-motion models capture divergence owing to phenotypic effects of many small substitutions on a phylogeny. These relatedness-based models can be used to ask whether there is support for phenotypes covarying with environments more than expected under models of genetic drift [66,67,69] and to assess non-neutral divergence along different axes of population structure. These approaches have been used to quantify the degree to which non-neutral genetic phenotypic change among populations is independent versus a consequence of shared history. For example, assessing how unexpected the phenotypes or polygenic scores of one set of populations are, conditional on another distinct subset [66,67]. These ideas have also been extended into explicit tests of non-neutral phenotypic or polygenic score change on admixture graphs [71] that could be used to detect repeated changes among populations.

In conclusion, methods to assess non-neutral, repeated evolutionary change across many populations are rapidly being developed. These developments mirror many of aspects of phylogenetic comparative methods, but extend them to situations where population history is not well represented by a single tree. In moving forward, we need to more explicitly test for convergence and incorporate more intuitive measures of when this convergence is surprising.

(b). Linked variation

Beyond single-locus tests or tests at the level of the phenotype, knowledge of the population genetic variation at a set of linked sites helps address questions related to convergence that may not be possible otherwise. As discussed above, convergent evolution at the level of a gene or allele is most surprising when selection repeatedly and independently pulls alleles up from rare frequency. By comparing haplotype patterns across populations, we can hope to build evidence towards demonstrating this as well as establishing independence to identify convergence.

One common signal leveraged in population genomic scans for selection is the hitchhiking effect. The rapid increase of a rare, beneficial allele gives little time for mutation and recombination to introduce genetic variation on the haplotypic background of the allele, resulting in a decrease in allelic diversity in this region [72,73]. Thus, a strong signal of a selective sweep at a locus is evidence that selection has led to a gain of information in the population. With multiple populations exposed to some novel selection pressure, linked variation and haplotype patterns not just within but among populations can be informative. Strong allele frequency differentiation among populations can be used as additional evidence of selection which can be linked to the specific selection pressure driving the change. However, seeing the signal of a selective sweep across several populations does not ensure that selection was independent. For example, there may have been recent selection for the trait once in the ancestor of the present-day populations (i.e. the scenario in figure 1b where the sweep went to fixation fully in the ancestor or the allele frequency change from x_2A to fixation was owing to drift). Additionally, there may have been selection in a single population and sufficient gene flow and genetic drift to increase the frequency of the selected haplotype with no additional selection in the recipient populations (i.e. figure 1c where now the increase in the recipient population was not owing to selection in population 2 but only migration pressure and drift).

Population genomic data helps dissect whether sweeps across multiple populations are indeed true examples of convergent adaptation. If, for example, populations adapt from different or independent mutations within the same gene or different genes that arose and swept, little overlap is expected in the haplotypes among these populations (figure 2). This builds support for the case that adaptation was probably independent and that information gain owing to selection was compounded across populations. Convergent adaptation owing to selection on the same mutation, i.e. independent adaptive allele frequency change on the same variant (independent substitutions but not independent mutations), may be also distinguishable from cases where most of the change is owing to shared selection. In [28], we developed an approach to distinguish between the ways convergent adaptation can arise using neutral allele frequency data from sites linked to beneficial loci. Specifically, we derived coancestry coefficients (terms proportional to the relatedness and kinship coefficients) both within and between populations experiencing the same selective pressure based on coalescent probabilities. We then used these terms to calculate the composite likelihoods of observing a set of neutral allele frequencies given a specific scenario of selection and selected allele sharing. Previously, we aimed to distinguish among convergent adaptation owing to convergent mutations, independent selection on shared ancestral variation, and independent selection on an introgressed variant, as well as a neutral model with no selection. In appendix Ab, we derive similar coancestry coefficients for the scenario where there has been a complete sweep in the ancestral population to exemplify how this approach can be extended to model scenarios that are not truly convergent adaptation in hopes to distinguish between these signals as well. Other authors have explored models and developed methods for sweeps from standing variation [74–76], sweeps from selected alleles spread by migration or introgression [77–80], and ancestral sweeps [81]. We hope that our approach, which combines insights from many of these models into a single framework, can aid investigators in identifying, and distinguishing among models of, convergent adaptation. Additionally, since our approach does not assume an underlying population tree, this may be particularly useful for closely related populations that may have short branching times and recent or ongoing gene flow.

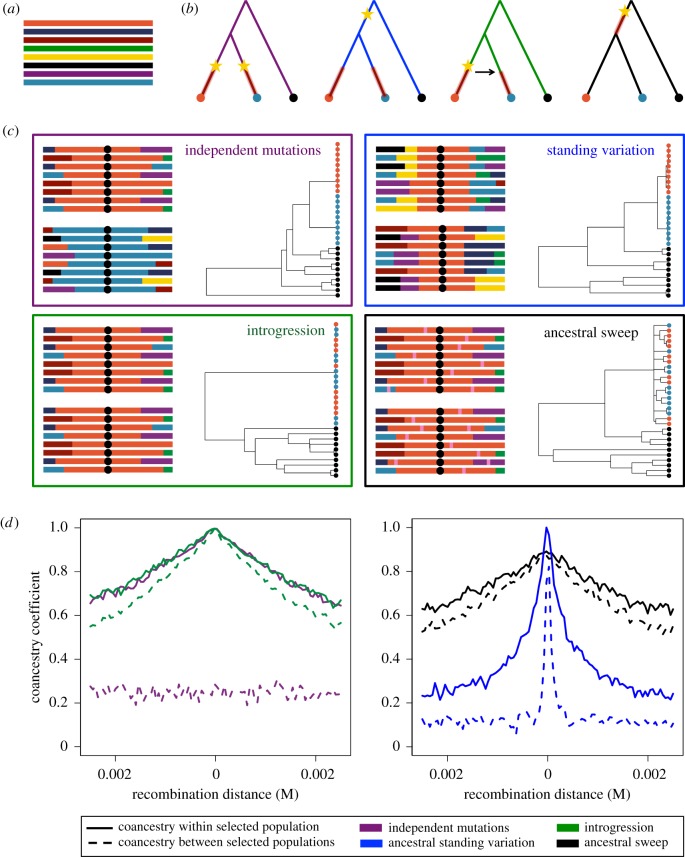
Figure 2.

Patterns generated under scenarios of convergent adaptation and not truly convergent (i.e. not independent) adaptation. (a) Haplotypic diversity in the ancestral population is shown. Each line represents an individual chromosome. (b) The four scenarios considered are depicted with yellow stars representing mutations at the beneficial locus, and red lines on the phylogenies when selection occurred. The scenarios are: (i) independent mutations, (ii) independent selection on ancestral standing variation, (iii) introgression, and (iv) selection in the ancestral population. (c) Panels for each of the four scenarios contain a cartoon representation of the haplotypic patterns surrounding the beneficial allele (black dot) in the two selected populations after fixation and a gene tree relating the populations at the beneficial allele. Pink regions in the haplotypes represent new mutations. (d) Within- and between-population conacestry coefficients for the four scenarios are shown as a function of recombination distance from the beneficial allele. Both gene trees and coancestry coefficients were derived from simulations briefly outlined in appendix Ab.

Now, to build intuition, we briefly summarize the types of patterns we expect to observe under various scenarios that result in an adaptive allele being fixed in two populations, as illustrated in figure 2b. We focus on four cases: (i) independent selection on independent mutations for a beneficial allele at the same locus, (ii) independent selection on an allele that was standing in the ancestor of the selected populations and independently in the daughter populations for a moderate amount of time, (iii) introgression followed by independent selection, and (iv) a complete sweep in the ancestral population of the two adapted populations prior to their splitting. The first three cases fall under our definition of convergent adaptation while the last would not because of its lack of independence or replication. For each scenario, we focus on three signals: the haplotype patterns in our two adapted populations (figure 2c), the gene tree at the beneficial allele for the two adapted populations plus an outgroup (figure 2c), and the coancestry coefficients that our approach uses, which are another statement about the haplotypic similarity within and between populations, as a function of recombination distance from the locus experiencing selection (figure 2d). The latter two signals shown were generated from simulations as outlined briefly in appendix Ab.

The difference between the independent mutations scenario and the others is perhaps the most striking. Here, the beneficial allele arose on different haplotypes in the two adapted populations and, after fixation, we observe high levels of similarity within the two populations, but none between. This sharing within a population that experienced selection is owing to the fact that variants linking the beneficial allele also increased in frequency. As we move further away from the selected locus, recombination is more likely to occur and this association breaks down. This is shown in the coancestry coefficients as a function of recombination distance from the selected site. In this case, there is an increase in coancestry within a selected population but no increase in coancestry (beyond neutral, shared population history) between the populations. We can also see this in the tree generated at the selected site. Here, all lineages within a population coalesce rapidly, while between them, the lineages do find a common ancestor faster than on the time-scale of typical, neutral lineages.

The other three scenarios have a key similarity. Now, there is some haplotypic similarity in both adapted populations because the beneficial allele has a single, shared origin. Still, there are features that differentiate these scenarios that may be useful to distinguish them. In the case that selection was on a variant that was standing in the ancestor of the adapted populations, there is a region of a shared, core haplotype between populations and, as a result, increased coancestry between the populations. However, we observe a faster decay in coancestry with increasing recombination distance between the populations than within a population. This is owing to the fact that while the allele was standing independently in both populations prior to the onset of selection, recombination broke down the original haplotype on which the selected allele arose. Seeing a strong sweep within populations, but only a partially shared haplotype among the populations, is evidence that selection has independently dragged up the same variant from low frequency. By contrast, the final two scenarios have higher amounts of sharing both within and between the adapted populations. In the introgression case, we expect little to no differentiation in the haplotypes between the populations if migration occurs during the sweep. The gene tree depicts that all lineages with the beneficial allele coalesce rapidly at the selected site, regardless of which population they were sampled from. In the coancestry coefficients, there is now a slow decay in the within-population coancestries and a similar decay between populations. The final scenario, which does not represent convergent adaptation but rather a single, ancestral sweep, looks very similar to introgression because there is a lot of sharing in haplotypes within and between populations. The key difference is, if selection occurred sufficiently far in the past, we will observe new mutations independently arising in the adapted populations (indicated by the pink bars on the haplotypes). Specifically, in the tree, we still observe all lineages at the selected site coalesce at the same time in the past, but now there are branches leading to our present-day lineages on which new mutations have occurred. Thus, to demonstrate that the beneficial allele swept in multiple populations, the between-population coalescent times should be much more recent than those in the rest of the genome. Observing very recent coalescence (i.e. short branch lengths) between and among populations in the swept region would allow us to rule out that the sweep is shared ancestrally or spread by neutral migration pressure. Such sweep patterns, that are independent among multiple populations, can provide evidence of adaptive convergence and the independent gain of information owing to selection.

4. Discussion

We emphasize the importance in carefully defining the questions we are trying to address in studying convergent adaptation. Convergent evolution has a wide range of overlapping definitions; it is obviously fine if our discussion does not line up with your definition (indeed one of the authors has varied in his definitions, [82,83]). However, we assert that when there has been convergent substitutions at a locus among taxa, it is of interest that selection favoured their increase in frequency multiple times, no matter their origin.

There is a growing body of theory on when we should expect various modes of convergent adaptation among distantly related populations (owing to independent mutations [84,85]) and among closely related populations (owing to independent mutations, standing variation, and the spread of alleles by migration [82,83,86–89]). Dissecting whether the same or different mutations gave rise to the adaptive alleles will help us gain insights into questions related to mutational target size or epistatic constraints, but these questions can be somewhat orthogonal to more basic questions about adaptation. As we learn more about repeated adaptation across populations, the need to differentiate convergent mutations from convergent allele frequency change will increase. For example, human populations have repeatedly adapted to different environments through changes in skin pigmentation. This convergent adaptation on the level of the phenotype comes from a mixture of selection on old standing variation, both derived and ancestral variants, and recent mutations [90–92]. In the case of repeated evolution probably involving highly polygenic traits (such as human height and the convergent evolution of small body size; [93,94]), populations may be convergently adapting via very similar shared sets of alleles. This may reduce the independent information we can hope to glean about the genetics of height, but establishing that the phenotypic change occurred convergently is still important.

We demonstrated a potential way to quantify the impressiveness of various instances of convergent adaptation. One fair question is whether expressing these ideas in terms of information gained by selection and surprise add something new to the discussion. We ourselves are still a little unsure. After all, log-likelihood ratios are regularly computed as a means of summarizing support for various selection models over the null model. However, usually the log-likelihood is viewed as a test statistic that should be compared to some null distribution, to see if the null model can be rejected. Indeed, we often tell ourselves that we should not be too invested in the value of log-likelihood ratio as it is influenced by our sample size, etc. However, in calculating log-likelihoods of a particular allele being fixed in different populations, the likelihood ratio is a statement about the outcome of an evolutionary process and its replications across populations. Therefore, thinking about the log-likelihood of outcomes across populations as representations of the information gained by selection, at least under some models, focuses us on the view that natural selection is a force that drives the origination of the improbable, and in the case of convergent adaptation, its repeated origination. More work is needed to demonstrate that this is indeed useful and how it could be practically applied, but the idea itself may have merit.

In this article, we focus on how population-level genomic data, specifically from closely related taxa, forces us to recognize new challenges in identifying convergent adaptation while also enabling us to address these issues in new ways. Additionally, the sharing of characters among closely related taxa brings its own set of opportunities. Repeated adaptation among recently diverged populations potentially allows us to use population genomics, genetic crosses, and association studies to map genotype to phenotype, as well as the option to perform experimental manipulations in replicated populations across relatively uniform genetic backgrounds. Population genetic tools can be useful in helping to assess the two criteria necessary to have convergent adaptation. There are many existing approaches, that often nicely parallel those from phylogenetics, to test that changes we observe are unusual, relative to some null model. More work is needed to fully flesh out the potential of these methods, but these tests can be incorporated into existing frameworks allowing the field to move forward with more explicit tests for convergent adaptation. We are excited by what new data and tools can help us learn about convergence. Still, it is important to emphasize that cases which meet these two criteria may help in identifying loci and traits that may be interesting to investigate further, but they might not be convergent adaptations on the phenotypic level. For example, two loci may have swept the same haplotype to fixation, we cannot be certain that the haplotypes, while sharing some alleles, do not also harbour different alleles conferring different phenotypic effects on fitness. Therefore, the hard work of linking the genotype and phenotype to fitness will remain an obstacle in describing convergent adaptation. However, the growing potential for identifying new cases of convergence in closely related populations offers a rich seam for these efforts.

Appendix A

(a) Information

Kimura [34] argued that Haldane’s [33] substitution load for a single selected allele is also related to the accumulation of genetic information. In this appendix, we discuss ideas about convergent allele frequency change in terms of information theory.

The information gain of the probability distribution p( ) over q( ) is defined as

$$\mathcal{I}=\sum _{x}p(x)\log \left[\frac{\hspace{0.17em}p(x)}{q(x)}\right].$$ A 1

This is the log-likelihood of x averaged over the probability distribution p( ). It measures how much more concentrated p( ) is on particular states in x compared to q( ). It is also called the Kullback–Leibler divergence, or relative entropy of the first model to the second model.

We can write the gain of information under our selection model compared to a neutral model as

$${\mathcal{I}}_{\mathrm{sel},\mathrm{neut}}=\sum _x{p}_{\mathrm{sel}}(x)\log \left[\frac{\hspace{0.17em}{p}_{\mathrm{sel}}(x)}{p_{\mathrm{neu}}(x)}\right],$$ A 2

i.e. the log-likelihood ratio under our selected compared to our neutral model averaged over outcomes of our selected model.

To see Kimura’s [34] argument, imagine an allele starting at frequency x₁ in the population. If it were neutral, it would fix in the population with probability x₁. If it is selected, it will fix with probability 1 (assuming x₁ ≫ 1/(2N_es), where N_e is the effective population size). Then, the gain of information under the selection model compared to the neutral model is

$$P(\text{fixed}\mid \text{sel})\log \left(\frac{P(\text{fixed}\mid \text{sel})}{P(\text{fixed}\mid \text{neutral})}\right)=\log \left(\frac{1}{x_1}\right),$$ A 3

as originally outlined by Kimura [34].

We can consider the gain of information in moving from frequency x₁ to x_2A, as in our population split case (figure 1b). Under genetic drift, the probability that a neutral allele starting from frequency x_1A ≤ x_2A reaches frequency x_2A before loss is (x₁/x₂). An advantageous, additive allele achieves this change deterministically (again assuming (x_1A ≫ (1/2N_es)). Therefore, we can write the gain of information of moving from frequency x_1A to x_2A under our selection model to our neutral model as

$$-\log \left(\frac{x_{2A}}{x_{1A}}\right).$$ A 4

This shows that our selective deaths in achieving this frequency change (equation (2.3)) in the ancestral population may also be thought of as a selective gain in information. (Note in expressing things this way there is an ambiguity in that we state that the frequency at the moment the populations split is x_2A. Therefore, an alternative formulation of the neutral probability may be the transitory stationary distribution at x_2A of the neutral diffusion starting from frequency x_1A. A different approach that would give us equation (A 4) is to think about the difference in the gain of information owing to selection in the system when going from frequency x₁ → 1 compared to going from x₂ → 1.)

Thus, we can decompose the total information gain under the selection model of going from frequency x_1A to x_2A and then from x_2A to fixation into L_D + L_A. Note that in doing this we have not specified the time it took selection to achieve this gain. If we have knowledge of the timing, this could be incorporated by using the allele-frequency transition probabilities for the neutral and selection model in equation (A 2). (Note that incorporating the timing would lead to the information gain to depend on the strength of selection.) Using transition probabilities would also allow us to incorporate genetic drift into the selection model, which would allow the amount of work done by selection to be averaged over likely values of the allele frequency change owing to the combined actions of genetic drift and selection. Such considerations would need more work if this were to be useful in a practical setting.

Similarly, the total information accumulated in fixing the allele in populations 1 and 2 in our admixture example (figure 1c) is

$$\begin{array}{rl}P(\text{fixed}\hspace{0.17em}1\hspace{0.17em}\mathrm{\&}\hspace{0.17em}2& \mid \text{sel})\log \left(\frac{P(\text{fixed}\hspace{0.17em}1\hspace{0.17em}\mathrm{\&}\hspace{0.17em}2\mid \text{sel})}{P(\text{fixed}\hspace{0.17em}1\hspace{0.17em}\mathrm{\&}\hspace{0.17em}2\mid \text{Neutral})}\right)\\ & =\log \left(\frac{1}{(x_{1}p)}\right)=-(\log (x_1)+\log (p)).\end{array}$$ A 5

Therefore, one measure of adaptive convergence may be the additional information gained by selection independently in different populations. In the context of information theory, equations (2.5) and (2.6) are called the coefficient of constraint which is a measure of how well we can predict the information in population 2 from that given to us by population 1.

Surprise! We can also formulate our results in terms of gain of information as the ‘surprise’ at our allelic state across populations. In information theory, the negative log probability of an outcome under a particular model is called the surprise (or the self information). The lower the probability of a particular outcome under a model, the greater the surprise when we see that outcome. Another good feature, following from that of log probabilities, is that surprise is additive so you are doubly surprised if you see the same rare event twice independently.

As everything is done under a effective deterministic selection model (i.e. starting from a frequency ≫ 1/(2N_es)), all of our statements about information gain only include the log probabilities under the neutral model. Therefore, they are the surprise at the outcome under the neutral model. Our measure of the work done by neutral probabilities can be decomposed into a product of conditional neutral, probabilities, e.g. equation (A 5) and so a sum of log probabilities. This has the nice feature that we can ask how surprised we are at the convergence in a second population given a change in the first population.

(b) Coancestry coefficients

Knowledge of variation linked to a selected site may enable us to address questions of convergence that would not be possible if we only observed the state of the selected populations. If we observe sister populations sharing a selective event, we can ask if the selection was independent or if the selective event occurred in their ancestor. If the selected event is shared and the sweep is recent, we might expect the regions around the selected site to be more similar than if the sweeps happened independently and are truly convergent. We can formalize this in terms of coancestry between populations.

We define coancestry coefficient f_ij as the probability that a pair of alleles sampled from populations i and i coalesce before the ancestral population of all sampled populations (see [28], for more details). Thinking about the populations in figure 1b, we can define the coancestry owing to both neutral processes and selection for populations 1 and 2 as $f_{12}^{(S)}$ where f₁₂ alone specifies the coancestry between the populations owing to drift and admixture. If the selective events occurred independently from a new mutation of the beneficial allele in both populations, the coancestry between them at loci near the selected allele is simply what we expect under neutrality, f₁₂.

The coancestry will increase if selection is on the same ancestral standing variant present in the ancestor of the populations, and is a function of the frequency of the standing variant, g (i.e. x_2A in figure 1b) and the amount of time, t, once populations 1 and 2 have split from their ancestor before selection started. Assuming the standing variant was previously neutral or was maintained in the population at some low frequency by balancing selection,

$$\begin{array}{rl}{f}_{12}^{(S)}& =y^2(e^{-2\mathrm{rt}}(\frac{1}{1+4\text{Nrg}}+\frac{4\text{Nrg}}{1+4\text{Nrg}}{f}_{12})+(1-e^{-2\mathrm{rt}})f_{12})\\ & +(1-y^2)f_{12},\end{array}$$ A 6

where y² represents the probability of both linked lineages failing to recombine off the beneficial allele. This can be approximated as $e^{-{\mathrm{rt}}_s}$ where t_s is the duration of the sweep phase. This increase in coancestry, that decays with distance from the selected site, is owing to the fact the region around the beneficial allele looks more similar if the variant is shared. However, as the amount of time the beneficial allele is standing independently in the sister populations before selection occurs increases, we expect this similarity to decrease as recombination is occurring independently in the populations. See [28] for full derivation.

If the selective event is shared completely (i.e. the sweep occurs in the ancestor of populations 1 and 2 before they split), there is a further increase in coancestry. In this case, the fraction of shared deaths is 1:

$$f_{12}^{(S)}=y^2+(1-y^2)f_{12}.$$ A 7

Even if the selective event is partially shared such that selection occurs in the ancestral population (for time t₁) and continues independently in the daughter populations (for time t₂), this takes the same form as (A 8) if t₁ + t₂ = t_s:

$$\begin{array}{rl}\hspace{0.17em}{f}_{12}^{(S)}& =e^{-{\mathrm{rt}}_2}(e^{-{\mathrm{rt}}_1}+(1-e^{-{\mathrm{rt}}_1})f_{12})+(1-e^{-{\mathrm{rt}}_2})f_{12}\\ & =y^2+(1-y^2)f_{12}.\end{array}$$ A 8

Therefore, it may not be possible to distinguish cases where the fraction of shared death is greater than zero such that the selective event is shared completely or partially. However, it may be possible to detect if truly convergent, i.e. there is no overlap in selected deaths.

Simulation details. We performed coalescent simulations under the four scenarios outlined above using mssel, a modified version of ms [95] that allows for the incorporation of selection at single site and stochastically generated allele frequency trajectories. See [28] for more details. These simulations were used to generate both coancestry coefficients averaged over 100 simulations and the gene trees. For all, we specified a 5% reduction in fitness for heterozygotes not carrying the beneficial allele and assumed a model of additivity. For the ancestral sweep model, we simulated a sweep that finished 0.1 coalescent generations in the past. For the standing variant model, we specified that the variant was standing at 1% frequency for 0.075 coalescent generations after the populations split. Additionally, for the migration model, we allowed for a fraction of 1 × 10⁻⁴ migrants per generation over the duration of the sweep from the source population into the recipient population.

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by the National Science Foundation Graduate Research Fellowship awarded to K.M.L. (grant no. 1148897) and by grants from the National Science Foundation (no. 1353380) and the National Institute of General Medical Sciences of the National Institutes of Health (grant no. NIH R01 GM108779) awarded to G.C.