Generalizing Performance Limitations of Relay Neurons: Application to Parkinson’s Disease

Abstract

Relay cells are prevalent throughout sensory systems and receive two types of inputs: driving and modulating. The driving input contains receptive field properties that must be transmitted while the modulating input alters the specifics of transmission. Relay reliability of a relay cell is defined as the fraction of pulses in the driving input that generate action potentials at the neuron’s output, and is in general a complicated function of the driving input, the modulating input and the cell’s properties. In a recent study, we computed analytic bounds on the reliability of relay neurons for a class of Poisson driving inputs and sinusoidal modulating inputs. Here, we generalize our analysis and compute bounds on the relay reliability for any modulating input. Furthermore, we show that if the modulating input is generated by a colored Gaussian process, closed form expressions for bounds on relay reliability can be derived. We applied our analysis to investigate relay reliability of thalamic cells in health and in Parkinson’s disease (PD). It is hypothesized that in health, neurons in the motor thalamus relay information only when needed and this capability is compromised in PD due to exaggerated beta-band oscillations in the modulating input from the basal ganglia (BG). To test this hypothesis, we used modulating and driving inputs simulated from a detailed computational model of the cortico-BG-thalamo-cortical motor loop and computed our theoretical bounds in both PD and healthy conditions. Our bounds match well with our empirically computed reliability and show that the relay reliability is larger in the healthy condition across the population of thalamic neurons. Furthermore, we show that the increase in power in the beta-band of the modulating input (output of BG) is causally related with the decrease in relay reliability in the PD condition.

I. INTRODUCTION

Relay neurons are present in several structures in the nervous system, including the thalamus and the spinal cord [2]–[4]. They receive two types of inputs: a driving input and a modulating input. The function of a relay neuron is to selectively relay information in the driving input, and the selectivity is regulated by the modulating input. For example, thalamocortical relay neurons in the motor thalamus relay information from the somatosensory cortex back to the cortical layers depending on a modulating input from the basal ganglia (BG) [5]–[8]. Information is considered to be relayed if a pulse in the driving input generates an action potential in the relay neuron, which we call a successful response. See Fig. 1.

Fig. 1. Successful and unsuccessful response.

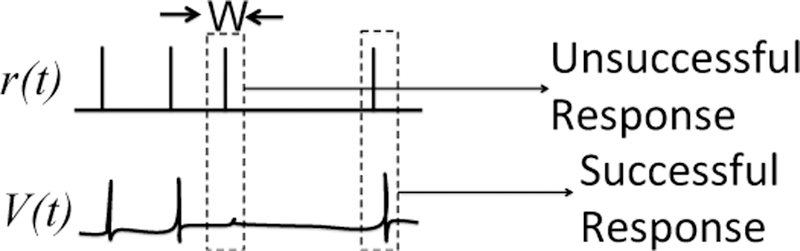
Examples of successful and unsuccesful response for a relay neuron. The neuron must produce one or more action potentials (i.e., a burst) within W ms of a pulse in driving input in order to successfully relay information.

In [1], we defined relay reliability as the ratio between the number of successful responses and the number of pulses in the driving input and we assumed that (i) the driving input is a series of δ-pulses (i.e., spike train) generated from a Poisson process with a refractory period and (ii) the modulating input belongs to a sinusoidal class of signals. Then, we derived analytic bounds on the relay reliability as a function of the driving input parameters, modulating input parameters and the neuron model parameters. Although a biophysical driving input may fall into the class of driving inputs used in [1] (i.e., spikes inputs from the sensorimotor cortical neurons generate a train of pulses), a modulating input from the BG may not always be exactly or even approximately sinusoidal. Therefore, in this study we first present a solution which yields bounds on relay reliability for any modulating input. Further, from our general solution, we provide a closed-form expression on the bounds as in [1] for modulating inputs generated from a bio-physically-plausible class of colored Gaussian processes.

We used the derived bounds to study relay reliability of thalamic neurons both in healthy and Parkinsonian (PD) conditions. It has been hypothesized that the relay reliability of thalamic neurons reduces in PD conditions because of exaggerated β-band (8–30 Hz) oscillations in the modulating input from the basal ganglia (BG) [1], [5], [9], [10]. Studies [5], [9] have shown through numerical simulations that, under PD conditions, the BG output has increased power in the β-band and the thalamic relay cells have lower reliability. However, an analytical connection between beta-band power and relay reliability was not derived.

We investigate this connection by estimating the reliability as a function of the power spectrum of the modulating input using our bounds in both PD and healthy conditions across a population of 10 thalamic neurons. For this, we used the modulating and driving inputs generated from a detailed computational model of the cortico-BG-thalamo-cortical motor loop [11] and computed the bounds on relay reliability. The reliability bounds matched the empirically computed relay reliability well and showed that relay reliability is higher in healthy than in PD conditions across the population of thalamic cells. Furthermore, our bounds show that the increment of power in the β-band of the modulating input from the BG is causally related with the decline in reliability in PD condition.

II. METHODS

A. Generalizing Relay Performance Analysis

In [1], we consider a state-space representation of an nth order biophysical-based model of a thalamic cell. The state vector, $\mathbf{x}\left(t\right)\triangleq {\left[V,h_1,\cdots ,h_{n-1}\right]}^T$, includes the output membrane voltage of the cell, V and n − 1 gating variables h₁, · · ·, h_n−1. We recall in [1] that a delta pulse of height I0 that arrives when the state $\mathbf{x}\left({\tau }_i^{-}\right)$ is in the region of interest (i.e., the region of the state space where the pulse of height I₀ can generate an action potential, Fig. 2) make the state to jump near the threshold point ${\mathbf{x}}_{th}\triangleq \overline{\mathbf{x}}+{\left[I_0,\mathbf{0}\right]}^T$ and where it evolves as:

$$\delta \mathbf{x}\left(t\right)=\sum _k{\mathbf{v}}_{\mathbf{k}}{\mathbf{u}}_{\mathbf{k}}^{\mathbf{T}}\left(\delta \mathbf{x}\left(0\right)+\mathbf{N}{\int }_0^t{e}^{-{\lambda }_k\tau }\delta u\left(\tau \right)\text{d}\tau \right)e^{{\lambda }_{k}t}.$$ (1)

Here δx(t) is measured with respect to x_th. See [1] for details and definitions of λ₁, · · ·, λ_n, v₁, · · ·, v_n, u₁, · · ·, u_n and N. $\delta u\left(\tau \right)$ is the time varying part of the modulating input measured starting at the arrival of a driving input pulse at time ${\tau }_i$.

Fig. 2. Region of interest.

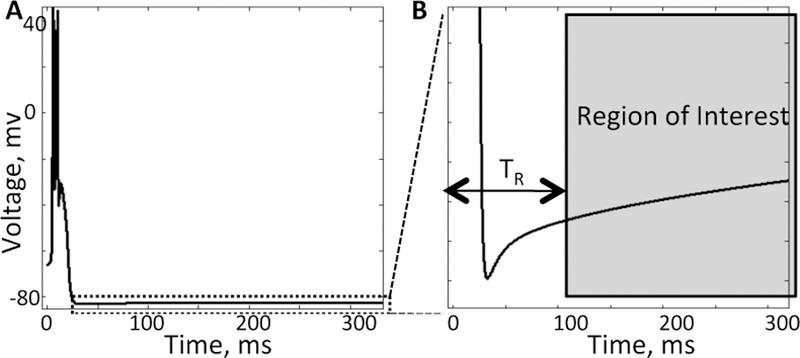
A) Evolution of the membrane potential of the thalamic neuron right after a burst of action potentials. B) Zoom in of the region of interest. Right after generating an action potential, the membrane potential hyperpolarizes and enters the refractory zone (i.e., it cannot generate an action potential). After time T_R the voltage recovers and the neuron is ready to fire again. In this study $T_R\simeq 100\hspace{0.17em}\text{ms}$.

In this study, we consider modulating inputs that belong to a more general class of signals that have small fluctuations about their mean value, i.e., $u_g\left(t\right)=E\left(u_g\right)+\delta u_g\left(t\right)$, where δu_g(t) is any stochastic small perturbation with mean 0. Therefore we set $\delta u\left(\tau \right)=\delta u_g\left(\tau +{\tau }_i\right)$ and, by using the Fourier transform, we have $\delta u_g\left(\tau +{\tau }_i\right)=\frac{1}{2\pi }\int \delta u_g\left(j\omega \right)e^{j\omega \tau }{e}^{j\omega {\tau }_i}d\omega$. Substituting this into (1) and integrating over $\tau$ we have:

$$\begin{gathered} \delta \mathbf{x}\left(t\right)=\sum _k({\mathbf{v}}_{\mathbf{k}}{\mathbf{u}}_{\mathbf{k}}^{\mathbf{T}}(\delta \mathbf{x}\left(0\right)+\frac{1}{2\pi }\mathbf{N}\times \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\int \frac{\delta u_g\left(j\omega \right)}{{\lambda }_k-j\omega }{e}^{j\omega {\tau }_i}(1-e^{-{\lambda }_{k}t+j\omega t})\text{d}\omega )e^{{\lambda }_{k}t}). \end{gathered}$$ (2)

The neuron will generate a spike if and only if the coefficient of $e^{{\lambda }_{1}t}$ is positive, i.e.,

$$\left(v_{1_1}{\mathbf{u}}_{\mathbf{1}}^{\mathbf{T}}\left(\delta \mathbf{x}\left(0\right)+\frac{1}{2\pi }\mathbf{N}\int \frac{\delta u_g\left(j\omega \right)}{{\lambda }_1-j\omega }{e}^{j\omega {\tau }_i}\text{d}\omega \right)\right)\ge 0.$$

By substituting $\delta \text{x}\left(0\right)=\delta {\text{x}}_{\text{o}}\left({\tau }_i\right)+{\left[I_0-I_{th},\text{0}\right]}^T$ we get

$$\begin{gathered} \left(v_{1_1}{\mathbf{u}}_{\mathbf{1}}^{\mathbf{T}}\left(\delta {\mathbf{x}}_{\mathbf{o}}({\tau }_i)+\frac{1}{2\pi }\mathbf{N}\int \frac{\delta u_g\left(j\omega \right)}{{\lambda }_1-j\omega }{e}^{j\omega {\tau }_i}\text{d}\omega \right) \\ \hspace{1em}\hspace{1em}+v_{11}{u}_{11}(I_0-I_{th}\right)\ge 0 \end{gathered}$$ (3)

where $\delta {\mathbf{x}}_{\mathbf{o}}\left(\tau \right)$, is the orbit in the region of interest with respect to the trajectory for u = E(u_g) with reference input r(t) = 0, such that

$$\delta {\mathbf{x}}_{\mathbf{o}}\left({\tau }_i\right)=\frac{1}{2\pi }\int -\mathbf{H}\left(j\omega \right){\overline{x}}_1\delta u_g\left(j\omega \right)e^{j\omega {\tau }_i}d\omega$$

For details see [1]. Now, substituting $\delta {\mathbf{x}}_{\mathbf{o}}\left({\tau }_i\right)$ in (3), we obtain

$$\begin{gathered} \frac{1}{2\pi }\int \left(v_{1_1}{\mathbf{u}}_{\mathbf{1}}^{\mathbf{T}}\mathbf{H}\left(j\omega \right){\overline{x}}_1+\frac{v_{1_1}{u}_{1_1}{x}_{t{h}_1}}{{\lambda }_1-j\omega }\right)\delta u_g{e}^{j\omega {\tau }_i}\text{d}\omega \\ \hspace{0.17em}\hspace{0.17em}\le \left(I_0-I_{th}\right)v_{1_1}{u}_{1_1} \end{gathered}$$ (4a)

Defining

$$G\left(t\right)\triangleq \frac{1}{2\pi v_{1_1}{u}_{1_1}}\int \left(v_{1_1}{\mathbf{u}}_{\mathbf{1}}^{\mathbf{T}}\mathbf{H}(j\omega ){\overline{x}}_1+\frac{v_{1_1}{u}_{1_1}{x}_{t{h}_1}}{{\lambda }_1-j\omega }\right)e^{j\omega {\tau }_i}\text{d}\omega$$ (4b)

$$\Rightarrow \left(G\ast \delta u_g\right)\left({\tau }_i\right)\le \left(I_0-I_{th}\right)sign\left(v_{1_1}{u}_{1_1}\right).$$ (4c)

Solutions of (4c) give the time instants when the neuron successfully spikes provided that a pulse in r(t) occurs and the state is in the region of interest. Therefore, the probability that the neuron spikes given the state is in region of interest is

$$P_{response}=\mathrm{Pr}((G\ast \delta u_g)({\tau }_i)\le I_0-I_{th})$$ (5)

for any general $u_g(t)=E\left(u_g\right)+\delta u_g\left(t\right)$. We note that it is assumed that $sign\left(v_{1_1}{u}_{1_1}\right)=1$, which is generally the case for biophysical neurons. However, unless more information about u_g(t) is provided, (4) cannot be solved further. Hence, we consider a plausible class of u_g(t) in the next section.

B. Colored Gaussian Modulating Inputs

We assumed that the modulating input is colored Gaussian noise, which implies that $\delta u_g\left(t\right)=h\left(t\right)\ast \eta \left(t\right)$, where η(t) is generated from a white Gaussian process with zero mean and unit variance and h(t) is a low pass filter. By substituting δu_g(t) in (4c) we obtain

$$\left(G\ast h\ast \eta \right)\left({\tau }_i\right)\le I_0-I_{th}.$$

Now, using properties of white Gaussian process we get:

$$\left(G\ast h\ast \eta \right)\left(t\right)~N\left(0,\frac{1}{2\pi }\int P_G\left(j\omega \right)P_h\left(j\omega \right)d\omega \right)$$ (6a)

$$\Rightarrow P_{response}=\mathrm{Pr}((G\ast h\ast \eta )({\tau }_i)\le I_0-I_{th})$$ (6b)

$$\therefore P_{response}=\frac{1}{2}+\frac{1}{2}erf\left(\frac{\sqrt{\pi }\left(I_0-I_{th}\right)}{\sqrt{\int P_G\left(j\omega \right)P_h\left(j\omega \right)dw)}}\right)$$ (6c)

where erf () is the error function, and P_G(jω) and P_h(jω) are the power spectrum of G(t) and h(t), respectively. Now, one can use equation (49) in [1] to derive a lower and upper bound on relay reliability from 6c as:

$$\frac{P_{response}}{1+\left(1-\alpha \right)P_{response}}\ge R\ge \alpha \cdot P_{response}$$ (7)

where, parameter α depends upon driving input average inter pulse interval T, refractory period T₀, and the time T_R to the region of interest (for details see Fig. 2 and [1], [12]).

III. RESULTS

We verified (6) by computing the bounds on the relay reliability across a population of neurons in the motor thalamus both in healthy and PD conditions, and then by comparing these bounds to reliability computed through numerical simulations. For this purpose, we used data generated by a detailed computational model of the cortico-BG-thalamo-cortical motor loop under both conditions.

A. Network Model of the Motor Loop

The Basal Ganglia Thalamocortical loop model used in [11] model is illustrated in Fig. 3. The four structures in the black boxes were explicitly modeled. Each modeled structure had neuronal population as represented inside the corresponding boxes in the Fig. 3. The model reproduced the experimental firing activity of the neurons in all the anatomical structures both in healthy and PD conditions.

Fig. 3. Cortico-BG-thalamo-cortical loop.

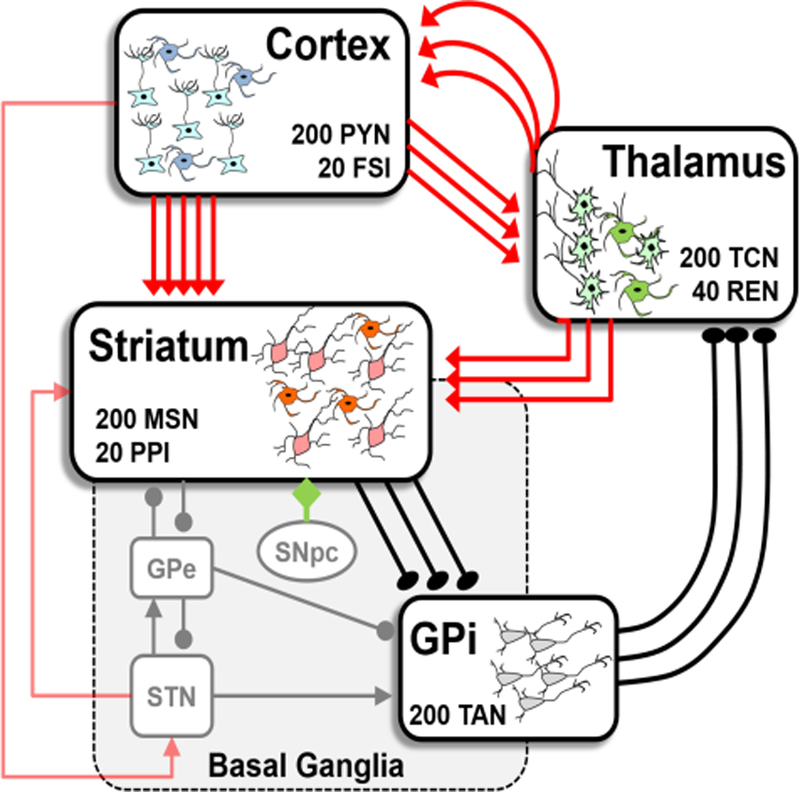
Red, black, and green arrows are glutamatergic, GABAergic, and dopaminergic projections, respectively. The anatomical structures explicitly modeled are depicted with black boxes (number of neurons reported inside each box), while the remaining nuclei are depicted with gray boxes. GPe (GPi)=external (internal) globus pallidus; SNpc=substantia nigra pars compacta; STN=subthalamic nucleus.

The network model a single-compartment model reported in [13] to represent the thalamocortical relay neuron. Briefly, the neuron was described by the following membrane equation

$$C_m\dot{V}=-g_L\left(V-E_L\right)-\sum _j{I}_j^{int}-I^{ex}-I^{in},$$ (8)

where V is the membrane potential, C_m = 1 µF / cm² is the specific capacitance of the membrane, g_L and E_L are the leakage conductance and reverse potential, respectively, and $I_j^{int}$ (in mA / cm²) denote the intrinsic currents. Finally, $I^{ex}=I_0{\sum }_i\delta (t={\tau }_i))$ and $I^{in}={10}^3\left(0.0005+\delta u_g\left(t\right)\right)\left(V-(V_{syn}=-85\right)$ denote the net glutamatergic and GABAergic synaptic current, respectively. The details of this model are given in [11], [13] and references therein.

For this neuron, we estimated that the time to region of interest T_R =100 ms. We note that the region of interest for the neuron is not equal to the orbit tube define in [1], but after an action potential occurs, the neuron’s state returns to a quasi-steady state where it remains for about 2000 ms and before ultimately going back to the orbit tube. We considered this quasi-steady state as the “region of interest”.

B. Modulating and Driving Inputs

To compute the modulating input δu_g(t) for our analysis, we first computed an ensemble sum of spike trains from 20 GPi neurons in [11]. Then, we subtracted the DC offset to remove the contribution of E(u_g) and we low-pass filtered the remaining signal using a 2nd order low-pass Butterworth filter with cut-off frequency 100 Hz to model effect of release of neurotransmitter and opening of synaptic gate. The resultant signal is our δu_g(t) (see Fig. 4A–B for healthy and PD conditions, respectively). Finally, we assessed whether δu_g(t) belongs to the class of colored Gaussian noise signals. Fig. 5 shows that, under healthy conditions, the histogram closely follows a Gaussian profile, suggesting that δu_g(t) does fall into the class of colored Gaussian noise signals. Under PD conditions, instead, the profile is related to a Gaussian distribution, even though it does not completely match a Gaussian curve. Correspondingly, Fig. 6A reports the power spectrum of the modulating input for both conditions and it shows that significant peaks in the β-band emerge under PD conditions, consistently with observations in PD patients and animals [14].

Fig. 4. Modulating and driving inputs.

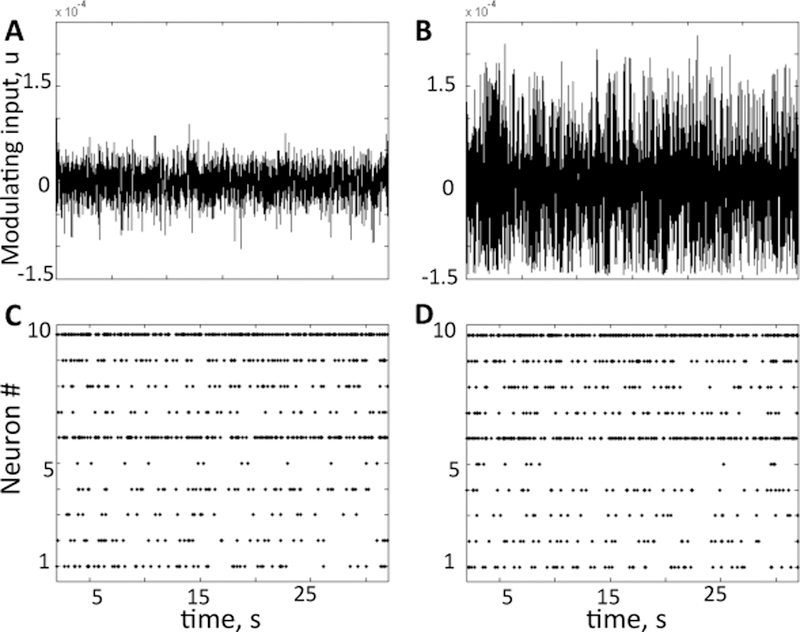
Modulating (A,B) and driving (C,D) inputs in healthy (A,C) and PD (B,D) conditions. The same modulating input drives all the thalamic neurons, while each neuron receives different cortical inputs, as in raster plot.

Fig. 5. Statistical properties of the modulating input.

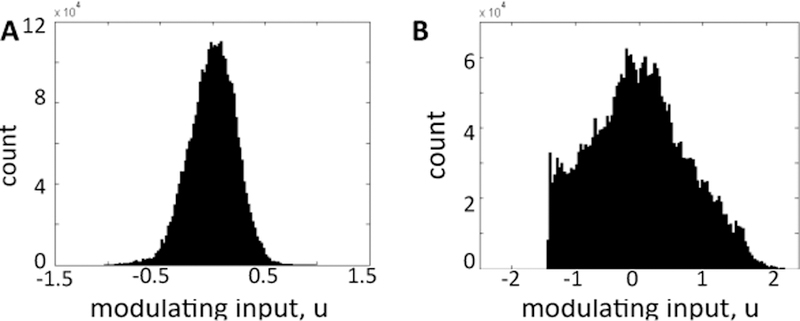
Histogram of the values of the modulating input in healthy (A) and PD (B) conditions.

Fig. 6. Modulating input and the neuron’s transfer function.

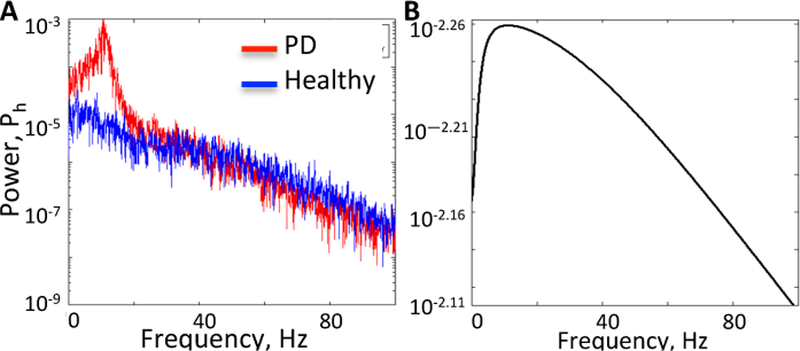
A) Power spectrum P_h(ω) of the modulating input in healthy and PD conditions. B) Power spectrum P_G(ω) of the transfer function of the thalamic neuron.

The driving input was computed from cortical spike trains generated from the pyramidal neuron models in the motor loop [11]. Specifically, we used an ensemble sum of spike trains from all the cortical neurons projecting onto the same thalamic neuron. Then, we chose instances where 2 or more cortical spikes fell into a 1 ms time bin because such a short inter-spike interval makes sure that these instances drive the thalamic neuron like an impulse allowing our analysis to be applicable. We use these instances as ${\tau }_i$ ‘s and used them to produce the driving input $r\left(t\right)={\sum }_i{I}_0\delta \left(t-{\tau }_i\right)$; I₀ = 17. The refractory period for these instances was T₀ =5 ms and the average inter spike interval varied from 2500 ms to 83 ms, depending on the thalamic neuron. Finally, using T₀, T, and T_R, we computed α as in [1]. A raster plot of reference inputs for all 10 thalamic neurons is plotted in Fig. 4C–D for healthy and PD conditions, respectively.

C. Computation of Relay Reliability

First, we computed G(ω), see Fig. 6B using the thalamic neuron describe above. Then, we computed I_th =16.35 and T_R=100 ms. Finally, we used (6) to compute the theoretical bounds for the modulating and driving inputs described in the previous section. We also simulated the full 9-dimensional model (8) and numerically computed the reliability. Fig. 7A–B report the theoretical bounds and empirically computed reliability for healthy and PD conditions, respectively. We note that the theoretical reliability matches quite well with the empirically computed reliability in both conditions across the neural population. We further calculated the theoretical reliability using the more general equation (5) (results not shown) and we found almost identical results using this equation as compared to (6), thus suggesting a general applicability of our closed form expression.

Fig. 7. Relay reliability in healthy and PD.

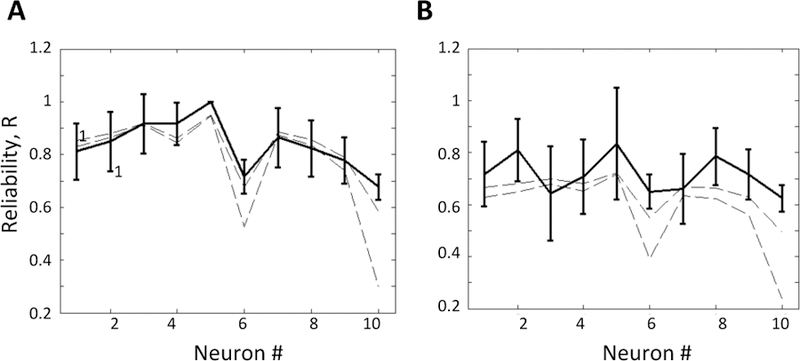
Theoretical and numerical bounds on the relay reliability in healthy (A) and PD (B) conditions. The theoretical bounds are calculated assuming a colored Gaussian modulating input. Solid black lines denote numerically computed relay reliability across 10 thalamic neurons with 95% error bars, dashed lines are theoretical lower and upper bound on the reliability across 10 thalamic neurons.

IV. CONCLUSIONS

In this paper, we generalized our results for relay reliability of a relay neuron for any modulating input, and we developed closed-form bounds on reliability when the modulating input is colored Gaussian noise. We applied our bounds using a detailed model of the cortico-BG-thalamo-cortical loop and showed that (i) the modulating input to the thalamus in the loop may belong to the set of colored Gaussian noise signals; (ii) the numerically computed relay reliability matches quite well with our theoretical bounds; and (iii) that the relay reliability decreases across the entire population of thalamic neurons in PD conditions and that a PD-elicited increase in the β-band power of the modulating input is the primary reason for decreased relay reliability, which may be related to the disease symptoms in a causal way.