Automatic Segmentation of Corneal Microlayers on Optical Coherence Tomography Images

Abstract

Purpose

To propose automatic segmentation algorithm (AUS) for corneal microlayers on optical coherence tomography (OCT) images.

Methods

Eighty-two corneal OCT scans were obtained from 45 patients with normal and abnormal corneas. Three testing data sets totaling 75 OCT images were randomly selected. Initially, corneal epithelium and endothelium microlayers are estimated using a corneal mask and locally refined to obtain final segmentation. Flat-epithelium and flat-endothelium images are obtained and vertically projected to locate inner corneal microlayers. Inner microlayers are estimated by translating epithelium and endothelium microlayers to detected locations then refined to obtain final segmentation. Images were segmented by trained manual operators (TMOs) and by the algorithm to assess repeatability (i.e., intraoperator error), reproducibility (i.e., interoperator and segmentation errors), and running time. A random masked subjective test was conducted by corneal specialists to subjectively grade the segmentation algorithm.

Results

Compared with the TMOs, the AUS had significantly less mean intraoperator error (0.53 ± 1.80 vs. 2.32 ± 2.39 pixels; P < 0.0001), it had significantly different mean segmentation error (3.44 ± 3.46 vs. 2.93 ± 3.02 pixels; P < 0.0001), and it had significantly less running time per image (0.19 ± 0.07 vs. 193.95 ± 194.53 seconds; P < 0.0001). The AUS had insignificant subjective grading for microlayer-segmentation grading (4.94 ± 0.32 vs. 4.96 ± 0.24; P = 0.5081), but it had significant subjective grading for regional-segmentation grading (4.96 ± 0.26 vs. 4.79 ± 0.60; P = 0.025).

Conclusions

The AUS can reproduce the manual segmentation of corneal microlayers with comparable accuracy in almost real-time and with significantly better repeatability.

Translational Relevance

The AUS can be useful in clinical settings and can aid the diagnosis of corneal diseases by measuring thickness of segmented corneal microlayers.

Introduction

Optical coherence tomography (OCT) is an imaging technique that captures the structures of the underlying tissue in vivo by measuring the backscattered light.1,2 It has revolutionized the field of ophthalmology imaging with its ability to provide in vivo high-resolution images of the ocular tissue in a noncontact and noninvasive manner. Measuring the thickness of different corneal microlayers can be used in the diagnosis of corneal diseases.3–6 The cornea microlayers have five microlayers, namely, the epithelium, the Bowman's, the stroma, the Descemet's membrane (DM), and the endotheiulm3 in addition to the basal-epithelium. The epithelium appears as a hyperreflective band, and the basal epithelium appears as a hyporeflective band compared with the overlying hyperreflective epithelium,7,8 due to its columnar shape oriented “in parallel” to the incident probe beam and the fact that it consists of only one layer of cells.9 The Bowman's microlayer is an acellular interface between the epithelium and the stroma,10 hence, it appears as hyporeflective band in between,11 while Endothelium/Descemet's complex appears as a hyporeflective band bounded by two smooth hyperreflective lines.12 There are six interfaces between the corneal microlayers, namely, the air-epithelium interface (EP), the basal-epithelial interface (BS), the epithelium-Bowman's interface (BW), the Bowman's-stroma interface (ST), the DM, and the endothelium-aqueous interface (EN). Measuring the thicknesses of those microlayers in vivo has proven to be valuable for the diagnosis of various corneal diseases, such as Fuchs dystrophy, keratoconus, corneal graft rejection, and dry eye.4,5,12–15 For example, thinning of Bowman's microlayer has been shown to be an accurate sign for the diagnosis of keratoconus.4,16 Also, measurement of the thicknesses of the endothelial/Descemet's microlayers has been shown to be an effective method for the early diagnosis of corneal graft rejection and Fuchs dystrophy.5,12 Thickening of the epithelium was described as an accurate sign of conjunctival corneal carcinoma in situ.14,17 Thickness measurement is done by segmenting the corneal interfaces in the OCT images. Manual segmentation of those interfaces is time-consuming, due to the large volume of the images captured by OCT, and it is highly subjective.18,19 Therefore, automated segmentation is needed. Nevertheless, the absence of a robust automated segmentation algorithm has precluded the use of OCT of the cornea in clinical settings. Developing automated algorithm will set the stage for the introduction of those novel diagnostic techniques to clinical practice. Existing segmentation methods of the cornea are limited because they only detect two or three interfaces.18–28 Eichel et al.19,27 reported a segmentation method to segment five interfaces. Eichel et al.19 segment the EP and EN interfaces using semiautomatic Enhanced Intelligent Scissors, and they use medial access transform to interpolate three inner corneal interfaces. However, this method requires user interaction and assumes fixed model between interfaces. Eichel et al.27 use Generalized Hough Transform to segment the EP and the EN interfaces, and they interpolate three inner corneal interfaces using medial access transform. However, this method assumes fixed shape for each of the EP and the EN interfaces and assumes a fixed model between interfaces. Additionally, most of the existing methods do not work in real-time19,28 and therefore are not suitable for clinical practice.

In this paper, we propose a novel automatic algorithm that segments six corneal interfaces in almost real-time. The proposed algorithm uses a general model for the corneal microlayer interfaces based on previous studies.18,22,27 Additionally, we validate the proposed algorithm against manual operators to assess its performance.

Methods

Data Sets

Forty-five consecutive patients were recruited in this study, including 35 patients with normal corneas and 10 patients with abnormal (i.e., pathological) corneas. The abnormal corneas included four corneas diagnosed with dry eye, three corneas diagnosed with keratoconus, and three corneas diagnosed with Fuchs dystrophy. All patients were diagnosed by a corneal specialist from Bascom Palmer Eye Institute (MAS). The patients signed a consent upon capturing the images and agreed to the usage of their data for research purposes. This research is approved by University of Miami Institutional Review Board. A data set consisting of 82 corneal OCT scans were collected from the patients (i.e., 72 scans from normal corneas and 10 scans from abnormal corneas). Three testing data sets of OCT images were used in the study. The first testing data sets consisted of 15 raw (i.e., unaveraged) OCT images, which were randomly selected from the OCT scans of the normal corneas with no repetition in the selected scan or selected image. The second testing data sets consisted of 50 raw (i.e., unaveraged) OCT images, which were randomly selected from the OCT scans of the normal corneas with no repetition in the selected scan or selected image. In the selection of the second testing data set, an OCT image was selected randomly from each scan of the normal corneas and the selected OCT images were analyzed. The images with low signal to noise ratio (SNR) and low contrast to noise ratio (CNR) were excluded. The images in both testing data sets were averaged using five frames per image with a custom developed software. The third testing data set consisted of 10 raw OCT images selected randomly from the OCT scans of the abnormal corneas with no repetition in the selected scan or selected image. The total number of the raw OCT images used in this study is 75, and the total number of the averaged OCT images is 60 (i.e., the grand total is 140 OCT images).

Capturing Machine

The corneal images were captured by a spectral-domain OCT (SD-OCT) machine (Envisu R2210, Bioptigen, Buffalo Grove, IL). The size of the captured images is 1024 × 1000 pixels. The used machine has a corrected depth of 1.58 mm using approximate refractive index for the whole cornea of 1.38, which corresponds to an axial digital resolution (i.e., pixel height) of 1.5 μm. However, the axial optical resolution of the machine is approximately 3 μm. The machine has a transversal width of 6 mm, which corresponds to a transversal digital resolution (i.e., pixel width) of 6 μm. A radial scan pattern was used for all the patients in the study.

Image Processing

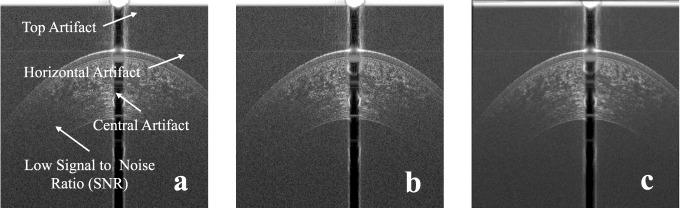
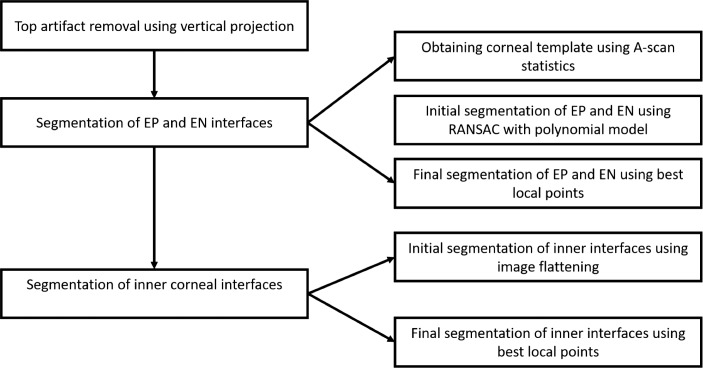
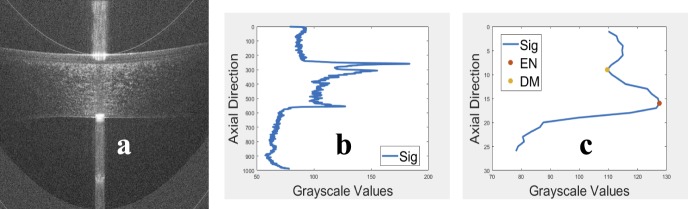
The SD-OCT image has common types of artifacts, namely, the top artifact, the central artifact, and the horizontal line artifact as shown in Figure 1a. The top and central artifacts are due to the back reflection at the corneal apex, which causes a saturation in the captured image at the center and the top part.18 The horizontal line artifact is due to the reconstruction algorithm, which is used to obtain the OCT image.18 The top part usually does not overlap with the cornea and can be removed without affecting the corneal shape. On the other hand, the central artifact overlaps with the cornea, and its removal can affect the corneal shape. Another common artifact is the low SNR at the peripheral parts of the image. In this paper, to enhance the segmentation of the inner interfaces, five raw frames for each OCT image in the test sets were registered using the EP and the EN interfaces, then they were averaged. Examples of raw and averaged OCT images are shown in Figures 1b and 1c, respectively. The steps of the proposed algorithm are in the following subsections, and they are illustrated in the flowchart in Figure 2.

Figure 1.

(a) Typical artifacts present on OCT images, (b) an example of a raw corneal OCT image, and (c) an example of an averaged corneal OCT image.

Figure 2.

The flowchart of the steps of the AUS.

Removal of Top Artifact

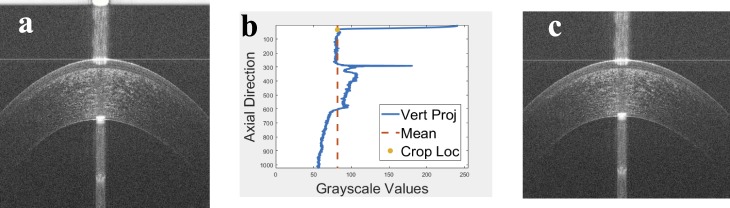
The top artifact of the raw OCT image shown in Figure 3a was identified and removed using the vertical projection shown in Figure 3b. The area above the mean at the beginning of the vertical projection (i.e., the vertical mean of the OCT image) was identified as the top artifact. Then, the OCT image was cropped by cutting this detected artifact as shown in Figure 3c.

Figure 3.

(a) An example of an OCT image with the top artifact, (b) the mean A-scan of the OCT image in Figure 3a with detected crop location, which is used to remove the top artifact, and (c) the image in Figure 3a after removing the top artifact.

Segmentation of the EP and the EN Interfaces

The cropped raw image was first pre-processed to obtain a corneal mask, which was used to detect the EP and the EN interfaces. For each A-scan 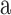of mean grayscale value of 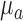and standard deviation 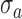, the points with grayscale values above 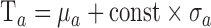were retained and other points were set to zero. Processing each A-scan individually ensured that some points were retained from each A-scan. The image, with pre-processed A-scan, is shown in Figure 4a. This step reduces the central artifact because the A-scans within the central artifact are processed independently and they have higher means, therefore, most of the points of those A-scans are set to zero. For each row 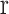, of the resulting image shown in Figure 4a, of mean grayscale value of 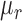and standard deviation 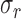, the points with values above were retained and other points were set to zero as shown in Figure 4b. This step reduces the horizontal line artifact, which has a higher mean; therefore, most of the points of the horizontal line artifact are set to zero. A 3 × 3 median filter was applied two times on the resultant image to reduce the scattered points as shown in Figure 4c. A post-processing step was done using the vertical projection of the image in Figure 4c to remove any outlier points at the top. An example of the final corneal mask is shown in Figure 4d.

Figure 4.

(a) The image in Figure 3a after setting the pixels in each A-scan below some threshold to zero, (b) the image in Figure 4a after setting the pixels in each row below some threshold to zero, (c) the image in Figure 4b after applying median filtering to remove the scattered noise points, and (d) the image in Figure 4c after post-processing to remove outlier points above the corneal apex.

The first nonzero point in each A-scan of the corneal mask was used to estimate the EP interface. A second order polynomial was used to estimate the EP interface where it provided good approximation for the interfaces of the cornea as suggested by LaRocca et al.,18 Zhang et al.,22 and Eichel et al.27 To obtain a robust estimation, the Random Sample Consensus (RANSAC)29 method was used to find the best fitted polynomial. The last nonzero point in each A-scan of the corneal mask was used to estimate the EN interface. RANSAC was used with a second order polynomial model to estimate the EN interface. An example of the estimated EP and EN interfaces is shown in blue and orange dotted lines, respectively, in Figure 5a.

Figure 5.

(a) Initial detection of the epithelium and endothelium in the image in Figure 4d, and (b) final detection of the epithelium and endothelium using the image in Figure 3c.

The raw OCT image was smoothed using a 3 × 3 weighted average filter.30 A search region was constructed for the EP interface by moving its estimate up and down using a fixed window of 5 pixels (i.e., 7.5 μm). Since the EP interface is bright, the point with maximum grayscale value within the vertical search window was selected. The final detected EP is obtained by fitting a second order polynomial to the selected points. The EN interface is obtained using the same steps. An example of the final detection of the EP and EN interfaces is shown in blue and orange solid lines, respectively, in Figure 5b.

Segmentation of Inner Interfaces

In this study, we used the raw images and the averaged images in the segmentation of the inner interfaces and compared between their segmentation results. The segmentation of the inner interfaces was done in three steps: the localization, the initial segmentation, and the final segmentation.

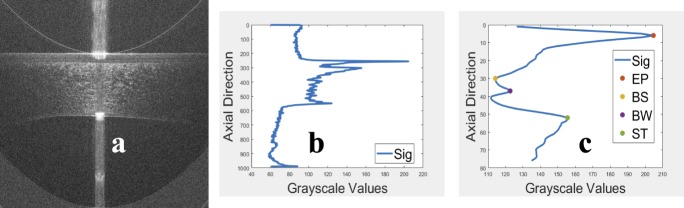
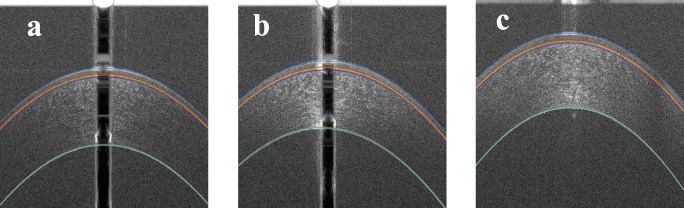
An image, with flat-EP, was obtained as shown in Figure 6a by shifting each A-scan of the raw (or averaged) image circularly such that the EP became a straight line. The central part, which has higher SNR, of the flat-EP image was vertically projected. Then, the vertical projection was smoothed using a 3 × 1 average filter as shown in Figure 6b. The EP location was detected as the first prominent peak in the vertical projection because the EP is hyperreflective.7,8 The BW and the ST locations were detected as the two prominent peaks just after the EP peak because the BW and ST are hyperreflective.10,11 The BS location was detected as the location of the minimum value between the EP peak and the BW peak because the BS is hyporeflective.9 The detected locations are shown in Figure 6c. To ensure the accuracy of the detected peaks for BW and ST interfaces, the search was limited into a fixed window of length of 70 pixels (i.e., approximately 105 μm) after the EP peak.

Figure 6.

(a) The image in Figure 3c after flattening the epithelium, (b) the mean A-scan of the image in Figure 6a, and (c) the detected locations of the epithelium, basal-epithelial, Bowman's, and stroma in the mean A-scan.

An image, with flat-EN, was obtained as shown in Figure 7a, then the central part was vertically projected as shown in Figure 7b. The EN location was detected as the last peak prominent in the vertical projection because the EN interfaces are hyperreflective.12 The DM was detected as the location of the minimum value just before the EN peak in the vertical projection as shown in Figure 7c because the DM is hyporeflective.12 The BS, the BW, and the ST interfaces were approximated by translating the detected EP interface to their corresponding locations since these interfaces are close to the EP interface. The DM interface was approximated by translating the detected EN interface to its location since it is close to the EN interface.

Figure 7.

(a) The image in Figure 3c after flattening the endothelium, (b) the mean A-scan of the image in Figure 7a, and (c) the detected locations of Descemet's and endothelium in the mean A-scan.

An example of the initial segmentation of the inner interfaces is shown in Figure 8a.

Figure 8.

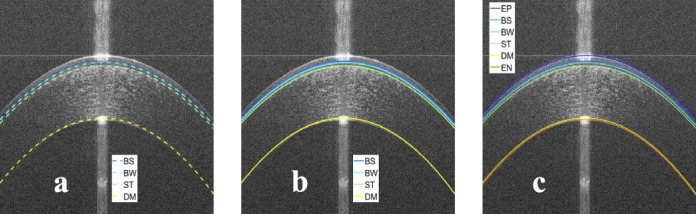
(a) Initial detection of the inner interfaces overlaid on the image in Figure 3c, (b) final detection of the inner interfaces overlaid on the image in Figure 3c, and (c) final detection of all interfaces overlaid on the image in Figure 3a.

The raw (or averaged) image was used to find the final segmentation of inner interfaces. A search region was constructed for each of the inner interfaces by moving its approximation up and down using a fixed window of length of 5 pixels (i.e., 7.5 μm). Since the BW and the ST interfaces are bright, the point with maximum grayscale value within the vertical search window was selected. Then, the final detection was obtained by fitting the selected points to a second order polynomial using least squares. Since the BS and the DM interfaces are dark interfaces, the point with minimum grayscale value within the vertical search window was selected. Then, the final detection was obtained by fitting the extracted points to a second order polynomial using least squares. Examples of the final segmentation of the inner interfaces and the final segmentation of all interfaces are shown in Figures 8b and 8c, respectively.

Study Design

Five trained manual operators (TMOs) and two corneal specialists participated in the study to validate the automatic segmentation algorithm (AUS) against the TMOs on normal and abnormal corneas. The validation was done quantitatively by measuring the repeatability of the TMOs and AUS, the reproducibility between the TMOs, and the reproducibility between the AUS and TMOs. Additionally, a subjective test was conducted by corneal specialists to subjectively assess both the manual and automatic segmentation.

The repeatability was measured by performing the manual and automatic segmentation twice on the same images then calculating the intraoperator error. The intraoperator error was calculated as the difference in pixels between the first segmentation and the second segmentation of the same operator (i.e., self-difference in pixels). The first and second TMOs were instructed to segment the images of the first testing data set, consisting of 15 raw OCT images and their averaged versions, twice.

The reproducibility of manual segmentation of one operator by another operator was measured by performing the manual segmentation on the same images then calculating the interoperator error. The interoperator error was calculated as the difference in pixels between the manual segmentation of one operator and the manual segmentation of another operator (i.e., mutual-difference in pixels). The interoperator error was calculated for all testing data sets. The first testing data set was already segmented for the repeatability, but it was used to assess the reproducibility. The third and fourth TMOs were instructed to segment the images of the second testing data set, consisting of 50 raw OCT images and their averaged versions, once. The third and fifth TMOs were instructed to segment the images of the third testing data set, consisting of 10 raw OCT images, once.

The reproducibility of manual segmentation by the automatic segmentation was assessed by calculating the segmentation error between the manual segmentation and the automatic segmentation on all testing data sets. The segmentation error was calculated as the difference in in pixels between the manual segmentation of some operator and the automatic segmentation (i.e., algorithm-operator difference in pixels). The segmentation error was calculated for all testing data sets. The first testing data set was already segmented by the AUS; therefore, the second and third testing data sets were segmented using the AUS.

The subjective test was conducted by two corneal specialists to assess the AUS against the TMOs. The subjective test included microlayer-segmentation grading to assess how good the segmentation matches the corneal microlayer interfaces. Also, the subjective test included regional-segmentation grading to assess how good the segmentation matches the corneal microlayer interfaces in central and peripheral regions of the cornea. The subjective test had scale from “1” to “5” where “5” represented excellent and “1” represented poor. The first specialist conducted the subjective test on the first testing data set and the second corneal specialist conducted the subjective test on the second testing data set.

In all comparisons, Wilcoxon rank sum test (WRST) was used with a significance level of 0.05. The nonparametric WRST was used since it exhibits no assumptions about the distribution of the data. A P-value of less than 0.05 was considered statistically significant. Values are presented as mean ± standard deviation.

All the methods and statistics have been implemented and run using MATLAB 2015b (MathWorks, Natick, MA), Windows 7 OS, and Dell Latitude E5570 (Intel Core i7-6820HQ CPU at 2.70 GHz, 32 GB RAM).

Results

Datasets Analysis

Forty-five consecutive patients, 25 males and 20 females, participated in the study. The ages ranged from 18 to 81 years with mean 40 ± 22 years. The first testing data set included 15 OCT images for normal corneas in which the top artifact was present in 15 images, the horizontal line artifact was present in 11 images, and the central artifact was present in 12 images. The second testing data set included 50 OCT images for normal corneas in which the top artifact was present in 44 images, the horizontal line artifact was present in 25 images, and the central artifact was present in 44 images. The third training data set included 10 OCT images for abnormal corneas in which the top artifact was present in 10 images, the horizontal line artifact was present in five images, and the central artifact was present in six images.

Intraoperator Error Results

The results of the intraoperator error using the averaged images and raw images are summarized in Tables 1 and 2. The WRST shows that the mean intraoperator error of the AUS is significantly less than the mean intraoperator error of the TMOs for both averaged (0.53 ± 1.80 vs. 2.32 ± 2.39 pixels; P < 0.0001) and raw images (0.46 ± 0.99 vs. 2.39 ± 2.68 pixels; P < 0.0001). Also, the intraoperator errors are significant across all interfaces. For all images, the mean intraoperator error of the AUS is significantly less than the mean intraoperator error of the TMOs (0.50 ± 1.45 vs. 2.36 ± 2.54 pixels; P < 0.0001). Given the axial resolution of the system, the AUS has a mean intraoperator error of 0.5 × 1.5 μm = 0.75 μm compared with 2.36 × 1.5 μm = 4.96 μm for the TMOs.

Table 1.

Intraoperator Error (Self-Difference in Pixels) on First Testing Data Set

Interface	Error on Averaged Images				Error on Raw Images
	First Operator Error	Second Operator Error	Mean Operator Errora	Automatic Segmentation Errora	First Operator Error	Second Operator Error	Mean Operator Errorb	Automatic Segmentation Errorb
EP	1.89 ± 1.47	1.75 ± 1.37	1.82 ± 1.42	0.08 ± 0.10*	2.15 ± 1.74	1.43 ± 1.19	1.79 ± 1.53	0.12 ± 0.18**
BS	1.99 ± 1.57	2.01 ± 1.55	2.00 ± 1.56	0.10 ± 0.23*	2.22 ± 2.05	1.81 ± 1.54	2.01 ± 1.82	0.38 ± 0.72**
BW	2.10 ± 1.70	1.66 ± 1.40	1.88 ± 1.57	0.05 ± 0.09*	2.40 ± 2.18	1.58 ± 1.32	1.99 ± 1.85	0.13 ± 0.34**
ST	2.89 ± 2.30	2.23 ± 1.84	2.56 ± 2.11	0.23 ± 0.38*	2.96 ± 2.52	2.03 ± 1.90	2.49 ± 2.27	0.19 ± 0.30**
DM	3.02 ± 3.59	2.86 ± 2.97	2.94 ± 3.29	1.39 ± 2.90*	3.20 ± 3.83	3.20 ± 3.75	3.20 ± 3.79	1.10 ± 1.60**
EN	2.80 ± 3.46	2.67 ± 3.15	2.75 ± 3.30	1.35 ± 2.94*	3.25 ± 3.82	2.53 ± 3.37	2.88 ± 3.62	0.87 ± 1.28**
Mean	2.45 ± 2.55	2.20 ± 2.22	2.32 ± 2.39	0.53 ± 1.80*	2.69 ± 2.85	2.10 ± 2.47	2.39 ± 2.68	0.46 ± 0.99**

^a*P < 0.0001.

^b**P < 0.0001 (significance level = 0.05).

Table 2.

Mean Intraoperator Error (Self-Difference in Pixels) on First Testing Data Set

Interface	Mean Operator Errora	Mean Automatic Segmentation Errora
EP	1.80 ± 1.48	0.10 ± 0.15*
BS	2.01 ± 1.70	0.24 ± 0.55*
BW	1.93 ± 1.72	0.09 ± 0.25*
ST	2.52 ± 2.19	0.21 ± 0.35*
DM	3.07 ± 3.55	1.25 ± 2.35*
EN	2.81 ± 3.46	1.11 ± 2.28*
Mean	2.36 ± 2.54	0.50 ± 1.45*

^a*P < 0.0001 (significance level = 0.05).

Interoperator Error Results

The results of interoperator errors are summarized in Table 3. The WRST shows that the mean interoperator error for the averaged images is significant compared with the mean interoperator error for the raw images (2.93 ± 3.02 vs. 3.17 ± 3.87 pixels; P < 0.0001). Also, the interoperator errors are significant across all interfaces except DM interface. The DM and the EN interfaces have the largest errors. Given the axial resolution, the mean interoperator error across all images is 3.05 ± 3.47 pixels, which is approximately 3.05 × 1.5 μm = 4.58 μm.

Table 3.

Interoperator Error (Mutual-Difference in Pixels) on First and Second Testing Data Sets^a

Interface	Error on Averaged Images			Error on Raw Images			Mean Error Over All Images
	First vs. Second Operators	Third vs. Fourth Operators	Meanb	First vs. Second Operators	Third vs. Fourth Operators	Meanb
EP	2.12 ± 1.65	1.39 ± 1.10	1.79 ± 1.47*	2.15 ± 1.76	1.81 ± 1.63	1.99 ± 1.71	1.89 ± 1.60
BS	3.99 ± 2.47	2.02 ± 1.55	3.09 ± 2.32*	3.53 ± 2.53	1.84 ± 1.65	2.78 ± 2.34	2.94 ± 2.34
BW	2.61 ± 2.17	1.33 ± 1.15	2.03 ± 1.89*	3.00 ± 2.88	1.45 ± 1.19	2.31 ± 2.42	2.17 ± 2.17
ST	3.43 ± 3.06	1.70 ± 1.48	2.66 ± 2.63*	3.98 ± 3.88	1.98 ± 1.73	3.22 ± 3.38	2.93 ± 3.02
DM	7.54 ± 4.13	2.25 ± 1.85	5.43 ± 4.28**	7.43 ± 6.03	2.53 ± 1.88	5.62 ± 5.46	5.52 ± 4.89
EN	3.38 ± 4.06	2.01 ± 1.90	2.81 ± 3.41*	4.41 ± 6.70	1.98 ± 1.58	3.48 ± 5.48	3.13 ± 4.54
Mean	3.84 ± 3.54	1.76 ± 1.55	2.93 ± 3.02*	4.08 ± 4.66	1.90 ± 1.64	3.17 ± 3.87	3.05 ± 3.47

^aFirst and second operators segmented the first testing data set, and the third and fourth operators segmented the second testing data set.

^b*P < 0.0001, **P = 0.0528 (significance level = 0.05).

Segmentation Error Results

The results of the segmentation errors between the AUS and the TMOs for normal corneas are summarized in Tables 4 and 5 for the averaged images and raw images, respectively. The WRST results show that the mean segmentation error of the AUS is significantly different than the mean interoperator error between the TMOs for the averaged images (3.44 ± 3.46 vs. 2.93 ± 3.02; P < 0.0001). The mean segmentation error of the AUS is significantly different than the mean interoperator error between the TMOs for the raw images (3.83 ± 4.11 vs. 3.17 ± 3.87; P < 0.0001). However, in both cases, the difference between the mean errors is less than one pixel for the averaged images (i.e., 0.51 pixel; 0.77 μm) and for the raw image (i.e., 0.66 pixel; 0.99 μm). Also, the segmentation error with the first TMO is significantly different than the segmentation error with the second TMO for both averaged and raw images (P < 0.0001). The segmentation error with the third TMO is significantly different than the segmentation error with the fourth TMO for both averaged and raw images (P < 0.0001). This means that the segmentation error is not enough to judge the segmentation of the AUS due to the subjectivity of the manual segmentation; therefore, the specialist subjective test was further conducted. Finally, the WRST shows that the mean segmentation error of the averaged images is significantly less than the mean segmentation error of the raw images (3.44 ± 3.46 vs. 3.83 ± 4.11 pixels; P < 0.0001).

Table 4.

Segmentation Error (Algorithm-Operator Difference in Pixels) on Averaged Images of First and Second Testing Data Sets^a

Interface	Error With First Operatorb	Error With Second Operatorb	Error With Third Operatorc	Error With Fourth Operatorc	Mean Error
EP	2.86 ± 2.00	2.65 ± 2.10*	1.35 ± 1.80	2.77 ± 2.07**	2.43 ± 2.09
BS	4.68 ± 2.54	2.12 ± 1.83*	5.58 ± 3.74	5.38 ± 3.00**	4.35 ± 3.14
BW	2.20 ± 2.05	1.96 ± 1.60*	2.26 ± 2.10	2.21 ± 2.23**	2.15 ± 2.00
ST	3.48 ± 3.16	2.98 ± 2.57*	3.39 ± 2.60	3.35 ± 2.83**	3.29 ± 2.81
DM	7.31 ± 4.56	3.49 ± 4.51*	4.55 ± 4.55	3.89 ± 3.52**	4.91 ± 4.63
EN	3.77 ± 5.02	4.18 ± 4.81*	2.52 ± 3.14	3.69 ± 3.80**	3.59 ± 4.40
Mean	4.05 ± 3.81	2.90 ± 3.26*	3.26 ± 3.42	3.54 ± 3.11**	3.44 ± 3.46

^aFirst and second operators segmented the first testing data set, and the third and fourth operators segmented the second testing data set.

^b*P < 0.0001.

^c**P < 0.0001 (significance level = 0.05).

Table 5.

Segmentation Error (Algorithm-Operator Difference in Pixels) on Raw Images of First and Second Testing Data Sets^a

Interface	Error With First Operatorb	Error With Second Operatorb	Error With Third Operatorc	Error With Fourth Operatorc	Mean Error
EP	2.46 ± 1.71	2.71 ± 2.17*	2.71 ± 2.42	3.60 ± 2.70**	2.84 ± 2.29
BS	4.44 ± 2.60	2.66 ± 2.40*	6.81 ± 4.26	5.23 ± 3.51**	4.66 ± 3.53
BW	2.00 ± 1.91	2.36 ± 2.28*	3.20 ± 3.14	2.50 ± 2.38**	2.47 ± 2.47
ST	3.12 ± 2.99	3.33 ± 3.35*	4.47 ± 3.57	3.92 ± 3.51**	3.61 ± 3.37
DM	8.53 ± 6.60	3.65 ± 5.70*	6.63 ± 4.84	4.07 ± 3.68**	5.79 ± 5.89
EN	3.97 ± 6.41	4.23 ± 5.66*	2.46 ± 2.23	4.01 ± 4.31**	3.78 ± 5.21
Mean	4.09 ± 4.74	3.16 ± 3.95*	4.34 ± 3.92	3.88 ± 3.48**	3.83 ± 4.11

^aFirst and second operators segmented the first testing data set, and the third and fourth operators segmented the second testing data set.

^b*P < 0.0001.

^c**P < 0.0001 (significance level = 0.05).

The results of the segmentation errors between the AUS and the TMOs for abnormal corneas are summarized in Table 6 for the raw OCT images. The mean segmentation error of the AUS is significantly different than the mean interoperator error between the TMOs (4.90 ± 4.27 vs. 1.90 ± 1.64; P < 0.0001). However, the difference between the mean errors (i.e., 3 pixels; 4.5 μm) is comparable with the optical resolution of the machine (i.e., 3 μm).

Table 6.

Interoperator Error (Mutual-Difference in Pixels) and Segmentation Error (Algorithm-Operator Difference in Pixels) on Third Testing Data Set

Interface	Interoperator Errora	Segmentation Error With Third Operatorb	Segmentation Error With Fifth Operatorb	Mean Segmentation Errora
EP	1.81 ± 1.63*	3.87 ± 2.88	3.45 ± 2.34**	3.67 ± 2.64
BS	1.84 ± 1.65*	6.79 ± 4.85	4.54 ± 3.48**	5.69 ± 4.38
BW	1.45 ± 1.19*	5.12 ± 4.93	3.64 ± 3.03**	4.39 ± 4.17
ST	1.98 ± 1.73*	5.53 ± 4.39	4.74 ± 3.38**	5.12 ± 3.92
DM	2.53 ± 1.88*	10.34 ± 6.16	4.58 ± 3.83**	7.63 ± 5.94
EN	1.98 ± 1.58*	4.16 ± 3.64	3.49 ± 3.14**	3.84 ± 3.42
Mean	1.90 ± 1.64*	5.74 ± 4.93	4.01 ± 3.21**	4.90 ± 4.27

^a*P < 0.0001.

^b**P < 0.0001 (significance level = 0.05).

Running Time Results

The AUS has mean running time of 0.19 ± 0.07 seconds per image compared with mean running time of 193.95 ± 194.53 seconds for the TMOs. The WRST shows that the running time of the AUS is significantly less than that of the TMOs (P < 0.0001).

Subjective Test

The results of the subjective test for microlayer grading in both the averaged and raw images are summarized in Tables 7 and 8, respectively. The mean subjective microlayer grading of the AUS is not significant from the mean subjective microlayer grading of the TMOs (4.94 ± 0.32 vs. 4.96 ± 0.24; P = 0.5081) for the averaged images and (4.92 ± 0.32 vs. 4.96 ± 0.25; P = 0.0525) for the raw images. The results of the subjective test for regional grading in both the averaged and raw images are summarized in Tables 9 and 10. The mean subjective regional grading of the AUS is significantly higher than the mean subjective regional grading of the TMOs (4.96 ± 0.26 vs. 4.79 ± 0.60; P = 0.0275) for the averaged images and (4.94 ± 0.23 vs. 4.69 ± 0.71; P = 0.0083) for the raw images.

Table 7.

Subjective Microlayer-Segmentation Grading on Averaged Images

Interface	First Specialist Grading on Averaged Images of First Testing Data Set			Second Specialist Grading on Averaged Images of Second Testing Data Set			Mean Operator Grading*	Mean Automatic Segmentation Grading*
	First Operator	Second Operator	Automatic Segmentation	Third Operator	Forth Operator	Automatic Segmentation
EP	5.00 ± 0.00	5.00 ± 0.00	5.00 ± 0.00	5.00 ± 0.00	5.00 ± 0.00	5.00 ± 0.00	5.00 ± 0.00	5.00 ± 0.00 a
BS	5.00 ± 0.00	4.93 ± 0.25	4.70 ± 0.70	4.80 ± 0.56	5.00 ± 0.00	5.00 ± 0.00	4.94 ± 0.27	4.80 ± 0.59 b
BW	5.00 ± 0.00	4.83 ± 0.46	4.87 ± 0.43	4.87 ± 0.35	5.00 ± 0.00	5.00 ± 0.00	4.92 ± 0.31	4.91 ± 0.36 c
ST	5.00 ± 0.00	4.83 ± 0.46	4.87 ± 0.43	5.00 ± 0.00	4.93 ± 0.26	5.00 ± 0.00	4.93 ± 0.29	4.91 ± 0.36 d
DM	4.97 ± 0.18	5.00 ± 0.00	5.00 ± 0.00	4.87 ± 0.35	5.00 ± 0.00	5.00 ± 0.00	4.97 ± 0.18	5.00 ± 0.00 e
EN	4.93 ± 0.37	5.00 ± 0.00	5.00 ± 0.00	5.00 ± 0.00	5.00 ± 0.00	5.00 ± 0.00	4.98 ± 0.21	5.00 ± 0.00 f
Mean	4.98 ± 0.18	4.95 ± 0.24	4.91 ± 0.38	4.92 ± 0.31	4.99 ± 0.11	5.00 ± 0.00	4.96 ± 0.24	4.94 ± 0.32 g

^*a P = NaN (i.e., not a number).

^bP = 0.0627.

^cP = 0.9914.

^dP = 0.7930.

^eP = 0.2206.

^fP = 0.4893.

^gP = 0.5081 (significance level = 0.05).

Table 8.

Subjective Microlayer-Segmentation Grading on Raw Images

Interface	First Specialist Grading on Raw Images of First Testing Data Set			Second Specialist Grading on Raw Images of Second Testing Data Set			Mean Operator Grading*	Mean Automatic Segmentation Grading*
	First Operator	Second Operator	Automatic Segmentation	Third Operator	Forth Operator	Automatic Segmentation
EP	5.00 ± 0.00	5.00 ± 0.00	5.00 ± 0.00	5.00 ± 0.00	5.00 ± 0.00	5.00 ± 0.00	5.00 ± 0.00	5.00 ± 0.00 a
BS	5.00 ± 0.00	5.00 ± 0.00	4.77 ± 0.57	5.00 ± 0.00	5.00 ± 0.00	5.00 ± 0.00	5.00 ± 0.00	4.84 ± 0.47 b
BW	4.97 ± 0.18	4.90 ± 0.40	4.87 ± 0.35	5.00 ± 0.00	5.00 ± 0.00	5.00 ± 0.00	4.96 ± 0.26	4.91 ± 0.29 c
ST	4.97 ± 0.18	4.90 ± 0.40	4.87 ± 0.35	4.73 ± 0.70	4.87 ± 0.35	4.93 ± 0.26	4.89 ± 0.41	4.89 ± 0.32 d
DM	4.97 ± 0.18	4.97 ± 0.18	5.00 ± 0.00	5.00 ± 0.00	4.60 ± 0.74	4.80 ± 0.56	4.91 ± 0.36	4.93 ± 0.33 e
EN	4.93 ± 0.25	5.00 ± 0.00	5.00 ± 0.00	5.00 ± 0.00	5.00 ± 0.00	4.87 ± 0.52	4.98 ± 0.15	4.96 ± 0.30 f
Mean	4.97 ± 0.16	4.97 ± 0.20	4.93 ± 0.31	4.96 ± 0.30	4.91 ± 0.36	4.93 ± 0.33	4.96 ± 0.25	4.92 ± 0.32 g

^*a P = NaN (i.e., not a number).

^bP = 0.0014.

^cP = 0.1813.

^dP = 0.5735.

^eP = 0.6197.

^fP = 0.9927.

^gP = 0.0525 (significance level = 0.05).

Table 9.

Subjective Regional-Segmentation Grading on Averaged Images

Interface	First Specialist Grading on Averaged Images of First Testing Data Set			Second Specialist Grading on Averaged Images of Second Testing Data Set			Mean Operator Grading*	Mean Automatic Segmentation Grading*
	First Operator	Second Operator	Automatic Segmentation	Third Operator	Forth Operator	Automatic Segmentation
Central	5.00 ± 0.00	4.97 ± 0.18	5.00 ± 0.00	5.00 ± 0.00	5.00 ± 0.00	5.00 ± 0.00	4.99 ± 0.11	5.00 ± 0.00 a
Peripheral	5.00 ± 0.00	4.87 ± 0.43	4.87 ± 0.43	4.33 ± 0.98	3.53 ± 0.92	5.00 ± 0.00	4.60 ± 0.79	4.91 ± 0.36 b
Mean	5.00 ± 0.00	4.92 ± 0.33	4.93 ± 0.31	4.67 ± 0.76	4.27 ± 0.98	5.00 ± 0.00	4.79 ± 0.60	4.96 ± 0.26 c

^*a P = 0.4893.

^bP = 0.0250.

^cP = 0.0275 (significance level = 0.05).

Table 10.

Subjective Regional-Segmentation Grading on Raw Images

Interface	First Specialist Grading on Raw Images of First Testing Data Set			Second Specialist Grading on Raw Images of Second Testing Data Set			Mean Operator Grading*	Mean Automatic Segmentation Grading*
	First Operator	Second Operator	Automatic Segmentation	Third Operator	Forth Operator	Automatic Segmentation
Central	5.00 ± 0.00	5.00 ± 0.00	4.97 ± 0.18	4.93 ± 0.26	5.00 ± 0.00	5.00 ± 0.00	4.99 ± 0.11	4.98 ± 0.15 a
Peripheral	4.97 ± 0.18	4.97 ± 0.18	4.87 ± 0.35	3.13 ± 0.52	3.40 ± 0.83	5.00 ± 0.00	4.40 ± 0.91	4.91 ± 0.29 b
Mean	4.98 ± 0.13	4.98 ± 0.13	4.92 ± 0.28	4.03 ± 1.00	4.20 ± 1.00	5.00 ± 0.00	4.69 ± 0.71	4.94 ± 0.23 c

^*a P = 1.0000.

^bP = 0.0016.

^cP = 0.0083 (significance level = 0.05).

Segmentation Results

To show the robustness of the proposed algorithm for different types of OCT images artifacts, some examples of the segmentations for normal corneas are shown in Figure 9, and some examples of the segmentation for abnormal corneas are shown in Figure 10. Also, examples of bad segmentation are shown in Figure 11 where the images have low SNR and CNR. To compare the AUS and the TMOs segmentations, the AUS is plotted against the TMOs segmentation. Figures 12, 13, and 14 show examples that highlight differences between TMOs and AUS segmentations.

Figure 9.

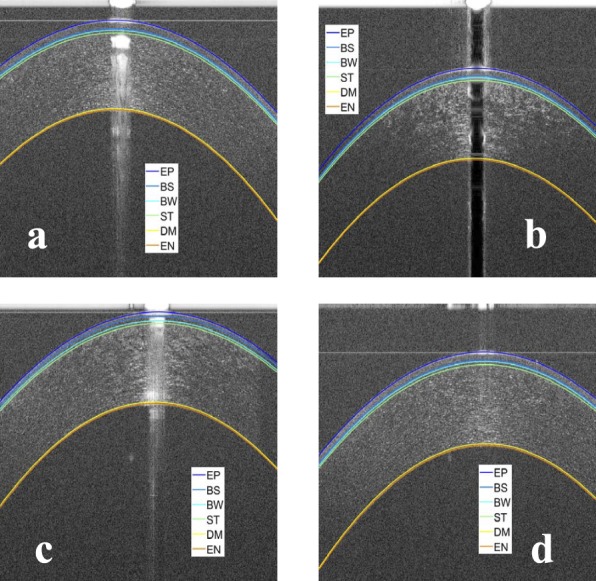
Examples of the results of the proposed segmentation algorithm for normal corneas. (a) Segmentation of an OCT image with dark central artifact and low SNR at the periphery, (b) segmentation of an OCT image with the cornea touching the top artifact, (c) segmentation of an OCT image with bright central artifact and low SNR at the periphery, and (d) segmentation of an OCT image with strong horizontal artifact and low SNR at the periphery.

Figure 10.

Examples of segmentation result for abnormal corneas: (a) an OCT image of a patient with a dry eye, (b) an OCT image of a patient with keratoconus, and (c) an OCT image of a patient with Fuchs dystrophy.

Figure 11.

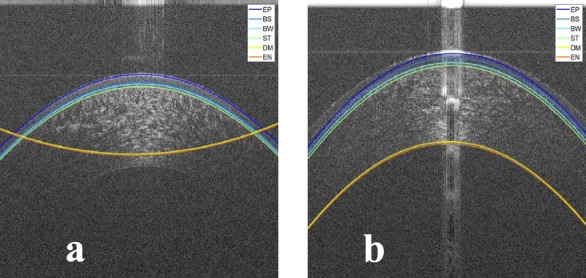
Examples of bad segmentation result for (a) an OCT image with low SNR at the epithelium and (b) an OCT image with very low SNR at the endothelium.

Figure 12.

Comparison between the manual segmentation of the first operator (red) and the automatic segmentation (blue) using an averaged OCT image. (a) The compared regions highlighted on the OCT image, (b) red window at the epithelium-air interface, (c) green window at the EN, and (d) blue window at the epithelium-air interface.

Figure 13.

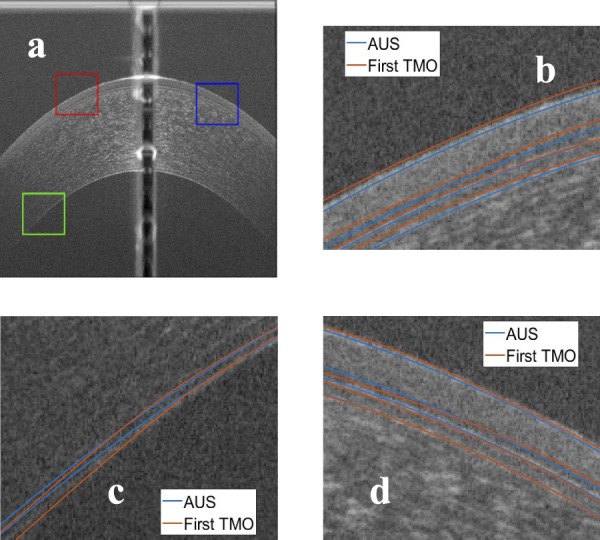
Comparison between the manual segmentation of the first operator (red) and the automatic segmentation (blue) using another averaged OCT image. (a) The compared regions highlighted on the OCT image, (b) red window at the epithelium-air interface, (c) green window at the EN, and (d) blue window at the epithelium-air interface.

Figure 14.

Comparison between the manual segmentation of the second operator (red) and the automatic segmentation (blue) using an averaged OCT image. (a) The compared regions highlighted on the OCT image, (b) red window at the epithelium-air interface, (c) green window at the EN, and (d) blue window at the epithelium-air interface.

Discussion

There is a strong evidence in the literature that measuring the thicknesses of corneal microlayers in vivo is valuable for the diagnosis of numerous corneal diseases, such as Fuchs dystrophy, keratoconus, and corneal graft rejection.4,5,12–15 Those studies have shown excellent potential in the diagnosis of these pathologies using thickness of corneal microlayers, but they have also disclosed limitations in the technology. Those most significant limitation is the lack of a robust AUS to extract quantitative data from the OCT images. Those limitations have precluded the use of corneal microlayer tomography in clinical settings.

In our experiments, it has been shown that the proposed AUS is able to segment all six corneal microlayer interfaces with excellent repeatability (i.e., less intraoperator error) that is significantly better than manual segmentation by the TMOs. Additionally, the AUS has mean segmentation error comparable to the mean interoperator error for normal corneas. We have noted that the AUS is less accurate when applied on abnormal corneas. Nevertheless, the segmentation error is comparable with the optical resolution of the machine. The subjective test results show that there is no significant difference between the segmentation of the AUS and the manual segmentation for both the averaged and raw images. The AUS is significantly better in peripheral regions than the manual operators because it can extrapolate the segmentation at low SNR regions. These results suggest that the AUS can replace the TMO in segmenting the corneal microlayer interfaces. Moreover, the comparison of the running time has shown that the AUS operates in almost real-time; while the TMOs have taken, on average, 1021 folds the time taken by the AUS to segment one image. This highlights the fact that manual segmentation is not practical in a clinical setting. On the other hand, the AUS could be adopted in clinical practices.

In our experiments, it has been shown that the registration and averaging significantly reduces the error. The intraoperator errors for the averaged images are significantly less than those for the raw images. The interoperator errors for the averaged images are significantly less than those for the raw images. The segmentation errors between the AUS and the TMOs for the averaged images are significantly less than the raw images. These results indicate the importance of the registration and averaging step in improving the segmentation quality.

In our experiments, it has been shown that the two interfaces with the largest segmentation errors are the DM and the EN interfaces. The results were consistent across all the experiments. This could be attributed to the low SNR of these interfaces, which makes the segmentation difficult. Therefore, the segmentation of the DM and the EN interfaces is very subjective, and this necessitates the usage of automatic segmentation, which has better repeatability.

Our AUS segments the six microlayer interfaces of the cornea, unlike most of the existing automatic segmentation methods in the literature that only segment two or three interfaces.18,20,22–25,28 Moreover, our AUS is faster than methods proposed by other authors. The comparison of running time results are summarized in Table 11. The AUS is almost real-time as it takes less than a quarter a second compared with other methods. The registration and averaging of images take running time of two seconds per image on average. The averaging is done on all images before segmenting them, and it is separate from the AUS; therefore, we could have excluded its time, but we included the averaging running time to give estimation of the total time. The comparison of the segmentation error between the AUS and other methods that detect three interfaces18,22,28 is summarized in Table 12. To fairly compare the methods, the error in pixels is expressed in micrometers to be independent of the machine pixel resolution. The segmentation error results for the proposed algorithm and Eichel et al.27 are summarized in Table 13. Our results are comparable with the reported methods, but our algorithm is a fully automated algorithm and segments all possible interfaces. Additionally, our algorithm does not impose any relationship or model between the interfaces as reported in the Eichel et al.27 method.

Table 11.

Comparison of Running Time Between the Proposed Automatic Segmentation and the Existing Methods

Method	Running Time (s)	Image Resolution	Number of Interfaces
Proposed Automatic Segmentation	0.19	1024 × 1000	6
Proposed Automatic Segmentation with Averaging	0.19 + 2.00 = 2.19	1024 × 1000	6
LaRocca et al.18	1.13	1024 × 1000	3
Zhang et al.22	0.52	1024 × 1000	3
Jahromi et al.28	7.99	—	3
Eichel et al.19	20	512 × 512	5
Eichel et al.27	—	—	—

Table 12.

Comparison of Segmentation Error (Algorithm-Operator Difference) Between the Proposed Automatic Segmentation and the Existing Methods Using Their Segmented Interfaces

Error in (μm)	Proposed Automatic Segmentation	Proposed Automatic Segmentation With Averaging	LaRocca et al.18	Zhang et al.22	Jahromi et al.28
EP error	2.84 × 1.5 = 4.26	2.43 × 1.5 = 3.65	0.60 × 3.4 = 2.04	0.44 × 3.4 = 1.50	0.33 × 13.3 = 4.39
BW error	2.47 × 1.5 = 3.71	2.15 × 1.5 = 3.23	0.90 × 3.4 = 3.06	0.72 × 3.4 = 2.45	0.42 × 13.3 = 5.59
EN error	3.78 × 1.5 = 5.67	3.59 × 1.5 = 5.39	1.7 × 3.4 = 5.78	1.59 × 3.4 = 5.41	0.80 × 13.3 = 10.64

Table 13.

Comparison of Segmentation Error (Algorithm-Operator Difference) Between the Automatic Segmentation and Eichel's Method27

Error in (μm)	Proposed Automatic Segmentation	Proposed Automatic Segmentation With Averaging	Eichel et al.27
EP error	2.84 × 1.5 = 4.26	2.43 × 1.5 = 3.65	3.92
BS error	4.66 × 1.5 = 6.99	4.35 × 1.5 = 6.53	—
BW error	2.47 × 1.5 = 3.71	2.15 × 1.5 = 3.23	4.59
ST error	3.61 × 1.5 = 5.42	3.29 × 1.5 = 4.94	2.86
DM error	5.79 × 1.5 = 8.69	4.91 × 1.5 = 7.37	5.94
EN error	3.78 × 1.5 = 5.67	3.59 × 1.5 = 5.39	6.52
Mean error	3.83 × 1.5 = 5.75	3.44 × 1.5 = 5.16	4.77

Limitations of the proposed algorithm include usage of a second order polynomial model for the corneal shape, and it is less accurate when applied on abnormal corneas. For future work, the algorithm will be validated on abnormal corneas with a more generic model for the corneal shape.

In conclusion, the proposed algorithm has a strong potential to improve the diagnosis of important corneal diseases by thickness measurement of the segmented corneal microlayer interfaces. Our algorithm might potentially allow the use of corneal microlayer tomography in clinical trials to set the stage for its introduction to everyday clinic flow.