Rates of niche and phenotype evolution lag behind diversification in a temperate radiation

Significance

Alternative models of evolutionary processes suggest different associations between species diversification and trait evolution, but limited empirical evidence is available to test these models across large clades at global extents. Here we investigate the relative timing of species diversification and niche and phenotypic evolution across a global plant radiation (Saxifragales) with enormous phenotypic and habitat variation. We demonstrate strong temporal lags among rates, with increased diversification occurring first, followed by niche and phenotype. Accelerated diversification rates are coincident with mid-Miocene expansion of temperate biomes. Later increases in niche and phenotypic evolutionary rates argue against density-dependent diversification alone, indicating a major role for ecological opportunity. These results have broad implications for understanding diversification processes and the origin of present-day temperate biotas.

Abstract

Environmental change can create opportunities for increased rates of lineage diversification, but continued species accumulation has been hypothesized to lead to slowdowns via competitive exclusion and niche partitioning. Such density-dependent models imply tight linkages between diversification and trait evolution, but there are plausible alternative models. Little is known about the association between diversification and key ecological and phenotypic traits at broad phylogenetic and spatial scales. Do trait evolutionary rates coincide with rates of diversification, are there lags among these rates, or is diversification niche-neutral? To address these questions, we combine a deeply sampled phylogeny for a major flowering plant clade—Saxifragales—with phenotype and niche data to examine temporal patterns of evolutionary rates. The considerable phenotypic and habitat diversity of Saxifragales is greatest in temperate biomes. Global expansion of these habitats since the mid-Miocene provided ecological opportunities that, with density-dependent adaptive radiation, should result in simultaneous rate increases for diversification, niche, and phenotype, followed by decreases with habitat saturation. Instead, we find that these rates have significantly different timings, with increases in diversification occurring at the mid-Miocene Climatic Optimum (∼15 Mya), followed by increases in niche and phenotypic evolutionary rates by ∼5 Mya; all rates increase exponentially to the present. We attribute this surprising lack of temporal coincidence to initial niche-neutral diversification followed by ecological and phenotypic divergence coincident with more extreme cold and dry habitats that proliferated into the Pleistocene. A lack of density-dependence contrasts with investigations of other cosmopolitan lineages, suggesting alternative patterns may be common in the diversification of temperate lineages.

Shifts in environmental regimes create ecological opportunities for lineages to diversify rapidly across the tree of life (1–4). However, reductions in diversification rates after initial bursts are commonly found in empirical systems (e.g., refs. 5–10). Although several models have been proposed to explain decreasing rates of species diversification, some of which are niche-neutral (7), slowdowns are most often attributed to ecological factors, especially filling of niche space and increasing competition (7, 11–13). Such density-dependent diversification should also drive rates of evolution of ecological niche and phenotypic traits that enable the exploration and partitioning of available habitat. Niche and some phenotypic attributes would then be expected to show correlated evolution during a radiation, as accelerated phenotypic evolution might enable species to exploit novel habitats. However, continuing ecological opportunity, as opposed to discrete historical events, may allow lineages to avoid saturation and should result in long-term and continuing high rates of diversification (e.g., refs. 1, 14, and 15). Further, niche-neutral diversification is also possible (e.g., ref. 13), especially when existing habitats expand without creating novel environments. Thus, it is unclear if there is a general relationship among species, ecological, and phenotypic diversification.

Surprisingly little is known about the relative timing of rate shifts among these facets of diversification at global scales and at critical points in Earth’s history. In some cases, associations between species diversification and rates of phenotypic (16–19) or ecological evolution (20–22) have been noted, while in others diversification and trait evolution are not linked (23–28). However, comparative case studies of macroevolutionary rates have examined these questions only at relatively narrow phylogenetic and spatial extents. Addressing pivotal questions of the timing of diversification of species, ecological niche, and phenotypic traits at global scales requires the study of widely distributed and diverse clades that are well-sampled for genetic, environmental, and phenotypic data. Such clades offer the opportunity for evolutionary replication of patterns and processes in different ecological and biogeographic regions. Challenges with assembling and analyzing global-scale biodiversity datasets spanning genotype, phenotype, and environment have so far limited investigations of possible associations among rates of species diversification and niche and phenotypic evolution to a few well-known clades of life [e.g., birds (9) and mammals (2)].

Here we compare the overall timing and rates of diversification and of niche and phenotypic evolution (i.e., niche and phenotypic lability) for a globally distributed plant clade, Saxifragales (approximately 2,400 species). This group is highly diverse in niche and phenotype, encompassing annual and perennial herbs, succulents, parasites, aquatics, shrubs, vines, lianas, epiphytes, and large trees. It harbors most of its diversity in temperate conditions (including montane and arid biomes) that expanded globally during cooling and drying trends in the last 15 My (15, 29, 30). In the context of both expanding and novel habitat, cold- and arid-adapted clades should experience rate increases for speciation, niche, and phenotypic traits, because the shift into new niches (via new niche-delimiting morphological traits) would provide opportunities for diversification outside of the ancestral niche. Continuing ecological opportunity may therefore provide a mechanism to escape density dependence (5–8). Saxifragales serve as an exemplar clade to examine macroevolutionary responses of lineages to the transition from a warmer, wetter Earth in the Eocene to early Miocene to colder, drier conditions that predominated afterward. Furthermore, because subclades of Saxifragales occupy diverse habitats, analysis of Saxifragales as a whole can serve as a useful multifaceted case study of the processes associated with diversification.

We built deeply sampled datasets comprising a phylogenetic backbone tree, a supermatrix covering most species in the clade, and ecological niche and phenotypic trait variables to estimate rates of species diversification and lability of ecological niche and phenotypic traits using macroevolutionary trait models. With this framework, we address the following key questions: (i) Is the macroevolutionary timing of diversification of a major, primarily temperate clade coincident with global cooling, aridification, and the proliferation of temperate habitats beginning in the late Miocene? (ii) Given this recent origin and continued expansion of major temperate biomes, have Saxifragales escaped density-dependent diversification downturns? (iii) Are shifts in niche and phenotypic lability tightly correlated with shifts in diversification rates, and, if not, in what sequence do these rate shifts occur?

Results

Biodiversity Data Assembly.

Using a phylogeny for Saxifragales inferred from a dataset of 301 genes and 627 species covering all major lineages (SI Appendix, Fig. S1) as a backbone constraint for a supermatrix analysis, we generated a tree comprising 1,736 species (72% of species diversity for Saxifragales; SI Appendix, Fig. S2), of which 1,455 (61%; SI Appendix, Fig. S3) were matched with occurrence data (736,703 occurrence records, an average of 317 occurrences per species). Major relationships recovered were consistent with recent phylogenetic work (31), including monophyly for all clades recognized as families. For the 23 phenotypic traits collected, 1,388 species (58%) had the minimum of 20% trait coverage we imposed for downstream analysis.

Niche and Phenotype Ordination.

The primary loadings on ordinated niche data captured temperature (SI Appendix, Table S1). Low values (Fig. 1, red and yellow) are associated with hotter and, to some extent, wetter habitats, as well as the hottest arid habitats; high values (Fig. 1, blue and green) are associated with cooler and drier habitats. Ordinated phenotype data (SI Appendix, Table S2) primarily captured a complex set of traits including plant height; woodiness; inflorescence, sepal, and petal shape descriptors; seed length; and several meristic traits (stamen, petal, and sepal number). Low ordinated phenotype values captured primarily low herbaceous rosette plants, and high values captured trees and shrubs.

Fig. 1.

Ancestral reconstruction across Saxifragales for PC1 of our dataset of 35 environmental variables; branches are colored in a rainbow scale from low ordinated values (red and yellow; hotter and to some extent wetter habitats, as well as the hottest arid habitats) to high ordinated values (green and blue; mostly colder and drier habitats). Black dots at nodes represent major ecological niche shifts (the upper 95th percentile of node–parent node differences). Red dots at nodes represent diversification shifts in the maximum credibility set. The inset density curves show tip rates for diversification (green), niche (orange), and phenotype (blue), all scaled from the minimum to the maximum reconstructed value. Around the edge are photographs of major representative habitats. Family codes are as follows: (a) Peridiscaceae, (b) Paeoniaceae, (c) Daphniphyllaceae, (d) Cercidiphyllaceae, (e) Altingiaceae, (f) Hamamelidaceae, (g) Iteaceae, (h) Grossulariaceae, (i) Saxifragaceae, (j) Cynomoriaceae, (k) Tetracarpaeaceae, (l) Aphanopetalaceae, (m) Penthoraceae, (n) Haloragaceae, and (o) Crassulaceae.

Niche and Phenotype: Conservatism and Correlated Evolution.

Although niche shifts are numerous throughout Saxifragales (Fig. 1), we found strong evidence for phylogenetic constraints on niche space, consistent with some degree of conservatism of both niche and phenotypic traits over >100 My of evolutionary time (λ test; niche: P = 8.3e-222; phenotype: p ∼ 0; SI Appendix, Figs. S4 and S5). To discern whether the phenotypic data captured potential niche-delimiting phenotypes, we asked whether the niche and phenotypic predictors were tightly correlated; we found strong evidence for correlated evolution between niche and phenotype (P = 4.1e-36) and their pairwise disparity (P < 2.2e-16; SI Appendix, Fig. S6).

Timing of Macroevolutionary Rates.

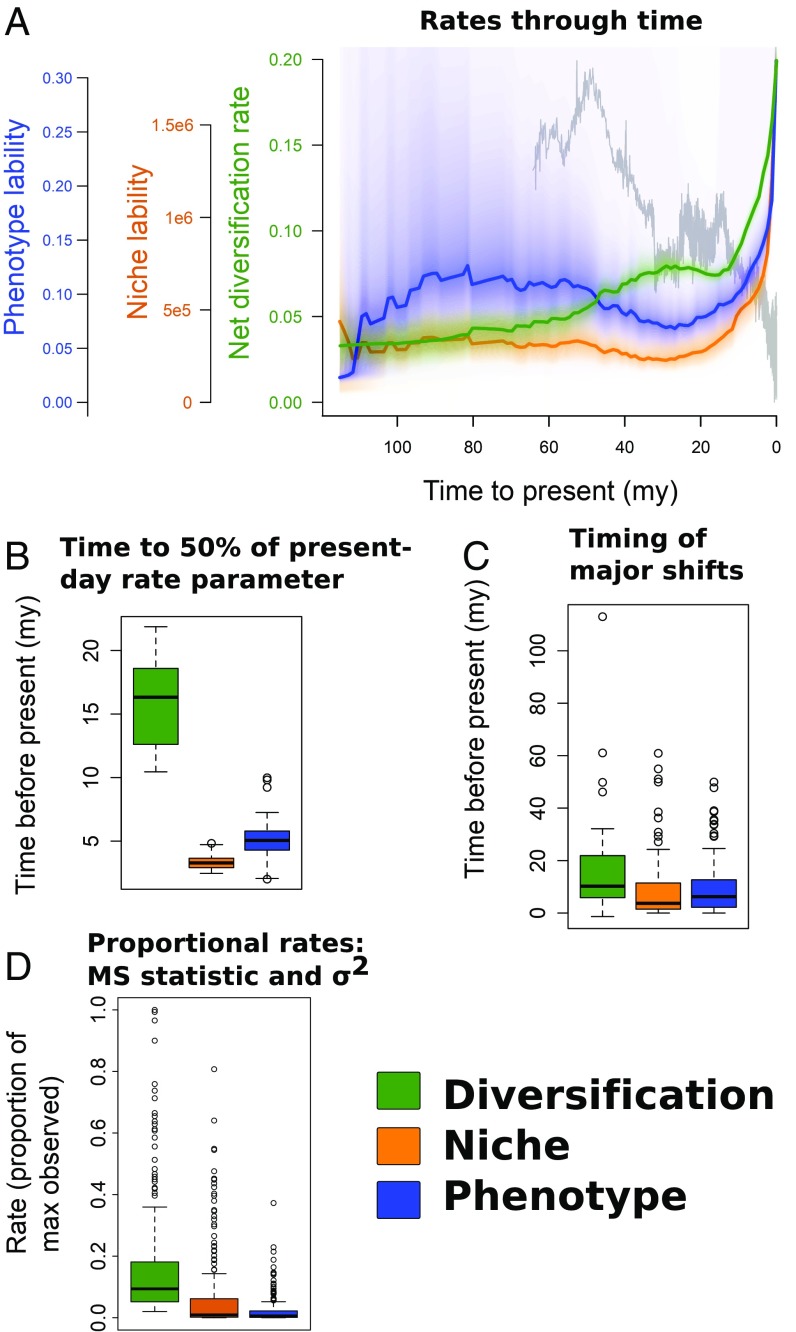
Net species diversification and rates of niche and phenotypic evolution (lability) as reconstructed by BAMM (Bayesian Analysis of Macroevolutionary Mixtures) all experienced strong increases toward the present, beginning in approximately the mid-Miocene (Fig. 2A and SI Appendix, Fig. S7), contemporaneous with the mid-Miocene Climatic Optimum (32–34). However, surprisingly, diversification rates through time show significantly earlier increases than for phenotypic and niche lability. Comparing the time to 50% of contemporaneous rates, we found diversification, niche, and phenotypic rates had significantly different timing [Fig. 2B; ANOVA P < 2e-16; all pairwise rate differences significant for Tukey honestly significant difference (HSD)], with niche and phenotypic rates lagging behind diversification. Phenotype also experienced a smaller lag either before, or more often after, niche rates for this and other analyses, although this ordering was sensitive to two alternative time calibration methods (Methods) and more often niche and phenotype timings were indistinguishable. Consistent with our rate estimates through time, shifts in diversification regimes were generally phylogenetically deeper than major ancestral shifts (upper 95th percentile) in niche and phenotype space (Fig. 2C; ANOVA P = 0.00036; all pairwise differences significant for Tukey HSD except niche vs. phenotype). Most major niche shifts (88.1% of the upper 95th percentile) and major phenotype shifts (84.6% of the upper 95th percentile) postdated 15 Mya.

Fig. 2.

(A) Median rates and rate distributions for net diversification, niche, and phenotypic macroevolutionary rates (colors shown in legend). The unit of diversification is speciation events per million years; niche and phenotypic rates are unitless. For relative comparability, the y axis is scaled from zero to the maximum median rate for all datasets. The gray curve in the background is a global temperature dataset (37). High niche evolutionary rates result from large scaling of the PCA ordination of environmental data (SI Appendix, Fig. S41). (B) Box plot showing the distributions of times to 50% of contemporaneous evolutionary rates from the mid-Miocene (15 Mya to present). (C) Box plot showing the distributions of times to present for either major shifts in ancestral reconstructions (environment, phenotype; 95th percentile of node–parent node differences) or shifts in the best shift configuration (diversification). (D) Box plot of evolutionary rates for MS (diversification) and σ² (niche and phenotype) as proportionally scaled to the maximum (contemporary) rates. Higher clade values for, for example, diversification indicate earlier rate increases. MS here parameterizes extinction as ε = 0.5; see SI Appendix, Figs. S8–S11 for evaluation of extinction fractions.

We also calculated the MS diversification statistic (35) and Ornstein–Uhlenbeck (OU) σ² trait rate parameters (36) for the entire tree and every subclade. In addition to the pure-birth MS statistic (ε = 0), we used a series of extinction proportions (ε = 0.1, 0.5, 0.9) to assess the impact of extinction on the MS results. We identified lags in evolutionary rates with early diversification increases followed by niche and then phenotype (Fig. 2D and SI Appendix, Figs. S8–S13), which was significant for all pairwise comparisons (Tukey HSD; rates scaled to a proportion of their contemporary rate for comparability; P < 0.002 for all comparisons). Higher extinction proportions reduced overall diversification rate scaling but pairwise comparisons remained significant.

Correlation Between Macroevolutionary Rates and Climate/Climatic Variation.

After the mid-Miocene Climatic Optimum, the timeframe in which we observed major increases in macroevolutionary rates (for diversification, niche, and phenotype), there was a very strong correlation between historical global temperature data (37) and macroevolutionary rates reconstructed by BAMM (fit using an exponential model; net diversification: F test P < 2.2e-16; R² = 0.8352; niche lability: P < 2.2e-16, R² = 0.845; phenotypic lability: P < 2.2e-16, R² = 0.779). We also observed a weaker, but significant, relationship between rates and variation in temperature (measured as the SD over moving 0.1-My intervals, fit using an exponential model; net diversification: F test P < 2.2e-16, R² = 0.2003; niche lability: P = 3.23e-2, R² = 0.03233; phenotypic lability: P = 6.25e-8, R² = 0.05527; SI Appendix, Figs. S14–S19). A combined model incorporating both temperature and temperature variability best explained the data (mean adjusted R² increase 0.0163, Akaike weight 0.705 for diversification, ∼1 for niche and phenotype), suggesting that temperature and temperature variability have independent explanatory power.

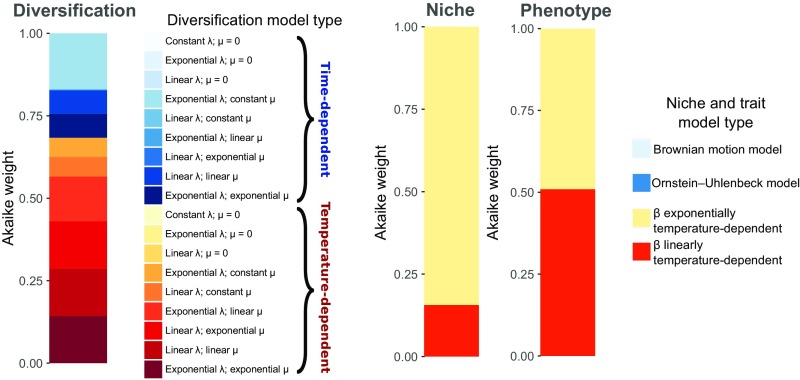
We fit likelihood models of temperature (n = 9) and time dependence (n = 9) in RPANDA [refs. 38–40; see Fig. 4 and SI Appendix, Tables S3–S5] to evaluate the association of diversification, niche, and phenotypic rates with historical temperature. For niche and phenotypic rates, support for temperature dependence was decisive (combined Akaike weights of linear and exponential models ∼1); Akaike weights moderately supported an exponential temperature relationship with niche lability (0.84), but support for either linear or exponential dependence was equivocal for phenotypic lability. For diversification rates, RPANDA was unable to distinguish a single best model. The best model (exponential speciation constant extinction with respect to time) did not include climate, but ΔAIC (Akaike information criterion) was only 0.325 and the ΔAkaike weight 0.025 compared with the second-best model (linear speciation and extinction with respect to temperature). The sum of Akaike weights for models with temperature was 0.6837 vs. 0.3163 for those without it (Fig. 4 and SI Appendix, Tables S3–S5 and S8–S10), indicating that the majority of the likelihood was in temperature-dependent models.

Fig. 4.

Visualization of RPANDA model fits, represented in relative terms as Akaike weights (y axis), as stacked bar graphs. For diversification, λ = speciation and μ = extinction. For niche and phenotype, β = rate parameter. For instance, “time-dependent exponential λ; constant μ” means that speciation is exponentially related to time and extinction is constant. Overall, red to orange colors represent temperature-dependent models, which occupy most of the likelihood. Blue colors represent temperature-neutral models. While all legend colors were plotted, not all are visible in the figure because some models have ∼0 weight.

Robustness to Priors.

Concern has been raised about the sensitivity of BAMM to prior specification (41); to assess this issue, we explored a series of extreme prior formulations on expected rate events and rate priors, varied over two orders of magnitude compared with the recommended BAMM priors (for further details see SI Appendix, Supporting Information Text and Figs. S20–S22). Expected event priors did not produce noticeable effects on rate curves. Rate priors had an effect particularly on early diversification estimates >40 My before present, with higher rate priors especially for niche and phenotypic analyses tending to result in an early burst of evolution ∼80 to 100 My before present that was absent with smaller prior values. This area of the rate curves was sensitive to dating procedure as well as prior (Methods and SI Appendix, Fig. S23), in sum suggesting greater uncertainty deeper in time. However, within the period of interest for this work (≤15 My before present), rate curves were essentially identical to those observed in recommended priors, and overall shape was robust to prior formulation and dating approach.

Niche- and Phenotype-Associated Diversification.

To assess whether observed rate patterns were associated with spatial variation in climate, we ran a series of trait-associated diversification tests with summary geographic data, using both the BAMM-based STRAPP (STructured Rate Permutations on Phylogenies) statistic and the semiparametric es-SIM statistic. We did not see significant associations of elevation (STRAPP: P = 0.868; es-SIM: P = 0.849) or latitude (STRAPP: P = 0.818; es-SIM: P = 0.194) with net diversification. Using STRAPP, we also did not find relationships of elevation and latitude with niche lability (elevation: P = 0.816; latitude: P = 0.101) or phenotypic lability (elevation: P = 0.386; latitude: P = 0.193). We also did not see a relationship between continental biogeography and diversification rates (STRAPP: P = 0.879), niche lability (STRAPP: P = 0.056), or phenotypic lability (STRAPP: P = 0.751).

These results are consistent with a worldwide response of Saxifragales to climatic cooling and aridification, without a clear association with temperate biomes alone (but see below). Ancestral reconstructions of climate space suggest that Saxifragales were already present in temperate habitats before Miocene cooling; the majority of the shifts into the most extreme areas of niche space (the upper 97.5th and lower 2.5th percentiles of contemporary values representing, respectively, the hottest desert and equatorial habitats and the coldest polar and montane habitats) are within the last 5 My (niche: 56.72%, phenotype: 61.54%; Fig. 1 and SI Appendix, Figs. S24 and S25).

Subclade Patterns.

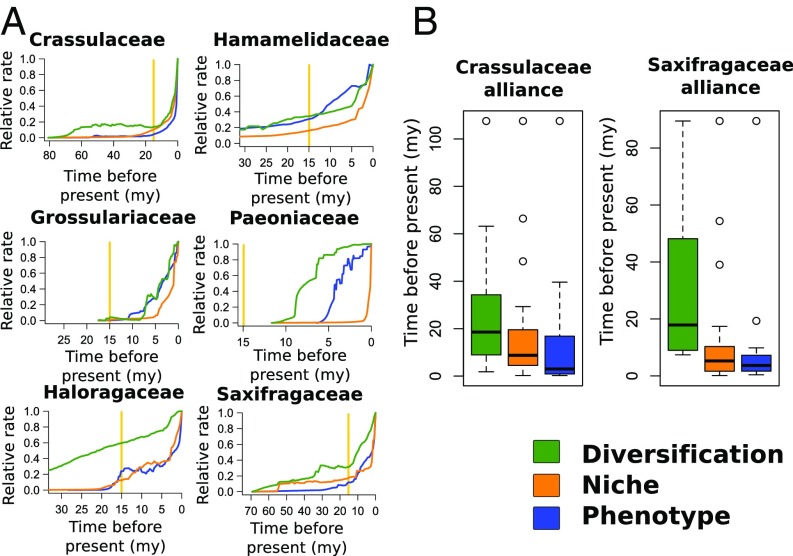
We generated a series of subclade rate plots for all families with more than 15 sampled species (Fig. 3A) to assess whether the global pattern we observed was general or driven by particular subclades. Diversification timing was equivocal for Hamamelidaceae and Grossulariaceae, with similar curves to niche rates after 15 My, but other examples clearly show that diversification rates predate shifts in other rates, with the timing consistent with that reported for the whole tree. Likewise, while niche and phenotype have a diverse set of timing patterns, patterns in each of two large clades (Saxifragaceae alliance and Crassulaceae alliance; cf. Fig. 3B where these taxa are defined, together comprising 97% of species diversity) show a precedence of niche rates consistent with our global analyses. Subclade plots also suggest a negative relationship between niche lability and clade median temperature (measured as the most recent common ancestor ancestral reconstruction of mean annual temperature; SI Appendix, Fig. S26). Consistent with this finding, we found that niche lability had a moderately significant association with habitat (STRAPP: P = 0.033). Other cladewise plots did not reveal a clear pattern for net diversification and phenotypic lability (SI Appendix, Figs. S27 and S28).

Fig. 3.

(A) Clade rates for major clades (all families with greater than 15 sampled taxa). Rate colors are shown in the legend; the yellow bars give the date of 15 My representing the Mid-Miocene Climatic Optimum. (B) Box plots showing the distribution of rate shifts for two large subclades of similar size, Crassulaceae alliance (Aphanopetalaceae + Crassulaceae + Haloragaceae + Penthoraceae + Tetracarpaeaceae) and the Saxifragaceae alliance (Grossulariaceae + Iteaceae + Saxifragaceae). For phylogenetic distribution of these shifts see SI Appendix, Supporting Information Text and Figs. S29–S31 and S37–S39.

Discussion

Our results demonstrate in a clade of flowering plants that rates of species diversification are not coincident with ecological and phenotypic evolution, which themselves are correlated. While rate parameters on niche, phenotype, and diversification all show strong mid-Miocene increases, we document a clear lag, where increases in diversification rates were followed by later increases in niche and phenotypic lability. This finding is robust when utilizing alternative methods and across sensitivity analyses and is based on one of the most densely sampled flowering plant clades to date, with a majority coverage of species for each of phylogenetic, niche, and trait attributes. Given the sensitivity of diversification methods to species sampling, missing species have been accounted for in all diversification analyses we implemented. At smaller phylogenetic scales, diversification without associated morphological trait change has been reported in tetrapods [lizards (25) and salamanders (26)]. We know of no similar examples documenting not only a lack of association but also a significant lag in timing, in a large, globally distributed clade representing any lineage of life. However, lags between species diversification and subsequent niche divergence have been reported in several bird lineages using sister comparison methods at smaller temporal and spatial scales (refs. 42 and 43, but see ref. 44).

The Timing of Opportunity.

Given the uncertainty in exactly defining rate shifts in rate-through-time plots alone, we analyzed rate analyses with a plurality of approaches. These included determination of the timing of significant rate shifts and of major shifts in ancestral reconstructions, with congruent results. Strong increases in rates of diversification and of niche and phenotypic evolution in Saxifragales were all dated to occur after the mid-Miocene Climatic Optimum. This timing is particularly significant given that from the late Cretaceous to the mid-Miocene the Earth was primarily covered in warm-tropical and subtropical habitats, with cool-temperate biomes limited to polar regions (33). After the mid-Miocene Climatic Optimum, a global cooling event marked the beginning of modern-day climate regimes and biomes, including a worldwide expansion of arid and cold-temperate biomes where Saxifragales are now most diverse (32, 34, 45–48). The observed coincidence of higher macroevolutionary rates with temperate habitat proliferation is consistent with increased ecological opportunities unavailable throughout much of the history of Saxifragales.

Consistent with increasing ecological opportunity, we found strong evidence that continuing climatic cooling and climatic variability had a significant positive correlation with all three macroevolutionary rates we tested. This relationship is also in line with simulation-based theoretical results (49), where diversification driven by niche conservatism is expected under directional climate change scenarios, and where climatic oscillation primarily drives diversification of taxa with higher niche lability. Further simulation results (13) support a causal relationship between environmental opportunities and both high diversification rates and rapid phenotypic evolution. Both processes act in Saxifragales at different timeframes, with a greater role in deeper divergences for niche conservatism (that is, lower niche macroevolutionary rates). While our quantitative analyses focused on paleotemperature data, aridification also increased during this period (50), which points to a combined role for decreasing temperature and precipitation in generating contemporary high evolutionary rates.

An Alternative to Density Dependence.

Our findings of (i) a lag between diversification rates and niche/phenotypic rates across major clades within Saxifragales and (ii) no clear downturn in diversification rates across any major clade within Saxifragales do not support simple models of density-dependent diversification. Rather, they are consistent with a model of primarily niche-neutral diversification, followed by greater levels of niche structuring as interspecific competition increases (13). Because most major niche and phenotypic shifts (Fig. 2C) as well as rate shifts (Fig. 3) postdate diversification shifts, diversification events at first likely occurred primarily in ancestral habitats. As habitats began to be more densely filled, this likely created competitive pressure. Coincident with this pressure was the increased availability of novel habitats through which to escape competition [also seen in simulated diversification events (13)]. Continued availability of novel habitats hence provides a potential explanation for the observed lag of niche and phenotypic macroevolutionary rates behind diversification. Both adaption to novel environments and saturation of established ones should eventually replace initially niche-neutral diversification, as niche partitioning and divergence begin to predominate, resulting in accelerated evolution of niche and of niche-associated phenotypic traits. While the overall phylogenetic pattern showed no evidence of density dependence, we did reconstruct falling diversification rates in BAMM for some lineages (SI Appendix, Figs. S29–S31), consistent with certain species of Saxifragales experiencing a density-dependent pattern not evident in the overall phylogeny.

We found limited evidence that global cooling disproportionately affected lineages in the most extreme temperate habitats, although Saxifragales are highly diverse and prominent members of these contemporary floras. We also did not see evidence of latitudinal or elevational associations with any of the macroevolutionary rate parameters we estimated, nor did we recover evidence for continent-specific rate patterns. These results may be consistent with the diversity of global responses to climatic cooling across clades despite similar rate patterns; substantial paleontological and modeling work suggests profound effects of Pleistocene conditions on many tropical biotas, as well as those closer in proximity to glaciated regions (51–55). However, we did see a significant relationship between occupied niche and niche lability; clades that originated in cooler climates generally showed greater increases in lability (SI Appendix, Fig. S21).

Habitat Patterns Through Time.

Much of the species diversity of Saxifragales in cold and arid habitats is in the large sister families Saxifragaceae and Grossulariaceae (primarily cold-adapted) and Crassulaceae (both arid- and cold-adapted, and largely succulent). Habitat ancestral reconstructions suggest that these groups were already present in cold and arid habitats before their mid-Miocene proliferation. The earliest divergence events in Crassulaceae are accompanied by ecological shifts and succulent specialization that largely occurred before the Miocene. These include parallel major shifts into desert and shrubland habitat in the African clades Crassula (50 Mya), Kalanchoe (12 Mya), the broader Kalanchoe group (13 Mya), the Macaronesian clade (24 Mya), and the New-World Acre clade (39 Mya). Likewise, a major shift toward temperate habitat occurs in the ancestor of Saxifragaceae and Grossulariaceae—temperate herbs and shrubs now diverse across the Northern Hemisphere in Arctic-alpine biomes—by 81 Mya, with a further shift into colder habitats in Grossulariaceae by 17 Mya, indicating these lineages had long been in cold habitats before the mid-Miocene. Finally, a shift toward temperate biomes in Hamamelidaceae, Altingiaceae, and Cercidiphyllaceae, comprising most of the remaining temperate shrub diversity, dates to at least 90 Mya. Because these dates for habitat shifts represent crown ages, the dates we report here are minimum age constraints on habitat shifts that could be considerably older. Two lineages—Peridiscaceae and Pterostemon, among the few tropical members of the clade—each experienced a habitat shift into more tropical environments >22 Mya, yet both are characterized by poor species diversity (∼0.6% of Saxifragales; see also ref. 56).

Beyond these early shifts, the majority of shifts into the most extreme habitats occurred within the last 5 My (SI Appendix, Fig. S24), consistent with the strong increases in habitat evolutionary rates in this timeframe. While not all species moved into colder, drier habitats, most shifts were into the most extreme parts of cold and dry habitats in which Saxifragales were ancestrally present (in extant species these represent, for instance, arid shrubland, Arctic tundra, and montane biomes). In most cases these frequent habitat shifts were preceded by diversification shifts. For example, a single diversification increase was reconstructed by BAMM in the Heuchera group (temperate and Arctic-alpine herbs of Saxifragaceae; 10 Mya), which was followed by one further diversification shift at 8 Mya and 12 major habitat shifts in descendant lineages. An increase in diversification rate at 43 Mya was followed by six major habitat shifts after 5 Mya in arid-adapted, primarily Australian Haloragaceae. Similar patterns occur in subclades of Grossulariaceae, Crassulaceae, Iteaceae, and Saxifragaceae. Hence, the phylogenetic placement of diversification shifts and habitat shifts across major clades was consistent with the pattern we constructed by time-averaged rate curves.

Assessment of Evolutionary Rates.

The robustness of methods to estimate diversification rates has seen significant discussion, with concerns raised by Moore et al. (41) and Meyer et al. (57) as well as methodological criticisms of these benchmarking methods by Rabosky et al. (58) and Rabosky (59). In the context of uncertainty about optimal methods for assessing macroevolutionary patterns, we applied a diversity of available methods, finding overall consistent results. Comparing clade-level estimates of the MS statistic (35) and σ² estimates from OU models (36), we found the same lag pattern as that seen in BAMM analyses. Likelihood model choice implemented in RPANDA (38–40) also favored temperature-dependent trait rates we identified based on BAMM rate curves. Likewise, we assessed a series of BAMM prior formulations and found our primary results robust. Across a diversity of methods, robustness analyses, and major subclades of Saxifragales, we found patterns that suggest a strong signal of diversification preceding trait evolution and related to historical climatic changes.

Conclusion.

Despite the widespread occurrence of rapid radiations across major clades of life (60) and a long interest in such patterns (e.g ref. 61), the evolutionary processes driving such radiations remain poorly understood (62, 63). As a largely temperate radiation, yet with representation across major terrestrial biomes, the results for Saxifragales may help identify radiation patterns common across other predominantly temperate groups and therefore relevant to the origin of present-day temperate biotas. The response of species diversification to climatic events has seen intensive research (e.g refs. 2, 3, and 64). The patterns shown here in Saxifragales suggest a different model from the majority of clades studied to date in which bursts of diversification are followed by slowdowns (5–10) and the greatest diversity is located in the tropics (e.g refs. 2, 9, and 65). Rather, continued expansion and formation of novel habitat may not only contribute to maintenance of high evolutionary rates into the present but also generate a lag between species diversification and niche and phenotypic evolutionary rate.

Methods

Phylogenetic Estimate.

To generate a robust phylogenetic backbone, we built a custom phylogenetic capture bait set of 301 protein-coding loci and obtained sequence data for 627 species of Saxifragales (SI Appendix, Table S6). These loci were assembled in aTRAM v. 2.0 (66, 67) using the SPAdes assembler (68) with five iterations, and using the aTRAM exon stitching pipeline (69). Species trees were estimated in ExaML (70) and ASTRAL-III v. 5.6.1 (71–73). Outgroup sampling broadly covered the rosids, the sister group of Saxifragales, using whole-genome and transcriptome data (74, 75).

To maximize species representation, we implemented a supermatrix approach combining this phylogenomic backbone with GenBank data. For the 627 species in the backbone phylogeny, we assembled 24 standard angiosperm loci (chosen based on a minimum taxon occupancy cutoff across Saxifragales; see SI Appendix, Supporting Information Text for a list and details) in aTRAM using off-target sequencing reads. A supermatrix comprising these contigs, as well as all Saxifragales GenBank data for the 24 loci, was assembled using PHLAWD (76). We conducted a likelihood search on this supermatrix using RAxML (77); given the topological similarity and few well-supported incongruences between trees obtained via concatenation and coalescent approaches (SI Appendix, Figs. S1 and S32), the backbone from ExaML was enforced as a constraint. For more details on data assembly and phylogeny reconstruction see SI Appendix, Supporting Information Text.

Time Calibration.

We used two approaches to time calibration of our phylogeny. First, we generated an ultrametric dated tree from the result of the supermatrix analysis using a secondary dating approach and the penalized likelihood method as implemented in treePL (78), hereafter referred to as the “treePL tree” (SI Appendix, Fig. S36). Node calibrations were based on median highest posterior density values reported from a recent comprehensive Bayesian analysis of angiosperm divergence times (79). We used the following constraints: crown Saxifragales (i.e., root age) = 112.99, stem Saxifragaceae = 85.69, stem Iteaceae = 91.03, crown woody clade (sensu ref. 80) = 95.93, and stem Haloragaceae = 72.09. The initial smoothing parameter was 100, and a thorough search was performed with “priming” to determine optimal run parameters and cross-validation. Second, we reduced our dataset to 94 phylogenetically representative taxa and the 50 most phylogenetically informative loci (based on Robinson–Foulds distance from the concatenated phylogeny; cf. ref. 81) to enable running a more computationally intensive Bayesian dating approach in BEAST (82, 83). We used a “congruification” approach (84, 85) in treePL to interpolate dates for nodes only sampled in the complete supermatrix phylogeny. Hereafter we refer to this as the “congruified BEAST” tree (SI Appendix, Fig. S3). The constraints we used are derived from vetted fossils in ref. 79: Altingiaceae, stem constraint 89.3 Mya; Haloragaceae, stem constraint 70.6 Mya; Iteaceae, stem constraint 89.0 Mya; Ribes, stem constraint 48.9 My; and the root age constraint above. For details on priors and the congruification approach, see SI Appendix, Supporting Information Text. Because dates and downstream results were similar for these two dating approaches, the BEAST approach is used for statistical tests in the main text; both are provided for comparison (Fig. 2; see SI Appendix, Figs. S23 and S33–S35; and Fig. 4; see SI Appendix, Tables S3–S5, and S7–S9).

Acquisition of Locality Records.

All locality data from each Saxifragales family were downloaded as DarwinCore archives from iDigBio and GBIF on January 16, 2017. Using Python csv tools, we removed records lacking geographic coordinates and disaggregated the data into individual species files (and into variety/subspecies files where these DarwinCore fields were provided). We manually examined the species files for the presence of fossil taxa, cultivars, and stray taxa erroneously placed in Saxifragales, and such records were removed. For more details on processing occurrence records see SI Appendix, Supporting Information Text.

Niche Predictor Assembly.

We assembled 35 environmental layers at 30-s resolution that capture features of climate, soil, landcover, and topography. These comprised 19 BioClim temperature and precipitation variables (http://www.worldclim.org/bioclim), seven soil layers (SoilGrids250m; ref. 86), six landcover classes (https://www.earthenv.org/landcover), and three topographical layers (elevation, GTOPO30; https://lta.cr.usgs.gov/GTOPO30; aspect and slope calculated from these in qGIS). The SoilGrid250m product was aggregated to 30-s resolution via averaging, resampled to the extent of other layers by nearest neighbor, and finally averaged across 5-, 15-, and 30-cm sampling depths (all steps in GDAL; https://www.gdal.org/). We implemented custom high-throughput Python methods based on GDAL to extract environmental conditions from observed points. Median values for each predictor were used in downstream analyses.

Morphological Trait Assembly.

We built upon a previous matrix (87) by extracting records from major global floras and primary literature to build a dataset of phenotypic traits broadly scorable across Saxifragales. These traits were (i) categorical: perennial/annual, woody/herbaceous, flowering season, leaf shape, inflorescence type, sepal number, sepal color, sepal shape, petal number, petal color, petal shape, and stamen number and (ii) continuous: plant height, petiole length, leaf length, leaf width, sepal length, sepal width, petal length, petal width, stamen length, style length, and seed length. We built an automated Python pipeline to standardize verbatim measurements and qualitative descriptors for downstream analysis. For continuous traits, after outlier measurements were discarded, the midpoint was taken [e.g., (1–)2–14 cm would yield 7 cm]. For categorical data, each text descriptor was standardized with a term synonymy list and coded sequentially from zero, and (for those taxa with multiple trait descriptors) a single trait value was randomly selected. For literature sources of trait data see SI Appendix, Supporting Information Text.

Ancestral Reconstruction.

We used the R package phytools (88) to perform ancestral reconstruction (command FastAnc). Based on model comparison with AIC_c, the OU model was favored for both niche and phenotype datasets, and we used this for all reconstructions. To identify exceptional shifts in reconstructed ancestral niche and phenotypic values (hereafter “major trait shifts”), we calculated the trait shift in each node in the phylogeny as the difference between reconstructed values for it and its parent node; major trait shifts were taken as those in the upper 95th percentile of reconstructed trait shifts.

Phenotypic Distance.

To treat discrete and continuous characters equally in a single distance metric, we built and summed two pairwise distance matrices on the interval [0, 1] for discrete and continuous characters, respectively: a Jaccard distance matrix and a Euclidean distance matrix divided by the maximum pairwise Euclidean distance found. We divided the result by 2, yielding a composite distance metric on the interval [0, 1], that is,

$$\left(\left(1-\frac{P\cap Q}{P\cup Q}\right)+\left(\sqrt{{\displaystyle \sum _{i=1}^d{\left|R_i-S_i\right|}^2}}\right)/max\left(\sqrt{{\displaystyle \sum _{i=1}^d{\left|R_i-S_i\right|}^2}}\right)\right)/2,$$

where P and Q are arrays of discrete characters and R and S are arrays of continuous characters. Axes with missing data were excluded for each pairwise comparison; we removed taxa with greater than 80% missing data. These calculations were implemented in Python and SciPy.

Ordination.

We ordinated all 35 environmental predictors using phylogenetic principle component analysis (PCA) as implemented in R library phytools, function phyl.pca. For phenotypic data, which comprised both continuous and discrete data, we applied the function phyl.pca to the composite distance matrix (that is, generalized multidimensional scaling). To complement traditional PCA loadings, we calculated R² values between each phenotypic trait and the first ordinated axis to estimate which phenotypes were most important.

Macroevolutionary Rate Analysis.

We used BAMM (89) along with a set of parametric and semiparametric test statistics to analyze macroevolutionary rates in Saxifragales. We used the BAMM diversification model to analyze net species diversification through time and the BAMM trait model to reconstruct evolutionary rates through time for ordinated niche and phenotypic data. For diversification, we derived prior settings from R library BAMMtools, function setBAMMpriors. We ran 50 million generations of Markov chain Monte Carlo (MCMC) in four chains with δT set as 0.01 and the swap period as 1,000 generations, sampling every 10,000th generation. MCMC scaling, move frequency, and initial values of parameters followed recommendations in BAMM documentation. We additionally set segLenth (likelihood grain) as 0.02 and the minimum clade size for shift inference for two to constrain estimates of rate shifts to internal branches. To account for nonrandom taxon sampling in diversification analyses, we used family-level sampling statistics (SI Appendix, Table S10) to specify clade sampling probabilities. The first 10% of generations were discarded as burn-in.

To understand evolutionary rates in niche and phenotypic traits (evolutionary lability) throughout Saxifragales, we also implemented complementary runs using the BAMM trait model on ecological and phenotypic data. For niche lability, we used the first axis of the phylogenetic PCA of niche predictors and ran the analysis for 250 million generations with a 10% burn-in. For lability in phenotypic trait data, we used the first axis of the phylogenetic multidimensional scaling of phenotypic traits and ran the analysis for two billion generations with a 75% burn-in. Settings followed those in the diversification analysis, with the exception that we did not adjust for family-level sampling, given that this is not implemented in the BAMM trait model. All of these analyses were run on both the congruified BEAST tree (SI Appendix, Figs. S29–S31) and the treePL tree (SI Appendix, Figs. S37–S39). For further details on the rate analyses see SI Appendix, Supporting Information Text.

We also assessed macroevolutionary rate timing by recursively calculating two simpler rate-invariant models across all tree subclades. We used the R package geiger (90, 91) to calculate (i) the MS statistic (ref. 35; cf. refs. 59 and 92), calculated using crown ages and corrected for missing taxa in each clade by the overall tree sampling percentage) and (ii) σ² rates from the favored OU model. To render these rates comparable, we scaled them to a proportion of the maximum (i.e., contemporary) rates, after removing the upper 99th percentile to discard a small number of outlier rates. For these relative rates, which were approximately exponentially distributed (SI Appendix, Figs. S8–S13), higher values mean rates closer to their contemporary maxima; hence, for each clade a higher relative rate implies an earlier rate increase.

Macroevolutionary Rates and Global Climate.

We used a regression approach to investigate relationships between global temperature and macroevolutionary rates estimated in BAMM. We used the 5-point mean δ¹⁸O of the Zachos deep-sea isotope dataset (37) extrapolated to global temperature (93). To measure temperature variability, we calculated the SD in a moving window analysis; on the basis of initial plots, we used a window width of 0.1 My. After comparing linear, quadratic, and exponential models using the AIC (94), we selected exponential models, treating each macroevolutionary rate as a response variable. To evaluate whether temperature and temperature variability had independent explanatory power, we built a combined exponential model with both treated as predictors and assessed both the increase in adjusted R² and AIC and Akaike weights for independent models and the combined model.

We also fit a series of explicit temperature-dependent likelihood models for traits and diversification (38, 39) as implemented in RPANDA (40). Because these models require complete temperature coverage for the nearly 113-My history of the clade, we used a longer δ¹⁸O dataset (95), calculating a 5-point mean and applying the temperature conversion as above. For diversification, we fit nine time-dependent models: constant, linear, and exponential pure birth as well as all possible combinations of linear and exponential birth with constant, linear, and exponential extinction. We also fit nine temperature-dependent models with the same birth–death functions as the time-dependent models. For temperature-dependent trait models, in both niche and phenotypic data we compared the fit of the first ordination axis on Brownian and OU trait models with both linear and exponentially temperature-dependent trait models. The niche data were scaled by 1,000⁻¹ to avoid likelihood optimization errors. We calculated AIC_c and Akaike weights to assess the best models and relative model fits, considering a model as decisively supported if it had a majority of the relative likelihood (Akaike weight >0.5).

Correlation of Rates with Niche, Traits, and Geography.

We tested whether diversification, niche, or phenotypic rates are related to biogeography (i.e., certain parts of geographic space have high evolutionary rates) using a series of geographic summary data (continental biogeography, latitude, and elevation). Using STRAPP (96) and ES-sim (97), we specifically tested for a relationship of macroevolutionary rates to the first axis of niche and trait ordinations, species mean latitude and elevation, and continent. For further details see SI Appendix, Supporting Information Text.

Data Availability.

Sequence data have been deposited at the Sequence Read Archive (ref. 98; for individual accession numbers see SI Appendix, Table S1). Alignments, trees, and other analysis products have been deposited at Dryad (99). Code for spatial analyses has been deposited at GitHub (100).