Mapping Solar System chaos with the Geological Orrery

Significance

The Solar System is chaotic, and precise solutions for the motions of the planets are limited to about 60 million years. Using a network of coring experiments that we call the Geological Orrery (after 18th century planetaria), we recover precise and accurate values for the precession of the perihelion of the inner planets from 223- to 199-million-year-old tropical lake sediments, circumventing the problem of Solar System chaos. Extension of the Geological Orrery from 60 million years ago to the whole Mesozoic and beyond would provide an empirical realm to constrain models of Solar System evolution, further test General Relativity and its alternatives, constrain the existence of additional past planets, and provide further tests of gravitational models.

Abstract

The Geological Orrery is a network of geological records of orbitally paced climate designed to address the inherent limitations of solutions for planetary orbits beyond 60 million years ago due to the chaotic nature of Solar System motion. We use results from two scientific coring experiments in Early Mesozoic continental strata: the Newark Basin Coring Project and the Colorado Plateau Coring Project. We precisely and accurately resolve the secular fundamental frequencies of precession of perihelion of the inner planets and Jupiter for the Late Triassic and Early Jurassic epochs (223–199 million years ago) using the lacustrine record of orbital pacing tuned only to one frequency (1/405,000 years) as a geological interferometer. Excepting Jupiter’s, these frequencies differ significantly from present values as determined using three independent techniques yielding practically the same results. Estimates for the precession of perihelion of the inner planets are robust, reflecting a zircon U–Pb-based age model and internal checks based on the overdetermined origins of the geologically measured frequencies. Furthermore, although not indicative of a correct solution, one numerical solution closely matches the Geological Orrery, with a very low probability of being due to chance. To determine the secular fundamental frequencies of the precession of the nodes of the planets and the important secular resonances with the precession of perihelion, a contemporaneous high-latitude geological archive recording obliquity pacing of climate is needed. These results form a proof of concept of the Geological Orrery and lay out an empirical framework to map the chaotic evolution of the Solar System.

In the introduction of his 1812 treatise on probability, Pierre-Simon de Laplace (1) envisioned the possibility of modeling the whole universe in a single equation (the gravitational laws). Using only knowledge of the present initial conditions, one could recover all of the past and predict all of the future. However, this paradigm of determinism does not apply to the Solar System. The validity of the solutions of Solar System gravitational models is constrained to about 0–60 Ma not only because of inherent limitations in the determination of initial conditions and parameters of the model but more fundamentally, because of the chaotic nature of the system for which initially close solutions diverge exponentially, in fact multiplying the uncertainties by a factor of 10 every 10 My (2, 3). Although there has been much recent progress, the powerful constraint imposed by chaos, at several levels, means that it is hopeless to attempt to retrace the precise history of the Solar System from only knowledge of the present as has been done until now. Conversely, geological data can constrain the astronomical solution back in time, thus allowing us to go beyond the horizon of predictability of the system. Geological data recording climate variations modulated by celestial mechanics potentially provide an empirical realm to test astronomical solutions that must conform to the past. Geological data from within the last 60 My seem to agree with astronomical solutions (4, 5) but provide little information on the Solar System beyond what is already known. The fundamental challenge is to find empirical data well beyond 60 Ma to provide anchors for extending the astronomical solutions, but this quest has been hampered by a lack of records with both sufficient temporal scope and independent age control. To circumvent the limitations of most geological data, we have developed an experimental system that uses a plexus of highly resolved data from multiple temporally correlative and complementary records termed “The Geological Orrery,” named after the mechanical planetaria—Orreries—of the 18th century from the fourth Earl of Orrery, Charles Boyle (6), and the “Digital Orrery,” a dedicated parallel-processing computer that was constructed to investigate the long-term motion of the Solar System that numerically confirmed its chaotic nature (7, 8). The Geological Orrery provides a procedure to fully map the actual gravitational history of the last ∼250 My of the Solar System and beyond, allowing reliable filtering and modification of astronomical solutions.

To a first approximation, the orbital planes of the planets are slowly deformed by the gravitational forces of the other bodies in the Solar System in a quasiperiodic way that can be decomposed into a series of secular fundamental frequencies representing roughly each planet’s contribution to the deformation of the orbits. These motions can be described in terms of the precession of perihelion in the orbital plane (g_i frequencies) and the precession of the orbital plane in space represented by the precession of the node (s_i frequencies). Differences of these secular frequencies of precession of perihelion g_i yield the “eccentricity cycles” familiar to paleoclimatologists, and the sums of the g_i frequencies with Earth’s axial precession constant, p, yield the “climatic precession” frequencies, today averaging about 21 ky (Table 1). Similarly, the difference frequencies of the secular fundamental frequencies of precession of the orbital nodes s_i yield the orbital inclination frequencies, and the sums of the s_i frequencies with p yield the familiar obliquity periods today near 41 ky.

Table 1.

Cycle nomenclature and origins of the climatic precession and eccentricity from the secular fundamental frequencies

Named lithological expression of cycles*	Description	Argument	Periods and informal names of Milankovitch or orbital cycle with today’s period†
Van Houten cycle	Precession frequency of Earth (p) + secular frequency of precession of perihelion of Mercury, Venus…	p + g1, p + g2, p + g3, p + g4, p + g5	∼21 ky (average 21.5 ky); 23.2-, 22.4-, 19.2-, 19.0-, 23.8-ky climatic precession
Short modulating cycle	Secular frequencies of precession of perihelion of Mars − that of Jupiter, etc.	g4 − g5, g3 − g2, g4 − g2, g3 − g2	∼100 ky (average 112.1 ky); 94.9-, 98.9-, 123.9-, 130.7-ky short orbital eccentricity cycles
McLaughlin cycle	Venus (g2) − Jupiter (g5)	g2 − g5	405-ky long orbital eccentricity Grand Cycle
None	Venus (g2) − Mercury (g1)	g2 − g1	696-ky Grand Cycle
None	Mercury (g1) − Jupiter (g5)	g1 − g5	973-ky Grand Cycle
Long modulating cycle	Mars (g4) − Earth (g3)	g4 − g3	2,365-ky Grand Cycle

^*From ref. 9.

^†Using the g1–g5 values from ref. 5, table 6 and p from refs. 29 and 33, table 1.

Here, we use the Geological Orrery to precisely determine the secular fundamental frequencies of the precession of perihelion of the inner planets and Jupiter from 199 to 220 Ma using climate proxy and geochronologic results from two major scientific coring experiments: (i) the Newark Basin Coring Project (NBCP) (9) that forms the basis of the Newark–Hartford Astrochronostratigraphic Polarity Timescale (NH APTS) (10) along with data from the adjacent Hartford Basin (SI Appendix) and (ii) the Colorado Plateau Coring Project (CPCP–1) (11, 12) (Fig. 1 and SI Appendix, Fig. S6 and Table S1).

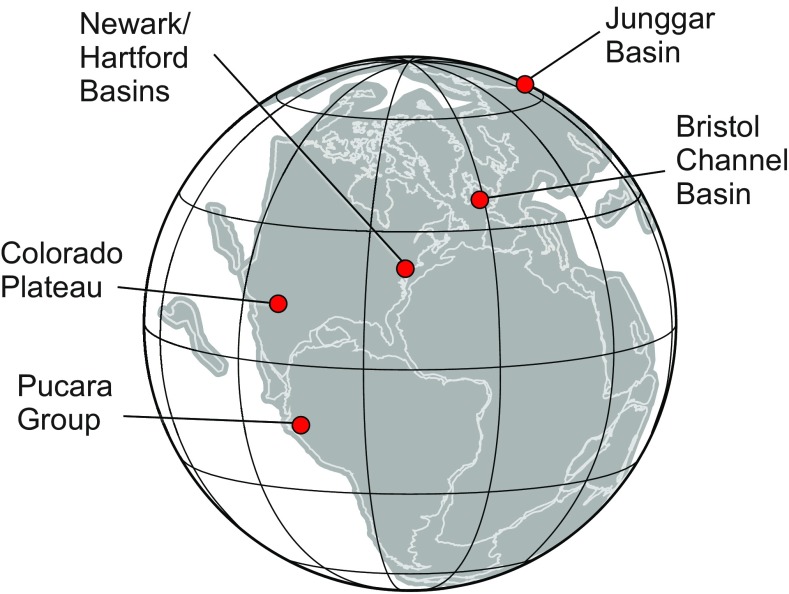
Fig. 1.

Map of Pangea at ∼200 Ma with locations discussed in text.

The NBCP experiment collected seven ∼1,000-m continuous cores and core holes in lacustrine to fluvial rift basin strata of the Newark Basin spanning most of the Late Triassic and the earliest Jurassic, which together with additional core and outcrop data (13–15) (SI Appendix, Figs. S1 and S6, and Table S1), tested the permeating nature of orbital pacing of lake depth in the paleotropics (0°–21° N) (16) through the lacustrine part of the section, previously inferred from scarce and discontinuous outcrops (17–19). Global correlation is achieved through 66 geomagnetic polarity intervals pinned in time by zircon chemical abrasion isotope dilution thermal ionization mass spectrometry (CA-ID-TIMS) U–Pb dates from three lava flow formations interbedded in the very latest Triassic and earliest Jurassic age part of the sequence (20, 21). Using largely a facies classification and a color scale, the NBCP experiment (19) supported the hypothesis that the rift lake depth was paced by orbital cycles, including a full range of climatic precession-related cycles. These include the ∼20-ky precessional and the ∼100- and 405-ky orbital eccentricity cycles with the latter and its mappable geological equivalent termed the McLaughlin Cycle (Table 1), then being used to tune the entire lacustrine part of the composite Newark–Hartford record (22). This, in turn, allowed the Triassic values of the secular fundamental frequencies of the precession of perihelion for Mercury (g1), Venus (g2), Earth (g3), and Mars (g4) (Table 1) to be roughly estimated (22). The tuned data also revealed even longer-period “Grand Cycles” (23) (Table 1), including one with a period of ∼1.7 My identified as the Mars–Earth cycle (g4 − g3) that today has a value of ∼2.4 My (5), the difference being attributed to chaotic diffusion in the behavior of the Solar System. However, these results lacked independent age control, allowing the possibility that hiatuses invisible to spectral analysis compromise both the timescale and the apparent eccentricity periodicities longer than 405 ky (24–27).

A major goal of the CPCP–1 experiment in the Triassic Chinle Formation in Petrified Forest National Park in Arizona was to provide an independent zircon U–Pb age-constrained paleomagnetic polarity stratigraphy that could be correlated to and test the NH APTS and the application of orbital theory on which it is based (11). CPCP–1 validated the NH APTS interval from ∼210 to 215 Ma and implicitly validated the age model for the younger interval bounded by zircon CA-ID-TIMS U–Pb dates from Newark Basin lavas for ∼600 ky around ∼201 Ma (21), making an independently dated sequence extending from ∼201 to 215 Ma in total. These geochronological data validate the NH APTS and provide direct dating of the 405-ky cycle at around 215 Ma (12) (SI Appendix, Fig. S7 and Table S2), and they provide the needed age control for examining Triassic–Early Jurassic orbital frequencies in the Newark–Hartford dataset and permit direct comparison with Neogene and Quaternary marine data.

Newark–Hartford Composite Results

The newly compiled Newark–Hartford dataset consists of four major depth series: depth rank (sedimentary facies related to water depth) and color from the recovered cores and down-hole sonic velocity and natural gamma radiation measurements providing instrumental complementary data (SI Appendix, Figs. S2 and S6). Data from cores and outcrops from the Newark and Hartford Basins allow seamless extension of the sequence into the Early Jurassic (Hettangian and Early Sinemurian) (12) (SI Appendix, Figs. S3–S6).

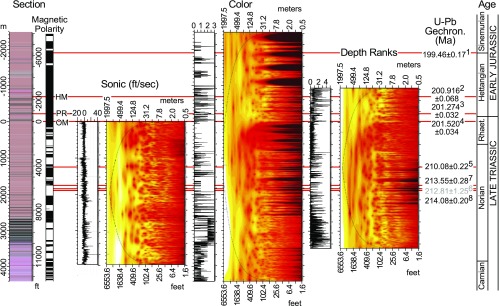
Wavelet spectra of these four depth series show similar patterns of periodicities in the depth domain with all of the thickness periodicities changing in frequency simultaneously (Fig. 2 and SI Appendix, Fig. S6), reflecting variations in accumulation rate. The most prominent frequency through most of the spectrum reflects the lithologically based McLaughlin Cycle, an expression of the 405-ky orbital eccentricity cycle (Table 2), which provided the basis for time calibration of the NH APTS (10). The zircon CA-ID-TIMS U–Pb dates from the Newark Basin lava flow formations and related intrusions show a pronounced (nearly an order of magnitude) (SI Appendix, Figs. S6 and S11) increase in accumulation rate at the beginning of the Central Atlantic Magmatic Province (CAMP) event (Fig. 2), above which the thickness frequencies correspondingly shift to much lower values in agreement with the visual observation of the increased thickness of the McLaughlin Cycles (13–15). The borehole geophysical data are complementary to the depth rank data, especially where the latter has reduced variability as shown by both wavelet and Multitaper Method (MTM) spectral analysis (Fig. 3 and Fig. 5). MTM analysis of X-ray fluorescence chemical data yields similar results on a subset of the thickness data (SI Appendix, Figs. S8 and S9). We regard this as a powerful verification that the main periodicities can be easily seen in all of the depth series by visual inspection without any tuning or nonuniform age model (Fig. 2).

Fig. 2.

Untuned Newark–Hartford wavelet spectra from core, holes, and outcrops (SI Appendix, Fig. S1 and Table S1). Crucial are the demonstrable and simultaneous shifts in all thickness periods, particularly pronounced in the lower two-thirds of the spectra. There is nearly an order of magnitude increase in accumulation rate above the lowest Basalt [Orange Mt. Basalt (Talcott Basalt in Hartford Basin) (OM)] at 0 m. Red horizontal lines mark positions of the lava flow formations of the CAMP. Zircon U–Pb CA-ID-TIMS ages are as follows: 1, based on paleomagnetic correlation to the Bristol Channel Basin Hettangian–Sinemurian Boundary at Global Boundary Stratotype Section and Point (GSSP) (43, 44) and then to the Pucara Group via ammonite biostratigraphy (46, 47); 2, Butner intrusion related to Hook Mt. Basalt (HM) (21); 3, Preakness Basalt [Holyoke Basalt in Hartford Basin (PR)] (21); 4, Palisade Sill feeder to OM (21); and 5–8, Chinle Formation (12).

Table 2.

Periods of the different arguments in the Newark–Hartford data using MTM analysis, FA, and corresponding values in the FA of the La2010d* and La2010a solutions (5) for Earth’s eccentricity (SI Appendix, Table S4)

Row	Argument (frequency)	MTM period (ky)	FA† period (ky)	La2010d*†‡ period (ky)	La2010a†§ period (ky)
1	g4 − g3	1,724.63	1,747.65	1,793.04	2,368.95
2	g1 − g5	923.04	923.16	957.56	967.42
3	g2 − g1	720.18	719.05	704.98	697.63
4	(g2 − g5) − (g4 − g3)	537.18	527.56	515.09	489.37
5	g2 − g5	405.17	404.97	404.58	405.63
6	(g2 − g5) + (g4 − g3)	336.53	335.13	330.08	346.42
7	g3 − g2	132.53	132.17	132.58	130.71
8	g4 − g2	122.96	123.08	123.47	123.88
9	g3 − g5	99.83	99.78	99.86	98.85
10	g4 − g5	94.43	94.49	94.62	94.89

^†All terms are recovered by FA in the 14 terms of larger amplitude (SI Appendix, Table S5), except g1 − g5 and g2 − g5 + (g4 − g3), which are of lower amplitude.

^‡La2010d* is taken over the interval 209–231 Ma.

^§La2010a is taken over the interval 0–20 Ma.

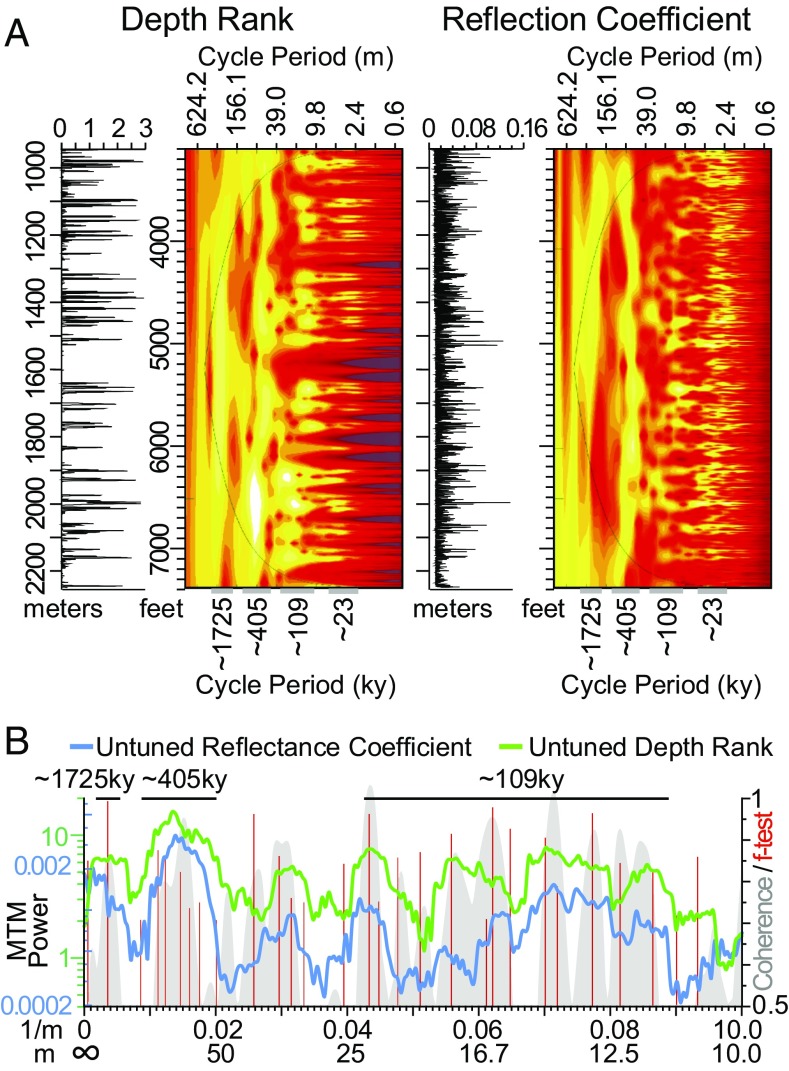
Fig. 3.

Comparison between untuned depth rank data from core and reflection coefficient (60) data (derived from borehole sonic velocity and density measurements from Rutgers and Somerset cores and holes of the NBCP; ref. 38) (SI Appendix) showing similarity in periods. The interval from ∼1,530 to ∼1,640 m lacks structure in depth ranks but shows clear periodicities similar to surrounding strata in the reflection coefficient data. (A) Comparison of wavelet spectra showing similar structure and periodicities. (B) MTM spectra of depth rank and reflection coefficient data showing similar cyclicity attributed to orbital eccentricity as well as the “F test” (f statistic values greater than 0.7 for both datasets; Analyseries 2.0 default: 6, 4pi tapers) and Blackman–Tukey coherence between the datasets (Analyseries 2.0 default: 30% autocorrelation; 80% confidence level). Note the close correspondence between frequencies with high coherence, high statistical significance, and high power.

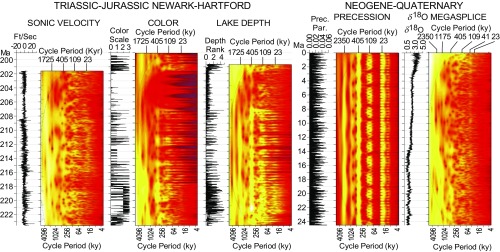
Fig. 5.

Comparison of time domain wavelet spectra of similar length from the Newark–Hartford dataset and the last ∼24 My of the Neogene and Quaternary (δ¹⁸O Megasplice) (details are in SI Appendix). The Newark–Hartford periods homologous to those in the precession index are apparent as is the difference in the Mars–Earth cycle between the more ancient solution and the modern solution. Note that periodicities at the lower frequencies show up as pulsing in amplitude in the higher frequencies. Precession is derived from clipped precession index of La2004 (29), and the δ¹⁸O Megasplice is from ref. 49.

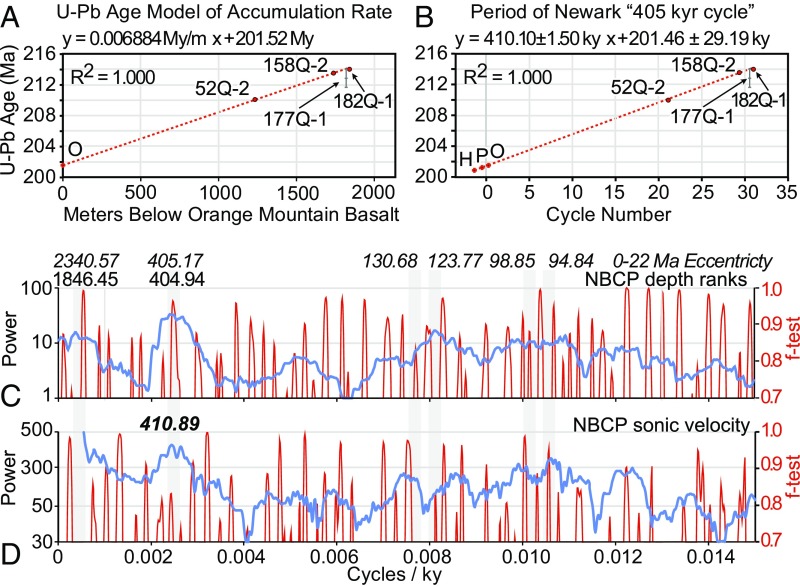
We convert the data from the core depth domain to the time domain with minimal modification using a simple model based on U–Pb dates imported from CPCP–1 via magnetostratigraphy and the lava flows within the section. This yields a spectrum with approximately the expected orbital periodicities (Fig. 4). A prominent cycle at ∼405 ky is present. By filtering the core depth series in this range to the thickness of this cycle (SI Appendix, Fig. S7 and Tables S2 and S3), we can determine its period without having to explicitly identify specific lithological McLaughlin Cycles as was done in ref. 12, which confirms the later results with different methods yielding a periodicity of 398 ± 12 ky using all of the dates and 410 ± 02 ky using only the three CPCP–1 dates in stratigraphic order and the Newark Basin CAMP dates (SI Appendix, Fig. S7 and Table S3). Therefore, regardless of the counting methodology, these results are indistinguishable from the 405-ky periodicity predicted to be stable over this time interval (5, 12).

Fig. 4.

Simple age model for untuned NBCP data using zircon U–Pb CA-ID-TIMS dates from basalt flows in the Newark Basin section (21) and CPCP–1 dates projected onto the Newark Basin section (12). Vertical gray bars guide the eye to periods from the La2004 solution of 0–22 Ma, with periods shown at the top of C for reference. (A) Accumulation rate determined using the Orange Mt. Basalt date (21) and the CPCP–1 dates with small uncertainties (12) (shown by diameter of point). (B) Duration of Jupiter–Venus Grand Cycle based on counting long (∼60-m) filtered cycles from untuned NBCP depth rank data (SI Appendix, Fig. S7 and Table S3); 52Q-1, 185Q-2, and 182Q-1 CPCP–1 dates, and 177Q-1 is the CPCP–1 date with large uncertainty that was not used. H, Hook Mt. Basalt; O, Orange Mt. Basalt; P, Preakness Basalt. (C and D) MTM spectra based on age model in A of untuned sequence of NBCP depth ranks (C) and sonic velocity (D) over the interval with independent dates with a prominent period at ∼405 ky, periods close to the short eccentricity cycle, and a period close to the Mars–Earth Grand Cycle.

Minimally tuned to the 405-ky periodicity, the wavelet spectra show that all of the frequencies seen in the depth domain are now aligned, and the datasets can be directly compared with the spectrum solution for the later Neogene plus Quaternary (Fig. 5 and SI Appendix, Figs. S10 and S12). Visual inspection of the wavelet spectra shows overall agreement in pattern in the high-power periods, except for those longer than 405 ky. In particular, the apparent homolog of the 2.4-My period in the Neogene plus Quaternary wavelet spectrum is distinctly offset to a shorter period of ∼1.7 My ascribed to the Mars–Earth orbital eccentricity Grand Cycle (g4 − g3) (Table 2) when it was first measured (22, 23). The 1.7-My cycle is not visible in the NBCP geophysical logs because of detrending issues with the six down-hole logs from which the composite logs are assembled (SI Appendix, Figs. S2 and S12). The possibility that the difference between the 1.7-My Triassic Period of g4 − g3 and its present 2.4-My period is due to hiatuses is eliminated by the CPCP–1 and Newark Basin lava flow U–Pb dates (SI Appendix, Fig. S7 and Tables S2 and S3).

Examining the interval between the 405-ky cycle and the 2.4-My cycle in the 0- to 24-Ma wavelet spectra, there are two bands of high power with a “ropy” appearance (Fig. 5 and SI Appendix, Fig. S12). They seem to have their homologs in a similar interval in the depth rank and color wavelet spectra in the Newark–Hartford spectra. These various Grand Cycles seem to correspond to the main terms of the eccentricity orbital solution (refs. 5, figure 5; 28; and 29, table 6) (SI Appendix, Table S4); predicted by combinations of the secular fundamental frequencies (Tables 1–3), these should correspond to the Jupiter–Mercury (g5 − g1 = 1/972.59 ky) and Venus–Mercury (g2 − g1 = 1/695.65 ky) cycles (Table 2 and SI Appendix, Table S4). To our knowledge, these have not previously been identified in any geological records. Because they are different in value from modern frequencies, assignment of these bands of spectral power to specific combinations of astronomical parameters raises the question of whether they could reflect geological noise or artifacts.

Table 3.

Secular fundamental frequencies and consistency relations

Row	Argument	MTM (″/y) Newark–Hartford	FA (″/y) Newark–Hartford	FA La2010d* residual (″/y)	La2010d* (″/y)	La2010 (″/y)
0	g5	4.257482†	4.257482†		4.257438	4.257482
1	g4 − g3‡	0.742	0.727‡	0.014†
2	(g1)§	5.662	(5.661)§	(0.050)§	(5.611)§	5.59
3	g2 − g1‡	1.795	1.796‡	0.006‡
4	(g2 − g5) − (g4 − g3)‡	2.456	2.473	−0.016‡
5	(g2)§	7.456	(7.458)§	−0.003†	7.461	7.453
6	g3 − g2‡	9.783	9.788‡	0.017‡
7	g4 − g2‡	10.526	10.516‡	0.014‡
8	(g3)§	17.240	(17.246)§	(0.010)§	(17.236)§	17.368
9	(g4)§	17.982	(17.973)§	(0.018)§	(17.955)§	17.916

^†Assumed values; g5 is considered a constant, and g2 is obtained from g2 − g5 to which the data are tuned.

^‡The g_i values obtained from the g_i − g5 terms as identified in the Newark–Hartford data.

^§Consistency check values computed with determined g_i values compared with the Newark–Hartford value from FA.

Secular Fundamental Frequencies of the Solar System

Fortunately, the question of the origin of the cycles in the Newark–Hartford dataset can be convincingly answered using refined Fourier analysis techniques in conjunction with the internal cross-checks afforded by the overdetermined components of the orbitally paced cycles themselves (SI Appendix, Table S7). MTM spectral analysis of the cycles with periods greater than 66 ky previously used for this sequence has been applied again here (Fig. 6, Table 2, and SI Appendix, Table S4). In addition, we have performed an independent analysis adopting a method developed for the quasiperiodic decomposition of the output of numerical integrations of dynamical systems called “Frequency Analysis” (FA) (30, 31) that has been widely used in various domains, including experimental physics (28, 29, 32). FA automatically extracts the frequencies and amplitudes of the periodic components of a signal without the need for manual selection of peaks sorted by decreasing amplitude. We applied FA to the whole Newark–Hartford depth rank dataset (200.65–225.565 Ma) after removing a 2-My running average using the computer code (SI Appendix). The FA results, limited to the 14 main terms (Table 2), are extremely close to the MTM analysis (Table 2 and SI Appendix, Table S4). Thus, we have obtained the same result using three different approaches (wavelet, MTM, and FA). The FA values will be used henceforth for additional quantitative analysis because of its reduced operator influence.

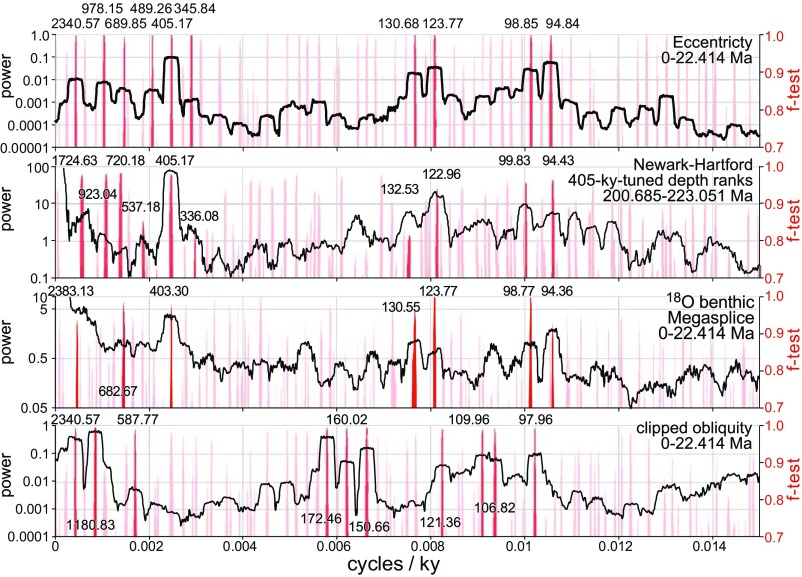
Fig. 6.

MTM spectra from the La2004 solution for eccentricity (29), 405-ky tuned Newark–Hartford depth rank data, the δ¹⁸O benthic Megasplice (50), and clipped La2004 solution for obliquity (33) (Analyseries 2.0 default: 6, 4 pi tapers). A 0- to 22-Ma interval instead of 0–24 Ma (as in the color data in Fig. 3) was used to conform to the depth rank data as opposed to the 0- to 24-Ma color data (Fig. 3). Periods above each spectrum are labeled where there is both high power and a high f significance level. Newark–Hartford data are tuned only to the 405-ky Jupiter–Venus cycle (g2 – g5), while the δ¹⁸O benthic Megasplice (50) is a composite of several records individually tuned to a suite of periodicities, including all of the major eccentricity periods from 405 to ∼100 ky for the older records and obliquity and the LR03 stack for the younger ones (50) (SI Appendix).

The MTM and FA analyses of the Newark–Hartford data exhibit striking similarities in the recovered values to periodic components of Earth's orbital eccentricity in numerical solutions of the past 20 My (compare columns 4 and 6 of Table 2) (e.g., ref. 29, table 6). This is similar to an earlier analysis that predated the independent age model (22). However, the important discrepancies with the past 20 My can now be taken more seriously, the most notable being in the g4 − g3 argument that has a present period of 2.364 My in the solution termed La2010a of ref. 5 but only 1.747 My in the Newark–Hartford data. It was argued in ref. 22 that this was the result of chaotic diffusion in the Solar System. We show here that this conclusion is most likely correct with a very high probability.

To a first approximation, the Solar System orbital motion can be considered quasiperiodic, and its long-term evolution can be represented by periodic terms of only 15 main frequencies: the frequencies g1, g2,…g8 [the secular fundamental frequencies of precession of perihelion of the planets (Mercury, Venus,…Neptune)] and s1–s4 and s6–s8 [the secular fundamental frequencies of precession of the nodes of the orbits of the planets (s5 is not present due to the conservation of angular momentum)]. Here, the secular frequencies are regarded as an average over 20 My. Insolation quantities on Earth are thus expressed in terms of these secular fundamental frequencies and additionally, the precession frequency of the spin axis of the Earth, p (29, 33, 34). In general, the secular fundamental frequencies do not appear directly in the physical variables but only as combinations of the frequencies (Tables 1 and 2 and SI Appendix, Table S4). For example, in Earth's orbital eccentricity, only differences of the form g_i − g_j are present and eventually, combinations of higher order of the g_i, with a zero sum of the coefficients (29). The largest-amplitude term in the Earth’s orbital eccentricity is the well-known g2 – g5 = 1/405-ky periodic term. Although the secular fundamental frequencies cannot be measured directly in sedimentary records due to a lack of resolution, the physical effects appear as the differences of frequencies, and these secular difference frequencies generate long-period beats that can be measured, with even longer periods than the g5 – g2 = 1/405-ky term. The geological record can thus be viewed as an interferometer in which the lower, measurable frequencies, the Grand Cycles, can be determined, although the higher frequencies that produce them cannot (Tables 1 and 2 and SI Appendix, Table S5). We thus can derive the secular fundamental frequencies pertaining to the precession of perihelion g1 through g4 directly from the geological data untethered from current values.

Chaotic Diffusion

Although over a few million years, the orbital evolution of the Solar System can be approximated by a quasiperiodic motion, as stated above, this is not true extending back in time to 200 Ma, where the chaotic diffusion of the system is noticeable. The main result is a small drift in the values of the secular frequencies of the system (5, 29, 30). This drift is small for individual frequencies, but its effects are greatly amplified in differences of close frequencies (i.e., beat cycles) as in the g4 – g3 Mars–Earth orbital eccentricity term. The period of this term is at present 2.364 My, while the observed value in the Newark Hartford data is apparently only 1.747 My (both FA results) (Table 2). Is this possible within the range of the predicted chaotic drift?

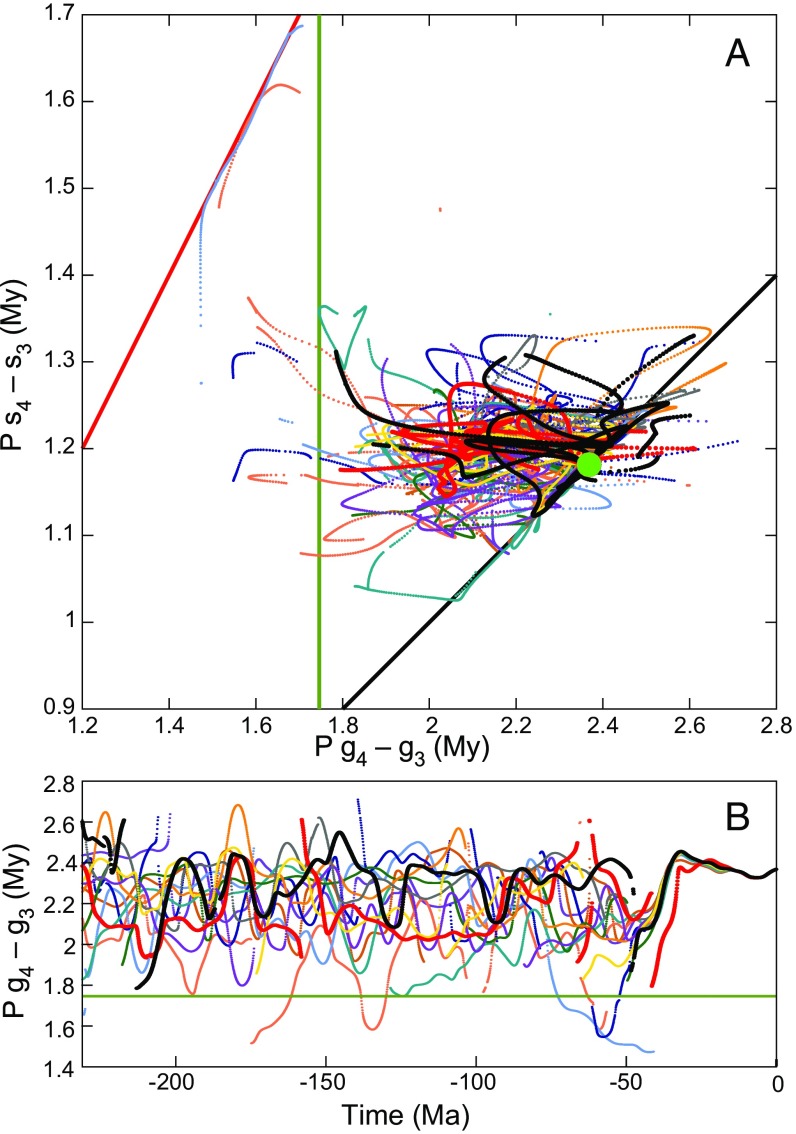
To answer this question, we cannot directly integrate the orbital solution back in time starting with the present initial conditions. Indeed, due to the chaotic behavior of the Solar System, the uncertainty in the solutions is multiplied by 10 every 10 My, and due to the sensitivity of the gravitational system to perturbations of the largest asteroids (minor planets) Ceres and Vesta, it will never be possible to retrieve precisely the planetary orbits beyond about 60 Ma (35). Nevertheless, the problem can be addressed in a probabilistic way by integrating the model beyond that time. While this does not provide the exact path of our Solar System but only a possibility for its past evolution, it does provide a gauge of the reasonableness of the geological data. We thus use 13 orbital solutions of the very precise models termed La2004 of ref. 29 and La2010 of ref. 5 with small variations in the initial conditions compatible with our present knowledge and examine the evolution of the Mars–Earth (g4 – g3) period from 0 to 250 Ma (Fig. 7A). The output is analyzed using FA with a sliding window of 20 My, with a 1-My offset between each interval (Fig. 7 and SI Appendix, Figs. S4 and S6). Among these 13 solutions, 4 of them have a (g4 – g3) period that goes below 1.75 My, and this is very nearly so for another 4. Thus, finding a 1.75-My value in the geological record in the 200- to 225-Ma time interval is entirely compatible with our best knowledge of Solar System motion.

Fig. 7.

Evolution of the period (P) of the g4 – g3 and s4 – s3 terms in 13 numerical solutions of the Solar System integrated over 250 My in the past. Frequencies values are obtained by FA over a sliding interval of 20 My, with an offset of 1 My between each interval. (A) The period of s4 – s3 is plotted with respect to the g4 – g3 period. The diagonal black line corresponds to the 2:1 resonance [P(g4 – g3) = 2P(s4 – s3), where P stands for “period of”], while the red line is the 1:1 resonance [P(g4 – g3) = P(s4 – s3)]. The green circle at (2.4, 1.2) is the present value for the Solar System and starting point of all solutions. (B) P(g4 – g3) is plotted for all 13 solutions. The black curve corresponds to La2010d (5), and the red curve is the La2004 (29). In both A and B, the green line is P(g4 – g3) = 1.75 My, the observed Newark–Hartford value.

After this first step, we search for a more quantitative estimate. The solution termed La2010d of ref. 5 comes close to the 1.75-My value in nearly the same time interval as the Newark–Hartford data, and we can consider it our reference solution we term La2010d*. We thus can compare how closely the Newark–Hartford data approximate La2010d* not only for the Mars–Earth (g4 – g3) cycle but also, for all of the major secular (difference) frequencies for Earth’s orbital eccentricity. Direct comparison of the FA results of La2010d* Earth’s eccentricity (Table 2 and SI Appendix, Table S4) with those of the Newark–Hartford data (columns 4 and 5 of Table 2) shows that the values of the periods are very close for all of the leading terms of the analyzed data (SI Appendix, Table S5). For a quantitative estimate, we use the frequencies expressed as arcsec per year rather than the period (in years), because they may be combined in a simpler way (Table 3 and SI Appendix, Table S4).

Fundamental Secular Frequencies

We can recover the fundamental secular frequencies from the Newark–Hartford data because of the great stability of the outer Solar System, notably Jupiter. The Newark–Hartford data are tuned to the g2 – g5 Venus–Jupiter 405-ky term, and we expect that FA (and MTM) should recover this value (column 4 of Table 2), which it does. While there is nothing new here, it verifies the consistency of our procedures. In addition, because the outer Solar System is very stable, the g5 frequency can be considered as a constant over the age of the Earth. The uncertainty in the 405 ky of one cycle in 250 My is due almost entirely to g2 (5). Indeed, the g5 value of La2010d*, obtained with FA, is 4.257438 ″/y, extremely close to the La2010a value of 4.257482 ″/y in ref. 5. With this assumption, supported by theory and computation, we can recover g1 from g1 − g5, g3 from g3 − g5, g4 from g4 − g5, and g2 from g2 − g5. For the last, the fact that we find a value close to the La2010a reference value is expected due to the tuning to g2 – g5 (Table 3). The recovered values for g1 through g4 are in column 4 of Table 3. We do not compare these values with the La2010a values but with the ones of La2010d* that should be much closer because this solution has drifted in a similar way due to chaotic diffusion (Fig. 7B). Indeed, the differences reported in column 5 of Table 3 are extremely small.

This should be sufficient to give us great confidence that the signal that we have recovered in the Newark–Hartford data is related to the Earth’s orbital eccentricity, but there is much more that can be recovered. Indeed, in the leading terms provided by FA, there are five additional terms in the FA of the La2010d* eccentricity solution. These terms, g4 − g3, g2 − g1, g2 − g5 − (g4 − g3 ), g3 − g2, and g4 − g2, are in column 6 of Table 3. We use these terms to test the consistency of the results. We compare the values obtained by FA on the Newark–Hartford data with the corresponding combination of the previously determined values for g1 through g4 (with g5 considered a constant). The differences are very small and are reported in column 5 of Table 3.

The correspondence of the 10 eccentricity terms reported in Table 3 is striking, and it is desirable to quantitatively examine whether such a close fit is due to chance. Among these 10 terms, we will not consider g5, because it is assumed constant. Also, we will not consider g2, because the Newark–Hartford data are tuned to the g2 – g5 term. We will not consider g4 – g3, as we chose the La2010d* solution, because g4 – g3 is close to g4 – g3 of the Newark–Hartford data of Early Mesozoic time. There remain seven frequencies in the Newark–Hartford data that are extremely close to the main La2010d* frequencies. Considering that these seven frequencies are among the 12 terms of largest amplitude of the Newark–Hartford data (after disregarding the g2 – g5 and g4 – g3 terms), we performed a statistical experiment with 33 billion draws of 12 frequencies in the [0.20 ″/y] interval. The probability that the close match of 7 of 12 terms of the Newark–Hartford to the La2010d* frequencies is due to chance is less than 5 × 10⁻⁸ and on the order of 10⁻¹¹ when only seven frequencies are considered (SI Appendix, Figs. S13 and S14). We can thus be very certain that the recovered frequencies in the Newark–Hartford data are actually the secular frequencies of the orbital motion of the Earth, and it is remarkable to see the high precision with which these frequencies are determined (Table 3). While similar values were calculated for the NBCP data in 1999 (22), these values are much more precise and accurate and pass the stringent tests inherent in the relationships among the secular frequencies, their expression in orbital eccentricity cycles, and their independent U–Pb-based age model. It is worth noting that the difference between La2010d* and the Newark–Hartford measurement for the secular fundamental frequency of the precession of perihelion for Mercury of 0.050 ″/y (Table 3) is nearly an order of magnitude less than the 0.430 ″/y contribution of General Relativity in the precession of perihelion of Mercury (e.g., refs. 2, table 4 and 36).

Other Geologic Expressions of the Mars–Earth (g4 – g3) Cycle in the Newark Basin

The existence of an ∼1.75-My cycle in the Triassic age strata of the Newark Basin was first inferred from outcrop data (18), although a 2-My period was estimated at that time. Based on this analysis, that intervals of maximum precessional variability at the peaks of this cycle contain all of the formally named members of the vast Passaic Formation, such as the Perkasie Member, which was originally recognized as distinctive in 1895 (37). These intervals also tend to be the units most easily mapped and the units with the most fossils (9), all of which are evidence of the tangibility of these Grand Cycles (SI Appendix, Figs. S15 and S16).

Synthetic seismic traces generated from the borehole data of the NBCP show the Grand Cycles (SI Appendix, Fig. S15). When tied to deep industry exploratory borehole records from the Newark Basin, themselves tied to seismic lies, both the Jupiter–Venus 405-ky and Mars–Earth 1.75-My cycles can be clearly seen as the most coherent components of the seismic profiles across the basin (38) (SI Appendix, Fig. S15). Presumably due to differences in cementation expressed in sonic parameters, the topographic expression of the deeply eroded tilted strata of the Newark Basin section also reveals the Grand Cycles, which can be seen from space, with ridges reflecting time intervals of high-precessional variability and valleys reflecting low-precessional variability that can be directly tied to the stratigraphy (SI Appendix, Fig. S16), much as bundles of plausibly obliquity-related rhythms can be seen in crater walls (39) or polar-layered deposits (40) on Mars.

Comparable Early Mesozoic Results

Thus far, Mesozoic records of astronomical forcing have tended to rely on “floating” astrochronologies or highly tuned records. By designing an experiment in a completely different region, CPCP–1, a globally exportable paleomagnetic and U–Pb-based correlative timescale was produced that validated the NH APTS. In so doing, we show the strong fidelity of the 405-ky Jupiter–Venus cycle as predicted by astronomical solutions, which in turn, allows us to recognize deviations from current astronomical solutions extrapolated from the ∼60-Ma limit of reliability, especially for the cycles with periods longer than 405 ky.

Pelagic ribbon-chert sequences from Japan have been correlated to the Newark–Hartford data through mainly biostratigraphic webs and carbon isotope stratigraphy (41). These show remarkably similar periods for the Mars–Earth orbital eccentricity cycle. As with the Newark and Hartford Basins, these were deposited in a tropical environment, albeit in the middle of the Panthalassic Ocean (41). In these data, the most prominent low-frequency cycle has a period that varies between 1.8 and 1.6 My, estimated by counting putative climate precession chert-clay couplets. As with the Newark–Hartford data, there does not seem to be any influence of obliquity.

The Early Jurassic age (Hettangian–Sinemurian) epicontinental marine Bristol Channel Basin (United Kingdom) sequence is precession dominated, expressing eccentricity cycles (42–45), and has a well-developed astrochronology and paleomagnetic polarity stratigraphy that parallels that in the Newark–Hartford composite. Based on polarity stratigraphy correlation to the NH APTS (43), the 405-ky cyclicity is in phase with that in the Newark–Hartford section and shows an amplitude modulation in phase with the g4 – g3 cycle in the radioisotopically anchored Newark–Hartford composite (43, 44). Paleomagnetic polarity correlation between the Newark–Hartford composite to the Bristol Channel section and ammonite-based correlation of the Hettangian–Sinemurian boundary from the Bristol Channel section to the marine Pucara Group (Peru) allows zircon U–Pb ages to be exported to the Bristol Channel and the Newark–Hartford Jurassic sections. The Pucara section has many zircon U–Pb CA-ID-TIMS dated ash layers with ages (46, 47) in agreement with both the Newark–Hartford and Bristol Channel Basin astrochronologies (44). An alternation in intensity of cycles attributed to climatic precession suggests a hint of obliquity pacing in the Bristol Channel data (42, 45) consistent with its higher-latitude position during the Early Jurassic (∼32° N) relative to the Newark–Hartford record (∼21° N) (10). A similar, stronger indication of obliquity is in results from higher-latitude Rhaetian coal-bearing sequences of the Sichuan Basin in China (48).

Comparison with the Cenozoic and Search for Obliquity Modulation

Comparisons of the recent compilation of benthic foraminifera δ¹⁸O data “Megasplice” (49) and modulators of obliquity with the astronomical solution for eccentricity and the Newark data are informative (Figs. 5 and 6). The wavelet spectrum of the δ¹⁸O benthic Megasplice has a less resolved structure than the Newark data. This is also seen in the MTM spectrum. The short orbital eccentricity cycles are well resolved as is the Jupiter–Venus 405-ky cycle; however, all of these cycles were used in tuning the geologically older records that comprise the Megasplice, while geologically younger parts used an age model based on the Lisiecki and Raymo (50) model termed LR04 that incorporated an ice model using the Laskar 1993 solution (La93) (51) for tuning the individual records that make up the LR04 stack; therefore, their agreement with the orbital solutions is not independent (Fig. 6). The obliquity modulating cycles (Fig. 6) are like the eccentricity cycles in that all of the frequencies are combination tones of s1, s2,…s5, which are related to precession of the node of each planetary orbit (e.g., s5 is related to the precession of the nodes of the orbit of Jupiter). We can even use the term Grand Cycles of obliquity to refer to the ensemble of long-period cycles.

The MTM spectrum of obliquity shows what should be expected in the Newark or δ¹⁸O benthic Megasplice if obliquity was a major component of the records. There is no obvious signal that can be assigned to combinations of the Grand Cycle s1, s2,…s5 secular frequencies in the Newark–Hartford data, although there could be confusion between the obliquity cycles around 100 ky and the short eccentricity cycles. Surprisingly, however, there is also no clear obliquity signal in the MTM spectrum of the δ¹⁸O benthic Megasplice as represented here either, although some beats, especially the 1.2-My (s4 − s3) Grand Cycle, are evident in the wavelet spectrum, and they have been reported from the older components of the δ¹⁸O benthic Megasplice, not examined here, and used to constrain astronomical solutions (52). Based on the wavelet spectrum, the obliquity Grand Cycles are smeared out in the younger part of the Megasplice record. This is despite the fact that obliquity and its longer-period modulators are known to be a significant part of the pacing of climate as seen in some of the records making up the Megasplice and high-latitude nonmarine records (52–54). Whether this reflects real aspects of the climate system, perhaps dampened by low CO₂; mixing of signals from different parts of the climate system; the δ¹⁸O proxy itself; or issues with tuning requires much additional work.

Grand Cycles and the Roadmap to Solar System Chaos

The results from the wavelet, MTM spectra, and FA of the Newark–Hartford data (Figs. 5 and 6 and Tables 2 and 3) are remarkable, because while the calculations of the Grand Cycles from the short eccentricity cycles in the 0- to 22-Ma data are due to their necessary linkage in the way that the astronomical solution is deconvolved and the secular frequencies are resolved, the succession of rock layers 210 My old has no such necessary linkage; it can only result from the sedimentary record of the climate response to the same physics that are imbedded in the 0- to 22-Ma eccentricity solution playing out in time. The differences between the current g1 through g4 values (column 7 of Table 3) and their Newark–Hartford FA determinations (column 4 of Table 3) are, therefore, significative and most parsimoniously explained as the result of chaotic diffusion in the gravitational interactions of the Solar System. In particular, the drift of g4 − g3 from the 2.36-My present value to the 1.75-My period observed in the Newark–Hartford data can be considered as direct geological evidence of the chaotic behavior of the Solar System.

Strong evidence for Grand Cycle orbital eccentricity pacing of climate is widespread in the lower latitudes during the Late Triassic and Early Jurassic. However, the results presented here suggest that the present astronomical solution for eccentricity does not fit the frequency data well for this time period (Table 3). We found a good match with the La2010d* solution, but it is expected that a more systematic search of the possible variations of the astronomical solutions could lead to an even better match. The important result for the Newark–Hartford data is to provide precise values for the Triassic–Jurassic secular fundamental frequencies g1 through g4 that could be considered as a reference point and used as an anchor for the search of orbital solutions that could match the past orbital evolution of the Solar System as recorded in the sedimentary data.

However, a major contributor to the chaotic behavior, in fact its signature (30), is related to the Mars–Earth secular resonance (g4 − g3) − 2(s4 − s3) (now in libration; i.e., oscillation in phase space) and its possible transitions to and from (g4 − g3) − (s4 − s3) (circulation; i.e., rotation in phase space), with the resulting 2:1 vs. 1:1 periods of the eccentricity and obliquity Grand Cycles (Fig. 7A). Because the Newark–Hartford data show no clearly discernible obliquity pacing, the mode of 2:1 vs. 1:1 resonance in the secular frequencies cannot presently be determined for this time interval. While there has been some recent progress with tantalizing results (55), the transition from the 2:1 vs. 1:1 periods has yet to be unambiguously observed in suitably long records, and it is possible that it has never occurred, although most numerical solutions show it. To obtain a result for the Triassic–Jurassic secular resonance, suitably long (>10-My) contemporaneous high-latitude records that would be expected to show a strong obliquity pacing are needed. For example, the continental and coal-bearing Triassic–Jurassic ∼70° N Junggar Basin section shows strong hints of obliquity forcing interpreted to be a 2:1 ratio of eccentricity to obliquity Grand Cycles (∼1.6:0.8 Ma), but that section lacks an independent geochronologic or paleomagnetic polarity timescale, although it does exhibit 405-ky periodicity (44). Cores spanning tens of millions of years from such a section would permit a high-resolution paleomagnetic polarity record to be developed from the basin (extremely difficult to do in outcrop in these gray and black strata because of weathering) that would allow correlation to the Newark–Hartford data and presumably resolve the mode of resonance in the eccentricity and obliquity Grand Cycles. This would be a full proof of concept of the Geological Orrery.

If the resonance is in the 2:1 ratio for the latest Triassic and earliest Jurassic as the preliminary interpretations suggest, this finding would only apply to that particular time, and we still cannot show when or if the 1:1 situation ever happens. There are strong hints that even longer astronomical cycles with periods of ∼8–9 and ∼36 My (41, 56) may modulate the Grand Cycles, and these modulations could be confused with actual changes in secular frequencies or tectonic influences in records that are too short. To examine these potential empirical phenomena will require careful concatenation of multiple long records with appropriate properties, including independent geochronology, all accurately recording low and high frequencies that pass the types of rigorous tests outlined here.

A complete Geological Orrery would consist of multiple sets of paired low- and high-latitude records (preferably cored to ensure superposition and continuity) spanning the Paleogene to Permian and beyond, with even deeper time highly desirable. When combined with the existing record from the last ∼60 My, the last ∼250 My of Solar System history would be covered. The empirical mapping of the secular frequencies of the Grand Cycles in eccentricity and obliquity over this time interval (including the transitions in secular resonances should they occur) would constitute an entirely new empirical realm to test Solar System evolution, astronomical solutions, and gravitational models. By constraining the past evolution of the speed of perihelion of Mercury g1, the results would provide mechanisms to constrain the evolution of the flattening parameter J2 of the Sun and further test General Relativity and its alternatives (3).The constraint on the past evolution of the other secular frequencies may be used to limit the existence of additional planets and examine predictions of galactic disk dark matter interactions with the Solar System (56, 57). The results would also be important in efforts to tune radiometric decay constants for geochronology and to produce accurate solar insolation targets beyond 60 Ma.

Materials and Methods

Core used in this analysis originates from three sedimentary basins in North America (SI Appendix, Fig. S1): the cores from the seven NBCP core sites (Newark Basin), the Passaic River Diversionary Tunnel Army Corps of Engineers (ACE) cores (Newark Basin), the Silver Ridge Core (Hartford Basin), the Park River Cores (Hartford Basin), the Metropolitan District Commission (MDC) cores (Hartford Basin), and the Colorado Plateau Coring Project, Petrified Forest National Park, 2013 1A (CPCP-PFNP13-1A) core (Colorado Plateau). Details of locations are given in SI Appendix, Table S1.

MTM spectra (Figs. 3, 4, and 6 and SI Appendix, Fig. S9) were developed using Analyseries (2.0), which was also used for filtering, interpolation, etc. (58), and the wavelet spectra (Figs. 2, 3, and 5 and SI Appendix, Figs. S6 and S12) were computed using the Matlab script of Torrence and Compo (59) (paos.colorado.edu/research/wavelets/). For all data, Analyseries (2.0) was used for interpolation and for the time series based on the Laskar 2004 solution (29), which in the case of the last 0–24 Ma, is not significantly different from more recent solutions (5). The FA method is described in refs. 30 and 31 and has been used with its implementation in the TRIP software, which is documented and freely available at https://www.imcce.fr/trip/. The TRIP source code used in this work is given in SI Appendix. Work on the NBCP and CPCP–1 cores was conducted at the Rutgers Core Repository as described in ref. 12, and CPCP–1 core analysis and documentation were conducted at the LacCore facility at the University of Minnesota (11).