Distinct differences in the nanoscale behaviors of the twist–bend liquid crystal phase of a flexible linear trimer and homologous dimer

Significance

The twist–bend (TB) liquid crystal phase is the newest nematic phase, having only been identified in 2011. Still, there are many outstanding mysteries about the nature of its nanoscale organization and behavior. We elucidate how the number of monomer units in a linear TB oligomer influences the structure of its nanoscale helix, an important TB phase structure–property relationship. While a TB dimer exhibits a temperature-dependent variation of its helix pitch, the analogous trimer features a temperature-independent helix pitch considerably shorter than that of the dimer and other known TB materials. This study illuminates the scope of possible variations that manifest in the TB phase and represents a substantial step in controlling its nanoscale behavior for technological applications.

Abstract

We synthesized the liquid crystal dimer and trimer members of a series of flexible linear oligomers and characterized their microscopic and nanoscopic properties using resonant soft X-ray scattering and a number of other experimental techniques. On the microscopic scale, the twist–bend phases of the dimer and trimer appear essentially identical. However, while the liquid crystal dimer exhibits a temperature-dependent variation of its twist–bend helical pitch varying from 100 to 170 Å on heating, the trimer exhibits an essentially temperature-independent pitch of 66 Å, significantly shorter than those reported for other twist–bend forming materials in the literature. We attribute this to a specific combination of intrinsic conformational bend of the trimer molecules and a sterically favorable intercalation of the trimers over a commensurate fraction (two-thirds) of the molecular length. We develop a geometric model of the twist–bend phase for these materials with the molecules arranging into helical chain structures, and we fully determine their respective geometric parameters.

Liquid crystal (LC) compounds with two or more rigid monomer units connected by flexible linkers can exhibit unique assemblies not encountered in other LCs. LC oligomers bridge the structure space between conventional small-molecule LCs and polymer LCs. This structural motif has generated considerable interest in the LC field because their chemical makeup induces odd–even effects and unique intercalated smectic phases (1, 2).

In addition, there have been a number of accounts of short oligomers which form the twist–bend (TB) LC phase (3–8), a phase which has only recently been identified (9). The TB phase is a nematic (N) characterized by heliconical orientational ordering of the LC director, where the molecules are inclined by a cone angle θ_H with respect to the helical axis z, and precess with azimuthal angle φ(z) around z, with nanoscale pitch p_H, but do so without any accompanying mass density wave in p_H (10). The nanoscale TB structure has been investigated in a number of LC systems with a variety of structural motifs, including flexible dimers (10–15), a bent-core mesogen (16), and mixtures of bent LC molecules with other LCs (11, 17–19). However, only one nanoscale structural investigation has previously been performed on TB-forming oligomers of three or more monomeric units (10), although in that case the compound was not a conventional linear trimer but a bent-core hybrid molecule. A number of studies have found through conventional X-ray diffraction techniques that trimers and tetramers tend to be heavily intercalated in the nematic and TB phases (4, 6), but to our knowledge, little other characterization of the nanoscale structure of the TB phase has been carried out on linear unbranched LC n-mers with n > 2.

Here, we describe the synthesis of an LC molecular trimer which we designate CB6OBO6CB. We perform a number of nanoscale characterization techniques, including resonant soft X-ray scattering (RSoXS), wide-angle X-ray diffraction (WAXS), and freeze-fracture transmission electron microscopy (FFTEM), and contrast the results to those of the analogous dimer molecule CB6OCB which also forms the TB phase (14). While CB6OCB exhibits a TB pitch which varies considerably from p_di = 100–170 Å, we find that CB6OBO6CB exhibits a pitch p_tri = 66–67 Å over the ∼20 °C range of its TB phase, making it effectively temperature-independent and small for a TB pitch, which we find extraordinary because this molecule is significantly longer than most other TB-forming LCs. We account for this fact by considering the degree of intercalation possible in CB6OBO6CB, which permits a sterically favorable interlocking of molecules over ∼2/3 of their molecular length, thereby constraining the flexibility and suppressing fluctuations of the helical structure. Our characterization further permits us to construct detailed geometric models of the TB phase in each of these materials and to make predictions about the behaviors of the analogous higher oligomers.

Results

CB6OBO6CB (or the “trimer” for conciseness), contains three rod-like monomer units linked by two flexible spacers (Fig. 1A). The odd number of atoms separating the monomer units ensures oligomer curvature, while the choice of the methylene link between the spacer and the monomeric cyanobiphenyl groups ensures a sufficient bend to make it a promising candidate to form the TB phase, by analogy to CB6OCB (the “dimer”) (14).

Fig. 1.

Molecular structure of CB6OBO6CB and CB6OCB and polarized light microscopy images of the trimer. (A) Molecular structure drawings of CB6OBO6CB and CB6OCB, which we denote trimer and dimer, respectively. Polarized light microscopy images of the trimer in the nematic phase (B) and the TB phase (C).

We characterized the phase behavior of CB6OBO6CB and positively identified the TB phase with a combination of polarized light microscopy (Fig. 1 B and C) differential scanning calorimetry (SI Appendix, Fig. S1), a binary phase diagram of the dimer and trimer (SI Appendix, Fig. S2), and a contact cell preparation of the trimer with CB7CB (9–11, 13) (SI Appendix, Fig. S3), a material well-known to exhibit the TB phase. We find the following LC phase behaviors on cooling: for CB6OBO6CB, I (isotropic) $\stackrel{169°\text{C}}{\to }$ N (nematic) $\stackrel{131°\text{C}*}{\to }$ TB $\stackrel{110°\text{C}}{\to }$ Cr (crystal) (the * symbol indicates a monotropic phase transition); and for CB6OCB, I $\stackrel{155°\text{C}}{\to }$ N $\stackrel{109°\text{C}}{\to }$ TB $\stackrel{99°\text{C}}{\to }$ Cr.

A typical uniaxial nematic texture forms on cooling from the isotropic phase of the trimer in a unidirectionally rubbed planar cell (Fig. 1B). On further cooling, the nematic phase transitions into another phase which exhibits a blocky optical texture that then develops into well-defined stripes and focal conic defects (Fig. 1C). These textures persist for ∼20 °C on steady cooling until the transition into the crystal phase. This behavior is fully consistent with the TB phase observed in LC dimers (9, 20).

The enthalpy of formation $\left(\mathrm{\Delta }H\right)$and the entropy change $\left(\mathrm{\Delta }S\right)$associated with the transitions are in the range of expected values for these types of transitions (Fig. 1). It is noteworthy, however, that the entropy change associated with the N–TB transition is greater than would be expected based on the behavior of dimeric materials as well as the temperature width of the preceding nematic phase (SI Appendix, Fig. S1 and refs. 5–7 and 21).

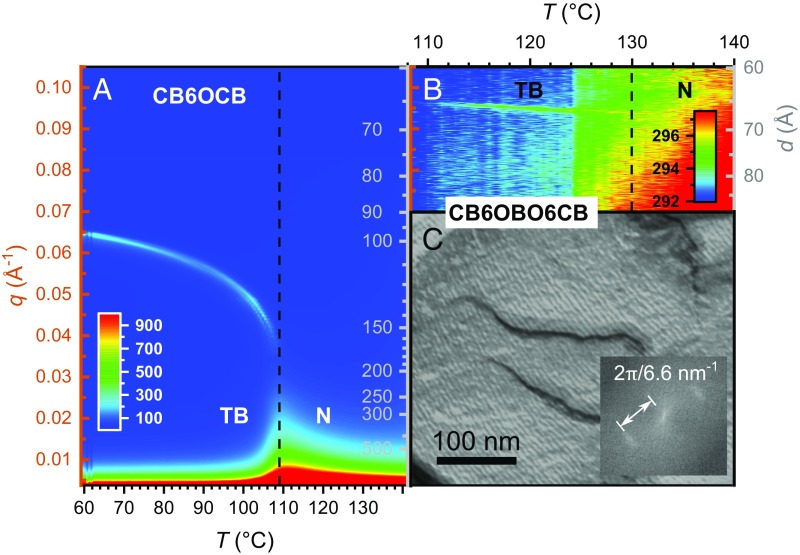
We subsequently performed RSoXS (13) on CB6OCB and CB6OBO6CB by taking 2D detector images on cooling from the nematic phase, where we observed no resonant scattering. We converted these 2D RSoXS detector images into plots of I(q) vs. q, the magnitude of the wave vector q, by azimuthally averaging the 2D diffractograms about q = 0. We then used the Nika X-ray data analysis and processing software to interpolate the 1D plots into a color map with q and the corresponding wavelength d(q) = 2π/q plotted as a function of temperature, with the intensity in the 1D plots represented by the color scale in Fig. 2 A and B. On cooling from the nematic, CB6OCB develops a peak at q(T = 108 °C) = 0.0375 Å⁻¹, corresponding to the TB helical pitch d(q) = p_di(T = 108 °C) ∼ 170 Å (Fig. 2A). The helical pitch rapidly decreases, then begins to saturate near p_di(T = 60 °C) ∼ 100 Å before it crystallizes. The determination of a TB pitch of ∼90 Å for CB6OCB by FFTEM in ref. 14 roughly accords with our RSoXS measurement, given that FFTEM experiments tend to exhibit the value of the pitch extrapolated to low temperature in the TB phase (19). CB6OBO6CB, on the other hand, exhibits a very different TB pitch behavior (Fig. 2B).

Fig. 2.

RSoXS color plots of CB6OCB and CB6OBO6CB with the q axis in orange and the d axis in gray, and an FFTEM image of CB6OBO6CB. (A and B) Color plots are composed of line scans in q of azimuthally averaged 2D detector images from RSoXS experiments taken as a function of temperature. The q and pitch d scales are the same across both plots. (A) CB6OCB exhibits usual temperature-dependent scattering behavior for conventional TB-forming dimer molecules. In the nematic phase, we observe no scattering features, as expected. On cooling to 108 °C, a peak appears near p_di(T = 108 °C) ∼ 170 Å corresponding to the TB helical pitch. On further cooling, the helical pitch drops dramatically, then more slowly approaches p_di(T = 60 °C) ∼ 100 Å before crystallization. (B) On cooling CB6OBO6CB from the nematic phase, a scattering* feature appears near 130 °C corresponding to a helical pitch of p_tri = 67–66 Å, remarkably short compared with that of CB6OCB and other known TB materials. The dashed line denoting the N–TB phase transition temperature was drawn where the TB phase scattering is clearly visible. The plot exhibits a slight discontinuity in the background scattering T = 124 °C, which is due to thermal drift in the cell absorbance while we stopped the q scans to perform a beamline energy scan. The half-width at half-height of the TB helix peak from the image contours gives HWHH ∼0.001 Å⁻¹, indicating a coherence length of ∼1,000 Å for the TB helix, consistent with the FFTEM image in C. (C) Representative FFTEM image of CB6OBO6CB in the TB phase exhibiting sinusoidal topographical modulations at p_tri,FFTEM = 6.6 nm. In different regions of the trimer sample, we observe topographical modulations with a variety of periodicities, but with the most frequently observed periodicity in the sample (when weighted by the area of occurrence) being 6.6 nm (SI Appendix, Fig. S5).

On cooling from the nematic phase, we begin to see unambiguous evidence of scattering from the TB helix at ∼130 °C. At 124 °C, we held the temperature fixed and varied the beamline energy about the carbon K-edge resonance to check that the scattering feature was indeed resonant (SI Appendix, Fig. S4), confirming that the structure of this phase is modulated in molecular orientation and not related to electron density (13). The scattering signal peaks at q_tri(high T) = 0.094 Å⁻¹, corresponding to a helical TB pitch of p_tri(high T) = 67 Å. On further cooling, this peak shifts very gradually to q_tri(low T) = 0.096 Å⁻¹, corresponding to a helical pitch of p_tri(low T) = 66 Å. The lack of significant temperature dependence of the pitch on cooling over the ∼20 °C temperature range is striking, and in stark contrast to other RSoXS measurements performed on TB dimers and their mixtures (13, 15, 18, 19). This TB scattering feature fades away as the sample crystallizes near 110 °C. We scanned all accessible RSoXS sample-detector configurations to check for other possible resonant scattering signals from q = 0.0012–0.10 Å⁻¹ (d = ∼60–5,000 Å) but found none. The value of the pitch obtained from RSoXS is in good agreement with our FFTEM measurement of p_tri,FFTEM = 66 Å (Fig. 2C and SI Appendix, Fig. S5) for the trimer, where we analyzed a number of images to obtain a statistical distribution of the observed periodicities throughout the sample, as described in ref. 19.

Using WAXS, we investigated the diffuse scattering in the trimer corresponding to correlations in mass density along (q_z,WAXS) and perpendicular to (q_⊥,WAXS) the TB helix axis. In the TB phase, the scattering feature along the helix axis is present near q_z,WAXS = 0.48 Å⁻¹ (SI Appendix, Fig. S6). This corresponds to d_z = 13 Å, or an intercalation of the trimer over nearly 1/3 of the molecular length. This is in agreement with the significant intercalation reported in previous studies of TB and smectic phases of LC linear oligomers (4, 6, 22). The q_⊥,WAXS feature corresponds to an average ∼5-Å lateral spacing between molecules of CB6OBO6CB.

We carried out birefringence measurements of the dimer and trimer (shown in SI Appendix, Fig. S7), then used the procedure developed by Meyer et al. (23) to calculate an optically derived cone angle from the birefringence as a function of temperature. The behavior of the optically derived cone angle in the dimer and trimer is similar to that found for CB7CB. At high temperature in the TB phase, the dimer exhibits a cone angle of ∼7°, while the trimer exhibits a cone angle of ∼10°. The cone angle saturates near 20° and 17° for the dimer and trimer, respectively, which is somewhat smaller than that found for CB7CB (19, 28).

Discussion

The striking differences in the nanoscale behavior of the TB phase in the dimer and trimer must be due to effects from the different number of rod-shaped monomer units in the molecules. A number of review studies have discussed the variations in physical and LC properties as a function of the number of monomer units in small LC oligomers (1, 2, 6, 24, 25), but beyond the work in the LC community, the literature on the properties of linear oligomer homologs is sparse. However, we presently have enough experimental detail to construct a model of the TB organization in each material and to speak to their differences.

The TB nanostructure is determined by a combination of molecular features, including the chemical makeup of the molecules and the relative dimensions of the monomer units, and structural features, including the TB pseudolayer spacing and helix pitch.

The “pseudolayer” spacing s in the TB phase is essentially the same feature as that found in aligned nematics, with scattering arcs in q_z elucidating the density modulation along the nematic director ẑ (26). We can determine s for the TB phase from the q_z,WAXS feature in WAXS experiments for both the dimer (14) and trimer (SI Appendix, Fig. S6), where s = d(q_z,WAXS) = 2π/q_z,WAXS. We find the pseudolayer spacing for the dimer is s_di = 11.6 Å (14) and for the trimer is s_tri = 13 Å, as denoted in Fig. 3 A and B. That s_di and s_tri are nearly 1/2 and 1/3 of their respective molecules indicates uniform intercalation of the molecules over their respective s and implies that the TB pseudolayers are spaced by the height of a single (tilted) alkyl-cyanobiphenyl or alkyl-biphenyl monomer unit making up the dimer or trimer. Interestingly, we find very little or no measurable temperature dependence of s in the nematic and TB phases of the trimer. Likewise, Paterson et al. (14) observe no discernible change in the equivalent s_di feature in the dimer through the nematic and TB phases. For this reason, in the following analysis we consider s to be constant through the temperature range of the TB phase.

Fig. 3.

Stick representations of the (A) CB6OCB dimer, (B) CB6OBO6CB trimer, and (C) the analogous theoretical polymer with corresponding low-temperature TB parameters and azimuthal precession Δφ set to 180° in each case for clarity. The molecules are uniformly intercalated, with the TB chains they form distinguishable and color-coded by the position of the chain–end interfaces. (A and B) The dimer and trimer systems both have end-to-end and arm-to-arm interactions, but only the trimer exhibits an additional 2/3 “interlocked” association (B) which tends to hinder molecular motion and flexibility in the TB helix. (C) The analogous polymer system forms an anticlinic (pseudo)lamellar phase which is a special case of the TB phase with Δφ = 180°. The polymer molecules are constructed by attaching the ends of many rod-like units that make up the middle monomer of the trimer (from the central carbon in one linker to the central carbon in the other). The pseudolayer spacing s_poly,est in the analogous polymer is estimated by tilting the middle rod-like unit of the trimer (16.6 Å) to a 30° angle.

The basic geometry of the helices of the trimer and dimer TB phases can be obtained by analyzing the X-ray and birefringence data in the light of the length of the linear subsegments of the molecules. From the values of the pitch p and s, we can determine the azimuthal precession φ per s at low temperature to be Δφ_di = 360° × s_di/p_di = 360° × (11.6 Å/100 Å) ∼ 42° and Δφ_tri = 360° × s_tri/p_tri = 360° × (13 Å/66 Å) ∼ 71°. For the sake of the geometric modeling that follows, we approximate by letting Δφ_di → 45° (an eightfold helix) and Δφ_tri → 72° (a fivefold helix). With this, we can construct the TB phase of the dimer as a series of octagons separated by the pseudolayer spacing s_di, with the rod-like arms of the dimer lying along the diagonal of the rectangular faces of the octagonal prism formed by connecting the corners of the octagonal pseudolayers with straight vertical lines, enforcing the azimuthal rotation of Δφ_di per s_di (Fig. 4A). Similarly, the TB phase of the trimer is modeled as a series of pentagons separated by s_tri, with the rod-like monomer units lying on the diagonal of the faces of the pentagonal prism formed, enforcing the azimuthal rotation of Δφ_tri per s_tri (Fig. 4B).

Fig. 4.

Geometric models of the CB6OCB dimer and CB6OBO6CB trimer in their respective TB phases. The molecules form pairs of interlocking chains which have the measured tilt angle and pitch. 3D space is filled by packing these chains on a hexagonal lattice in the x–y plane having a lattice parameter that gives the correct density. (A) A geometric construction that governs the structure of the TB phase formed by the dimer at low temperature. The chains are divided into two subsets, with the ends of the red molecules in the chains meeting at the corner of a red octagon, and the ends of the purple molecules meeting at the corner of a purple octagon. The molecular ends in the dimer overlap by 15.8–12.4 Å = 3.4 Å, and the rod-like arms are tilted from the helix axis ẑ along the diagonal of an outer rectangular face of the octagonal prism by the TB cone angle θ_TB,di = 21.2°. (B) A geometric construction governing the structure of the TB phase formed by the trimer at low temperature. The chains are divided into three subsets with the ends of the blue molecules in the chains meeting at a blue pentagon, and likewise for the green and yellow chains. The chemical makeup of a rod-like middle-monomer is depicted in gray overlaying a middle segment of the blue leftmost trimer chain. The molecular ends of the trimer overlap by 16.0–13.9 Å = 2.1 Å (16.0 Å being the averaged monomer length), which is significantly less than that found for the dimer. The rod-like units of the trimer are tilted along the diagonal of the outer face of the pentagonal prism by the cone angle θ_TB,tri = 27.2°. The polygonal prisms in (A and B) enforce the respective azimuthal precessions Δφ per pseudolayer s. Once the single chains are constructed, they may be rotated around the center line of the polygons to change their helical phase. In this 3D packing sketch, the phase is assumed to be the same for all helices, with the differently colored helices positioned randomly in their packing. We depict a possible 3D packing of the helical chains on a hexagonal lattice in (A and B) (gray planes), although the actual packing motif may be different.

We can obtain the TB cone angle θ_TB from the optical birefringence measurements of the materials in the nematic and TB phases. On cooling from the nematic phase to the TB phase, we observe a decrease in birefringence, which is due to a collective tilt θ_optical of the molecules from ẑ and can be determined by the method of Meyer et al. (23). This measured θ_optical is not, however, the TB cone angle θ_TB, as θ_optical measures the tilt of the molecular plane of the molecule away from ẑ, and θ_TB is defined by the angle between the helix axis ẑ and the local director n̂. θ_TB comes from a combination of the intrinsic bend angle of the molecule and the tilting of the molecules from ẑ. We can therefore determine θ_TB at low temperature using θ_optical and the experimentally determined geometric constraints enforced by the polygonal constructions of Fig. 4. By doing this, we find θ_TB,di = 21.2° (θ_optical,di ∼ 20°) and θ_TB,tri = 27.2° (θ_optical,tri ∼ 17°) at low temperature in the TB phase (see SI Appendix, Fig. S8 for derivation).

Although we are not invoking any specific relation the crystal structure, SI Appendix, Fig. S6 shows the sharpening of the pseudolayer diffuse scattering near q_z ∼0.45 Å⁻¹, giving s_di in the TB phase, into a Bragg reflection peak in the crystal at q_z = 0.48 Å⁻¹, which suggests that the helices in the trimer TB and crystal phases are similar. This is likely to be less so for the dimer.

By solving our geometric constructions of the TB phase, we may also determine the effective monomer length m_eff in the TB helix (the length of the diagonal of the rectangular face of the polygonal prisms in Fig. 4). This length may in general be different from the full length of the rod-like monomer unit m_calc making up the dimer and trimer, if there is overlap or separation between end groups, for instance. Solving from the geometric constraints in the TB model of the dimer (Fig. 4A), we find m_di,eff = 12.4 Å. The length of one of the rod-like monomers making up the dimer, as measured in its extended all-trans conformation from the central carbon in the linker to the end nitrogen group, is calculated to be m_di,calc = 15.8 Å. Here, we consider only the extended all-trans conformer of the dimer as an approximation to the conformational diversity expected in the TB phase, since the condensed and locally orientationally aligned TB phase tends to favor extended conformations over more kinked conformers. This indicates an overlapping of the end groups for the dimer of m_di,calc – m_di,eff = 3.4 Å at low temperature in the TB phase, or a bit more than the atomic diameter of an end nitrogen. We expect that on heating, in addition to the cone angle decreasing, the ends of the dimers will tend to pull apart, leading to the flexibility in the helix structure and the dramatic pitch increase that we observe at high temperatures in the TB phase (Fig. 2A).

Using a similar treatment for the trimer as for the dimer, we determine the effective monomer length in the TB phase of the trimer to be m_tri,eff = 13.9 Å. Because the end- and middle-monomer groups of the trimer are not of equal lengths, we can determine the average monomer length using the Spartan calculation of the extended all-trans conformation of the trimer by averaging the lengths of the individual monomer segments. We do this because we only observe a single scattering peak from the pseudolayer spacing, which implies that the end- and middle-monomer units that make up the trimer are uniformly distributed in 3D space. Here again, we consider the extended all-trans conformer of the trimer in our model as an approximation, for the same reasons that we do for the dimer (as mentioned above). The length of an end monomer is measured from the central carbon in a carbon linker to its nearest nitrogen atom, and the length of a middle monomer is measured from the central carbon of one alkyl linker to the central carbon of the other linker. From this, we find m_tri,calc = (2 × 15.7 Å + 16.6 Å)/3 = 16 Å. And now, m_tri,calc – m_tri,eff = 2.1 Å, indicating a smaller overlap of the molecular ends in the trimer than that found in the dimer. Indeed, the mismatch in the lengths of the end- and middle monomers of the trimer will tend to pull the shorter end monomers apart by association with the longer middle monomers (Fig. 3B). From the above discussion, we can conclude that the molecules in the TB phase of the dimer and the trimer exhibit mutual end-group interactions which leads to an effective heliconical chain-like arrangement of the molecules, as depicted in Fig. 4.

We can compare intermolecular interactions which occur in the TB phases of the dimer and trimer. A common feature of these phases is the short-range pseudolayer lamellar order with spacing s, corresponding to a length unit along z equal to that of a tilted rigid section of the molecule projected onto the z axis. This periodicity indicates a molecular preference to be intercalated by displacement along z of an integral number of such units. In the TB phases there are two kinds of interactions that give rise to this preference: (i) upper ends of molecules strongly associate with lower ends of other molecules, and (ii) the molecular bends tend to associate with both molecular ends and bends. These associations, evident in the models of Figs. 3 and 4, are physical correlations, held together by combination of van der Waals and electrostatic forces, thereby contributing to flexibility, elasticity, and fluctuations in the structure of the TB helix. The trimer system has more chemically bonded monomers per unit length in the TB helix than there are in the dimer. For the trimer, at each pseudolayer interface (any pentagon in Fig. 4B) there are two-thirds chemically bonded monomer bends (chemically bonded with an alkyl linker) and one-third terminally associated monomers (end-to-end physical association), whereas for the dimer, at each pseudolayer interface (any octagon in Fig. 4A) there are one-half chemically bonded monomers and one-half terminally associated monomer units. This effect tends to increase the rigidity of the TB helix, thereby reducing (and essentially eliminating) the temperature dependence of the helix pitch in the TB phase of the trimer.

From our experiments, a number of interesting trends in the structure of the TB phase of this oligomeric family emerge. For instance, the pseudolayer spacing increases from the dimer to the trimer (s_di = 11.6 Å; s_tri = 13 Å). This trend indicates that s will increase in the higher oligomers, but is not likely to exceed the theoretical pseudolayer spacing s_poly,est ∼ 14.4 Å of the comparable polymer which is composed of the middle-monomer units of the trimer tilted at a comparable angle (30°), as depicted in Fig. 3C. This is because the comparable polymer, in the anticlinic (pseudo)lamellar system, has (effectively) no molecular ends that may overlap, in contrast to the dimer and trimer which have a mixture of inner and terminal connections between rod-shaped elements which do overlap. In addition, the TB pitch tends to decrease from the dimer to the trimer [p_di(low T) ∼ 100 Å; p_tri(low T) ∼ 66 Å], implying that the pitch will tend to decrease in the higher oligomers in this family and approach a value not smaller than p_poly = 2•s_poly,est. The pitch will also become more temperature-independent with the increasing number of monomers in the oligomer as the amount of intermolecular locks increases. Additionally, the azimuthal precession Δφ per s increases from the dimer to the trimer (Δφ_di ∼ 42°; Δφ_tri ∼ 71° at low T). From this observation, we can expect that Δφ will tend to increase in the higher oligomers of this family, and asymptotically approach a value perhaps not exceeding Δφ_poly = 180°, since the comparable polymer in an anticlinic (pseudo)lamellar phase has p_poly and s_poly (and therefore Δφ_poly), fixed by the chemical structure. Our investigation of this dimer and trimer outlines the possible trends in their oligomeric family and for other linear main-chain oligomeric series with similar molecular constructions. It is important to stress, however, that the behavior of the TB nanostructure of different oligomer families may depend qualitatively on the chemical structure of those oligomers, as well as on the number of monomer segments, their relative dimensions, and preferred orientations. Clearly, it is of great interest to explore the features of the TB nanostructure more systematically as a function of these variables.

Finally, we evaluate the possible 3D packing motifs of the heliconical chains formed from the dimer and trimer. Consider the hexagonal lattice represented in the gray-shaded planes in Fig. 4. Each site on this lattice has a heliconical chain passing through it, and the constructions in Fig. 4 result if we assume that all of the chains pass through the plane with the same phase φ. The assumption that all of the chains have the same phase is motivated by the X-ray diffraction crystal structures of Hori et al. (27) for their dimer material II-3, which exhibits a helical state in its crystal phase with an azimuthal rotation of Δφ_II-3 = 90° per layer, with a layer spacing of s_II-3 = 9.7 Å, a tilt of the mesogenic cores of θ_II-3 = 45° relative to the helix axis, and a pitch of p_II-3 = 38.7 Å. The crystal structure of II-3 is similar to that sketched for the TB phase of the trimer in Fig. 4B, but with II-3 having its helical chains on squares rather than on pentagons and tiling a square lattice to fill 3D space. In this crystal structure, the helical phase φ in a given plane normal to the helix axis is the same for all of the chains, a geometrical consequence of the large monomer tilt of II-3 and the steric constraints of packing the rod-shaped units with a large tilt. The large inherent tilt of the rod-like monomer units in the dimer and trimer makes it likely that their helical chains are likewise precessing in phase with one another, as depicted in Fig. 4. Although we find that this evidence points to the organization depicted in Fig. 4, it is possible that the helical chains are instead randomly spatially arranged or arranged in more complex fashions, although we cannot speak to these organizational motifs in the present study.

Recently, Al-Janabi et al. (8) published an investigation of the phase behavior of the trimer that we study here. A comparison of our data for our trimer and theirs (which they call B6₃) shows that their differential scanning calorimetry measurements, phase diagram, and nonresonant X-ray scattering features are nearly the same as ours. The only difference appears to be that they obtained different optical textures than expected for a TB phase. On this basis, and the lack of miscibility between their trimer and another material with a TB phase, they chose not to identify the lower-temperature nematic phase as a TB phase. However, as we report, our RSoXS experiments demonstrate an orientation modulation at 66 Å only near the carbon K-edge resonance, and not off the energy resonance (SI Appendix, Fig. S4). The TB phase is the only known LC phase in this range of length scales (and, correspondingly, q values) that exhibits resonant scattering for p and the absence of scattering for p in nonresonant conditions. The likelihood of having a splay-bend nematic or similar modulated nematic with a nonzero density modulation, but lacking a nonresonant scattering signal, is too remote to consider and has already been discussed in detail in ref. 13. In addition to this evidence, our polarized light microscopy images are decidedly typical of the TB phase, exhibiting the blocky texture and the rope texture in a unidirectionally rubbed cell, with the textures alone having been used by many research groups to identify the TB phase. And finally, a binary phase diagram (SI Appendix, Fig. S2) and a contact cell preparation with the trimer and the well-known TB-forming material CB7CB (SI Appendix, Fig. S3) clearly demonstrate miscibility of these compounds in the nematic and TB phases. It is with this evidence that we confidently identify the lower-temperature nematic phase of CB6OBO6CB as the TB phase.

Conclusions

We synthesized and characterized the TB-forming LC trimer CB6OBO6CB and its analogous dimer CB6OCB. The trimer exhibits a monotropic TB phase with a temperature-independent heliconical pitch p_tri = 67–66 Å. Our characterization and analysis of these materials suggest the importance of the number of chemically linked segments in a molecule for controlling the elasticity and fluctuations in the TB nanostructure. We constructed a geometric picture of the TB phase for the dimer and trimer which indicates that they are formed by a helical chain motif which is linked together by an association and overlapping of the molecular ends. The nanoscale properties of their TB phases differ significantly because the trimer exhibits an additional molecular association over 2/3 its length which does not exist in the dimer. This work evokes the possibility for designing LCs which exhibit a specific temperature-independent TB pitch for technological applications in which a fixed pitch over a wide temperature range is preferred, such as nanotemplating or chiral separation techniques. It also opens up a rich phase space of possible molecular designs motifs for the TB phase by not only varying the chemical makeups and number of monomer units, but by also varying the relative physical dimensions and orientations of the monomers in the oligomer, likely yielding further exciting material properties.

Materials and Methods

The synthesis of CB6OBO6CB is described in detail in SI Appendix.

The thermal behavior of CB6OBO6CB was investigated by differential scanning calorimetry using a Mettler Toledo DSC822^e differential scanning calorimeter equipped with a TSO 801RO sample robot and calibrated using indium and zinc standards. The heating profile in each run was heat, cool, and reheat at 10 °C min⁻¹ with a 3-min isotherm between heating and cooling segments. Thermal data were normally extracted from the second heating trace. Initial phase characterization was performed with polarized light microscopy, using an Olympus BH2 polarizing light microscope equipped with an Instec hot stage. Birefringence measurements of CB6OCB and CB6OBO6CB were carried out using polarized light microscopy, with the samples filled into 4.2-μm-thick unidirectionally rubbed glass cells (23). The birefringence at a given temperature was determined using the average of three distinct measurements from a Berek optical compensator.

RSoXS experiments were performed at the Advanced Light Source at Lawrence Berkeley National Laboratories beamline 11.0.1.2 with linearly polarized X-ray photons. RSoXS cells were assembled by placing a 100-nm silicon nitride window, supported by a silicon substrate on a hot plate with the temperature above the clearing temperature. The LC material was placed onto the substrate, with another identical substrate placed on top of the material to form a sandwich cell. This cell was mounted onto a custom-made copper hot stage, which permitted heating the sample in situ. The hot stage was placed inside a vacuum chamber (P < 10⁻⁶ Torr) due to the extremely short attenuation length of soft X-rays in air. The X-ray energy was tuned between 270 and 290 eV in our experiments. We took detector images of CB6OCB and CB6OBO6CB on cooling from the nematic phase. The data from the detector were reduced using the Igor Pro-based NIKA data reduction software package (28, 29). WAXS experiments were performed using a Forvis Technologies Compact SAXS/WAXS Diffractometer. The LC was filled into thin-wall 1-mm-diameter quartz capillaries, which were mounted inside an Instec hot stage. The hot stage was sealed with Kapton tape, which contributes a background signal at $q\approx 0.4$ Å⁻¹. The incident beam energy was 10 keV.

FFTEM experiments were carried out by sandwiching the LC between 2 mm × 3 mm glass planchettes, which induce mostly random planar anchoring of the molecules at the glass interfaces. We cooled the cell from the isotropic (I) to the desired LC phase and monitored the sample in the microscope. The cell was then rapidly quenched to T < −180 °C by immersion in liquid propane and fractured under high vacuum at −140 °C. The exposed LC surface was subsequently coated with 2 nm of platinum deposited at 45° for imaging contrast, followed by ∼25 nm of carbon deposited at 90° to increase the mechanical rigidity of the replica. After removing the LC material, the Pt–C replica was placed on a copper TEM grid and imaged in a Philips CM 10 100-keV TEM, allowing the topography of the fracture plane to be observed. TEM images were obtained with a 1K × 1K Gatan Bioscan digital camera. The surfaces facing the platinum shadowing direction accumulate more platinum and therefore produce darker shadows in the TEM images.

We estimated the end-to-end length of CB6OBO6CB trimer and CB6OCB dimer in their extended all-trans conformations. Dihedrals connecting the rings to the alkyl chains were initially manually set at their expected energy minima—values of 0° for CR-CR-O-CT and 90° for CR-CR-CT-CT (where CR is an aromatic ring carbon atom, O is an oxygen atom, and CT the tetrahedral alkyl chain carbon). The trimer and the dimer were optimized to reach an equilibrium geometry, in vacuum in the ground state, using the semiempirical AM1 method as an initial approximation. Subsequently, a second fully relaxed geometry optimization was initiated using the ab initio Hartree–Fock method with 6–31G* basis set.

Molecular end-to-end lengths for both the trimer and dimer were then determined by measuring the distance from one terminal nitrogen atom to the other and adding the length of two nitrogen radii. The end-to-end nitrogen–nitrogen distance of the trimer was l_tri = 46.0 Å, and was l_di = 30.4 Å for the dimer, very close to that estimated for the dimer in ref. 14. We then determined the end-to-end molecular dihedral angles of the trimer by comparing one nitrogen–oxygen plane to the other nitrogen–oxygen plane, finding it to be 134.08°. To find the dihedral angle of the dimer, we compared the nitrogen–oxygen plane to a C_b–nitrogen plane (where C_b is the benzylic carbon attached to the cyanobiphenyl unit) and determined it to be 0.28°.

All molecular modeling calculations were performed with Spartan’16 molecular calculation and modeling software.