Significance
Measles vaccine is a highly effective healthcare intervention, but getting vaccine to those in need remains a major problem. Complicating the issue, high-burden countries typically have low-quality infrastructure, severely limiting the number of infections detected and therefore limiting our understanding of local epidemiology. Here we show that statistical disease models can be fitted to sparse case data from Pakistan using a fast linear regression approach. This method yields estimates of the effects of past interventions, the seasonal likelihood of measles transmission, and the magnitude of future outbreaks under different intervention policies. We use these models to understand in general when and where vaccine should be distributed, and these results were used to inform Pakistan’s 2018 vaccination campaign planning.
Keywords: measles elimination, time series, mathematical model, vaccine
Abstract
Measles remains a major contributor to preventable child mortality, and bridging gaps in measles immunity is a fundamental challenge to global health. In high-burden settings, mass vaccination campaigns are conducted to increase access to vaccine and address this issue. Ensuring that campaigns are optimally effective is a crucial step toward measles elimination; however, the relationship between campaign impact and disease dynamics is poorly understood. Here, we study measles in Pakistan, and we demonstrate that campaign timing can be tuned to optimally interact with local transmission seasonality and recent incidence history. We develop a mechanistic modeling approach to optimize timing in general high-burden settings, and we find that in Pakistan, hundreds of thousands of infections can be averted with no change in campaign cost.
Measles is a significant source of global disease burden and child mortality, estimated to have caused 7 million infections and 90,000 deaths in 2016 (1). Although an effective, safe, and cost-efficient measles vaccine has existed since the 1960s, vaccination in high-burden settings remains a challenge due largely to poor healthcare infrastructure and access (1–3). As a result, measles vaccine dissemination is a pressing global health and social justice issue.
While routine immunization (RI) at 9 mo and 15 mo of age is the World Health Organization (WHO) recommended vaccination schedule (2), high-burden settings rely heavily on mass vaccination campaigns, termed supplemental immunization activities (SIAs), to provide measles vaccine more broadly (3). In these campaigns, health workers advertise and run fixed postvaccination sites to target all children in a specified age range with the aim to vaccinate susceptible children missed by RI (3). SIAs are logistically complicated and implementing them successfully requires a combination of operational excellence, planning, and knowledge of region-specific needs. While understanding and optimizing SIA implementation is therefore a difficult general problem, it is a critical contributor to measles burden control and an important step toward global measles elimination.
In this report we analyze measles in Pakistan, a high-burden setting (4), and show that SIA impact is strongly dependent on timing. We present a general time-series susceptible–infected–recovered (TSIR) model (5) which explicitly accounts for SIAs in the process of inferring the underlying susceptible population, transmission seasonality, and future infections. Fitting this model to laboratory-confirmed measles cases from 2012 to 2017, we show that Pakistan has significant annual measles transmission seasonality with a high-transmission season beginning in October and continuing through the following April. This seasonality has implications for SIA timing, and using the model to extrapolate from 2018 to 2021, we show that an SIA conducted in November prevents on average more infections than an equivalent campaign run in January. Finally, by extending the model to the province level, we show that optimal SIA timing is spatially heterogeneous, and we discuss implications of this result for future SIA planning in Pakistan and elsewhere.
Measles Transmission Seasonality in Pakistan
Measles is a highly virulent disease, and laboratory-confirmed measles cases in Pakistan have more than doubled from 2016 to 2017 (4). Pakistan’s most recent Demographic and Health Survey (DHS) (2012–2013) estimates measles vaccination coverage in 1- to 2-y olds at nationwide, with significant subnational heterogeneity (–) (6). Given this relatively low RI coverage, informed and effective SIAs are needed to slow and potentially interrupt measles transmission.
Mechanistic modeling allows us to understand measles seasonality while estimating underlying susceptible populations and forecasting policy outcomes. TSIR models of measles are well studied (7–10) and have been used to understand measles transmission in a variety of settings (11, 12). While modern TSIR methods typically use Markov chain Monte Carlo (13) or related algorithms (14, 15) to calibrate to incidence data, we forgo this complexity and instead extend the more computationally robust linear-regression approach (5) to the high-burden context by incorporating past interventions.
Considering time in semimonthly increments corresponding to a measles infection’s typical duration (1, 16), we model , the susceptible population at time , and , the corresponding infection prevalence at time , as a discrete, stochastic dynamical system,
| [1] |
| [2] |
| [3] |
Here, is an assumed known estimate of births missed by RI at time , is the fraction of the susceptible population reached by any SIA at time , models inhomogeneous population mixing (5), and is the average number of infectious contacts per person at time which we assume has an annual periodicity. Transmission uncertainty is accounted for by , a zero-mean, log-normal random process, and laboratory-confirmed cases, , are assumed to be drawn from a binomial distribution where is the laboratory-reporting rate, an unknown probability for cases to be selected for laboratory study. In Eq. 1 children missed by RI, , contribute to while infections and SIAs serve to decrease . Simultaneously, Eq. 2 models new infections occurring at rate as infectious and susceptible populations interact.
Since measles SIAs happen relatively infrequently, Pakistan’s campaign history can be used to reduce to the estimation of a single parameter. Subnational vaccination campaigns have been conducted six times in Pakistan since 2012 with wide variation in target population (17). Here we assume that nonzero where is the known target population fraction and is an unknown SIA efficacy parameter common to all campaigns from 2012 to 2017.
Given the observed series and corresponding [via RI coverage estimates (6) and birth-rate estimates (18–20)] (Methods), the model can be fitted to data in a two-step linear-regression process described in Methods and SI Appendix, section 2. Model calibration yields estimates of , , , and with uncertainty due both to underreporting and to transmission stochasticity.
Fitting the model to national-level reports yields , indicating, in qualitative agreement with similar estimates from high-burden settings (21), that a single laboratory-confirmed case corresponds on average to infections in the population. Simultaneously, we find , indicating that inhomogeneous population mixing is a small but statistically significant effect. Past SIA efficacy is estimated to be , which shows that campaign efforts have had a significant effect on measles susceptibility in Pakistan.
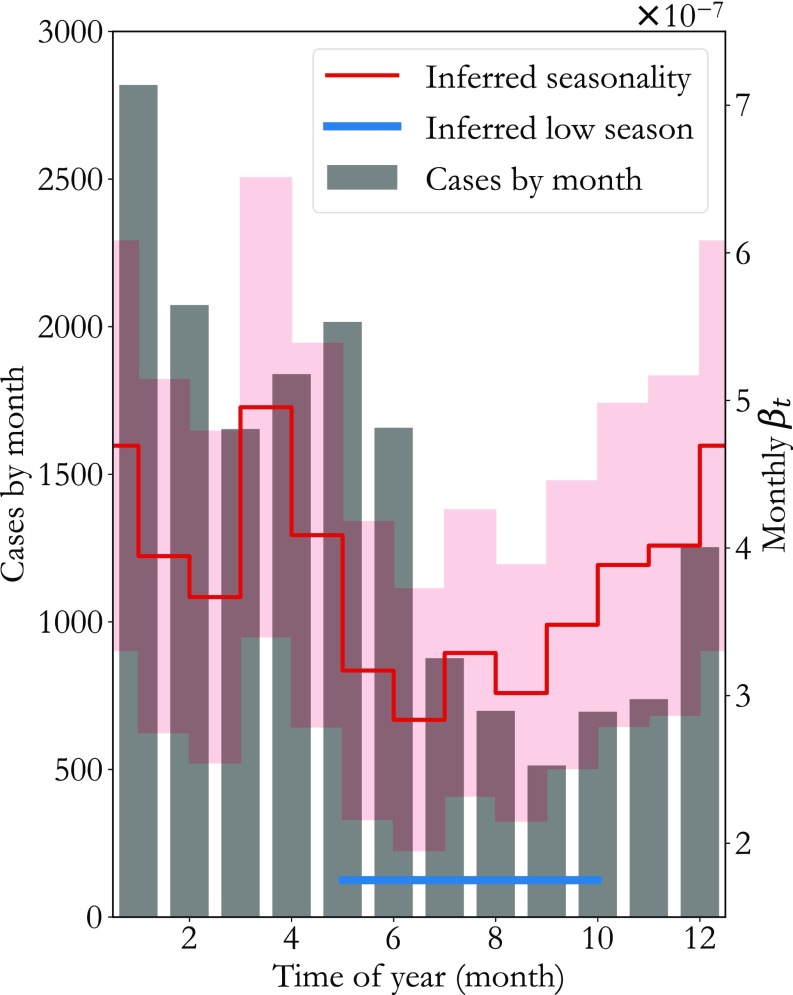
In Fig. 1, national-level reports from 2012 to 2017 are aggregated by month (gray bars), showing that the majority of measles cases occur in the first half of the year. The inferred consistent with this case distribution is averaged by month and overlaid in red (SD cloud), showing that low transmission occurs between May and October (blue), Pakistan’s hot, summer rainy season. This correlation between measles transmission and rainfall or temperature agrees with findings from research in other settings (11, 22) and suggests that transmission fluctuates in part due to weather-related variation in contact rates.
Fig. 1.
Measles transmission seasonality in Pakistan. Laboratory-confirmed cases from 2012 to 2017 aggregated by month are plotted as gray bars. The corresponding inferred force of infection (red trace, SD cloud) shows that transmission varies by as much as throughout the year, with a low-transmission season (blue line) from May through September, Pakistan’s summer rainy season.
Seasonal population migration and associated changes in population density have also been correlated with measles incidence in urban settings (23, 24). We test this hypothesis in SI Appendix, section 2 by computing annual variation in nighttime light satellite imagery brightness (25) near Pakistan’s largest cities, Karachi and Lahore. As shown in SI Appendix, Fig. S6, our inferred is highly correlated (Pearson correlation 0.725) with this measure of Pakistan’s urban population density, suggesting that annual rural-to-urban migration is also a driver of Pakistan’s transmission seasonality.
Interestingly, the increase in transmission precedes the rise in cases by 2–3 mo. This phase difference is in quantitative agreement with seasonality studies of measles in the preelimination United States (26), suggesting that although a measles infection’s duration is only 2–3 wk, high transmission is required for a considerable time before enough infections have occurred to spark an outbreak. Operationally speaking, this is a valuable insight since lows in the aggregated case count alone might incorrectly suggest that Pakistan’s low measles transmission season ranges from July to November.
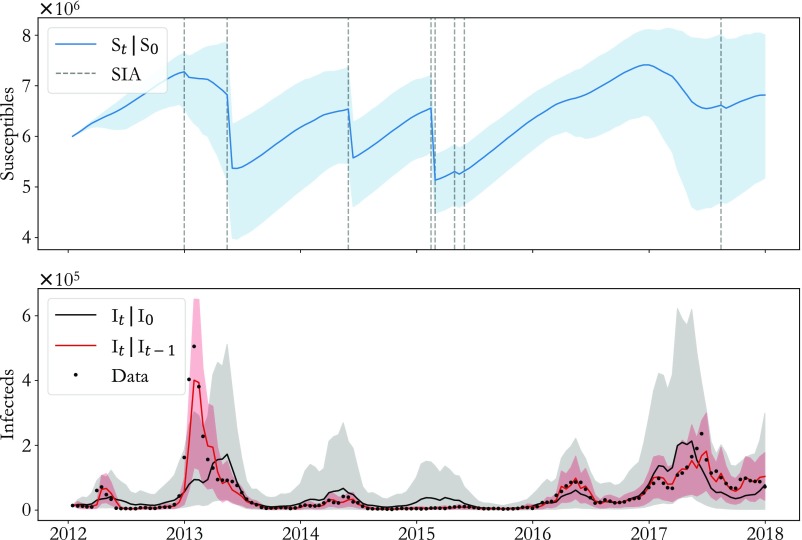
Model seasonality and corresponding extrapolation ability are tested against laboratory reporting-rate scaled cases (black dots) in Fig. 2. In red, predicted given shows that the model is capable of reliable semimonthly prediction () with relatively low uncertainty (red cloud, CI). A more substantial test of the model is shown in black, where is predicted for a full 6 y starting with in January 2012. This long-term model prediction has larger uncertainty (gray cloud, CI) as expected and captures the major outbreaks in 2013, 2016, and 2017 (), demonstrating that the inferred seasonality is consistent with the observed dynamics. The corresponding inferred is plotted in blue, showing stark decreases in susceptible population following SIAs (gray dashed lines) with heterogeneity between SIAs due largely to differences in target population. Finally, in SI Appendix, section 3, we demonstrate that when data past March 2017 are withheld from model fitting, out-of-sample model extrapolation successfully predicts the severity and timing of the 2017 outbreak.
Fig. 2.
Testing model performance. (Lower) Semimonthly (red) and 6-y (black) model extrapolations are compared with laboratory reporting-rate scaled cases demonstrating that the model predicts outbreak timing and magnitude. (Upper) The underlying susceptible population (blue) corresponding to the long-term projection highlights the potentially strong effect of SIAs (gray dashed lines). For all traces, shaded regions indicate CIs.
Optimal SIA Timing
An effective vaccination campaign immunizes susceptible individuals to stifle measles transmission before it occurs. SIAs accomplish this in the model by decreasing both in Eq. 1 and the resulting in Eq. 2. Intuitively, based on the seasonality of Fig. 1, we expect that SIAs in Pakistan will have greatest impact in October or November since the susceptible population built up over the summer low-transmission season can be immunized before high transmission begins. Using the model, we demonstrate that this intuition is qualitatively correct, but a given population’s recent measles history also affects optimal SIA timing.
Hypothetical SIA policies can be quantitatively compared by calculating projected infections. Here, we focus on SIAs run in 2018 over the course of a full month with half the population targeted in each semimonthly model period, and we compute the sample distribution of total infections from 10,000 model runs starting with the data at the end of 2017 and forecasting for 3 y. The 2018–2021 forecasting period was selected since, in practice, multiple SIAs will be run in -y periods, and we are interested in comparing effects of single SIAs for simplicity. All hypothetical campaigns have efficacy equal to the inferred 2012–2017 efficacy, , to isolate the effects of SIA timing.
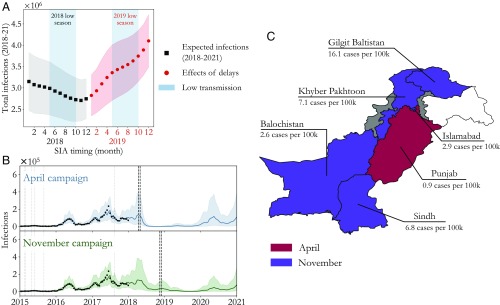
Expected infections under hypothetical 2018 SIA policies are plotted in black in Fig. 3A. As anticipated based on the seasonality, a November SIA has greatest impact, with fewer infections on average than an otherwise equivalent campaign run in January. Moreover, if the extra 10 mo to prepare leads to increases in SIA efficacy, we find that November rapidly becomes even more strongly favored (SI Appendix, Fig. S6). Throughout the low-transmission season (shaded blue region), campaigns become more and more effective. This is as we would expect since susceptible population buildup results in a wider-reaching campaign with greater herd-immunity effects (SI Appendix, section 5).
Fig. 3.
Optimizing SIA timing in Pakistan. (A) Comparing total expected infections in 2018–2021 (black, SE shading) under different SIA policies shows that November minimizes measles burden by taking advantage of susceptible buildup over the low-transmission season (blue region). As a result however, delays into the 2018–2019 high-transmission season (red, SE shading) are costly. (B) Model projections for pre– (April) and post–low-transmission season (November) SIAs (black dashed lines) demonstrate the tradeoff between 2018 and 2020 outbreak control. As a result, 2017 measles burden also plays a significant role in timing optimization. (C) Extending the model to the province level allows us to compare April and November SIA timing subnationally. Preference for April is mapped in red while preference for November is mapped in purple; gray provinces [Federally Administered Tribal Areas and Azad Kashmir, representing less than of Pakistan’s total population (20)] are inaccessible to health workers while white areas indicate disputed territory. Heterogeneity in the 2017 laboratory-confirmed measles cases per 100,000 (indicated) is reflected in the timing optimization.
As a direct consequence of this, however, delays past November rapidly incur large costs since the 2018–2019 high-transmission season depletes the susceptible population and mitigates the effect of an SIA. This is demonstrated in Fig. 3A by extending the analysis to equivalent campaigns in 2019. Expected infections under these policies are plotted in red, and we find that a campaign delayed from November 2018 to May 2019 results in over 600,000 more measles infections on average over the 2018–2021 period.
Fig. 3B plots extrapolated model traces for SIAs before (in April, blue) and after (in November, green) the 2018 low-transmission season for more detailed comparison. While the April SIA mitigates infections in 2018, this comes at the expense of a large outbreak in 2020. On the other hand, the November SIA decreases the severity of the predicted 2020 outbreak at the expense of infections in 2018. This tradeoff indicates that transmission seasonality’s contribution to the optimal SIA timing acts in concert with the expected severity of upcoming outbreaks, an expectation which depends directly on measles’ recent history in a population. For Pakistan as a whole, 2017 was a relatively severe measles year, indicating that natural infection has decreased the susceptible population. Consistent with this intuition, model extrapolation predicts that 2020’s outbreak will be larger on average than 2018’s, and the November SIA is preferable as a result.
The interplay between seasonality and recent history is highlighted if we apply the model to Pakistan’s provinces individually. To do this, the model is fitted to province-level data assuming the national-level transmission seasonality of Fig. 1 with a contact rate scaled by the fraction of Pakistan’s population within the province. The assumption that measles transmission behaves qualitatively similarly across the country is necessary since individual provinces report too few laboratory-confirmed cases to reliably infer province-level transmission parameters. Province-level models are tested by the methods of Fig. 2 in SI Appendix, section 4. They show comparable predictive performance to the national-level model, indicating that the seasonality assumptions are valid.
Subnationally, Pakistan’s recent measles history has significant heterogeneity. For example, in Pakistan’s two most populated provinces, Punjab and Sindh, laboratory-confirmed measles cases per 100,000 in 2017 were at 0.9 and 6.8, respectively. While this is due in part to RI coverage differences between Punjab and Sindh (6), this also indicates that 2017 was an outbreak year in Sindh but not in Punjab. This heterogeneity is mirrored in province-level optimal SIA timing: Comparing April and November SIAs where data are available, we see in Fig. 3C that in provinces with high 2017 case counts the November campaign is more effective (purple) while in Punjab the April SIA performs better (red). Thus, in line with intuition from the national level, optimizing SIA timing requires a balance between contributions due to seasonality and incidence history. The modeling approach presented here offers a robust means to solve this optimization problem in high-burden contexts.
Discussion
Measles vaccination campaign optimization is a complex general problem. Here, we have studied data from Pakistan to demonstrate that SIA timing is a critical factor and that two SIAs with equivalent efficacy and cost may have significantly different impacts solely as a result of their start date. With that in mind, transmission seasonality and recent measles burden, the drivers of optimal campaign timing, should be considered alongside operational constraints in future SIA planning.
From a methodological perspective, the TSIR model used in this work is a robust tool for evaluating competing SIA polices. While disease models with mass vaccination have been studied in the past (27–29), generalization of a least-squares–based model calibration method (5) to the high-burden context offers a simple, data-driven SIA optimization approach. Model extensions such as age structure (30), subnational spatial correlation (10), and disease importation (7) are active areas of research. These studies, in conjunction with the method presented here, may contribute to other aspects of SIA optimization, an important problem for measles eradication with widespread global health implications.
Methods
Pakistani Demographic and Surveillance Data.
Population estimates for 2010 and 2015 and live-birth estimates for 2010, 2012, 2015, and 2020 were obtained from WorldPop (18–20). These were aggregated to the district level and linearly interpolated over time. Rates for the first dose of measles vaccine were estimated using the 2012–2013 DHS (6) and treated as constant over the 2012–2017 model period, while second-dose rates were estimated using caregiver-reported dose histories associated with laboratory-rejected cases.
Laboratory-confirmed and -rejected cases were obtained from Pakistan’s WHO-affiliated laboratory. The rejected cases and corresponding self-reported dose histories were used to estimate rates of second-dose measles vaccine coverage in all provinces. Combining these estimates of demographic quantities gives
where and are first- and second-dose measles vaccine coverage over time, and is the estimated live births. The above model assumes the first vaccine dose has a seroconversion rate and the second dose has a seroconversion rate (16). For more details, see SI Appendix, section 1.
Fitting and Testing the Model.
Model fitting to an observed series proceeds in two steps, accounting for uncertainty due to underreporting and transmission individually. In the first step, Eq. 1 is used to construct a weighted least-squares regression of against which yields, for a given , estimates of and the relative fluctuations in the susceptible population. Further assuming that susceptible fluctuations are small and , i.e., that seasonality varies only within a year, Eq. 2 defines a generalized linear autoregression of . Solving this regression problem yields estimates of and the remaining parameters including the variance due to transmission uncertainty.
As mentioned in the main text, we assume , where is a known measure of target SIA population (17) and is an efficacy parameter common to all SIAs from 2012 to 2017. Since the regression approach above can be carried out given a hypothetical , we take an approach similar to the profile-likelihood optimization used by others (14, 15). In other words, a range of s are tested by repeated model fitting and subsequent goodness-of-fit optimization. For mathematical details of the full model calibration procedure and related sensitivity testing see SI Appendix, section 2.
Code and Data Availability.
All analysis was done in Python 3.6.2, and the associated code can be found in the GitHub repository, https://github.com/NThakkar-IDM/campaign_timing (31). All data came from open-source providers noted in the references with the exception of the laboratory reports which can be obtained only with permission from the World Health Organization Country Office in Pakistan. To obtain permission, contact the corresponding author (N.T.) or submit a request to the WHO directly (details can be found in the WHO data policy, https://www.who.int/publishing/datapolicy/en/).
Supplementary Material
Acknowledgments
We thank Pakistan’s Expanded Program on Immunization for providing the laboratory-reported data, Kurt Frey for useful conversations and significant help with compiling Pakistan’s past SIA calendar, Hil Lyons for assistance with computing birth rates from the DHS, and Caitlin Cornell for useful edits to the manuscript.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
Data deposition: The code used in this paper has been deposited in the GitHub repository, https://github.com/NThakkar-IDM/campaign_timing.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1818433116/-/DCSupplemental.
References
- 1.World Health Organization (2018) Measles fact sheet. Available at http://www.who.int/mediacentre/factsheets/fs286/en/. Accessed June 15, 2018.
- 2.World Health Organization (2017) Summary of the WHO position on measles vaccine. Available at http://www.who.int/immunization/policy/position_papers/measles/en/. Accessed June 15, 2018.
- 3.World Health Organization (2016) Planning and implementing high-quality supplementary immunization activities for injectable vaccines. http://www.who.int/immunization/diseases/measles/en/. Accessed June 15, 2018.
- 4.World Health Organization (2017) Measles cumulative report for 2017. http://www.emro.who.int/vpi/publications/measles-monthly-bulletin.html. Accessed June 15, 2018.
- 5.Finkenstädt B, Grenfell BT (2000) Time series modelling of childhood diseases: A dynamical systems approach. J R Stat Soc Ser C Appl Stat 49:187–205. [Google Scholar]
- 6.National Institute of Population Studies - NIPS/Pakistan and ICF International (2013) Pakistan Demographic and Health Survey 2012-13. Available at https://dhsprogram.com/publications/publication-FR290-DHS-Final-Reports.cfm. Accessed October 26, 2017.
- 7.Grenfell BT, Bjørnstad ON, Kappey J (2001) Travelling waves and spatial hierarchies in measles epidemics. Nature 414:716–723. [DOI] [PubMed] [Google Scholar]
- 8.Bjørnstad ON, Finkenstädt BF, Grenfell BT (2002) Dynamics of measles epidemics: Estimating scaling of transmission rates using a time series SIR model. Ecol Monogr 72:169–184. [Google Scholar]
- 9.Grenfell BT, Bjørnstad ON, Finkenstädt BF (2002) Dynamics of measles epidemics: Scaling noise, determinism, and predictability with the TSIR model. Ecol Monogr 72:185–202. [Google Scholar]
- 10.Xia Y, Bjørnstad ON, Grenfell BT (2004) Measles metapopulation dynamics: A gravity model for epidemiological coupling and dynamics. Am Nat 164:267–281 [DOI] [PubMed] [Google Scholar]
- 11.Ferrari MJ, et al. (2008) The dynamics of measles in sub-Saharan Africa. Nature 451:679–684. [DOI] [PubMed] [Google Scholar]
- 12.Dalziel BD, et al. (2016) Persistent chaos of measles epidemics in the prevaccination United States caused by a small change in seasonal transmission patterns. PLoS Comput Biol 12:e1004655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Morton A, Finkenstädt BF (2005) Discrete time modelling of disease incidence time series by using Markov chain Monte Carlo methods. J R Stat Soc Ser C Appl Stat 54:575–594. [Google Scholar]
- 14.Ramsay JO, Hooker G, Campbell D, Cao J (2007) Parameter estimation for differential equations: A generalized smoothing approach. J R Stat Soc Ser B Stat Methodol 69:741–796. [Google Scholar]
- 15.Ionides EL, Nguyen D, Atchadé Y, Stoev S, King AA (2015) Inference for dynamic and latent variable models via iterated, perturbed Bayes maps. Proc Natl Acad Sci USA 112:719–724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Plotkin S, Orenstein W, Offit P, Edwards KM (2017) Plotkin’s Vaccines (Elsevier, Philadelphia: ), 7th Ed. [Google Scholar]
- 17.World Health Organization (2018) Summary of measles-rubella supplementary immunization activites, 2000-2018. Available at http://www.who.int/immunization/monitoring_surveillance/data/en/. Accessed October 26, 2017.
- 18.Tatem AJ. (2017) WorldPop, open data for spatial demography. Sci Data 4:170004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tatem AJ, et al. (2014) Mapping for maternal and newborn health: The distributions of women of childbearing age, pregnancies and births. Int J Health Geographics 13:2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gaughan AE, Stevens FR, Linard C, Jia P, Tatem AJ (2013) High resolution population distribution maps for Southeast Asia in 2010 and 2015. PLoS One 8:e55882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Simons E, et al. (2012) Assessment of the 2010 global measles mortality reduction goal: Results from a model of surveillance data. Lancet 379:2173–2178. [DOI] [PubMed] [Google Scholar]
- 22.Altizer S, et al. (2006) Seasonality and the dynamics of infectious diseases. Ecol Lett 9:467–484. [DOI] [PubMed] [Google Scholar]
- 23.Bharti N, et al. (2011) Explaining seasonal fluctuations of measles in Niger using nighttime lights imagery. Science 334:1424–1427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bharti N, Djibo A, Tatem AJ, Grenfell BT, Ferrari MJ (2016) Measuring populations to improve vaccination coverage. Sci Rep 6:34541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.National Oceanic and Atmospheric Administration (2018) Version 1 VIIRS day/night band nighttime lights. Available at https://www.ngdc.noaa.gov/eog/viirs/. Accessed February 4, 2019.
- 26.Yorke JA, Nathanson N, Pianigiani G, Martin J (1979) Seasonality and the requirements for perpetuation and eradication of viruses in populations. Am J Epidemiol 109:103–123. [DOI] [PubMed] [Google Scholar]
- 27.d’Onofrio A. (2002) Pulse vaccination strategy in the SIR epidemic model: Global asymptotic stable eradication in presence of vaccine failures. Math Comput Model 36:473–489. [Google Scholar]
- 28.Gao S, Chen L, Nieto JJ, Torres A (2006) Analysis of a delayed epidemic model with pulse vaccination and saturation incidence. Vaccine 24:6037–6045. [DOI] [PubMed] [Google Scholar]
- 29.Briat C, Verriest EI (2009) A new delay-SIR model for pulse vaccination. Biomed Signal Process Control 4:272–277. [Google Scholar]
- 30.Kuniya T. (2011) Global stability analysis with a discretization approach for an age-structured multigroup SIR epidemic model. Nonlinear Anal Real World Appl 12:2640–2655. [Google Scholar]
- 31.Thakkar N. (2019) Data from “A time series model for forecasting measles vaccination campaign impact.” GitHub. Available at https://github.com/NThakkar-IDM/campaign_timing. Deposited February 11, 2019.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.