Abstract
The main aim was to determine the differences between four training games and competitive matches (CM) according to position and compared to the most demanding passages (MDP) of competitive match play. Global Positioning System data were obtained from 21 football players belonging to the reserve squad of a Spanish La Liga club during the 2015/16 season. The training games were small-sided games (SSGs) with 5 and 6 and large-sided games with 9 and 10 outfield players per team. The players were categorized based on positional groups: full back (FB), central defender (CD), midfielder (MF), offensive midfielder (OMF), and forward (FW). The variables recorded were the distance covered (DIS), DIS at high speed (HSR; >19.8 km·h-1), DIS at sprint (SPR; >25.2 km·h-1), high metabolic load distance (HMLD; >25.5 W·kg-1) all in m·min-1, average metabolic power (AMP; W·kg-1) and number of high-intensity accelerations (ACC; >3 m·s-2) and decelerations (DEC; <-3 m·s-2), both in n·min-1. The MDP was analysed using a rolling average method for AMP as a criterion variable, where maximal values were calculated for time windows of 5 and 10 minutes of CM and after that compared with the training game formats. As the SSG format increases, all the rest of the variables increase and the number of cases with significant interposition differences also increases (effect size [ES]: DIS: 0.7-2.2; HSR: 0.7-2.1; SPR: 0.8-1.4; HMLD: 0.9-2.0; AMP: 0.8-1.9; ACC: 0.8-1.7; DEC: 0.5-1.7). The large-sided game 10v10 + 2 goalkeepers over-stimulates sprint values relative to MDP (all: 121.0% of MDP, ES=0.5-1.8). This study provides useful information for coaching staff on the heightened impact of different training game formats on physical load, considering positional differences in relation to the MDP of competitive match play.
Keywords: Small-sided games, GPS, Peak intensity, Match demands, Football
INTRODUCTION
Football is a sport with high-intensity episodes combined with long periods, approximately 70% of the total match time, in low-intensity ranges [1]. The total distance covered ranges between 9.5 and ~12 km in a competitive match [2-3], of which a distance between 220 and 1900 m is covered at high speed (~19.8 km·h-1) while distances between 200 and 500 m are covered at sprint (~25.0 km·h-1) [1-2-3]. In the course of the game the players change activity around 1400 times [4-5], which might entail accelerations and decelerations in some cases of high intensity (2.5 m·s-2) between 50 and 100 times per game [3-6]. However, all these values are an average of the mean activity performed by a player in competition [9].
It is known that the intra- and inter-player variability of physical demand is high [7], especially to the extent that the speed ranges chosen for the analysis are higher due to contextual variables involved in games [8]. Then the average values usually used to describe the physical performance pattern of competing players may hide most demanding passages of play (MDP) that exceed these values [9] and which, if not addressed, might underestimate some periods of real competitive match (CM) intensity. To describe the MDP in competition in both rugby league [10] and football [11] a number of time windows have been proposed [12] for calculating the power law relationship [13], while the rolling average [14] is the best way to find the most intense periods of a CM. A number of variables have been used to describe this MDP in football such as m·min-1 [11-15], metabolic power and cumulative accelerations and decelerations [16]. However, to the authors’ knowledge there are no research studies in which the MDP are analyzed considering several dependent variables simultaneously.
One of the advantages of various-sided training games is that they can be modified to adjust their load and intensity [17], something which might be considered when scheduling training sessions. The MDP have recently been compared with training game formats in football [11-15]. To do this, variables that describe displacement intensity (e.g. total distance or distance at high speed per minute) and mechanical work (AU per minute) in tasks played at 4v4, 6v6, 8v8 and 10v10 have been calculated. The study concluded that SSG formats over-stimulated musculoskeletal demand mechanical work variables with respect to the MDP in competition and under-stimulated the distance covered at high speed.
The existence of a positional profile in competition demands is not new [7]; the MDP are also specific to the position occupied by the player on the playing field [15-18]. Interest is growing [11] in learning whether, as in the case of competition, SSGs stimulate different positional groups in a particular way. Specifically, in this paper [11], the positional groups that were most and least overloaded during SSGs were central defender and midfielder respectively. However, due to their training applications, it would be handy to be able to describe the MDP using several variables simultaneously.
The main aim was to estimate the differences between four training game formats with goalkeepers and CM according to position-specific activity and duration compared to MDP using AMP as a criterion variable. This study might help coaches to learn whether proposed tasks underload, replicate or overload the requirements of the MDP of competitive match play, something which might be considered when scheduling training sessions.
MATERIALS AND METHODS
Participants
Data were collected for 21 football players (20.4 ± 1.2 years, 1.79 ± 0.06 m, 70.2 ± 6.5 kg) belonging to the reserve squad of a Spanish La Liga club. The players were grouped according to their playing position as central defender (CD: n=4), full back (FB: n=6), midfielder (MF: n=3), offensive midfielder (OMF: n=3), and forward (FW: n=5). Although ethics committee clearance was not required [19], prior to the commencement of the study all the subjects were informed of the aims and requirements of the research and the players gave their informed consent for participation in the research study. The study conformed nevertheless to the recommendations of the Declaration of Helsinki.
Design
GPS (Global Positioning System) data were collected during the 2015/16 competitive season to establish the position-specific demands of small-sided games, large-sided games and CM, expressing their demands relative to practice time (m·min-1 or n·min-1) and values relative to the MDP of competitive match play (% of MDP). For calculating the MDP, the time-window was 5 min for the small-sided games (SSG5: small-sided game 5v5 + 2 goalkeepers (Gks) and SSG6: small-sided game 6v6 + 1 joker + 2 goalkeepers) and 10 min for the large-sided games (LSG9: large-sided game 9v9 + 2 goalkeepers; LSG10 and CM); the time windows used are the usual ones for each game format. These data were drawn from the daily player monitoring in which player activities were routinely measured over the course of the season.
Based on the recommendations of Akenhead et al. [2], training load data were analysed with respect to the number of days before or after a match (MD minus or plus). The training sessions that are contextualized below were composed of integrated content (e.g. tactical, technical and physical factors were amalgamated): MD+1 was the session the day after the competition where players split into two training groups. The first group included players who had completed >60 min of competition. The aim of this session was to recover from the previous match, so the recovery term was used: MD+1R. Players conducted low-impact activity combined with recovery exercises. The second group included players who had completed <60 min of competition. This group worked within a technical circuit followed by a positional game and a small-sided game (SSG) with goalkeepers (area: 30-60 m2 per player). This session attempted to replicate competition loads, so the compensatory term was used: MD+1C. MD-4 was the session four days before the competition and aimed to develop the players’ strength and power capabilities. This consisted of a gym workout followed by positional games and an SSG with goalkeepers (area: 25-50 m2 per player). MD-3 was the session three days before the competition and aimed to tactically prepare players for the next match. The structure consisted of a moderate intensity positional game (area: 70-100 m2) and concluded with an 11 v 11 match (72 × 65 m). MD-2 was the session two days before the competition. The load was focused on technical-tactical elements. The structure of the session was as follows: control and passing sequences, a positional game with a low number of players per team, and tactical exercises. MD-1 was the session before the competition and was primarily geared towards activation drills replicating the tactical competition scenarios and concluded with set pieces [20].
Data were collected throughout 37 CM (13 wins, 15 losses, and 9 draws). The team usually played in a 1-4-3-3 formation, with a Gk, two FBs, two CDs, one MF, two OMFs and three FWs. Only data from players who completed the 1st or 2nd half of the CM were analysed. Players with fewer than 6 full halves completed were not included in the analysis and nor were Gks.
Physical Variables
The variables recorded were the distance covered (m·min-1), distance covered at high speed running (HSR: >19.8 km·h-1, m·min-1); distance covered at sprinting (SPR: >25.2 km·h-1, m·min-1); the number of high-intensity accelerations and decelerations (ACC/DEC: > 3 m·s-2, n·min-1); the high metabolic load distance (HMLD: >25.5 W·kg-1, m·min-1); and the average metabolic power (AMP: W·kg-1); the intensity thresholds used were established based on previous studies [1-21-22-23].
Procedure
The activity profile of the players was monitored during each training game format and CM using a portable 10 Hz GPS unit (Viper Pod, 50 g, 88 x 33 mm, STATSports Viper, Northern Ireland) as used in previous studies [24-25]. The accuracy of these devices has been studied recently, with 2.53 ± 6.03% estimation error in distance covered, with accuracy (%) improving as the distance covered increases and the speed of movement decreases [26]. The GPS model used in this study was worn in a purpose-designed vest inside a mini pocket positioned in the centre area of the upper back, just above the shoulder blades, thus not affecting mobility of the upper limbs and torso. Upon completion of each training session and CM, GPS data were extracted using the appropriate proprietary software (Viper, STATSports, Northern Ireland).
In order to calculate the intensity of the four training game formats and CM in relation to the MDP of competitive match play, the moving average duration method was used with the AMP variable. AMP is based on energy expenditure by players. The measures combine the energy expenditure associated with constant speed activity as well as acceleration and deceleration activity [1-27]. This variable has been analysed as an indicator of metabolic expenditure in previous papers [28-29-30]. Given the possible limitations of this variable, Rampinini et al. [31] analysed the recording capacity of 10 Hz GPS units and found a strong correlation with the criterion device (laser device, standard error = 2.4 to 2.9%). Therefore, this metric is a precise measure for evaluating external demands in football where high-intensity random efforts occur at both high and low speeds [16]. STATSports software was then used for the computation of a moving average over the AMP variable using two different durations (5 and 10 min) and the maximum value for each duration was recorded. As a result, for each individual match the period with the highest AMP values was selected and analysed for each of the two moving average durations.
Training game formats and competitive matches
A total of 635 individual records (n= 408 for training game formats and n= 227 for CM) were obtained. The distribution of records in each training game format and CM for each of the positions is shown in Table 1.
TABLE 1.
Number of records in each game format and competitive matches according to the players’ position.
| Player’s position | SSG5 | SSG6 | LSG9 | LSG10 | Official match | Total |
|---|---|---|---|---|---|---|
| CD | 10 | 9 | 27 | 34 | 42 | 122 |
| FB | 18 | 26 | 31 | 41 | 60 | 176 |
| MF | 12 | 13 | 22 | 24 | 40 | 111 |
| OMF | 8 | 10 | 20 | 23 | 34 | 95 |
| FW | 9 | 15 | 24 | 32 | 51 | 131 |
| Total | 57 | 73 | 124 | 154 | 227 | 635 |
CD = central defender; FB = full back; MF = midfielder; OMF = offensive midfielder; FW = forward; SSG5 = small-side game 5v5 + 2 goalkeepers; SSG6 = small-side game 6v6 + 1 joker + 2 goalkeepers; LSG9 = large-sided game 9v9 + 2 goalkeepers; LSG10 = large-sided game 10v10 + 2 goalkeepers.
Only the most standardized training game formats over the season were used for analysis: 1) SSG5: dimensions: 33 x 40 m, and duration: 05:39 ± 01:12 min:s; 2) SSG6: dimensions: 33 x 40 m, and duration: 05:57 ± 01:24 min:s; 3) LSG9: dimensions: 72 x 65 m, and duration: 12:03 ± 02:44 min:s; 4) LSG10: dimensions: 105 x 65 m, and duration: 10:41 ± 02:32 min:s. Training game formats were performed on a natural grass surface and the ball was always available by prompt replacement when out with the aim of maximizing effective playing time [32]. Analysed game formats were conducted in the final part of the sessions. SSG5 and SSG6 were performed in sessions MD + 1C and MD-4, while LSG9 and LSG10 were performed in MD-3. Training game formats included the offside rule. The demands were studied according to the position of the players during match play. Data from jokers and Gks were not included in the analysis. Pauses between repetitions in the training game formats were excluded.
The SSG5 and SSG6 were relativized to the values obtained in the MDP of the CM with the time window of 5 min, while the LSG9 and LSG10 were relativized through comparison with the time window of 10 min. Also, the average of CM was compared with the MDP of 10 min. Unlike previous studies [11], the determination of MDP made possible through the moving average duration method was not used in the various-sided games with goalkeepers studied.
Statistical analysis
The data are presented as means and standard deviations (mean ± SD). The homogeneity of variances was examined by means of Levene’s test. The presence of significant differences among training game formats and CM was determined by means of a 2-tailed repeated-measures analysis of variance applied to each of the dependent variables in relation to the position (CD, FB, MF, OMF and FW) and training game formats (SSG5, SSG6, LSG9, LSG10 and CM). Whenever a significant difference was found, post hoc Bonferroni’s test was used, whereas Dunnett’s T3 post hoc test was applied when the variances were not homogeneous. All the statistical analysis was performed using SPSS 16.0 (SPSS Inc., Illinois, USA) for Windows, with significance being set at p<0.05. Effect sizes (ES) were calculated to determine meaningful differences with magnitudes classed as trivial (<0.2), small (>0.2-0.6), moderate (>0.6-1.2), large (>1.2- 2.0) and very large (>2.0-4.0) [33].
RESULTS
Regardless of the position occupied by the players, in Table 2 we can observe the absolute demands imposed in the different training game formats and CM studied. The meaningful differences (ES) in the variables studied between training game formats were the following: DIS: 0.6-1.6; HSR: 0.5-1.7; SPR: 0.5-1.1; HMLD: 0.4-1.2; AMP: 0.4-1.4; ACC: 0.4-3.8; DEC: 0.3-4.9. The LSG formats over-stimulate all of the variables compared with CM; nevertheless, the SSG formats only over-stimulate ACC and DEC variables.
TABLE 2.
Relative values ± SD (in min-1) of the variables in the game formats and competitive matches.
| Variable | Position | SSG5 | SSG6 | LSG9 | LSG10 | Official Match | ES;p |
|---|---|---|---|---|---|---|---|
| DIS | CD | 103.8 ± 8.7 | 98.9 ± 8.5 | 106.9 ± 9.5⊗ | 114.7 ± 7.7*,†,∆,⊗ | 101.3 ± 5.8b | ES: 0.9-2.0; p<0.001 |
| FB | 110.9 ± 4.2b | 108.7 ± 9.2b,c | 112.5 ± 8.2⊗ | 119.1 ± 7.7*,†,∆, ⊗ | 105.0 ± 5.9b | ES: 0.8-2.1; p<0.001 | |
| MF | 109.0 ± 5.8 | 98.3± 12.1 | 117.8 ± 12.8a,b,† | 126.0 ± 9.5a,b,e*,†, ⊗ | 114.8 ± 7.5a,b,e,† | ES: 0.7-2.6; p=0.004 | |
| OMF | 110.9 ± 8.7 | 111.6 ± 2.1b,c | 121.2 ± 13.2a,b,e | 129.6 ± 12.2a,b,e,*, ⊗ | 113.9 ± 8.7a,b,e | ES: 0.7-1.6; p<0.001 | |
| FW | 101.3 ± 4.9 | 92.6 ± 10.9 | 108.5 ± 11.0†, ⊗ | 115.5 ± 11.5*,†, ⊗ | 95.7 ± 11.1 | ES: 0.6-2.0; p<0.001 | |
| all | 108.0 ± 7.1 | 101.8 ± 11.8 | 113.0 ± 12.0*,†, ⊗ | 120.2 ± 11.1*,†,∆, ⊗ | 105.4 ± 10.7 | ES: 0.6-1.6; p<0.001 | |
| ES;p | ES: 0.0-2.2; p=0.004 | ES: 0.4-2.2; p=0.001 | ES: 0.3-1.3; p=0.001 | ES: 0.3-1.6; p=0.001 | ES: 0.1-2.0; p<0.001 | ||
| HSR | CD | 1.1 ± 1.1 | 2.2 ± 1.3 | 5.8 ± 3.1*,† | 7.3 ± 3.7c,*,†, ⊗ | 4.7 ± 1.2*,† | ES: 0.4-1.9; p<0.001 |
| FB | 2.5 ± 1.8 | 3.4 ± 2.8 | 9.7 ± 4.4a,c,d,*,†, ⊗ | 11.4 ± 3.7a,c,*,†, ⊗ | 7.0 ± 1.9a,c | ES: 0.4-2.7; p<0.001 | |
| MF | 1.5 ± 1.2 | 2.2 ± 1.8 | 3.4 ± 2.5 | 4.5 ± 2.6*,† | 4.7 ± 1.5*,† | ES: 0.1-2.2; p<0.001 | |
| OMF | 2.7 ± 1.7 | 2.4 ± 1.7 | 6.5 ± 3.9c,* | 9.1 ± 4.5c,*,† | 6.4 ± 2.1a,c,* | ES: 0.6-1.7; p<0.001 | |
| FW | 1.8 ± 1.3 | 1.8 ± 1.8 | 7.1 ± 3.4c,*,† | 10.7± 6.0c,*,†, ⊗ | 6.5 ± 2.5a,c,*,† | ES: 0.7-1.8; p<0.001 | |
| all | 1.9 ± 1.6 | 2.6 ± 2.3 | 6.7 ± 4.1*,† | 8.9 ± 4.8*,†,∆, ⊗ | 5.9 ± 2.1*,† | ES: 0.5-1.7; p<0.001 | |
| F(p) | ES: 0.1-1.1; p=0.083 | ES: 0.4-0.6; p=0.232 | ES: 0.6-1.7; p<0.001 | ES: 0.1-2.1; p<0.001 | ES: 0.2-1.3; p<0.001 | ||
| SPR | CD | 0.1 ± 0.2 | 0.0 ± 0.0 | 1.2 ± 1.7*,† | 1.9 ± 1.9c,*,† | 1.1 ± 0.5c,d,*,† | ES: 0.4-1.7; p<0.001 |
| FB | 0.0 ± 0.2 | 0.4 ± 0.9 | 2.0 ± 2.0c,*,† | 3.3 ± 2.1a,c,d,*,†, ⊗ | 1.6 ± 0.8a,c,d,*,† | ES: 0.6-1.9; p<0.001 | |
| MF | 0.0 ± 0.1 | 0.2 ± 0.5 | 0.5 ± 1.3 | 0.6 ± 1.1 | 0.7 ± 0.5* | ES: 0.1-1.6; p=0.149 | |
| OMF | 0.1 ± 0.2 | 0.5 ± 0.8 | 0.8 ± 1.0 | 1.6 ± 1.6* | 0.9 ± 0.5* | ES: 0.6-1.1; p=0.008 | |
| FW | 0.0 ± 0.0 | 0.0 ± 0.1 | 1.1 ± 1.1*,† | 3.0 ± 2.9c,*,†,∆ | 1.5 ± 0.9a,c,d,*,† | ES: 0.8-1.2; p<0.001 | |
| all | 0.0 ± 0.2 | 0.2 ± 0.6 | 1.2 ± 1.6*,† | 2.2 ± 2.3*,†,∆, ⊗ | 1.2 ± 0.8*,† | ES: 0.5-1.1; p<0.001 | |
| F(p) | ES: 0.3-0.7; p=0.622 | ES: 0.1-0.9; p=0.205 | ES: 0.4-0.9; p=0.005 | ES: 0.1-1.5; p<0.001 | ES: 0.1-1.3; p<0.001 | ||
| HMLD | CD | 18.0 ± 3.7 | 15.3 ± 1.9 | 18.6 ± 4.2†, ⊗ | 20.6 ± 4.1†, | 15.8 ± 1.8 | ES: 0.5-1.4; p<0.001 |
| FB | 22.1 ± 4.1 | 22.9 ± 5.4a,b,c, ⊗ | 24.7 ± 5a,c, ⊗ | 25.7 ± 4.9a,c, ⊗ | 19.1 ± 3.1a,b | ES: 0.3-1.7; p=0.004 | |
| MF | 18.5 ± 3.2 | 17.8 ± 4.7 | 19.1 ± 4.7 | 21.2 ± 3.7 | 18.8 ± 3.2a,b | ES: 0.5-0.8; p=0.075 | |
| OMF | 21.3 ± 5.5 | 21.8 ± 4.3 | 25.9 ± 5.9a,c | 28.2 ± 5.4a,b,c,*, ⊗ | 22.5 ± 4.5a,b,c,e | ES: 0.4-1.3; p<0.001 | |
| FW | 19.9 ± 0.9†, ⊗ | 16.2 ± 3.4 | 22.3 ± 4.2†, ⊗ | 24.5 ± 5.5a,*,†, | 16.3 ± 4.4 | ES: 0.4-1.7; p<0.001 | |
| all | 20.2 ± 4.1 | 19.3 ± 5.4 | 22.2 ± 5.6†, ⊗ | 24.1 ± 5.5*,†,∆, ⊗ | 18.3 ± 4.1 | ES: 0.3-1.2; p<0.001 | |
| F(p) | ES: 0.2-1.0; p=0.047 | ES: 0.2-1.6; p<0.001 | ES: 0.7-1.5; p<0.001 | ES: 0.5-1.6; p<0.001 | ES: 0.9-2.0; p<0.001 | ||
| AMP | CD | 10.2 ± 0.9 | 9.5 ± 0.8 | 10.0 ±0.9⊗ | 10.6 ± 0.8†, ⊗ | 9.2 ± 0.5 | ES: 0.5-2.1; p<0.001 |
| FB | 11.2 ± 0.6a, ⊗ | 11.2 ± 1.2a,b,c, ⊗ | 10.9 ± 0.9a, ⊗ | 11.4 ± 0.8a, ⊗ | 9.8 ± 0.6a,b | ES: 0.2-2.3; p<0.001 | |
| MF | 10.8 ± 0.6 | 9.8 ± 1.2 | 10.7 ± 1.2 | 11.4 ± 0.9a,†, ⊗ | 10.5 ± 0.8a,b,e | ES: 0.7-1.6; p<0.001 | |
| OMF | 11.1 ± 1.1 | 11.1± 0.6 | 10.8± 1.2⊗ | 12.2 ± 1.1a,b,c,e,*, ⊗ | 10.5 ± 0.8a,b,e | ES: 1.1-1.8; p<0.001 | |
| FW | 10.4 ± 0.4⊗ | 9.3 ± 1.1 | 11.5 ± 1.2a,†, ⊗ | 10.9 ± 1.1†, ⊗ | 8.8 ± 1.2 | ES: 0.5-2.2; p<0.001 | |
| all | 10.8 ± 0.8⊗ | 10.3 ± 1.4 | 10.3 ± 1.0⊗ | 11.2 ± 1.1*,†,∆, ⊗ | 9.7 ± 1.0 | ES: 0.4-1.4; p<0.001 | |
| F(p) | ES: 0.1-1.4; p=0.020 | ES: 0.1-1.6; p<0.001 | ES: 0.6-1.4; p<0.001 | ES: 0.9-1.7; p<0.001 | ES: 0.0-1.6; p<0.001 | ||
| ACC | CD | 3.6 ± 0.8∆,□, ⊗ | 2.9 ± 0.6⊗ | 2.3 ± 0.4⊗ | 2.2 ± 0.4⊗ | 1.8 ± 0.2b | ES: 0.9-4.6; p<0.001 |
| FB | 4.0 ± 0.9∆,□, ⊗ | 4.1 ± 0.9a,b,∆,□, ⊗ | 2.5 ± 0.5⊗ | 2.4 ± 0.6b, ⊗ | 1.7 ± 0.4b | ES: 0.1-4.0; p<0.001 | |
| MF | 4.3 ± 0.7∆,□, ⊗ | 3.9 ± 0.9b,∆,□, ⊗ | 2.4 ± 0.6 | 2.3 ± 0.5 | 2.1 ± 0.4a,b,e | ES: 0.5-4.5; p<0.001 | |
| OMF | 4.3 ± 0.8∆,□, ⊗ | 4.2 ± 1.3 | 3.0 ± 0.6a.b.c,e, ⊗ | 2.9 ± 0.6a,b,c,e, ⊗ | 2.2 ± 0.4a,b,e | ES: 0.1-4.2; p<0.001 | |
| FW | 3.8 ± 0.6†,∆,□, ⊗ | 2.7 ± 0.6∆,□, ⊗ | 2.1 ± 0.6⊗ | 2.1 ± 0.5⊗ | 1.4 ± 0.5 | ES: 1.8-4.6; p<0.001 | |
| all | 4.0 ± 0.8∆,□, ⊗ | 3.6 ± 1.0∆,□, ⊗ | 2.5 ± 0.6⊗ | 2.3 ± 0.6⊗ | 1.8 ± 0.5 | ES: 0.4-3.8; p<0.001 | |
| F(p) | ES: 0.0-0.9; p=0.304 | ES: 0.1-1.6; p<0.001 | ES: 0.9-1.5; p<0.001 | ES: 0.8-1.5; p<0.001 | ES: 0.2-1.7; p<0.001 | ||
| DEC | CD | 3.6 ± 0.4∆,□, ⊗ | 3.1 ± 0.8□, ⊗ | 2.2 ± 0.3⊗ | 2.1 ± 0.4 | 1.7 ± 0.2 | ES: 0.8-7.6; p<0.001 |
| FB | 4.2 ± 0.8∆,□, ⊗ | 4.4 ± 1.1a,b,∆,□, ⊗ | 2.7 ± 0.5a,b, ⊗ | 2.5 ± 0.5a,b, ⊗ | 1.9 ± 0.3a,b | ES: 0.2-3.8; p<0.001 | |
| MF | 4.2 ± 0.9∆,□, ⊗ | 3.9 ± 1.2∆,□, ⊗ | 2.4 ± 0.6 | 2.4 ± 0.6b | 2.1 ± 0.4a,b | ES: 0.3-3.8; p<0.001 | |
| OMF | 4.2 ± 0.6∆,□, ⊗ | 4.0 ± 1.1 | 2.8 ± 0.4a,b,c, ⊗ | 2.8 ± 0.7a,b,c, ⊗ | 2.1 ± 0.4a,b | ES: 0.2-4.7; p<0.001 | |
| FW | 4.4 ± 0.5†,∆,□, ⊗ | 3.1 ± 0.8∆,□, ⊗ | 2.2 ± 0.5⊗ | 2.0 ± 0.5⊗ | 1.6 ± 0.5 | ES: 1.8-5.6; p<0.001 | |
| all | 4.1 ± 0.7∆,□, ⊗ | 3.8 ± 1.1∆,□, ⊗ | 2.5 ± 0.5⊗ | 2.4 ± 0.6⊗ | 1.8 ± 0.4 | ES: 0.3-4.8; p<0.001 | |
| F(p) | ES: 0.3-1.8; p=0.142 | ES: 0.4-1.3; p=0.001 | ES: 0.2-1.7; p<0.001 | ES: 0.5-1.4; p<0.001 | ES: 0.0-1.1; p<0.001 |
CD = central defender; FB = full back; MF = midfielder; OMF = offensive midfielder; FW = forward; SSG5 = small-side game 5v5 + 2 goalkeepers; SSG6 = small-side game 6v6 + 1 joker + 2 goalkeepers; LSG9 = large-sided game 9v9 + 2 goalkeepers; LSG10 = large-sided game 10v10 + 2 goalkeepers; a > CD; b > FW; c > MF; d > OMF; e > FB; * >SSG5; † >SSG6; ∆ >LSG9; □ > LSG10; ⊗ >competitive match; DIS = distance covered (m); HSR = distance covered at high speed running (m >19.8 km·h-1); SPR = distance covered at sprinting (m >25.2 km·h-1); HMLD = high metabolic load distance (25.5 W·kg-1); AMP = average metabolic power; ACC = number of accelerations at high intensity (n >3 m·s-2); DEC = number of decelerations at high intensity (n <-3 m·s-2).
Table 2 shows the mean ± SD of the results obtained for the four training game formats and the CM, differentiating the positional groups. ACC and DEC demands were greater in SSGs (SSG5 and SSG6; ACC: ES: 1.4-3.8; DEC: ES: 1.7-4.8). As the SSGs increase the number of players, all the rest of the variables increase and the number of cases with significant interposition differences (p<0.05) also increases (ES: DIS: 0.7-2.2; HSR: 0.7-2.1; SPR: 0.8-1.4; HMLD: 0.9-2.0; AMP: 0.8-1.9; ACC: 0.8-1.7; DEC: 0.5-1.7).
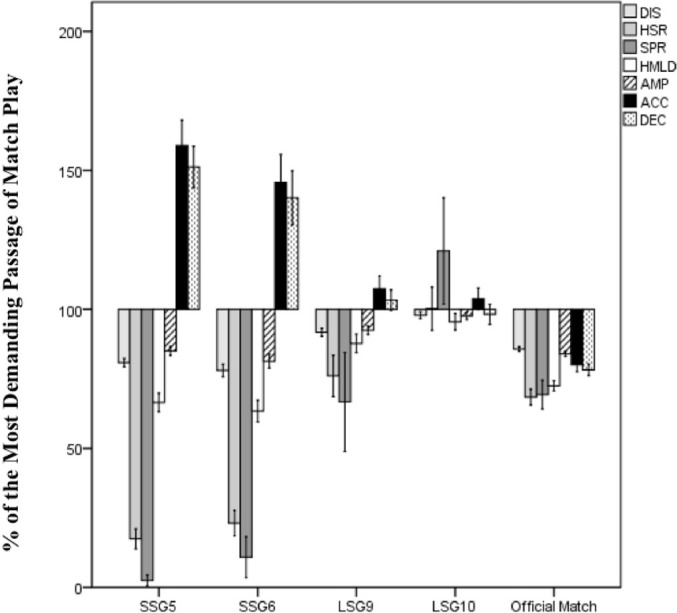
Figure 1 shows the different training game formats and CM by relativizing load to MDP for all players’ positions. The SSG5 format over-stimulates mechanical values (ACC: 158.8%, ES: 0.3-1.0; DEC: 151.2%, ES: 1.1-1.5) while the variables DIS, HMLD and AMP over-stimulate 50% according to the MDP (DIS: 80.8%, ES: 0.2-1.7; HMLD: 66.5%, ES: 0.3-0.5; AMP: 85.0%, ES: 0.1-0.8); however, HSR and SPR did not exceed 20% according to the MDP (HSR: 17.4%, ES: 0.3-0.9; SPR: 2.4%, ES: 0.5-0.9). The results obtained in the SSG6 format of the values and the differences (ES) between positions were similar to what was observed in the SSG5 format (DIS: 77.9%, ES: 0.3-1.6; HSR: 22.7%, ES: 0.3-0.9; SPR: 10.7%, ES: 0.2-1.0; HMLD: 63.4%, ES: 0.5-1.2; AMP: 81.4%, ES: 0.5-1.3; ACC: 146.0%, ES: 0.5-1.6; DEC: 140.7%, ES: 0.5-0.9). In the LSG9, the load values were exceeded in the ACC and DEC variables close to 100% according to the MDP (ACC: 107.4%, ES: 0.2-1.0; DEC: 103.3%, ES: 0.1-0.8), while the rest of the variables did not exceed the MDP (DIS: 91.7%, ES: 0.2-0.3; HSR: 76.1%, ES: 0.1-0.8; SPR: 66.6%, ES: 0.0-0.3; HMLD: 87.7%, ES: 0.1-0.7; AMP: 92.4%, ES: 0.2-0.6). The LSG10 format over-stimulates sprint values (121.0%, ES: 0.5-1.8), while the rest of the variables have values close to 100% of MDP (DIS: 97.8%, ES: 0.7-2.3; HSR: 100.2%, ES: 0.5-2.5; AMP: 97.6%, ES: 0.6-1.8; ACC: 103.8%, ES: 0.3-0.9; DEC: 98.1%, ES: 0.5-0.6). The CM values were lower according to the MDP in all variables, obtaining values between 65 and 85% with significant differences between positions (ES) smaller compared to the other formats (DIS: 85.7%, ES: 0.3-0.6; HSR: 68.4%, ES: 0.2-0.6; SPR: 69.3.7%, ES: 0.2-0.6; HMLD: 72.4%, ES: 0.2-0.6; AMP: 83.9%, ES: 0.2-0.5; ACC: 80.1%, ES: 0.3-0.4; DEC: 78.2%, ES: 0.1-0.4).
FIG. 1.
Game formats and competitive match percentages (%) according to the MDP for all players’ positions.
SSG5 = small-side game 5v5 + 2 goalkeepers; SSG6 = small-side game 6v6 + 1 joker + 2 goalkeepers; LSG9 = large-sided game 9v9 + 2 goalkeepers; LSG10 = large-sided game 10v10 + 2 goalkeepers; * >SSG5; † >SSG6; ∆>LSG9; □>LSG10; ⊗ >competitive match; DIS = distance covered; HSR = high speed running (m >19.8 km·h-1); SPR = sprint (m >25.2 km·h-1); HMLD = high metabolic load distance (m); AMP = average metabolic power; ACC = accelerations (n >3 m·s-2); DEC = decelerations (n <-3 m·s-2).
Finally, Table 3 shows the mean ± SD of the training game formats and CM relative to the MDP according to the position. The variables such as ACC (SSG5: 158.8 %, ES: 1.1; SSG6: 146.0%, ES: 3.4) and DEC (SSG5: 151.2%, ES: 1.0; SSG6: 140.7%, ES: 3.8) showed a high percentage load relative to MDP. In HSR the values relative to MDP are close to 100.0% (all: 100.0%, ES: 0.5-2.5). In DIS, FB obtains the highest values with significant differences (p<0.05) compared to MF and OMF in SSG5 (ES: 1.4-1.7) and with MF in SSG6 (ES: 1.6). In HSR, in LSG9 and LSG10, MF shows the lowest values obtaining significant differences (p<0.05) with CD, FB (ES: -0.8 and - 0.8, respectively) and CD (ES: -0.8). In CM, MF in SPR obtains the highest values according to the MDP (80.5%, ES: 0.6). FB shows in SSG6 the highest values in HMLD (ES: 1.1) and AMP (ES: 1.1-1.3). In ACC, significant interposition differences (p<0.05) are observed in SSG6 (ES: 1.3-1.5), LSG9 (ES: 1.1) and LSG10 (ES: 0.7-1.0).
TABLE 3.
Game formats and competitive match percentage according to the MDP.
| Variable | Position | SSG5 (%) | SSG6 (%) | LSG9 (%) | LSG10 (%) | Official Match (%) | ES;p |
|---|---|---|---|---|---|---|---|
| DIS | CD | 82.2 ± 6.9 | 78.3 ± 6.7 | 90.7 ± 8.1*,†, ⊗ | 97.4 ± 6.6*,†,∆, ⊗ | 86.1 ± 4.9† | ES: 0.9-2.9; p<0.001 |
| FB | 83.3 ± 3.1c,d | 81.6 ± 6.9c | 91.9 ± 6.7*,†, ⊗ | 97.4 ± 6.3*,†,∆, ⊗ | 86.3 ± 4.9*,† | ES: 0.8-2.4; p<0.001 | |
| MF | 77.4 ± 4.1 | 69.8 ± 8.6 | 90.3 ± 9.8*,† | 96.5 ± 7.3*,†, ⊗ | 87.9 ± 5.7*,† | ES: 0.7-3.4; p<0.001 | |
| OMF | 77.4 ± 6.1 | 77.8 ± 1.5 | 91.0 ± 9.9* | 97.3 ± 9.2*,†, ⊗ | 85.5 ± 6.5 | ES: 0.7-2.3; p<0.001 | |
| FW | 82.1 ± 6.4 | 78.7 ± 11.8 | 93.3 ± 9.5*,†, ⊗ | 100.4 ± 10*,†, ⊗ | 83.2 ± 9.6 | ES: 0.7-2.1; p<0.001 | |
| ES;p | ES: 0.2-1.7; p=0.012 | ES: 0.3-1.6; p=0.004 | ES: 0.2-0.3; p=0.505 | ES: 0.4-0.5; p=0.359 | ES: 0.3-0.6; p=0.019 | ||
| HSR | CD | 12.1 ± 12.6 | 24.0 ± 14.8 | 91.2 ± 48.4c,*,† | 113.5 ± 56.7c,*,†, ⊗ | 73.1 ± 1.9*,† | ES: 0.4-2.0; p=0.004 |
| FB | 17.8 ± 12.6 | 24.2 ± 20.2 | 88.4 ± 39.9c,*,†, ⊗ | 103.1 ± 34.2*,†, ⊗ | 63.9 ± 16.9*,† | ES: 1.5-2.9; p<0.001 | |
| MF | 19.3 ± 14.9 | 29.5 ± 21.6 | 55.3 ± 41.1* | 73.6 ± 41.7*,† | 76.9 ± 24.7*,† | ES: 0.1-2.5; p<0.001 | |
| OMF | 24.3 ± 14.5 | 21.4 ± 17.9 | 69.2 ± 42.4* | 97.5 ± 47.7*,† | 68.9 ± 22.8* | ES: 0.6-1.9; p<0.001 | |
| FW | 13.1 ± 9.9 | 13.7 ± 13.1 | 69.3 ± 33.7*,† | 104.5 ± 58.9*,†, ⊗ | 63.2 ± 24.3*,† | ES: 0.7-1.7; p<0.001 | |
| ES;p | ES: 0.3-0.9; p=0.328 | ES: 0.3-0.9; p=0.249 | ES: 0.1-0.8; p=0.013 | ES: 0.2-0.8; p=0.041 | ES: 0.2-0.6; p=0.018 | ||
| SPR | CD | 2.6 ± 7.3 | 0.5 ± 1.6 | 79.6 ± 109.8*,† | 124.0 ± 122.0*,† | 69.0 ± 34.5*,† | ES: 0.4-1.1; p<0.001 |
| FB | 1.4 ± 5.0 | 11.7 ± 23.6 | 74.7 ± 76.3*,† | 121.5 ± 80.1*,†, ⊗ | 59.1 ± 30.3*,† | ES: 0.6-1.8; p=0.004 | |
| MF | 2.1 ± 7.3 | 21.3 ± 52.1 | 64.6 ± 174.8 | 90.1 ± 154.3 | 80.5 ± 45.2a,e,*,† | ES: 0.1-0.7; p=0.104 | |
| OMF | 7.3 ± 13.2 | 33.3 ± 48.8 | 57.5 ± 77.9 | 116.8 ± 119.7* | 67.6 ± 41.5* | ES: 0.6-1.1; p=0.006 | |
| FW | 0.4 ± 0.0 | 1.2 ± 4.6 | 53.7 ± 53.4*,† | 143.7 ± 140.2*,†,∆ | 72.9 ± 46.9*,† | ES: 0.8-1.2; p<0.001 | |
| ES;p | ES: 0.3-0.8; p=0.343 | ES: 0.2-0.9; p=0.193 | ES: 0.1-0.3; p=0.875 | ES: 0.2-0.4; p=0.610 | ES: 0.2-0.6; p=0.011 | ||
| HMLD | CD | 69.6 ± 14.5 | 58.9 ± 7.6 | 85.8 ± 19.3† | 95.5 ± 19.1*,†, ⊗ | 73.4 ± 8.6† | ES: 0.5-2.1; p=0.004 |
| FB | 69.0 ± 12.8 | 71.5 ± 16.9b | 92.6 ± 18.8*,†, ⊗ | 96.3 ± 18.4*,†, ⊗ | 71.7 ± 11.5 | ES: 0.2-1.6; p<0.001 | |
| MF | 63.3 ± 11.1 | 60.8 ± 16.3 | 78.9 ± 19.6† | 87.4 ± 15.1*,† | 77.5 ± 13.4b,† | ES: 0.5-1.7; p<0.001 | |
| OMF | 61.7 ± 16.1 | 63.1 ± 12.4* | 87.4 ± 19.9*,†, ⊗ | 95.3 ± 18.5 | 75.1 ± 15.2b | ES: 0.4-1.9; p=0.004 | |
| FW | 66.7 ± 2.9 | 54.4 ± 11.5 | 91.5 ± 17.1*,†, ⊗ | 100.6 ± 22.5*,†, ⊗ | 66.9 ± 18.1† | ES: 0.4-2.6; p<0.001 | |
| ES;p | ES: 0.0-0.5; p=0.525 | ES: 0.5-1.1; p=0.009 | ES: 0.1-0.7; p=0.093 | ES: 0.2-0.7; p=0.158 | ES: 0.2-0.7; p=0.005 | ||
| AMP | CD | 85.4 ± 7.5 | 79.5 ± 6.6 | 91.2 ± 8.5†, ⊗ | 96.9 ± 7.2*,†, ⊗ | 84.3 ± 4.8 | ES: 0.7-2.5; p=0.004 |
| FB | 87.1 ± 5.2 | 87.4 ± 9.4b,c | 93.4 ± 7.5*, ⊗ | 97.6 ± 7.4*,†, ⊗ | 83.9 ± 5.3 | ES: 0.8-2.2; p<0.001 | |
| MF | 82.5 ± 5.0 | 74.9 ± 9.4 | 89.5 ± 10† | 94.9 ± 7.5*,†, ⊗ | 85.8 ± 6.5† | ES: 0.6-2.4; p<0.001 | |
| OMF | 82.1 ± 8.0 | 83.2 ± 4.2 | 92.6 ± 9.8*, ⊗ | 97.7 ± 8.5*,† ⊗ | 84.5 ± 6.4 | ES: 0.6-1.9; p<0.001 | |
| FW | 86.8 ± 3.7 | 77.2 ± 9.0 | 94.9 ± 9.4†, ⊗ | 100.4 ± 10.4*,†, ⊗ | 81.3 ± 10.6 | ES: 0.6-1.8; p<0.001 | |
| ES;p | ES: 0.1-0.8; p=0.153 | ES: 0.5-1.3; p=0.001 | ES: 0.2-0.6; p=0.276 | ES: 0.3-0.6; p=0.180 | ES: 0.2-0.5; p=0.022 | ||
| ACC | CD | 143.4 ± 33.9∆,□, ⊗ | 116.8 ± 25.8⊗ | 98.7 ± 18.3⊗ | 96.0 ± 16.8⊗ | 79.2 ± 7.3 | ES: 0.9-4.0; p=0.004 |
| FB | 166.8 ± 39.8∆,□, ⊗ | 171.1 ± 38.9a,b,*,∆,□, ⊗ | 113.5 ± 24.1⊗ | 108.9 ± 26.2c, ⊗ | 80.0 ± 19.8 | ES: 1.7-2.4; p<0.001 | |
| MF | 153.1 ± 24.3∆,□, ⊗ | 140.8 ± 33.2∆,□, ⊗ | 94.1 ± 24.7 | 90.2 ± 22.0 | 81.1 ± 15.1 | ES: 0.4-3.9; p<0.001 | |
| OMF | 153.1 ± 30.4⊗ | 148.3 ± 45.9 | 117.7 ± 22.6c, ⊗ | 113.7 ± 24.7a,c, ⊗ | 85.5 ± 16.9 | ES: 0.1-3.0; p<0.001 | |
| FW | 176.9 ± 30.8†,∆,□, ⊗ | 123.9 ± 29.7⊗ | 110.7 ± 34.3⊗ | 107.5 ± 26.8⊗ | 76.4 ± 28.7 | ES: 1.7-3.5; p<0.001 | |
| ES;p | ES: 0.3-1.9; p=0.231 | ES: 0.2-1.9; p<0.001 | ES: 0.2-1.0; p=0.005 | ES: 0.2-1.0; p=0.001 | ES: 0.3-0.4; p=0.079 | ||
| DEC | CD | 144.4 ± 17.1∆,□, ⊗ | 124.5 ± 31.9⊗ | 100.2 ± 15.2⊗ | 93.8 ± 19.3⊗ | 77.8 ± 9.6 | ES: 0.8-5.8; p=0.004 |
| FB | 152.4 ± 28.7∆,□, ⊗ | 159.1 ± 39.9∆,□, ⊗ | 109.3 ± 21.4⊗ | 99.7 ± 17.6⊗ | 78.3 ± 12.7 | ES: 0.2-3.3; p<0.001 | |
| MF | 142.4 ± 31.1∆,□, ⊗ | 129.4 ± 40.6⊗ | 91.9 ± 22.5 | 93.6 ± 25 | 80.8 ± 14.3 | ES: 0.4-3.2; p<0.001 | |
| OMF | 143.8 ± 22.4∆,□, ⊗ | 137.6 ± 37.1 | 108.2 ± 16.0⊗ | 110.0 ± 27.2⊗ | 82.7 ± 15.9 | ES: 0.2-3.5; p<0.001 | |
| FW | 181.1 ± 21.1†,∆,□, ⊗ | 129.2 ± 33∆,□, ⊗ | 104.5 ± 26.4⊗ | 94.3 ± 24.6⊗ | 73.5 ± 22.9 | ES: 1.8-4.8; p<0.001 | |
| ES;p | ES: 1.1-1.4; p=0.026 | ES: 0.6-0.9; p=0.042 | ES: 0.1-0.8; p=0.029 | ES: 0.5-0.6; p=0.033 | ES: 0.1-0.4; p=0.095 |
CD = central defender; FB = full back; MF = midfielder; OMF = offensive midfielder; FW = forward; SSG5 = small-side game 5v5 + 2 goalkeepers; SSG6 = small-side game 6v6 + 1 joker + 2 goalkeepers; LSG9 = large-sided game 9v9 + 2 goalkeepers; LSG10 = large-sided game 10v10 + 2 goalkeepers; a > CD; b > FW; c > MF; d > OMF; e > FB; * >SSG5; † >SSG6; ∆>LSG9; □>LSG10; ⊗ >competitive match; DIS = distance covered (m); HSR = high speed running (m >19.8 km·h-1); SPR = sprint (m >25.2 km·h-1); HMLD = high metabolic load distance (m >25 W·kg-1); AMP = average metabolic power (W·kg-1); ACC = accelerations (n >3 m·s-2); DEC = decelerations (n <-3 m·s-2).
DISCUSSION
The main purpose of this study was to examine the demands on the players in different game formats according to their position, setting out the results relative to the minutes of play (m·min-1 or n·min-1) and relative to the percentage (%) of the MDP of competitive match play. To our knowledge, no study has used different variables to describe the MDP of match play based on the use of AMP as a criterion variable. The main conclusions of the paper are: 1) there are different demands on the players depending on their position on the field in the training game formats and CM; 2) training game formats present different demands on the players, increasing them as the number of players in the training game format rises, except for the ACC and DEC variables, where the values are reduced; 3) the average values of the CM variables in the training game formats are between 70% and 80% of the MDP; 4) LSG10 played with a 10-minute duration replicate most of the demands of the MDP, achieving over-stimulating sprint demands, whilst the training game formats with the lowest number of players over-stimulate ACC and DEC; and 5) demands related to the MDP also vary depending on the position of the player. The demands, in relative or absolute terms/values, related to the demands of maximum effort in competition vary according to the position of the players in the field: from these absolute criteria in small formats and with relative criteria in large formats, the differences between demands are reduced in different game positions.
Currently, prescribing training based on a game’s average demands might leave some of the most demanding phases of the game uncovered, with a potential drop in poor performance and an increase in injury risk [9-15]. The results of this study support the hypothesis that the average demands of CM are between the values from 70 to 80% of MDP and are also position-dependent. Following the training planning proposal of Martin-Garcia et al. [20], SSG5 and SSG6 are in MD-4 and LSG9 and LSG10 are in MD-3.
The results show that over-stimulation and under-stimulation of MDP demands were replicated partially in a similar way during the game formats. It can be observed that in the situations in which a smaller number of players participated (SSG5 and SSG6), high-intensity acceleration and deceleration demands reached values of 150% with respect to the MDP. These results support the hypothesis that SSGs might be game formats in which players stimulate their ability to perform high-intensity acceleration and deceleration actions [34]. In contrast, and in line with previous papers [35], the variables that represent the locomotive variables (DIS, HSR and SPR) are not stimulated in game formats with few players, providing under-stimulation of actions carried out at high speed [36], while increasing their demand as game size and the number of players involved increase, reaching approximate values of 125% in the sprint variable in LSG10. The development of the sprint variable in the LSG10 format may be due to the reduced number of interruptions; the players' training dynamic is more joyful without the pressure of competition.
The results show that the demands imposed in different game formats differ according to the position occupied by the players in competition when the demands are expressed in absolute values [15] and also in relative values (% of MDP). It should be noted that physical demands have an opposite effect in their interpretation depending on whether they are considered as relative or absolute values. While in formats with few players (e.g., SSG5 and SSG6) the demands are similar in absolute values between positional groups, differences emerge when they are relativized to a percentage with respect to the MDP. In contrast, there were no positional group-based differences between LSG9 and LSG10 when expressed relative to the MDP in the distance covered by the players, while there were significant differences when the results were expressed in absolute values.
The use of training matches that replicate the structure of competition is a common practice in football training. This type of LSG is usually held in the mid-week sessions [17], at which general principles of the game are addressed with inter-sectoral relationships, looking for higher specificity that encourages learning transference [37]. The results of this research study show that intensity in LSG formats in relation to the MDP was the highest for all the variables except for ACC and DEC. During this type of game format, the players are able to reproduce the MDP (values close to 100% of MDP) and even exceed these values (all players in LSG10; 121%) in the distance covered at sprint. Once again it was found that the demands in LSG formats were position-dependent, respecting the differences between positions in the MDP, because the differences between positions were reduced when the demands were expressed as a percentage of MDP.
One of the main limitations of this paper is that the MDP was only studied using the AMP criterion variable in the period of greatest demand. It is likely that if the MDP had been identified based on the highest value of other variables, the values obtained with respect to the MDP would have been different. In addition, we believe that using more time windows (e.g., 1, 3, 7, 12 or 15 minutes) would have made it possible to explore in greater depth how the values relating to the competition percentage vary, as has been proposed in a previous paper [11] when the authors analysed total distance, the distance covered at high speed and the mechanical load in different training game formats and CM.
This study provides useful information for coaching staff on the impact of game formats on physical load, taking into account positional differences in relation to the MDP of competitive match play. The results highlight the importance of expressing the demands of the game formats relative to the MDP of each position. Only the acceleration and deceleration variables greatly exceed the values in the MDP during the SSGs, while the demands of other variables do not do so in any cases; however, they are the formats where the greatest number of players over-stimulate the HSR and SPR variables.
PRACTICAL IMPLICATIONS
Based on these results, it may be necessary to include varied types of tasks to overload the player during the training process. Distance, distance covered at high speed and distance covered when sprinting are the variables that have the lowest MDP percentage while performing the game formats studied, especially in the smallest formats of training games. Hence it may be necessary to design other types of tasks where these variables can be stimulated or complemented with other types of activities where they can be stimulated.
Acknowledgments
The authors thank all the athletes who participated in the study. The authors did not report any potential conflicts of interest. This work was not supported by a funding source.
Conflict of interest
The authors did not report any potential conflicts of interest.
REFERENCES
- 1.Osgnach C, Poser S, Bernardini R, Rinaldo R, di Prampero PE. Energy cost and metabolic power in elite soccer: a new match analysis approach. Med Sci Sports Exerc. 2010;42(1):170–8. doi: 10.1249/MSS.0b013e3181ae5cfd. [DOI] [PubMed] [Google Scholar]
- 2.Akenhead R, Hayes PR, Thompson KG, French D. Diminutions of acceleration and deceleration output during professional football match play. J Sci Med Sport. 2013;16(6):556–561. doi: 10.1016/j.jsams.2012.12.005. [DOI] [PubMed] [Google Scholar]
- 3.Mallo J, Mena E, Nevado F, Paredes V. Physical demands of top-class soccer friendly matches in relation to a playing position using global positioning system technology. J Hum Kinet. 2015;47(1):179–188. doi: 10.1515/hukin-2015-0073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Krustrup P, Mohr M, Ellingsgaard H, Bangsbo J. Physical demands during an elite female soccer game: importance of training status. Med Sci Sports. 2005;37(7):1242–1248. doi: 10.1249/01.mss.0000170062.73981.94. [DOI] [PubMed] [Google Scholar]
- 5.Mohr M, Krustrup P, Andersson H, Kirkendal D, Bangsbo J. Match activities of elite women soccer players at different performance levels. J Strength Cond Res. 2008;22(2):341–349. doi: 10.1519/JSC.0b013e318165fef6. [DOI] [PubMed] [Google Scholar]
- 6.Dalen T, Jørgen I, Gertjan E, Havard HG, Ulrik W. Player load, acceleration, and deceleration during forty-five competitive matches of elite soccer. J Strength Cond Res. 2016;30(2):351–359. doi: 10.1519/JSC.0000000000001063. [DOI] [PubMed] [Google Scholar]
- 7.Castellano J, Blanco-Villaseñor A. Análisis de la variabilidad del desplazamiento de futbolistas de élite durante una temporada competitiva a partir de un modelo lineal mixto generalizado. Cuad Psico Deporte. 2015;15(1):161–168. [Google Scholar]
- 8.Gregson W, Drust B, Atkinson G, Salvo VD. Match-to-match variability of high-speed activities in premier league soccer. Int J Sports Med. 2010;31(4):237–242. doi: 10.1055/s-0030-1247546. [DOI] [PubMed] [Google Scholar]
- 9.Gabbett TJ, Kennelly S, Sheehan J, Hawkins R, Milsom J, King E, Ekstrand J. If overuse injury is a ‘training load error’, should undertraining be viewed the same way? Br J Sports Med. 2016;50:1017–1018. doi: 10.1136/bjsports-2016-096308. [DOI] [PubMed] [Google Scholar]
- 10.Delaney JA, Duthie GM, Thornton HR, Scott TJ, Gay D, Dascombe BJ. Acceleration-Based Running Intensities of Professional Rugby League Match Play. Int J Sports Physiol Perform. 2016;11(6):802–809. doi: 10.1123/ijspp.2015-0424. [DOI] [PubMed] [Google Scholar]
- 11.Lacome M, Simpson BM, Cholley Y, Lambert P, Buchheit M. Small-Sided Games in Elite Soccer: Does One Size Fit All? Int J Sports Physiol Perform. 2017:1–24. doi: 10.1123/ijspp.2017-0214. [DOI] [PubMed] [Google Scholar]
- 12.Delaney JA, Thornton HR, Burgess DJ, Dascombe BJ, Duthie GM. Duration-specific running intensities of Australian Football match-play. J Sports Sci Med. 2017;20(7):689–694. doi: 10.1016/j.jsams.2016.11.009. [DOI] [PubMed] [Google Scholar]
- 13.Katz J, Katz L. Power laws and athletic performance. J Sports Sci. 1999;17(6):467–476. doi: 10.1080/026404199365777. [DOI] [PubMed] [Google Scholar]
- 14.Varley MC, Elias GP, Aughey RJ. Current match-analysis techniques’ underestimation of intense periods of high-velocity running. Int J Sports Physiol Perform. 2012;7(2):183–185. doi: 10.1123/ijspp.7.2.183. [DOI] [PubMed] [Google Scholar]
- 15.Abbott W, Brickley G, Smeeton NJ. Positional differences in GPS outputs and perceived exertion during soccer training games and competition. J Strength Cond Res. 2018 doi: 10.1519/JSC.0000000000002387. [DOI] [PubMed] [Google Scholar]
- 16.Delaney JA, Thornton HR, Rowell AE, Dascombe BJ, Aughey RJ, Duthie GM. Modelling the decrement in running intensity within professional soccer players. Sci Med in Football. 2017:1–7. [Google Scholar]
- 17.Clemente FM, Lourenço Martins FML, Mendes RS. Developing aerobic and anaerobic fitness using small-sided soccer games: Methodological proposals. J Strength Cond Res. 2014;36(3):76–87. [Google Scholar]
- 18.Martín-García A, Casamichana D, Díaz AG, Cos F, Gabbett TJ. Positional Differences in the Most Demanding Passages of Play in Football Competition. J Sports Sci Med. 2018;17(4):563. [PMC free article] [PubMed] [Google Scholar]
- 19.Winter EM, Maughan RJ. Requirements for ethics approvals. J Sports Sci. 2009;27:985. doi: 10.1080/02640410903178344. [DOI] [PubMed] [Google Scholar]
- 20.Martín-García A, Gómez Díaz A, Bradley PS, Cos F, Casamichana D. The Quantification of a Professional Football Teams External Load Using a Microcycle Structure. J Strength Cond Res. 2018;32(12):3511–3518. doi: 10.1519/JSC.0000000000002816. [DOI] [PubMed] [Google Scholar]
- 21.Owen AL, Djaoui L, Newton M, Malone S, Mendes B. A contemporary multi-modal mechanical approach to training monitoring in elite professional soccer. Sci Med in Football. 2017;1(3):216–221. doi: 10.1080/24733938.2021.1942539. [DOI] [PubMed] [Google Scholar]
- 22.Stevens TG, de Ruiter CJ, Twisk JW, Savelsbergh GJ, Beek PJ. Quantification of in-season training load relative to match load in professional Dutch Eredivisie football players. Sci Med in Football. 2017:1–9. [Google Scholar]
- 23.Tierney PJ, Young A, Clarke ND, Duncan MJ. Match play demands of 11 versus 11 professional football using Global Positioning System tracking: Variations across common playing formations. Hum Mov Sci. 2016;49:1–8. doi: 10.1016/j.humov.2016.05.007. [DOI] [PubMed] [Google Scholar]
- 24.Bowen L, Gross AS, Gimpel M, Li FX. Accumulated workloads and the acute: chronic workload ratio relate to injury risk in elite youth football players. Br J Sports Med. 2016;51(5):452–459. doi: 10.1136/bjsports-2015-095820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Fox R, Patterson SD, Waldron M. The relationship between heart rate recovery and temporary fatigue of kinematic and energetic indices among soccer players. Sci Med in Football. 2017;1(2):132–138. [Google Scholar]
- 26.Beato M, Bartolini D, Ghia G, Zamparo P. Accuracy of a 10 Hz GPS Unit in Measuring Shuttle Velocity Performed at Different Speeds and Distances (5-20 M) J Hum Kinet. 2016;54(1):15–22. doi: 10.1515/hukin-2016-0031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.di Prampero PE, Fusi S, Sepulcri L, Morin JB, Belli A, Antonutto G. Sprint running: a new energetic approach. J Exp Biol. 2005;208(14):2809–16. doi: 10.1242/jeb.01700. [DOI] [PubMed] [Google Scholar]
- 28.Brown DM, Dwyer DB, Robertson SJ, Gastin PB. Metabolic power method: Underestimation of energy expenditure in field-sport movements using a global positioning system tracking system. Int J Sports Physiol Perform. 2016;11(8):1067–1073. doi: 10.1123/ijspp.2016-0021. [DOI] [PubMed] [Google Scholar]
- 29.Buchheit M, Manouvrier C, Cassirame J, Morin JB. Monitoring locomotor load in soccer: is metabolic power, powerful? Int J Sports Med. 2015;36(14):1149–1155. doi: 10.1055/s-0035-1555927. [DOI] [PubMed] [Google Scholar]
- 30.Hader K, Mendez-Villanueva A, Palazzi D, Ahmaidi S, Buchheit M. Metabolic power requirement of change of direction speed in young soccer players: not all is what it seems. PloS one. 2016;11(3):e0149839. doi: 10.1371/journal.pone.0149839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rampinini E, Alberti G, Fiorenza M, Riggio M, Sassi R, Borges T, Coutts A. Accuracy of GPS devices for measuring high-intensity running in field-based team sports. Int J Sports Med. 2015;36(1):49–53. doi: 10.1055/s-0034-1385866. [DOI] [PubMed] [Google Scholar]
- 32.Casamichana D, Castellano J. Time-motion, heart rate, perceptual and motor behaviour demands in small-sided soccer games: Effects of pitch size. J Sport Sci. 2010;28(14):1615–1623. doi: 10.1080/02640414.2010.521168. [DOI] [PubMed] [Google Scholar]
- 33.Batterham AM, Hopkins WG. Making meaningful inferences about magnitudes. Int J Sports Physiol Perform. 2006;1(1):50–57. [PubMed] [Google Scholar]
- 34.Castellano J, Casamichana D. Differences in the number of accelerations between small-sided games and friendly matches in soccer. J Sports Sci Med. 2013;12(1):209. [PMC free article] [PubMed] [Google Scholar]
- 35.Castellano J, Casamichana D, Dellal A. Influence of game format and number of players on heart rate responses and physical demands in small-sided soccer games. J Strength Cond Res. 2013;27(5):1295–1303. doi: 10.1519/JSC.0b013e318267a5d1. [DOI] [PubMed] [Google Scholar]
- 36.Casamichana D, Castellano J, Castagna C. Comparing the physical demands of friendly matches and small-sided games in semiprofessional soccer players. J Strength Cond Res. 2012;26(3):837–43. doi: 10.1519/JSC.0b013e31822a61cf. [DOI] [PubMed] [Google Scholar]
- 37.Delgado-Bordonau J, Mendez-Villanueva A. Tactical periodization: Mourinho’s best kept secret. Soccer NSCAA J. 2012;3:28–34. [Google Scholar]