Concepts and tools for mechanism and selectivity analysis in synthetic organic electrochemistry

Significance

It seems opportune to accompany the present revival of synthetic organic electrochemistry by drawing attention of synthetic chemists to the heterogeneous nature of electrochemical reactions. Quantitative analysis of the successive layers in between working electrode and solution––electrical double layer, forced convection–diffusion layer, and reaction–diffusion layers––allows the mastering of the relationships between mechanism and product selectivity. The multiple connections between catalysis and electrochemical reactions are emphasized and illustrated by typical examples. Advantage is taken of the recent advances in activation of small molecules in response to modern energy and environment challenges with extension to synthetic organic electrochemical reactions.

Abstract

As an accompaniment to the current renaissance of synthetic organic electrochemistry, the heterogeneous and space-dependent nature of electrochemical reactions is analyzed in detail. The reactions that follow the initial electron transfer step and yield the products are intimately coupled with reactant transport. Depiction of the ensuing reactions profiles is the key to the mechanism and selectivity parameters. Analysis is eased by the steady state resulting from coupling of diffusion with convection forced by solution stirring or circulation. Homogeneous molecular catalysis of organic electrochemical reactions of the redox or chemical type may be treated in the same manner. The same benchmarking procedures recently developed for the activation of small molecules in the context of modern energy challenges lead to the establishment and comparison of the catalytic Tafel plots. At the very opposite, redox-neutral chemical reactions may be catalyzed by injection (or removal) of an electron from the electrode. This class of reactions has currently few, but very thoroughly analyzed, examples. It is likely that new cases will emerge in the near future.

Synthetic organic electrochemistry is reported to be presently enjoying a vigorous revival (1–8). If this is indeed the case, it would seem apropos to accompany this event in two ways. One is to single out from past knowledge particularly important concepts and techniques, which have been insufficiently utilized, ignored, or inadequately taken into account (9, 10). The other is to try making modern organic electrosynthesis embrace notions and methods that have been acquired through recent dedication to oxidative and reductive activation of small molecules in response to modern energy and environment challenges. Since one important issue is to help homogeneous chemists get acquainted to electrochemical approaches, the first of our tasks might be to explain what are the nature and consequences of the fundamentally heterogeneous character of electrochemical processes. To start with, electron transfers that initiate the electrochemical process indeed take place at the interface between a solid (with the exception of mercury) electronic conductor electrode and an ionic-conducting solution. Transport of reactants and products to and from the electrode surface also takes place in a heterogeneous context, giving rise to concentration profiles between electrode surface and bulk of the bathing solution. Simultaneously, the electron transfer formation of the primary intermediates is usually coupled with a cascade of chemical reactions leading to competitive formation of several products. These events may occur at the electrode surface in an adsorbed state or are more commonly coupled with mass transport in solution. Selectivity is accordingly the result of the kinetic competition between various pathways. Deciphering the mechanism of the global electrochemical process is thus intimately related to measuring and planning product selectivity. This immediately raises the question of the relations that may and should exist between analyses of preparative-scale electrolysis on the one hand and application of nondestructive techniques such as cyclic voltammetry, on the other. The latter are based on a tasting-type electrolysis in which a vanishingly small charge is passed, sufficient to record a current-potential response but small enough to leave the substrates and cosubstrates (of the order of one part per million) almost untouched. Competition of the electrochemical/chemical events with diffusional transport under precisely mastered conditions allows analysis of the kinetics within extended time windows (from minutes to submicroseconds). However, for irreversible processes, these approaches are blind on reaction bifurcations occurring beyond the kinetically determining step, which are precisely those governing the selectivity of the reaction. This is not the case of preparative-scale electrolysis accompanied by identification and quantitation of products. It thus appears as a necessary complement of nondestructive techniques in the determination of the reaction mechanism. Combination of the two approaches also allows making out the parameters that govern selectivity and therefore opens routes to optimizing the production of a target product. The conditions of preparative-scale electrolysis, where the most rapid conversion of the reactants is sought by minimizing the ratio between the volume of solution and the electrode surface area, as well as speeding the stirring or circulation of the solution, are the exact opposite of those of nondestructive techniques. However, the physico-mathematical description of the concentration profile of reactants, intermediates, and products is based on the same combination of mass transport, chemical reaction equations, and boundary conditions in both cases. Unlike the time-dependent cyclic voltammetric responses, the electrolysis case is simplified by the fact that diffusional transport occurs under steady-state conditions caused by forced convection resulting from stirring or circulation of the solution.

These various points are expounded in the next sections. Attention is focused on one of the two electrodes rather than on the problems raised by the association of the two electrodes in the electrolysis cell, for which excellent accounts are available (11, 12).

Heterogeneous and Chemical Nature of Electrochemical Processes. Electrical Double Layer, Diffusion Layer, and Reaction–Diffusion Layer

As detailed in SI Appendix, an electrical double layer builds up at the interface between electrode and the ionic bathing solution (ref. 13, pp. 12, 13). The site where electron transfer between the electrode and the reactant takes place is usually assumed to be in the middle of the compact double layer. The potential that the reactant “sees” is thus somewhat smaller than the potential difference between electrode and solution imposed by the operator. There might thus be a small influence of the double layer on the kinetics of the electrode electron transfer that starts the electrochemical process. This is a minor issue in the practice of preparative-scale electrolysis since the electrode potential is usually poised at a sufficiently negative value (for reductions, positive for oxidations) for the concentration of the substrate to be transformed to be zero at the electrode surface.

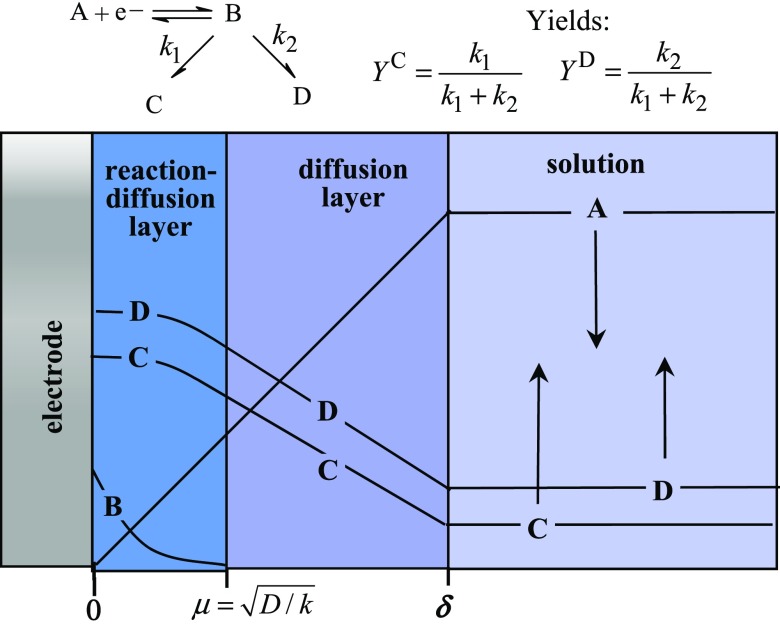
The solution contains excess supporting electrolyte that suppresses the contribution of migration in the mass transport of charged reactive species. Mass transport thus essentially involves diffusion and convection. The convection mode is in fact forced by stirring or circulation of the solution. It follows that a steady-state diffusion regime is established as pictured in Fig. 1. It is characterized (13) by a diffusion layer thickness, δ, which decreases with the rates of stirring or circulation. Exhaustive potential or current-controlled electrolysis is the most common regime in current laboratory practice. If, in the case of a simple $\text{A}+{\mathrm{e}}^{-}\text{B}$ reaction, the electrode potential is poised such that the A concentration at the electrode is zero, the consumption of A and the production of B in the solution is represented by exponential functions of time:

$$C_{\text{A}}^b=C^0\exp \left(-\frac{t}{t_C}\right),C_{\text{B}}^b=C^0\left[1-\exp \left(-\frac{t}{t_C}\right)\right],$$

where $t_C$ is the time constant of the cell: $t_C=V\delta /S/D$. V is the volume of solution, S the electrode surface area, D the average reactants’ diffusion coefficient, $C_{\text{A}}^b$ and $C_{\text{B}}^b$, the bulk concentrations of A and B, respectively, and $C^0$ the initial bulk concentration of $C_{\text{A}}^b$. In current laboratory practice, δ is on the order of 10⁻³–10⁻² cm. They are much thicker than electrical double layers (by a factor on the order of 10⁵–10⁶).

Fig. 1.

Electrolysis under force convection for a simple competitive reaction scheme. Steady-state concentration profiles and expression of the yields.

There is still another type of layer manifesting the heterogeneous nature of the electrochemical processes. It is related to the chemical reactions that accompanied the formation of the intermediate resulting from the first electron transfer step. This is represented in Fig. 1 for the simple case where a first-order reaction (with a rate constant k) follows the initial electron transfer. The diffusion–reaction layer thickness is $\sqrt{D/k}$ as shown in the figure for a fast reaction. The intermediate B is confined within this reaction–diffusion layer owing to a balance resulting from the compensation of diffusion and chemical reaction:

$$C_{\text{B}}=C^0\sqrt{D/k}\exp \left(-x\sqrt{D/k}\right)/\delta ,$$

where x is the distance from the electrode surface. For a fast reaction with, e.g., a rate constant $k={10}^7{\text{s}}^{-1}$ and a typical diffusion coefficient $D={10}^{-5}\cdot {\text{cm}}^2\cdot {\text{s}}^{-1}$, the reaction–diffusion layer thickness is 10⁻⁶ cm, much smaller than the usual diffusion-layer thicknesses but much larger than electrical double layers.

In the converse situation where $\sqrt{D/k}>>\delta$, the reaction takes place in the bulk of the solution. The system may then be analyzed according to the usual procedures of homogeneous chemistry. These are the conditions in which the “the pool method” (14) is run. An oxidant or reductant is prepared electrochemically in conditions (temperature, solvent) where it is stable and then, in a second stage, allowed to react with appropriate substrates in conditions where it can exert its full oxidative or reductive power.

Mechanism and Selectivity. Intrinsic and Operational Actors

In most cases, the chemistry accompanying the electron transfer between electrode and substrate involves more reactions than a single $\text{B}\to \text{C}$ step. The organic radicals or ion radicals resulting from this initial step are indeed very often chemically unstable. A first type of reaction that may affect the first electron transfer intermediate B is its reduction (or oxidation) at the electrode. In most cases, the second electron transfer is energetically more costly than the first and there is therefore no difficulty in preventing the occurrence of the second reaction by an appropriate adjustment of the electrode potential. The chemical reactions affecting the intermediate formed after a first electron transfer fall into two categories. One involves acid–base reactions in a broad (Lewis + Brönsted) sense. Their occurrence is a consequence of the intermediate being more basic, for a reduction, and more acidic, for an oxidation, than the parent reactant. This excess basicity (or acidity) is thus removed either by addition of an acid (or a base) or by elimination of a base (or an acid), which may occur in a stepwise manner or in a concerted manner (15). In a large number of cases, the second intermediate thus formed, C, is easier to reduce (or to oxidize) than the first. The result is a global exchange of two electrons per molecule, according to an ECE (electrochemical–chemical–electrochemical)-type mechanism (SI Appendix). A second series of reactions is related to the radical character of the intermediate. Dimerization is one of the most important reactions in this category, but other reactions, such as cyclization, H-atom abstractions (HAT), reactions with nucleophiles, etc. are also worth considering. The two types of chemistry may be combined, as when an acid–base reaction produces a secondary radical that undergoes a typical radical reaction (13).

This extremely rich set of chemical possibilities combined with the sequencing of the various steps interrogates the relationship between mechanism and selectivity. A systematic description of the electrochemical reactions of the various functional groups is clearly beyond the scope of the present article. Extensive reviews of these topics are available, as well as strategies targeting particular classes of molecules (16). We may instead focus on uncovering the parameters that govern the competition between reaction pathways leading to different final products. The simplest case involves the concentration profiles shown in Fig. 1 and the very simple expression of the yields (ref. 13 and SI Appendix). They are independent of operational parameters such as concentration of substrate and of stirring or circulation rates. This is no longer the case when competition involves reactions with different order as detailed in the next section on the example of the direct reduction of CO₂ in N,N′-dimethylformamide (DMF) on an inert electrode, which is a typical illustration of such situations. This example indeed contains the main ingredients of a mechanism/selectivity venture including, besides different order competing steps, the occurrence of ECE-disproportionation (“DISP”) type processes. It is also worth noting that the coupling of chemical steps with electron transfer not only affects currents and chemical selectivities but also the potentials at which electron transfer occurs. Potential-dependent selectivity may therefore not be only governed by the standard potentials of the electron transfer step but may have to take account of the effects of the accompanying reactions.

Example: Direct Electrolysis of CO₂ in an Aprotic Solvent on an Inert Electrode

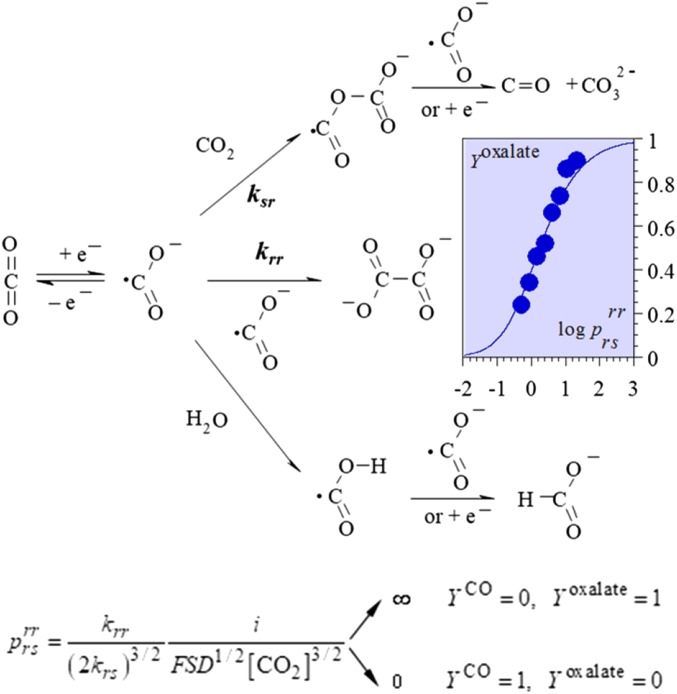
In the scheme of Fig. 2, the upper and the lower pathways may involve competitively, as second electron transfer, an electrode reaction (“ECE”), or a solution reaction (“DISP”).Competition involves the radical–radical and radical substrate dimerization pathways (rate constants: k_rr and k_sr, respectively). The latter requires a second electron uptake, which occurs at the electrode surface (ECE pathway) because of the high instability of the CO₂^•− anion radical (17). Electrolysis is run at the foot of the very negative CO₂ reduction wave (17), implying that CO₂ concentration is practically constant. Under these conditions the competition is governed by the single dimensionless parameter $p_{rs}^{rr}$, the expression of which (Fig. 2) reflects the competition between a first-order and a second-order reaction (ref. 13, pp. 152–154).

Fig. 2.

Oxalate (as opposed to CO and carbonate) yield in the preparative electrolysis of CO₂ in DMF on a mercury electrode at a current density of 1.6 mA/cm² at 0 °C as a function of CO₂ concentration. The fitting with the theoretical curve implies that k_rr/k_rs^3/2 = 8.5 × 10⁵ M^1/2s^−1/2 and D = 10⁻⁵ cm²/s.

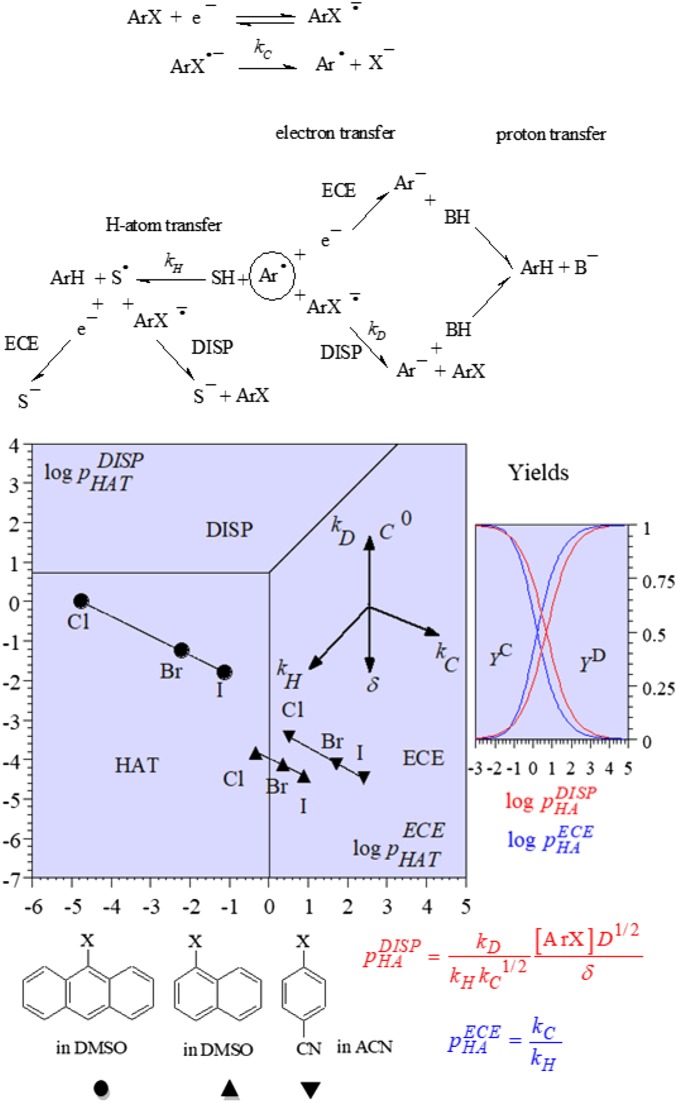
H Atom vs. Electron + Proton Transfer. Mechanism Derives from Preparative Electrolysis Rather than from Cyclic Voltammetry

The products from the two competing pathways in Fig. 3 are the same, but it might be important to know which is followed when a third reaction leads to the product of interest in competition with H atom or electron + proton transfers. Nondestructive techniques, such as cyclic voltammetry, are obviously not appropriate for distinguishing between the two pathways. Product distribution analysis may in contrast provide an answer if electrolysis is carried out in a light organic solvent with the addition of heavy water, or conversely, in a perdeuterated solvent with light water added. In the first case, the ratio of ArD over ArH produced is a measure of the relative importance of the electron + proton transfer pathway and the H-atom pathway. In the second case, it is, conversely, a measure of the relative importance of the H-atom pathway and the electron + proton transfer pathway. This strategy has been applied to the reduction of aromatic halides and the results are displayed (Fig. 3) under the form of a unitless 2D zone diagram which governs the competition between H-atom transfer and ECE- and DISP electron transfers, respectively. The values of the parameters, and of the rate constants they contained, were obtained by adjustment of the yield measured in deuteration experiments to the working curves shown in Fig. 3. This analysis provides a means to understand the competition between H-atom transfer and electron transfer + protonation in general. It also provides guidelines for optimizing deuterium incorporation reactions (13).

Fig. 3.

Reductive electrolysis of aromatic halides. The representative points are derived from deuteration experiments carried out at a potential located past the cyclic voltammetric peak potential. The compass rose on the top right summarizes the effect of the various rate and operational parameters.

Catalysis and Electrochemical Processes

Catalysis may interfere in the electrochemistry realm and vice versa in various different manners and the denominations of these different modes derive more from usage than from rationality.

“Electrocatalysis” is currently used to name catalysis of electrochemical reactions by surface states of the electrode (typical example: Platinum is a good electrocatalyst of H₂ evolution from the reduction of protons).

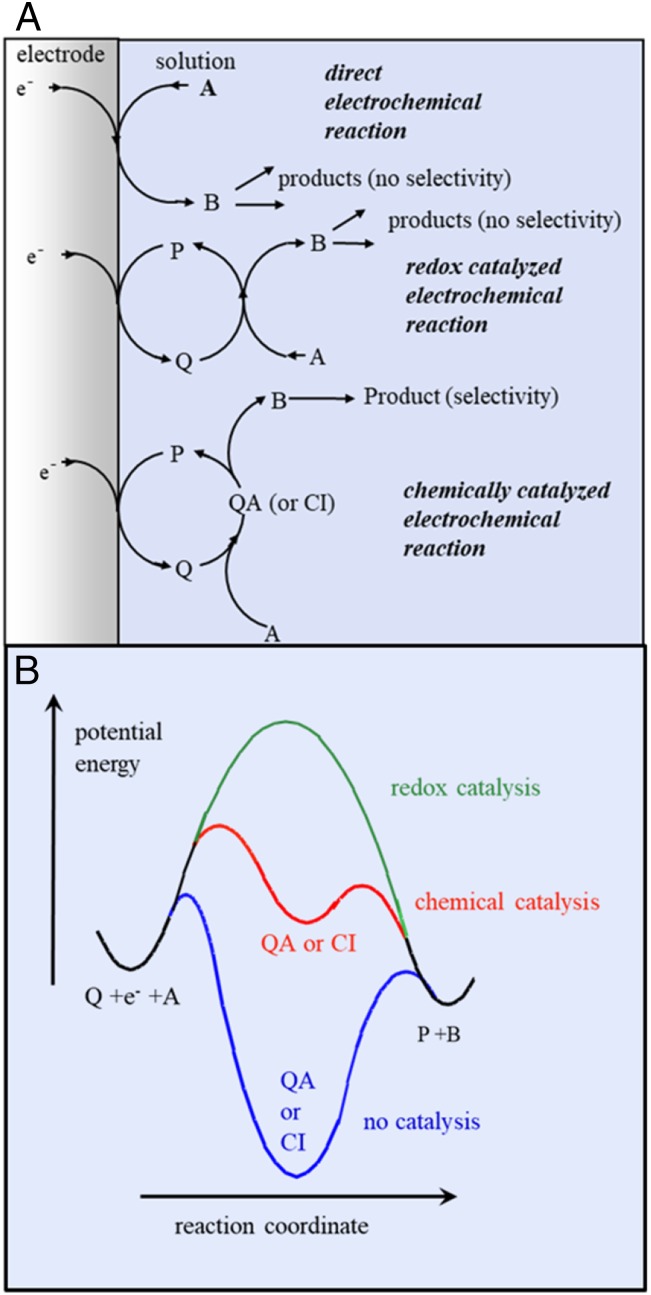
“Molecular catalysis of electrochemical reactions” clearly defines the target, namely, an electrochemical reaction that is uncomfortably slow and which is speeded up by a molecular catalyst dispersed in the solution or confined within a film deposited on the electrode surface (refs. 13, p. 252, and 18). It can be of two types (Fig. 4A). In “redox catalysis” the catalyst is a molecule that shuttles an electron to or from the electrode to the substrate with which it exchanges electron in an outersphere manner. It could be viewed as a physical catalysis in the sense that the catalytic boosting of the current is only due to the 3D dispersion of the electron exchanging species as opposed to the 2D nature of the direct electrode electron exchange [or this reason it is often called “mediator” (19)]. The outersphere/innersphere terminology has been introduced for electron transfer to or from coordination complexes, according to the absence or occurrence of a ligand change in the coordination sphere of the central metal (20). This notion has been extended to the organic realm, outersphere meaning that electron transfer is not concerted with a bond breaking or a bond-making event as opposed to the innersphere case. “Chemical catalysis” covers the innersphere case, often implying the transient formation of a Sabatier adduct between catalyst and substrate (Fig. 4B). Chemical catalysis appears as more efficient than redox catalysis (red curve vs. green curve), provided the adduct is not too stable, which would impede closing the catalytic loop (blue curve). Selectivity of indirect (catalyzed) electrochemical reactions is expected to be different from direct reaction in the case of chemical catalysis due to the specific interaction between the substrates and the catalyst, and we may also anticipate stereoselectivity in the case of chemical catalysis as opposed to redox catalysis. Less obvious is the prediction that the selectivity of redox-catalyzed reactions may be different from the selectivity obtained in direct reactions (21, 22). The physical reasons underlying this prediction derive from the development of a space-dependent concentration profile of the product selection intermediate which forms is a function of the nature and rate of the step that produces this key intermediate and of the rates of the follow-up steps. There is another circumstance where catalysis and electrochemist may be connected. Instead of having a catalyst couple that catalyzes an electrochemical reaction, we may have an electrochemical reaction that catalyzes a nonredox chemical reaction, which, globally, does not include any electron exchange. These reactions will be discussed in a further section.

Fig. 4.

Molecular catalysis of electrochemical reactions. (A) Reactions schemes and (B) potential energy profiles.

Catalyst Benchmarking and Optimization in Molecular Catalysis of Electrochemical Reactions. Catalytic Tafel Plots

The choice between several catalysts of a target reaction is intuitively directed toward the one that gives rise to the largest current at the less negative potential (for reductions, positive for oxidation). The latter parameter––the overpotential, η––is simply and precisely defined as the difference between the electrode potential, E, and a fixed potential, often chosen as the standard potential of the reaction to be catalyzed. Another parameter represents the rate at which the catalyst is able to convert reactants to product and is best expressed by the turnover frequency, defined as the ratio of the number of molecules transformed by the number of catalyst molecules effectively used in this transformation per unit of time: $TOF=N_{product}/N_{active\hspace{0.17em}cat}$, where “TOF” is “turnover frequency.” Catalyst molecules effectively engaged in the catalytic process are not all molecules present in the solution but only those that are located in a thin reaction–diffusion layer adjacent to the electrode surface as shown in Fig. 5A. For the simple reaction scheme at the top of the figure, the concentration profiles are as shown in Fig. 5A for constant substrate concentration $\left(C_{sub}^b\right)$ electrolysis and the turnover frequency is

$$\begin{array}{l}TOF=\frac{TO{F}_{\mathit{max}}}{1+\text{exp}\left[\frac{F}{RT}\left(E-E_{cat}^0\right)\right]}=\frac{TO{F}_{\mathit{max}}}{1+\text{exp}\left[\frac{F}{RT}\left(E_{\mathit{targe}t}^0-E_{cat}^0\right)\right]\text{exp}\left(-\frac{F}{RT}\eta \right)},\\ \hspace{0.17em}\text{with:}\hspace{0.17em}TO{F}_{\mathit{max}}=k_{cat}{C}_{sub}^b.\end{array}$$

Fig. 5.

Homogeneous molecular catalysis of an electrochemical reaction. (A) Concentrations profiles. (B) catalytic Tafel plots.

This relationship, represented by catalytic Tafel plots in Fig. 5B, confirms and quantifies the intuition that TOF and overpotential depend on each other. Comparing the catalytic Tafel plots offers a rational of benchmarking catalysts, independently of the particular experimental conditions used in each case, as pictured in Fig. 5B. Such catalytic Tafel plots can be obtained by running of several electrolysis at successive electrode potentials. The same plots may be obtained in a less tedious manner by means of cyclic voltammetry for reaction schemes as simple as the scheme in Fig. 5 or for more complicated schemes leading however to a single product. In the case where several products are obtained, the combined use of the two approaches is a powerful tool to decipher mechanisms and master selectivity.

The electrochemical reduction of vicinal dihalides into the corresponding olefins (detailed in SI Appendix) is an example showing that catalytic Tafel plots, previously used mostly for catalysis of the electrochemical conversion of small molecules, can be applied to a typical organic electrolytic process (23).

Selectivity in Aryl Halides Reduction Catalyzed by Electrogenerated Nickel Complexes. Comparison with Direct Reduction

As discussed earlier, the direct reduction of aryl halides (ArX) involves a two-electron cleavage leading to ArH according to an ECE–DISP-HAT mechanism. In principle, one can also consider the formation of a biaryl product Ar–Ar arising from dimerization of the Ar^• radical inter mediate. However, a complete analysis of the ECE-DISP-DIM competition problem shows that the maximal expected yield of the dimer is in the range of 10% in agreement with experimental results (24). Interestingly, when catalyzed by electrogenerated coordinatively unsaturated nickel complexes, the reduction of bromobenzene leads to formation of biphenyl (85% yield). A detailed mechanistic investigation showed that the reaction proceeds from electrogenerated Ni(0) complex and by a catalytic process (25, 26).

Electrochemically Catalyzed Reactions

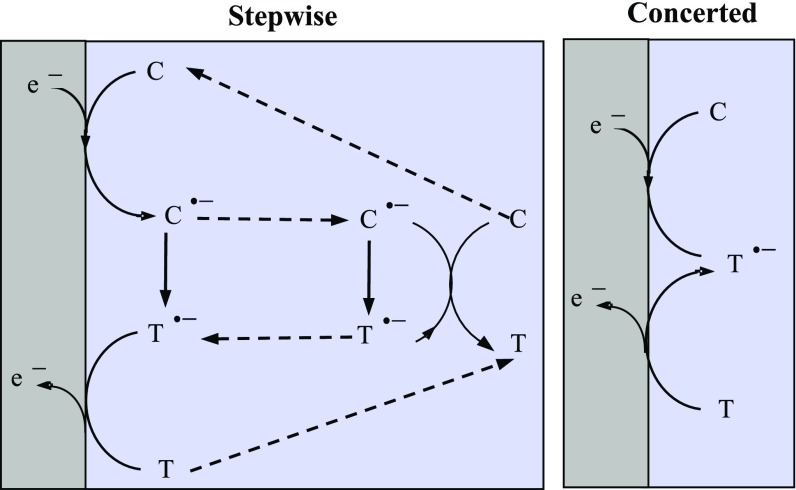
The simplest example of such reactions deals with cis-trans isomerization of olefins (27, 28) as shown in Fig. 6. The notations are inspired by cis-trans isomerizations involving neutral reactants trigged by a reductive electron transfer. It applies to any isomerization process reductively or oxidatively triggered. The reaction to be catalyzed electrochemically is a downhill process hampered by a large activation barrier. Isomerization becomes thermodynamically and kinetically easy after injection removal of one electron (as represented in the scheme, and can be symmetrically adapted to oxidatively triggered reactions). After the substrate C has acquired one electron at the electrode, the resulting anion radical, C^•− is converted into its isomer T^•−, which reacts with C, starting a solution chain process. It finally gives back the borrowed electron to the electrode, thus completing the isomerization process thanks to electron transfer catalysis. Situations may be encountered in which the intermediate C^•− does not exist, and therefore electron transfer and structural change are concerted, as in the right-hand version of the scheme. Even if C^•− does exist, its intermediacy may be bypassed when the driving force of its conversion into T^•− is very large, resulting in the same concerted process (13).

Fig. 6.

cis-trans isomerization of olefins.

S_RN1 Aromatic Nucleophilic Substitution

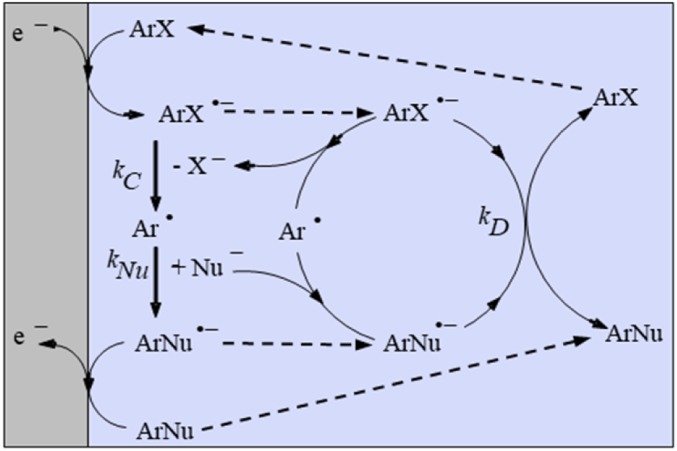
It might be surprising at first glance that substitution of a halide ion or other leaving groups by a nucleophile may occur at an aromatic carbon $\left(\text{ArX}+{\text{Nu}}^{\text{-}}\to \text{ArNu}+{\mathrm{X}}^{-}\right)$ as indeed occurs with a large number of substrate–nucleophile couples (29). Actually, these “S_RN1” aromatic substitutions do not involve the aromatic substrate itself as the reacting electrophile (Fig. 7). They require stimulation by solvated electrons, light, or an electrode (30). The first electrochemical example described (31) involved 4-bromobenzophenone as substrate and thiophenolate ion as nucleophile. Mixing of the two reactants did not produce any reaction over more than 48 h. Upon transfer of the reaction mixture in an electrochemical cell and poising the cathode potential at a value corresponding to the reduction of 4-bromobenzophenone, the reaction was completed in a few minutes with an almost quantitative yield and a very small electron consumption (corresponding to the difference between the yield observed and 100%). This experiment, as well as other observations, suggested the mechanism depicted above. In the absence of nucleophile, the aryl halide undergoes a two-electron reductive cleavage according to an ECE–DISP-HAT mechanism as previously discussed (13). In poor-H-atom–donating solvents, such as liquid NH₃ (32), the competition involves the (e⁻+H⁺) ECE–DISP pathways. Its outcome can be simply obtained by replacing HAT by substitution in Fig. 6 and k_H by k_Nu in the competition parameters introduced at this time (13).

Fig. 7.

S_RN1 aromatic nucleophilic substitution.

Besides the two examples just discussed, relatively few cases, clearly identified as electrochemically induced chemical reactions, have been presently described (26, 33–37). There is little doubt that this situation type will change in the near future at the time of the present revival of synthetic organic electrochemistry.

Conclusions

With the exception of “pool” strategies where reductants or oxidants, prepared electrochemically, are used as homogeneous reactants, in current preparative electrochemical processes, the reactions that follow the initial electron transfer and lead to the products are intimately coupled with reactant transport. The heterogeneous nature of electrochemical processes thus translates into concentrations profiles between electrode and solution for substrates, intermediates, and products. They can be characterized semiquantitatively by diffusion layers and reaction–diffusion layer and also by a complete mathematical analysis, which allows a full characterization of mechanistic and selectivity parameters. A simplifying factor of this endeavor is the steady-state character of the diffusion process thanks to its coupling with convection forced by stirring or solution circulation. Homogeneous molecular catalysis of organic electrochemical reactions of the redox or chemical type may be treated in the same manner. They are eligible for the same benchmarking procedures as recently developed for the activation of small molecules in the context of modern energy challenges, notably the establishment and comparison of the catalytic Tafel plots (turnover frequency vs. overpotential) characterizing the various catalysts to be compared. At the very opposite, redox neutral chemical reactions may be catalyzed by injection (or removal) of an electron from the electrode. This class of reactions has currently few, but very thoroughly analyzed, examples. It is likely that new examples will emerge in the near future.