Linear magnetoresistance in the low-field limit in density-wave materials

Significance

Magnetoresistance has a history of revealing key electronic characteristics of materials. From early measurements on noble metals to definitive characterization of localization effects in semiconductors to recent studies of topological materials, the magnetoresistive response provides an experimental technique to explore the Fermi surface in detail, and to predict and craft physical properties through its sign, functional form, and potential quantum character. Linear magnetoresistance in density-wave systems has eluded clear explanation for over half a century. Here, we present measurements that lead to a general explanation based on unusual current paths tied to the formation of long-range charge or spin order. This mechanism potentially extends to the large magnetoresistance observed in semimetals like Bi, graphite, and WTe₂.

Abstract

The magnetoresistance (MR) of a material is typically insensitive to reversing the applied field direction and varies quadratically with magnetic field in the low-field limit. Quantum effects, unusual topological band structures, and inhomogeneities that lead to wandering current paths can induce a cross-over from quadratic to linear MR with increasing magnetic field. Here we explore a series of metallic charge- and spin-density-wave systems that exhibit extremely large positive linear MR. By contrast to other linear MR mechanisms, this effect remains robust down to miniscule magnetic fields of tens of Oersted at low temperature. We frame an explanation of this phenomenon in a semiclassical narrative for a broad category of materials with partially gapped Fermi surfaces due to density waves.

The evolution of the electronic transport under the influence of a magnetic field can be deeply revealing of the fundamental properties of a material. Classically, the transverse magnetoresistance ρ_xx(H_z) evolves quadratically with magnetic field H, saturating at high fields if the hole and electron densities are not compensated (1–3). The asymptotic behavior in the low-field limit of ω_cτ << 2π, where ω_c is the cyclotron frequency and τ is the relaxation time, arises from the Onsager reciprocity relation, which requires σ_ij(H) = σ_ji(−H). The leading term in the magnetoresistance (MR) at low field is thus Δρ = ρ(H) − ρ(H = 0) ∼ H² (1, 2).

Other functional forms have been observed, most notably the symmetric linear form of Δρ ∼ |H|, which is nonanalytic at H = 0 but is allowed in the high-field limit, ω_cτ >> 2π. There are several well-established electronic and geometric mechanisms for generating this behavior in the high-field limit (1–10), which can be separated into two classes. The first is due to special features at the Fermi surface, such as sufficiently low electron density to permit condensation of the electrons into the lowest spin-split Landau level (4), linear dispersion from a Dirac cone with infinitesimally small carrier mass (5), Umklapp scattering (6), and magnetic breakdown (7). The second class is predominantly geometric in nature, such as an average over a combination of open and closed electron trajectories in polycrystals (2), guiding center diffusion in weak disorder (8), or strong mobility fluctuations due to irregular current paths from a strongly inhomogeneous medium or conductive grain boundaries (9, 10). Neither class addresses linear MR in the low-field regime where ω_cτ << 2π, the focus of our experiments.

While MR in metallic paramagnets and ferromagnets is typically small and negative, as the magnetic field quenches spin fluctuations and reduces spin scattering of itinerant carriers, large positive linear MR has been reported over the years in systems with charge-density-wave (CDW) order. This includes 2H-NbSe₂ (7), Nb₃Te₄ (11), (PO₂)₄(WO₃)₈ (12), and RTe₃ (R = Tb and Ho) (13). The linear MR in the low-field limit has been attributed to a wide range of mechanisms, from magnetic breakdown (7) to scattering of CDW fluctuations at Fermi surface hot spots (13). Here we argue that there exists a universal mechanism to create linear MR in the low-field/low-temperature limit. The salient features are a consequence of itinerant carriers turning sharp corners of the Fermi surface. This mechanism is greatly enhanced in both charge- and spin-density-wave (SDW) systems, as the formation of correlated electronic states opens a gap at the Fermi surface, removing sheets of open electron paths while keeping only small electron/hole pockets/ellipsoids with small orbits of sharp curvature. The change in the Fermi surface topology provides a generic approach to creating linear MR in the low-field limit in correlated electron systems.

Results

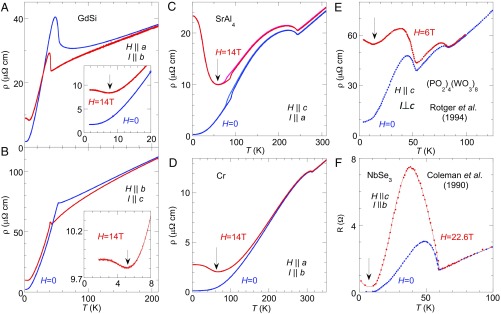
We present in Fig. 1 detailed ρ(T, H) data on the density-wave systems GdSi, SrAl₄, and Cr, in addition to comparisons to NbSe₃ and (PO₂)₄(WO₃)₈ derived from the literature. GdSi and Cr have SDWs driven by Fermi surface nesting with Néel transitions at T_N = 54.5 and 311.5 K, respectively (14–18). SrAl₄ develops a CDW state below T_CDW = 245 K (19), with no confounding contributions from spin order. All of the SDW and CDW ordering wave vectors are incommensurate: Q ∼ (0, 0.483, 0.092) in GdSi (14–16), Q ∼ (0.952, 0, 0) in Cr (18), and Q ∼ (0, 0, 0.11) in SrAl₄ (19). GdSi turns into a field-induced ferromagnet at H_c = 20.7 T (15), while the SDW in Cr extends to beyond 16 T (17). We measure ρ_xx(H_z, T) over a wide magnetic-field range and temperatures from 0.35 to 350 K (Figs. 1 and 2).

Fig. 1.

Finite-field magnetoresistance anomaly in the zero-temperature limit in CDW/SDWs. Transverse MR ρ_xx(T, H_z) at zero (blue) and high (red) fields are contrasted for (A and B) GdSi (H || a and b, respectively), (C) SrAl₄, (D) Cr, (E) (PO₂)₄(WO₃)₈ (data from ref. 12), and (F) NbSe₃ (data from ref. 22). The CDW and SDW transitions manifest as the resistance anomalies at higher temperature. Arrows point to where the in-field low-temperature resistance anomaly starts to grow with decreasing temperature. SrAl₄ has an extra structural transition at T ∼ 80 K as indicated by the temperature hysteresis (19). For our samples, the ratio of ρ(300 K)/ρ(2 K) = 25 for GdSi with I||b, 58 for GdSi with I||c, 77 for SrAl₄, and ρ(350 K)/ρ(2 K) = 92.4 for Cr. This resistance anomaly at finite fields and zero temperature was also observed in semimetals Bi, graphite (20), and WTe₂ (21).

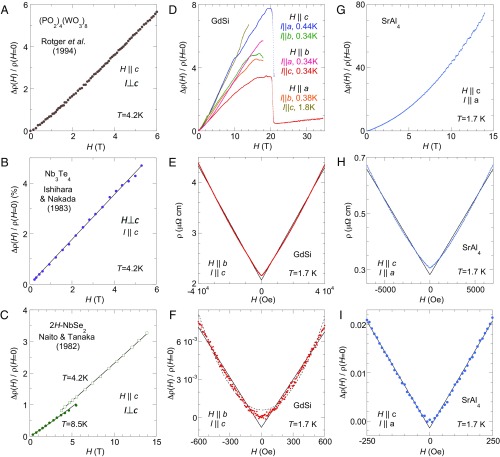
Fig. 2.

Linear transverse MR at low field. Positive linear MR as exemplified by five different CDW and SDW systems: (A) (PO₂)₄(WO₃)₈ (data from ref. 12), (B) Nb₃Te₄ (data from ref. 11), and (C) 2H-NbSe₂ (data from ref. 7), in addition to (D–F) GdSi, and (G–I) SrAl₄. Linear MR varies over a field range spanning more than three decades, with (D and G) Δρ/ρ ∼ 800% in GdSi and ∼7,500% in SrAl₄; (E and H) Δρ/ρ ∼ 100%; and (F and I) Δρ/ρ ∼ 1%. Black solid and dashed lines are even-parity linear (∼|H|) and quadratic fits to the data, respectively. GdSi undergoes a first-order spin-flip transition at ∼3 T for both H||a and H||c (15). Hence we focus on its MR behavior under the H||b geometry where the spin canting under field is continuous.

All of the listed materials exhibit a resistivity anomaly at the density-wave (DW) ordering temperature for both zero and high fields (Fig. 1). In addition to the DW anomaly, these systems also show a finite-field resistivity anomaly ρ_xx(T, H_z = constant) in the zero-temperature limit, which grows with decreasing T and extrapolates to its greatest value at T = 0. The onset temperature for the resistivity anomalies are marked by arrows in Fig. 1. Similar high-field, low-temperature ρ(T, H = constant) anomalies have been reported in semimetallic Bi, graphite, and WTe₂ (20, 21), and were attributed to metal–insulator transitions (20). The finite-field, low-temperature anomalies we consider here exist in highly conductive CDW and SDW systems with only partially gapped Fermi surfaces. Our proposed mechanism based on carriers turning sharp Fermi surface corners provides a different explanation for the zero-temperature resistance anomaly of Fig. 1. We argue that its relationship to linear or quadratic MR depends on the structure of the Fermi surface and the degree of disorder, and can be applied to both DW systems and semimetals.

We feature in Fig. 2 two of the most prominent linear MR cases available to us, the pure SDW system GdSi and the pure CDW system SrAl₄, as well as linear MR from three different CDW systems in the literature: (PO₂)₄(WO₃)₈, Nb₃Te₄, and 2H-NbSe₂ (7, 11, 12). In all cases, a strong MR with a positive, linear field dependence was observed in the low-temperature limit. The magnitude of the effect is large: e.g., an MR ratio Δρ_ii(H)/ρ_ii(0) = 3.5–8 (i = a, b, c) at H = 20 T for GdSi and ∼75 at H = 14 T for SrAl₄, with Δρ(H)/ρ(0) still ∼1–2% at a few hundreds of Oersted. The nearly linear behavior spans more than three decades of field range, and is clearly present even for ω_cτ << 2π.

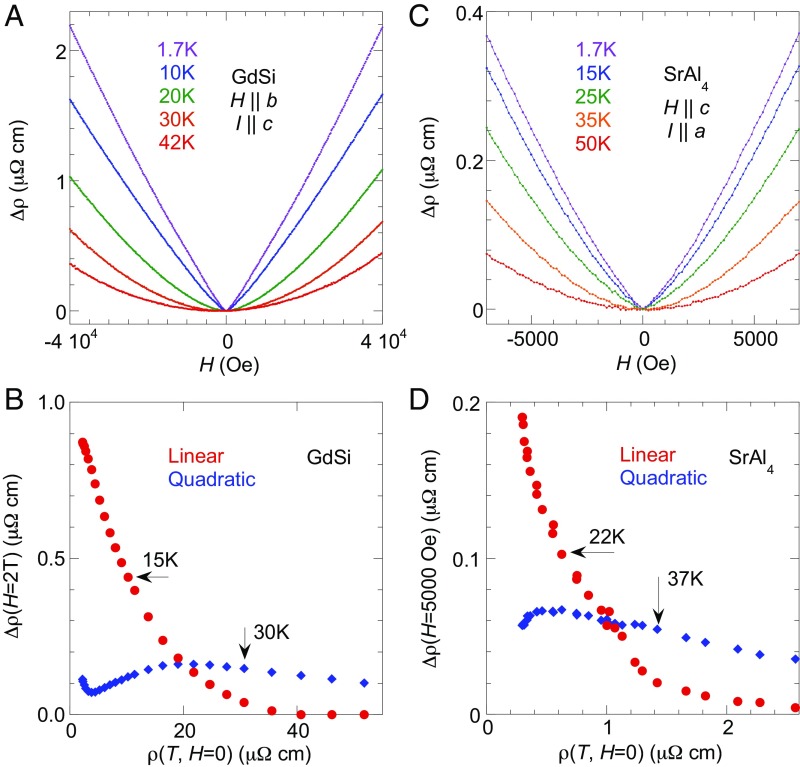
For both GdSi and SrAl₄, the linear MR in the low-temperature limit evolves into a parabolic field dependence at more elevated temperatures (Fig. 3), similar to RTe₃ in the literature (13). Although MR is often fit to a power law with a temperature-dependent exponent (7, 13), our attempts to perform a scaling analysis such as the Kohler plot to collapse all ρ(T, H) data onto a universal curve were not successful. Instead, there likely exist contributions from multiple electron- and hole-like conduction bands at the gapped Fermi surface, with potentially different functional forms under field.

Fig. 3.

Temperature evolution of linear and quadratic components in the prominent examples of the SDW system GdSi and the CDW system SrAl₄. (A and C) Representative curves of Δρ(H, T) are plotted together for varying temperatures. Fitting each curve with a sum of linear and quadratic terms, Δρ(H, T) = A(T)|H| + B(T)H², gives the coefficients A(T) and B(T). (B and D) These coefficients are compared for their contributions [linear with A(T)H and quadratic with B(T)H²] to the MR under a field of 2 T for GdSi and 0.5 T for SrAl₄, respectively.

We adopt a phenomenological approach to disentangle linear and quadratic components, fitting the measured MR as ρ(H, T) = ρ(T, H = 0) + A(T)|H| + B(T)H² as a function of field at various temperatures. We note that this form is distinct from a simple cross-over between linear and quadratic dependencies, and that this procedure is only valid to a magnitude of Δρ that is comparable to ρ(H = 0). As plotted in Fig. 3 B and D for GdSi and SrAl₄, respectively, contributions from A(T) and B(T) to the MR are very different, although they are both insensitive to the range of fitting for 0.5 T < H < 4 T in GdSi, and for 0.1 T < H < 0.7 T in SrAl₄. In both systems, the linear component A(T)H dominates over the quadratic term B(T)H² at low temperature, but A(T)H drops dramatically with increasing values of the zero-field resistivity, ρ(T, H = 0). We plot A(T)H and B(T)H² against ρ(T, H = 0) instead of T itself in Fig. 3 B and D to highlight the monotonic behavior of A(ρ(T, H = 0)). By comparison, A(T) would saturate at low temperature, as demonstrated by all of the systems in Fig. 1. B(T) does not change appreciably over a wide range of temperatures. The strong linear behavior approaching the zero-temperature limit is consistent with observations regarding Nb₃Te₄ and (PO₂)₄(WO₃)₈ (11, 12).

The rapid diminution of A(T) at elevated temperature argues against phonon- (6) or excitation-based (13) scattering mechanisms as sources for the linear MR. It is also important to note that the low-temperature resistivity anomaly in ρ(T, H = constant) becomes more prominent in clean systems with higher residual resistivity ratio (RRR) values. In NbSe₃, for example, the resistivity anomaly was only observed in samples with RRR values of 284 and 87, but not of 31 (22). Previous experiments (23) on a Cr sample with an RRR of 1,760 found an MR ratio ∼3,000 at 15 T and 4.2 K, which would nearly double the room-temperature resistance at zero field. This MR anomaly significantly surpasses the anomaly in our Cr sample with an RRR ∼ 85 (Fig. 1D). ρ(H) in Cr in general has a power exponent between 1 and 2 (23) depending on the degree of disorder and the relative field and crystalline directions.

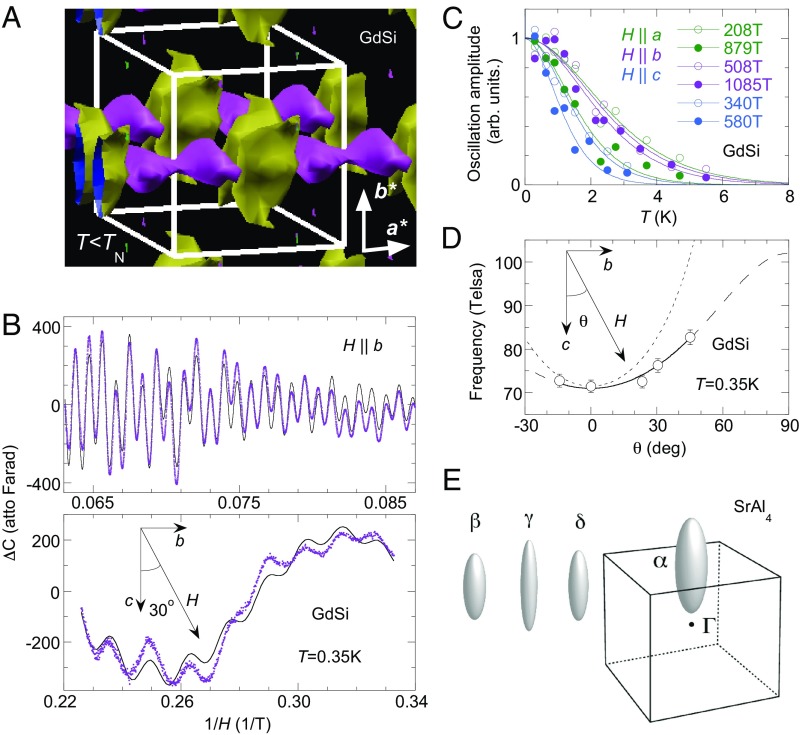
The similarity in behavior between CDW and SDW systems (Figs. 1–3) suggests that both the low-temperature MR anomaly and its subset of low-field linear MR, Δρ ∼ |H|, may arise from a generic mechanism that is intrinsic to general features of the Fermi surface. We have performed density-functional theory (DFT) calculations for GdSi in the gapped SDW phase and, as illustrated in Fig. 4, we find that its Fermi surface is marked by closed, bowtie or pinwheel-like volumes. These small volumes and their associated tight electron orbits contrast with the paramagnetic phase which has extended Fermi surfaces with nesting characteristics (14, 16). Similarly, the gapped Fermi surface of SrAl₄ is also closed in the form of several ellipsoids whose sizes are as small as 0.5% of the Brillouin zone volume (ref. 19 and schematically reproduced here in Fig. 4).

Fig. 4.

Closed Fermi surfaces in GdSi and SrAl₄ with small orbitals. (A) Three-dimensional schematics of DFT-calculated Fermi surface in the SDW phase of GdSi (T < T_SDW, Methods). All forms are closed with no open surfaces. (B) Raw data of quantum oscillations as a function of inverse magnetic field, expressed in measured cantilever capacitance. (Top) Along the b axis, the fitting (solid line) reveals F = 1,085, 508, and 432 T, with respective Dingle temperatures T_D = 2.8, 4.7, and 2.8 K. (Bottom) The detected quantum oscillation frequency of F = 76 T in the lowest branch. (C) Temperature dependence of major quantum oscillations along three crystalline axes, revealing carrier masses from 0.75 to 1.34 m_e. (D) The angular evolution of the frequency branch in the b–c plane with the lowest F₀ = 71.5 T along the c axis. The short-dashed line in a functional form of F₀/cos(θ) indicates the expectation from a tubular-shaped Fermi surface, while the solid curve (and long-dashed-line extension) is a fit of data to the expected form of an ellipsoidal Fermi surface. (E) A schematic of the dHvA oscillation reconstructed Fermi surface of SrAl₄ in the gapped CDW phase. Reproduced from ref. 19. Copyright (2016), with permission from Elsevier.

To validate our band structure calculations for GdSi, we probe the Fermi surface via cantilever torque magnetometry-based de Haas–van Alphen (dHvA) oscillations (Fig. 4) at the National High Magnetic Field Laboratory. Along the b axis, the three highest frequencies observed are 1,085, 508, and 432 T, which, respectively, enclose ∼12, 6, and 5% of the cross-sectional areas of the first Brillouin zone in the a–c plane. No frequency higher than 1,000 T was observed along either the c or a axes. The lowest frequency measured is 71.5 T for H along the c axis, which was also detected through a significant part of the b–c plane (Fig. 4F). The slowly varying form of F(θ) suggests an ellipsoidal Fermi surface that should present a small orbital for H along the b axis, although a corrugated cylinder cannot be ruled out without data over the full angular range. The 71.5-T frequency would represent an orbital of lateral size 0.05–0.1 Å⁻¹, enclosing 0.53% of the cross-sectional area of the first Brillouin zone in the a–b plane.

Discussion

Both GdSi and SrAl₄ have similarly high electron densities n in the gapped phase, with Hall coefficients R_H on the order of several 10⁻¹⁰ m³/C (refs. 14 and 19). With ρ(T = 1.7 K, H = 0) of GdSi and SrAl₄, of 2.2 and 0.31 μΩ cm, respectively, and carrier masses all around unity, the cyclotron frequency ω_c is typically small. For GdSi with seven conduction electrons per formula unit (three Gd 5d-6s and four Si 3s-3p electrons), we estimate on average for all carriers ω_cτ = H/ρnec = 4 × 10⁻³ at H = 2 T for our sample. The criteria for quantum linear MR (5) are thus not satisfied under our measurement conditions. Additionally, itinerant carriers would not have time to circle a full Fermi surface orbital. Instead they would only follow a small arc before being scattered away by either phonons or disorder to an incoherent state on the Fermi surface.

In general, a small arc would induce a very small directional change to the propagation of the carrier. However, the local curvature of the orbit could become large enough that within τ a carrier could round a sharp corner to change its direction by a significant fraction of 2π before being scattered away. The turning process at sharp corners would dominate the magnetoresistive contributions from all other carriers at flat parts of Fermi surface because the curvature of a sharp corner could define a large but local angular frequency ω. Despite the corner representing only a portion of a full revolution, the most significant contribution to the MR would come from the effectively large ω_cτ. Carrier movement on other, flatter regions of the Fermi surface only weakly contributes to the MR with a conventional quadratic dependence.

Although the importance of local curvature has been recognized in the literature, most often it still leads to predictions of quadratic MR because of assumptions of finite-sized rounding of the Fermi surface feature (24, 25), perfectly suited to explain the large quadratic MR in the semimetals Bi, graphite, and WTe₂ with their respective small Fermi surface pockets (20, 21). However, Pippard pointed out that there exists linear MR for a square Fermi surface with an infinitely sharp corner (3). Intuitively, this linear dependence can be understood by noting that in the reciprocal space, the global cyclotron frequency ω_c linearly increases with H, while the orbital size remains unchanged. Thus, the number of electrons moving along the orbital of the Fermi surface that can access the sharp corner within the mean scattering time before colliding, τ, increases linearly with field, and so does the MR. The MR behaves linearly as long as the mean-free-path length in reciprocal space, l_k, is much larger than the radius of the sharp corner, r_k, so that rounding is not relevant.

The field limit below which Δρ/ρ is no longer observable serves to estimate the curvature of the sharpest corner on the Fermi surface. The Onsager–Lifshitz relation connects orbit radii in reciprocal space, r_k, and real space, r, by $r_k=\left(eH/c\hslash \right)r$. When the carriers’ mean-free path, l, becomes comparable to r at the corner with decreasing H, the linear MR disappears. With disorder, the sharp turning points in the band structure could be broadened on the scale of the mean-free path: $r_k\sim 1/l$. Using these two expressions to constrain r_k, and taking l ∼ 1,000 Å and H = 10–100 Oe, we estimate r_k ∼ 10⁻⁴ Å⁻¹ in the SrAl₄ and GdSi systems. Features so small are at or beyond the resolution limit of present quantum oscillation techniques. We also note that our general mechanism of linear MR does not require an orbit of the same curvature around a full circumference, but only a sharp corner.

The Pippard approach does not address how sharp corners in the band structure survive in real materials, especially as different branches of the original Fermi surface hybridize via the CDW. An alternative way to create sharp band structure features in a CDW or SDW may arise from avoided crossings of nested pockets. The momentum required to scatter from one branch of the Fermi surface to an (approximately orthogonal) branch is extracted by Umklapp scattering from the CDW or SDW order. Hence a (possibly disorder-assisted) tunneling process could play the role required by Pippard’s mechanism to act as a source/sink of particles on the two branches. This would be a nonlinear process in terms of the ratio of the impurity potential to the gap––i.e., essentially using strong coupling impurities to reform the (hidden) Fermi surface of the parent metal, and to scatter between the intersecting branches. The idea is similar to the “Umklapp” mechanism, except that it would not require thermal excitation of particle–hole pairs.

It follows that the competition between coherent turning of sharp corners on the Fermi surface and incoherent collisions with phonons is the origin of the high-field resistivity anomaly in ρ(T, H = constant) exhibited in Fig. 1. τ decreases by collisions with either disorder or phonons. With a decreasing mean-free path with increasing temperature, fewer electrons will be able to circle the sharp corner before collisions; hence the MR initially decreases. The MR eventually begins to increase again due to enhanced phonon scattering at elevated temperature. With a disorder-shortened l_k closer to r_k of the turning corner, the power-law exponent of the field dependence would be expected to change from 1 to 2.

This mechanism for large, positive, and linear MR is well suited for explaining the behavior of a broad family of DW materials, and potentially other metallic incommensurate antiferromagnets in which large patches of Fermi surface are gapped out by the formation of long-range order (26). By removing sheet-like Fermi surfaces for open electron paths upon ordering, closed electron or hole pockets represent a generic topology for the remaining density of states. Although only representing a small portion of the Fermi surface, they can manifestly dominate the response to an applied field. In fact, as seen for SrAl₄, its linear MR at T = 1.7 K is of order 7,500% by H = 14 T, effectively matching the total electrical resistivity at room temperature.

Methods

Aligned single crystals of GdSi, Cr, and SrAl₄ were prepared in bar shapes of 1–3-mm length for magnetotransport measurements. Electrical leads were attached by silver epoxy in a four-lead geometry. High-field MR was measured using LakeShore LS372 resistance bridges and a 3708 preamplifier in either an 18-T superconducting magnet or a 35-T dc magnet (Cell 12) at the National High Magnetic Field Laboratory (NHMFL), Tallahassee, FL, using Helium-3 cryostat inserts to reach 0.34 K. The lower-field data were taken with similar electronics in a 14-T Physical Property Measurement System (PPMS; Quantum Design, Inc.) for 1.7 K ≤ T ≤ 350 K. All low-field data were taken following protocols to remove potential trapped flux in the superconducting magnet. Nevertheless, we estimate that the zero-field value is only precise to 20 Oe.

We also characterize germane Fermi surface features of GdSi via dHvA measurements at the NHMFL, using cantilever torque magnetometry with Andeen-Hagerling AH2700A capacitance bridges in an 18-T superconducting magnet down to T = 0.34 K. A monotonic polynomial background was first removed, and the oscillating spectra were Fourier transformed to detect major frequencies. The data were further fit to the Lifshitz–Kosevich formula, as the oscillating amplitude from torque magnetometry depends on temperature and field as ∼TH^−1/2exp(−αT_D/H)/sinh(−αT/H), where T_D is the Dingle temperature, and coefficient α = 14.69(m/m_e) Tesla/K, with the carrier mass m normalized by the free-electron mass m_e. This provides the fitting functional form in Fig. 4 for both carrier mass and Dingle temperature.

Density-functional theory calculation employed a 1 × 2 × 1 supercell with a halved first Brillouin zone of nonmagnetic GdSi. This procedure approximates the real Q ∼ (0, 0.493, 0.092) with a commensurate (0, 1/2, 0) antiferromagnetic order (14).