Developmental integration and evolution of labile plasticity in a complex quantitative character in a multiperiodic environment

Significance

Many quantitative characters undergo continuous reversible development, or labile plasticity, which may be determined by multiple components of plasticity acting on different time scales. Thermal adaptation in mammals includes transient fat deposition and fur growth, shivering and sweating or panting, and movement between warm and cold microhabitats, adapting individuals to annual and daily temperature cycles. With a single component of plasticity, adaptation is constrained by filtering environmental frequencies above the development rate and by component costs of plasticity. For a character with multiple components of plasticity, some patterns of development integration among the components can alleviate these constraints and facilitate evolutionary changes that greatly improve labile plasticity tracking complex environmental cycles in the optimum phenotype.

Abstract

Labile plasticity in a complex quantitative character is modeled, with multiple components contributing to net plasticity in the character. Each component has a specific development rate, norm of reaction, and cost of plasticity. For example, thermal adaptation in mammals includes seasonal fat deposition and fur growth, short-term shivering and sweating or panting, and movement between warm and cold sites. Norms of reaction do not reveal patterns of developmental integration, which must be investigated by studies of developmental dynamics in a changing environment. In a periodic environment, a labile character with a single component of plasticity is constrained by filtering environmental frequencies above the development rate and by the cost of plasticity. With multiple components of plasticity, some patterns of integration can alleviate these constraints to greatly improve fidelity of the mean phenotype tracking multiperiodic cycles in the optimum phenotype. This occurs by environmental signal amplification or inhibition through developmental integration among components and by an augmented development rate of net plasticity in the character that reduces environmental frequency filtering. When development of a component with high cost of plasticity is regulated partly by the norm of reaction of another component, evolution can diminish the reaction norm slope of the costly component without curtailing its development, thereby reducing the loss of fitness from its cost of plasticity. Apparent maladaptation in a component of plasticity may be an integral part of an adaptive pattern of developmental integration by mutual inhibition between components and compensatory evolution of a negative component reaction norm slope.

Animal and plant species generally respond to multiple environmental cycles affecting individual survival and reproduction, using a variety of labile plastic mechanisms of morphology, physiology, and behavior acting on different time scales (1). For example, plants have diurnal cycles of photosynthesis, stomate opening, and, in some species, flower opening, influencing water, oxygen, and ${\mathrm{C}\mathrm{O}}_2$ metabolism; deciduous plants shed and regrow foliage annually; and flowering plants usually have a distinct flowering season. In many long-lived vertebrates, secondary sexual characters develop maximally during annual reproductive seasons, including male behavioral and morphological mating displays, and combat characters such as antlers in male cervids which develop and shed annually; female primates of some species develop sexual swellings and coloration in internal, hormonally driven, quasilunar cycles of ovulation (2).

Ecologically important traits often are complex quantitative characters influenced by multiple mechanisms of labile plasticity that undergo continuous reversible development on different time scales. For example, thermal adaptation of animals to ambient temperature changes usually involves a combination of morphological, physiological, and behavioral mechanisms (3, 4). In mammals, adaptation to annual temperature cycles occurs morphologically by development of winter fat and fur, and physiologically and behaviorally by summer or winter estivation or hibernation; adaptation to daily temperature cycles and hourly temperature fluctuations involves a combination of nocturnal torpor, diurnal or nocturnal surface or subterranean burrowing, panting, sweating, shivering, piloerection, peripheral vasodilation and vasoconstriction, and movement between microhabitats such as sun and shade or land and water. Labile plasticity in all these components jointly regulates individual body temperature, but details of their developmental integration remain largely unknown. Multiple labile plastic mechanisms have been described for other complex characters, such as parental behavior (5) and reactions of aquatic organisms to hypoxia (6).

Previous analytical theory of phenotypic plasticity has largely been restricted to characters with a single component of fixed plasticity, using genetic norms of reaction to describe the static equilibrium development of phenotypes across a range of constant environments (7–13). It is therefore important to model developmental integration of components of plasticity in a complex character, to analyze how the dynamics of labile plasticity in the character depend on developmental integration of the components, and how the dynamics evolve in response to multiple environmental cycles of different frequency. Here, I model developmental integration in a complex quantitative character with labile plastic components having different development rates, norms of reaction, and costs of plasticity in a multiperiodic environment. For any pattern of developmental integration, the components are selected jointly and evolve together, based on their contributions to net labile plasticity in the character. I compare models with different patterns of developmental integration to answer the questions: How does developmental integration of components of net labile plasticity in a complex quantitative character influence (i) the norm of reaction of the mean phenotype, (ii) the evolution of component norms of reaction, and (iii) the ability of net labile plasticity in the mean phenotype to track the optimum phenotype in a multiperiodic environment?

For simplicity, I consider organisms with a generation time exceeding the period of the longest ecologically relevant environmental cycle and assume that evolution of plasticity is slow. The models thus apply to long-lived species with lifespans of several years or more, such as large vertebrates, and to short-lived species with multiple generations restricted to a particular season, such as insects with multiple summer generations and a dormant winter phase.

Multiperiodic Environment

The dominant environmental oscillations influencing most organisms are a combination of annual, lunar, and daily cycles in temperature, precipitation, and insolation driven by planetary rotations of the earth around the sun, the moon around the earth, and the earth around its axis. The amplitudes of environmental cycles with these three frequencies are largely determined by latitude, altitude, and the local topography and ecosystem (14). I model a single key environmental variable, ${\epsilon }_t$, such as regional temperature, experienced by all individuals in a population at time $t$. For convenience, the environment is scaled to have a mean of zero, $\overline{\epsilon }=0$. A multiperiodic environment is represented as a sum of periodic components, with time measured in years, and $i^{th}$ periodic component having amplitude ${\alpha }_i$ and frequency ${\omega }_i$,

$${\epsilon }_t=\sum _i{\alpha }_i\sin \left(2\pi {\omega }_{i}t\right).$$ [1a]

The periodic environment drives cycles in the optimum phenotype, ${\theta }_t$, which is assumed to be a linear function of the environment with intercept $A$ in the average environment and slope $B$,

$${\theta }_t=A+B{\epsilon }_t.$$ [1b]

Single Component of Labile Plasticity

Evolutionary models of phenotypic plasticity in quantitative characters typically use norms of reaction to analyze fixed plasticity in which the environment at a critical stage of development early in the life of an individual determines its final adult phenotype that is subject to natural selection (7–13). In contrast, characters with labile plasticity undergo continuous reversible development in response to environmental fluctuations, the dynamics of which cannot be described by norms of reaction alone.

I first summarize a basic model of development and evolution of a labile character with a single component of labile plasticity (15) and apply these to a periodic environment. The norm of reaction of a genotype, $a+\varphi \left(\epsilon \right)$, describes its expected phenotype as an intercept, $a$, in the average environment, plus a function of the environment in which it develops (1). For simplicity, the norm of reaction is assumed to be linear, with slope $b$, so that $\varphi \left(\epsilon \right)=b\epsilon$. In a variable environment, ${\epsilon }_t$, with fluctuations in the optimum phenotype, the labile component of an individual phenotype, denoted as ${\zeta }_t$, develops toward its norm of reaction at rate $\lambda$, in proportion to its deviation from the norm of reaction, $d{\zeta }_t/dt=-\lambda \left[{\zeta }_t-b{\epsilon }_t\right]$.

Further assumptions are: (i) All individuals in a population experience the same environment, as a stationary autocorrelated process; and (ii) the generation time of the population, $T$, greatly exceeds the time scales of development, $1/\lambda$, and of environmental fluctuations. The labile plasticity asymptotically approaches the reaction norm slope, $b$, multiplied by a weighted average of past environments, with weights decreasing exponentially into the past at the rate of development, ${\zeta }_t=b{f}_t$, where $f_t=\lambda \underset{0}{\overset{\infty }{\int }}{e}^{-\lambda s}{\epsilon }_{t-s}ds$. Labile plasticity in an individual phenotype closely tracks the optimum phenotype when it develops rapidly and has a reaction norm slope $b$ close to $B$.

The reaction norm slope of the mean phenotype in the population evolves to $\overline{b}=B{\left[1+\frac{{\gamma }_b}{\gamma }/\text{E}{f}_t^2\right]}^{-1}$, where ${\gamma }_b/\gamma$ describes the cost of plasticity by stabilizing selection against $b$, relative to the strength of stabilizing selection on the phenotype (16), and $\text{E}$ denotes expectation. At evolutionary equilibrium, $\overline{b}$ has the same sign but a smaller magnitude than $B$, reduced by the cost of plasticity and increased by variance in $f_t$.

For a multiperiodic environment, assumption (ii) entails that $T$ greatly exceeds the period of the longest ecologically relevant environmental cycle, so that

$$f_t=\sum _i{\alpha }_i\left[\frac{\sin \left(2\pi {\omega }_{i}t\right)-\left(2\pi {\omega }_i/\lambda \right)\cos \left(2\pi {\omega }_{i}t\right)}{1+{\left(2\pi {\omega }_i/\lambda \right)}^2}\right],$$ [1c]

$$\text{E}{f}_t^2=\frac{{\alpha }_i^2/2}{1+{\left(2\pi {\omega }_i/\lambda \right)}^2}.$$ [1d]

In an environment with a only a single cycle of frequency $\omega$ much greater than the development rate, $2\pi \omega /\lambda >1$ (when multiple periods of the cycle occur within the time scale of development, $1/\lambda$), plasticity in the mean phenotype, $\overline{b}{f}_t$, cannot closely track fluctuations in the optimum phenotype, $B{\epsilon }_t$. This occurs for two reasons. First, $f_t$ has a significantly diminished amplitude and lags substantially behind the environment, ${\epsilon }_t$. Second, with an appreciable cost of plasticity, the inequality also implies a substantial evolutionary reduction in the reaction norm slope $\overline{b}$ compared with $B$, unless the cycles have very large amplitude, ${\alpha }_i>{\left(2\pi {\omega }_i/\lambda \right)}^2$. In a multiperiodic environment with cycles of different frequency having comparable amplitude, or with a smooth continuous frequency spectrum, the development rate constitutes a threshold frequency, above which environmental cycles are filtered out by averaging over the time scale of development. Thus, environmental frequencies below the development rate play a dominant role in the development and evolution of labile plasticity in a character with a single component of plasticity.

This model assumes that the norm of reaction, and developmental dynamics toward it, are linear. Models of fixed plasticity readily encompass nonlinear reaction norms (8–10, 17–19), but contain no explicit developmental dynamics and therefore cannot describe labile plasticity in a quantitative character in a fluctuating environment. Nonlinearity of reaction norms and developmental dynamics greatly complicate the analysis of labile plasticity. Linear models for labile plasticity provide a foundation on which more general nonlinear theories can be built.

Developmental Integration and Component Dynamics

Phenotypic integration among characters has long been studied, showing that patterns of phenotypic covariance among characters reflect their functional and developmental relationships (20–24). Integration of plasticity among characters also has been investigated (25, 26), and network graphs have been used to describe patterns of developmental integration and phenotypic evolution (27–29).

I model a complex quantitative character of an individual as a sum of a constant additive genetic effect or breeding value, $a$, in the average environment, a constant microenvironmental effect $e$ (including nonadditive genetic effects) that is independent among individuals with mean $ē=0$ and variance ${\sigma }_e^2$ in each (macro)environment (30), and a net labile plasticity that is the sum of multiple plastic components, ${\zeta }_{j,t}$ for $j=\mathrm{1,2},\dots ,l$,

$$z_t=a+e+\sum _j{\zeta }_{j,t}.$$ [2a]

The mean phenotype in the population is

$${\overline{z}}_t=ā+\sum _j{\overline{\zeta }}_{j,t}.$$ [2b]

To understand how the net labile plasticity in such a complex character develops, it is necessary to analyze the dynamics of its components. However, with multiple components of net plasticity in a character, the details of their developmental interactions remain largely unknown. I therefore analyze a general model with each component developing at its specific rate in proportion to a linear combination of component deviations from their specific norms of reaction, describing regulatory mechanisms shared among the components,

$$\frac{d{\zeta }_{j,t}}{dt}=-{\lambda }_j\sum _k{D}_{jk}\left[{\zeta }_{k,t}-b_k{\epsilon }_t\right].$$ [2c]

The matrix $D$ describes the pattern of developmental integration among the components, allowing the component dynamics to be written in vector-matrix form

$$\frac{d{\zeta }_t}{dt}=-{⧅}_{\lambda }D\left({\zeta }_t-b{\epsilon }_t\right),$$ [2d]

where ${⧅}_{\lambda }$ is a diagonal matrix with component development rates, ${\lambda }_1,\dots ,{\lambda }_l$, on the diagonal and zeros elsewhere, and column vectors ${\zeta }_t={\left({\zeta }_{1,t},\dots ,{\zeta }_{l,t}\right)}^{\top }$ and $b={\left(b_1,\dots ,b_l\right)}^{\top }$ are defined with ^⊤ designating transpose. If the development of each component is self-regulating ($D_{jj}>0$), then $D$ can be rescaled by dividing each element of the $j^{th}$ row by $D_{jj}$ and rescaling the development rates to $D_{jj}{\lambda }_j$, leaving ${⧅}_{\lambda }D$ unchanged. Thus, in general, we can set $D_{jj}=1$.

The formal solution of Eq. 2d is

$${\zeta }_t=e^{-{⧅}_{\lambda }Dt}{\zeta }_0+{\int }_0^t{e}^{-{⧅}_{\lambda }D\left(t-u\right)}{\epsilon }_{u}du{⧅}_{\lambda }Db,$$ [2e]

where the matrix exponentials are defined by the power series for the exponential. To avoid any component diverging to $\pm \infty$, it is necessary to postulate that all eigenvalues of ${⧅}_{\lambda }D$ have nonnegative real parts.

If ${⧅}_{\lambda }D$ is positive definite so that all its eigenvalues have positive real parts, assuming that $T$ greatly exceeds the longest time scale of development and the longest period of environmental cycles, and using the change of variable $s=t-u$, the solution converges asymptotically (as $T$ and $t\to \infty$) to

$${\zeta }_t={\int }_0^{\infty }{e}^{-{⧅}_{\lambda }Ds}{\epsilon }_{t-s}ds{⧅}_{\lambda }Db.$$ [2f]

In a periodic environment, this represents an asymptotically stable cycle in the components of net plasticity in the mean phenotype.

In a constant environment, ${\epsilon }_t=\epsilon$, Eq. 2d indicates that, for any positive definite matrix ${⧅}_{\lambda }D$, the components of net plasticity achieve constant equilibrium values, ${\zeta }_{j,t}=b_j\epsilon$; hence, from Eq. 2b, the population norm of reaction is

$$\overline{z}=ā+\left(\sum _j{\overline{b}}_j\right)\epsilon .$$ [2g]

Selection and Evolution of Component Reaction Norms

Stabilizing selection around a fluctuating optimal phenotype ${\theta }_t$ is described by a quadratic function for the expected Malthusian fitness of individuals with phenotype $z_t$ in environment ${\epsilon }_t$,

$$m\left(z_t,{\epsilon }_t\right)=m_{max}\left({\epsilon }_t\right)-\frac{\gamma }{2}{\left(z_t-{\theta }_t\right)}^2-\sum _j\frac{{\gamma }_j}{2}{b}_j^2.$$ [3a]

The summation gives the net cost of plasticity by stabilizing selection with strength ${\gamma }_j$ acting against the reaction norm slope of the $j^{th}$ plastic component, $b_j$. Many characters have a small or undetectable cost of plasticity (31), but it has been suggested that costs of plasticity may be substantial in some characters (32–34).

The population mean fitness at time $t$ is obtained by averaging the individual fitness over the distribution of individual phenotypes, $z_t$, and the joint distribution of genotypic reaction norm parameters, $a,b_1,\dots ,b_l$.

$$\begin{array}{ccc}\hfill \overline{m}\left({\overline{z}}_t,{\epsilon }_t\right)& =\hfill & m_{max}\left({\epsilon }_t\right)-\frac{\gamma }{2}\left[{\left({\overline{z}}_t-{\theta }_t\right)}^2+{\sigma }_{z,t}^2\right]\hfill \\ \hfill & \hfill & -\sum _j\frac{{\gamma }_j}{2}\left({\overline{b_j}}^2+G_{jj}\right).\hfill \end{array}$$ [3b]

The component reaction norm parameters are assumed to have constant additive genetic variances, $G_{aa},G_{jj}$, and covariances, $G_{aj},G_{jk}$, in the average environment, $\overline{\epsilon }=0$. If the distribution of individual microenvironment $e$ is normal, and the joint distribution of genetic parameters is multivariate normal, then the phenotypic distribution in the population at any time is also normal. However, the results do not depend on normality. The phenotypic variance, ${\sigma }_{z,t}^2$, depends on the genetic (co)variances of reaction norm parameters and the developmental integration pattern of the components; ${\sigma }_{z,t}^2$ generally changes with the environment, but does not depend on the mean reaction norm parameters in a population (11, 15).

Evolution of the mean reaction norm parameters, $ā,{\overline{b}}_1,\dots ,{\overline{b}}_l$, is governed by their additive genetic variance–covariance matrix, $G$, the selection gradient of mean fitness with respect to the mean reaction norm parameters, and the population generation time, $T$, measured as the mean age of mothers at reproduction (9, 15, 35),

$$\frac{d}{dt}\left(\begin{array}{c}\hfill ā\hfill \\ \hfill \overline{b}\hfill \end{array}\right)=\frac{1}{T}\left(\begin{array}{cccc}\hfill G_{aa}\hfill & \hfill G_{a1}\hfill & \hfill \dots \hfill & \hfill G_{al}\hfill \\ \hfill G_{a1}\hfill & \hfill G_{11}\hfill & \hfill \dots \hfill & \hfill G_{1l}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill G_{al}\hfill & \hfill G_{1l}\hfill & \hfill \dots \hfill & \hfill G_{ll}\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\nabla }_{ā}\hfill \\ \hfill {\nabla }_{\overline{b}}\hfill \end{array}\right)\overline{m},$$ [3c]

where ${\nabla }_{ā}=\partial /\partial ā$ and ${\nabla }_{\overline{b}}={\left(\partial /\partial \overline{b_1},\dots ,\partial /\partial \overline{b_l}\right)}^{\top }$. The selection gradients on the mean reaction norm parameters are

$${\nabla }_{ā}\overline{m}=-\gamma \left({\overline{z}}_t-{\theta }_t\right),$$ [3d]

$${\nabla }_{\overline{b}}\overline{m}=-\gamma \left({\overline{z}}_t-{\theta }_t\right){\nabla }_{\overline{b}}\sum _j{\overline{\zeta }}_{j,t}-\left(\begin{array}{c}\hfill {\gamma }_1{\overline{b}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\gamma }_l{\overline{b}}_l\hfill \end{array}\right).$$ [3e]

Assuming a long generation time and low genetic variability of plasticity, so that evolution of plasticity is slow, and provided that $G$ is not singular, the evolutionary equilibrium of mean reaction norm parameters is obtained by setting to zero the expected selection gradient averaged over 1 year. $\text{E}{\nabla }_{ā}\overline{m}=0$ always produces $ā=A$, the average value of the optimum phenotype (Eq. 1b). The remaining equations, $\text{E}{\nabla }_{\overline{b}}\overline{m}=0$, must be solved simultaneously to obtain the evolutionary equilibrium of component reaction norm slopes, ${\overline{b}}_1,\dots ,{\overline{b}}_l$, for particular models of development.

No Integration

Development.

In the absence of developmental integration, each component of net plasticity develops toward its specific norm of reaction independently of the others. The matrix of developmental interactions is therefore simply the identity matrix, $D=I$, with diagonal elements one and off-diagonal elements zero, so that ${⧅}_{\lambda }D={⧅}_{\lambda }$. The labile plasticity of each component approaches an asymptotic solution identical to that for a character with only a single component (15),

$${\zeta }_{j,t}=b_j{f}_{j,t}\text{with}{f}_{j,t}={\lambda }_j{\int }_0^{\infty }{e}^{-{\lambda }_{j}s}{\epsilon }_{t-s}ds.$$ [4a]

In the multiperiodic environment of Eq. 1a,

$$f_{j,t}=\sum _i{\alpha }_i\left[\frac{\sin \left(2\pi {\omega }_{i}t\right)-\left(2\pi {\omega }_i/{\lambda }_j\right)\cos \left(2\pi {\omega }_{i}t\right)}{1+{\left(2\pi {\omega }_i/{\lambda }_j\right)}^2}\right],$$ [4b]

and the mean phenotype is (from Eqs. 2b and 4b)

$$\overline{z_t}=ā+\sum _j{\overline{b}}_j{f}_{j,t}.$$ [4c]

Evolution.

Despite developing independently, the component norms of reaction are selected and evolve jointly based on their contributions to net plasticity in the character. From Eq. 3e, the $j^{th}$ equation of $\text{E}{\nabla }_{\overline{b}}\overline{m}=0$ is

$$\sum _k\text{E}{f}_{j,t}{f}_{k,t}{\overline{b}}_k-B\text{E}{\epsilon }_t{f}_{j,t}+\left({\gamma }_j/\gamma \right){\overline{b}}_j=0.$$ [4d]

For the periodic environment of Eq. 1a,

$$\text{E}{f}_{j,t}{f}_{k,t}=\sum _i\frac{{\alpha }_i^2}{2}\left\{\frac{1+\left(2\pi {\omega }_i/{\lambda }_j\right)\left(2\pi {\omega }_i/{\lambda }_k\right)}{\left[1+{\left(2\pi {\omega }_i/{\lambda }_j\right)}^2\right]\left[1+{\left(2\pi {\omega }_i/{\lambda }_k\right)}^2\right]}\right\},$$ [4e]

$$\text{E}{\epsilon }_t{f}_{j,t}=\text{E}{f}_{j,t}^2=\sum _i\frac{{\alpha }_i^2/2}{1+{\left(2\pi {\omega }_i/{\lambda }_j\right)}^2}.$$ [4f]

Defining $E_{ij}=\text{E}{f}_{j,t}{f}_{k,t}$, the set of Eqs. 4d can be solved in matrix form as

$$\left(\begin{array}{c}\hfill {\overline{b}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\overline{b}}_l\hfill \end{array}\right)=B{\left(\begin{array}{ccc}\hfill E_{11}+\frac{{\gamma }_1}{\gamma }\hfill & \hfill \dots \hfill & \hfill E_{1l}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill E_{1l}\hfill & \hfill \dots \hfill & \hfill E_{ll}+\frac{{\gamma }_l}{\gamma }\hfill \end{array}\right)}^{-1}\left(\begin{array}{c}\hfill E_{11}\hfill \\ \hfill ⋮\hfill \\ \hfill E_{ll}\hfill \end{array}\right).$$ [4g]

With only two components, this is

$$\left(\begin{array}{c}\hfill {\overline{b}}_1\hfill \\ \hfill {\overline{b}}_2\hfill \end{array}\right)=\frac{B}{H}\left(\begin{array}{c}\hfill \left(E_{22}+\frac{{\gamma }_2}{\gamma }\right)E_{11}-E_{12}{E}_{22}\hfill \\ \hfill \left(E_{11}+\frac{{\gamma }_1}{\gamma }\right)E_{22}-E_{12}{E}_{11}\hfill \end{array}\right),$$ [4h]

where $H=\left(E_{11}+\frac{{\gamma }_1}{\gamma }\right)\left(E_{22}+\frac{{\gamma }_2}{\gamma }\right)-E_{12}^2$.

Serial Integration

Development.

The components of net plasticity are integrated sequentially. The first component develops toward its specific norm of reaction autonomously in response to ambient environmental cycles. Each subsequent component in the series is developmentally integrated with the previous ones, such that

$$\frac{d{\zeta }_{j,t}}{dt}=-{\lambda }_j\sum _{k=1}^j{D}_{jk}\left[{\zeta }_{k,t}-b_k{\epsilon }_t\right].$$ [5a]

For example, mammalian thermal adaptation appears to combine slow development of fat and fur in response to seasonal temperature cycles, rapid development of shivering and sweating (or panting) (among other physiological mechanisms) in response to daily and hourly changes in individual body temperature determined by both of these components, and, finally, individual movement between warm and cold microhabitats in response to body temperature affected by all of the components.

The developmental interaction matrix $D$ is then a lower triangular matrix, so that

$${⧅}_{\lambda }D=\left(\begin{array}{cccc}\hfill {\lambda }_1\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill {\lambda }_2{D}_{21}\hfill & \hfill {\lambda }_2\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\lambda }_l{D}_{l1}\hfill & \hfill {\lambda }_l{D}_{l2}\hfill & \hfill \dots \hfill & \hfill {\lambda }_l\hfill \end{array}\right),$$

with eigenvalues being the component development rates, ${\lambda }_1,\dots ,{\lambda }_l$. Thus, there exists a stable asymptotic equilibrium of labile plasticity in the components (Eq. 2f). This can be evaluated by using spectral analysis of the matrix, assuming that the eigenvalues are distinct, so that ${⧅}_{\lambda }D=Q{⧅}_{\lambda }{Q}^{-1}$, where the matrix $Q$ has columns that are the right eigenvectors of ${⧅}_{\lambda }D$. Expanding the matrix exponential, it can then be shown that the asymptotic solution for the components of net plasticity is

$${\zeta }_t=\left(Q{⧅}_{\lambda }^{-1}{⧅}_f{Q}^{-1}{⧅}_{\lambda }\right)Db,$$ [5b]

where ${⧅}_f$ is a diagonal matrix with elements $f_{1,t},\dots ,f_{l,t}$ on the main diagonal defined in Eqs. 4a and 4b and zero elsewhere. With only two serially integrated components of net plasticity,

$$Q=\left(\begin{array}{cc}\hfill {\lambda }_1/{\lambda }_2-1\hfill & \hfill 0\hfill \\ \hfill D_{21}\hfill & \hfill 1\hfill \end{array}\right),$$

and the asymptotic developmental trajectories are

$${\zeta }_{1,t}=b_1{f}_{1,t},$$ [5c]

$${\zeta }_{2,t}=b_2{f}_{2,t}+b_1{D}_{21}\frac{f_{2,t}-f_{1,t}}{{\lambda }_1/{\lambda }_2-1}.$$ [5d]

The first component develops autonomously as in Eq. 4a, and labile plasticity of the second component is modified from $b_2{f}_{2,t}$ because of its developmental integration with the first component. The mean phenotype in a fluctuating environment (Eq. 2b) is

$${\overline{z}}_t=ā+{\overline{b}}_1\left(f_{1,t}+D_{21}\frac{f_{1,t}-f_{2,t}}{{\lambda }_1/{\lambda }_2-1}\right)+{\overline{b}}_2{f}_{2,t}.$$ [5e]

Evolution.

From Eq. 3e, setting $\text{E}{\nabla }_{\overline{b}}\overline{m}=0$ produces for two components a pair of coupled equations for the component reaction norms,

$$\left(\begin{array}{cc}\hfill C_1+\frac{{\gamma }_1}{\gamma }\hfill & \hfill C_2\hfill \\ \hfill C_2\hfill & \hfill E_{22}+\frac{{\gamma }_2}{\gamma }\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\overline{b}}_1\hfill \\ \hfill {\overline{b}}_2\hfill \end{array}\right)=B\left(\begin{array}{c}\hfill C_3\hfill \\ \hfill E_{22}\hfill \end{array}\right),$$ [5f]

$$\begin{array}{ll}\hfill C_1& =E_{11}+2D_{21}\frac{E_{11}-E_{12}}{{\lambda }_1/{\lambda }_2-1}+D_{21}^2\frac{E_{11}-2E_{12}+E_{22}}{{\left({\lambda }_1/{\lambda }_2-1\right)}^2}\hfill \\ \hfill C_2& =E_{12}+D_{21}\frac{E_{12}-E_{22}}{{\lambda }_1/{\lambda }_2-1}\hfill \\ \hfill C_3& =E_{11}+D_{21}\frac{E_{11}-E_{22}}{{\lambda }_1/{\lambda }_2-1},\hfill \end{array}$$

where $E_{jk}$ is defined in Eq. 4e, after Eq. 4f. These formulas have the solution

$$\left(\begin{array}{c}\hfill \overline{b_1}\hfill \\ \hfill {\overline{b}}_2\hfill \end{array}\right)=\frac{B}{H}\left(\begin{array}{c}\hfill \left(E_{22}+\frac{{\gamma }_2}{\gamma }\right)C_3-C_2{E}_{22}\hfill \\ \hfill \left(C_1+\frac{{\gamma }_1}{\gamma }\right)E_{22}-C_2{C}_3\hfill \end{array}\right),$$ [5g]

where $H=\left(C_1+\frac{{\gamma }_1}{\gamma }\right)\left(E_{22}+\frac{{\gamma }_2}{\gamma }\right)-C_2^2$.

Complete Integration

Development.

The components of net plasticity are fully integrated such that each develops at its specific rate in proportion to the deviation of net plasticity from the net norm of reaction,

$$\frac{d{\zeta }_{j,t}}{dt}=-{\lambda }_j\sum _{k=1}^l\left[{\zeta }_{k,t}-b_k{\epsilon }_t\right].$$ [6a]

Summing both sides shows that net plasticity in the character develops as

$$\frac{d}{dt}\sum _j{\zeta }_{j,t}=-\mathrm{\Lambda }\left[\sum _j{\zeta }_{j,t}-\left(\sum _j{b}_j\right){\epsilon }_t\right],$$ [6b]

where $\mathrm{\Lambda }=\sum _j{\lambda }_j$. The development rate of net plasticity with completely integrated components is the sum of the component development rates.

The net plasticity of the character in an individual approaches an asymptotic form,

$$\sum _j{\zeta }_{j,t}=\left(\sum _j{b}_j\right)f_t\text{with}{f}_t=\mathrm{\Lambda }{\int }_0^{\infty }{e}^{-\mathrm{\Lambda }s}{\epsilon }_{t-s}ds.$$ [6c]

In the periodic environment of Eq. 1a,

$$f_t=\sum _i{\alpha }_i\left[\frac{\sin \left(2\pi {\omega }_{i}t\right)-\left(2\pi {\omega }_i/\mathrm{\Lambda }\right)\cos \left(2\pi {\omega }_{i}t\right)}{1+{\left(2\pi {\omega }_i/\mathrm{\Lambda }\right)}^2}\right].$$ [6d]

With complete integration of the components of net plasticity (Eq. 6a), the developmental integration matrix $D$ has all elements unity, so that

$${⧅}_{\lambda }D=\left(\begin{array}{ccc}\hfill {\lambda }_1\hfill & \hfill \dots \hfill & \hfill {\lambda }_1\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\lambda }_l\hfill & \hfill \dots \hfill & \hfill {\lambda }_l\hfill \end{array}\right).$$

The sole nonzero eigenvalue of this matrix is $\mathrm{\Lambda }$; hence, the component dynamics do not converge to a unique solution, but depend on initial conditions. Their dynamics can be evaluated by expanding the matrix exponentials in Eq. 2e, noting that (${{⧅}_{\lambda }}^{\mathrm{D)}n}={\mathrm{\Lambda }}^{n-1}{⧅}_{\lambda }D$, so that $e^{-{⧅}_{\lambda }Dt}=I+{\mathrm{\Lambda }}^{-1}\left(e^{-\mathrm{\Lambda }t}-1\right){⧅}_{\lambda }D$, yielding the asymptotic solution for the component dynamics

$${\zeta }_{j,t}=c_j+\frac{{\lambda }_j}{\mathrm{\Lambda }}\left(\sum _j{b}_j\right)f_t,$$ [6e]

where the constant $c_j={\zeta }_{j,0}-\frac{{\lambda }_j}{\mathrm{\Lambda }}{\sum }_k{\zeta }_{k,0}$ depends on initial conditions. However, ${\sum }_j{c}_j=0$, consistent with asymptotic stability of net plasticity in the mean phenotype.

The mean phenotype in the population in a fluctuating environment, from Eqs. 2b and 6c, is

$$\overline{z_t}=ā+\left(\sum _j{\overline{b}}_j\right)f_t.$$ [6f]

Evolution.

The $j^{th}$ equation of $\text{E}{\nabla }_{\overline{b}}\overline{m}=0$, from Eq. 3e, is

$$\sum _k{\overline{b}}_k\text{E}{f}_t^2-B\text{E}{\epsilon }_t{f}_t+\frac{{\gamma }_j}{\gamma }{\overline{b}}_j=0,$$ [6g]

and for the periodic environment (Eq. 1a)

$$\text{E}{\epsilon }_t{f}_t=\text{E}{f}_t^2=\sum _i\frac{{\alpha }_i^2/2}{1+{\left(2\pi {\omega }_i/\mathrm{\Lambda }\right)}^2}.$$ [6h]

Multiplying all terms of Eq. 6g by $\gamma /{\gamma }_j$, and summing, yields the evolutionary equilibrium slope of the population norm of reaction,

$$\sum _j{\overline{b}}_j=B{\left[1+\frac{1}{\text{E}{f}_t^2{\sum }_j\left(\gamma /{\gamma }_j\right)}\right]}^{-1}.$$ [6i]

Substituting Eq. 6i back into [6g] gives the evolutionary equilibrium of the component reaction norm slopes,

$${\overline{b}}_j=\frac{\gamma /{\gamma }_j}{{\sum }_j\left(\gamma /{\gamma }_k\right)}B{\left[1+\frac{1}{\text{E}{f}_t^2{\sum }_j\left(\gamma /{\gamma }_k\right)}\right]}^{-1}.$$ [6j]

Negative Complete Integration

Development.

The developmental integration matrix $D$ has diagonal elements 1, off-diagonal elements $-1/\left(l-1\right)$, and is singular. For $l=2$ components, ${⧅}_{\lambda }D$ has eigenvalues 0 and $\mathrm{\Lambda }={\lambda }_1+{\lambda }_2$, so the matrix exponential in Eq. 2e can be expanded as for complete integration to find

$$\left(\begin{array}{c}\hfill {\zeta }_{1,t}\hfill \\ \hfill {\zeta }_{2,t}\hfill \end{array}\right)=\frac{{\lambda }_2{\zeta }_{\mathrm{1,0}}+{\lambda }_1{\zeta }_{\mathrm{2,0}}}{\mathrm{\Lambda }}\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \end{array}\right)+\frac{b_1-b_2}{\mathrm{\Lambda }}\left(\begin{array}{c}\hfill {\lambda }_1\hfill \\ \hfill -{\lambda }_2\hfill \end{array}\right)f_t,$$ [7a]

where $f_t$ is defined in Eq. 6c. This shows that labile plasticity in one of the components must be apparently maladaptive, counteracting the adaptation of net plasticity in the character. The difference between the two components has asymptotically stable dynamics, while the sum depends on initial conditions,

$$\begin{array}{ll}\hfill {\zeta }_{1,t}-{\zeta }_{2,t}& =\left(b_1-b_2\right)f_t\hfill \\ \hfill {\zeta }_{1,t}+{\zeta }_{2,t}& =\frac{2}{\mathrm{\Lambda }}\left({\lambda }_2{\zeta }_{\mathrm{1,0}}+{\lambda }_1{\zeta }_{\mathrm{2,0}}\right)+\frac{{\lambda }_1-{\lambda }_2}{\mathrm{\Lambda }}\left(b_1-b_2\right)f_t.\hfill \end{array}$$ [7b]

Evolution.

Using Eqs. 7b and 3e, $\text{E}{\nabla }_{\overline{b}}\overline{m}=0$ produces a pair of coupled equations for the component reaction norms,

$$\begin{array}{l}\hfill \left[{\left(\frac{{\lambda }_1-{\lambda }_2}{\mathrm{\Lambda }}\right)}^2\left({\overline{b}}_1-{\overline{b}}_2\right)-\left(\frac{{\lambda }_1-{\lambda }_2}{\mathrm{\Lambda }}\right)B\right]\text{E}{f}_t^2\left(\begin{array}{c}\hfill 1\hfill \\ \hfill -1\hfill \end{array}\right)=\left(\begin{array}{c}\hfill \frac{{\gamma }_1}{\gamma }{\overline{b}}_1\hfill \\ \hfill \frac{{\gamma }_2}{\gamma }{\overline{b}}_2\hfill \end{array}\right),\\ \hfill \end{array}$$ [7c]

where $\text{E}{f}_t^2$ is defined in Eq. 6h. Adding these equations gives ${\gamma }_2{\overline{b}}_2=-{\gamma }_1{\overline{b}}_1$, showing that one of the component reaction norm slopes must be negative, again implying apparently maladaptive plasticity. Multiplying the first of Eqs. 7c by $\gamma /{\gamma }_1$, the second by $\gamma /{\gamma }_2$, and subtracting them finally yields the evolutionary equilibrium,

$$\begin{array}{l}\hfill {\overline{b}}_1-{\overline{b}}_2=\left(\frac{{\lambda }_1-{\lambda }_2}{\mathrm{\Lambda }}\right)B{\left[{\left(\frac{{\lambda }_1-{\lambda }_2}{\mathrm{\Lambda }}\right)}^2-\frac{1}{\left(\frac{\gamma }{{\gamma }_1}+\frac{\gamma }{{\gamma }_2}\right)\text{E}{f}_t^2}\right]}^{-1}.\\ \hfill \end{array}$$ [7d]

Numerical Results

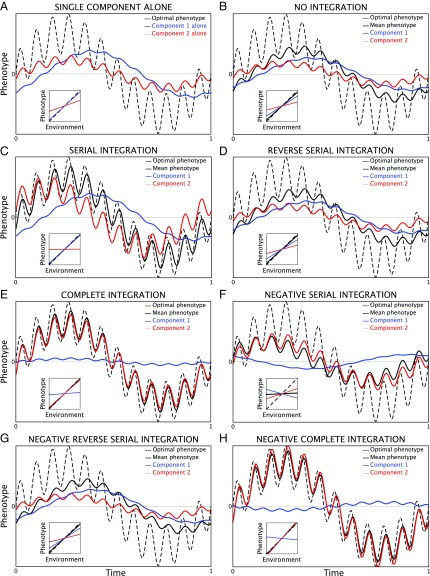
Table 1 and Fig. 1 compare numerical results for development models with one or two components of net plasticity in a labile character. The same two components are used throughout, with constant rates of development and costs of plasticity, in response to the same biperiodic environment. Component 1 develops slowly with a low cost, and component 2 develops rapidly with a high cost. In each case, the reaction norm slopes of the component(s) and of the mean phenotype are at evolutionary equilibrium, shown in Table 1, which also presents the mean squared deviation of the mean phenotype from the optimum phenotype, averaged over 1 year, and the cost of plasticity. For ease of visualization, the environment includes yearly and monthly cycles instead of the more usual yearly and daily cycles.

Table 1.

Evolutionary equilibrium reaction norms, environmental tracking, and cost of plasticity, for a character with two components of labile plasticity in a biperiodic environment

Development model	$D_{21}$, $D_{12}$	${\overline{b}}_1/B$	${\overline{b}}_2/B$	$\frac{\overline{b_1}+{\overline{b}}_2}{B}$	$\frac{\text{MSD}}{B^2}$	Cost
Component 1 alone		0.9067			0.4323	0.0164
Component 2 alone			0.3519		0.3100	0.1239
No integration	0, 0	0.6380	0.2605	0.8984	0.2835	0.0760
Serial integration	1, 0	0.9067	0.0156	0.9224	0.0787	0.0167
Reverse serial integration	0, 1	0.6237	0.2714	0.8950	0.2664	0.0814
Complete integration*	1, 1	0.9466	0.0189	0.9655	0.0770	0.0183
Negative serial integration	−1, 0	−0.2827	0.3281	0.0455	0.2850	0.1093
Negative reverse serial	0, −1	0.6540	0.2477	0.9017	0.3013	0.0699
Negative complete†	−1, −1	−1.2195	0.0244	−1.1951	0.0779	0.0303

Optimum phenotype cycles annually and monthly with {frequency, amplitude}: $\left\{{\omega }_1,{\alpha }_1\right\}=\left\{\mathrm{1,1}\right\}$ and $\left\{{\omega }_2,{\alpha }_2\right\}=\left\{\mathrm{12,0.5}\right\}$ (Fig. 1). Component 1 develops slowly with low cost, $\left\{{\lambda }_1,{\gamma }_1/\gamma \right\}=\left\{\mathrm{5,0.02}\right\}$. Component 2 develops rapidly with high cost, $\left\{{\lambda }_2,{\gamma }_2/\gamma \right\}=\left\{\mathrm{60,1}\right\}$. Developmental integration coefficients, $D_{21},D_{12}$. Reaction norm slopes of components, ${\overline{b}}_1/B$, ${\overline{b}}_2/B$, and mean phenotype, $\frac{{\overline{b}}_1+{\overline{b}}_2}{B}$. Mean squared deviation of mean phenotype from optimum, $\frac{\text{MSD}}{B^2}$. Cost = $\frac{{\gamma }_1}{\gamma }\frac{{\overline{b}}_1^2}{B^2}+\frac{{\gamma }_2}{\gamma }\frac{{\overline{b}}_2^2}{B^2}$ for two components, or one term for a component alone.

^**Singular. Observable reaction norm slopes of components $\frac{\left\{{\lambda }_1,{\lambda }_2\right\}}{{\lambda }_1+{\lambda }_2}\frac{{\overline{b}}_1+{\overline{b}}_2}{B}=\left\{0.0742,0.8912\right\}$ and mean phenotype $\frac{{\overline{b}}_1+{\overline{b}}_2}{B}$ as listed (Eqs. 6e and 6f).

^†Singular. Observable reaction norm slopes of components $\frac{\left\{{\lambda }_1,-{\lambda }_2\right\}}{{\lambda }_1+{\lambda }_2}\frac{{\overline{b}}_1-{\overline{b}}_2}{B}=\left\{-0.0957,1.1482\right\}$ and mean phenotype $\frac{{\lambda }_1-{\lambda }_2}{{\lambda }_1+{\lambda }_2}\frac{{\overline{b}}_1-{\overline{b}}_2}{B}=1.0525$ (Eqs. 7a and 7b).

Fig. 1.

Evolutionary equilibrium of labile plasticity in a quantitative character in a biperiodic environment. All panels have the same parameters for the environment and the components of plasticity in a character (Table 1). Insets show the norms of reaction of the components and the mean phenotype. (A) The character has only one component of plasticity, either component 1 alone or component 2 alone (Eqs. 1c and 1d). Subsequent panels have two components of net plasticity in the character, with different patterns of developmental integration. (B) No integration (Eqs. 4). (C) Serial integration (Eqs. 5). (D) Reverse serial integration. (E) Complete integration (Eqs. 6). (F) Negative serial integration (Eqs. 5). (G) Negative reverse serial integration. (H) Negative complete integration (Eqs. 7). For complete and negative complete integration, E and H, Insets show observable reaction norms in the Table 1 footnotes.

For a character with a single component mechanism of plasticity, component 1 evolves a reaction norm slope close to $B$, because of its low cost of plasticity; slow development prevents it from tracking the monthly cycle, an example of environmental frequency filtering by development rate. In contrast, rapid development of component 2 allows it to respond to both the annual and monthly cycles, but because of its high cost of plasticity, the response is rather limited. A character with either of the single components alone cannot closely track the optimum phenotype (Fig. 1A). Comparing the components alone shows that reaction norm slopes do not reliably indicate the fidelity of the mean phenotype in tracking the optimum. Component 1 alone has a high reaction norm slope but does not track the environment as closely as component 2 alone with a much lower reaction norm slope (Table 1).

For a character with two components of net plasticity that lack developmental integration, the component reaction norm slopes evolve lower than when they exist alone. The reaction norm slope of the mean phenotype evolves slightly smaller than that of component 1 alone. Nevertheless, the mean phenotype with two components tracks the optimum more closely than with either component alone (Table 1 and Fig. 1B).

Two components of net plasticity that are developmentally integrated, serially or completely, only modestly increase the reaction norm slope of the mean phenotype, but dramatically improve fidelity of the mean phenotype tracking the optimum (Table 1 and Fig. 1 B and C). This is achieved in rather different ways by the two patterns of developmental integration. In both cases, component 2 evolves a reaction norm slope near zero, practically eliminating the loss of fitness from its high cost of plasticity (Eq. 3b), but the two patterns differ greatly in the labile plasticity of their components. With serial integration, the autonomously developing component 1 evolves an almost identical reaction norm slope and displays virtually the same labile plasticity as when it exists alone, while component 2 makes up most of the distance to the optimum phenotype left by component 1. With complete integration, the response of component 1 is diminished, and component 2 is largely responsible for the net plasticity in the mean phenotype (Fig. 1 B and C). Component 2 contributes greatly to net plasticity in both cases because it develops (rapidly) in response to the deviation of net plasticity from the norm of reaction of the mean phenotype, rather than only its deviation from its own norm of reaction (Eqs. 5a and 6a). With complete integration, component 2 closely tracks the optimum phenotype, while component 1 develops little, because each component contributes to net plasticity in proportion to its development rate (Eq. 6e).

With serial integration, close tracking of the optimum phenotype by the mean phenotype is facilitated when the first, autonomously developing component in the series has slow development and a small cost of plasticity. For reverse serial integration, with the order of the two components reversed and the fast component 2 developing autonomously, environmental frequency filtering by the slow component 1 prevents it from responding accurately to the high-frequency environmental cycle not covered by component 2 (Fig. 1 A and B). Hence, with reverse serial integration, net plasticity in the mean phenotype is only slightly better at tracking the optimum than with no integration (Table 1 and Fig. 1 B and D).

Negative serial and negative reverse serial integration produce net plasticity slightly worse at tracking the optimum than no integration, but better than either component alone (Table 1 and Fig. 1 F and G). In negative serial integration, component 1 evolves a negative reaction norm slope to compensate for the negative integration with component 2; consequently, labile plasticity in slow component 1 is apparently maladaptive, counter to the main adaptive trend of net plasticity in the mean phenotype. This does not occur in negative reverse serial integration because slow component 1 cannot track the high-frequency environmental cycle. With negative complete integration, component 1 again evolves a negative reaction norm slope and displays apparently maladaptive labile plasticity (Fig. 1 F and H). For any parameters, with negative complete integration, labile plasticity in one component must be apparently maladaptive (Eq. 7a).

Complete and negative complete integration both have singular ${⧅}_{\lambda }D$ matrices with eigenvalues $\mathrm{\Lambda }$ and 0; hence, the reaction norm slopes may differ from Table 1 column headings and listed coefficients (Eq. 2g). Reaction norm slopes listed for each component could in principle be observed by experimentally disabling the other component. Reaction norm slopes that would be observed in experiments with intact organisms appear in the Table 1 footnotes and Fig. 1, Insets. With negative complete integration, the observable reaction norm of the mean phenotype shows hyperplasticity, with slope greater than $B$.

Discussion

Norms of reaction, describing the expected phenotype of a genotype or population as a function of a constant environment of individual development, constitute one of the main tools for investigation of phenotypic plasticity (1). However, the norm of reaction of the mean phenotype in a population takes the same form for any pattern of developmental integration with stable developmental dynamics (Eq. 2g). This occurs because norms of reaction describe only the static equilibrium of phenotypic plasticity across a range of constant environments. Thus, the reaction norms of components of a complex character do not reveal the pattern of developmental integration of the components or the dynamics of the net labile plasticity in the character.

For a character with multiple components of labile plasticity, in a changing environment the net labile plasticity depends on the development rates, the pattern of developmental integration, and the norms of reaction of the components (Eqs. 2c and 2d). Empirical studies of developmental integration among components of plasticity in a complex quantitative character therefore must focus on developmental dynamics of the components, as well as component norms of reaction, and their manifestation in the net labile plasticity of the character in a changing environment.

Environmental Frequency Filtering.

Previous results for a character with a single component of labile plasticity (15), applied here to a periodic environment, illuminate the property of filtering environmental frequencies above the development rate, by averaging over the time scale of development (Eq. 1c, Table 1, and Fig. 1A). Environmental frequency filtering can be reduced by an augmented development rate conferred by certain patterns of developmental integration of the components and the resulting evolution, discussed below.

A complex character, with multiple components of net plasticity that differ substantially in development rate and cost of plasticity, has a greatly expanded potential for evolutionary adaptation to a multiperiodic environment. Developmental integration of components of plasticity in a complex character can alleviate constraints on adaptation both directly through its impact on development and indirectly by facilitating evolution in component norms of reaction, as follows.

Environmental Signal Modulation.

Developmental integration in the present models entails that developmental feedback (or regulation) from component norms of reaction is shared among components (Eq. 2c). All components contribute to the mean phenotype tracking the optimum, driven by a key environment variable, and respond to the same or similar environmental signals. Positive integration ($D_{jk}>0$) tends to amplify the environmental signal controlling development of a component, while negative integration inhibits the signal. The asymmetric pattern of serial developmental integration (Fig. 1C) displays environmental signal amplification in its purest form, without changing the development rates (eigenvalues) of the process (Eq. 5b).

Augmented Development Rate of Net Plasticity.

Symmetric or mutual integration ($D_{jk}$ and $D_{kj}>0$) increases the development rate of net plasticity in the mean phenotype. With complete integration, the development rate of net plasticity is the sum of component development rates (Eq. 6b); no other form of integration achieves a higher development rate of net plasticity. An augmented development rate of net plasticity reduces environmental frequency filtering, allowing the mean phenotype to respond to higher-frequency environmental cycles.

Evolutionary Reduction of Costs of Plasticity.

Signal amplification by developmental integration, through sharing regulation among component norms of reaction, allows the reaction norm slope of a component with a high cost of plasticity to evolve to near zero, as it continues to develop in response to a changing environment, largely eliminating the loss of fitness from its cost of plasticity. This is demonstrated by serial integration and complete integration (Table 1 and Fig. 1 C and E).

With certain patterns of developmental integration, evolution of component reaction norms facilitates close tracking of the optimum phenotype by the mean phenotype of a complex character in a multiperiodic environment, while simultaneously reducing the loss of fitness from component costs of plasticity. Hence, natural selection on a character with multiple components of labile plasticity should cause joint evolution of component reaction norms and their pattern of developmental integration.

In the numerical examples, serial integration constitutes a key adaptation which could evolve directly from no integration (Fig. 1 B and C). Serial integration therefore may provide a plausible hypothesis for developmental integration of fast and slow components of mammalian thermal adaptation. In contrast, negative complete integration seems to be an isolated adaptive peak that cannot easily evolve from no integration (Fig. 1 B and F–H).

Apparent Maladaptation.

With negative complete integration of two components, for any parameters, at evolutionary equilibrium, one component reaction norm slope must be negative, and one component of labile plasticity must appear maladaptive (Eqs. 7a and 7c). Apparent maladaptation of the slow component (Fig. 1H) is an integral part of developmental regulation of the fast component, involving mutual inhibition of development, and compensatory evolution (36–38) of a negative reaction norm slope of the slow component. This convoluted pattern of development nevertheless allows net plasticity in the mean phenotype to closely track the optimum phenotype (Table 1). Thus, apparent maladaptation of a component of net plasticity in a complex character cannot be taken literally, without understanding the developmental integration of the components. This may explain some observations of apparent maladaptive evolution in a subset of genes with plastic expression (39, 40).