Ice sheet contributions to future sea-level rise from structured expert judgment

Significance

Future sea level rise (SLR) poses serious threats to the viability of coastal communities, but continues to be challenging to project using deterministic modeling approaches. Nonetheless, adaptation strategies urgently require quantification of future SLR uncertainties, particularly upper-end estimates. Structured expert judgement (SEJ) has proved a valuable approach for similar problems. Our findings, using SEJ, produce probability distributions with long upper tails that are influenced by interdependencies between processes and ice sheets. We find that a global total SLR exceeding 2 m by 2100 lies within the 90% uncertainty bounds for a high emission scenario. This is more than twice the upper value put forward by the Intergovernmental Panel on Climate Change in the Fifth Assessment Report.

Abstract

Despite considerable advances in process understanding, numerical modeling, and the observational record of ice sheet contributions to global mean sea-level rise (SLR) since the Fifth Assessment Report (AR5) of the Intergovernmental Panel on Climate Change, severe limitations remain in the predictive capability of ice sheet models. As a consequence, the potential contributions of ice sheets remain the largest source of uncertainty in projecting future SLR. Here, we report the findings of a structured expert judgement study, using unique techniques for modeling correlations between inter- and intra-ice sheet processes and their tail dependences. We find that since the AR5, expert uncertainty has grown, in particular because of uncertain ice dynamic effects. For a +2 °C temperature scenario consistent with the Paris Agreement, we obtain a median estimate of a 26 cm SLR contribution by 2100, with a 95th percentile value of 81 cm. For a +5 °C temperature scenario more consistent with unchecked emissions growth, the corresponding values are 51 and 178 cm, respectively. Inclusion of thermal expansion and glacier contributions results in a global total SLR estimate that exceeds 2 m at the 95th percentile. Our findings support the use of scenarios of 21st century global total SLR exceeding 2 m for planning purposes. Beyond 2100, uncertainty and projected SLR increase rapidly. The 95th percentile ice sheet contribution by 2200, for the +5 °C scenario, is 7.5 m as a result of instabilities coming into play in both West and East Antarctica. Introducing process correlations and tail dependences increases estimates by roughly 15%.

Global mean sea-level rise (SLR), which during the last quarter century has occurred at an accelerating rate (1), averaging about +3 mm⋅y⁻¹, threatens coastal communities and ecosystems worldwide. Adaptation measures accounting for the changing hazard, including building or raising permanent or movable structures such as surge barriers and sea walls, enhancing nature-based defenses such as wetlands, and selective retreat of populations and facilities from areas threatened by episodic flooding or permanent inundation, are being planned or implemented in several countries. Risk assessment for such adaptation efforts requires projections of future SLR, including careful characterization and evaluation of uncertainties (2) and regional projections that account for ocean dynamics, gravitational and rotational effects, and vertical land motion (3). During the nearly 40 y since the first modern, scientific assessments of SLR, understanding of the various causes of this rise has advanced substantially. Improvements during the past decade include closing the historic sea-level budget, attributing global mean SLR to human activities, confirming acceleration of SLR since the nineteenth century and during the satellite altimetry era, and developing analytical frameworks for estimating regional and local mean sea level and extreme water level changes. Nonetheless, long-term SLR projections remain acutely uncertain, in large part because of inadequate understanding of the potential future behaviors of the Greenland and Antarctic ice sheets and their responses to future global climate change. This limitation is especially troubling, given that the ice sheet influence on SLR has been increasing since the 1990s (4) and has overtaken mountain glaciers to become the largest barystatic (mass) contribution to SLR (5). In addition, for any given future climate scenario, the ice sheets constitute the component with the largest uncertainties by a substantial margin, especially beyond 2050 (6).

Advances since the Fifth Assessment Report (AR5) of the Intergovernmental Panel on Climate Change (7) include improved process understanding and representation in deterministic ice sheet models (8, 9), probabilistic projections calibrated against these models and the observational record (10), and new semiempirical models, based on the historical relationship between temperature and sea-level changes. Each of these approaches has limitations that stem from factors including poorly understood processes, poorly constrained boundary conditions, and a short (∼25 y) satellite observation record of ice sheets that does not capture the time scales of internal variability in the ice sheet climate system. As a consequence, it is unclear to what extent recent observed ice sheet changes (11) are a result of internal variability (ice sheet weather) or external forcing (ice sheet climate).

Where other methods are intractable for scientific or practical reasons, structured expert judgement (SEJ), using calibrated expert responses, provides a formal approach for estimating uncertain quantities according to current scientific understanding. It has been used in a wide range of applications, including natural and anthropogenic hazards such as earthquakes, volcanic eruptions, vector-borne disease spread, and nuclear waste security (12). That said, it should not be regarded as a substitute for fundamental research into driving processes, but instead as a source of complementary insights into the current state of knowledge and, in particular, the extent of the uncertainties (12). An SEJ study conducted in advance of the AR5 (13) (hereafter BA13) provided valuable insights into the uncertainties around ice sheet projections, as assessed at that time.

Since then, regional- and continental-scale, process-based modeling of ice sheets has advanced substantially (8, 9, 14–16), with the inclusion of new positive feedbacks that could potentially accelerate mass loss, and negative feedbacks that could potentially slow it. These include solid Earth and gravitational processes (17, 18), Antarctic marine ice cliff instability (19), and the influences of organic and inorganic impurities on the albedo of the Greenland Ice Sheet (20). The importance of these feedbacks is an area of continuing research. Therefore, alternative approaches must be exploited to assess future SLR and, critically, its associated uncertainties (21), to serve the more immediate needs of the science and policy communities.

Here, we report the findings of an SEJ exercise undertaken in 2018 via separate, 2-d workshops held in the United States and United Kingdom, involving 22 experts (hereafter SEJ2018). Details of how experts were selected are provided in SI Appendix, Note 1. The questions and format of the workshops were identical, so that the findings could be combined using an impartial weighting approach (Methods). SEJ (as opposed to other types of expert elicitation) weights each expert using objective estimates of their statistical accuracy and informativeness (22), determined using experts’ uncertainty evaluations over a set of seed questions from their field with ascertainable values (Methods). The approach is analogous to weighting climate models based on their skill in capturing a relevant property, such as the regional 20th century surface air temperature record (23). In SEJ, the synthetic expert (i.e., the performance weighted [PW] combination of all of the experts’ judgments) in general outperforms an equal weights (EW) combination in terms of statistical accuracy and informativeness, as illustrated in SI Appendix, Fig. S3. The approach is particularly effective at identifying those experts who are able to quantify their uncertainties with high statistical accuracy for specified problems rather than, for example, experts with restricted domains of knowledge or even high scientific reputation (12).

The participating experts quantified their uncertainties for three physical processes relevant to ice sheet mass balance: accumulation, discharge, and surface runoff. They did this for each of the Greenland, West Antarctic, and East Antarctic ice sheets (GrIS, WAIS, and EAIS, respectively), and for two schematic temperature change scenarios. The first temperature trajectory (denoted L) stabilized in 2100 at +2 °C above preindustrial global mean surface air temperature (defined as the average for 1850–1900), and the second (denoted H) stabilized at +5 °C (SI Appendix, Fig. S1). The experts generated values for four dates: 2050, 2100, 2200, and 2300. Experts also quantified the dependence between accumulation, runoff, and discharge within each of the three ice sheets, and between each ice sheet for discharge only, for the H scenario in 2100. We used temperature trajectories rather than emissions scenarios to isolate the experts’ judgements about the relationship between global mean surface air temperature change and ice sheet changes from judgements about climate sensitivity.

An important and unique element of SEJ2018 was the elicitation of intra- and inter-ice sheet dependencies (SI Appendix, Note 1.5). Two features of dependence were elicited: a central dependence and an upper tail dependence. The former captures the probability that one variable exceeds its median given that the other variable exceeds its median, whereas the latter captures the probability that one variable exceeds its 95th percentile given that the other exceeds its 95th percentile. It is well known that these two types of dependence are, in general, markedly different, a property that is not captured by the usual Gaussian dependence model. The latter always imposes tail independence, regardless of the degree of central dependence, and can produce large errors when applied inappropriately (24). For example, if GrIS discharge exceeds its 95th percentile, what is the probability that runoff will also exceed its 95th percentile? This probability may be substantially higher than the independent probability of 5%, and ignoring tail dependence may lead to underestimating the probability of high SLR contributions. On the basis of each expert’s responses, a joint distribution was constructed to capture the dependencies among runoff, accumulation, and discharge for GrIS, WAIS, and EAIS, with dependence structures chosen, per expert, to capture central and tail dependences (Methods and SI Appendix, Note 1.5). In BA13, heuristic dependency values were applied on the basis of simple assumptions about the response of processes to a common forcing.

To help interpret the findings, experts were also asked to provide qualitative and rank-order information on what they regard to be the leading processes that could influence ice dynamics and surface mass balance (snowfall minus ablation); henceforth, this is termed the descriptive rationale. Further details can be found in the SI Appendix. The combined sea-level contribution from all processes and ice sheets was determined assuming either independence or dependence. Here, we focus on the findings with dependence; we examine the effect of the elicited dependencies and the approach taken in SI Appendix, Note 1.5.

The ice sheet contributions were expressed as anomalies from the 2000–2010 mean states, which were predefined (SI Appendix, Table S7). The baseline sea-level contribution for this period was prescribed as 0.76 mm⋅y⁻¹ (0.56, 0.20, and 0.00 mm⋅y⁻¹ for GrIS, WAIS, and EAIS, respectively) and has been added to the elicited values discussed here. This is close to an observationally derived value of 0.79 mm⋅y⁻¹ for the same period, which was published subsequently to the SEJ workshops (4).

Results and Discussion

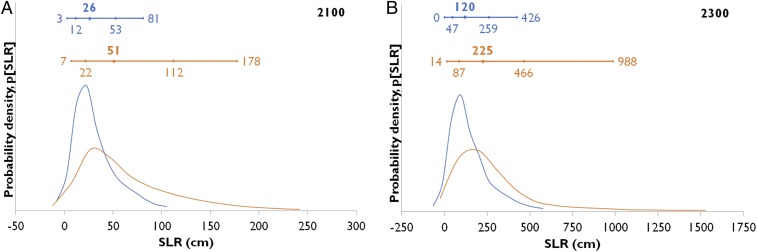
Fig. 1 shows the probability density functions (PDFs) for both temperature trajectory scenarios for the combined ice sheet contributions, assuming some dependencies exist between ice sheet processes, as elicited from the expert group (SI Appendix, Note 1.5). The associated numerical values are detailed in Table 1, and plots for all four epochs are provided in SI Appendix, Fig. S2. They display similar characteristics to Fig. 1. The PDFs were generated using Monte Carlo sampling from the intrinsic range obtained from the expert responses (22). All PDFs are non-Gaussian and exhibit an extended upper tail, especially for the H temperature scenario. We believe this reflects the experts’ joint view that large amplitude, nonlinear instabilities could be triggered at this higher temperature, even by 2050. For example, for 2050, the median [and likely range, defined as the 17–83% probability range, as in the AR5 (25)] of the ice sheet contributions are 10 cm (5–18 cm) for the L scenario and 12 cm (6–24 cm) for the H scenario. The tail behavior is discussed further in SI Appendix, Note 1.1. By 2100, the differences between the scenarios grow larger, with projected contributions of 26 cm (12–53 cm) and 51 cm (22–113 cm; Fig. 2 and Table 1).

Fig. 1.

PDFs for the L (blue) and H (red) temperature scenarios for the combined ice sheet SLR contributions at (A) 2100 and (B) 2300. All four time intervals are shown in SI Appendix, Fig. S2. The horizontal bars show the fifth, 17th, 50th (median), 83rd, and 95th percentile values. The baseline rate of 0.76 mm⋅a⁻¹ is included. Note that there is more than a factor five change in the x axis scales.

Table 1.

Projected sea-level rise contributions from each ice sheet and combined

Year and ice sheet	Low				High
	Mean ± SD	50%	5–95%	17–83%	Mean ± SD	50%	5–95%	17–83%
2050
PW01 SLR	11 ± 8	10	1–27	5–18	15 ± 12	12	1–38	6–24
GrIS	7 ± 5	5	2–18	3–11	9 ± 7	6	2–27	4–14
WAIS	7 ± 8	5	0–23	1–7	5 ± 6	4	0–18	1–10
EAIS	0 ± 2	0	−4–4	−2–1	0 ± 4	0	−6–7	−3–2
2100
PW01 SLR	32 ± 25	26	3–81	12–53	67 ± 56	51	7–178	22–112
GrIS	19 ± 16	13	2–57	7–31	33 ± 30	23	2–99	10–60
WAIS	13 ± 16	8	−3–44	2–23	27 ± 33	18	−5–93	3–46
EAIS	3 ± 6	0	−8–12	−3–4	6 ± 17	2	−11–46	−4–11
2200
PW01 SLR	89 ± 72	72	5–231	30–149	204 ± 260	130	5–750	40–251
GrIS	49 ± 47	34	5–149	19–79	77 ± 69	55	3–216	23–122
WAIS	37 ± 45	26	−24–128	1–76	80 ± 113	51	−25–324	−3–138
EAIS	4 ± 15	2	−15–34	−6–10	48 ± 158	6	−29–398	−10–19
2300
PW01 SLR	155 ± 137	120	0–426	47–259	310 ± 322	225	14–988	87–466
GrIS	78 ± 75	55	7–237	30–145	130 ± 117	98	7–349	39–225
WAIS	67 ± 88	44	−47–248	6–131	117 ± 136	83	−36–384	7–228
EAIS	10 ± 41	3	−29–96	−8–24	63 ± 195	10	−53–498	−14–51

Individual ice sheet and total sea-level contributions for both temperature scenarios and for the four periods considered: 2050, 2100, 2200, and 2300. All values assume the dependencies elicited for the 2100 H case. Because the PDFs are not Gaussian, the mean and median values differ; the latter is a better measure of central tendency. All values are cumulative from 2000 and include the baseline imbalance for 2000–2010 of 0.76 mm y⁻¹. The AR5-defined likely range (17–83%) is provided alongside the 90% credible interval. PW01 denotes the performance weighted combination of experts based on their calibration score.

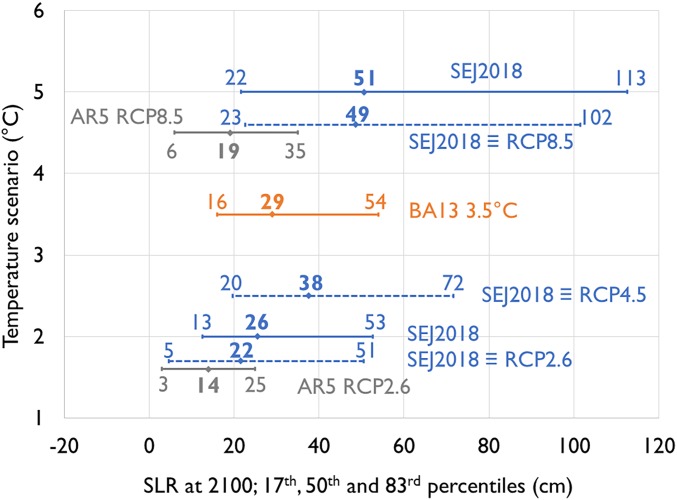
Fig. 2.

Median and likely range (17th–83rd percentile as used in the AR5) estimates of the ice sheet SLR contributions for different temperature scenarios and different studies. AR5 RCP ice sheet contributions are shown for RCP 2.6 and RCP 8.5 by combining contributions from the different sources (gray bars). BA13 is shown for the elicited temperature increase of 3.5 °C by 2100 (orange bar). This study (SEJ2018, in blue) is shown for the L and H temperature scenarios using solid lines. Dashed lines are interpolated from the L and H findings, using stochastic resampling of the distributions assuming a linear relationship between pairs of L and H samples.

The relative contribution of each ice sheet to total SLR (used here to refer to the sum of the three ice sheet contributions) depends on the temperature scenario. To demonstrate this, we compare the mean projections for the three ice sheets for the overall 2100 H distribution, for the same distribution conditional on the total contribution being above the median total projection (>51 cm), and the same distribution conditional on the total being above the 90th percentile (>141 cm). In the unconditional distribution, GrIS dominates the mean projection, contributing 33 cm (49%) of the 67-cm total, compared with 27 cm for WAIS and 6 cm for EAIS: proportions that approximately mirror the present-day contributions (4). The GrIS share declines for larger total contributions. For the mean of the upper half of total SLR projections, GrIS contributes 49 cm (46%) of 106 cm total compared with 44 cm for WAIS and 13 cm for EAIS; for the mean of the top decile, GrIS contributes 60 cm (30%) of the 194-cm total compared with 95 cm for WAIS and 39 cm for EAIS.

Statistically, the declining GrIS share and declining GrIS/AIS ratio reflect a higher mean estimate but slightly less skewed distribution for GrIS than for WAIS, and a long tail for EAIS (Fig. 3), as well as the assessed dependence structure between different terms. Physically, this is likely a result of the role of highly nonlinear dynamic processes coming into play for marine sectors of the AIS that are needed to achieve the higher values of total SLR, whereas at lower total SLR values, more linear processes dominate. It is also noteworthy that the fifth percentiles for both temperature scenarios and for all epochs are less than their current values, suggesting a scenario in which increased snowfall, primarily over the AIS (Table 1), plausibly compensates for any changes in ice dynamics and enhanced melting over the GrIS.

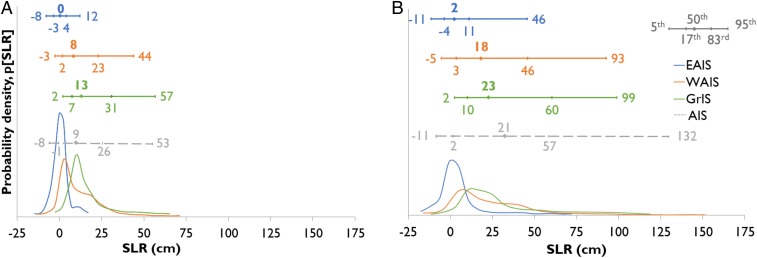
Fig. 3.

Individual ice sheet contributions to SLR for 2100 L (A) and H (B) temperature scenarios, assuming dependences between the ice sheets in terms of the processes of accumulation, runoff, and discharge. PDFs were generated from 50,000 realizations of the relevant SEJ distributions. Horizontal bars indicate the fifth, 50th, and 95th percentile values (i.e., the 90% credible range). Also shown are the likely range (17th–83rd percentile) as defined in the AR5 and the total AIS contribution (WAIS plus EAIS assuming the inter ice sheet dependencies elicited). Note that this is not simply the sum of WAIS and EAIS contributions because of inter-ice sheet dependencies. The AIS values are compared with a recent emulator approach (30) in SI Appendix, Fig. S11.

Direct comparison with the AR5 is complicated by the use of different external forcings. Our L scenario is slightly warmer than the median projection for Representative Concentration Pathway (RCP) 2.6, and cooler than the median projection for RCP 4.5 at 2100 (2081–2100 global mean warming of +1.9 °C compared with medians of +1.6 °C and +2.4 °C, for RCP 2.6 and RCP 4.5, respectively), whereas our H scenario is roughly comparable to the median projection for RCP8.5 (2081–2100 global mean warming of +4.5 °C compared with a median of +4.3 °C for RCP 8.5), although with different trajectories (SI Appendix, Fig. S1). Our two temperature scenarios were chosen to assess the potential consequences, in terms of SLR, of the goal of the COP21 Paris agreement to keep global temperatures below +2 °C above preindustrial and of a scenario closer to business as usual, as opposed to matching a specific RCP. For comparison, the AR5 likely range ice sheet SLR contribution for RCP8.5 at 2100 is 6–35 cm, with a median of 19 cm (7) (Fig. 2). As mentioned, comparing our findings with those from the AR5 requires transforming temperatures and percentiles to match those used in the AR5. Nonetheless, given these caveats, it is clear the SEJ median and upper value of the likely range (83rd percentile) are statistically significantly larger than the corresponding AR5 values (Fig. 2). Our likely range upper bound is almost three times the AR5 value for RCP 8.5 (94 vs. 35 cm, estimated by summing the individual components considered in the AR5 and, hence, assuming perfect dependence). This is driven, primarily, by larger uncertainty ranges for the WAIS and GrIS contributions (Fig. 3), possibly resulting from experts’ consideration of the aforementioned nonlinear processes. We note also that the uncertainties have grown substantially in comparison with BA13, where the elicited temperature increase above preindustrial was +3.5 °C (indicated by the orange line in Fig. 2). In comparison, our current findings result in a larger uncertainty range at a lower temperature increase (Fig. 2). There has been recent consideration of the benefits of limiting warming to +1.5 °C (26) and what difference this would make compared with the Paris Agreement +2 °C. The reduction in the sea-level contribution from the ice sheets at this lower temperature for our study is broadly in line with the findings of the Intergovernmental Panel on Climate Change Special Report on 1.5 °C, which obtained a value of 10 cm reduction in global mean sea level from all sources (26).

Another important point is the positive skews of the distributions, which result in long upper tails that are less apparent in the AR5 values (limited to the likely range). For example, the median values obtained here and in the AR5 for RCP2.6 differ by 8 cm (Fig. 2), but the 83rd percentile from the SEJ is about 100% larger (51 vs. 25 cm). This becomes even more important if considering probabilities beyond the likely range defined in the AR5, such as the very likely range (the 90th percentile confidence interval). This is apparent from the values in Table 1. Kurtosis provides a quantitative measure of tail behavior and is discussed in SI Appendix, Note 1.1.

Fig. 3 illustrates the PDFs for 2100 L and H temperature trajectories for each ice sheet. The 90% credible intervals for the GrIS and WAIS (approximately equivalent to the very likely range in Intergovernmental Panel on Climate Change terminology) are broadly similar to one another in both scenarios (c.f. the 90% credible interval bars in Fig. 3 A and B). For the 2100 L and H scenarios, the EAIS uncertainty ranges are about a factor of three and two smaller, respectively. Median values for the GrIS and WAIS are broadly comparable (13/8 cm for L and 23/18 cm for H), whereas the EAIS median values are 0 and 2 cm for L and H, respectively. Both the WAIS and GrIS show a strong skew with a long positive tail, which is absent for the EAIS for 2100 L but begins to emerge for 2100 H. There is, consequently, a substantial difference between the high-end, 95th percentile values considered here versus the 83rd percentile value presented in the AR5, which is far more pronounced than differences between the fifth and 17th percentiles (Fig. 3). For WAIS under 2100 H, the difference between the 83rd and 95th percentile is a factor two (Fig. 3 and Table 1), and a factor four for the EAIS. This is also seen when considering the total SLR from the ice sheets. For 2200 H, the 83rd and 95th percentiles are 251 and 750 cm, respectively (Table 1). By limiting consideration only to the likely range, the AR5 results miss this tail behavior, which is a critical component of risk management.

The present SEJ demonstrates a shift in expert opinion since BA13 (i.e., in 2012), when it was found that the GrIS had the narrowest 90% credible range but the largest median SLR rate (13). Here, the GrIS still has the largest median value (for both L and H), but the upper tail of the distribution is now comparable to that of the WAIS (Fig. 3A). It is difficult to determine the basis for this, but we note that the experts overwhelmingly believe that the recent (last 2 decades) acceleration in mass loss from the GrIS is predominantly a result of external forcing, rather than internal variability. Of the 22 experts, 18 judge the acceleration is largely or entirely a result of external forcing (SI Appendix, Fig. S9A and Table S6). This is an important and statistically significant shift from the findings in BA13. In contrast, for the WAIS, opinion remains divided, with seven experts indicating their view that it is largely a result of internal variability, seven placing more weight on external forcing, and eight giving equal weights to each. This reflects the earlier conclusions of BA13.

The findings of SEJ2018 cannot be directly compared with BA13 because the target questions differ, as do the temperature scenarios. The closest comparison that can be made between SEJ2018 and BA13 is for the latter’s cumulative 5/50/95% SLR values of 10/29/84 cm for 2010–2100, which comprised two-thirds from GrIS, one-third from WAIS, and a negligible amount from EAIS, for a temperature increase based on experts’ judgement of +3.5 °C (13). For SEJ2018, we obtain −5/18/73 cm for +2 °C rise and −1/43/170 cm for +5 °C rise (integrated over 2000–2100). Fig. 2 compares the likely range in BA13 and the various temperature markers used here and in the AR5. It is evident that opinion has shifted toward a stronger ice sheet response and a larger credible range, for a given temperature change, than was considered plausible by the experts 6 y ago.

The rather high median and 95% values for 2100 SLR (Fig. 2 and Table 1), found here, likely reflect recent studies that have explored, in particular, AIS sensitivity to CO₂ forcing during previous warm periods (27, 28) and new positive feedback processes such as the Marine Ice Cliff Instability (19), alongside the increasing evidence for a secular trend in Arctic climate (29) and subsequent increasing GrIS mass loss (4). A recent study (30) has used an emulator approach to reexamine the potential role of the Marine Ice Cliff Instability in explaining past sea level and how this affects projections, and we can compare our AIS results with the projections reported in ref. 30. Our results lie between the emulation with Marine Ice Cliff Instability and without, lying closer to the latter for the median values (SI Appendix, Fig. S11). Uncertainties for the H temperature scenario grow rapidly beyond 2100, with 90th percentile credible ranges of −10 to 740 cm and −9 to 970 cm for 2200 and 2300, respectively. Limiting projections to the likely range largely obscures the real, and potentially critical, extent of the deep uncertainties evident in this study.

Global Total SLR Projections.

To place these results in the context of total SLR projections, including contributions from ocean thermal expansion, glaciers, and land-water storage, we use a probabilistic SLR projection framework (3). Specifically, we substitute Monte Carlo samples from the PW01 joint probability distribution in SEJ2018 for the ice sheet values used in Kopp et al. (3), while keeping the remaining projections for other components of SLR. For thermal expansion and glaciers, these projections are driven by CMIP5 model projections, using an approach similar to that of AR5. For land-water storage, the projections are based on semiempirical relationships among population, dam construction, and groundwater withdrawal (3). We combine the L scenario ice sheet projections with the other components from the +2.0 °C scenario developed by Rasmussen et al. (31), and for the H scenario with those for RCP 8.5 from Kopp et al. (3).

Compared with other SLR projections for 2050 developed over the last 6 y (32), the 2050 L projections are broadly comparable (very likely range of 16–49 cm), whereas the 2050 H projections are somewhat fatter tailed, with the very likely range extending up to 61 cm (Table 2). This compares with the 20 studies compiled by Horton et al. (32), which spanned from 12 cm at the low end of fifth percentile projections to 48 cm at the high end of 95th percentile projections. There are relatively few +2 °C studies to compare with our 2100 L projections, but those that are compiled in Horton et al. (32) range from 0.2 m at the low end of fifth percentile projections to 1.1 m at the high end of the 95th percentile projections. The SEJ2018 distributions fall on the high side of this range, with a median projection of 0.7 m and a 90th percentile range of 0.4–1.3 m.

Table 2.

Total global-mean sea-level rise projections

Centimeters above 2000 CE	50%	17–83%	5–95%	1–99%
2050 L	30	22–40	16–49	10–61
2050 H	34	26–47	21–61	16–77
2100 L	69	49–98	36–126	21–163
2100 H	111	79–174	62–238	43–329

Produced by combining PW01 ice sheet projections with thermal expansion, glacier, and land water storage distributions from Kopp et al (3).

The 2100 H projections fall within the existing range of RCP 8.5 projections, which have extended upward in recent years, substantially beyond the AR5 range. The 2100 H median projection of 1.1 m falls midway between the AR5 projection of 0.7 m and the 1.5 m that Kopp et al. (6) projected using the Antarctic ice sheet projections of DeConto and Pollard (19), which provided an initial attempt at explicit, continental-scale physical modeling of ice shelf hydrofracturing and marine ice cliff instability. The very likely range of 0.6–2.4 m falls within the 0.4–2.4-m low-fifth percentile to high-95th percentile range in the compilation of Horton et al. (32). This comparison emphasizes the skewness of the expert distribution: although the median projection falls in the middle of recently published projections, the 95th percentile tracks the high end of published projections. Although none of these studies is entirely independent of the others, taken together, they provide strong support for recent coastal planning scenarios that anticipate SLR well above the AR5 range (33–35).

Conclusions.

This study suggests that experts’ judgments of uncertainties in projections of the ice sheet contribution to SLR have grown during the last 6 y and since publication of the AR5. This is likely a consequence of a focused effort by the glaciological community to refine process understanding and improve process representation in numerical ice sheet models. It may also be related to the observational record, which indicates continued increase in mass loss from both the AIS and GrIS during this time. This negative learning (36, 37) may appear a counter intuitive conclusion, but is not an uncommon outcome: as understanding of the complexity of a problem improves, so can uncertainty bounds grow. We note that for risk management applications, consideration of the upper tail behavior of our SLR estimates is crucial for robust decision making. Limiting attention to the likely range, as was the case in the Intergovernmental Panel on Climate Change AR5, may be misleading and will likely lead to a poor evaluation of the true risks. We find it plausible that SLR could exceed 2 m by 2100 for our high-temperature scenario, roughly equivalent to business as usual. This could result in land loss of 1.79 M km², including critical regions of food production, and displacement of up to 187 million people (38). A SLR of this magnitude would clearly have profound consequences for humanity.

Materials and Methods

Experts were convened in two separate 2-d workshops, one in Washington, DC, drawing on experts working in North America, followed by one near London, drawing on European experts. The experts were notified in advance of the objectives of the exercise and received examples of questions to be asked, along with a description of the method to be applied for analyzing their responses (SI Appendix, Note 4). To minimize misunderstandings and ambiguities and to clarify issues and aspects of the problem, group discussion of the target questions was allowed before experts individually (and privately) completed each of the three categories of questions. These comprised seed questions used for calibration of the experts, target questions for eliciting judgments on topics for which our goal was to quantify uncertainties, and a set of descriptive rationale questions, through which experts could articulate or summarize their reasoning about the target items (SI Appendix, Note 3). The period for answering questions was unlimited, but in practice was about 6–8 h overall. At the conclusion of the first day, responses were collated and preliminary probability distributions were developed from EW and from performance weights combination solutions, using the Classical Model Decision Maker approach (22). These preliminary outcomes were presented to the experts on the second day, and they were given an opportunity to discuss and, if they wished, to revise their initial judgments. Although a broad discussion revealed what motivated many of the responses and provided a basis for our interpretation here of the key contributory factors, few experts changed any of their responses after this provisional presentation.

After the elicitation, the target item uncertainty distributions were recalculated with the Classical Model to conform to the goal of achieving optimal statistical accuracy with minimal credible bounds (e.g., high informativeness). This is accomplished by forming a weighted combination of those experts for which the hypothesis that their probabilistic assessments were statistically accurate would be not rejected at the 0.01 level (denoted PW01). The threshold 0.01 was chosen to achieve robust representation of experts from both workshops while enforcing standard scientific constraints on statistical hypotheses. On this basis, the judgments of six US and two European experts were preferred, and the outcomes of pooling their judgments are shown in SI Appendix, Table S1, for each of the temperature scenarios. Instead of choosing a statistical rejection threshold based on standard hypothesis testing, the Classical Model also allows choosing an optimal threshold that maximizes the statistical accuracy and informativeness of the resulting combination. The effect of this optimization is a moderate reduction in the 90th percentile credible range relative to the PW01 combination.

The Classical Model Decision Maker combined score is an asymptotic strictly proper scoring rule if experts get zero weight when their P value drops below some threshold (22). This means that, with such a cutoff, an expert receives their maximal expected weight in the long run by, and only by, stating percentiles that reflect their true beliefs. The weight of an expert is determined by his/her statistical accuracy and informativeness. For comparison, an equally weighted combination of the eight preferred experts (denoted EW01) is formed. EW01’s credible intervals are wider than those of PW01 (SI Appendix, Note 1.1). We use PW01 here to provide robust representation from both panels, as explained here. All combinations concern the experts’ joint distributions, based on the elicited dependence information. Expert scoring is shown in SI Appendix, Table S3, where further details can be found. Rutgers, Princeton University, and Resources for the Future (RFF) considered this study to be exempt from requiring informed consent.

Code Availability.

The Classical Model code is freely available at www.lighttwist.net/wp/. Code to localize the SLR projections from this study is available at github.com/bobkopp/LocalizeSL.

Data Availability.

The anonymized responses of the experts to the SEJ questionnaire, alongside workshop materials and presentations are available at https://data.bris.ac.uk/data/dataset/23k1jbtan6sjv2huakf63cqgav.