Partition Coefficients for the SAMPL5 Challenge using Transfer Free Energies

Abstract

SAMPL challenges[1–4] provide excellent opportunities to assess theoretical approaches on new data sets with a goal of gaining greater insight towards protein and ligand modeling. In the SAMPL5 experiment, cyclohexane-water partition coefficients were determined using a vertical solvation scheme in conjunction with the SMD continuum solvent model. Several DFT functionals partnered with correlation consistent basis sets were evaluated for the prediction of the partition coefficients. The approach chosen for the competition, a B3PW91 vertical solvation scheme, yields a mean absolute deviation of 1.9 logP units and performs well at estimating the correct hydrophilicity and hydrophobicity for the full SAMPL5 molecule set.

Introduction

Theoretical approaches can be a useful partner for predicting physiochemical properties important in experimental design, from drug development, to studies in toxicology and environmental science. Such predictive approaches can provide guidance in high-throughput screening for rational design [5, 6]. An important step in establishing such utility, however, is to ensure that the approaches are suitable and well-tested.

A popular route towards rationale design is the use of mathematical models to determine quantitative structure-activity relationships (QSAR) or quantitative structure-property relationships (QSPR), based on parameters or descriptors that correlate physical and chemical properties with experimental observations. Though useful, it is difficult for these predictive models to determine properties coupled with changes in the electronic environment such as those that arise from solute-solute and solute-solvent interactions.

Measurements of solvation properties of molecules in different solution phases and the distribution equilibria between the phases are of strong interest in drug discovery as these properties are critical for drug profiling. Promising drug candidates can be discarded as a result of inaccurate predictions of such properties; particularly of interest are the partition (P) and distribution (D) coefficients. The partition coefficient (P) between two phases x and y, respectively, is the ratio of the concentration of solute C in each phase, where the subscript 0 represents the neutral, unionized state of the solute.

$$\text{P}=\frac{{\left[{\text{C}}_0\right]}_y}{{\left[{\text{C}}_0\right]}_x}\hspace{1em}\hspace{1em}\text{D}=\frac{{\Sigma }_i{\left[{\text{C}}_i\right]}_y}{{\Sigma }_i{\left[{\text{C}}_i\right]}_x}$$

In contrast, the distribution coefficient (D) is the actual partitioning or distribution of the total analytical concentration between two solvents at a fixed pH, which includes all chemical states in solution (i.e., unionized and ionized states). Although many QSAR and QSPR techniques exist, because these approaches are based on defining statistical relationships via parameters trained to fit known experimental properties, this may not be the most suitable approach for predicting properties for molecules that undergo chemical transformations in different environments, such as compounds with multiple protonation states or compounds that can undergo structural rearrangements [7–9]. Additionally, many QSAR and QSPR models are paramertized to predict octanol/water partition coefficients as there is an abundance of reliable experimental data for available to parameterize this predictive approach. For this, it is ideal to have a simple approach that relies on less parameterization and is transferable for use with other solvents.

The partition coefficient between two immiscible solvents, such as water and cyclohexane, is expressed as the equilibrium distribution between the concentrations of a solute in each solvent and is related to the change in energy associated with the solute-solvent interactions, which is expressed as the free energy difference, ΔG, of the solute in each solvent,

$$\log P=\log \left(\frac{{\left[\text{solute}\right]}_{\text{cyclohexane}}}{{\left[\text{solute}\right]}_{\text{water}}}\right)=\left(\mathrm{\Delta }{G}_{\text{water}}-\mathrm{\Delta }{G}_{\text{cyclohexane}}\right)\frac{{\log }_{10}e}{kT}$$

where e is Euler’s number, k is Boltzmann’s constant, and T is temperature. Predicting the free energy of solvation for a molecule using chemometric techniques can be challenging due to the difficulties in parameterizing the solute-solvent interactions, with the many intermolecular forces that contribute to solvation.

Another route that can be used to predict the partition coefficient is to use quantum mechanical (QM) approaches, accounting for solvation via either an explicit or implicit route. For explicit solvation, individual solvent molecules are included in a calculation. While these approaches can account for non-covalent solute-solvent interactions, they can become computationally intensive due to the number of solvent molecules that may be needed within the solvation shell as well as the amount of sampling that would be required. For implicit solvation, a representation of the solvent is utilized which neglects explicit contributions of the solute-solvent interactions, resulting in a lower computational cost approach. Implicit solvation approaches, continuum solvent models, are commonly used and include the Conductor-like Polarizable Continuum Model (CPCM)[10], the COnductor-like Screening MOdel (COSMO)[11], and the Solvation Model based on Density (SMD)[12], for predicting the free energies of hydration. Of these solvation models, SMD is a more portable model for the prediction of solvation free energies, as it uses the electron density of the solute in contrast to partial charges as used in CPCM and COSMO. In previous studies predicting the free energies of solvation of small molecules, it has been shown that the increasing quality of a basis set can improve the prediction, including ab initio approaches[13] as well as in hybrid QM and molecular mechanics (MM) approaches such as the QM/MM-non-Boltzmann-Bennett method [14, 15].

For this investigation, emphasis is on the 13 molecule subset (Batch 0) of the SAMPL5 distribution coefficient molecule set. Using this subset, a variety of hybrid DFT functionals with different basis sets were used to predict the cyclohexane-water partition coefficient. A vertical solvation approach, using gas-phase optimized geometries to predict the free energy in solution, was used for predicting the cyclohexane-water transfer free energy needed for the calculation of the partition coefficient. The approach that was chosen was applied to the full molecule set of 53 compounds, which corresponds to Submission #40 in the SAMPL5 Distribution Coefficient Challenge.

Methods

The initial structures issued with the SAMPL5 challenge data set were used as the reference state for all calculations. Gas phase geometry optimizations and frequency calculations were performed on the 53 molecules of the SAMPL5 set (shown in Figure 1) using B3LYP[16–18] in conjunction with cc-pVTZ basis sets [19–22]. B3LYP/cc-pVTZ was selected due to its well-established success in the prediction of ground state gas-phase structures for molecules such as those in the SAMPL5 set. Frequencies were examined to ensure that equilibrium stationary points were reached. For second-row species such as sulfur, the recommended form of the correlation consistent basis sets, the augmented tight-d basis sets, cc-pV(T+d)Z, [23] was used to avoid the deficiencies noted in the original form of the correlation consistent basis sets for second-row atoms. The correlation consistent basis sets were selected due to their demonstrated behavior with a broad range of functionals[24–33], known to converge with respect to increasing basis set size (i.e., cc-pVnZ, where n=D, T, Q) to the Complete Basis Set (CBS), or Kohn-Sham limit, for numerous properties such as thermochemical properties. Though DFT structures are generally known to reach convergence using a triple-zeta basis set, for molecules that include sulfur or transition metal species or molecules of increasing size, energetic properties determined using DFT may not reach convergence unless a basis set of at least quadruple-zeta quality basis sets are used. Thus, basis sets through quadruple-zeta quality were considered in this work.

Figure 1.

Structure of the 53 compounds investigated in the SAMPL5 challenge. The 13 molecules represent (left) correspond to the Batch 0 subset.

Many prior studies seeking to predict the solvation free energies of small organic molecules often chose hybrid DFT methods, however, an optimal functional or optimal functional class has not yet been agreed upon [12, 34–44]. In order to identify which functional would serve best for the blind prediction, single point calculations were carried out on the optimized geometries using several different hybrid DFT functionals, (B97-1[45], B98[46], B3PW91[16, 47], M05[48], M05-2X[49], M06[50], M06-2X, M06-HF[51], ωB97[52], and ωB97X-D[53]) in combination with the cc-pVnZ basis sets (where n=D, T, and Q) for the subset of 13 molecules (noted Batch 0 in Figure 1). These functionals can be classified as three different types of hybrid functionals: global hybrid generalized gradient approximation (GH-GGA) includes B97-1, B98, and B3PW91; global hybrid meta-GGA (GH-mGGA) includes M05, M05-2X, M06, M06-2X, and M06-HF; and range separated hybrid (RSH)-GGA includes ωB97 and ωB97X-D. These functionals were chosen due to their popularity and utility for organic species, as well as to provide a variety of classes of hybrid functionals. All calculations were performed using the “Ultrafine” integration grid as it is known that HM-GGA functionals are sensitive to the integration grid size [54] and finer grids can improve numerical accuracy. These single point calculations were carried out in implicit solvent using the SMD solvation model for both water and cyclohexane. The partition coefficients were estimated from the difference in the transfer free energy in water and in cyclohexane. All calculations were performed with the Gaussian09 package [55].

Results and Discussion

For the Batch 0 subset of molecules, several hybrid DFT functionals were tested with double, triple, and quadruple-ζ level basis sets. In these calculations, only a single conformation, protonation state, and tautomer were considered thus there is not a statistical uncertainty associated with the calculations. Rather, there is model uncertainty that arises from the assumption of a single geometry, the DFT method, the basis set, and the solvent model. From the results shown in Table 1, overall, each approach predicts the partition coefficient within a mean absolute deviation (MAD) in the range of 1.5 to 2.0 logP units in reference to experiment, which corresponds to a 2.0 to 2.7 kcal mol⁻¹ variation in the transfer free energy. While QSPR methods are able to predict within 0.3 to 1.0 log units from experiment, the physical significance of the predictions are questionable as these models have adroit tactics at modeling noise [56].

Table 1.

Comparison of Predicted LogP with Experimental LogD.

SAMPL5 ID	logD Exp.		B97-1				B98				B3PW91				M05				M05-2X				M06				M06-2X				M06-HF				ωB97				ωB97X-D
			DZa	TZ	QZ		DZ	TZ	QZ		DZ	TZ	QZ		DZ	TZ	QZ		DZ	TZ	QZ		DZ	TZ	QZ		DZ	TZ	QZ		DZ	TZ	QZ		DZ	TZ	QZ		DZ	TZ	QZ
003	1.9 ± 0.1		3.1	2.7	2.6		3.0	2.6	2.5		3.0	2.7	2.6		3.0	2.7	2.6		2.8	1.9	2.0		3.0	2.7	2.7		2.8	2.3	2.3		1.8	1.4	1.3		2.9	2.5	2.4		2.8	2.5	2.4
015	−2.2 ± 0.3		−3.1	−3.6	−3.6		−3.1	−3.6	−3.7		−3.2	−3.6	−3.7		−3.1	−3.5	−3.7		−3.5	−4.6	−4.4		−3.1	−3.4	−3.4		−3.5	−4.0	−3.9		−4.6	−5.3	−5.1		−3.3	−3.9	−4.0		−3.5	−3.9	−3.9
017	2.5 ± 0.3		1.3	1.0	1.0		1.2	1.0	1.0		1.0	0.9	0.9		1.3	1.2	1.1		0.6	−0.1	0.0		1.3	1.2	1.2		0.6	0.3	0.5		−1.0	−1.4	−1.3		0.9	0.6	0.6		0.9	0.7	0.6
020	1.6 ± 0.3		0.9	0.3	0.1		0.9	0.2	0.1		0.8	0.2	0.1		0.9	0.4	0.2		0.5	−0.8	−0.8		0.9	0.4	0.3		0.5	−0.2	−0.2		−0.6	−1.5	−1.6		0.7	−0.1	−0.2		0.6	−0.1	−0.2
037	−1.5 ± 0.1		−3.9	−4.2	−4.3		−4.0	−4.3	−4.4		−4.0	−4.3	−4.3		−3.7	−4.0	−4.1		−4.4	−5.1	−5.0		−4.0	−4.2	−4.2		−4.4	−4.8	−4.7		−5.4	−6.2	−6.0		−4.1	−4.5	−4.5		−4.2	−4.5	−4.5
045	−2.1 ± 0.2		−1.1	−1.5	−1.6		−1.1	−1.6	−1.7		−1.2	−1.6	−1.7		−1.0	−1.4	−1.5		−1.4	−2.4	−2.4		−1.0	−1.4	−1.4		−1.4	−1.9	−1.9		−2.4	−3.1	−3.0		−1.3	−1.8	−1.9		−1.4	−1.8	−1.9
055	−1.5 ± 0.1		−2.6	−3.1	−3.2		−2.7	−3.2	−3.3		−2.7	−3.2	−3.2		−2.6	−3.0	−3.1		−2.9	−−3.8	−3.8		−2.7	−3.1	−3.1		−2.9	−3.4	−3.4		−3.6	−4.2	−4.1		−2.7	−3.2	−3.3		−2.8	−3.3	−3.4
058	0.8 ± 0.1		2.7	2.3	2.2		2.7	2.2	2.2		2.6	2.2	2.2		2.8	2.4	2.3		2.3	1.3	1.3		2.8	2.4	2.4		2.3	1.8	1.8		1.0	0.5	0.4		2.5	2.0	2.0		2.4	2.0	2.0
059	−1.3 ± 0.3		−0.4	−0.5	−0.5		−0.4	−0.5	−0.5		−0.5	−0.6	−0.6		−0.3	−0.4	−0.4		−0.6	−1.0	−1.0		−0.3	−0.4	−0.4		−0.6	−0.8	−0.7		−1.4	−1.5	−1.5		−0.5	−0.7	−0.7		−0.6	−0.7	−0.7
061	−1.5 ± 0.1		−0.8	−1.2	−1.3		−0.8	−1.3	−1.4		−0.9	−1.3	−1.4		−0.7	−1.2	−1.3		−1.0	−1.9	−1.9		−0.8	−1.3	−1.4		−1.0	−1.6	−1.7		−1.7	−2.4	−2.5		−1.0	−1.6	−1.7		−1.0	−1.5	−1.6
068	1.4 ± 0.3		1.5	0.9	0.8		1.5	0.8	0.7		1.4	0.8	0.7		1.6	1.0	0.9		1.2	0.0	0.0		1.7	1.1	1.1		1.2	0.5	0.5		−0.3	−0.8	−1.0		1.3	0.5	0.4		1.2	0.6	0.5
070	1.6 ± 0.3		5.5	5.1	5.0		5.5	5.1	5.0		5.3	4.9	4.9		5.5	5.3	5.0		5.0	4.1	4.0		5.6	5.4	5.3		5.0	4.6	4.6		3.3	2.8	2.6		5.2	4.8	4.7		5.2	4.8	4.7
080	−2.2 ± 0.2		1.1	0.5	0.4		1.0	0.4	0.3		1.1	0.5	0.4		1.2	0.7	0.6		0.8	−0.3	−0.3		1.1	0.5	0.5		0.8	0.1	0.1		0.1	−0.8	−0.7		1.0	0.3	0.2		0.8	0.2	0.2
MSDb			0.5	0.1	0.0		0.5	0.0	−0.1		0.4	0.0	−0.1		0.6	0.2	0.1		0.1	−0.8	−0.8		0.5	0.2	0.2		0.1	−0.4	−0.3		−0.9	−1.5	−1.6		0.3	−0.2	−0.3		0.2	−0.2	−0.3
MADc			1.5	1.5	1.5		1.5	1.5	1.5		1.5	1.5	1.5		1.5	1.5	1.5		1.5	1.6	1.6		1.5	1.5	1.5		1.5	1.5	1.5		1.6	1.9	1.9		1.5	1.5	1.5		1.5	1.5	1.5

^aThe columns labeled DZ, TZ, and QZ correspond to the cc-pVDZ, cc-pVTZ, and cc-pVQZ basis sets.

^bThe mean signed deviation of the predicted logP from the experimental logD.

^cThe mean absolute deviation of the predicted logP from the experimental logD.

For the Batch 0 subset of molecules and the functionals considered, there is not a systematic underestimation or overestimation in the prediction of the logP. The predicted logP for the GH-GGA and RSH-GGA functionals are similar, with a MAD of 1.5 logP units. Each of the tested approaches are able to predict the correct sign of logP in water and cyclohexane (hydrophobicity/hydrophilicity) for each molecule, with the exception of molecules 017, 020, 058, 068, and 080. Predicting the correct sign of logP is important as this reflects the preference of the molecule to reside in either the organic or aqueous phase.

The lowest MAD observed in this study is 1.5 logP units, which is given by eight out of the ten functionals tested. As shown in Table 1, most of the functionals result in a low mean signed deviation (MSD) compared with the magnitude of the MAD. This indicates that there is not a consistent deviation from the experimental values. Rather, the small magnitude of the MSD is the result of deviations above and below experiment such that they largely cancel for the Batch 0 subset of molecules. The largest MSDs observed are for the M06-HF functional with the magnitude of the MSDs within 50% or more of the MADs. Thus, the M06-HF functional has a larger systematic error resulting in underestimation of the logP value, i.e. negative MSDs in comparison to the other functionals. The calculated values for logP are plotted with respect to the molecule number in Figure 2 while the numerical results are shown in Table 1. As shown, the quality of the basis set used does not impact the predictions of hydrophobicity or hydrophilicity since the sign of the deviations is mostly unchanged when changing basis. For M06-HF, although it appears that the calculated logP is consistently underestimated with the TZ and QZ basis sets, the functional tends to predict molecules to be more hydrophilic than those predicted with the other functionals. This bias towards hydrophilicity would become a problem for high-throughput drug screening as ideal compounds are neither too hydrophobic nor too hydrophilic. Predictions that are too hydrophilic could result in discarding potential compounds.

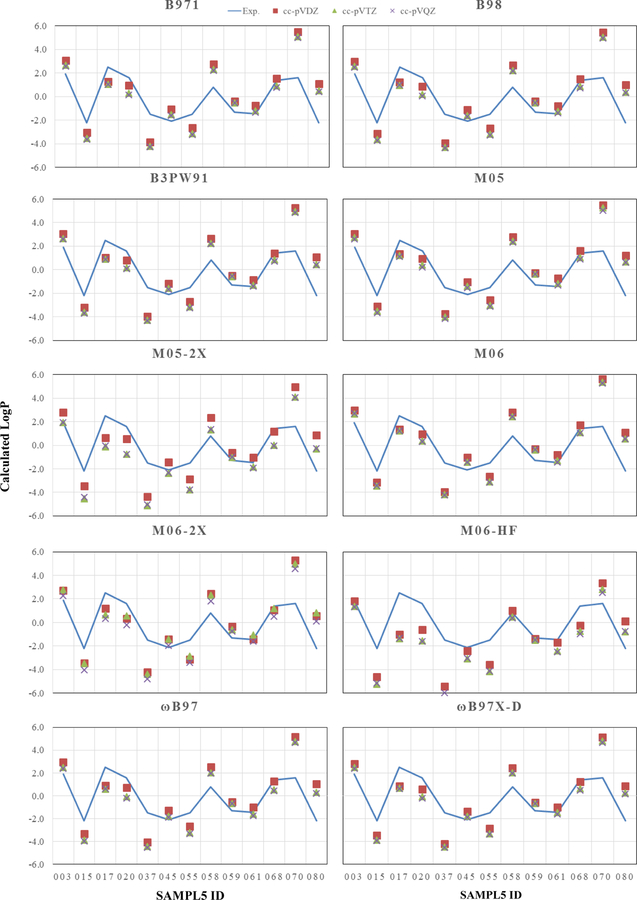
Figure 2.

Subset of Molecules (Batch0) LogP: Effect of Increasing Basis Sets.The predicted logP with respect to increasing basis set size (DZ, TZ, QZ) are represented by the red box, green triangle, and purple ‘X’, respectively.

The correlation consistent basis sets used for this work were constructed in a systematic fashion to recover correlation energy for ab initio methods and overall convergence is commonly demonstrated for properties determined with increasing size of basis sets. As illustrated in Figure 2, the increasing quality of the basis sets lowers the logP values. This behavior is clearly convergent, yet convergence to the Kohn-Sham limit does not necessarily result in improved results with respect to experiment.

In examining the Batch 0 subset, trends in the predictions of logP for each molecule are consistent for each functional with only a few exceptions. Molecules 020, 068, and 070 have deviations that differ in sign as a function of basis set and functional. This is simply the result of the predictions being so close to experiment that even a small variation in the predicted logP values can change the sign of the deviation. Increasing the basis set size typically improves the predictions of logP for the HG-GGA functionals and the RSH-GGA functionals, while the magnitude of the signed deviation increases slightly for the GH-mGGA functionals. Overall, the small variation between the logP values obtained with the TZ and QZ basis sets indicates that the TZ basis set is already near the Kohn-Sham limit. A greater percentage of exact exchange from the functionals may help in the prediction of logP, for example, from M05 to M05-2X, a better prediction of logP is obtained for molecules 003, 045, 058, 059, 070, and 080. However, for some molecules too much exact exchange overestimates the solvation in water and underestimates the logP by at least 1.0 to 2.0 logP units. For example, each functional underestimates the logP for molecules 015, 017, 020, 037, and 055, as each overestimates the solvation in water relative to cyclohexane. Additionally for these molecules, increasing the size of the basis set predicts the molecules to be more hydrophilic. In these cases, the functionals perform best using a DZ basis set. In the case for molecule 068, each functional predicts within experimental error using a DZ basis set, with the exclusion of M06-HF.

Overall, similar predictions of logP are obtained with the GH-GGA functionals and the RSH-GGA functionals. For the GH-mGGA functionals, predictions of logP obtained using M05 and M06 are similar. Using M05-2X and M06-2X yield similar predictions of logP as well. M06-HF stands out the most in contrast to the other functionals as it consistently overestimates the solvation of the molecule in water. From the results, it is evident that increasing the amount of exact exchange, as well the quality of the basis set, overestimates the solvation energy in water relative to the solvation energy in cyclohexane. It is believed that this bias in overestimation in water is due to the parameter fitting for the SMD solvation model. The SMD solvation model, which was reported to achieve an accuracy for predicting the solvation free energies (mean unsigned error of 0.6 to 1.0 kcal/mol for neutral solutes), was more heavily parameterized against molecules solvated in water in contrast to cyclohexane [12]. This situation can be advantageous for molecules that are slightly hydrophobic. However, this is not optimal since there is a consistent overestimation of the energy from being solvated in water as this results in misleading predictions of the equilibrium distribution of a molecule in different solvents. Although there are cases in which the GH-mGGA functionals perform best, the GGA functionals were constructed with less parameter fitting and may serve as a stronger class of functionals for initial starting guesses when predicting the solvation properties of molecules in which experiment is unavailable.

B3PW91 was chosen as the method for predicting the transfer free energy of the remaining SAMPL5 subsets because of its overall consistent behavior across the period table, and for a number of energetic properties. Some of the molecules within the SAMPL5 set contain sulfur. Previous studies have shown that for molecules containing sulfur, the BP3W91 functional yields more accurate energetics than the B3LYP functional when using correlation consistent basis sets [25, 57]. The results submitted for the SAMPL5 challenge are shown in Table 2. Using B3PW91 and a quadruple-ζ basis level basis set has an MAD of 1.9 and was able to estimate the logP within 2.0 logP units from the experimental logD for about 60% of the molecule set. Although this approach lacks contributions from other protonation states, tautomers, and additional protomers, it provided a good starting estimate of logP. Regarding the outliers that this approach predicted over 2.0 logP units in reference to the experimental logD, it is believed that the prediction can be improved by including the chemical contributions from tautomerization, protonation, as well as with additional conformational sampling as many of the outliers that are greater than 3.0 logP units from the experimental logD are less rigid than other molecules within the dataset. For several of the molecules, the source of the larger deviations are known whereas other relationships between the prediction and the structure will require further investigations. The largest outlier is molecule 083, with a deviation of 9.0 logP units, is a result of modeling of the incorrect tautomer. The tautomeric state issued in the SAMPL5 data set was not the preferred tautomer. The results obtained from using the triple-ζ and the quadruple-ζ level basis sets are very similar. Rather than using a quadruple-ζ level basis set, it is recommended to use a triple-ζ level size and the correlation consistent basis sets that include tight d functions for molecules containing sulfur [33].

Table 2.

Overview of the Results Submitted to the SAMPL5 Challenge.

SAMPL5 ID	LogDExp.	LogPCalc.
002	1.4 ± 0.3	−1.0
003	1.9 ± 0.1	2.6
004	2.2 ± 0.3	4.1
005	−0.9 ± 0.1	1.1
006	−1.0 ± 0.1	−0.9
007	1.4 ± 0.3	3.5
010	−1.7 ± 0.4	−2.4
011	−3.0 ± 0.1	3.2
013	−1.5 ± 0.4	3.1
015	−2.2 ± 0.3	−3.7
017	2.5 ± 0.3	0.9
019	1.2 ± 0.4	5.9
020	1.6 ± 0.3	0.1
021	1.2 ± 0.3	0.7
024	1.0 ± 0.4	1.9
026	−2.6 ± 0.1	−2.8
027	−1.9 ± 0.1	2.7
033	1.8 ± 0.2	3.4
037	−1.5 ± 0.1	−4.3
042	−1.1 ± 0.3	0.7
044	1.0 ± 0.4	0.9
045	−2.1 ± 0.2	−1.7
046	0.2 ± 0.3	−1.0
047	−0.4 ± 0.3	0.2
048	0.9 ± 0.4	0.8
049	1.3 ± 0.1	1.9
050	−3.2 ± 0.6	−5.4
055	−1.5 ± 0.1	−3.2
056	−2.5 ± 0.1	−1.6
058	0.8 ± 0.1	2.2
059	−1.3 ± 0.3	−0.6
060	−3.9 ± 0.2	−1.7
061	−1.5 ± 0.1	−1.4
063	−3.0 ± 0.4	−6.0
065	0.7 ± 0.2	−1.4
067	−1.3 ± 0.3	0.4
068	1.4 ± 0.3	0.7
069	−1.3 ± 0.3	−0.1
070	1.6 ± 0.3	4.9
071	−0.1 ± 0.5	−0.9
072	0.6 ± 0.3	3.3
074	−1.9 ± 0.3	−6.3
075	−2.8 ± 0.3	−1.4
080	−2.2 ± 0.2	0.4
081	−2.2 ± 0.3	−5.3
082	2.5 ± 0.4	6.4
083	−1.9 ± 0.4	−10.9
084	0.0 ± 0.2	2.6
085	−2.2 ± 0.4	0.7
086	0.7 ± 0.2	1.1
088	−1.9 ± 0.3	−1.0
090	0.8 ± 0.2	1.0
092	−0.4 ± 0.3	−1.1
	MSDa	0.5
	MADb	1.9

^aThe mean signed deviation of the predicted logP from the experimental logD.

^bThe mean absolute deviation of the predicted logP from the experimental logD.

Conclusion

In this study, several DFT functionals were used to predict the partition coefficients in cyclohexane and water of molecules in the SAMPL5 molecule set, a diverse set of molecules, representing a variety of protonation states and tautomerization states. Using the SMD implicit solvation model and a vertical solvation approach, the free energy of transfer was predicted, resulting in a mean absolute deviation of 1.9 logP units from the experimental logD. The results highlight that the performance of density functionals does not consistently overestimate or underestimate the logP for some molecules in the SAMPL5 set. Functionals in the GH-GGA and the RSH-GGA class perform similarly, whereas the performance of GH-mGGA does not provide similar results as GH-GGA and RSH-GGA functionals. The results show that functionals that include a larger percentages of exact exchange tend to predict logP values that overestimate the hydrophilicity. For molecules that are similar to those studied in this work, using a GH-GGA functional, such as B3PW91, in conjunction with cc-pVTZ can be used for predicting transfer free energy of small organic molecules.

Moving forward, alternative strategies should be considered to try to improve the predictions. The acid dissociation constants for many of the ionizable compounds are not known. It is possible that these theoretical predictions could be improved by accounting for the multiple ionization states as this would more accurately estimate the distribution [58]. Although assumptions were made regarding the protonation, tautomeric, and conformational states, the results highlight the ability of hybrid DFT approaches and the SMD implicit solvent model for estimating logP. As these approaches are able to predict close to experimental logD, the predicted logP underestimates the energetic contributions related to the structural and environmental heterogeneity in solution that is reflective of experiment. To attempt to further reduce the logP deviations from the experimental logD, the performance of ab initio electronic correlation methods could be considered for predicting the logP. While the use of these electronic structure methods would increase the computational cost, these predictions may provide a stronger approach that allows for systematic improvement.